Seismotectonic Properties and Zonation of the Far-Eastern Eurasian Plate Around the Korean Peninsula

Abstract

Regional seismotectonics provides crucial information for seismic hazard analysis, which is difficult to address with short-term earthquake records. The far-eastern Eurasian plate around the Korean Peninsula presents a stable intraplate environment with diffuse seismicity, of which responsible tectonics and active faults are difficult to identify. Combined analysis of instrumental and historical earthquake records is required for assessment of long-term seismicity properties. Seismotectonic provinces are identified from the spatial distribution of seismicity properties controlled by the medium properties and stress field. The boundaries of the seismotectonic provinces are defined considering the medium properties that can be inferred from geological, geophysical and tectonic features. The Gutenberg–Richter frequency–magnitude relationships and maximum magnitudes for the seismotectonic provinces are determined using instrumental and historical earthquake records. The validity of maximum magnitude estimation is tested with synthetic data. A parametric method, the Tate–Pisarenko method, produces more accurate estimates than non-parametric methods. A modified Tate–Pisarenko method is proposed for estimation of maximum magnitudes for incomplete short-term earthquake catalogs. The maximum magnitude of events for the whole region is approximately the same as the average of the maximum magnitudes of events for subdivided provinces, causing apparent variation in maximum magnitudes depending on the number of seismotectonic provinces. Consideration of a reasonable number of seismotectonic provinces may be needed for proper assessment of seismic hazard potentials is recommended. The combined analysis of historical and instrumental earthquake records suggests maximum magnitudes greater than 7 around the peninsula.

Appendix 1: Determination of \(M_{\max }\)

1.1 Parametric Determination: The Tate–Pisarenko (TP) Method

An event catalog composed of n events is considered. The magnitudes of the events are $M_j$ ($j=1,2,\ldots ,n$) in an ascending order. We define the probability, G(M, Y) that F(M) is less than a certain constant Y (Pisarenko et al. 1996; Kijko and Graham 1998):

$$\begin{aligned}&G(M,Y)=\mathrm {Probability}[F(M)\le Y]=Y, \end{aligned}$$

(22)

where the constant Y ranges between 0 and 1. The probability for the case that $F(M_n)$ is less than Y is given by

$$\begin{aligned}&G(M_n,Y)=\mathrm {Probability}[F(M_n)\le Y]=Y^n. \end{aligned}$$

(23)

The differentiation of $G(M_n,Y)$ with respect to Y corresponds to $F(M_n)$:

$$\begin{aligned}&\frac{\mathrm{d}G(M_n,Y)}{\mathrm{d}Y}=nY^{n-1}=g(M_n,Y). \end{aligned}$$

(24)

Here, function $g(M_n)$ is given by

$$\begin{aligned} g(M_n,Y)&= {} \mathrm {Probability}[f(M_n)\le Y] \nonumber \\&= {} \mathrm {Probability}[f(M_1)\le Y, f(M_2)\le Y, \ldots , f(M_n)\le Y] \nonumber \\&= {} \int f(M)\, \mathrm{d}m \\&= {} F(M_n) \nonumber \end{aligned}$$

(25)

The expected value of $F(M_n)$, $S_n$, is given by

$$\begin{aligned}&S_n=\int _0^1 F(M_n) \,Y \, \mathrm{d}Y=\int _0^1 g(M_n,Y) \, Y \, \mathrm{d}Y=\frac{n}{n+1}. \end{aligned}$$

(26)

Here, the expected value $S_n$ is used as the representative value of $F(M_n)$.

The magnitude $M_n$ can be written using a Taylor expansion:

$$\begin{aligned}&M_n=F^{-1}\left( S_n\right) = F^{-1}\left( 1\right) +\left. \frac{\mathrm{d}F^{-1}(S)}{\mathrm{d}S}\right| _{S=1}(S_n-1)+\ldots , \end{aligned}$$

(27)

where $F^{-1}(1)$ is equal to $M_{\max }$, and $S_n=F(M_n)=n/(n+1)$. Also, we have

$$\begin{aligned}&\left. \frac{\mathrm{d}F^{-1}(S)}{\mathrm{d}S}\right| _{S=1}=\frac{1}{ \left. \frac{\mathrm{d}F(M)}{\mathrm{d}M}\right| _{M=F^{-1}(1)}}=\frac{1}{f(M_{\max })}. \end{aligned}$$

(28)

Thus, Eq. (27) becomes

$$\begin{aligned}&M_n=M_{\max }+\frac{1}{f(M_{\max })}\times \left( \frac{-1}{n+1}\right) . \end{aligned}$$

(29)

From Eqs. (29) and (16), the maximum magnitude ($M_{\max }$) can be rewritten as

$$\begin{aligned}&M_{\max }=M_n+\left( \frac{1}{n+1}\right) \times \frac{1- \exp \left[ -\beta (M_{\max }-M_{\min }) \right] }{\beta \exp \left[ -\beta (M_{\max }-M_{\min }) \right] }, \end{aligned}$$

(30)

which can be approximated for a large n as

$$\begin{aligned}&M_{\max }=M_n+\left( \frac{1}{n}\right) \times \frac{1- \exp \left[ -\beta (M_{\max }-M_{\min }) \right] }{\beta \exp \left[ -\beta (M_{\max }-M_{\min }) \right] }. \end{aligned}$$

(31)

1.2 Non-Parametric Determination Based on Order Statistics (NPOS)

The expected value of magnitude, E(M), can be calculated using

$$\begin{aligned}&E(M)=\int _{M_{\min }}^{M_{\max }} M f(M) \mathrm{d}M=M_{\max }-\int _{M_{\min }}^{M_{\max }} F(M)\, \mathrm{d}M. \end{aligned}$$

(32)

The cumulative probability density function, F(M), is given by

$$\begin{aligned}&F(M)=\mathrm {Probability}[M \le M_u], \end{aligned}$$

(33)

where $M_u$ is a given magnitude. Equation (33) suggests that

$$\begin{aligned}&F(M_n)=\mathrm {Probability}[M_1 \le M_u, M_2 \le M_u, \ldots , M_n \le M_u]=\left[ F(M)\right] ^n. \end{aligned}$$

(34)

Thus, we have

$$\begin{aligned}&E(M_n)=M_{\max }-\int _{M_{\min }}^{M_{\max }} \left[ F(M)\right] ^n\, \mathrm{d}M. \end{aligned}$$

(35)

The integration over magnitude up to $M_{\max }$ corresponds to integration over magnitude up to $M_n$, and the expected value of $E(M_n)$ is replaced to be $M_n$. We have

$$\begin{aligned}&M_{\max }=M_n+\int _{M_{\min }}^{M_n} \left[ F(M)\right] ^n\, \mathrm{d}M, \end{aligned}$$

(36)

where the cumulative probability function, F(M), can be written as (Cooke 1979; Kijko and Singh 2011)

$$\begin{aligned}&F(M)=\frac{i}{n}, \quad \, \mathrm {for} \,\,(1\le i \le n). \end{aligned}$$

(37)

The expression for $M_{\max }$ in Eq. (36) can be written in a discrete form using Eq. (37):

$$\begin{aligned} M_{\max } &= M_n+\sum _{i=1}^{n-1} \left( \frac{i}{n} \right) ^n (M_{i+1}-M_i) \nonumber \\= & {} M_n+M_n-\sum _{i=0}^{n-1} \left[ \left\{ \left( 1-\frac{i}{n} \right) ^n -\left( 1-\frac{i+1}{n} \right) ^n\right\} M_{n-i} \right] . \end{aligned}$$

(38)

From the definition of natural logarithm, we have

$$\begin{aligned}&\lim _{n\rightarrow \infty } \left( 1+\frac{1}{n}\right) ^n=e. \end{aligned}$$

(39)

Equation (38) becomes

$$\begin{aligned}&M_{\max }=2 M_n-(1-\mathrm{e}^{-1})\sum _{i=0}^{n-1} (\mathrm{e}^{-i} M_{n-i}). \end{aligned}$$

(40)

1.3 The Robson–Whitlock (RW) Method

This method uses the largest two magnitudes in the catalog (Robson and Whitlock 1964). From Eq. (29), we deduce a relationship for an event catalog that is composed of $n-1$ events:

$$\begin{aligned}&M_{n-1}'=M_{\max }+\frac{1}{f(M_{\max })}\times \left( \frac{-1}{n}\right) . \end{aligned}$$

(41)

Here, when we select $n-1$ events from n events, the average of the observed maximum magnitudes in the selected catalogs:

$$\begin{aligned}&M_{n-1}'=\frac{(n-1)M_n+M_{n-1}}{n}. \end{aligned}$$

(42)

Thus, from Eqs. (29), (41) and (42), we have

$$\begin{aligned}&M_{\max }=(n+1)M_n-n M_{n-1}'=2M_n-M_{n-1}. \end{aligned}$$

(43)

Table 1 Seismicity properties and maximum magnitude estimates of instrumental earthquakes for the 7-province-composite seismotectonic province model

Table 2 Seismicity properties and maximum magnitude estimates of instrumental earthquakes for the 17-province-composite seismotectonic province model

Table 3 Seismicity properties and maximum magnitude estimates of historical earthquakes for the 7-province-composite seismotectonic province model

Table 4 Seismicity properties and maximum magnitude estimates of historical earthquakes for the 17-province-composite seismotectonic province model

Fig. 1

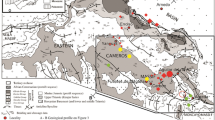
a Geological and tectonic structures around the Korean Peninsula (e.g., Chough et al. 2000). b An enlarged map of the study region. The major geological provinces are denoted: GM Gyeonggi massif, GB Gyeongsang basin, IFB Imjingang fold belt, NM Nangrim massif, OCB Okcheon belt, OJB Ongjin basin, YM Yeongnam massif, YIB Yeonil basin (YIB). The ambient compression stress field (Choi et al. 2012) and capable faults in the peninsula (Choi 2012) are denoted. The regions of paleo-rifting in the East Sea and the paleo-continental-collision in the Yellow Sea are shaded

Fig. 2

Regional variation in the seismic and geophysical properties of the crust of the Korean Peninsula: a crustal thickness (Hong et al. 2008), b crustal P amplification (Hong and Lee 2012), c crustally-guided shear-wave attenuation factors (Lg ${Q_{0}}$) (Hong and Choi 2012), d Moho P (Pn) velocities (Hong and Kang 2009), e shear-wave velocities at a depth of 6.75 km (Choi et al. 2009), f upper-crustal $V_{P}/V_{S}$ ratios (Jo and Hong 2013), g Bouguer gravity anomalies (Cho et al. 1997), and h heat flows (Lee et al. 2010).

Fig. 3

a Instrumental seismicity from 1978 to 2013 and b historical seismicity from 1393 to 1904 around the Korean Peninsula. Offshore events were recorded limitedly in the historical earthquake catalog. The spatial distribution of seismicity is similar between instrumental and historical earthquakes

Fig. 4

Distribution of earthquakes as a function of magnitude: a instrumental earthquakes and b historical earthquakes. Historical earthquakes with magnitudes of 4.0–4.5 appear to have been under-recorded

Fig. 5

a Focal depth distribution of instrumental earthquakes. Most earthquakes occur at depths less than 20 km. b Focal mechanism solutions for earthquakes around the Korean Peninsula. Strike-slip earthquakes striking in NE are dominant around the peninsula. Reverse-faulting earthquakes striking in NS are observed in the region off the east coast of the peninsula, and normal-faulting earthquakes striking in EW are observed in the region around the northwestern peninsula

Fig. 6

a Distribution of event magnitudes as a function of time in short-period ($T_A$) and long-period ($T_B$) catalogs. The expected maximum magnitudes for short and long periods are $M_{\max }^{\mathrm{exp},A}$ and $M_{\max }^{\mathrm{exp},B}$. An excessively large earthquake with magnitude of $M_{\max }^{\mathrm{obs}, A}$, satisfying $M_{\max }^{\mathrm{obs},A}=M_{\max }^{\mathrm{exp},B}$, is included in the short-period catalog. b The Gutenberg–Richter frequency–magnitude relationships for short-period and long-period catalogs. The numbers of events with magnitudes $M\ge M_{\min }$ for short- and long-period catalogs are $N_\mathrm{ana}^A$ and $N_\mathrm{ana}^B$. The maximum magnitude for the long period is determined using the b value of the short-period catalog

Fig. 7

Minimum magnitudes ($M_{\min }$) ensuring the completeness of earthquake catalogs: a instrumental earthquake catalog and b historical earthquake catalog. The minimum magnitudes of the instrumental and historical earthquakes are determined to be 2.5 and 4.7, respectively

Fig. 8

Synthetic tests of maximum magnitude estimation for synthetic earthquake catalogs with the minimum magnitude of 2.5 and b value of 0.92. a Variations of maximum magnitude estimates for synthetic earthquake catalogs with various numbers of events. The maximum magnitudes are determined by four methods (TP, NPOS, RW, RWC). The accuracy of estimated maximum magnitudes increases with the number of events in the catalogs. b Comparison of maximum magnitude estimates among four methods. Method TP yields the most accurate estimates with large standard deviations

Fig. 9

Synthetic tests of maximum magnitude estimation for synthetic earthquake catalogs with the minimum magnitude of 4.7 and b value of 0.82. a Variations of maximum magnitude estimates for synthetic earthquake catalogs with various numbers of events. The maximum magnitudes are determined by four methods (TP, NPOS, RW, RWC). b Comparison of maximum magnitude estimates among four methods

Fig. 10

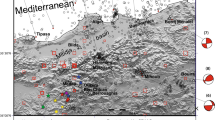
The spatial distribution of seismicity densities based on a the instrumental earthquakes with magnitudes greater than or equal to 2.5, and b the historical earthquakes with magnitudes greater than or equal to 4.7. High seismicity is observed at similar inland regions between the instrumental and historical catalogs (regions A, B, C, D). Low seismicity is observed in the northeastern peninsula (region H) and Gyeonggi massif (region G). The historical earthquakes display a characteristic high seismicity around the Seoul metropolitan area (region I), and weak seismicity in offshore regions (regions E, F, J, K, L)

Fig. 11

a Seismotectonic province models composed of 17 and 7 provinces over the reference seismicity density map. The 7-province-composite model is a simplified model of the 17-province-composite model. b The 17-province-composite model over seismic and geophysical properties. The seismotectonic province model generally agrees with the regional variation of seismic and geophysical properties

Fig. 12

Maximum magnitude estimates based on the instrumental earthquake records for a the 7-province-composite seismotectonic province model and b the 17-province-composite seismotectonic province model

Fig. 13

Maximum magnitude estimates based on the historical earthquake records for a the 7-province-composite seismotectonic province model and b the 17-province-composite seismotectonic province model