Dirac’s Theorem and Multigraded Syzygies

Abstract

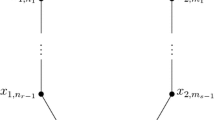
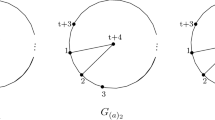
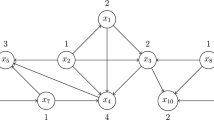
Let G be a simple finite graph. A famous theorem of Dirac says that G is chordal if and only if G admits a perfect elimination order. It is known by Fröberg that the edge ideal I(G) of G has a linear resolution if and only if the complementary graph $G^c$ of G is chordal. In this article, we discuss some algebraic consequences of Dirac’s theorem in the theory of homological shift ideals of edge ideals. Recall that if I is a monomial ideal, $HS _k(I)$ is the monomial ideal generated by the kth multigraded shifts of I. We prove that $HS _1(I)$ has linear quotients, for any monomial ideal I with linear quotients generated in a single degree. For and edge ideal I(G) with linear quotients, it is not true that $HS _k(I(G))$ has linear quotients for all $k\ge 0$. On the other hand, if $G^c$ is a proper interval graph or a forest, we prove that this is the case. Finally, we discuss a conjecture of Bandari, Bayati, and Herzog that predicts that if I is polymatroidal, $HS _k(I)$ is polymatroidal too, for all $k\ge 0$. We are able to prove that this conjecture holds for all polymatroidal ideals generated in degree two.