Steady-state electron trajectories in a free electron laser with ion-channel and axial magnetic field in the presence of self-fields

Abstract

A theory of self-fields in a one-dimensional helical wiggler free electron laser with ion-channel guiding and axial magnetic field is presented. The steady-state orbits under the influence of self-field are derived and discussed. The $\mathrm{\Phi }$ function that determines the rate of change of axial velocity with energy is derived. The numerical results show the effects of self-fields and the two electron-beams guiding devices (ion-channel and axial magnetic field) on the trajectories when used separately and simultaneously. The study shows that new unstable orbits, in the first part of the group I and II orbits, are found. A detailed stability analysis of orbits is presented.

Introduction

A Raman free-electron laser (FEL) produces coherent radiation by passage of a cold intense relativistic electron beam through a wiggler magnetic field which is spatially periodic along the beam axis. Since a high density and low energy electron beam is required in Raman regime, an axial magnetic field or ion-channel is usually employed to focus on the beam. The steady-state trajectories for the electron in a FEL with an axial magnetic field and one-dimensional or three-dimensional helical wiggler were studied [1–5]. The trajectories in the one-dimensional idealized wiggler are valid for particles near the axis (i.e. $r<<{\mathit{\lambda }}_{\text{w}}$).

Ion-channel guiding as an alternative to the conventional axial magnetic field guiding [6–8], was first proposed for use in FELs by Takayama and Hiramatsu [9]. Experimental results of a FEL with ion-channel guiding have been reported by Ozaki et al. [10]. Jha and Wurtele [11] developed a three-dimensional code for FEL simulation that allows for the effects of an ion-channel. The trajectory of an electron and gain in a combined idealized helical wiggler and ion-channel was studied [12–14]. FEL with realizable helical wiggler and ion-channel guiding was studied in Refs. [15] and [16].

In Raman regime, equilibrium self-electric and self-magnetic fields have significant effects on the steady-state orbits. It has been shown that self-field can induce chaos in a helical FEL [17–20]. The self-fields in a FEL with helical wiggler and axial magnetic field have been treated in both linear [21] and nonlinear [22] theory. The effects of self-fields on the stability of steady-state trajectories were studied in a FEL with a one-dimensional helical wiggler and axial magnetic field [23, 24] or ion-channel guiding [25, 26].

In recent years, electron trajectories and gain in a planar and helical wiggler FEL with ion-channel guiding and axial magnetic field were studied, detailed analysis of the stability and negative mass regimes were considered [27–29]. The purpose of this paper is to study the effects of the self-fields on electron trajectories in a FEL with ion-channel guiding and axial magnetic field. This work is organized as follows: In “Steady-state orbits” steady-state trajectories are obtained in the absence of self-fields. In “Self-field calculation and steady-state orbits in the presence of self-fields”, self-fields are calculated using Poisson^’s equation and Ampere^’s law. Equilibrium orbits are found under the influence of self-fields. Limiting forms for cases with only one type of guiding (ion-channel or solenoidal) are also presented. Then, an equation is derived for the function $\mathrm{\Phi }$. In “Numerical studies”, the results of a numerical study based on the equations derived are presented. The last section, is reserved to the conclusions. In “Appendix”, a stability analysis of steady-state trajectories has been performed.

Steady-state orbits

The evolution of the motion of a single electron in a FEL is governed by the relativistic Lorentz equation

$$\frac{\text{d}\left(\mathit{\gamma }m\mathit{v}\right)}{\text{d}t}=-e\left[{\mathit{E}}_{\text{i}}+\frac{1}{c}\mathit{v}\times \left({\mathit{B}}_{\text{w}}+B_0{\mathit{e}}_{\text{z}}\right)\right],$$

(1)

where ${\mathit{E}}_{\text{i}}$ is the transverse electrostatic field of an ion-channel and it can be written as

$${\mathit{E}}_{\text{i}}=2\mathit{\pi }e{n}_{\text{i}}\left(x\widehat{\mathit{x}}+y\widehat{\mathit{y}}\right),$$

(2)

and ${\mathit{B}}_{\text{w}}$ is the idealized helical wiggler magnetic field and can be described by

$${\mathit{B}}_{\text{w}}={\mathit{B}}_{\text{w}}\left(\widehat{\mathit{x}}cos{k}_{\text{w}}z+\widehat{\mathit{y}}sin{k}_{\text{w}}z\right),$$

(3)

and $B_0$ is the axial static magnetic field. Here, $B_{\text{w}}$ denotes the wiggler amplitude, $k_{\text{w}}\left(=2\mathit{\pi }/\phantom{2\mathit{\pi }{\mathit{\lambda }}_{\text{w}}}{\mathit{\lambda }}_{\text{w}}\right)$ is the wiggler wave number, ${\mathit{\lambda }}_{\text{w}}$ is the wiggler wavelength (period), $n_{\text{i}}$ is the density of positive ions having charge e.

By assuming a relativistic electron moving along the z axis of a helical wiggler magnetic field and separating into components, we can write Eq. (1) as

$$\frac{\text{d}\left(\mathit{\gamma }m{v}_x\right)}{\text{d}t}=-2\mathit{\pi }{n}_{\text{i}}{e}^{2}x-\frac{e}{c}\left(B_0{v}_y-v_z{B}_{\text{w}}sin{k}_{\text{w}}z\right),$$

(4)

$$\frac{\text{d}\left(\mathit{\gamma }m{v}_y\right)}{\text{d}t}=-2\mathit{\pi }{n}_{\text{i}}{e}^{2}y-\frac{e}{c}\left(-B_0{v}_x+v_z{B}_{\text{w}}cos{k}_{\text{w}}z\right),$$

(5)

$$\frac{\text{d}\left(\mathit{\gamma }m{v}_z\right)}{\text{d}t}=-\frac{e}{c}\left(v_y{B}_{\text{w}}cos{k}_{\text{w}}z-v_x{B}_{\text{w}}sin{k}_{\text{w}}z\right),$$

(6)

where $\mathit{\gamma }$ is the relativistic factor. Steady-state solutions are obtained by requiring that $v_{\text{z}}\cong v_{||}=\text{constant}$, $x\sim sin{k}_{\text{w}}z$, and $y\sim cos{k}_{\text{w}}z$. In this manner, steady-state solutions of the form $v_{\text{x}}=v_{\text{w}}cos{k}_{\text{w}}z$ and $v_y=v_{\text{w}}sin{k}_{\text{w}}z$, where

$$v_{\text{w}}=\frac{k_{\text{w}}{v}_{||}^2{\mathit{\Omega }}_{\text{w}}}{{\mathit{\omega }}_{\text{i}}^2+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)},$$

(7)

${\mathit{\omega }}_{\text{i}}={\left(2\mathit{\pi }{n}_{\text{i}}{e}^2/\phantom{2\mathit{\pi }{n}_{\text{i}}{e}^2\mathit{\gamma }m}\mathit{\gamma }m\right)}^{1/\phantom{12}2}$, is the ion-channel frequency and ${\mathit{\Omega }}_{0,\text{w}}=e{B}_{0,\text{w}}/\phantom{e{B}_{0,\text{w}}\mathit{\gamma }mc}\mathit{\gamma }mc$, are the cyclotron frequencies due to the axial guide and wiggler magnetic fields.

The self-electric and self-magnetic fields are induced by the steady-state charge density and current of the non-neutral electron beam. In order to model these self-fields, the assumption of a homogeneous electron density profile has been made,

$$n_{\text{b}}\left(r\right)=\left\{\begin{array}{c}\hfill n_{\text{b}}=const.r\le r_{\text{b}}\\ \hfill 0r>r_{\text{b}},\\ \hfill \end{array}\right.$$

(8)

where $n_{\text{b}}$ is the number density of the electrons and $r_{\text{b}}$ is the beam radius.

Self-field calculation and steady-state orbits in the presence of self-fields

The self-electric field can be obtained by Poisson^’s equation

$${\mathit{E}}^{\left(s\right)}=-2\mathit{\pi }e{n}_{\text{b}}r\widehat{\mathit{r}}=-2\mathit{\pi }e{n}_{\text{b}}\left(x\widehat{\mathit{x}}+y\widehat{\mathit{y}}\right).$$

(9)

The self-magnetic field is obtained by Ampere^’s law,

$$\mathrm{\nabla }\times \mathit{B}=\frac{4\mathit{\pi }}{c}{\mathit{J}}_{\text{b}},$$

(10)

where ${\mathit{J}}_{\text{b}}=-e{n}_{\text{b}}\left({\mathit{v}}_{\perp }+v_{||}{\widehat{\mathit{e}}}_z\right)$ is the beam current density and ${\mathit{v}}_{\perp }$ is the transverse velocity. The Eq. (10) can be solved by using the methods used in Ref. [20] (or Refs. [24] and [25]) in cylindrical coordinates. This yield

$${\mathit{B}}_{\text{s}}^{\left(1\right)}={\mathit{B}}_{\text{s|}|}+{\mathit{B}}_{\text{sw}}^{\left(1\right)},$$

(11)

where

$${\mathit{B}}_{\text{s}\mathit{\theta }}=-2\mathit{\pi }e{n}_{\text{b}}\frac{v_{||}}{c}r{\widehat{\mathit{e}}}_{\mathit{\theta }}=2\mathit{\pi }e{n}_{\text{b}}\frac{v_{||}}{c}\left(y\widehat{\mathit{x}}-x\widehat{\mathit{y}}\right),$$

(12)

$${\mathit{B}}_{\text{sw}}^{\left(1\right)}=\frac{2{\mathit{\omega }}_{\text{b}}^2\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}{{\mathit{\omega }}_{\text{i}}^2+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}{\mathit{B}}_{\text{w}},$$

(13)

and ${\mathit{\omega }}_{\text{b}}={\left(2\mathit{\pi }{n}_{\text{b}}{e}^2/\phantom{2\mathit{\pi }{n}_{\text{b}}{e}^2\mathit{\gamma }m}\mathit{\gamma }m\right)}^{1/\phantom{12}2}$. The self-magnetic field induced by transverse velocity ${\mathit{B}}_{\text{sw}}^{\left(1\right)}$, which is generated by the wiggler magnetic field, is known as wiggler induced self-magnetic field that is proportional to the wiggler magnetic field. The total new magnetic field up to first-order correction, may be written as

$${\mathit{B}}^{\left(1\right)}={\mathit{B}}_{\text{w}}+{\mathit{B}}_{\text{s}}^{\left(1\right)}+B_0{\widehat{\mathit{e}}}_z={\mathit{\lambda }}^{\left(1\right)}{\mathit{B}}_{\text{w}}+2\mathit{\pi }e{n}_{\text{b}}\frac{v_{||}}{c}\left(y\widehat{\mathit{x}}-x\widehat{\mathit{y}}\right)+B_0{\widehat{\mathit{e}}}_z,$$

(14)

where

$${\mathit{\lambda }}^{\left(1\right)}=1+\frac{2{\mathit{\omega }}_{\text{b}}^2\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}{{\mathit{\omega }}_{\text{i}}^2+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}.$$

(15)

So, the Eqs. (4–6) can be solved by considering the self-electric and self-magnetic fields by first-order correction. Therefore, the transverse velocity can be obtained by first-order correction which produces a new self-magnetic field ${\mathit{B}}_{\text{sw}}^{\left(2\right)}=K{\mathit{\lambda }}^{\left(1\right)}{\mathit{B}}_{\text{w}}$, where

$$K=\frac{2{\mathit{\omega }}_{\text{b}}^2\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}{{\mathit{\omega }}_{\text{i}}^2+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}.$$

(16)

and ${\mathit{\gamma }}_{||}={\left(1-v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}^{-1/\phantom{-12}2}$. This process may be continued to find the higher order terms. Finally, the total wiggler-induced magnetic field becomes

$${\mathit{B}}_{\text{sw}}=\underset{n\to \infty }{lim}{\mathit{B}}_{\text{sw}}^{\left(n\right)}=K\mathit{\lambda }{\mathit{B}}_{\text{w}},$$

(17)

where

$$\mathit{\lambda }=\underset{n\to \infty }{lim}{\mathit{\lambda }}^{\left(n\right)}=\underset{n\to \infty }{lim}\sum _{i=0}^{n-1}{K}^i+\underset{n\to \infty }{lim}\frac{2{\mathit{\omega }}_{\text{b}}^2\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}{{\mathit{\omega }}_{\text{i}}^2+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}{K}^n.$$

(18)

If the absolute value of $K$ is <1, then the series in Eq. (18) will converge to $1/\phantom{1\left(1-K\right)}\left(1-K\right)$, and the last term in the right-hand side will goes to zero. In this case, Eq. (18) may be expressed in the following form

$$\mathit{\lambda }=\frac{{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}{{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]}^{}+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}.$$

(19)

The equation of motion of a electron, in the presence of self-fields ${\mathit{E}}^{\left(s\right)}$, ${\mathit{B}}_{\mathit{\theta }}^{\left(s\right)}$, and ${\mathit{B}}_{\text{w}}^{\left(s\right)}$, may be written as

$$\frac{\text{d}{v}_{\text{x}}}{\text{d}t}=-\left[{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left(1-\frac{v_{||}{v}_{\text{z}}}{c^2}\right)\right]x+\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}sin{k}_{\text{w}}z-{\mathit{\Omega }}_0{v}_{\text{x}},$$

(20)

$$\frac{\text{d}{v}_{\text{y}}}{\text{d}t}=-\left[{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left(1-\frac{v_{||}{v}_{\text{z}}}{c^2}\right)\right]y-\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}cos{k}_{\text{w}}z+{\mathit{\Omega }}_0{v}_{\text{y}},$$

(21)

$$\frac{\text{d}{v}_z}{\text{d}t}=\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}\left(v_{y}cos{k}_{\text{w}}z-v_{x}sin{k}_{\text{w}}z\right)+\frac{{\mathit{\omega }}_{\text{b}}^2{v}_{||}}{2c^2}\left(v_{x}x+v_{y}y\right).$$

(22)

Assuming solutions of the form $x\sim sin{k}_{\text{w}}z$ and $y\sim cos{k}_{\text{w}}z$ and $v_z\cong v_{||}$, we will find the steady-state solutions $v_x=v_{\text{w}}cos{k}_{\text{w}}z$ and $v_y=v_{\text{w}}sin{k}_{\text{w}}z$, where

$$v_{\text{w}}=\frac{k_{\text{w}}{v}_{||}^2{\mathit{\Omega }}_{\text{w}}}{{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]}^{}+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)}.$$

(23)

It should be noted that the assumption of constant $\mathit{\gamma }$ is consistent with the on-axial helical orbits that have a constant radius and, therefore, a constant kinetic energy. Equation (23) shows resonant enhancement in the magnitude of the transverse velocity when

$${\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)\approx 0.$$

(24)

Steady-state trajectories may be classified according to the type of guiding. There are three main categories:

• 1. When the value of axial magnetic field is zero $\left({\mathit{\Omega }}_0=0\right)$; that is, a FEL with a helical wiggler and an ion-channel guiding. In this type of guiding Eq. (23) becomes,

  $$v_{\text{w}}=\frac{k_{\text{w}}{v}_{||}^2{\mathit{\Omega }}_{\text{w}}}{{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]}^{}-k_{\text{w}}^2{v}_{||}^2}.$$

  (25)

  This type of guiding, was studied in the absence of self-fields in Refs. [12–14] and in the presence of self-fields in Refs. [25] and [26].

• 2. When the density of positive ions is zero $\left({\mathit{\omega }}_{\text{i}}=0\right)$; that is, a FEL with a helical wiggler and an axial magnetic field. In this type of guiding Eq. (23) becomes,

  $$v_{\text{w}}=\frac{k_{\text{w}}{v}_{||}^2{\mathit{\Omega }}_{\text{w}}}{k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)-{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]}.$$

  (26)

  This type of guiding, was studied in the absence of self-fields in Refs. [1–3] and in the presence of self-fields in Refs. [23] and [24].

• 3. When both the ion-channel and the axial magnetic field are present; that is, a helical wiggler FEL with an ion-channel and an axial magnetic field. When both types of guiding are present, $v_{\text{w}}$ is given by Eq. (23). This case contains three types: (a) two guiding frequencies are taken to be equal (${\mathit{\Omega }}_0={\mathit{\omega }}_{\text{i}}$), (b) the ion-channel frequency is taken to be constant, (c) the axial magnetic field frequency is taken to be constant.

  $\mathrm{\Phi }$ function is defined as the variation of the axial velocity divided by the electron energy. By substituting the value of $v_{\text{w}}$ in the relation of the conservation law of energy $\mathit{\gamma }=1-v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2-v_{\text{w}}^2/\phantom{v_{\text{w}}^2{c}^2}{c}^2$, we obtain

  $$\frac{1}{{\mathit{\gamma }}^2}=1-\frac{v_{||}^2}{c^2}-\frac{k_{\text{w}}^2{v}_{||}^4{\mathit{\Omega }}_{\text{w}}^2}{{\left\{{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)\right\}}^2}.$$

  (27)

Implicit differentiation of this equation leads to

$$\frac{\text{d}{v}_{||}}{\text{d}\mathit{\gamma }}=\frac{c^2}{\mathit{\gamma }{\mathit{\gamma }}_{||}^2{v}_{||}}\mathrm{\Phi },$$

(28)

where ${\mathit{\gamma }}_{||}={\left(1-v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}^{-1/\phantom{-12}2}$ and

$$\mathrm{\Phi }=1-\frac{{\mathit{\beta }}_{\text{w}}^2\left[\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)\left(1+{\mathit{\gamma }}_{||}^2\right)+k_{\text{w}}{v}_{||}{\mathit{\Omega }}_0{\mathit{\gamma }}_{||}^2-{\left(v_{||}/\phantom{v_{||}c}c\right)}^4{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^2\right]}{{\mathit{\omega }}_{\text{i}}^2\left(1+2{\mathit{\beta }}_{\text{w}}^2\right)+k_{\text{w}}{v}_{||}{\mathit{\Omega }}_0\left(1+{\mathit{\beta }}_{\text{w}}^2\right)-{\mathit{\omega }}_{\text{b}}^2\left(1+2{\mathit{\beta }}_{\text{w}}^2\right)-k_{\text{w}}^2{v}_{||}^2-{\left(v_{||}/\phantom{v_{||}c}c\right)}^2{\mathit{\omega }}_{\text{b}}^2}.$$

(29)

In the absence of an axial static magnetic field $\left({\mathit{\Omega }}_0=0\right)$, we have

$$\mathrm{\Phi }=1-\frac{{\mathit{\beta }}_{\text{w}}^2\left[\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)\left(1+{\mathit{\gamma }}_{||}^2\right)-{\left(v_{||}/\phantom{v_{||}c}c\right)}^4{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^2\right]}{{\mathit{\omega }}_{\text{i}}^2\left(1+2{\mathit{\beta }}_{\text{w}}^2\right)-{\mathit{\omega }}_{\text{b}}^2\left(1+2{\mathit{\beta }}_{\text{w}}^2\right)-k_{\text{w}}^2{v}_{||}^2-{\left(v_{||}/\phantom{v_{||}c}c\right)}^2{\mathit{\omega }}_{\text{b}}^2},$$

(30)

and in the absence of ion-channel $\left({\mathit{\omega }}_{\text{i}}=0\right)$, we have

$$\mathrm{\Phi }=1-\frac{{\mathit{\beta }}_{\text{w}}^2\left[k_{\text{w}}{v}_{||}{\mathit{\Omega }}_0{\mathit{\gamma }}_{||}^2-{\mathit{\omega }}_{\text{b}}^2\left(1+{\mathit{\gamma }}_{||}^2\right)+-{\left(v_{||}/\phantom{v_{||}c}c\right)}^4{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^2\right]}{k_{\text{w}}{v}_{||}{\mathit{\Omega }}_0\left(1+{\mathit{\beta }}_{\text{w}}^2\right)-{\mathit{\omega }}_{\text{b}}^2\left(1+2{\mathit{\beta }}_{\text{w}}^2\right)-k_{\text{w}}^2{v}_{||}^2-{\left(v_{||}/\phantom{v_{||}c}c\right)}^2{\mathit{\omega }}_{\text{b}}^2},$$

(31)

where ${\mathit{\beta }}_{\text{w}}=v_{\text{w}}/\phantom{v_{\text{w}}{v}_{||}}{v}_{||}$.

Numerical studies

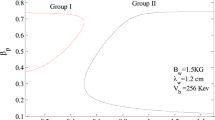
In this section, a numerical study the effects of self-fields on steady-state relativistic electron trajectories in a FEL with a helical wiggler magnetic field in the presence of an axial magnetic field and/or an ion-channel is presented. For numerical calculations, parameters are ${\mathit{\lambda }}_{\text{w}}=3.14cm$, ${\mathit{\gamma }}_0=3$, $B_{\text{w}}=1kG$, and $n_{\text{b}}={10}^{12}c{m}^{-3}$. A six-order polynomial equation is obtained for $v_{||}/\phantom{v_{||}c}c$ by Eq. (27). There are six roots for $v_{||}/\phantom{v_{||}c}c$ for any sets of parameters and only the three real positive roots will be considered here. The steady-state trajectories may be divided into two classes corresponding to the cases in which: $v_{\text{w}}<0$ referred to as group I, and $v_{\text{w}}>0$ referred to as group II. The stability of steady-state orbits is investigated in “Appendix”.

When values of ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}}{k}_{\text{w}}c$ and ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}}{k}_{\text{w}}c$ are equal

Figure 1 shows $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized ion-channel frequency, that is equal to the normalized axial magnetic field frequency $\left({\mathit{\omega }}_{\text{i}}={\mathit{\Omega }}_0\right)$. Group I and Group II orbits are defined by the conditions $\left({\mathit{\Omega }}_0={\mathit{\omega }}_{\text{i}}\right)<k_{\text{w}}{v}_{||}\left(\sqrt{5+4\left({\mathit{\omega }}_{\text{b}}^2/\phantom{{\mathit{\omega }}_{\text{b}}^2{k}_{\text{w}}^2{c}^2}{k}_{\text{w}}^2{c}^2\right)\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}-1\right)/\phantom{k_{\text{w}}{v}_{||}\left(\sqrt{5+4\left({\mathit{\omega }}_{\text{b}}^2/\phantom{{\mathit{\omega }}_{\text{b}}^2{k}_{\text{w}}^2{c}^2}{k}_{\text{w}}^2{c}^2\right)\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}-1\right)2}2$ and $\left({\mathit{\Omega }}_0={\mathit{\omega }}_{\text{i}}\right)>k_{\text{w}}{v}_{||}\left(\sqrt{5+4\left({\mathit{\omega }}_{\text{b}}^2/\phantom{{\mathit{\omega }}_{\text{b}}^2{k}_{\text{w}}^2{c}^2}{k}_{\text{w}}^2{c}^2\right)\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}-1\right)/\phantom{k_{\text{w}}{v}_{||}\left(\sqrt{5+4\left({\mathit{\omega }}_{\text{b}}^2/\phantom{{\mathit{\omega }}_{\text{b}}^2{k}_{\text{w}}^2{c}^2}{k}_{\text{w}}^2{c}^2\right)\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)}-1\right)2}2$, respectively. Dotted lines show the unstable trajectories that are investigated in “Appendix”. The results in the absence of self-fields are shown for comparison, with circles lines. The main discrepancy in the presence of the self-fields is found for the first part of the group I orbits, with $0<\left({\mathit{\omega }}_{\text{i}}={\mathit{\Omega }}_0\right)/\phantom{\left({\mathit{\omega }}_{\text{i}}={\mathit{\Omega }}_0\right)k_{\text{w}}c}{k}_{\text{w}}c<0.17$, and the first part of the group II orbits, which exhibit an orbital instability not found in the absence of the self-fields. The first part of the group I orbits is important in experiments with FELs, while, the first part of the group II orbits is not important. Because, injection into the first part of the group II orbits has two problems. First, electrons exhibit strong oscillations about their steady state orbit value, and second, the transverse orbit excursions are large due to their large transverse velocity. Figure 1 shows that minimum value of the ion-channel density (or the axial magnetic field) is required for the stability in group I. The variation of ${\mathit{\omega }}_{\text{i}}^{\text{min}}$ (or ${\mathit{\Omega }}_0^{\text{min}}$) with the electron density, for group I orbits, is shown in Fig. 2. To explain Fig. 2, it should be noted that by increasing the beam density $\left(n_{\text{b}}\right)$ and the kinetic energy of electron $\left(\mathit{\gamma }\right)$, the self-fields increase, therefore, a stronger ion-channel density (or axial magnetic field) is required for the onset of instability.

Fig. 1

Axial velocity $v_{||}/\phantom{v_{||}c}c$as a function of the normalized axial magnetic field frequency that is equal to the ion-channel frequency. With self-field (solid lines); without self-field (circles lines); unstable orbits (dotted lines)

Fig. 2

Variation of $({\mathit{\omega }}_{\text{i}}^{\text{min}}={\mathit{\Omega }}_0^{\text{min}})/\phantom{({\mathit{\omega }}_{\text{i}}^{\text{min}}={\mathit{\Omega }}_0^{\text{min}})k_{\text{w}}}{k}_{\text{w}}c$ with electron density $n_{\text{b}}$ for group I orbits

The variation of factor $\mathit{\lambda }$ with the normalized ion-channel frequency, that is equal to the normalized axial magnetic field frequency, is shown in Fig. 3. Dotted lines show the unstable orbits. As this figure shows, for the upper branch of the group I orbits, $\mathit{\lambda }$ is below unity and acts as a diamagnetic correction to the wiggler magnetic field. The magnitude of the diamagnetic effect for stable orbits increases gradually with increasing the normalized ion-channel frequency (or the normalized axial magnetic field). In group II orbits, $\mathit{\lambda }$ is above unity and acts as a paramagnetic correction to the wiggler magnetic field. When $n_{\text{i}}\left(or{B}_0\right)\to \infty$, the value of $\mathit{\lambda }$ approaches to unity, therefore, the defocusing effect of self-fields is negligible in comparison with the strong focusing effect of the ion-channel (or the axial magnetic field) for a high density ion-channel (or axial magnetic field).

Fig. 3

Variation of factor $\mathit{\lambda }$ with the normalized axial magnetic field frequency that is equal to the ion-channel frequency. Unstable orbits (dotted lines)

Figure 4 shows $\mathrm{\Phi }$ as a function of the normalized ion-channel frequency which is equal to the normalized axial magnetic field. Dotted lines show the unstable orbits. In Fig. 4, for group I orbits, $\mathrm{\Phi }$ increases monotonically from unity at zero of the guiding frequency and exhibits a singularity at the transition to orbit instability. The behavior of $\mathrm{\Phi }$ for the group II orbits is interesting, since it is negative. This implies the existence of a negative-mass regime in which the axial velocity increases with decreasing energy.

Fig. 4

Graph of function $\mathrm{\Phi }$ versus the normalized axial magnetic field frequency that is equal to the ion-channel frequency. Unstable orbits (dotted lines)

When values of ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}}{k}_{\text{w}}c$ is held constant

Figure 5 shows $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field when ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Group I and Group II orbits are defined by the conditions ${\mathit{\omega }}_{\text{i}}^2<{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]-k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)$ and ${\mathit{\omega }}_{\text{i}}^2>{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]-k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)$, respectively. Dotted lines show the unstable orbits. The results in the absence of self-fields are shown for comparison, with circles lines. In the presence of the self-fields, the first part of the group II orbits is unstable. So, when value of ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ is <0.371, the first part of the group I orbits is unstable. The reason is that values of the ion-channel density and axial magnetic field are small and can not focus the electron beam. Ion-channel focusing, in a FEL, can take place under the Budker condition ($n_{\text{b}}>n_{\text{i}}>>n_{\text{b}}/\phantom{n_{\text{b}}{\mathit{\gamma }}_0^2}{\mathit{\gamma }}_0^2$). Ion-channel is produced by passing beam with density of $n_{\text{b}}$ through the preionized plasma with density of $n_{\text{i}}$. The condition $n_{\text{b}}>n_{\text{i}}$ is necessary for the complete expulsion of the plasma electrons by the electron beam. In this paper, the density of electron beam is taken at $n_{\text{b}}={10}^{12}{\text{cm}}^{-3}$, therefore, the density of the electron beam is larger than the ion-channel density for the group I orbits. The group II orbits require electron densities, which are not attainable in relativistic electron beams. This limitation can be overcome by using laser-produced ion-channels with higher densities of orders of magnitude.

Fig. 5

Axial velocity $v_{||}/\phantom{v_{||}c}c$as a function of the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field for ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. With self-field (solid lines); without self-field (circles lines); unstable orbits (dotted lines)

Figure 6 shows $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field when ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4,0.8,1.2$. Dotted lines show the unstable orbits. Figure 6 also shows how group I and group II orbits are affected by the change in the normalized axial magnetic field frequency. When the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ is higher than 1.25, group I orbits are eliminated. Figure 7 shows factor $\mathit{\lambda }$ as a function of the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field when ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Dotted lines show the unstable orbits. As Fig. 3, it can be seen that for the upper branch of the group I orbits, $\mathit{\lambda }$ is below unity (diamagnetic effect) while for the group II orbits, $\mathit{\lambda }$ is above unity (paramagnetic effect). Figure 8 shows $\mathrm{\Phi }$ as a function of the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field which is constant with ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$.

Fig. 6

Axial velocity $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field for ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$ (solid lines), ${\mathit{\Omega }}_{}/\phantom{{\mathit{\Omega }}_{}{k}_{\text{w}}c}{k}_{\text{w}}c=0.8$ (circles lines), and ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=1.2$ (triangles lines). Unstable orbits (dotted lines)

Fig. 7

Variation of factor $\mathit{\lambda }$ with the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field for ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Unstable orbits (dotted lines)

Fig. 8

Graph of function $\mathrm{\Phi }$ versus the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an axial magnetic field for ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Unstable orbits (dotted lines)

When values of ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}}{k}_{\text{w}}c$ is held constant

Figure 9 shows $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel when ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Group I and Group II orbits are defined by the conditions ${\mathit{\Omega }}_0<\left[-{\mathit{\omega }}_{\text{i}}^2+\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)+k_{\text{w}}^2{v}_{||}^2\right]/\phantom{\left[-{\mathit{\omega }}_{\text{i}}^2+\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)+k_{\text{w}}^2{v}_{||}^2\right]k_{\text{w}}{v}_{||}}{k}_{\text{w}}{v}_{||}$ and ${\mathit{\Omega }}_0>\left[-{\mathit{\omega }}_{\text{i}}^2+\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)+k_{\text{w}}^2{v}_{||}^2\right]/\phantom{\left[-{\mathit{\omega }}_{\text{i}}^2+\left(1+v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)+k_{\text{w}}^2{v}_{||}^2\right]k_{\text{w}}{v}_{||}}{k}_{\text{w}}{v}_{||}$, respectively. Dotted lines show the unstable orbits. The results in the absence of self-fields are shown for comparison, with circles lines. In the presence of the self-fields, the lower branch of the group II orbits is unstable. In this case, when value of ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ is <0.185, the first part of the group I orbits is unstable. Figure 10 shows $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel when ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4,0.6,0.8$. Dotted lines show the unstable orbits. Figure 10 also shows how group I and group II orbits are affected by the change in the normalized ion-channel frequency. Group I orbits is eliminated, when the normalized ion-channel frequency ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c$ is higher than 1.03. Figure 11 shows factor $\mathit{\lambda }$ as a function of the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel when ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Dotted lines show the unstable orbits. Figure 12 shows $\mathrm{\Phi }$ as a function of the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel which is constant with ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$.

Fig. 9

Axial velocity $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel for ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. With self-field (solid lines); without self-field (circles lines); unstable orbits (dotted lines)

Fig. 10

Axial velocity $v_{||}/\phantom{v_{||}c}c$ as a function of the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ the presence of an ion-channel for ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$ (solid lines), ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.6$ (circles lines), and ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.8$ (triangles lines). Unstable orbits (dotted lines)

Fig. 11

Variation of factor $\mathit{\lambda }$ with the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel for ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Unstable orbits (dotted lines)

Fig. 12

Graph of function $\mathit{\Phi }$ versus the normalized axial magnetic field frequency ${\mathit{\Omega }}_0/\phantom{{\mathit{\Omega }}_0{k}_{\text{w}}c}{k}_{\text{w}}c$ in the presence of an ion-channel for ${\mathit{\omega }}_{\text{i}}/\phantom{{\mathit{\omega }}_{\text{i}}{k}_{\text{w}}c}{k}_{\text{w}}c=0.4$. Unstable orbits (dotted lines)

Conclusion

It this paper, the steady-state electron trajectory for a helical wiggler FEL with the axial magnetic field and the ion-channel guiding in the presence of self-fields has been analyzed numerically. A six-degree polynomial equation is obtained for the axial velocity. Also, an equation for the function $\mathit{\Phi }$ is obtained, which determines the variation of axial velocity divided by the electron energy. The chosen parameters for this system are characterized by ${\mathit{\lambda }}_{\text{w}}=3.14\text{cm}$, ${\mathit{\gamma }}_0=3$, $n_{\text{b}}={10}^{12}{\text{cm}}^{-3}$and $B_{\text{w}}=1\text{kg}$. The necessary and sufficient conditions for orbit stability have been established. For this condition, we have considered variation of the relativistic factor $\mathit{\gamma }$ in the stability analysis of orbits. It was shown that self-fields can make parts of the steady-state orbits unstable. Numerical calculations are made to illustrate the effects of the two electron-beam guiding devices on the trajectories when applied separately and simultaneously in the presence of self-fields.

Appendix: Orbits stability analysis

The Hamiltonian of a single electron $H=\mathit{\gamma }m{c}^2+\mathit{\pi }{e}^2\left(n_{\text{b}}-n_i\right)\left(x^2+y^2\right)$ shows that energy is a constant of motion but $\mathit{\gamma }$ changes with distance from the axis $\mathit{\gamma }$. For orbit stability analysis we need to perturb the trajectory, which changes the distance from the axis leading to changes in the relativistic factor $\mathit{\gamma }$.

Transforming to a frame rotating with the wiggler field, we define

$$\left\{\begin{array}{c}{\widehat{\mathit{e}}}_1=\widehat{\mathit{x}}cos{k}_{\text{w}}z+\widehat{\mathit{y}}sin{k}_{\text{w}}z\hfill \\ {\widehat{\mathit{e}}}_2=-\widehat{\mathit{x}}sin{k}_{\text{w}}z+\widehat{\mathit{y}}cos{k}_{\text{w}}z\hfill \\ {\widehat{\mathit{e}}}_3=\mathit{z},\hfill \end{array}\right.$$

(32)

and write the equation of motion of the electron as follows:

$$\begin{array}{cc}\hfill {\ddot{x}}_1=& -\left[{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left(1-\frac{v_{||}{v}_z}{c^2}\right)+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)\right]x_1+\left(2k_{\text{w}}{v}_3-{\mathit{\Omega }}_0\right){\dot{x}}_2+k_{\text{w}}{\dot{v}}_3{x}_2\hfill \\ \hfill +\frac{{\mathit{\omega }}_{\text{i}}^2}{c^2}\left({\dot{x}}_1{x}_1+{\dot{x}}_2{x}_2\right)\left({\dot{x}}_1-k_{\text{w}}{v}_3{x}_2\right),\\ \hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\ddot{x}}_2=& -\left[{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left(1-\frac{v_{||}{v}_z}{c^2}\right)+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)\right]x_2-{\mathit{\Omega }}_{\text{w}}{v}_3+\left({\mathit{\Omega }}_0-2k_{\text{w}}{v}_3\right){\dot{x}}_1-k_{\text{w}}{\dot{v}}_3{x}_1\hfill \\ \hfill +\frac{1}{c^2}\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)\left({\dot{x}}_1{x}_1+{\dot{x}}_2{x}_2\right)\left({\dot{x}}_2+k_{\text{w}}{v}_3{x}_1\right),\\ \hfill \end{array}$$

(34)

$${\ddot{x}}_3=\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}\left({\dot{x}}_2+k_{\text{w}}{v}_3{x}_1\right)+\frac{{\mathit{\omega }}_i^2}{c^2}\left({\dot{x}}_1{x}_1+{\dot{x}}_2{x}_2\right)v_3,$$

(35)

where dots represent differentiation with respect to time, and $\text{d}\mathit{\gamma }/\phantom{\text{d}\mathit{\gamma }\text{d}t}\text{d}t$ is substituted from the following equation

$$\frac{\text{d}\mathit{\gamma }}{\text{d}t}=-\frac{e}{m{c}^2}\left(\mathit{v}·\mathit{E}\right)=-\frac{\mathit{\gamma }}{c^2}\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)\left(x_1{\dot{x}}_1+x_2{\dot{x}}_2\right),$$

(36)

The steady-state orbits are obtained by requiring the double derivates to be zero, this will yield

$$\begin{array}{c}{x}_{10}={\dot{x}}_{10}={\dot{x}}_{20}=0,\hfill \\ x_{20}=-\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}{v}_{30}{\left[{\mathit{\omega }}_i^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+k_{\text{w}}{v}_{30}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{30}\right)\right]}^{-1},\hfill \\ {\dot{x}}_{30}=\text{const}.\hfill \end{array}$$

(37)

Velocity components of the steady state orbits can also be shown to be $v_{10}=v_{\text{w}}$, $v_{20}=0$ and $v_{30}=v_{||}$ with $v_{\text{w}}$ given by Eq. (23).

Stability analysis is performed by assuming small perturbations of steady-state solutions as $x_1=\mathit{\delta }{x}_1,$${\dot{x}}_1=\mathit{\delta }{\dot{x}}_1,$$x_2=x_{20}+\mathit{\delta }{x}_2,$${\dot{x}}_2=\mathit{\delta }{\dot{x}}_2,$${\dot{x}}_3=v_3=v_{30}+\mathit{\delta }{v}_3$, and $\mathit{\gamma }={\mathit{\gamma }}_0+\mathit{\delta }\mathit{\gamma }$. Equations (33)–(35) can now be linearized to obtain

$$\begin{array}{cc}\hfill \mathit{\delta }{\ddot{x}}_1=& -\left[{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+k_{\text{w}}{v}_{30}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{30}\right)\right]\mathit{\delta }{x}_1+\left[2k_{\text{w}}{v}_{30}-{\mathit{\Omega }}_0-\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)k_{\text{w}}{v}_{30}{x}_{20}^2/\phantom{\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)k_{\text{w}}{v}_{30}{x}_{20}^2{c}^2}{c}^2\right]\mathit{\delta }{\dot{x}}_2\hfill \\ \hfill +k_{\text{w}}\mathit{\delta }{\dot{v}}_{30}{x}_{20},\\ \hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \mathit{\delta }{\ddot{x}}_2=& -\left[{\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+k_{\text{w}}{v}_{30}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{30}\right)\right]\mathit{\delta }{x}_2+\left[\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+{\mathit{\Omega }}_0{k}_{\text{w}}{v}_{30}\right)x_{20}+\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}{v}_{30}\right]\left(\mathit{\delta }\mathit{\gamma }/\phantom{\mathit{\delta }\mathit{\gamma }\mathit{\gamma }}\mathit{\gamma }\right)\hfill \\ \hfill +\left({\mathit{\Omega }}_0-2k_{\text{w}}{v}_{30}\right)\mathit{\delta }{\dot{x}}_1+\left[\left(2{\mathit{\omega }}_{\text{b}}^2{v}_{||}/\phantom{2{\mathit{\omega }}_{\text{b}}^2{v}_{||}{c}^2}{c}^2-k_{\text{w}}{\mathit{\Omega }}_0+2k_{\text{w}}^2{v}_{30}\right)x_{20}-\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}\right]\mathit{\delta }{v}_3,\\ \hfill \end{array}$$

(39)

$$\mathit{\delta }{\ddot{x}}_3=\left[\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}+\frac{{\mathit{\omega }}_{\text{i}}^2}{c^2}{v}_{30}{x}_{20}\right]\mathit{\delta }{\dot{x}}_2+\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}{k}_{\text{w}}{v}_{30}\mathit{\delta }{x}_1.$$

(40)

The quantities $\mathit{\delta }\mathit{\gamma }/\phantom{\mathit{\delta }\mathit{\gamma }{\mathit{\gamma }}_0}{\mathit{\gamma }}_0$ and $\mathit{\delta }\mathit{\lambda }$ can be calculated as follows:

$$\frac{\mathit{\delta }\mathit{\gamma }}{{\mathit{\gamma }}_0}=\frac{{\mathit{\gamma }}_0^2}{c^2}\left[v_{10}\mathit{\delta }{\dot{x}}_1-k_{\text{w}}{v}_{30}{v}_{10}\mathit{\delta }{x}_2+\left(v_{30}-k_{\text{w}}{x}_{20}{v}_{10}\right)\mathit{\delta }{v}_3\right],$$

(41)

$$\mathit{\delta }\mathit{\lambda }=\left(B_1-\mathit{\lambda }{B}_3/\phantom{B_1-\mathit{\lambda }{B}_3{B}_5}{B}_5\right)\mathit{\delta }{v}_3+\left({\mathit{\gamma }}_0^2/\phantom{{\mathit{\gamma }}_0^2{c}^2}{c}^2\right)\left(B_2-\mathit{\lambda }{B}_4/\phantom{B_2-\mathit{\lambda }{B}_4{B}_5}{B}_5\right)\left[v_{10}\mathit{\delta }{\dot{x}}_1-k_{\text{w}}{v}_{30}{v}_{10}\mathit{\delta }{x}_2+\left(v_{30}-k_{\text{w}}{x}_{20}{v}_{10}\right)\right]$$

where $B_1=2{\mathit{\omega }}_{\text{b}}^2\left(v_{||}/\phantom{v_{||}c}c\right)+{\mathit{\Omega }}_0-2k_{\text{w}}{v}_{||}$, $B_2=-{\mathit{\omega }}_{\text{i}}^2+{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}-k_{\text{w}}{v}_{||}{\mathit{\Omega }}_0$, $B_3=-2{\mathit{\omega }}_{\text{b}}^2\left(v_{||}/\phantom{v_{||}c}c\right)+{\mathit{\Omega }}_0-2k_{\text{w}}{v}_{||}$, $B_4=-{\mathit{\omega }}_{\text{i}}^2+{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]-k_{\text{w}}{v}_{||}{\mathit{\Omega }}_0$, and $B_5={\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\left[1+\left(v_{||}^2/\phantom{v_{||}^2{c}^2}{c}^2\right)\right]+k_{\text{w}}{v}_{||}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{||}\right)$.

Differentiating between Eqs. (38) and (39) with respect to time and using Eq. (26) and its time derivation, the following two coupled equations can be obtained:

$$\mathit{\delta }{\stackrel{⃛}{x}}_1=-P\mathit{\delta }{\dot{x}}_1+Q\mathit{\delta }{\ddot{x}}_2,$$

(42)

$$\mathit{\delta }{\stackrel{⃛}{x}}_2=-R\mathit{\delta }{\dot{x}}_2-S\mathit{\delta }{\ddot{x}}_2+T\mathit{\delta }{x}_1,$$

(43)

where

$$P={\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+k_{\text{w}}{v}_{30}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{30}\right)-\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}{k}_{\text{w}}^2{v}_{30}{x}_{20},$$

(44)

$$Q=2k_{\text{w}}{v}_{30}-{\mathit{\Omega }}_0-\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)k_{\text{w}}{v}_{30}{x}_{20}^2/\phantom{\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2\right)k_{\text{w}}{v}_{30}{x}_{20}^2{c}^2}{c}^2+k_{\text{w}}{x}_2\left(\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}+{\mathit{\omega }}_{\text{i}}^2{v}_{30}{x}_{20}/\phantom{{\mathit{\omega }}_{\text{i}}^2{v}_{30}{x}_{20}{c}^2}{c}^2\right),$$

(45)

$$\begin{array}{cc}\hfill R& ={\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+k_{\text{w}}{v}_{30}\left({\mathit{\Omega }}_0-k_{\text{w}}{v}_{30}\right)+\left({\mathit{\gamma }}^2/\phantom{{\mathit{\gamma }}^2{c}^2}{c}^2\right)\left[D_1{k}_{\text{w}}{v}_{30}{v}_{10}-{\mathit{\Omega }}_{\text{w}}{v}_{||}^2{k}_{\text{w}}{v}_{10}\left(B_2-\mathit{\lambda }{B}_4/\phantom{B_2-\mathit{\lambda }{B}_4{B}_5}{B}_5\right)\right]\hfill \\ \hfill & -D_2\left(\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}+{\mathit{\omega }}_{\text{i}}^2{v}_{30}{x}_{20}/\phantom{{\mathit{\omega }}_{\text{i}}^2{v}_{30}{x}_{20}{c}^2}{c}^2\right),\hfill \\ \hfill \end{array}$$

(46)

$$S=\left({\mathit{\gamma }}^2/\phantom{{\mathit{\gamma }}^2{c}^2}{c}^2\right)\left[-D_1{v}_{10}+{\mathit{\Omega }}_{\text{w}}{v}_{30}\left(B_2-\mathit{\lambda }{B}_4/\phantom{B_2-\mathit{\lambda }{B}_4{B}_5}{B}_5\right)\right]-{\mathit{\Omega }}_0+2k_{\text{w}}{v}_{30},$$

(47)

$$T=D_2\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}{k}_{\text{w}}{v}_{30},$$

(48)

and

$$D_1=\left({\mathit{\omega }}_{\text{i}}^2-{\mathit{\omega }}_{\text{b}}^2{\mathit{\gamma }}_{||}^{-2}+{\mathit{\Omega }}_0{k}_{\text{w}}{v}_{30}\right)x_{20}+\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}{v}_{30}$$

(49)

$$\begin{array}{c}{D}_2=\left({\mathit{\gamma }}^2/\phantom{{\mathit{\gamma }}^2{c}^2}{c}^2\right)\left(v_{30}-k_{\text{w}}{x}_{20}{v}_{10}\right)D_1+\left(2{\mathit{\omega }}_{\text{b}}^2{v}_{||}/\phantom{2{\mathit{\omega }}_{\text{b}}^2{v}_{||}{c}^2}{c}^2-k_{\text{w}}{\mathit{\Omega }}_0+2k_{\text{w}}^2{v}_{30}\right)x_{20}-\mathit{\lambda }{\mathit{\Omega }}_{\text{w}}\hfill \\ -{\mathit{\Omega }}_{\text{w}}{v}_{||}\left[\left(B_1-\mathit{\lambda }{B}_3/\phantom{B_1-\mathit{\lambda }{B}_3{B}_5}{B}_5\right)\right.+\left({\mathit{\gamma }}^2/\phantom{{\mathit{\gamma }}^2{c}^2}{c}^2\right)\left(v_{30}-k_{\text{w}}{x}_{20}{v}_{10}\right)\left(B_2-\mathit{\lambda }{B}_4/\phantom{B_2-\mathit{\lambda }{B}_4{B}_5}{B}_5\right),\hfill \end{array}$$

(50)

The necessary condition for stability of the electron orbit may be obtained by assuming that all displacements (oscillating with the same frequency) are represented by

$$\mathit{\delta }{x}_j=A_j{e}^{i\mathit{\omega }t},j=1,2,3,$$

(51)

where $A_j$ is the complex amplitude. Equations (28) and (29) lead to the following two algebraic equations:

$$i\left({\mathit{\omega }}^3-\mathit{\omega }P\right)A_1-{\mathit{\omega }}^{2}Q{A}_2=0,$$

(52)

$$\left({\mathit{\omega }}^{2}S+T\right)A_1+i\left({\mathit{\omega }}^3-\mathit{\omega }R\right)A_2=0.$$

(53)

The necessary and sufficient condition for a nontrivial solution consists of the determinant of coefficients in Eqs. (51) and (52) equated to zero. Imposing this condition yields

$${\mathit{\omega }}^4+\left(QS+P+R\right){\mathit{\omega }}^2+\left(PR-QT\right)=0.$$

(54)

This is a quadratic equation is ${\mathit{\omega }}^2$, and the system will be stable if both roots are real and positive. The stability conditions are, therefore, given by

$$\left\{\begin{array}{c}{\left(P+R+QS\right)}^2-4\left(PR-QT\right)>0,\hfill \\ \left(P+R+QS\right)>0,\hfill \\ \left(PR-QT\right)>0.\hfill \end{array}\right.$$

(55)

Dotted lines in figures show the unstable parts of the trajectories.