Skip to main content
Springer Nature Link
Log in

Bounds on the number of cycles of length three in a planar graph

  • Published:
Israel Journal of Mathematics Aims and scope Submit manuscript

Abstract

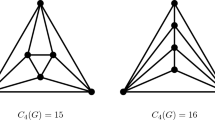
LetG be ap-vertex planar graph having a representation in the plane with nontriangular facesF 1,F 2, …,F r. Letf 1,f 2, …,f r denote the lengths of the cycles bounding the facesF 1,F 2, …,F r respectively. LetC 3(G) be the number of cycles of length three inG. We give bounds onC 3(G) in terms ofp,f 1,f 2, …,f r. WhenG is 3-connected these bounds are bounds for the number of triangles in a polyhedron. We also show that all possible values ofC 3(G) between the maximum and minimum value are actually achieved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. B. Grünbaum,Convex Polytopes, Wiley-Interscience, New York, 1967.

    MATH  Google Scholar 

  2. B. Grünbaum,Polytopes, graphs, and complexes, Bull. Amer. Math. Soc.76 (1970), 1131–1201.

    Article  MATH  MathSciNet  Google Scholar 

  3. S. L. Hakimi and E. F. Schmeichel,On the number of cycles of length k in a maximal planar graph, J. Graph Theory3 (1979), 69–86.

    Article  MATH  MathSciNet  Google Scholar 

  4. S. L. Hakimi and E. F. Schmeichel,The number of triangles in a triangulation of a set of points in the plane, Elem. Math.35 (1980), 137–142.

    MathSciNet  Google Scholar 

  5. F. Harary,Graph Theory, Addison-Wesley, Reading, Mass., 1969.

    Google Scholar 

  6. E. F. Schmeichel and S. L. Hakimi,On planar graphical degree sequences, SIAM J. Appl. Math.32 (1977), 598–609.

    Article  MATH  MathSciNet  Google Scholar 

  7. H. Whitney,Non-separable and planar graphs, Trans. Amer. Math. Soc.34 (1932), 339–362.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Northwestern University, 60201, Evanston, IL, USA

    S. L. Hakimi & E. F. Schmeichel

  2. San José State University, 95192, San José, CA, USA

    S. L. Hakimi & E. F. Schmeichel

Authors
  1. S. L. Hakimi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. E. F. Schmeichel
    View author publications

    You can also search for this author inPubMed Google Scholar

Additional information

This research was supported in part by the U.S.A.F. Office of Scientific Research, Systems Command, under Grant AFOSR-76-3017 and the National Science Foundation under Grant ENG79-09724.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hakimi, S.L., Schmeichel, E.F. Bounds on the number of cycles of length three in a planar graph. Israel J. Math. 41, 161–180 (1982). https://doi.org/10.1007/BF02760664

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02760664

Keywords