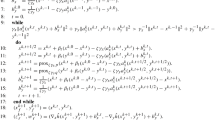Abstract
An error analysis is provided for discrete Lagrangian cell problems where the exact objective function for each cell is approximated by a simpler expression. Easily-calculated rigorous and heuristic bounds are given for the error in the value of the objective function. The solution itself, however, can be significantly distorted.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. Charnes and W.W. Cooper, “A note on the ‘Fail-Safe’ properties of the ‘Generalized Lagrange Multiplier Method’”, and H. Everett, “Comment on preceeding note”,Operations Research 13 (1965) 674–678.
Richard H. Day, “Allocating weapons to target complexes by means of nonlinear programming”,Operations Research 14 (1966) 992–1013.
H. Everett, III, “Generalized Lagrange multiplier method for solving problems of optimum allocation of resources”,Operations Research 11 (1963) 399–417.
G.G. Furman and H.J. Greenberg, “Optimal weapon allocation with overlapping area defenses”,Operations Research 21 (1973) 1291–1308.
S. Kaplan, “Solution of the Lorie—Savage and similar integer programming problems by the generalized Lagrange multiplier method”,Operations Research 14 (1966) 1130–1136.
F. Lemus and K.H. David, “An optimum allocation of different weapons to a target complex”,Operations Research 11 (1963) 787–794.
E.P. Loane, “An algorithm to solve finite separable single-constrained optimization problems”,Operations Research 19 (1971) 1477–1493.
G.J. Silverman, “Primal decomposition of mathematical programs by resource allocation — I and II”,Operations Research 20 (1972) 58–93.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Schweitzer, P.J. Optimization with an approximate Lagrangian. Mathematical Programming 7, 191–198 (1974). https://doi.org/10.1007/BF01585515
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01585515