Potential Energy Surface Mapping of Charge Carriers in Ionic Conductors Based on a Gaussian Process Model

Abstract

The potential energy surface (PES) of a charge carrier in a host crystal is an important concept to fundamentally understand ionic conduction. Such PES evaluations, especially by density functional theory (DFT) calculations, generally require vast computational costs. This chapter introduces a novel selective sampling procedure to preferentially evaluate the partial PES characterizing ionic conduction. This procedure is based on a machine learning method called the Gaussian process (GP), which reduces computational costs for PES evaluations. During the sampling procedure, a statistical model of the PES is constructed and sequentially updated to identify the region of interest characterizing ionic conduction in configuration space. Its efficacy is demonstrated using a model case of proton conduction in a well-known proton-conducting oxide, barium zirconate (BaZrO₃) with the cubic perovskite structure. The proposed procedure efficiently evaluates the partial PES in the region of interest that characterizes proton conduction in the host crystal lattice of BaZrO₃.

1 Introduction

Atomic transport phenomena in solids such as atomic diffusion and ionic conduction are generally governed by thermally activated processes. Based on transition state theory (TST) [1,2,3], the mean frequency of an elementary process (ν) with a single saddle point state, a so-called an atomic or ionic jump, is approximated by $\nu = \nu_{0} { \exp }({-}\Delta E^{\text{mig}} /k_{\text{B}} T)$, where ν ₀ is the vibrational prefactor, k _B is the Boltzmann constant, T is the temperature, and ΔE ^mig is the potential barrier, i.e., the change in the potential energy (PE) from the initial state to the saddle point state. ν ₀ is typically a constant value in the range of 10¹²–10¹³ s⁻¹ associated with a lattice vibration [3,4,5,6,7,8]. Consequently, ΔE ^mig mainly determines the rate of an atomic jump in a solid.

In general, atomic transfer is composed of several types of atomic jumps, which form a complicated three-dimensional (3D) network in the crystal lattice. Therefore, it is necessary to grasp the entire potential energy surface (PES) of a mobile atom or ion. However, a theoretical PES evaluation, e.g., based on density functional theory (DFT), generally requires huge computational costs, particularly in the case of a host crystal with a low crystallographic symmetry. The nudged elastic band (NEB) method [9, 10] is a well-established technique to avoid evaluating the entire PES, in which only the minimum energy paths (MEPs) are focused on in the PES. Because of its efficiency and versatility, the NEB method is used conventionally to clarify the atomic-scale-picture and the kinetics of atomic transfer in crystals.

However, the NEB method has some practical limitations. First, the initial and final states of all elementary paths in a crystal must be specified. That is, all local energy minima in the crystal and all conceivable elementary paths between adjacent local energy minima must be known in advance. As the crystallographic symmetry of the host crystal decreases, the number of local energy minima and conceivable elementary paths rapidly increase. Consequently, satisfying the requirements in the NEB method is very difficult without a priori information on the entire PES. In cases without a priori information, physical and chemical knowledge (e.g., ionic radii, chemical bonding states, electrostatic interaction, and interstitial and bottleneck sizes) are generally used. However, a key elementary path determining the rate of atomic diffusion or ionic conduction is sometimes missed in such an arbitrary manner. In addition, the NEB method requires huge computational costs for low-symmetry crystals, even if only the MEPs in the PES are evaluated. For example, in our recent study on proton conduction in tin pyrophosphate (SnP₂O₇) with space group of P2_1/C , we evaluated 143 possible elementary paths connecting 15 local energy minima by the NEB method [11]. An alternative method that is both robust and efficient is desirable to analyze complicated atomic transfers consisting of many elementary paths in a low-symmetry crystal.

This chapter introduces a novel selective sampling procedure for PES mapping based on a machine learning technique [12]. This sampling procedure preferentially evaluates a partial PES in the region of interest characterizing ionic conduction. The region of interest is defined in two ways: (1) a low-PE region forming long-range migration pathways throughout the crystal lattice in the PES and (2) a low-force norm region (low-FN region), which includes all the local minima and saddle points in the PES. It should be noted that other mathematically definable and efficient choices could be considered as the region of interest. See the synthetic 2D PES and FN surface (FNS) for the definitions of the region of interest (Fig. 2.1).

Fig. 2.1

Synthetic two-dimensional (a) PES and (b) FNS of a charge carrier in a host crystal lattice. Region of interest is defined as the low-PE region in the PES and the low-FN region in the FNS

The proposed sampling procedure has three key features. (1) A statistical model of the PES or FNS is developed as a Gaussian process (GP) [13, 14]. The statistical model is iteratively updated by repeatedly (i) sampling at a point where the predicted PE or FN is low and (ii) incorporating the newly calculated PE or FN value at the sampled point. (2) The statistical PES or FNS model is used to identify the subset of grid points at which the PEs or FNs are relatively low. Here a selection criterion is introduced for this advanced purpose, because GP applications have generally targeted the single global minimum or maximum point (not a subset). (3) The procedure allows us to estimate how many points in the region of interest remain unsampled, i.e., lets us know when sampling should be terminated.

These features are possible by exploiting an advantage of the GP that it provides not only the predicted PE or FN value but also the uncertainty at each grid point. Figure 2.2 illustrates selective sampling sequences using a one-dimensional synthetic PES where nine grid points in the low-PE region should be selectively sampled from all (50) points as an example. Roughly speaking, the grid point most likely to be located in the low-PE region is sampled at each step based on the predicted PEs (red solid curve) and the uncertainties (pale blue area). In the early steps, the predicted PEs are uncertain with large discrepancies from the true PES (black solid curve), resulting in selecting grid points with large uncertainties. As the sampling proceeds, the predicted PE curve gradually approaches the true one and the uncertainty decreases. Eventually, the grid points in the low-PE region are selectively sampled in the latter steps.

Fig. 2.2

Schematic illustration of the proposed selective sampling procedure in a one-dimensional configuration space with synthetic data [12]. In each plot, the x- and y-axes represent the configuration space and the PEs, respectively. Red area in plot (a) represents the low-PE region. In this example, the goal is to efficiently identify and evaluate the PEs at the nine points in the low-PE region. Plot (b) indicates the initialization step, where two points (filled red squares) are randomly selected and their PEs are evaluated. Remaining 16 plots [plots (c) to plot (r)] indicate steps 1–16 of the procedure

The uncertainty in the GP model is useful also to determine when to terminate sampling. The termination criterion should be determined based on the existence probability of unsampled low-PE points, for which the information on the uncertainty is indispensable. As a model case, herein the efficacy of the proposed procedure is demonstrated using proton conduction in a proton-conducting oxide, barium zirconate (BaZrO₃) [15,16,17,18].

2 Problem Setup

2.1 Entire Proton PES in BaZrO₃

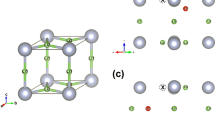
The entire PES of a proton in BaZrO₃ evaluated using DFT calculations with structural optimization is initially shown for the problem setup of the demonstration study. Figure 2.3 shows the crystal structure of BaZrO₃ [space group: $Pm{\bar{3}}m$ (221)] and its asymmetric unit satisfying 0 ≤ x, y, z ≤ 0.5, y ≤ x, and z ≤ y. x, y, and z denote the 3D fractional coordinates of a proton introduced into the host lattice. Ba, Zr, and O ions occupy the 1a, 1b, and 3c sites, respectively, using the origin setting shown in Fig. 2.3. A 40 × 40 × 40 grid is introduced in the unit cell (the grid interval is nearly equal to 0.1 Å), which contains 64,000 grid points in total. Due to the high crystallographic symmetry of BaZrO₃, the asymmetric unit has only 1771 grid points. Among these points, three coincide with Ba, Zr, or O ion. Removing these three points reduces the remaining grid points to 1768.

Fig. 2.3

Crystal structure and the asymmetric unit of BaZrO₃ with the cubic perovskite structure

The DFT calculations for the PES (and FNS) evaluation of a proton in BaZrO₃ are based on the projector augmented wave (PAW) method as implemented in the VASP code [19,20,21,22]. The generalized gradient approximation (GGA) parameterized by Perdew, Burke, and Ernzerhof is used for the exchange-correlation term [23]. The 5s, 5p, and 6s orbitals for Ba, 4s, 4p, 5s, and 4d for Zr, 2s and 2p for O, and 1s for H are treated as valence states. The supercell consisting of 3 × 3 × 3 unit cells (135 atoms) is used with a 2 × 2 × 2 mesh for the k-point sampling. Only the atomic positions in a limited region corresponding to the 2 × 2 × 2 unit cells around the introduced proton are optimized with fixing all other atoms and the proton. The atomic positions are optimized until the residual forces converge to less than 0.02 eV/Å.

Figure 2.4a shows the calculated proton PES in the low-PE region below 0.3 eV. The blue regions around the O ions are the most stable proton sites and are located ~1 Å from the O ions. The OH distance is almost equivalent to that in water, indicating that OH bond formation stabilizes the protons in BaZrO₃. There are four equivalent proton sites per O ion, which are connected by the low-PE points around the O ions. The rotational path around the O ions consists of four equivalent quarter-rotational paths, where the calculated potential barrier is 0.18 eV. On the other hand, the hopping path connecting adjacent rotational orbits is located at the periphery of the edges of the ZrO₆ octahedra. The calculated potential barrier of the hopping path is 0.25 eV, which is higher than that of the rotational path. The two kinds of paths form a three-dimensional proton-conducting network throughout the crystal lattice. Consequently, protons exhibit a long-range migration via repeated rotation and hopping, where the hopping path is the rate-determining path in proton conduction.

Fig. 2.4

(a) Calculated proton PES in the low PE region below 0.3 eV in reference to the most stable point [12]. (b) Grid points at which the force norm acting on a proton is less than 0.2 eV/Å

2.2 Problem Statement

Figure 2.4(a) indicates that the partial PES of a proton in the low-PE region below 0.3 eV is necessary and sufficient to estimate the proton diffusivity and conductivity in the crystal lattice of BaZrO₃. In the low-PE region, there are 353 grid points to be evaluated by DFT calculations, corresponding to the lowest 20% of the grid points. Therefore, the first task is to selectively sample all the low-PE grid points as efficiently as possible. Hereafter this is referred to task 1. Task 2 is based on the force norm (FN) acting on a proton at each grid point. The FN is calculated along with the PE by the DFT calculations. In this task, the region of interest is defined as grid points with an FN below a threshold (i.e., 0.2 eV/Å in the present study), denoted by blue spheres in Fig. 2.4(b). There are only 15 grid points in the low-FN region in the asymmetric unit. The region of interest in task 2 is much smaller than that in task 1, hopefully leading to more efficient sampling.

Prior to the detailed description of the proposed procedure in Sect. 2.3, this problem is generalized and mathematically formulated using the identification of the low-PE region as an example. There are N grid points, $i = 1, \ldots ,N$, in the asymmetric unit of the host crystal lattice. The PE of a proton at grid point i is denoted by E _i . Using the parameter 0 < α < 1, the low-PE region is defined as the set of αN points where the PEs are lower than those at other (1−α)N points. The goal is to identify all αN grid points in the low-PE region as efficiently as possible. For simplicity, α is assumed to be prespecified. However, it can be adaptively determined, as demonstrated in Sect. 2.4.3.

When θ _α represents the PE threshold of the low-PE region, the subsets of P _α and N _α are defined as

$$ P_{\alpha }\,{:\!=} \{ i \in \{ 1, \ldots ,N\} |E_{i} < \theta_{\alpha } \} $$

(2.1)

$$ N_{\alpha }\,{:\!=} \{ i \in \{ 1, \ldots ,N\} |E_{i} \ge \theta_{\alpha } \} . $$

(2.2)

The task is formally stated as the problem of identifying all points in P _α . Using statistical terminology, the points in P _α and N _α are called “positive” and “negative” points, respectively. Note that P _α , N _α , and θ _α are unknown unless the PEs at all grid points are actually computed. During the sampling process, these quantities are estimated based on the PEs at points sampled in the earlier steps. Our estimates of positive and negative sets are denoted as $\hat{P}_{\alpha }$ and $\hat{N}_{\alpha }$, respectively. The former indicates the set of points at which the PEs have been sampled and computed in earlier steps. The latter represents the set of points at which the PEs have yet to be computed. The proposed selective sampling procedure can be interpreted as the process of sequentially updating these two sets of points. Specifically, we begin at $\hat{P}_{\alpha } = {\emptyset }$ and $\hat{N}_{\alpha } = \{ 1, \ldots ,N\}$. The two sets are updated as

$$ \hat{P}_{\alpha } \leftarrow \hat{P}_{\alpha } \cup \{ i^{{\prime }} \} , $$

(2.3)

$$ \hat{N}_{\alpha } \leftarrow \hat{N}_{\alpha } \backslash \{ i^{{\prime }} \} , $$

(2.4)

where i′ is the sampled point in the step. When the termination criterion is satisfied, $\hat{P}_{\alpha }$ has a high probability of containing all points in P _α . The estimated θ _α is also defined as $\hat{\theta }_{\alpha }$. Section 2.3.3 shows how to estimate θ _α from the prespecified α. Note that the θ _α estimation is unnecessary in task 2 because the FN threshold is directly specified by the FN value.

3 GP-Based Selective Sampling Procedure

Here the proposed sampling procedure based on the GP is described using the PES-based task (task 1) as an example. Specifically, the key features are explained in the following subsections: the GP-based PE statistical model (Sect. 2.3.1), the selection criterion of the next grid point (Sect. 2.3.2), the estimation of the PE threshold (Sect. 2.3.3), and the criterion for sampling termination (Sect. 2.3.4). Note that the threshold estimation (Sect. 2.3.3) is irrelevant to task 2 for the low-FN identification.

3.1 Gaussian Process Models

We adopt a GP model [13, 14] as the statistical model of the PES. Using a GP model, the potential energy E _i is represented as

$$ E_{i} \sim N(\mu_{i} ,\sigma_{i}^{2} ),\quad i = 1, \ldots ,N, $$

(2.5)

where N(μ _i , σ ² _i ) denotes the normal distribution with mean μ _i and variance σ ² _i . A GP model is a type of regression model. Consider a d-dimensional vector of descriptors for each point, where the vector is denoted as ${\varvec{\upchi}}_{i} \in {\mathbb{R}}^{d} \,\,{\text{for}}\,\,i = 1, \ldots ,N$. The mean and variance of the PE at the ith point, which are given in Eqs. (2.8) and (2.9), respectively, are represented as functions of χ _i . The GP model employs the so-called kernel function $k:{\mathbb{R}}^{d} \times {\mathbb{R}}^{d} \to {\mathbb{R}}$. For two different points indexed by i and j, k(χ _i , χ _j ) is roughly interpreted as the similarity between these two points. One of the most commonly used kernel functions is the RBF kernel, which is given by

$$ k({\varvec{\upchi}},{\varvec{\upchi}}^{{\prime }} ) = \sigma_{\text{f}}^{ 2} \exp ( - \left\| {{\varvec{\upchi}} - {\varvec{\upchi}}^{{\prime }} } \right\|/2l^{2} ), $$

(2.6)

where σ _f, l > 0 are tuning parameters, and ǁ · ǁ represents the L ₂ norm. Furthermore, for n points indexed by 1, …, n, let ${\mathbf{K}} \in {\mathbb{R}}^{nn}$ be the so-called kernel matrix defined as

$$ {\mathbf{K}}\,{:\!=} \left[ {\begin{array}{*{20}c} {k({\varvec{\upchi}}_{1} ,{\varvec{\upchi}}_{1} )} & \cdots & {k({\varvec{\upchi}}_{1} ,{\varvec{\upchi}}_{n} )} \\ \vdots & \ddots & \vdots \\ {k({\varvec{\upchi}}_{n} ,{\varvec{\upchi}}_{1} )} & \cdots & {k({\varvec{\upchi}}_{n} ,{\varvec{\upchi}}_{n} )} \\ \end{array} } \right]. $$

(2.7)

For any point in the configuration space whose descriptor vector is represented as ${\varvec{\upchi}} \in {\mathbb{R}}^{d}$, the GP model provides the predictive distribution of its PE in the form of a normal distribution $N[\mu ({\varvec{\upchi}}),\sigma^{2} ({\varvec{\upchi}})]$. Here, the mean function $\mu :{\mathbb{R}}^{d} \to {\mathbb{R}}$ is given as

$$ \mu ({\varvec{\upchi}})\,{:\!=} {\varvec{\upkappa}}({\varvec{\upchi}})^{\text{T}} {\mathbf{K}}^{ - 1} {\mathbf{E}}, $$

(2.8)

where ${\varvec{\upkappa}}({\varvec{\upchi}})\,{:\!=} [k({\varvec{\upchi}},{\varvec{\upchi}}_{1} ), \ldots ,k({\varvec{\upchi}},{\varvec{\upchi}}_{n} )]^{\text{T}}$ and ${\mathbf{E}}\,{:\!=} [E_{1} , \ldots ,E_{n} ]$, while the variance function $\sigma^{2} :{\mathbb{R}}^{d} \to {\mathbb{R}}$ is given as

$$ \sigma^{2} ({\varvec{\upchi}})\,{:\!=} k({\varvec{\upchi}},{\varvec{\upchi}}) - {\varvec{\upkappa}}({\varvec{\upchi}})^{\text{T}} {\mathbf{K}}^{ - 1} {\varvec{\upkappa}}({\varvec{\upchi}}). $$

(2.9)

At each step, the GP model of PES is fitted based on $\{ ({\varvec{\upchi}}_{i} ,E_{i} )\}_{{i \in \hat{P}_{\alpha } }}$, which is the set of points whose PEs have already been computed by DFT calculations in earlier steps.

3.2 Selection Criterion

Given a GP model in the form of Eq. (2.5) for each point, the subsequent task is to select the next point at which the PE is most likely to be lower than the estimated threshold $\hat{\theta }_{\alpha }$. (The following subsection discusses how to estimate the threshold.) For this task, some techniques developed in the context of Bayesian optimization [24, 25], which are used to minimize or maximize an unknown function, can be borrowed. There are two main options that can be adapted for our task in the Bayesian optimization literature. The first is to select the point at which the probability that the PE is lower than $\hat{\theta }_{\alpha }$ is maximized. This is called the “probability of improvement”, which is formulated as

$$ i^{{\prime }}\,{:\!=} \arg \mathop {\hbox{max} }\limits_{{i \in \hat{N}_{\alpha } }}\Phi [\hat{\theta }_{\alpha } ;\mu ({\varvec{\upchi}}_{i} ),\sigma^{2} ({\varvec{\upchi}}_{i} )], $$

(2.10)

where $\Phi (\cdot;\mu ,\sigma^{2} )$ is the cumulative distribution function of $N(\mu ,\sigma^{2} )$. The second option is the “expected improvement”. Similarly, it is formulated as

$$ i^{{\prime }}\,{:\!=} \arg \mathop {\hbox{min} }\limits_{{i \in \hat{N}_{\alpha } }} \int_{ - \infty }^{{\hat{\theta }_{\alpha } }} {E\phi [E;\mu ({\varvec{\upchi}}_{i} ),\sigma^{2} ({\varvec{\upchi}}_{i} )]dE} , $$

(2.11)

where $\phi (\cdot;\mu ,\sigma^{2} )$ is the probability density function of $N(\mu ,\sigma^{2} )$. This study employs the second option, although the performance difference between Eqs. (2.10) and (2.11) is negligible in our experience.

3.3 PE Threshold

PE threshold θ _α should be estimated because it is unknown prior to evaluating the entire PES. The contingency table (Table 2.1) is here considered to obtain an estimate $\hat{\theta }_{\alpha }$ of the threshold θ _α . TP, FP, FN, and TN denote the true positive, false positive, false negative, and true negative, respectively. The notation # indicates the event number. Note that the FN is not the “force norm” acting on a proton in this context. The numbers for these four events can be rephrased as:

Table 2.1 Contingency table defining TP, FP, FN, and TN

• #TP: The number of sampled points in the low-PE region.

• #FP: The number of sampled points in the high-PE region.

• #FN: The number of not-yet-sampled points in the low-PE region.

• #TN: The number of not-yet-sampled points in the high-PE region.

These four numbers depend on the estimated PE threshold $\hat{\theta }_{\alpha }$. Recalling the equation of $P_{\alpha } /(P_{\alpha } + N_{\alpha } ) = \alpha$, the following relationship should be maintained

$$ [\# TP(\hat{\theta }_{\alpha } ) + \# FN(\hat{\theta }_{\alpha } )]/N = \alpha . $$

(2.12)

Because E _i for $i \in \hat{P}_{\alpha }$ is already evaluated, we simply obtain

$$ \# TP(\hat{\theta }_{\alpha } ) = \sum\limits_{{i \in \hat{P}_{\alpha } }} {I(E_{i} < \hat{\theta }_{\alpha } )} , $$

(2.13)

where I(·) is the indicator function defined by I(z) = 1 if z is true and I(z) = 0 if z is false. On the other hand, $\# {\text{FN}}(\hat{\theta }_{\alpha } )$ must be estimated based on the statistical model Eq. (2.6) because E _i is unknown for $i \in \hat{N}_{\alpha }$

$$ \# {\text{FN(}}\hat{\theta }_{\alpha } )\approx \mathop {\text{FN}}\limits^{ \wedge } (\hat{\theta }_{\alpha } )\,{:\!=} \sum\limits_{{i \in N_{\alpha } }} {\Phi [\hat{\theta }_{\alpha } ;\mu ({\varvec{\upchi}}_{i} ),\sigma^{2} ({\varvec{\upchi}}_{i} )]} . $$

(2.14)

The estimate of the threshold $\hat{\theta }_{\alpha }$ is determined for each step so that it satisfies Eq. (2.12) where the quantities on the left-hand side are given by Eqs. (2.13) and (2.14).

3.4 Termination Criterion

When sampling is terminated, $\hat{P}_{\alpha }$ should ideally contain all the points in P _α , i.e., $\hat{P}_{\alpha } \supseteq P_{\alpha }$. As easily noted from the contingency table, this requirement can be rewritten as $\# {\text{FN}}(\hat{\theta }_{\alpha } ) = 0$. This indicates that the estimated false negative rate (FNR) defined as

$$ {\text{F}}\widehat{\text{N}}{\text{R}}\,:\!= \frac{{\# \mathop {\text{FN}}\limits^{ \wedge } (\hat{\theta }_{\alpha } )}}{{\# {\text{TP}}(\hat{\theta }_{\alpha } ) + \# \mathop {\text{FN}}\limits^{ \wedge } (\hat{\theta }_{\alpha } )}}, $$

(2.15)

can assess the badness of the sampled points. ${\text{F}}\widehat{\text{N}}{\text{R}}$ in Eq. (2.15) can be interpreted as the proportion of points where the PEs have yet to be evaluated. At each step, $\# {\text{TP}}(\hat{\theta }_{\alpha } )$ is computed by Eq. (2.13) and $\# {\text{FN}}(\hat{\theta }_{\alpha } )$ is estimated by Eq. (2.14). Then, the sampling is terminated if ${\text{F}}\widehat{\text{N}}{\text{R}}$ is close to zero (e.g., <10⁻⁶).

4 Results of Selective Sampling

4.1 Low-PE Region Identification

The performances of several sampling procedures for α = 0.2 are compared in the low-PE region identification problem. Specifically, the following six sampling methods are assessed: (1) GP1(xyz), (2) GP2(xyz + 1st NNs), (3) GP3(xyz + prePES), (4) random, (5) prePES, and (6) ideal. The first three are the proposed GP-based selective sampling methods with different descriptors. In GP1, the 3D coordinates (x _i , y _i , and z _i ) in the host crystal lattice are used as the descriptors of the ith point (denoted as xyz). In GP2, the first nearest neighbor (1st NN) distances to the Ba, Zr, and O atoms from each point are used as additional descriptors (denoted as 1st NNs). In GP3, a preliminary PES (denoted as prePES) is used as an additional descriptor. The preliminary PES means a rough but quick approximation of the PES obtained using less accurate but more efficient computational methods. For prePES, the PE values at all N points obtained by single-point DFT calculations are used. Random indicates naive random sampling, where a point is selected randomly at each step. prePES denotes a selective sampling method based only on the preliminary PES. Specifically, points are sequentially selected in ascending order of the preliminary PEs obtained by single-point DFT calculations. Finally, ideal indicates the ideal sampling method, which can only be realized when the actual PEs at all the points are known in advance.

In GP1 to GP3, two points are randomly selected to initialize the GP model. The average and the standard deviation over ten runs with different random seeds are discussed. The tuning parameters of the GP models are set to σ _f = l = 0.5. According to our preliminary experiments, the performances are insensitive to the tuning parameter choices.

Figure 2.5 compares the efficiencies of the six sampling methods. The number of points successfully sampled from the low-PE region (#TP) is plotted as a function of the number of PE computations based on DFT (#TP + #FP). The results of the three different GP-based sampling methods (GP1 to GP3) indicate the importance of choosing the descriptors. Using the 3D coordinates (GP1) as the descriptors is only slightly better than using the random method. On average, GP1 requires 1539.6 ± 31.2 DFT computations until all the points in the low-PE region are identified. GP2 has an improved performance, suggesting that additional appropriate descriptors are generally advantageous. GP2 requires 1269.4 ± 100.3 DFT computations to identify all the low-PE grid points. GP3 has a markedly enhanced performance. GP3 requires only 394.1 ± 5.2 DFT computations, indicating that the preliminary PES is a very helpful descriptor. On the other hand, prePES has a much poorer performance and requires 1479 DFT computations. Thus, the preliminary PES alone is insufficient to effectively identify the low-PE region. The importance of the preliminary PES is discussed in more detail below.

Fig. 2.5

Efficiencies of the six sampling methods for α = 0.20 [12]. Number of grid points successfully sampled from the low-PE region (#TP) is plotted versus the number of PE evaluations by DFT (#TP + #FP)

Figure 2.6 demonstrates the differences between the sampling sequences of the GP1, GP3, prePES, and ideal methods. GP1 erroneously selects many points in the high-PE region. In contrast, GP3 preferentially selects points in the low-PE region, and only a small number of points are mistakenly selected from the high-PE region. Although the prePES method preferentially selects points in the low-PE region, it fails to identify all of them. Surprisingly, the sampling sequence of GP3 is almost identical to that in the ideal sampling, despite the unknown low-PE region beforehand. This indicates that the GP model in GP3 successfully estimates the PES in the low-PE region.

Fig. 2.6

Selected grid points (gray dots) at 100, 200, 300, and 400 steps by the different sampling methods in the model crystal lattice of BaZrO₃ for α = 0.20 [12]. Yellow surface in each plot is the isosurface corresponding to the PE threshold at α = 0.20

Figure 2.5 indicates that the preliminary PES obtained by single-point DFT calculations is highly valuable as a descriptor when it is used along with three-dimensional coordinates (x, y, z) in GP modeling. However, using the preliminary PES alone cannot identify the low-PE region in the prePES sampling. The results are only slightly better than random. In the earlier steps, the sampling curve of prePES almost overlaps with the ideal sampling curve, but it gradually deviates as the sampling proceeds. Eventually, 1479 steps are necessary to find all points in the low-PE region using prePES. This is 4.2-fold decline compared to the ideal sampling case (353 points). The inefficiency of prePES is attributed to the relationship between the DFT calculations with and without structural optimization.

Figure 2.7 shows the rank correlation between the actual and preliminary PEs, where the points with low PEs are located below the horizontal dotted line. The prePES sampling method selects points in ascending order of the preliminary PEs, meaning that the points are selected from left to right in Fig. 2.7(a). Therefore, most of the N grid points (all points located in the shaded region) must be sampled to select all the points in the low-PE region. On the other hand, in GP3 with xyz and prePES as descriptors, the average number of sampling steps required to identify all the points in the low-PE region is only 394.1, which is only a 1.1-fold increase compared to the ideal sampling method.

Fig. 2.7

Rank correlation between the actual and the preliminary PEs [12]. Open circles and crosses show the grid points in P _α and N _α , respectively. Blue and red symbols indicate sampled points at 400 steps in (a) prePES and (b) GP4, respectively. GP4 method samples all the positive points at 400 steps with a small number of False ositive points (i.e., sampled points not in the low-PE region). In (b), there are no False Negative points

4.2 Low-FN Region Identification

The previous subsection demonstrates several types of sampling methods, which use different descriptors to identify the low-PE region. GP3, which employs descriptors of xyz and prePES, exhibits the best performance and is comparable to ideal sampling. However, the region of interest (i.e., the low-PE region) comprises 20% of the configuration space. Thus, the computational cost can be reduced by 80% at most.

To further reduce computational costs, it is necessary to redefine a smaller region of interest. The mean frequency of atomic or ionic jumps in a solid is determined mainly by the change in PE from the initial point to the saddle point. As both of these points can be mathematically defined as points with a zero gradient in the PES, the region of interest can be redefined as the region where the force norm (FN) acting on a proton is small. In this model case, the FN threshold is set to 0.2 eV/Å, which leads to 15 grid points in the low-FN region (See Fig. 2.4b).

The efficiencies of four sampling methods are compared for the low-FN region identification problem: (1) GP4(xyz), (2) GP5(xyz + preFNS), (3) preFNS, and (4) ideal. GP4(xyz) and GP5(xyz + preFNS) are GP-based selective sampling procedures where the three-dimensional coordinates (x, y, z) and/or the preliminary FNS (denoted as “preFNS”) are used as descriptors. The preliminary FNS is the FN values at all N points computed by single-point DFT calculations, which should have a higher contribution to the sampling performance. The preFNS method indicates a selective sampling where the grid points are sequentially selected in the ascending order of the preliminary FNs. The average and the standard deviation over ten runs with different random seeds are discussed for GP4(xyz) and GP5(xyz + preFNS). The tuning parameters of the GP models σ _f and l are optimized for each method.

Figure 2.8 compares the performances of several sampling methods. The GP-based sampling (GP4 and GP5) can selectively sample the grid points in the low-FN region requiring 199.7 ± 68.6 and 116.0 ± 30.6 DFT computations to identify all the low-FN grid points, respectively. Both methods show higher efficiencies than that of PES-based GP3(xyz + prePES). These enhanced performances are due to the smaller region of interest defined on the basis of the FNS. Analogous to the preliminary PES, the preliminary FNS evaluated by single-point DFT calculations is a valuable descriptor, which improves the sampling performance in GP-based sampling. However, the naive sampling based on the preFNS shows a much worse performance as it requires 955 DFT computations.

Fig. 2.8

Efficiencies of the four FN-based samplings: GP4(xyz), GP5(xyz + preFNS), preFNS, and ideal. Number of grid points successfully sampled from the low-FN region (#TP) is plotted versus the number of FN computations by DFT (#TP + #FP). Green line is the result in GP5 using the 16 lowest FN points in preFNS as the initial grid points

Figure 2.9 shows the rank correlation between the actual and preliminary FNs. The open red circles denote the 15 grid points in the low-FN region. In the preFNS sampling, the points are selected from left to right in the figure. Consequently, all 955 points located in the shaded region must be sampled to select all positive points. The difference in the rank depends on whether structural optimization is performed, implying that the local structural relaxation around a proton in oxides is important.

Fig. 2.9

Rank correlation between the actual and the preliminary FNs. Red open circles and crosses show grid points in P _α and N _α , respectively. Blue and black crosses denote False Positive and True Negative points at step 955 in the preFNS sampling method, respectively

Although using the low-FN region as the region of interest improves the sampling performance, the performance still deviates from that of ideal sampling. Figure 2.10 shows the step numbers where each of the low-FN grid points (Nos. 1–15) are sampled in ten runs of GP4 and GP5. Two grid points (Nos. 6 and 8) are relatively difficult to sample, degrading the sampling performance. This is probably because these points are isolated from the other low-FN points (Fig. 2.10c). Consequently, the FNS statistical model cannot predict that these two points are likely to be in the low-FN region.

Fig. 2.10

Step numbers where each of the low-FN grid points is sampled in ten runs of (a) GP4 and (b) GP5 (red crosses). Green open diamonds in (b) are the results in GP5 using the 16 lowest FN points in preFNS (bottom 1%) as the initial grid points. (c) Two most difficult grid points to sample among the low-FN grid points (No. 6: black spheres, No. 8: white spheres)

To overcome this difficulty, information on the preliminary FNS is exploited not only as a descriptor in the FNS statistical model. Specifically, the initial grid points for the GP-based methods are not selected randomly, but in the ascending order of the preliminary FNs. The green open diamonds in Fig. 2.10b show the results by GP5 sampling using the 16 lowest FN points in the preFNS as the initial grid points. The two grid points (Nos. 6 and 8) are sampled at step 2 and step 86, respectively, resulting in 95 DFT computations to sample all low-FN points (See the green line in Fig. 2.8). Thus, fully exploiting information about the preliminary FNS can improve the sampling performance.

4.3 Practical Issues

Here two critical issues, which limit practicality, are discussed in the case of the low-PE region identification (task 1): (1) when to terminate sampling and (2) how to determine the PE threshold α.

The first issue is common in GP-based sampling methods. One practical advantage of statistical models such as the GP model is that the number of remaining points to be sampled can be estimated by estimating the FNR. Figure 2.11 shows the profiles of the estimated FNR and threshold as functions of the number of DFT computations in GP3. These plots indicate that the estimated FNR almost coincides with the ground truth line. Additionally, the estimated threshold converges to the true value as the sampling proceeds. These results suggest that the estimated FNR should be a useful termination criterion.

Fig. 2.11

Profiles of the estimated (a) FNRs and (b) PE thresholds for GP3 sampling [12]

Another practical issue is how to choose an appropriate α, which depends on the focused system. In the case of proton conduction in an oxide, the low-PE region should be defined such that a proton-conducting network exists throughout the crystal lattice within the region. According to the actual PEs, the low-PE regions are isolated when α < 0.15, but they are abruptly connected when α = 0.20. This means that a proper α value should be around 0.20 in the present study. If such an appropriate α value is initially unknown, the α value can be set in a stepwise manner. To demonstrate this approach, the performance of GP3 is investigated as α is increased from 0.05 to 0.20 in a stepwise manner (The results are shown in Fig. 2.12). In this scenario, α is increased by 0.05 when the estimated FNR becomes smaller than 10⁻⁶.

Fig. 2.12

(a) Efficiency of GP3(xyz + prePES) sampling when α is increased in a stepwise manner from 0.05 to 0.20 in 0.05 increments [12]. Number of grid points successfully sampled from the low-PE region (#TP) is plotted versus the number of DFT computations (#TP + #FP). (b), (c) Profiles of the estimated FNRs and PE thresholds versus the number of DFT computations [12]

Figure 2.12(b) indicates that the convergence of the estimated FNR is slightly slower than the ground truth FNR in the first step with α = 0.05. This is why more than 250 DFT computations are required to ensure that all points in P _0.05 are successfully sampled. On the other hand, when α = 0.10, 0.15, or 0.20, the convergences of the FNRs are almost as fast as the ground truth FNRs. It should be noted that the true positive points abruptly increase when the α value is switched, indicating that the positive points for higher α are sampled in earlier steps. Although this stepwise strategy is less efficient than directly specifying α = 0.20, it is much more efficient than the prePES and random sampling methods.

5 Conclusions

In this chapter, a machine learning-based selective sampling procedure for PES evaluation is introduced and applied to proton conduction in BaZrO₃ to demonstrate its efficacy. The region of interest governing the ionic conduction is defined in the two ways: (1) a low-PE region and (2) a low-FN region.

For the low-PE region, the performance of the selective sampling based on the GP model greatly depends on the descriptors. Employing the preliminary PES (prePES) is significantly effective, which is evaluated by single-point DFT computations in a smaller supercell. The GP3(xyz + prePES) sampling requires 394 DFT computations to sample all the low-PE grid points (353 points) in a grid with 1768 points for the asymmetric unit of BaZrO₃ crystal. This is a 78% reduction in the computational costs. However, the defined region of interest, i.e., the low-PE region, comprises 20% of the configuration space. Consequently, the reducible computational cost is limited to 80%.

The region of interest should, therefore, be redefined as it becomes smaller in the configuration space. For the low-FN region, the region of interest contains only 15 grid points, whose volume is less than 1% of the configuration space. Among the several sampling methods to identify the low-FN region, GP5(xyz + preFNS) shows the best performance. It requires only 116 DFT computations to identify all grid points in the low-FN region. Furthermore, the computational cost can be further reduced to 95 DFT computations using the 16 lowest FN grid points in the preFNS as the initial points. This means that exploiting the information on the preFNS can reduce the computational cost by 95%.

Thus, preliminary information (i.e., prePES and preFNS) significantly contributes to the sampling performance. Therefore, a machine learning-based approach hybridized with a low-cost PES and/or FNS evaluation should be a solid methodology for preferential PES evaluation in the region of interest. In addition, using the FNR, which is defined in Eq. (2.15), solves two critical issues, which are when to terminate sampling and how to determine an appropriate α value (equivalent to the PE threshold).