Abstract
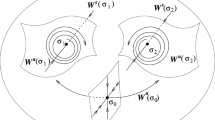
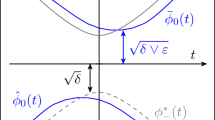
We outline a singular-perturbations approach to the graph-valued stochastic averaging results of Freidlin-Wentzell and Freidlin-Weber. We specifically consider the Freidlin-Weber problem (a Newtonian particle in a double-well potential). To show the Freidlin-Weber convergence result, we develop a perturbed test function via a boundary-layer PDE near the homoclinic orbit. Solvability of this PDE is equivalent to the glueing conditions of Freidlin-Wentzell. Details of our calculations will appear elsewhere.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
W. M. Boothby, An Introduction to Differentiable Manifolds and Riemannian Geometry. Academic Press Inc., Orlando, FL, second edition, 1986.
A. N. Borodin, “A limit theorem for the solutions of differential equations with a random right-hand side,” Teor. Verojatnost. i Primenen., vol. 22, no. 3, pp. 498–512, 1977.
A. N. Borodin and M. I. Freidlin, “Fast oscillating random perturbations of dynamical systems with conservation laws,” Ann. Inst. H. Poincaré Probab Statist., vol. 31, no. 3, pp. 485–525, 1995.
L. C. Evans, “The perturbed test function method for viscosity solutions of nonlinear PDE,” Proc. Roy Soc. Edinburgh Sect. A, vol. III, no. (3–4), pp. 359–375, 1989.
S. N. Evans and R. B. Sowers, “Pinching and twisting Markov processes,” Annals of Probability, to appear.
M. Freidlin and M. Weber, “Random perturbations of nonlinear oscillators,” Ann. Probab, vol. 26, no. 3, pp. 925–967, 1998.
M. Freidlin and M. Weber, “A remark on random perturbations of the nonlinear pendulum,” Ann. Appl. Probab, vol. 9, no. 3, pp. 611–628, 1999.
M. I. Freidlin and A. D. Wentzell, “Random perturbations of Hamiltonian systems,” Mem. Amer. Math. Soc, 109(523):viii+82, 1994.
I. I. Gihman, “Concerning a theorem of N. N. Bogolyubov,” Ukrain. Mat. >Z, vol. 4, pp. 215–219, 1952.
R. Z. Khasminskii, “Diffusion processes with a small parameter,” Izv. Akad. Nauk SSSR Sen Mat., vol. 27, pp. 1281–1300, 1963.
R. Z. Khasminskii, “A limit theorem for solutions of differential equations with a random right hand part,” Teor. Verojatnost. i Primenen, vol. 11, pp. AAA–A62, 1966.
R. Z. Khasminskii, “Stochastic processes defined by differential equations with a small parameter,” Teor. Verojatnost. i Primenen, vol. 11, pp. 240–259, 1966.
T. G. Kurtz, “A limit theorem for perturbed operator semigroups with applications to random evolutions,” J. Functional Analysis, vol. 12, pp. 55–67, 1973.
T. G. Kurtz, “An abstract averaging theorem,” J. Functional Analysis, vol. 23, no. 2, pp. 135–144, 1976.
H. J. Kushner. Approximation and Weak Convergence Methods for Random Processes with Applications to Stochastic System Theory, MIT Press, Cambridge, MA, 1984.
A. I. Ne<ishtadt, “Probability phenomena due to separatrix crossing,” Chaos, vol. 1, no. 1, pp. 42–48, 1991.
G. C. Papanicolaou and W. Kohler, “Asymptotic theory of mixing stochastic ordinary differential equations,” Comm. PureAppl. Math., vol. 27, pp. 641–668, 1974.
G. C. Papanicolaou and W. Kohler, “Asymptotic analysis of deterministic and stochastic equations with rapidly varying components,” Comm. Math. Phys., vol. 45, no. 3, pp. 217–232, 1975.
R. B. Sowers, “Stochastic averaging near a homoclinic orbit with multiplicative noise,” submitted.
R. B. Sowers, “Stochastic averaging with a flattened Hamiltonian: A Markov process on a stratified space (a whiskered sphere),” Trans. Amer. Math. Soc, vol. 354, no. 3, pp. 853–900, (electronic), 2002.
R. L. Stratonovich, Topics in the Theory of Random Noise, Vol. I: General Theory of Random Processes. Nonlinear Transformations of Signals and Noise. Gordon and Breach Science Publishers, New York, 1963. Revised English edition. Translated from the Russian by Richard A. Silverman.
J. Walsh, “A diffusion with discontinuous local time,” in Temps Locaux, Astérisque, vol. 52–53. Société Mathématique de France, Paris, 1978.
G. Wolansky, “Limit theorem for a dynamical system in the presence of resonances and homoclinic orbits,” J. Differential Equations, vol. 83, no. 2, pp. 300–335, 1990.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer Science+Business Media Dordrecht
About this paper
Cite this paper
Sowers, R.B. (2003). Stochastic Averaging Near Homoclinic Orbits Via Singular Perturbations. In: Namachchivaya, N.S., Lin, Y.K. (eds) IUTAM Symposium on Nonlinear Stochastic Dynamics. Solid Mechanics and Its Applications, vol 110. Springer, Dordrecht. https://doi.org/10.1007/978-94-010-0179-3_7
Download citation
DOI: https://doi.org/10.1007/978-94-010-0179-3_7
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-010-3985-7
Online ISBN: 978-94-010-0179-3
eBook Packages: Springer Book Archive