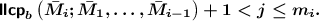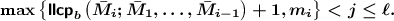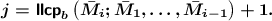Security of Full-State Keyed Sponge and Duplex: Applications to Authenticated Encryption

Abstract

We provide a security analysis for full-state keyed Sponge and full-state Duplex constructions. Our results can be used for making a large class of Sponge-based authenticated encryption schemes more efficient by concurrent absorption of associated data and message blocks. In particular, we introduce and analyze a new variant of SpongeWrap with almost free authentication of associated data. The idea of using full-state message absorption for higher efficiency was first made explicit in the Donkey Sponge MAC construction, but without any formal security proof. Recently, Gaži, Pietrzak and Tessaro (CRYPTO 2015) have provided a proof for the fixed-output-length variant of Donkey Sponge. Yasuda and Sasaki (CT-RSA 2015) have considered partially full-state Sponge-based authenticated encryption schemes for efficient incorporation of associated data. In this work, we unify, simplify, and generalize these results about the security and applicability of full-state keyed Sponge and Duplex constructions; in particular, for designing more efficient authenticated encryption schemes. Compared to the proof of Gaži et al., our analysis directly targets the original Donkey Sponge construction as an arbitrary-output-length function. Our treatment is also more general than that of Yasuda and Sasaki, while yielding a more efficient authenticated encryption mode for the case that associated data might be longer than messages.

1 Introduction

Since its introduction, the Sponge construction by Bertoni, Daemen, Peeters and Van Assche [4] has faced an immense increase in popularity. As “simple” hash function mode, it is the fundament of the SHA-3 standard Keccak [5], but also its keyed variants have become very popular modes of operation for a permutation to build a wide spectrum of symmetric-key primitives: reseedable pseudorandom number generators [7], pseudorandom functions and message authentication codes (PRFs/MACs) [9, 11], Extendable-Output Functions (“XOFs”) [24] and authenticated encryption (AE) modes [10, 11]. The keyed Sponge principle also got adopted in Spritz, a new RC4-like stream cipher [26], and in 10 out of 57 submissions to the currently running CAESAR competition on authenticated encryption [1, 3]. These use cases reinforce the fact that Sponge-based constructions will continue to play an important role, not only in the new hashing standard SHA-3, but in various next-generation cryptographic algorithms.

The classical Sponge construction consists of a sequential application of a permutation p on a state of b bits. This state is partitioned into an r-bit rate or outer part and a c-bit capacity or inner part, where $b=r+c$. In the absorption phase, message blocks of size r bits are absorbed by the outer part and the state is transformed using p, while in the squeezing phase, digests are extracted from the outer part r bits at a time. In the indifferentiability framework of Maurer, Renner and Holenstein [20], Bertoni et al. [6] proved that the Sponge construction is secure up to the $O(2^{c/2})$ birthday-type bound. The capacity part is left untouched throughout the evaluation of the Sponge construction: a violation of this paradigm would make the indifferentiability security result void.

In this work, we strive for optimality, and investigate the most efficient ways of using Sponges for message authentication and authenticated encryption in a provably secure manner. In both directions, we consider a generalization of the currently known schemes to full-state absorption, the most efficient usage of the underlying permutation, and we show that these schemes are secure. Due to the full-state absorption, we cannot anymore rely on the classical indifferentiability result of the Sponge (as was for instance done in [2, 10]), and a new security analysis is required. We will elaborate on both directions in the following.

Message Authentication. Bertoni et al. [9] introduced the keyed Sponge as a simple evaluation of the Sponge function on the key and the message, Sponge$(K\Vert M)$, and proved security beyond $O(2^{c/2})$. Chang et al. considered a slight variant of the keyed Sponge where the key is processed in the inner part of the Sponge, and observed that it can be seen as the Sponge based on an Even-Mansour blockcipher. At FSE 2015, Andreeva, Daemen, Mennink and Van Assche [2] considered a generic and improved analysis of both the outer- and inner-keyed Sponge. So far, however, these constructions have only been considered with the classical r-bit absorption.

The idea of using full-state message absorption for achieving higher efficiency was first made explicit in the Donkey Sponge MAC construction [11],¹ but without any formal security proof. The recently introduced Donkey-inspired MAC function Chaskey [22] did get a formal security analysis, but its proof is thwarted towards Chaskey and does not apply to the Donkey Sponge.

A thorough analysis of the full-state message absorption keyed Sponge had to wait for Gaži, Pietrzak and Tessaro [17], who prove nearly tight security up to $O(\ell q(q+N)/2^b + q(q+\ell +N)/2^c )$, where the adversary makes q queries of maximal length $\ell$, and makes N primitive calls. However, their analysis only applies to the fixed-output-length variant, and the proof does not directly seem to extend to the original arbitrary-output-length keyed Sponge. In this work, we provide a direct proof for this more general case.

In more detail, we present a generalized scheme, dubbed Full-state Keyed Sponge (FKS), whose security implies the security of Donkey Sponge in the ideal permutation setting, and prove that it is secure up to approximately $\frac{2(q\ell )^2}{2^b} + \frac{2q^2\ell }{2^c} + \frac{\mu N}{2^{k}}$, where k is the size of the key, and $\mu$ is a parameter called the “multiplicity”. We note that usage of the outer-keyed Sponge makes no longer any difference from the usage of the inner-keyed variant in the presence of full-state absorption (see also Sect. 8). Our proof of FKS follows the modular approach of Andreeva et al., but due to the full-state absorption, we cannot rely on the indifferentiability result of [6], and present a new and more detailed analysis.

Authenticated Encryption. Encryption via the Sponge can be done (and is typically done) via the Duplex construction [10], a stateful construction consisting of an initialization interface and a duplexing interface. The initialization interface can be called to initialize an all-zero state; the duplexing interface absorbs a message of size $<r$ bits and squeezes $\le r$ bits of the outer part. The security of the Duplex traces back to the indifferentiability of the classical Sponge, yielding a $O(2^{c/2})$ security bound.

Bertoni et al. [10] showed that the Duplex, in turn, allows for authenticated encryption in the form of SpongeWrap. This mode is, de facto, the basis of the majority of Sponge-based submissions to the CAESAR competition. Jovanovic et al. [18] re-investigated Sponge-based authenticated encryption schemes, starring NORX, and derived beyond birthday-bound security. These results are, however, all for the usual r-bit absorption. Yasuda and Sasaki [27] have considered several full-state and partially full-state Sponge-based authenticated encryption schemes for efficient incorporation of associated data, directly lifting Jovanovic et al.’s security proofs. The concurrent absorption mode proposed by Yasuda and Sasaki (Fig. 3 in [27]) fails to utilize the full-state absorption when the associated data becomes longer than the message, forcing the mode switch from a full-state mode to the classical r-bit absorbing Sponge mode; hence, we refer to this as a partially full-state AE mode. Full-state data absorption was also proposed by Reyhanitabar, Vaudenay and Vizár [25] in their compression function based AE mode p-OMD.

We generically aim to optimize the efficiency in Sponge-based authenticated encryption. To this end, we first formalize the Full-state Keyed Duplex (FKD) construction. It differs from the original Duplex in the fact that (i) the key is explicitly used to initialize the state (In this, the $\mathrm {FKD}$ is similar to the Monkey Duplex [11]) and (ii) the absorption is performed on the entire state. Note that the possibility to absorb in the entire state enforces the explicit usage of the key. Next, we prove that $\mathrm {FKD}$ is provably secure, i.e., indistinguishable from a random oracle with the same interfaces. As before, we cannot rely on the classical indifferentiability proof due to the full-state absorption; however, we show how to adapt the FKS proof to a special case directly related to the security of $\mathrm {FKD}$.

We exemplify the better absorption capabilities of $\mathrm {FKD}$ by the introduction of a Full-state SpongeWrap (FSW). The FSW construction is more general than that of Yasuda and Sasaki, who only considered specific AE constructions, and interestingly, our approach also yields a more efficient (truly full-state) authenticated encryption mode irrespective of the relative lengths of messages and their associated data.

Organization of the Paper. Notations and preliminary concepts are presented in Sect. 2. We present the Full-state Keyed Sponge and Full-state Keyed Duplex in Sect. 3. The security model is discussed in Sect. 4. In Sect. 5 we prove security of FKS and in Sect. 6 of $\mathrm {FKD}$. The introduction of the Full-state SpongeWrap, and the application of $\mathrm {FKD}$ to this construction is given in Sect. 7. Section 8 provides a brief discussion on related-key security and our security models.

2 Notations and Conventions

The set of all strings of length b is denoted as $\{0,1\}^{b}$ for any $b \ge 1$ and the set of all finite strings of arbitrary length is denoted as $\{0,1\}^{*}$. We will denote the empty string of length 0 as $\varepsilon$. For any positive b, we let $\{0,1\}^{<b} = \bigcup _{i=0}^{b-1} \{0,1\}^{i}$ denote set of all strings of length less than b including $\varepsilon$. For two strings $X,Y \in \{0,1\}^{*}$ we let $X \,\Vert \,Y$ denote the string obtained by concatenation of X and Y. For a string $X \in \{0,1\}^{x}$ we let $\mathsf {left}_{\ell } \left( {X} \right)$ denote the $\ell$ leftmost bits of X and $\mathsf {right}_{r} \left( {X} \right)$ the r rightmost bits of X such that $X=\mathsf {left}_{\chi } \left( {X} \right) \,\Vert \,\mathsf {right}_{x-\chi } \left( {X} \right)$ for any $0 \le \chi \le x$. For integral b, r, c such that $b=r+c$, and for $t\in \{0,1\}^{b}$, we let $\mathsf {outer}\left( {t}\right) = \mathsf {left}_{r} \left( {t} \right)$ and $\mathsf {inner}\left( {t}\right) = \mathsf {right}_{c} \left( {t} \right)$.

For a non-empty finite set $\mathcal {S}$ let denote sampling an element a from $\mathcal {S}$ uniformly at random. We let |Z| denote the cardinality if Z is a set and the length if Z is a string. We let $\mathrm {Perm}\left( {b}\right)$ denote the set of all permutations of b-bit strings and $\mathrm {Func}\left( {b}\right)$ the set of all functions over b-bit strings.

Given two strings X, Y, let

$$\mathsf {llcp}_b\left( {X},{Y} \right) = \max _{i \ge 0}\left\{ i \;:\; \mathsf {left}_{ib} \left( {X} \right) = \mathsf {left}_{ib} \left( {Y} \right) \right\} $$

denote the length of the longest common prefix between X and Y in b-bit blocks. For a string X and a non-empty set of strings $\left\{ Y_1,\ldots , Y_n \right\}$ let

$$\mathsf {llcp}_b\left( {X};{Y_1,\ldots , Y_n} \right) = \max \left\{ \mathsf {llcp}_b\left( {X},{Y_1} \right) , \ldots , \mathsf {llcp}_b\left( {X},{Y_n} \right) \right\} .$$

For any two pairs of integers $(i,j),(i',j')$, we say that $(i',j')<(i,j)$ if either $i'<i$ or if $i'=i$ and $j'<j$. We say that $(i',j') \le (i,j)$ if $(i',j')<(i,j)$ or if $(i',j')=(i,j)$. In other words, we use lexicographical ordering to determine ordering of integer-tuples.

3 Sponge Constructions

3.1 Full-State Keyed Sponge

We consider the Full-state Keyed Sponge (FKS) construction that is using a public permutation $p: \{0,1\}^{b} \rightarrow \{0,1\}^{b}$. It is furthermore parameterized with r, k, which are required to satisfy $r<b$ and $k\le b-r=: c$. The parametrization is sometimes left implicit if it is clear from the context. FKS gets as input a key $K\in \{0,1\}^{k}$, a message $M\in \{0,1\}^{*}$, and a natural number z, and it outputs a string $Z\in \{0,1\}^{z}$:

$$\begin{aligned} \mathrm {FKS}^p(K,M,z)=\mathrm {FKS}_K^p(M,z)=Z\,. \end{aligned}$$

It operates on a state $t\in \{0,1\}^{b}$, which is initialized using the key K. The message M is first padded to a length a multiple of b bits, using $\mathrm {pad}_b(M)=M\Vert 10^{b-1-|M|\mathrm{mod}b}$, which is then viewed as m b-bit message blocks $M^1\Vert ...\Vert M^m$.² These message blocks are processed one-by-one, interleaved with evaluations of p. After the absorption of M, the outer r bits of the state are output and the state is processed via p until a sufficient amount of output bits are obtained. FKS is depicted in Fig. 1, and Algorithm 1 provides a formal specification of FKS.

Fig. 1.

The FKS construction.

3.2 Full-State Keyed Duplex

We present the Full-state Keyed Duplex (FKD) construction, a generalization of the Duplex of Bertoni et al. [8, 10]. $\mathrm {FKD}$ is also parameterized by a public permutation $p: \{0,1\}^{b} \rightarrow \{0,1\}^{b}$ and values r, k, which are required to satisfy $r<b$ and $k\le b-r=: c$. Again, the parametrization is sometimes left implicit if clear from the context. An instance of $\mathrm {FKD}$, denoted by D, consists of two interfaces: $D.\mathrm {initialize}$ and $D.\mathrm {duplexing}$. $D.\mathrm {initialize}$ gets as input a key $K\in \{0,1\}^{k}$ and outputs nothing, while $D.\mathrm {duplexing}$ gets as input a message $M\in \{0,1\}^{<b}$ and a natural number $z\le r$, and it outputs a string $Z\in \{0,1\}^{z}$. $\mathrm {FKD}$ is depicted in Fig. 2, and the formal specification is given in Algorithm 2. $\mathrm {FKD}$ is a generalization of FKS where $D.\mathrm {initialize}$ is used to initialize the state, and messages are absorbed into the state and/or digests are squeezed out of the state using $D.\mathrm {duplexing}$ calls.

Fig. 2.

The $\mathrm {FKD}$ construction.

4 Security Models and Tools

Multiplicity. Let $\{(x_i,y_i)\}_{i=1}^{\sigma }$ be a set of $\sigma$ evaluations of a permutation p. Following Andreeva et al. [2], we define the total maximal multiplicity as $\mu =\mu _{\mathrm {fwd}}+\mu _{\mathrm {bwd}}$, where

$$\begin{aligned} \mu _{\mathrm {fwd}}&= \max _a |\{i\in \{1,\ldots ,\sigma \} \;:\; \mathsf {outer}\left( {x_i}\right) =a\}|,\\ \mu _{\mathrm {bwd}}&= \max _a |\{i\in \{1,\ldots ,\sigma \} \;:\; \mathsf {outer}\left( {y_i}\right) =a\}|. \end{aligned}$$

The multiplicity is a quantity that characterises the data that are available to the adversary during the attack. We have $2 \le \mu \le 2\sigma$ per definition, however the upper bound $2\sigma$ is never reached in practical applications of sponge-based constructions. Being a sum of forward and backward multiplicities, the total multiplicity can be seen as a measure of adversary’s ability to control the outer part of the permutation inputs and outputs respectively. In case of sponge-based designs, the backward multiplicity can be expected to be approximately $\sigma 2^{-r}$ while the forward multiplicity varies with concrete applications [2].

4.1 Adversaries and Patarin’s Coefficient-H Technique

We consider an information-theoretic adversary $\varvec{A}$ that has access to one or more oracles X; this is denoted by $\varvec{A}^{X}$ and the notation $\varvec{A}^{X}\Rightarrow 1$ means that $\varvec{A}$, after interaction with X, returns 1. It is a classical fact (for a simple proof see [14]) that in the information-theoretic setting, adversaries can be assumed to be deterministic without loss of generality.

We use Patarin’s Coefficient-H technique [23]; more precisely, a revisited formulation of it by Chen and Steinberger [14]. Consider a deterministic information-theoretic adversary $\varvec{A}$ whose goal is to distinguish two oracles X and Y:

$$\begin{aligned} \varDelta _{\varvec{A}}\left( {X};{Y}\right) = \left| \Pr \left[ {\varvec{A}^X \Rightarrow 1} \right] - \Pr \left[ {\varvec{A}^Y \Rightarrow 1} \right] \right| . \end{aligned}$$

Here, X and Y are randomized algorithms; the randomization depends on the specific scenario and for now is left implicit. The interaction with any of the two systems X or Y is summarized in a transcript $\tau$. Denote by $D_X$ the probability distribution of transcripts when interacting with X, and similarly, $D_Y$ the distribution of transcripts when interacting with Y. A transcript $\tau$ is called attainable if $\Pr \left[ {D_Y=\tau } \right] >0$, meaning that it can occur during interaction with Y. Denote by $\mathcal {T}$ the set of all attainable transcripts. The Coefficient-H technique states the following, for the proof of which we refer to [14].

Lemma 1

(Coefficient-H Technique) [14, 23]. Consider a fixed deterministic adversary $\varvec{A}$. Let $\mathcal {T}=\mathcal {T}_\mathrm {good}\cup \mathcal {T}_\mathrm {bad}$ be a partition into good transcripts $\mathcal {T}_\mathrm {good}$ and bad transcripts $\mathcal {T}_\mathrm {bad}$. If there exists an $\varepsilon$ such that for all $\tau \in \mathcal {T}_\mathrm {good}$,

$$\begin{aligned} \frac{\Pr \left[ {D_X=\tau } \right] }{\Pr \left[ {D_Y=\tau } \right] } \ge 1-\varepsilon , \end{aligned}$$

then, $\varDelta _{\varvec{A}}\left( {X};{Y}\right) \le \varepsilon + \Pr \left[ {D_Y\in \mathcal {T}_\mathrm {bad}} \right]$.

The two partitions of $\mathcal {T}$ are labeled as $\mathcal {T}_\mathrm {good}$ and $\mathcal {T}_\mathrm {bad}$ to aid the intuitiveness of the proof. The transcripts in $\mathcal {T}_\mathrm {good}$ are “good” in the sense that they give us a high value of ${\Pr \left[ {D_X=\tau } \right] }/{\Pr \left[ {D_Y=\tau } \right] }$ and thus small $\varepsilon$ while the “bad” transcripts from $\mathcal {T}_\mathrm {bad}$ fail to do so.

4.2 Security Models for FKS and FKD

Let $RO ^\infty :\{0,1\}^{*}\rightarrow \{0,1\}^{\infty }$ be a random oracle which takes inputs of arbitrary but finite length and returns random infinite strings, where each output bit is selected uniformly and independently for every input M.

Let F be either FKS or $\mathrm {FKD}$, which is based on a permutation $p: \{0,1\}^{b} \rightarrow \{0,1\}^{b}$ and a key $K\in \{0,1\}^{k}$. We will define the security of F in two settings: the public permutation setting, where the adversary has query access to the permutation (security comes from the secrecy of K), and the secret permutation setting (with no explicit key K), where the adversary has no access to the underlying permutation and the security comes from the secrecy of the permutation.

We use the notations $F_K^p$ and $F_0^\pi$ to refer to the public permutation and secret permutation based schemes, respectively; where, $\pi$ is a secret random permutation.

In both settings, we consider an adversary that aims to distinguish the real F from an ideal (reference) primitive—an oracle $RO$ with the same interface. For $F=\mathrm {FKS}$ the corresponding ideal primitive $RO$ is defined by $RO _{\mathrm {FKS}}(M,z) =\mathsf {left}_{z} \left( { RO ^{\infty }(M)} \right)$. For $F=\mathrm {FKD}$ the corresponding reference primitive $RO ^{}_{\mathrm {FKD}}$ is a stateful oracle with two interfaces: (1) $RO ^{r}_{\mathrm {FKD}}.\mathrm {initialize}()$ that initializes the state of the oracle, $\mathrm {St}$, to the empty string, and (2) $RO ^{r}_{\mathrm {FKD}}.\mathrm {duplexing}(M, z)$ that, on input $M \in \left\{ 0, 1\right\} ^{<b}$ and a natural number z, first updates the state as $\mathrm {St}\leftarrow \mathrm {St} || pad_b(M)$ and then outputs $\mathsf {left}_{z} \left( { RO ^{\infty }(\mathrm {St})} \right)$.

We define the distinguishing advantage of any adversary $\varvec{A}$ against F based on a public permutation by

The distinguishing advantage of $\varvec{A}$ against F based on a secret permutation is defined by

The resource parameterized advantage functions are defined as usual. Let be the maximum advantage over all adversaries that make q queries to the left oracle, all of maximal length $\ell$ permutation calls if $F=\mathrm {FKS}$ or that make at most q ${\mathrm {initialize}}()$ calls to the left oracle and issue at most $\ell$ duplexing queries after each initialization if $F=\mathrm {FKD}$ with total maximal multiplicity $\mu$ in both cases, and that make N direct queries to the public permutation. To simplify the analysis, we assume that each of the q oracle queries in fact consists of exactly $\ell$ permutation (or that the adversary indeed makes $\ell$ duplexing calls after each initialization). This is without loss of generality, it can simply be achieved by giving extra squeezing outputs to the adversary. Similarly, we define , noticing that in this case $N=0$, thus it is omitted from the resources.

4.3 Security Model for Even-Mansour

Our proof relies on a reduction to the security of a low-entropy single-key Even-Mansour construction [15, 16]. In more detail, let $p:\{0,1\}^{b}\rightarrow \{0,1\}^{b}$ be a permutation and $K\in \{0,1\}^{k}$ be a key. The Even-Mansour blockcipher is defined as

$$\begin{aligned} E_K^p(M) = p(M \oplus (0^{b-k}\,\Vert \,K)) \oplus (0^{b-k}\,\Vert \,K). \end{aligned}$$

We define the distinguishing advantage of any adversary $\varvec{A}$ against E based on a public permutation p as

Let be the maximum advantage over all adversaries that make q queries to the left oracle, with total maximal multiplicity $\mu$, and that make N direct queries to the public permutation.

5 Security Analysis of FKS

We prove the following result for $\mathrm {FKS}$:

Theorem 1

Let $b,r,c,k>0$ be such that $b=r+c$ and $k\le c$. Let $\mathrm {FKS}$ be the scheme of Sect. 3.1. Then,

The proof follows to a certain extent the modular approach of [2], and in particular also uses the observation that $\mathrm {FKS}^p_K$ can alternatively be considered as $\mathrm {FKS}_0^{E_K^p}$, a clever observation used before by Chang et al. [13]. Note that this observation only works for $k\le c$: it consists of xoring two dummy keys $K\oplus K$ in-between every two adjacent permutation calls, and if $k>c$ this would entail a difference in the squeezing blocks of $\mathrm {FKS}$. This trick splits the security of $\mathrm {FKS}^p_K$ into the security of the Even-Mansour blockcipher and the security of $\mathrm {FKS}$ with secret primitive. Looking back at [2], the security of Inner-keyed Sponge/Outer-keyed Sponge [2] with secret permutations was simply reverted to the classical indifferentiability result of [6]. Because this is a rather loose approach, and additionally because the indifferentiability bound cannot be used for $\mathrm {FKS}$ due to its full-state absorption, we consider the security of $\mathrm {FKS}$ with secret primitive in more detail and derive an improved bound.

Proof

(Proof of Theorem 1 ). Consider any adversary $\varvec{A}$ with resources $(q,\ell , \mu , N)$. Note that $\mathrm {FKS}^p_K = \mathrm {FKS}^{E_K^p}_0$. Therefore, by a modular argument,

for some adversary $\varvec{B}$ with resources $(q,\ell ,\mu )$ and adversary $\varvec{C}$ with resources $(q \ell ,\mu ,N)$. Note that $\varvec{B}$ also has access to p, but queries to this oracle are meaningless as its left oracle ($\mathrm {FKS}^\pi _0$ or $RO _{\mathrm {FKS}}$) is independent of p.

In [2], it is proven that for any $\varvec{C}$. In Lemma 2, we prove that for any adversary $\varvec{B}$.    $\square$

Lemma 2

Let $b,r,c>0$ be such that $b=r+c$. Let $\mathrm {FKS}$ be the scheme of Sect. 3.1. Then,

Proof

Given that the padding is publicly known and injective, we can generalize the setting, and assume that the ${i}^{\mathrm {th}}$ query $M_i$ has length divisible by b and that $M_i^{m_i} \ne 0^b$, i.e. we assume that all the queries are already padded. More detailed, for $1\le i\le q$, we let $m_i = |M_i|/b$ and $M_i = M_i^1 \,\Vert \,M_i^2 \,\Vert \,\ldots \,\Vert \,M_i^{m_i}$ s.t. $|M_i^j|=b$ for $1 \le j \le m_i$. We further assume, that the adversary always asks for output of length divisible by r and that every query induces exactly $\ell$ primitive calls. This is without loss of generality: we can simply output “free bits” to the adversary. We will denote the b-bit state of $\mathrm {FKS}$ just before the ${j}^{\mathrm {th}}$ application of $\pi$ is made when processing the ${i}^{\mathrm {th}}$ query as $s_i^j$ for $1\le j \le \ell$. Similarly, we will denote the b-bit state of $\mathrm {FKS}$ just after the ${j}^{\mathrm {th}}$ application of $\pi$ in ${i}^{\mathrm {th}}$ query as $t_i^j$ for $1\le j \le \ell$. We will call the former in-states and the latter out-states. Note that every in-state $s_i^j$ is determined by the out-state $t_i^{j-1}$ and the block of query $M_i^j$ as $s_i^j=t_i^{j-1} \oplus M_i^j$ in the absorbing phase or just by $t_i^j$ in the squeezing phase as depicted in Fig. 3.

Fig. 3.

Processing the ${i}^{\mathrm {th}}$ query.

To aid the simplicity of further analysis we additionally define initial dummy out-states $t_i^0=0^b$ and extended queries $\bar{M}_i = M_i \,\Vert \,0^{(\ell - m_i)b}$ for $1 \le i \le q$. Now we can express every in-state, be it absorbing or squeezing, as $s_i^j = t_i^{j-1} \oplus \bar{M}_i^j$. We will group the out-states of ${i}^{\mathrm {th}}$ query as $T_i=\{t_i^0, t_i^1, \ldots , t_i^{\ell }\}$. Because each query induces exactly $\ell$ calls to $\pi$, we know that a query $M_i$ will be answered by a string $Z_i=Z_i^1 \,\Vert \,\ldots \,\Vert \,Z_i^{z_i}$ with $z_i = \ell - m_i +1$ and $|Z_i^j| = r$ for $1 \le j \le z_i$. In particular, we have that $Z_i^j = \mathsf {outer}\left( {t_i^{m_i+j-1}}\right)$.

The RP-RF Switch. We start by replacing the random permutation $\pi \xleftarrow {\$}\mathrm {Perm}\left( {b}\right)$ by a random function $f \xleftarrow {\$}\mathrm {Func}\left( {b}\right)$ in the experiment. This will contribute the term $(q \ell )^2/2^b$ to the final bound by a standard hybrid argument so we have .

Patarin’s Coefficient-H Technique. We will use the coefficient-H technique to show that . The two systems an adversary is trying to distinguish are $\mathrm {FKS}_0^f$ and $RO _{\mathrm {FKS}}$. We will refer to the former as X and to the latter as Y. In either of the worlds, the adversary makes q queries $M_1,\ldots ,M_q$ and learns the responses $Z_1,\ldots ,Z_q$. The transition from queries $M_i$ to $\bar{M}_i$ is injective, and additionally the length $m_i$ of $M_i$ is implicit from $\bar{M}_i$. Therefore, we can summarize the interaction of the adversary with its oracle (X or Y) with a transcript $(\bar{M}_1,\ldots ,\bar{M}_q,Z_1,\ldots ,Z_q)$.

To facilitate the analysis, we will disclose additional information $T_1, \ldots , T_q$ to the adversary at the end of the experiment. In the real world, these are the out-states $T_i=\{t_i^0, t_i^1, \ldots , t_i^{\ell }\}$ as discussed in the beginning of the proof. In the ideal world, these are dummy variables that satisfy the following intrinsic properties of the Sponge construction:

• 1. $t_i^0 = 0^b$ for $1 \le i \le q$,

• 2. if $\mathsf {llcp}_b\left( {\bar{M}_i},{\bar{M}_{i'}} \right) = n$ for $1 \le i,i' \le q$ then $t_i^j=t_{i'}^j$ for $1 \le j \le n$,

• 3. $\mathsf {outer}\left( {t_i^{j+m_i-1}}\right) = Z_i^j$ for $1 \le i \le q$ and $1 \le j \le z_i$,

but are perfectly random otherwise. Note that in both worlds, $Z_1,\ldots ,Z_q$ are fully determined by $T_1,\ldots ,T_q$, so we can drop them from the transcript. Thus a transcript of adversary’s interaction with $\mathrm {FKS}$ will be $\tau =(\bar{M}_1,\ldots ,\bar{M}_q, T_1, \ldots , T_q)$.

With respect to Lemma 1, we will show that there exists a definition of bad transcripts $\mathcal {T}_\mathrm {bad}$, such that $\Pr \left[ {D_X=\tau } \right] / \Pr \left[ {D_Y=\tau } \right] = 1$ for any $\tau \in \mathcal {T}_\mathrm {good}=\mathcal {T}\backslash \mathcal {T}_\mathrm {bad}$, and thus .

Definition of a Bad Transcript. Stated formally, a transcript $\tau$ is labeled as bad if

$$\begin{aligned} \begin{aligned}&\exists (1,1)\le (i,j),(i',j') \le (q,\ell ) \; \text {such that:}\\&\qquad \qquad j\ne j' \vee \mathsf {llcp}_b\left( {\bar{M}_i},{\bar{M}_{i'}} \right) < j =j' \le \ell ,\\&\qquad \qquad t_i^{j-1} \oplus \bar{M}_i^j = t_{i'}^{j'-1} \oplus \bar{M}_{i'}^{j'}. \end{aligned} \end{aligned}$$

(1)

This formalization of a bad transcript comes with an intuitive, informal interpretation; as long as all relevant inputs $s_i^j = t_i^{j-1} \oplus \bar{M}_i^j$ to the random function f induced by the Sponge function are distinct the output of the Sponge will be distributed uniformly. We do not require uniqueness of all in-states because the adversary can trivially force their repetition by issuing queries with common prefixes, as we have argued earlier. However these collisions are not a problem because uniqueness of the queries implies that $\mathsf {llcp}_b\left( {\bar{M}_i},{\bar{M}_{i'}} \right) <\max \{m_i,m_{i'}\}$ for any two queries $\bar{M}_i,\bar{M}_{i'}$. Even if the adversary truncates an old query and thus forces an old absorbing in-state s to be squeezed for output, it is still not a problem because the adversary has not seen the image f(s) before. Note that albeit in-states do not exist in the ideal world, they can be defined by the same relation as in the real world, i.e. $s_i^j = t_i^{j-1} \oplus \bar{M}_i^j$.

Bounding the Ratio of Probabilities of Good Transcripts. In the ideal world, the out-states $\{t_i^0\}_{i=0}^{q}$ are always assigned a value trivially. Beside that, we will also trivially assign a single randomly sampled value to multiple state variables, that are affected by the common prefixes of the queries. The remaining out-states are sampled uniformly at random. It follows that there are exactly $\eta (\tau ) = \sum _{i=1}^q \ell - \mathsf {llcp}_b\left( {M_i};{M_1,\ldots ,M_{i-1}} \right)$ b-bit values in any transcript $\tau$, that are sampled independently and uniformly. We thus have $\Pr \left[ {D_Y = \tau } \right] = 2^{-\eta (\tau ) b }$ for any $\tau$.

Let $\varOmega _X$ be the set of all possible real-world oracles. We have that $|\varOmega _X| = 2^{b2^b}$. Let $\mathsf {comp}_{X}\left( {\tau } \right) \subseteq \varOmega _X$ be the set of all oracles compatible with the transcript $\tau$, i.e. the set of the real-world oracles that are capable of producing $\tau$ in an experiment. We will compute the probability of seeing $\tau$ in the real world as $\Pr \left[ {D_X = \tau } \right] = |\mathsf {comp}_{X}\left( {\tau } \right) |/|\varOmega _X|$. Note that a real-world oracle is completely determined by the underlying function f.

If $\tau \in \mathcal {T}_\mathrm {good}$, then every in-state $s_i^j = t_i^{j-1} \oplus \bar{M}_i^j$ that does not trivially collide with some other in-state $s_{i'}^{j'}$ due to common prefix of $\bar{M}_i^j$ and $\bar{M}_{i'}^{j'}$ must be distinct. The number of domain points of f that have an image assigned by $\tau$ is easily seen to be $\eta (\tau ) = \sum _{i=1}^q \ell - \mathsf {llcp}_b\left( {M_i};{M_1,\ldots ,M_{i-1}} \right)$. A compatible function f can therefore have arbitrary image values on the remaining $2^b - \eta (\tau )$ domain points. Thus we compute $|\mathsf {comp}_{X}\left( {\tau } \right) | = 2^{b \left( 2^b - \eta (\tau )\right) }$ and

$$\Pr \left[ {D_X = \tau } \right] = \frac{|\mathsf {comp}_{X}\left( {\tau } \right) |}{|\varOmega _X|} = \frac{2^{b \left( 2^b - \eta (\tau )\right) }}{2^{b2^b}} = 2^{-\eta (\tau ) b} = \Pr \left[ {D_Y = \tau } \right] .$$

Bounding the Probability of a Bad Transcript in the Ideal World. We can bound the probability of $\tau$ being bad (cf. (1)) by first bounding the collision probability of an arbitrary but fixed pair of in-states $s_i^j, s_{i'}^{j'}$ (i.e. the event $s_{i}^{j}=s_{i'}^{j'}$ occurs) and then summing this probability for all possible values of $(i,j),(i',j')$ with $(i',j') \ne (i,j)$. Because this probability varies significantly, we will split all in-states into three classes and bound probabilities of individual collisions between these classes.

We will associate to each in-state $s_i^j$ a label $\mathsf {stamp}_{i}^{j}$. We set $\mathsf {stamp}_{i}^{j} = \mathtt {free}$ if $1 < j = \mathsf {llcp}_b\left( {\bar{M}_i};{\bar{M}_1, \ldots , \bar{M}_{i-1}} \right) + 1 \le m_i$ such that $m_{i^*} < j$ for some $i^* < i$. We will set $\mathsf {stamp}_{i}^{1} = \mathtt {initial}$ for $1 \le i \le q$ and $\mathsf {stamp}_{i}^{j} = \mathtt {fixed}$ in the remaining cases. Informally, we have $\mathsf {stamp}_{i}^{j} = \mathtt {free}$ whenever the adversary forces $\mathsf {outer}\left( {t_i^{j-1}}\right) =Z_{i^*}^{j-m_{i^*}-1}$ by reusing exactly first $j-1$ blocks of a previous query $\bar{M}_{i^*}$ in $\bar{M}_i$ and sets $\bar{M}_i^j \ne \bar{M}_{i^*}^j = 0^b$. By doing this, it freely but non-trivially chooses $\mathsf {outer}\left( {s_i^j}\right) =\mathsf {outer}\left( {s_{i*}^j \oplus \bar{M}_{i*}^j \oplus \bar{M}_i^j}\right)$. Note that if the adversary puts $\bar{M}_i^j=\bar{M}_{i^*}^j$, this is not counted as a free state (the states will in fact be the same). We have $\mathsf {stamp}_{i}^{j} = \mathtt {initial}$ for the initial in-state of every query.

As the condition (1) is symmetrical w.r.t. (i, j) and $(i',j')$, and as it cannot be satisfied if $(i,j)=(i',j')$, it can be rephrased as

$$\begin{aligned} \begin{aligned}&\exists (1,1)\le (i',j')<(i,j)\le (q,\ell ) \; \text {such that:}\\&\qquad \qquad \mathsf {llcp}_b\left( {\bar{M}_i};{\bar{M}_1, \ldots , \bar{M}_{i-1}} \right) < j \le \ell ,\, s_i^j = s_{i'}^{j'}. \end{aligned} \end{aligned}$$

(2)

Doing so is without loss of generality, as each $s_i^j$ with $j \le \mathsf {llcp}_b\left( {\bar{M}_i};{\bar{M}_1, \ldots , \bar{M}_{i-1}} \right)$ is identical with some previous state that has already been checked for collisions with $s_{i'}^{j'}$ for every possible $(i',j')$. In the further analysis, we will be working with (2) rather than with (1).

We will now bound the probability of collision of an arbitrary pair of in-states $(s_i^j, s_{i'}^{j'}) = (t_i^{j-1} \oplus \bar{M}_i^j, t_{i'}^{j'-1} \oplus \bar{M}_{i'}^{j'})$ with $\mathsf {stamp}_{i}^{j}=\mathtt {fixed}$. We fix arbitrary i and investigate the following three cases for j. In each case we treat every $(i',j')<(i,j)$.

• Case 1:

  

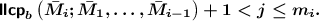
  In this case, $t_i^{j-1}$ is undetermined when the adversary issues the query $\bar{M}_i$. This implies that it will be independent from all $t_{i'}^{j'-1}$ for any $(i',j')<(i,j)$. The probability of the collision $t_i^{j-1} \oplus \bar{M}_i^j = t_{i'}^{j'-1} \oplus \bar{M}_{i'}^{j'}$ is easily seen to be $2^{-b}$.

• Case 2:

  

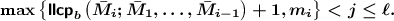
  Here $t_i^{j-1}=$ $Z_i^{j-m_i} \,\Vert \,\mathsf {inner}\left( {t_i^{j-1}}\right)$ and $\bar{M}_i^j = 0^b$. Although the adversary learns the value of $Z_i^{j-m_i}$ during the experiment, this is independent of all $s_{i'}^{j'}$ with $(i',j')<(i,j)$ (because $j +1 > \mathsf {llcp}_b\left( {\bar{M}_i};{\bar{M}_1, \ldots , \bar{M}_{i-1}} \right)$). Even if $\mathsf {stamp}_{i'}^{j'} \in \{\mathtt {free}, \mathtt {initial}\}$ and $\mathsf {outer}\left( {s_{i'}^{j'}}\right) = \alpha$ for some value $\alpha$ chosen by the adversary, the collision $Z_i^{j-m_i} \,\Vert \,\mathsf {inner}\left( {t_i^{j-1}}\right) = \alpha \,\Vert \,\mathsf {inner}\left( {s_{i'}^{j'}}\right)$ happens with probability $2^{-b}$.

• Case 3:

  

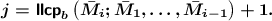
  If $j = \mathsf {llcp}_b\left( {\bar{M}_i},{\bar{M}_{i'}} \right) + 1$, the in-state $s_{i'}^{j'=j}$, call it a twin-state of $s_i^j$, cannot collide with $s_i^j$, as by the second trivial property $t_i^{j-1} = t_{i'}^{j-1}$ and by $j - 1= \mathsf {llcp}_b\left( {\bar{M}_i},{\bar{M}_{i'}} \right)$ we have $\bar{M}_i^j \ne \bar{M}_{i'}^j$. Note that if there was an $i^*<i$ with $m_{i^*} \le \mathsf {llcp}_b\left( {\bar{M}_i},{\bar{M}_{i^*}} \right) = j-1$ and $j \le m_i$ then we would have $\mathsf {stamp}_{i}^{j}=\mathtt {free}$. However if we had the same situation but with $j> m_i$ then $\bar{M}_i$ and $\bar{M}_{i^*}$ would be identical. So $\mathsf {outer}\left( {t_i^{j-1}}\right)$ has not been set and revealed to the adversary by any previous output value and for any non-twin, in-state $s_{i'}^{j'}$, the probability of collision is at most $2^{-b}$ by a similar argument as in Case 1.

There are no more than $q\ell$ choices for (i, j) and no more than $q\ell$ possible $(i',j')$ for every (i, j) so the overall probability that the condition (2) will be evaluated due to a pair of in-states with $\mathsf {stamp}_{i}^{j} = \mathtt {fixed}$ is at most $(q\ell )^2/2^b$.

If $\mathsf {stamp}_{i}^{j}=\mathtt {free}$ then $\mathsf {outer}\left( {s_i^{j}}\right)$ is under adversary’s control. However the value of $\mathsf {inner}\left( {t_i^{j-1}}\right)$ is always generated at the end of the experiment. By a case analysis similar to the previous one we can verify that the probability of a collision due to a pair of in-states with $\mathsf {stamp}_{i}^{j}=\mathtt {free}$ is not bigger than $2^{-c}$. It is apparent from the definition of a $\mathtt {free}$ in-state that there is at most one such in-state for each query. Having $q\ell$ in-states in total, there are at most $q(q\ell )$ pairs with $\mathsf {stamp}_{i}^{j}=\mathtt {free}$ and the probability of $\tau \in \mathcal {T}_\mathrm {bad}$ due to such a pair is at most $q^2\ell / 2^c$.

If $\mathsf {stamp}_{i}^{j}=\mathtt {initial}$ then $s_i^j$ cannot non-trivially collide with any other $\mathtt {initial}$ in-state. A collision with a non-$\mathtt {initial}$ state $s_{i'}^{j'}$ implies that $t_{i'}^{j'-1} = \bar{M}_{i'}^{j'} \oplus \bar{M}_{i}^1$. If $j'>m_{i'}$ or if there is some $M_{i^*}$ with $m_{i^*} < j' <= \mathsf {llcp}_b\left( {M_{i'}},{\bar{M}_{i^*}} \right) + 1$, then $\mathsf {outer}\left( {t_{i'}^{j'-1}}\right)$ is known to the adversary. However $\mathsf {inner}\left( {t_{i'}^{j'-1}}\right)$ is always generated at the end of the experiment. By a case analysis similar to the one we carried out earlier, it can be verified that the collision $s_i^1 = s_{i'}^{j'}$ occurs with probability no bigger than $2^{-c}$. There is exactly one $\mathtt {initial}$ in-state in each query, so similarly as with the $\mathtt {free}$ in-states, the overall probability of a transcript being bad due to a pair with an $\mathtt {initial}$ in-state is at most $q^2\ell /2^c$. By summing all the partial collision probabilities we obtain that $\Pr \left[ {D_Y \in \mathcal {T}_{bad}} \right] \le (q\ell )^2/2^b + 2q^2\ell /2^c$.    $\square$

6 Security Analysis of $\mathrm {FKD}$

For $\mathrm {FKD}$, we prove the following result:

Theorem 2

Let $b,r,c,k>0$ be such that $b=r+c$ and $k\le c$. Let $\mathrm {FKD}$ be the scheme of Sect. 3.2. Then,

The proof uses Lemma 3 to transform a $\mathrm {FKD}$ adversary into an $\mathrm {FKS}$ adversary, similarly to [8, 10]. While this would be sufficient to prove the security of the Duplex construction, the bound induced solely by Lemma 3 suffers from a quantitative degradation: we have that , resulting in a bound $\frac{2q^2\ell ^4}{2^b} + \frac{2q^2\ell ^3}{2^c} + \frac{\mu N}{2^{k}}$ according to Theorem 1. In reality, there will be a quantitative gap between the security of $\mathrm {FKD}$ construction and that of $\mathrm {FKS}$ present, but it will be smaller. This is because an $\mathrm {FKS}$ adversary constructed from an $\mathrm {FKD}$ adversary issues queries of a specific structure which is far from general. In below proof for $\mathrm {FKD}$, we use this property. In more detail, we derive a specific class of “constrained adversaries” and generalize the proof of Lemma 2 to these adversaries.

Proof

(Proof of Theorem 2 ). Consider any adversary $\varvec{A}$ with resources $(q,\ell , \mu , N)$. We have that $\mathrm {FKD}^p_K = \mathrm {FKD}^{E_K^p}_0$. Therefore, by a modular argument,

for some adversary $\varvec{B}$ with resources $(q,\ell ,\mu )$ and adversary $\varvec{C}$ with resources $(q, \ell ,\mu ,N)$. Note that $\varvec{B}$ also has access to p, but these queries are meaningless as its left oracle ($\mathrm {FKD}^\pi _0$ or $RO ^{}_{\mathrm {FKD}}$) is independent of p.

In [2], it is proven that . In Corollory 3 we show that any $\mathrm {FKD}$ adversary $\varvec{B}$ can be turned into a special “constrained” adversary $\varvec{B'}$ against $\mathrm {FKS}$ with resources $(q\ell ,\ell ,\mu )$:

In Lemma 4, we prove that for any such adversary $\varvec{B'}$.    $\square$

For the remainder of the proof, we introduce the mapping $Q_{\mathrm {FKS}}: (\{0,1\}^{<b})^+ \rightarrow \{0,1\}^{*}$. For any $b>0$ and for all $X_1, \ldots , X_n \in \{0,1\}^{<b}$ we let

$$Q_{\mathrm {FKS}}(X_1,\ldots ,X_n) = \mathrm {pad}_b(X_1) \,\Vert \,\ldots \,\Vert \,\mathrm {pad}_b(X_{n-1})\,\Vert \,X_n.$$

Lemma 3

(Duplexing lemma) [10]. Let $b,r,c,k>0$ be such that $b=r+c$ and $k\le c$. Let $D=\mathrm {FKD}^p$ as defined in Sect. 3.2. Then for the ${i}^{\mathrm {th}}$ duplexing query $(M_i,z_i)$ made after the last $D.{\mathrm {initialize}}(K)$ we have

$$Z_i = D.\mathrm {duplexing}\left( {M_i,z_i} \right) = \mathrm {FKS}^p(K,Q_{\mathrm {FKS}}(M_1,\ldots ,M_i), z_i).$$

Moreover, the mapping $Q_{\mathrm {FKS}}: (\{0,1\}^{<b})^+ \rightarrow \{0,1\}^{*}$ is injective.

The proof of the lemma uses similar arguments as that of Bertoni et al. [10]. A complete proof can be found in the full version of this paper [21].

The result of Lemma 3 can be used to reduce any $\mathrm {FKD}$ adversary to a constrained FKS adversary. More specifically, any adversary $\varvec{A}$ against $\mathrm {FKD}$ that makes q initialize calls and duplexes $\ell$ blocks after each initialization can be reduced to a constrained FKS adversary $\varvec{A'}=R_{\mathrm {FKS}}(\varvec{A})$. To answer the ${j}^{\mathrm {th}}$ duplexing query $(M_i^j,z_i^j)$ made by $\varvec{A}$ after the ${i}^{\mathrm {th}}$ initialize call, $\varvec{A'}$ queries its own oracle with $(Q_{\mathrm {FKS}}(M_i^1, \ldots , M_i^j),z_i^j)$. $\varvec{A'}$ copies the output of$\varvec{A}$ at the end of the experiment.

Corollary 3

Let $\varvec{A}$ be an adversary against $\mathrm {FKD}$ that makes q initialize calls and duplexes $\ell$ blocks after each initialization and $R_{\mathrm {FKS}}(\varvec{A})$ the constrained FKS adversary as defined above. It follows from Lemma 3, that .

We denote by $\mathcal {A}'_{q,\ell }$ the set of constrained adversaries against $\mathrm {FKS}$, that were induced by some $\mathrm {FKD}$ adversary that makes q initialize calls and duplexes $\ell$ blocks after each initialization:

Lemma 4

Let $b,r,c>0$ be such that $b=r+c$. Let $\mathrm {FKS}$ be the scheme of Sect. 3.1. Then,

for any constrained adversary $\varvec{A'}\in \mathcal {A}'_{q,\ell }$.

The proof follows to large extent the framework of the proof of Lemma 2. We show in particular, that although the constrained adversary makes $q\ell$ queries, each query induces only a single $\mathtt {free}$ or $\mathtt {initial}$ state; the remaining internal in-states, if any, are always identical to the in-states of a previous query and they thus do not contribute to the probability of observing a bad transcript. This gives us at most $q\ell$ $\mathtt {free}$ or $\mathtt {initial}$ in-states and the bound follows. A complete proof can be found in the full version of this paper [21].

7 Full-State SpongeWrap and its Security

Our results from Sect. 6 can be used to prove security of modified, more efficient versions of existing Sponge-based AE schemes. As an interesting instance, we introduce Full-state SpongeWrap, a variant of the authenticated encryption mode SpongeWrap [8, 10], offering improved efficiency with respect to processing of associated data (AD).

7.1 Authenticated Encryption for Sequences of Messages

We will focus on authenticated encryption schemes that act on sequences of AD-message pairs. Following Bertoni et al.³ [8, 10]we will think of an authenticated encryption scheme as an object W surfacing three APIs:

• $W.{\mathrm {initialize}}(K,N)$: calling this function will initialize W with a secret key from the set of keys $\mathcal {K}$ and a nonce from the set of nonces $\mathcal {N}$.

• $W.{\mathrm {wrap}}(A,M)$: this function inputs an AD-message pair (A, M) and outputs a ciphertext-tag pair (C, T), where $|C|=|M|$ and T is a $\tau$-bit tag authenticating (A, M) and all the queries processed by W so far (i.e. since the last initialization call).

• $W.{\mathrm {unwrap}}(A, C, T)$: this function accepts a triple of AD, ciphertext and tag, and outputs a message M if C is an encryption of M and T is a valid tag for (A, M), and all the previous queries processed by W so far; otherwise it outputs an error symbol $\bot$.

Here, the AD, messages and ciphertexts are finite strings and we have $|C|=|M|$. $\tau$ is a positive integer and we call it the expansion of W. We require that W is initialized before making the first wrapping or unwrapping call. For a given key K, we will use $W_K$ to refer to the corresponding keyed instance, omitting K from the list of inputs; that is, $W.{\mathrm {initialize}}(K,N)=W_K.{\mathrm {initialize}}(N)$.

Security of Authenticated Encryption. We follow Bertoni et al. [8, 10] for defining the security of AE. We split the twofold security goal of AE into two separate requirements: privacy and authenticity.

Let W be a scheme for authenticated encryption, as described above, that internally makes calls to a public random permutation p. We formalize the privacy of W by an experiment in which an adversary $\varvec{A}$ is given access to $p, p^{-1}$ and an oracle O that provides two interfaces: $O.{\mathrm {initialize}}(N)$ and $O.{\mathrm {wrap}}(A, M)$. We have $O \in \{W_K, RO _W\}$, where $W_K$ is an instance of the real scheme with the key K, and $RO _W$ is an ideal primitive that acts as follows: it keeps a list of strings $St \in {(\left\{ 0, 1\right\} ^*)}^*$ as its internal state. On calling $RO _W.{\mathrm {initialize}}(N)$ the list St is set to the empty list and then the nonce N is added to the list (denote this operation by $St \leftarrow St || N$); now each call $RO _W.{\mathrm {wrap}}(A, M)$ will first update the list as $St \leftarrow St || (A, M)$ and then will output $\mathsf {left}_{|M|+\tau } \left( { RO ^\infty (\left\langle St \right\rangle )} \right)$, where $\left\langle St \right\rangle$ denotes an injective encoding of the list St into a string in $\left\{ 0, 1\right\} ^*$. (Note that the list St preserves the boundaries between N and all the queried AD-message pairs).

The adversary must distinguish between the two worlds: the real world where it is interacting with $W_K$ and the ideal world where it is interacting with $RO _W$. The advantage of the adversary in doing so is defined as

It is assumed that the adversary meets the nonce-requirement, i.e. that every $\mathrm {initialize}()$ it makes is done with a fresh nonce.

For the definition of authenticity property, consider an experiment where an adversary $\varvec{A}$ is given access to the oracle $W_K$ and is allowed to ask the queries $W_K.{\mathrm {initialize}}(N)$ and $W_K.{\mathrm {wrap}}(A,M)$. It is assumed that $\varvec{A}$ respects the nonce-requirement in the wrapping queries. $\varvec{A}$ is again allowed to query p. The adversary can also attempt forgeries at any time during the experiment; we say that the adversary forges if it outputs a sequence $(N,(A_1,C_1,T_1), \ldots , (A_n,C_n,T_n))$ such that after calling $W.{\mathrm {initialize}}(K,N)$ and then $W.{\mathrm {unwrap}}(A_i,C_i,T_i)$ for $1 \le i \le n-1$, $W.{\mathrm {unwrap}}(A_n,C_n,T_n)$ does not return $\bot$. The sequence $(N,(A_1,C_1,T_1),$ $\ldots , (A_n,C_n,T_n))$ must be such that the adversary has not obtained $(C_n,T_n)$ from a wrapping query that followed an initialization with N and a series of wrapping queries $(A_1,M_1), \ldots , (A_n,M_n)$ with some $M_1,\ldots ,M_n$. The adversary does not have to use a unique nonce in the forgery. Note that it can be assumed w.l.o.g. that every forgery attempt is either a fresh nonce followed by a single AD-ciphertext-tag triplet or of the form $(N,(A_1,C_1,T_1), \ldots , (A_n,C_n,T_n))$ with $(N,(A_1,C_1,T_1),$ $\ldots , (A_{n-1},C_{n-1},T_{n-1}))$ being learned by the adversary from a sequence of previous wrapping queries. We define the advantage of $\varvec{A}$ as

We let be the maximum advantage over all adversaries that make q initialize queries to the left oracle, and after each initialization do wrapping queries that induce at most $\ell$ permutation calls (including the initialization) and with total maximal multiplicity $\mu$, and that make N direct queries to the public permutation, and that make at most $q_v$ forgery attempts. We similarly let .

7.2 Full-State SpongeWrap

The Full-State SpongeWrap (FSW) is a permutation mode for authenticated encryption of AD-message sequences as described in Sect. 7.1. It is parametrized by a b-bit permutation p, the maximal message block size r, the key size k, the nonce size n, and the tag size $\tau > 0$. We require that $k\le b-r=:c$ and $n<r$. The set of keys is $\mathcal {K} = \{0,1\}^{k}$ and the set of nonces is $\mathcal {N} = \{0,1\}^{n}$. The $\mathrm {FSW}$ construction uses an instance of $\mathrm {FKD}$ internally to process the inputs block by block. To ensure domain separation of different stages of processing a query, we use three frame bits placed at the same position in each ${\mathrm {duplexing}}$ call to $\mathrm {FKD}$ as explained in Table 1.

The main motivation of the FSW is concurrent absorption of message and AD to achieve maximal efficiency in terms of minimizing the number of permutation calls made. Since we can only process r bits of a message input at a time, we can use the remainder of the state for the frame bits and a block of AD. This implies the lengths of message and AD blocks processed with each permutation call; $r+1$ bits for padded message block, 3 frame bits and (having in mind that the input to $\mathrm {FKD}$ is always padded) this leaves us at most $(b-1)-(r+1)-3=c-5$ bits for a block of AD. To minimize the number of permutation calls made in all possible situations, we further specify special treatment for the wrap/unwrap queries with more AD blocks than message blocks. An informal outline of a wrap/unwrap query is given in Algorithm 3. This outline nicely illustrates how the frame bits are used for domain separation.

Table 1. Labeling and usage of the frame bits within $\mathrm {FSW}$.

We next give a complete algorithmic description of the $\mathrm {FSW}$. To keep it compact, we introduce the following notations. For any $L \in \{0,1\}^{\le r}$, $R \in \{0,1\}^{\le c-5}$ and $F \in \{0,1\}^{3}$, we let

$$\begin{aligned} Q(L,F,R) = \mathrm {pad}_{r+1}(L) \,\Vert \,F \,\Vert \,R. \end{aligned}$$

(3)

Note that $r+4 \le |Q(L,F,R)| \le b-1$ for any L, F, R. We let $(L,R) = \mathsf {lsplit}({X,n})$ for any $X\in \{0,1\}^{*}$ such that $L = \mathsf {left}_{\min (|X|,n)} \left( {X} \right)$ and $\mathsf {right}_{|X|-|L|} \left( {X} \right)$. We let $X_1\,\Vert \,X_2 \,\Vert \,\ldots \,\Vert \,X_m \xleftarrow {r} X$ denote partitioning a string X in such a way that $X=X_1\,\Vert \,X_2 \,\Vert \,\ldots \,\Vert \,X_m$, $|X_i|=r$ for $1\le i < m$ and $0<|X_m|\le r$. Note that $m=\lceil |X| / r \rceil$. We will use the abbreviation $D.\mathrm {dpx}( {M,z} )$ for the interface $D.\mathrm {duplexing}\left( {M,z} \right)$ of an $\mathrm {FKD}$ D. The interfaces of $\mathrm {FSW}[p,r,k,n,\tau ]$ are defined in Algorithm 4. A schematic depiction of how the wrap interface processes various types of inputs can be found in the full version of this paper [21].

7.3 Security of FSW

The security of $\mathrm {FSW}$ is relatively easy to analyze, thanks to the result from Sect. 6.

Lemma 5

Let $W = \mathrm {FSW}[p,r,k,n,\tau ]$ be an instance of $\mathrm {FSW}$ as described in Sect. 7.2. Denote any query to $W.{\mathrm {initialize}}$ and a list of subsequent queries to $W.{\mathrm {wrap}}$ by $(N,(A_1,M_1), \ldots ,(A_n,M_n))$. Then, $\mathrm {FSW}$ injectively maps this sequence to a sequence of corresponding $\mathrm {FKD}$ duplexing queries $(Q_1,\ldots ,Q_d)$.

Fig. 4.

The tree of all possible frame bits sequences for a single AD-message pair (top-left). The composition of an $\mathrm {FKD}$ query $Q_i$ (bottom-right).

We prove the injectivity of the mapping by showing how it can be inverted. Thanks to the way the frame bits are used (Fig. 4), it is possible to determine which duplexing calls belong to a single wrap query. More than that, we can also determine the boundaries of message and AD using the frame bits and then we can reconstruct them thanks to the use of the padding. The full proof can be found in the full version of this paper [21].

Theorem 3

Let $b,r,c,k,n,\tau >0$ be such that $b=r+c$, $k\le c$ and $n<r$. Let $\mathrm {FSW}$ be the scheme of Sect. 7.2. Then,

We start by defining the $RO\mathrm {FSW}$—an idealized $\mathrm {FSW}$ that internally uses the $RO ^{r}_{\mathrm {FKD}}$ instead of $\mathrm {FKD}$ (and thus does not use p at all). By Thm. 2 we have that

We consequently analyse the security of $RO\mathrm {FSW}$, which is a relatively straightforward task because it internally uses a $RO ^{r}_{\mathrm {FKD}}$. We obtain and . A complete proof can be found in the full version of this paper [21].

8 Discussion

Related-Key Security. Our treatment of the security of the full-state constructions is in the traditional model where the adversary has no control over selection of the secret keys or relations among different keys. If one considers the stronger model of related-key attack security then care must be taken in utilizing these schemes. Indeed, if an adversary has access to two instances $F_1=\mathrm {FKS}^p_{K_1}$ and $F_2=\mathrm {FKS}^p_{K_2}$, and it knows the relation $\varDelta = K_1 \oplus K_2$, then it can make the outputs of $F_1$ and $F_2$ collide trivially by asking two b-bit queries $F_1(M)$ and $F_2(M\oplus \varDelta )$.

Although it is outside the scope of this paper to treat related-key security thoroughly, we informally propose some easy solutions to prevent trivial related-key attacks like the one mentioned before. We start by noticing that the inner-keyed Sponge construction [2] is not susceptible to this problem, as the secret key and the adversarial data blocks never overlap; hence, a simple way of thwarting such trivial related-key attacks is to always prepend the input data with a block of b zeroes. Thus the adversary can no longer xor an arbitrary value directly to the key prior to the application of the permutation. If the original adversarial resources were $(q,\ell ,\mu ,N$), we can without any further argumentation use the bound with the resources $(q,\ell +1,\mu ,N)$ for this new construction.

Another possibility would be to slightly modify the constructions and partition the input data into an r-bit starting block and b-bit blocks afterward. The initial block would be xored to the outer r bits of the initial state. Our security analysis would carry over to this construction with minimal modifications.

Generalized Security Model. The security analyses of $\mathrm {FKS}$ and $\mathrm {FKD}$ cover those of the original Sponge and Duplex constructions as special cases. Beyond that, for the security analysis of $\mathrm {FKD}$ itself, we have generalized the security model of the original Duplex construction from Bertoni et al. [9, 10]. While in the analysis of Bertoni et al. the analysis of the multiple-initializations scenario is left rather implicit, we include it explicitly in our model.

This generalized setting seems more closely matching the use of the Duplex construction in several AE schemes which do not require sessions and new session keys, where one would initialize the Duplex (or $\mathrm {FKD}$) construction for every query. This is well demonstrated by the example of $\mathrm {FSW}$. More precisely, the way we design and analyze the security of $\mathrm {FSW}$ allows for a very versatile use. $\mathrm {FSW}$ can be used to secure AD-message pairs in a single session [12], i.e. using a single initialize call during the lifetime of the key or alternatively every AD-message pair can be preceded by an initialize call with a unique nonce. In fact, $\mathrm {FSW}$ can be used for anything between these two extremes; for example, a setting where every AD-message pair is processed with a unique nonce, but can get fragmented into smaller sub-pairs. The security analysis of $\mathrm {FSW}$ covers each of these use cases.

On the Keying of the Sponge. As we have claimed in the introduction, the difference in the security of the outer-keyed and inner-keyed Sponges vanishes in presence of the full state absorption. On one hand, using a key of more than c bits does not increase the security level, as the extra bits cannot be used by the low-entropy Even-Mansour construction. On the other hand, absorbing several b-bit blocks of the key only results into a derived key of effective length of c bits. We remark that both the outer- and inner-keyed Sponges can be seen as special cases of FKS, by using more restrictive padding rules that only place the message blocks in the outer part of the state.

Boosting Sponge-based AE. Out of 57 CAESAR candidates, 10 are using a Sponge-based design. The method we used to enhance SpongeWrap can be straightforwardly adjusted to boost the performance of five of these 10 schemes: Keyak, Ketje, STRIBOB, CBEAM and ICEPOLE [3]. This is because all the said designs are using frame bits for domain separation. The other designs cannot benefit from our modifications, either due to a domain separation method relying on intangibility of the inner part of the state (NORX), or due to producing tag from the inner part of the state (Ascon, Primates), or because they are already using the inner part of the state (Artemia) or because the designs do not follow the general structure of the Sponge Wrap (Pi Cipher) [3]. We note that if Ketje was to benefit from the technique we have introduced, it would be necessary to increase the number of rounds of the underlying permutation.