Abstract
Wang et al. (CCS 2017) recently proposed a protocol for malicious secure two-party computation that represents the state-of-the-art with regard to concrete efficiency in both the single-execution and amortized settings, with or without preprocessing. We show here several optimizations of their protocol that result in a significant improvement in the overall communication and running time. Specifically:
-
We show how to make the “authenticated garbling” at the heart of their protocol compatible with the half-gate optimization of Zahur et al. (Eurocrypt 2015). We also show how to avoid sending an information-theoretic MAC for each garbled row. These two optimizations give up to a 2.6\(\times \) improvement in communication, and make the communication of the online phase essentially equivalent to that of state-of-the-art semi-honest secure computation.
-
We show various optimizations to their protocol for generating AND triples that, overall, result in a 1.5\(\times \) improvement in the communication and a 2\(\times \) improvement in the computation for that step.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
In recent years, we have witnessed amazing progress in secure two-party computation, in both the semi-honest and malicious settings. In the semi-honest case, there has been an orders-of-magnitude improvement in protocols based on Yao’s garbled circuit [39] since the initial implementation by Malkhi et al. [26]. This has resulted from several important techniques, including oblivious-transfer extension [16], pipelining [13], hardware acceleration [6], free-XOR [19] and other improved garbling techniques [17, 32], etc. Similarly, the concrete efficiency of secure two-party computation in the malicious case has also improved tremendously in both the single-execution [1, 8, 10, 14, 18, 20,21,22,23, 28, 30, 34,35,36,37, 41] and amortized [15, 24, 25, 31, 33] settings. Whereas initial implementations in the malicious case could evaluate up to 1,000 gates at the rate of 1 gate/second [32], the current state-of-the-art protocol by Wang et al. [37] (the WRK protocol) can compute tens of millions of gates at a rate up to 700,000\(\times \) faster. With this steady stream of improvements, it has become more and more difficult to squeeze out additional performance gains; as an illustrative example, Zahur et al. [40] introduced a highly non-trivial optimization (“half-gates”) just to reduce communication by 33%.
We show several improvements to the WRK protocol that, overall, improve its performance by 2–3\(\times \). Recall their protocol can be divided into three phases: a function-independent phase (Ind.) in which the parties know an upper bound on the number of gates in the circuit to be evaluated and the lengths of their inputs; a function-dependent phase (Dep.) in which the parties know the circuit, but not their inputs; and an online phase in which the parties evaluate the circuit on their respective inputs. Our results can be summarized as follows:
-
We show how to make the “authenticated garbling” at the heart of the online phase of the WRK protocol compatible with the half-gate optimization of Zahur et al. We also show that it is possible to avoid sending an information-theoretic MAC for each garbled row. These two optimizations result in up to a 2.6\(\times \) improvement in communication and, somewhat surprisingly, result in a protocol for malicious secure two-party computation in which the communication complexity of the online phase is essentially equivalent to that of state-of-the-art semi-honest secure computation.
-
The function-dependent phase of the WRK protocol involves the computation of (shared) “AND triples” between the parties. We show various optimizations of that step that result in a 1.5\(\times \) improvement in the communication and a 2\(\times \) improvement in the computation. Our optimizations also simplify the protocol significantly.
We can combine these improvements in various ways, and suggest in particular two instantiations of protocols with malicious security: one that minimizes the total communication across all phases, and one that trades off increased communication in the function-independent phase for reduced communication in the function-dependent phase. These protocols improve upon the state-of-the-art by a significant margin, as summarized in Table 1. For example, compared to the protocol of Nielsen et al. [28] we achieve the same communication across the function-dependent and online phases, but improve the total communication by more than 6\(\times \); compared to the prior work with the best total communication [12], we achieve a 1.5\(\times \) improvement overall and, at the same time, push almost all communication to the function-independent preprocessing phase. (Our protocol also appears to be significantly better than that of Hazay et al. [12] in terms of computation. See Sect. 6 for a more detailed discussion.)
The multi-party case. It is natural to wonder whether we can extend our improved technique for authenticated garbling to the multi-party case, i.e., to improve upon [38]. Unfortunately, we have not yet been able to do so. In Sect. 7, we discuss some of the difficulties that arise.
1.1 Outline
In Sect. 2 we provide some background about the WRK protocol. We provide the high-level intuition behind our improvements in Sect. 3. In Sect. 4, we describe in detail our optimizations of the online phase of the WRK protocol, and in Sect. 5 we discuss our optimizations of the preprocessing phase. In Sect. 6, we compare our resulting protocols to prior work.
2 Background
We begin by describing some general background, followed by an in-depth review of the authenticated-garbling technique introduced in [37]. In the section that follows, we give a high-level overview of our optimizations and improvements.
We use \(\kappa \) and \(\rho \) to denote the computational and statistical security parameters, respectively. We sometimes use “\(:=\)” to denote assignment.
Information-theoretic MACs. As in prior work, we authenticate bits using a particular information-theoretic MAC. Let  be a value known to \(\mathsf {P}_\mathsf {B}\) that is chosen at the outset of the protocol. We say a bit b known to \(\mathsf {P}_\mathsf {A}\) is authenticated to \(\mathsf {P}_\mathsf {B}\) if \(\mathsf {P}_\mathsf {B}\) holds a key \(\mathsf{K}[b]\) and \(\mathsf {P}_\mathsf {A}\) holds the corresponding tag
be a value known to \(\mathsf {P}_\mathsf {B}\) that is chosen at the outset of the protocol. We say a bit b known to \(\mathsf {P}_\mathsf {A}\) is authenticated to \(\mathsf {P}_\mathsf {B}\) if \(\mathsf {P}_\mathsf {B}\) holds a key \(\mathsf{K}[b]\) and \(\mathsf {P}_\mathsf {A}\) holds the corresponding tag  . We abstractly denote such a bit by
. We abstractly denote such a bit by  ; i.e., for some fixed
; i.e., for some fixed  , when we say the parties hold
, when we say the parties hold  we mean that \(\mathsf {P}_\mathsf {A}\) holds \((b, \mathsf{M}[b])\) and \(\mathsf {P}_\mathsf {B}\) holds \(\mathsf{K}[b]\) such that
we mean that \(\mathsf {P}_\mathsf {A}\) holds \((b, \mathsf{M}[b])\) and \(\mathsf {P}_\mathsf {B}\) holds \(\mathsf{K}[b]\) such that  . We analogously let \([b]_\mathsf{B}\) denote a bit b known to \(\mathsf {P}_\mathsf {B}\) and authenticated to \(\mathsf {P}_\mathsf {A}\).
. We analogously let \([b]_\mathsf{B}\) denote a bit b known to \(\mathsf {P}_\mathsf {B}\) and authenticated to \(\mathsf {P}_\mathsf {A}\).
A pair of authenticated bits  , each known to a different party, form an authenticated share of
, each known to a different party, form an authenticated share of  . We denote this by
. We denote this by  , where the value in the left slot is known to \(\mathsf {P}_\mathsf {A}\), and the value in the right slot is known to \(\mathsf {P}_\mathsf {B}\). Both authenticated bits and authenticated shares are XOR-homomorphic.
, where the value in the left slot is known to \(\mathsf {P}_\mathsf {A}\), and the value in the right slot is known to \(\mathsf {P}_\mathsf {B}\). Both authenticated bits and authenticated shares are XOR-homomorphic.
Authenticated bits can be computed efficiently based on oblivious transfer [28, 29]. We abstract away the particular protocol used to generate authenticated bits, and design our protocols in the  -hybrid model (cf. Fig. 1) in which there is an ideal functionality that provides them.
-hybrid model (cf. Fig. 1) in which there is an ideal functionality that provides them.
Opening authenticated values. An authenticated bit  known to \(\mathsf {P}_\mathsf {A}\) can be opened by having \(\mathsf {P}_\mathsf {A}\) send b and \( \mathsf{M}[b]\) to \(\mathsf {P}_\mathsf {B}\), who then verifies that
known to \(\mathsf {P}_\mathsf {A}\) can be opened by having \(\mathsf {P}_\mathsf {A}\) send b and \( \mathsf{M}[b]\) to \(\mathsf {P}_\mathsf {B}\), who then verifies that  . As observed in prior work [9], it is possible to open n authenticated bits with less than n times the communication. Specifically, \(\mathsf {P}_\mathsf {A}\) can open
. As observed in prior work [9], it is possible to open n authenticated bits with less than n times the communication. Specifically, \(\mathsf {P}_\mathsf {A}\) can open  by sending \(b_1, \ldots , b_n\) along with \(h:=H( \mathsf{M}[b_1], \ldots , \mathsf{M}[b_n])\), where H is a hash function modeled as a random oracle. \(\mathsf {P}_\mathsf {A}\) then simply checks whether
by sending \(b_1, \ldots , b_n\) along with \(h:=H( \mathsf{M}[b_1], \ldots , \mathsf{M}[b_n])\), where H is a hash function modeled as a random oracle. \(\mathsf {P}_\mathsf {A}\) then simply checks whether  .
.
We let  denote the process of opening one or more authenticated bits in this way, and overload this notation so that
denote the process of opening one or more authenticated bits in this way, and overload this notation so that  denotes the process of having each party open its portion of an authenticated share.
denotes the process of having each party open its portion of an authenticated share.
Circuit-dependent preprocessing. We consider boolean circuits with gates represented as a tuple \((\alpha , \beta , \gamma , T)\), where \(\alpha \) and \(\beta \) are (the indices of) the input wires of the gate, \(\gamma \) is the output wire of the gate, and  is the type of the gate. We use \(\mathcal {W}\) to denote the output wires of all AND gates, \(\mathcal {I} _1,\mathcal {I} _2\) to denote the input wires for each party, and \(\mathcal {O} \) to denote the output wires.
is the type of the gate. We use \(\mathcal {W}\) to denote the output wires of all AND gates, \(\mathcal {I} _1,\mathcal {I} _2\) to denote the input wires for each party, and \(\mathcal {O} \) to denote the output wires.
Wang et al. [37] introduced an ideal functionality called  (cf. Fig. 2) that is used by the parties in a circuit-dependent, but input-independent, preprocessing phase. This functionality sets up information for the parties as follows:
(cf. Fig. 2) that is used by the parties in a circuit-dependent, but input-independent, preprocessing phase. This functionality sets up information for the parties as follows:
-
1.
For each wire w that is either an input wire of the circuit or an output wire of an AND gate, generate a random authenticated share
 . We refer to the value
. We refer to the value  as the mask on wire w.
as the mask on wire w. -
2.
For the output wire \(\gamma \) of each XOR gate
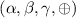 , generate a random authenticated share
, generate a random authenticated share 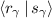 whose value
whose value 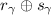 is the XOR of the masks on the input wires \(\alpha , \beta \).
is the XOR of the masks on the input wires \(\alpha , \beta \). -
3.
For each AND gate \((\alpha , \beta , \gamma , \wedge )\), generate a random authenticated share
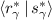 such that
such that 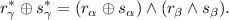
We refer to a triple of authenticated shares  for which
for which  as an authenticated AND triple. These are just (authenticated) Beaver triples [4] over the field \({\mathbb {F}}_2\).
as an authenticated AND triple. These are just (authenticated) Beaver triples [4] over the field \({\mathbb {F}}_2\).
Authenticated garbling. We now describe the idea behind the authenticated garbling technique from the WRK protocol. We assume the reader is familiar with basic concepts of garbled circuits, e.g., point-and-permute [5], free-XOR [19], etc.
Following the preprocessing phase described above, every wire w is associated with a secret mask \(\lambda _w\), unknown to either party. If the actual value on that wire (when the circuit is evaluated on the parties’ inputs) is \(z_w\), then the masked value on that wire is defined to be \(\hat{z}_w = z_w \oplus \lambda _w\). We focus on garbling a single AND gate \((\alpha , \beta , \gamma , \wedge )\). Assume \(\mathsf {P}_\mathsf {A}\) is the circuit garbler and \(\mathsf {P}_\mathsf {B}\) is the circuit evaluator. Say the garbled wire labels are \((\mathsf{L}_{\alpha , 0}, \mathsf{L}_{\alpha , 1})\) and \((\mathsf{L}_{\beta ,0},\mathsf{L}_{\beta , 1})\) for wires \(\alpha \) and \(\beta \), respectively. Since we apply the free-XOR optimization, \(\mathsf {P}_\mathsf {A}\) also holds \(\varDelta \) such that  for any wire w. The protocol inductively ensures that the evaluator \(\mathsf {P}_\mathsf {B}\) knows the wire labels \(\mathsf{L}_{\alpha , \hat{ z}_\alpha }, \mathsf{L}_{\alpha , \hat{ z}_\beta }\) and masked values \(\hat{ z}_\alpha , \hat{ z}_\beta \) for both input wires. Note that the correct masked value for the output wire is then
for any wire w. The protocol inductively ensures that the evaluator \(\mathsf {P}_\mathsf {B}\) knows the wire labels \(\mathsf{L}_{\alpha , \hat{ z}_\alpha }, \mathsf{L}_{\alpha , \hat{ z}_\beta }\) and masked values \(\hat{ z}_\alpha , \hat{ z}_\beta \) for both input wires. Note that the correct masked value for the output wire is then

and we need to ensure that \(\mathsf {P}_\mathsf {B}\) learns this value.
To achieve this, \(\mathsf {P}_\mathsf {A}\) generates a garbled gate consisting of 4 rows (one for each  )
)

with bit \(\hat{ z}_{u,v}\) defined as

Here, \([\mathsf{L}_{\gamma ,\hat{ z}_{u,v}}]\) is \(\mathsf {P}_\mathsf {A}\)’s share of the garbled label; \(r_{u,v}\) is \(\mathsf {P}_\mathsf {A}\)’s share of the bit \(\hat{ z}_{u,v}\); and \(\mathsf {P}_\mathsf {B}\) holds the corresponding share \(s_{u,v}\) such that  . The value \( \mathsf{M}[r_{u,v}]\) is the MAC authenticating the underlying bit to \(\mathsf {P}_\mathsf {B}\). Also note that the definition of \(\hat{ z}_{u,v}\) indicates that when \(u=\hat{ z}_\alpha \) and \(v=\hat{ z}_\beta \) then \(\hat{ z}_{u, v} = \hat{ z}_\gamma \).
. The value \( \mathsf{M}[r_{u,v}]\) is the MAC authenticating the underlying bit to \(\mathsf {P}_\mathsf {B}\). Also note that the definition of \(\hat{ z}_{u,v}\) indicates that when \(u=\hat{ z}_\alpha \) and \(v=\hat{ z}_\beta \) then \(\hat{ z}_{u, v} = \hat{ z}_\gamma \).
Suppose the evaluator \(\mathsf {P}_\mathsf {B}\) holds \((u, \mathsf{L}_{\alpha , u})\) and \((v, \mathsf{L}_{\beta , v})\), where \(u = \hat{ z}_\alpha \) and \(v = \hat{ z}_\beta \). Then \(\mathsf {P}_\mathsf {B}\) can evaluate this AND gate by decrypting \(G_{u, v}\) to obtain \(r_{u,v}\) and \(\mathsf {P}_\mathsf {A}\)’s share of \(\mathsf{L}_{\gamma ,\hat{ z}_{u,v}}\). After verifying the MAC on \(r_{u,v}\), party \(\mathsf {P}_\mathsf {B}\) can combine these values with its own shares to reconstruct the masked output value \(\hat{ z}_{u,v}\) (that is, \(\hat{ z}_\gamma \)) and its corresponding label \(\mathsf{L}_{\gamma ,\hat{ z}_{u,v}}\) (that is, \(\mathsf{L}_{\gamma , \hat{ z}_\gamma }\)).
Assuming that the authenticated bits and shares of the labels can be computed securely, the above protocol is secure against malicious adversaries. In particular, even if \(\mathsf {P}_\mathsf {A}\) cheats and causes \(\mathsf {P}_\mathsf {B}\) to abort during evaluation, any such abort depends only on the masked values on the wires. Since the masks are random and unknown to either party, this means that any abort is input-independent. The MACs checked by \(\mathsf {P}_\mathsf {B}\) ensure correctness, namely that evaluation has resulted in the correct (masked) output-wire value.
From authenticated shares to shared labels. Another important optimization in the WRK protocol is to compute shares of labels efficiently using authenticated shares. Assume the parties hold an authenticated share  of some mask
of some mask  . It is then easy to compute a share of \(\lambda \varDelta _{\mathsf A} \), since
. It is then easy to compute a share of \(\lambda \varDelta _{\mathsf A} \), since

Since \(\mathsf {P}_\mathsf {A}\) has r, \(\varDelta _{\mathsf A} \), and \(\mathsf{K}[s]\) while \(\mathsf {P}_\mathsf {B}\) has \( \mathsf{M}[s]\), the two parties can locally compute shares of \(\lambda \varDelta _{\mathsf A} \) (namely, \([\lambda \varDelta _{\mathsf A} ]\)) given only  .
.
We can use this fact to compute shares of labels for a secret masked bit efficiently. Assuming the global authentication key (i.e., \(\varDelta _{\mathsf A} \)) is also used as the free-XOR shift, then it holds that  . Therefore, the task of computing shares of labels reduces to the task of computing shares of \(\hat{ z}_{u,v}\varDelta _{\mathsf A} \), since \(\mathsf{L}_{\gamma ,0}\) is known to \(\mathsf {P}_\mathsf {A}\).
. Therefore, the task of computing shares of labels reduces to the task of computing shares of \(\hat{ z}_{u,v}\varDelta _{\mathsf A} \), since \(\mathsf{L}_{\gamma ,0}\) is known to \(\mathsf {P}_\mathsf {A}\).
Notice that

If the parties hold an authenticated AND triple ( ) and a random authenticated share
) and a random authenticated share  such that
such that  ,
,  ,
,  , and
, and  . The parties can then locally compute shares of \(\lambda _\alpha \varDelta _{\mathsf A} \), \(\lambda _\beta \varDelta _{\mathsf A} \), \(\lambda _\gamma \varDelta _{\mathsf A} \), and \((\lambda _\alpha \wedge \lambda _\beta )\varDelta _{\mathsf A} \), and finally compute shares of \(\hat{ z}_{u,v}\varDelta _{\mathsf A} \) by linearly combining the above shares.
. The parties can then locally compute shares of \(\lambda _\alpha \varDelta _{\mathsf A} \), \(\lambda _\beta \varDelta _{\mathsf A} \), \(\lambda _\gamma \varDelta _{\mathsf A} \), and \((\lambda _\alpha \wedge \lambda _\beta )\varDelta _{\mathsf A} \), and finally compute shares of \(\hat{ z}_{u,v}\varDelta _{\mathsf A} \) by linearly combining the above shares.
3 Overview of Our Optimizations
We separately discuss our optimizations for the authenticated garbling and the preprocessing phases. Details and proofs can be found in Sects. 4 and 5.
3.1 Improving Authenticated Garbling
As a high level, the key ideas behind authenticated garbling are that (1) it is possible to share garbled circuits such that neither party knows how rows in the garbled tables are permuted (since no party knows the masks on the wires); moreover, (2) information-theoretic MACs can be used to ensure correctness of the garbled tables. In the original protocol by Wang et al., these two aspects are tightly integrated: each garbled row includes an encryption of the corresponding MAC tag, so the evaluator only learns one such tag for each gate.
Here, we take a slightly different perspective on how authenticated garbling works. In particular, we (conceptually) divide the protocol into two parts:
-
In the first part, the parties compute a shared garbled circuit, without any authentication, and let the evaluator reconstruct and evaluate that garbled circuit. We stress here that, even though there is no authentication, corrupting one or more garbled rows does not allow a selective-failure attack for the same reason as in the WRK protocol: any failure depends only on the masked wire values, but neither party knows those masks. This part is achieved by the encrypted wire labels alone, which have the form
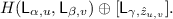 These require \(4\kappa \) bits of communication per gate.
These require \(4\kappa \) bits of communication per gate. -
In the second part, the evaluator holds masked wire values for every wire of the circuit. It then checks correctness of all these masked values. For example, it will ensure that for every AND gate, the underlying (real) values on the wires form an AND relationship. Such verification is needed for masked values that \(\mathsf {P}_\mathsf {B}\) obtains during the evaluation of the garbled circuit. The WRK protocol achieves this by encrypting authenticated shares of the form
 in each row of a garbled table. The evaluator decrypts one of the rows and checks the appropriate tag. These encrypted tags contribute \(4\rho \) bits of communication per gate.
in each row of a garbled table. The evaluator decrypts one of the rows and checks the appropriate tag. These encrypted tags contribute \(4\rho \) bits of communication per gate.
With this new way of viewing authenticated garbling, we can optimize each part independently. By doing so, we are able to reduce the communication of the first part to \(2\kappa +1\) bits per gate, and reduce the communication of the second part to 1 bit per gate. In the process, we also reduce the computation (in terms of hash evaluations) by about half. In the following, we discuss intuitively how these optimizations work.
Applying row-reduction techniques. In garbled circuits, row reduction refers to techniques that use fewer than four garbled rows per garbled gate [11, 27, 32, 40]. We review the simplest row-reduction technique here, describe the challenge of applying the technique to authenticated garbling, and then show how we overcome the challenge. This will serve as a warm-up to our final protocol that is compatible with the half-gate technique.
In classical garbling, a garbled AND gate can be written as (in our notation):
The idea behind GRR3 row reduction [27] is to choose wire labels so \(G_{0,0} = 0^\kappa \). That is, the garbler chooses
The garbler now needs to send only \((G_{0,1}, G_{1,0}, G_{1,1})\), reducing the communication from \(4\kappa \) to \(3\kappa \) bits. If the evaluator has input wires with masked values (0, 0), it can simply set \(G_{0,0}=0^\kappa \) and then proceed as before.
In authenticated garbling, the preprocessing results in shares of \(\{\hat{ z}_{u,v} \varDelta _{\mathsf A} \}\). Hence, if \(\mathsf {P}_\mathsf {A}\) could compute \(\mathsf{L}_{\gamma ,0}\) then the parties could locally compute shares of the \(\{G_{u,v}\}\) (since \(\mathsf {P}_\mathsf {A}\) knows all the \(\mathsf{L}_{\alpha ,u}, \mathsf{L}_{\beta ,v}\) values and their hashes). \(\mathsf {P}_\mathsf {A}\) could then send its shares to \(\mathsf {P}_\mathsf {B}\) to allow \(\mathsf {P}_\mathsf {B}\) to recover the entire garbled gate. Unfortunately, \(\mathsf {P}_\mathsf {A}\) cannot compute \(\mathsf{L}_{\gamma ,0}\) because \(\mathsf {P}_\mathsf {A}\) does not know \(\hat{ z}_{0,0}\)! Indeed, that value depends on the secret wire masks, unknown to either party.
Summarizing, row-reduction techniques in general compute one (or both) of the output-wire labels as a function of the input-wire labels and the secret masks, making them a challenge for authenticated garbling.
Our observation is that although \(\mathsf {P}_\mathsf {A}\) does not know \(\hat{ z}_{0,0}\), the garbling requires only \(\hat{ z}_{0,0} \varDelta _{\mathsf A} \) for which the parties do have shares. Let \(S_A\) and \(S_B\) denote the parties’ shares of this value, so that \(S_A \oplus S_B = \hat{ z}_{0,0} \varDelta _{\mathsf A} \). Our main idea is for the parties to “shift” the entire garbling process by the value \(S_B\), as follows:
-
1.
\(\mathsf {P}_\mathsf {A}\) computes \(\mathsf{L}_{\gamma ,0} := H(\mathsf{L}_{\alpha ,0}, \mathsf{L}_{\beta ,0}) \oplus S_A\). Note this value differs from the standard garbling value by a shift of \(S_B\). Intuitively, instead of choosing \(\mathsf{L}_{\gamma ,0}\) so that \(G_{0,0}=0^\kappa \), we set implicitly set \(G_{0,0}=S_B\). Although \(\mathsf {P}_\mathsf {A}\) does not know \(S_B\), it only matters that the evaluator \(\mathsf {P}_\mathsf {B}\) knows it.
-
2.
Based on this value of \(\mathsf{L}_{\gamma ,0}\), the parties locally compute shares of the garbled gate \(G_{0,1}, G_{1,0}, G_{1,1}\) defined above, and open them to \(\mathsf {P}_\mathsf {B}\).
-
3.
When \(\mathsf {P}_\mathsf {B}\) evaluates the gate on input \(\mathsf{L}_{\alpha ,u}, \mathsf{L}_{\beta ,v}\), if \((u,v) \ne (0,0)\) then evaluation is the same as usual. If \((u,v) = (0,0)\) then \(\mathsf {P}_\mathsf {B}\) sets \(G_{0,0} = S_B\). This is equivalent to \(\mathsf {P}_\mathsf {B}\) doing the usual evaluation but shifting the result by \(S_B\).
Using the half-gate technique. The state-of-the-art in semi-honest garbling is the half-gate construction of Zahur et al. [40]. It requires \(2\kappa \) bits of communication per AND gate, while being compatible with free-XOR. We describe this idea, translated from the original work [40] to be written in terms of masks and masked wire values so as to match our notation.
The circuit garbler computes a garbled gate as:
and computes the 0-label for that gate’s output wire as:
If the evaluator \(\mathsf {P}_\mathsf {B}\) holds masked values u, v and corresponding labels \(\mathsf{L}_{\alpha ,u}, \mathsf{L}_{\beta ,v}\), it computes:

This results in the value
which is the correct output \(\mathsf{L}_{\gamma ,\hat{ z}_{u,v}} = \mathsf{L}_{\gamma ,0} \oplus \hat{ z}_{u,v} \varDelta _{\mathsf A} \).
As before, this garbling technique is problematic for authenticated garbling, because the garbler \(\mathsf {P}_\mathsf {A}\) cannot compute \(\mathsf{L}_{\gamma ,0}\) as specified. (\(\mathsf {P}_\mathsf {A}\) does not know the wire masks, so cannot compute the term \((\lambda _\alpha \lambda _\beta \oplus \lambda _\gamma ) \varDelta _{\mathsf A} \).)
However, the parties holdFootnote 1 shares of this value; say, \(S_A \oplus S_B = (\lambda _\alpha \lambda _\beta \oplus \lambda _\gamma )\varDelta _{\mathsf A} \). We can thus conceptually “shift” the entire garbling procedure by \(S_B\) to obtain the following interactive variant of half-gates:
-
1.
\(\mathsf {P}_\mathsf {A}\) computes the output wire label as
$$ \mathsf{L}_{\gamma ,0} := H(\mathsf{L}_{\alpha ,0}) \oplus H(\mathsf{L}_{\beta ,0}) \oplus S_A, $$which is “shifted” by \(S_B\) from what the half-gates technique specifies.
-
2.
The parties locally compute shares of \(G_0, G_1\) as per the half-gates technique described above. These shares are opened to \(\mathsf {P}_\mathsf {B}\), so \(\mathsf {P}_\mathsf {B}\) learns \((G_0, G_1)\).
-
3.
To evaluate the gate on inputs \(\mathsf{L}_{\alpha ,u}, \mathsf{L}_{\beta ,v}\), the evaluator \(\mathsf {P}_\mathsf {B}\) performs standard half-gates evaluation and then adds \(S_B\) as a correction value. This results in the correct output-wire label, since:
$$\begin{aligned} \mathsf{Eval}(\mathsf{L}_{\alpha ,u},\mathsf{L}_{\beta ,v}) \oplus S_B&= \mathsf{Eval}(\mathsf{L}_{\alpha ,u},\mathsf{L}_{\beta ,v}) \oplus (\lambda _\alpha \lambda _\beta \oplus \lambda _\gamma )\varDelta _{\mathsf A} \oplus S_A \\&= H(\mathsf{L}_{\alpha ,0}) \oplus H(\mathsf{L}_{\beta ,0}) \oplus \hat{ z}_{u,v} \varDelta _{\mathsf A} \oplus S_A \\&= \mathsf{L}_{\gamma ,0}\oplus \hat{ z}_{u,v} \varDelta _{\mathsf A} \\&= \mathsf{L}_{\gamma , \hat{ z}_{u,v}}. \end{aligned}$$
Authentication almost for free. In the WRK scheme, suppose the actual values on the wires of an AND gate are \(z_\alpha , z_\beta , z_\gamma \) with \(z_\alpha \wedge z_\beta = z_\gamma \). During evaluation, \(\mathsf {P}_\mathsf {B}\) learn masked values \(\hat{ z}_\alpha = z_\alpha \oplus \lambda _\alpha \), \(\hat{ z}_\beta = z_\beta \oplus \lambda _\beta \), and \(\hat{ z}_\gamma = z_\gamma \oplus \lambda _\gamma \). For correctness it suffices to show that
Note the parties already have authenticated shares of \(\lambda _\alpha , \lambda _\beta , \lambda _\gamma \), and \((\lambda _\alpha \wedge \lambda _\beta )\), so they can also derive authenticated shares of related values.
In the WRK scheme the garbler \(\mathsf {P}_\mathsf {A}\) prepares an authenticated share (MAC) of \(\hat{ z}_{\alpha ,\beta }\) corresponding to each of the 4 possible values of \(\hat{ z}_\alpha , \hat{ z}_\beta \). It encrypts this share so that it can only be opened using the corresponding wire labels. \(\mathsf {P}_\mathsf {B}\) can then decrypt and verify the relevant \(\hat{ z}_{\alpha ,\beta }\) value (and take it to be the masked output value \(\hat{ z}_\gamma \)).
Our approach is to apply a technique suggested for the SPDZ protocol [9]: evaluate the circuit without authentication and then perform batch authentication at the end. Thus, in our new protocol authentication works as follows:
-
1.
\(\mathsf {P}_\mathsf {B}\) evaluates the circuit, obtaining (unauthenticated) masked values \(\hat{ z}_\alpha \) for every wire \(\alpha \).
-
2.
\(\mathsf {P}_\mathsf {B}\) reveals the masked values of every wire (1 bit per wire). Revealing these to \(\mathsf {P}_\mathsf {A}\) does not affect privacy because the masks are hidden from both parties (except for certain input/output wires where one or both of the parties already know the underlying values).
-
3.
\(\mathsf {P}_\mathsf {A}\) generates authenticated shares of only the relevant \(\hat{ z}_{\alpha ,\beta }\) values and sends them. \(\mathsf {P}_\mathsf {B}\) verifies the authenticity of each share. This is equivalent to sending a MAC of \(\mathsf {P}_\mathsf {A}\)’s shares. As described in Sect. 2, this can be done by sending only a hash of the MACs.
This technique for authentication adds an extra round, but it makes the authentication almost free in terms of communication. \(\mathsf {P}_\mathsf {B}\) sends 1 bit per wire and \(\mathsf {P}_\mathsf {A}\) sends only a single hash value to authenticate.
Details of the optimizations described above can be found in Sect. 4.
3.2 Improving the Preprocessing Phase
We also improve the efficiency of preprocessing in the WRK protocol significantly; specifically: (1) we design a new protocol for generating so-called leaky-AND triples. Compared to the best previous protocol by Wang et al., it reduces the number of hash calls by 2.5\(\times \) and reduces communication by \(\kappa \) bits. (2) we propose a new function-dependent preprocessing protocol that can be computed much more efficiently. We remark that the second optimization is particularly suitable for RAM-model secure computation, where CPU circuits are fixed ahead of time.
To enable the above optimizations, we set \(\mathsf {lsb}(\varDelta _{\mathsf A}):=1\) and  , where \(\mathsf {lsb}(x)\) denotes the least significant bit of x.
, where \(\mathsf {lsb}(x)\) denotes the least significant bit of x.
A new leaky-AND protocol. The output of a leaky-AND protocol is a random authenticated AND triple  with one caveat: the adversary can choose to guess the value of
with one caveat: the adversary can choose to guess the value of  . A correct guess remains undetected while an incorrect guess will be caught. (See Fig. 4 for a formal definition.) The leaky-AND protocol by Wang et al. works in two steps. Two parties first run a protocol whose outputs are triples that are leaky without any correctness guarantee; then a checking procedure is run to ensure correctness. The leakage is later eliminated by bucketing. In our new protocol, we observe that these two steps can be computed at the same time, reducing the number of rounds as well as the amount of computation (i.e., H-evaluations). Moreover, computing and checking can be further improved by adopting ideas from the half-gate technique. Details are below.
. A correct guess remains undetected while an incorrect guess will be caught. (See Fig. 4 for a formal definition.) The leaky-AND protocol by Wang et al. works in two steps. Two parties first run a protocol whose outputs are triples that are leaky without any correctness guarantee; then a checking procedure is run to ensure correctness. The leakage is later eliminated by bucketing. In our new protocol, we observe that these two steps can be computed at the same time, reducing the number of rounds as well as the amount of computation (i.e., H-evaluations). Moreover, computing and checking can be further improved by adopting ideas from the half-gate technique. Details are below.
Recall that in the half-gate approach, if a wire is associated with wire labels  , the first row of the gate computed by the garbler has the form
, the first row of the gate computed by the garbler has the form

for some C. An evaluator holding \((b, \mathsf{L}_{b})\) can evaluate it as

Correctness ensures that  , which means that after the evaluation the two parties hold shares of bC. Note that when free-XOR is used with shift \(\varDelta _{\mathsf A} \), then a pair of garbled labels \((\mathsf{L}_0, \mathsf{L}_1)\) and the IT-MAC for a bit (i.e., (\(\mathsf{K}[b], \mathsf{M}[b]\))) have the same structure. Therefore the above can be reformulated and extended as follows:
, which means that after the evaluation the two parties hold shares of bC. Note that when free-XOR is used with shift \(\varDelta _{\mathsf A} \), then a pair of garbled labels \((\mathsf{L}_0, \mathsf{L}_1)\) and the IT-MAC for a bit (i.e., (\(\mathsf{K}[b], \mathsf{M}[b]\))) have the same structure. Therefore the above can be reformulated and extended as follows:

Assuming the two parties have an authenticated bit \([b]_\mathsf{B}\), then  . If we view \(C_1\) and \(C_2\) as shares of some value
. If we view \(C_1\) and \(C_2\) as shares of some value  , then this can be interpreted as a way to select on a shared value such that the selection bit b is known only to one party and at the same time the output (namely,
, then this can be interpreted as a way to select on a shared value such that the selection bit b is known only to one party and at the same time the output (namely,  ) is still shared.
) is still shared.
Now we are ready to present our protocol. We will start with a set of random authenticated bits  . We want the two parties to directly compute shares of
. We want the two parties to directly compute shares of

Assuming  , revealing \(d=\mathsf {lsb}(S)\) allows the parties to “fix” these random authenticated shares to a valid triple (by computing
, revealing \(d=\mathsf {lsb}(S)\) allows the parties to “fix” these random authenticated shares to a valid triple (by computing  ). Once the parties hold shares of S (for example, \(\mathsf {P}_\mathsf {A}\) holds \(S_1\) and \(\mathsf {P}_\mathsf {B}\) holds
). Once the parties hold shares of S (for example, \(\mathsf {P}_\mathsf {A}\) holds \(S_1\) and \(\mathsf {P}_\mathsf {B}\) holds  ), checking the correctness of d also becomes easy: d is valid if and only if
), checking the correctness of d also becomes easy: d is valid if and only if  from \(\mathsf {P}_\mathsf {A}\) equals to
from \(\mathsf {P}_\mathsf {A}\) equals to  from \(\mathsf {P}_\mathsf {B}\). A wrong d can pass the equality check only if the adversary guesses the other party’s \(\mathsf{\varDelta }\) value. Now the task is to compute shares of S, where S can be rewritten as
from \(\mathsf {P}_\mathsf {B}\). A wrong d can pass the equality check only if the adversary guesses the other party’s \(\mathsf{\varDelta }\) value. Now the task is to compute shares of S, where S can be rewritten as

Here, we will focus on how to compute shares of

Now we apply the half-gate observation: \(\mathsf {P}_\mathsf {A}\) has  and \(\mathsf {P}_\mathsf {B}\) has
and \(\mathsf {P}_\mathsf {B}\) has  , and we have
, and we have

Therefore, this value can be computed by \(\mathsf {P}_\mathsf {A}\) sending one ciphertext to \(\mathsf {P}_\mathsf {B}\). Given the above observations, the final protocol can be derived in a straightforward way. Overall this new approach improves communication by 1.2\(\times \) and improves computation by 2\(\times \).
For details and a security proof corresponding to the above, see Sect. 5.1.
New function-dependent preprocessing. Here we show how to further improve the efficiency of function-dependent preprocessing. Recall that in the WRK protocol, each AND triple is derived from B leaky-AND triples, for \(B \approx \frac{\rho }{\log C}\); these triples are then used to multiply authenticated masked values for each AND gate of the circuit. Our observation is that we can reduce the number of authenticated shares needed per gate from \(3B+2\) to \(3B-1\). This idea was initially used by Araki et al. [3] in the setting of honest-majority three-party computation. See Sect. 5.2 for details.
4 Technical Details: Improved Authenticated Garbling
Since we already discussed the main intuition of the protocol in the previous section, we will present our main protocol in the  -hybrid model. Detailed protocol description is shown in Fig. 3. Each step in the protocol can be summarized as follows:
-hybrid model. Detailed protocol description is shown in Fig. 3. Each step in the protocol can be summarized as follows:
-
1.
Parties generate circuit preprocessing information using
 .
. -
2.
\(\mathsf {P}_\mathsf {A}\) computes its own share of the garbled circuit and sends to \(\mathsf {P}_\mathsf {B}\).
-
3–4.
Parties process \(\mathsf {P}_\mathsf {A}\) and \(\mathsf {P}_\mathsf {B}\)’s input and let \(\mathsf {P}_\mathsf {B}\) learn the corresponding masked input wire values and garbled labels.
-
5.
\(\mathsf {P}_\mathsf {B}\) locally reconstructs the garbled circuit and evaluates it.
-
6–8.
\(\mathsf {P}_\mathsf {B}\) sends all masked wire values (including all input, output, and internal wires) to \(\mathsf {P}_\mathsf {A}\); two parties check the correctness of all masked wire values.
-
9.
\(\mathsf {P}_\mathsf {A}\) reveals the masks of output wires to \(\mathsf {P}_\mathsf {B}\), who can recover the output.
Note that steps 2 through 9 are performed in the online phase, with \(2\kappa +2\) bits of communication per AND gate, \(\kappa +1\) bits of communication per input bit, and 1 bit of communication per output bit.
4.1 Proof of Security
We start by stating our main theorem.
Theorem 1
If H is modeled as a random oracle, the protocol in Fig. 3 securely computes f against malicious adversaries in the  -hybrid model.
-hybrid model.
Before proceeding to the formal proof, we first introduce two important lemmas. The first lemma addresses correctness of our distributed garbling scheme in the semi-honest case; the second lemma addresses correctness of the whole protocol when \(\mathsf {P}_\mathsf {A}\) is corrupted.
Lemma 1
When both parties follow the protocol honestly then, after step 5, for each wire w in the circuit \(\mathsf {P}_\mathsf {B}\) holds  .
.
Proof
We prove this by induction on the gates in the circuit.
Base case. It is easy to verify from step 3 and step 4 that the lemma holds for input wires.
Induction step. XOR-gates are trivial and so focus on an AND gate \((\alpha , \beta , \gamma , \wedge )\). First, the garbled tables are computed distributively, therefore we first write down the table after \(\mathsf {P}_\mathsf {B}\) merged its own share as follows. Note that we ignore the gate id (\(\gamma \)) for simplicity.
\(\mathsf {P}_\mathsf {A}\) locally computes the output garbled label for 0 values, namely \(\mathsf{L}_{\gamma ,0}\) as:
\(\mathsf {P}_\mathsf {B}\), who holds \((z_\alpha \oplus \lambda _\alpha , \mathsf{L}_{\alpha , z_\alpha \oplus \lambda _\alpha })\) and \((z_\beta \oplus \lambda _\beta , \mathsf{L}_{\beta , z_\beta \oplus \lambda _\beta })\) by the induction hypothesis, evaluates the circuit as follows:
Observe that
and
Therefore, we conclude that
This means that, with respect to \(\mathsf {P}_\mathsf {A}\)’s definition of \(\mathsf{L}_{\gamma ,z_\gamma \oplus \lambda _\gamma }\), \(\mathsf {P}_\mathsf {B}\)’s label is always correct. The masked value is correct because the least-significant bit of \(\varDelta _{\mathsf A}\) is 1; thus,
Lemma 2
Let \(x {\mathop {=}\limits ^\mathrm{def}}\hat{ x}_w\oplus \lambda _w\) and \(y{\mathop {=}\limits ^\mathrm{def}}\hat{ y}_w\oplus \lambda _w\), where \(\hat{ x}_w\) is what \(\mathsf {P}_\mathsf {B}\) sends in step 3, \(\hat{ y}_w\) is what \(\mathsf {P}_\mathsf {A}\) sends in step 4, and \(\lambda _w\) is defined by  . If \(\mathsf {P}_\mathsf {A}\) is malicious, then \(\mathsf {P}_\mathsf {B}\) either aborts or outputs f(x, y).
. If \(\mathsf {P}_\mathsf {A}\) is malicious, then \(\mathsf {P}_\mathsf {B}\) either aborts or outputs f(x, y).
Proof
After step 5, \(\mathsf {P}_\mathsf {B}\) obtains a set of masked values \(z_w\oplus \lambda _w\) for all wires w in the circuit. In the following, we will show that if these masked values are not correct, then \(\mathsf {P}_\mathsf {B}\) will abort with all but negligible probability.
Again we will prove by induction. Note that the lemma holds for all wires \(w\in \mathcal {I} _1\cup \mathcal {I} _2\), according to how x, y are defined, as well as for XOR-gates. In the following, we will focus on an AND gate \((\alpha ,\beta ,\gamma ,\wedge )\). Now, according to induction hypothesis, we already know that \(\mathsf {P}_\mathsf {B}\) hold correct values of \((z_\alpha \oplus \lambda _\alpha , z_\beta \oplus \lambda _\beta )\).
Recall that the checking is done by computing
The correctness of input masked values means that
Since \(\mathsf {Open}\) does not abort, \(c=0\), which means that \(\hat{ z}_\gamma = z_\alpha \wedge z_\beta \oplus \lambda _\gamma = z_\gamma \oplus \lambda _\gamma \). This means that the output masked wire value is also correct.
Given the above two lemmas, the proof of security of our main protocol is relatively easy. We provide all details below.
Proof
We consider separately a malicious \(\mathsf {P}_\mathsf {A}\) and \(\mathsf {P}_\mathsf {B}\).
Malicious \(\mathsf {P}_\mathsf {A}\). Let  be an adversary corrupting \(\mathsf {P}_\mathsf {A}\). We construct a simulator
be an adversary corrupting \(\mathsf {P}_\mathsf {A}\). We construct a simulator  that runs
that runs  as a subroutine and plays the role of \(\mathsf {P_{A}}\) in the ideal world involving an ideal functionality \(\mathcal {F}\) evaluating f.
as a subroutine and plays the role of \(\mathsf {P_{A}}\) in the ideal world involving an ideal functionality \(\mathcal {F}\) evaluating f.  is defined as follows.
is defined as follows.
-
1.
 plays the role of
plays the role of 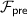 and records all values that
and records all values that 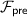 sends to two parties.
sends to two parties. -
2.
 receives all values that
receives all values that 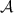 sends.
sends. -
3.
 acts as an honest \(\mathsf {P}_\mathsf {B}\) using input \(y:=0\).
acts as an honest \(\mathsf {P}_\mathsf {B}\) using input \(y:=0\). -
4.
For each wire \(w\in \mathcal {I} _1\),
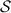 receives \(\hat{ x}_w\) and computes \(x_w := \hat{ x}_w\oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by
receives \(\hat{ x}_w\) and computes \(x_w := \hat{ x}_w\oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by  in the previous steps.
in the previous steps. -
6.
 picks random bits for all \(\hat{ z}_w\) and send them to
picks random bits for all \(\hat{ z}_w\) and send them to 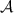 .
. -
7–9.
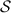 acts as an honest \(\mathsf {P}_\mathsf {B}\) If an honest \(\mathsf {P}_\mathsf {B}\) would abort,
acts as an honest \(\mathsf {P}_\mathsf {B}\) If an honest \(\mathsf {P}_\mathsf {B}\) would abort,  aborts; otherwise
aborts; otherwise  computes the input x of
computes the input x of  . from the output of
. from the output of 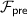 and the values
and the values 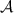 sent.
sent.  then sends x to \(\mathcal {F}\).
then sends x to \(\mathcal {F}\).
We show that the joint distribution of the outputs of  and the honest \(\mathsf {P}_\mathsf {B}\) in the real world is indistinguishable from the joint distribution of the outputs of
and the honest \(\mathsf {P}_\mathsf {B}\) in the real world is indistinguishable from the joint distribution of the outputs of  and \(\mathsf {P}_\mathsf {B}\) in the ideal world. We prove this by considering a sequence of experiments, the first of which corresponds to the execution of our protocol and the last of which corresponds to execution in the ideal world, and showing that successive experiments are computationally indistinguishable.
and \(\mathsf {P}_\mathsf {B}\) in the ideal world. We prove this by considering a sequence of experiments, the first of which corresponds to the execution of our protocol and the last of which corresponds to execution in the ideal world, and showing that successive experiments are computationally indistinguishable.
-
\(\mathbf {Hybrid_{1}}\). This is the hybrid-world protocol, where we imagine
 playing the role of an honest \(\mathsf {P_{B}}\) using \(\mathsf {P}_\mathsf {B}\)’s actual input y, while also playing the role of
playing the role of an honest \(\mathsf {P_{B}}\) using \(\mathsf {P}_\mathsf {B}\)’s actual input y, while also playing the role of  .
. -
\(\mathbf {Hybrid_{2}}\). Same as \(\mathbf {Hybrid_{1}}\), except that in step 6, for each wire \(w\in \mathcal {I} _1\) the simulator
 receives \(\hat{x}_w\) and computes \(x_w := \hat{x}_w\oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by
receives \(\hat{x}_w\) and computes \(x_w := \hat{x}_w\oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by  . If an honest \(\mathsf {P}_\mathsf {B}\) would abort in any later step,
. If an honest \(\mathsf {P}_\mathsf {B}\) would abort in any later step,  sends \(\mathsf {abort}\) to \(\mathcal {F}\); otherwise it sends \(x=\{x_w\}_{w\in \mathcal {I} _1}\) to \(\mathcal {F}\).
sends \(\mathsf {abort}\) to \(\mathcal {F}\); otherwise it sends \(x=\{x_w\}_{w\in \mathcal {I} _1}\) to \(\mathcal {F}\).The distributions on the view of
 in \(\mathbf {Hybrid_{1}}\) and \(\mathbf {Hybrid_{2}}\) are identical. The output \(\mathsf {P}_\mathsf {B}\) gets are the same due to Lemma 1 and Lemma 2.
in \(\mathbf {Hybrid_{1}}\) and \(\mathbf {Hybrid_{2}}\) are identical. The output \(\mathsf {P}_\mathsf {B}\) gets are the same due to Lemma 1 and Lemma 2. -
\(\mathbf {Hybrid_{3}}\). Same as \(\mathbf {Hybrid_{2}}\), except that
 uses \(y'=0\) in step 3 and ignore what
uses \(y'=0\) in step 3 and ignore what  sends back. Then in step 6,
sends back. Then in step 6,  sends random bits instead of the value for \(z_w\oplus \lambda _w\).
sends random bits instead of the value for \(z_w\oplus \lambda _w\).The distributions on the view of
 in \(\mathbf {Hybrid_{3}}\) and \(\mathbf {Hybrid_{2}}\) are again identical (since the \(\{s_w\}_{w \in \mathcal {I} _2}\) are uniform).
in \(\mathbf {Hybrid_{3}}\) and \(\mathbf {Hybrid_{2}}\) are again identical (since the \(\{s_w\}_{w \in \mathcal {I} _2}\) are uniform).
Note that \(\mathbf {Hybrid_{3}}\) corresponds to the ideal-world execution described earlier. This completes the proof for a malicious \(\mathsf {P}_\mathsf {A}\).
Malicious \(\mathsf {P}_\mathsf {B}\). Let  be an adversary corrupting \(\mathsf {P}_\mathsf {B}\). We construct a simulator
be an adversary corrupting \(\mathsf {P}_\mathsf {B}\). We construct a simulator  that runs
that runs  as a subroutine and plays the role of \(\mathsf {P_{B}}\) in the ideal world involving an ideal functionality \(\mathcal {F}\) evaluating f.
as a subroutine and plays the role of \(\mathsf {P_{B}}\) in the ideal world involving an ideal functionality \(\mathcal {F}\) evaluating f.  is defined as follows.
is defined as follows.
-
1.
 plays the role of
plays the role of  and records all values sent to both parties.
and records all values sent to both parties. -
2.
 acts as an honest \(\mathsf {P}_\mathsf {A}\) and send the shared garbled tables to \(\mathsf {P}_\mathsf {B}\).
acts as an honest \(\mathsf {P}_\mathsf {A}\) and send the shared garbled tables to \(\mathsf {P}_\mathsf {B}\). -
3.
For each wire \(w\in \mathcal {I} _2\),
 receives \(\hat{ y}_w\) and computes \(y_w := \hat{ y}_w\oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by
receives \(\hat{ y}_w\) and computes \(y_w := \hat{ y}_w\oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by  in the previous steps.
in the previous steps. -
4.
 acts as an honest \(\mathsf {P}_\mathsf {A}\) using input \(x=0\).
acts as an honest \(\mathsf {P}_\mathsf {A}\) using input \(x=0\). -
6–8.
 acts as an honest \(\mathsf {P}_\mathsf {A}\). If an honest \(\mathsf {P}_\mathsf {A}\) would abort,
acts as an honest \(\mathsf {P}_\mathsf {A}\). If an honest \(\mathsf {P}_\mathsf {A}\) would abort,  abort.
abort. -
9.
 sends y computed in step 3 to \(\mathcal {F}\), which returns \(z=f(x,y)\).
sends y computed in step 3 to \(\mathcal {F}\), which returns \(z=f(x,y)\).  then computes \(z':=f(0, y)\) and defines \(r'_w=z_w\oplus z'_w\oplus r_w\) for each \(w\in \mathcal {O} \).
then computes \(z':=f(0, y)\) and defines \(r'_w=z_w\oplus z'_w\oplus r_w\) for each \(w\in \mathcal {O} \).  then acts as an honest \(\mathsf {P}_\mathsf {A}\) and opens values \(r'_w\) to
then acts as an honest \(\mathsf {P}_\mathsf {A}\) and opens values \(r'_w\) to  . If an honest \(\mathsf {P}_\mathsf {A}\) would abort,
. If an honest \(\mathsf {P}_\mathsf {A}\) would abort, 
 outputs whatever
outputs whatever  outputs.
outputs.
We now show that the distribution on the view of  in the real world is indistinguishable from the distribution on the view of
in the real world is indistinguishable from the distribution on the view of  in the ideal world. (Note \(\mathsf {P}_\mathsf {A}\) has no output.)
in the ideal world. (Note \(\mathsf {P}_\mathsf {A}\) has no output.)
-
\(\mathbf {Hybrid_{1}}\). This is the hybrid-world protocol, where
 acts as an honest \(\mathsf {P_{A}}\) using \(\mathsf {P}_\mathsf {A}\)’s actual input x, while playing the role of
acts as an honest \(\mathsf {P_{A}}\) using \(\mathsf {P}_\mathsf {A}\)’s actual input x, while playing the role of  .
. -
\(\mathbf {Hybrid_{2}}\). Same as \(\mathbf {Hybrid_{1}}\), except that in step 3,
 receives \(\hat{ y}_w\) and computes \(y_w := \hat{ y}_w \oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by
receives \(\hat{ y}_w\) and computes \(y_w := \hat{ y}_w \oplus r_w\oplus s_w\), where \(r_w, s_w\) are the values used by  . If an honest \(\mathsf {P}_\mathsf {A}\) abort in any step, send \(\mathsf {abort}\) to \(\mathcal {F}\).
. If an honest \(\mathsf {P}_\mathsf {A}\) abort in any step, send \(\mathsf {abort}\) to \(\mathcal {F}\). -
\(\mathbf {Hybrid_{3}}\). Same as \(\mathbf {Hybrid_{2}}\), except that in step 4,
 acts as an honest \(\mathsf {P}_\mathsf {A}\) with input \(x=0\).
acts as an honest \(\mathsf {P}_\mathsf {A}\) with input \(x=0\).  sends x computed in step 3 to \(\mathcal {F}\), which returns \(z=f(x,y)\).
sends x computed in step 3 to \(\mathcal {F}\), which returns \(z=f(x,y)\).  then computes \(z':=f(0, y)\) and defines \(r'_w=z_w\oplus z'_w\oplus r_w\) for each \(w\in \mathcal {O} \).
then computes \(z':=f(0, y)\) and defines \(r'_w=z_w\oplus z'_w\oplus r_w\) for each \(w\in \mathcal {O} \).  then acts as an honest \(\mathsf {P}_\mathsf {A}\) and opens values \(r'_w\) to
then acts as an honest \(\mathsf {P}_\mathsf {A}\) and opens values \(r'_w\) to  . If an honest \(\mathsf {P}_\mathsf {A}\) would abort,
. If an honest \(\mathsf {P}_\mathsf {A}\) would abort,  \(\mathcal {S} _{}\) outputs whatever
\(\mathcal {S} _{}\) outputs whatever  outputs.
outputs.The distributions on the view of
 in \(\mathbf {Hybrid_{3}}\) and \(\mathbf {Hybrid_{2}}\) are identical.
in \(\mathbf {Hybrid_{3}}\) and \(\mathbf {Hybrid_{2}}\) are identical.
Note that \(\mathbf {Hybrid_{3}}\) is identical to the ideal-world execution.
5 Technical Details: Improved Preprocessing
In this section, we provide details for our two optimizations of the preprocessing phase. The first optimization improves the efficiency to compute a leaky AND gate. Leaky AND gate is a key component towards a preprocessing with full security. This functionality  outputs triples with guaranteed correctness but the adversary can choose to guess the x value from the honest party: an incorrect guess will be caught immediately; while a correct guess remain undetected.
outputs triples with guaranteed correctness but the adversary can choose to guess the x value from the honest party: an incorrect guess will be caught immediately; while a correct guess remain undetected.
The second optimization focuses on how to combine leaky triples in a more efficient way. In particular, we observe that a recent optimization in the honest-majority secret sharing protocol by Araki et al. [3], can be applied to our setting too. As a result, we can roughly reduce the bucket size by one.
5.1 Improved Leaky AND
Before giving the details, we point out a minor difference in the leaky-AND functionality ( ) as compared to [37]. As shown in Fig. 4, instead of letting
) as compared to [37]. As shown in Fig. 4, instead of letting  directly learn the value of x, the functionality allows
directly learn the value of x, the functionality allows  to send a query in a form of \((P_1, p_2, P_3)\) and return if
to send a query in a form of \((P_1, p_2, P_3)\) and return if  . It can be seen that this special way is no more than a query on x and two queries on \(\mathsf{\varDelta }\), and the
. It can be seen that this special way is no more than a query on x and two queries on \(\mathsf{\varDelta }\), and the  cannot learn any information on y or z.
cannot learn any information on y or z.
The main intuition of the protocol is already discussed in Sect. 3.2. We will proceed to present the protocol, in Fig. 5.
Theorem 2
The protocol in Fig. 5 securely realizes  in the
in the  -hybrid model.
-hybrid model.
Proof
As the first step, we will show that the protocol is correct if both parties are honest. We recall that
-
1.
\(G_1:= H(\mathsf{K}[x_2]\oplus \varDelta _{\mathsf A})\oplus H(\mathsf{K}[x_2])\oplus C_\mathsf{A}\)
-
2.
\(G_2:= H(\mathsf{K}[x_1]\oplus \varDelta _{\mathsf B})\oplus H(\mathsf{K}[x_1])\oplus C_\mathsf{B}\)
-
3.
\(C_\mathsf{A}:= y_1\varDelta _{\mathsf A} \oplus \mathsf{K}[y_2]\oplus \mathsf{M}[y_1]\)
-
4.
\(C_\mathsf{B} := y_2\varDelta _{\mathsf B} \oplus \mathsf{M}[y_2]\oplus \mathsf{K}[y_1]\)
Note that
When \(x_2 = 0\), we have
When \(x_2 = 1\), we have
Therefore,
Similarly,
Taking these two equations, we know that
Since \(\mathsf {lsb}(\varDelta _{\mathsf A} \oplus \varDelta _{\mathsf B}) = 1\), it holds that
Therefore, \((x_1\oplus x_2)\wedge (y_1\oplus y_2) = d\oplus z_1\oplus r = z_1\oplus z_2\).
Now we will focus on the security of the protocol in the malicious setting. First note that the protocol is symmetric, therefore we only need to focus on the case of a malicious \(\mathsf {P}_\mathsf {A}\). The local computation of both parties is deterministic, with all inputs sent from  . Therefore, all messages sent during the protocol can be anticipated (emulated) by
. Therefore, all messages sent during the protocol can be anticipated (emulated) by  after
after  sending out the shares. This is not always possible if
sending out the shares. This is not always possible if  uses local random coins or if
uses local random coins or if  has private inputs. This fact significantly reduces the difficulty of the proof. Intuitively,
has private inputs. This fact significantly reduces the difficulty of the proof. Intuitively,  will be able to immediately catch
will be able to immediately catch  cheating by comparing what it sends with what it would have sent (which
cheating by comparing what it sends with what it would have sent (which  knows by locally emulating). The majority of the work then is to extract
knows by locally emulating). The majority of the work then is to extract  ’s attempt to perform a selective failure attack.
’s attempt to perform a selective failure attack.
Define a simulator  as follows.
as follows.
-
0a.
 interacts with
interacts with  and obtains \(\mathsf {P}_\mathsf {A}\)’s share of
and obtains \(\mathsf {P}_\mathsf {A}\)’s share of  .
.  also gets \(\varDelta _{\mathsf A} \) from
also gets \(\varDelta _{\mathsf A} \) from 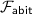 .
. 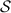 randomly picks \(\varDelta _{\mathsf B} \) and \(\mathsf {P}_\mathsf {B}\)’s share of
randomly picks \(\varDelta _{\mathsf B} \) and \(\mathsf {P}_\mathsf {B}\)’s share of 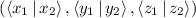 in a way that makes it consistent with \(\mathsf {P}_\mathsf {A}\)’s share.
in a way that makes it consistent with \(\mathsf {P}_\mathsf {A}\)’s share.  now randomly picks d and computes \([r]_\mathsf{B}:=[z_2]_\mathsf{B}\oplus d\).
now randomly picks d and computes \([r]_\mathsf{B}:=[z_2]_\mathsf{B}\oplus d\). -
0b.
Using values
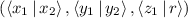 from both parties,
from both parties, 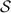 locally emulates all messages sent by each party, namely \((G_1, d_1, L_1)\) sent by an honest \(\mathsf {P}_\mathsf {A}\) and \((G_2, d_2, L_2)\) sent by an honest \(\mathsf {P}_\mathsf {B}\).
locally emulates all messages sent by each party, namely \((G_1, d_1, L_1)\) sent by an honest \(\mathsf {P}_\mathsf {A}\) and \((G_2, d_2, L_2)\) sent by an honest \(\mathsf {P}_\mathsf {B}\). -
1.
 plays the role of
plays the role of 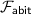 and sends out
and sends out 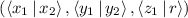 as defined above.
as defined above. -
2.
 acts as an honest \(\mathsf {P}_\mathsf {B}\) and receive \(G_1'\) sent by
acts as an honest \(\mathsf {P}_\mathsf {B}\) and receive \(G_1'\) sent by  .
.  computes \(P_1=G'_1\oplus G_1\).
computes \(P_1=G'_1\oplus G_1\). -
3.
 randomly picks a \(G_2\) and send it to
randomly picks a \(G_2\) and send it to  .
. -
4.
 acts as an honest \(\mathsf {P}_\mathsf {B}\) and receives \(d'_1\).
acts as an honest \(\mathsf {P}_\mathsf {B}\) and receives \(d'_1\).  computes \(p_2:=d'_1\oplus d_1\).
computes \(p_2:=d'_1\oplus d_1\). -
5.
 plays the role of
plays the role of  and obtain \(L_1\).
and obtain \(L_1\).  computes \(P_3=L'_1\oplus L_1\).
computes \(P_3=L'_1\oplus L_1\).  sends \((P_1,p_2,P_3)\) to
sends \((P_1,p_2,P_3)\) to  as the selective failure attack query. If
as the selective failure attack query. If  abort,
abort,  plays the role of
plays the role of  and aborts. If the value d in the protocol equals to r defined in step 0a,
and aborts. If the value d in the protocol equals to r defined in step 0a,  returns 0; otherwise
returns 0; otherwise  returns 1.
returns 1. -
6.
 sends \((P_1,p_2,P_3)\) to
sends \((P_1,p_2,P_3)\) to  as the selective failure query. If
as the selective failure query. If  returns fail,
returns fail,  sends 0 to
sends 0 to  as the output of
as the output of 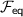 .
.
Note that messages that  sends to
sends to  in the protocol are changed from \((G_2, d_2, L_2)\) to \((G_2, d_2\oplus x_2\mathsf {lsb}(P_1), L_2\oplus x_2P_1\oplus d'\varDelta _{\mathsf B})\), where \(d'=p_2\oplus x_2\cdot \mathsf {lsb}(P_1)\) and the equality checking in step 5 changed from comparing \(L_1=L_2\) to
in the protocol are changed from \((G_2, d_2, L_2)\) to \((G_2, d_2\oplus x_2\mathsf {lsb}(P_1), L_2\oplus x_2P_1\oplus d'\varDelta _{\mathsf B})\), where \(d'=p_2\oplus x_2\cdot \mathsf {lsb}(P_1)\) and the equality checking in step 5 changed from comparing \(L_1=L_2\) to
that is
This is the same form as the selective failure query in  .
.
5.2 Improved Function-Dependent Preprocessing
In this section, we will focus on improving the preprocessing in the Leaky AND triple generation ( ) hybrid model. The main observation is that in the protocol of WRK, each wire is associated with a mask (in the authenticated share format). Then the AND of input masks are computed using one AND triple. This is a waste of randomness, since we also directly construct all triples in place for all wires. Note that the idea is similar to Araki et al. [3]. The detailed protocol is presented in Fig. 6.
) hybrid model. The main observation is that in the protocol of WRK, each wire is associated with a mask (in the authenticated share format). Then the AND of input masks are computed using one AND triple. This is a waste of randomness, since we also directly construct all triples in place for all wires. Note that the idea is similar to Araki et al. [3]. The detailed protocol is presented in Fig. 6.
Note that although the above optimization aims to reduce the overall cost of the protocol, but it turns out that even in this case, most of the computation and communication (including computation of all authenticated bits as well as all leaky-AND triples in step 5) can be still done in the function-independent phase. The function-dependent cost is increased by only \(\kappa \) bits per AND gate only. Therefore, here we have an option to trade-off between total communication and communication in the offline stage. By increasing the function-dependent cost by \(\kappa \) bits per gate, we reduce bucket size by 1. We believe both versions can be useful depending on the application, and the concrete cost of both versions of the protocol are presented in the performance section.
6 Performance
In this section, we discuss the concrete efficiency of our protocol. We consider two variants of our protocol that optimize the cost of different phases: The first version of our protocol is optimized to minimize the total communication; the second version is optimized to minimize the communication in the function-dependent phase. (The cost of the online phase is identical in both versions.)
6.1 Communication Complexity
Table 2 shows the communication complexity of recent two-party computation protocols in the malicious setting. Numbers for these protocols are obtained from the respective papers, while numbers for our protocol are calculated. We tabulate both one-way communication and total communication. If parties’ data can be sent at the same time over a full-duplex network, then one-way communication is a better reflection of the running time. In general, for a circuit that requires a bucket size of B, we can obtain an estimation of the concrete communication cost: our first version has function dependent cost of \(3\kappa \) per gate, and function independent cost of \((4B-2)\kappa + (3B-1)\rho \) per gate; our second version has a function dependent cost of \(2\kappa \) per gate, and a function independent cost of \((4B+2)\kappa + (3B+2)\rho \) per gate.
We see that our protocol and the protocol by Nielsen et al. [28] are the only ones that, considering the function-dependent phase and the online phase, have cost similar to that of the state-of-the-art semi-honest garbled-circuit protocol. In other words, the overhead induced by malicious security can be completely pushed to the preprocessing stage. Compared to the protocol by Nielsen et al., we are able to reduce the communication in the preprocessing stage by 6\(\times \) in the single-execution setting, and by 3.4\(\times \) in the amortized setting. Our protocol also has the best total communication complexity in both settings, excepting the work of [18, 33] which are 6% better but do not support function-independent preprocessing.
6.2 Computational Complexity
Since the WRK protocol represents the state-of-the-art as far as implementations are concerned, we compare the computational complexity of our protocol to theirs. We also include a comparison to the more recent protocol by Hazay et al. [12] (the HIV protocol), which has not yet been implemented.
Comparing to the WRK protocol. Our protocol follows the same high-level approach as the WRK protocol. Almost all H-evaluations in our protocol can be accelerated using fixed-key AES, as done in [6]. We tabulate the number of H-evaluations for both protocols in Table 3. Due to our improved  , we are able to achieve a 2–2.5\(\times \) improvement.
, we are able to achieve a 2–2.5\(\times \) improvement.
Comparing to the HIV protocol. As noted by the authors, the HIV protocol has polylogarithmic computational overhead compared to semi-honest garbled circuits. This is due to their use of the MPC-based zero-knowledge proof by Ames et al. [2]. On the other hand, in our protocol, the computation is linear in the circuit size. Furthermore, almost all cryptographic operations in our protocol can be accelerated using hardware AES instructions.
Taking an AES circuit as example, the ZK protocol by Ames et al. for a circuit of that size has a prover running time of around 70 ms and a verifier running time of around 30 ms. Therefore, even if we ignore the cost of computing and sending the garbled circuit, the oblivious transfers, and other operations, the end-to-end running time of the HIV protocol will still be at least 100 ms. On the other hand, the entire WRK protocol runs within 17 ms for the same circuit. As our protocol results in at least a 2\(\times \) improvement, our protocol will be at least an order of magnitude faster than the HIV protocol.
7 Challenges in Extending to the Multi-Party Case
Wang et al. [38] have also shown how to extend their authenticated-garbling protocol to the multi-party case. In this section, we discuss the challenges involved in applying our new techniques to that setting. Note that Ben-Efraim [7] recently proposed new techniques for multi-party garbling, making it compatible with some of the half-gate optimizations. Despite being based on half-gates, they still require 4 garbled rows per AND gate, and thus their work still leaves open the question of reducing the communication complexity of the online phase in the multi-party case.
In the multi-party WRK protocol, there are \(n-1\) garbling parties and one evaluating party. For each wire, each garbler chooses their own set of wire labels (called “subkeys”). As in the 2-party case, the preprocessing defines some authenticated bits, and as a result all parties can locally compute additive shares of any garbler’s subkey corresponding to any authenticated value.
In each gate, each garbler \(P_i\) generates standard Yao garbled gate consisting of 4 rows. Each row of \(P_i\)’s gate is encrypted by only \(P_i\)’s subkeys, and the payload of the row is \(P_i\)’s shares of all garblers’ subkeys. That way, the evaluator can decrypt the correct row of everyone’s garbled gates, obtain everyone’s shares of everyone’s subkeys, and combine them to get everyone’s appropriate subkey for the output wire.
Now suppose we modify things so each garbler generates a half-gates-style garbled gate instead of a standard Yao garbled gate. The half-gate uses garbler \(P_i\)’s subkeys as its “keys” and encodes \(P_i\)’s shares of all subkeys as its “payloads”. Now the protocol may not be secure against an adversary corrupting the evaluator and a garbler. In particular, half-gates garbling defines \(G_0 = H(\mathsf{L}_{\alpha ,0}) \oplus H(\mathsf{L}_{\alpha ,1}) \oplus \lambda _\beta \varDelta \). When \(P_i\) is acting as garbler, these \(\mathsf{L}_{\alpha ,u}\) values correspond to \(P_i\)’s subkeys. Now suppose \(P_i\) colludes with the evaluator. If the evaluator comes to learn \(G_0\) (which is necessary to evaluate the gate in half of the cases), then the adversary can learn the secret mask \(\lambda _\beta \) since it is the only unknown term in \(G_0\). Clearly revealing the secret wire mask breaks the privacy of the protocol. This is not a problem with Yao garbled gates, where each row can be written as \(G_{u,v} = H(\mathsf{L}_{\alpha ,u}, \mathsf{L}_{\beta ,v}) \oplus \text {[payload already known to garbler]}\). The secret masks do not appear in the garbled table, except indirectly through the payloads (subkey shares).
It is even unclear if row-reduction can be made possible. In the multi-party setting, the garbler has no control over the “payload” (i.e., output wire label) of the garbled gate when using row-reduction. Indeed, this is what makes it possible to reduce the size of a garbled gate. This is not a problem in the two-party case, where there is only one garbler who has control over all garbled gates and all wire labels. He generates a garbled table, and then computes his output wire label (subkey) as a function of the payload in the table. However, in the multi-party case, \(P_i\) generates a half-gate whose payloads include \(P_i\)’s shares of \(P_j\)’s subkeys! We would need \(P_j\)’s choice of subkeys to depend on the payloads of \(P_i\)’s garbling (for all i and j!). It is not clear how this can be done, and even if it were possible it would apparently require additional rounds proportional to the depth of the circuit.
Notes
- 1.
Note that \((\lambda _\alpha \lambda _\beta \oplus \lambda _\gamma ) = \hat{ z}_{0,0}\), the same secret value as in the previous example.
References
Afshar, A., Mohassel, P., Pinkas, B., Riva, B.: Non-interactive secure computation based on cut-and-choose. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 387–404. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_22
Ames, S., Hazay, C., Ishai, Y., Venkitasubramaniam, M.: Ligero: lightweight sublinear arguments without a trusted setup. In: ACM CCS 2017, pp. 2087–2104. ACM Press (2017)
Araki, T., Barak, A., Furukawa, J., Lichter, T., Lindell, Y., Nof, A., Ohara, K., Watzman, A., Weinstein, O.: Optimized honest-majority MPC for malicious adversaries - breaking the 1 billion-gate per second barrier. In: 2017 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 22–26 May 2017, pp. 843–862. IEEE Computer Society Press (2017)
Beaver, D.: Efficient multiparty protocols using circuit randomization. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 420–432. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_34
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols. In: Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, pp. 503–513. ACM (1990)
Bellare, M., Hoang, V.T., Keelveedhi, S., Rogaway, P.: Efficient garbling from a fixed-key blockcipher. In: 2013 IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 19–22 May 2013, pp. 478–492. IEEE Computer Society Press (2013)
Ben-Efraim, A.: On multiparty garbling of arithmetic circuits. Cryptology ePrint Archive, Report 2017/1186 (2017). https://eprint.iacr.org/2017/1186
Brandão, L.T.A.N.: Secure two-party computation with reusable bit-commitments, via a cut-and-choose with forge-and-lose technique. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 441–463. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_23
Damgård, I., Pastro, V., Smart, N.P., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B., Nordholt, P.S., Orlandi, C.: MiniLEGO: efficient secure two-party computation from general assumptions. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 537–556. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_32
Gueron, S., Lindell, Y., Nof, A., Pinkas, B.: Fast garbling of circuits under standard assumptions. In: Ray, I., Li, N., Kruegel: C. (eds.) ACM CCS 2015, Denver, CO, USA, 12–16 October 2015, pp. 567–578. ACM Press (2015)
Hazay, C., Ishai, Y., Venkitasubramaniam, M.: Actively secure garbled circuits with constant communication overhead in the plain model. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part II. LNCS, vol. 10678, pp. 3–39. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_1
Huang, Y., Evans, D., Katz, J., Malka, L.: Faster secure two-party computation using garbled circuits. In: USENIX Security 2011 (2011)
Huang, Y., Katz, J., Evans, D.: Efficient secure two-party computation using symmetric cut-and-choose. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 18–35. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_2
Huang, Y., Katz, J., Kolesnikov, V., Kumaresan, R., Malozemoff, A.J.: Amortizing garbled circuits. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 458–475. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_26
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Kolesnikov, V., Mohassel, P., Rosulek, M.: FleXOR: flexible garbling for XOR gates that beats free-XOR. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 440–457. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_25
Kolesnikov, V., Nielsen, J.B., Rosulek, M., Trieu, N., Trifiletti, R.: DUPLO: unifying cut-and-choose for garbled circuits. In: ACM CCS 2017, pp. 3–20. ACM Press (2017)
Kolesnikov, V., Schneider, T.: Improved garbled circuit: free XOR gates and applications. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 486–498. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70583-3_40
Kreuter, B., Shelat, A., Shen, C.H.: Billion-gate secure computation with malicious adversaries. In: USENIX Security 2012 (2012)
Lindell, Y.: Fast cut-and-choose based protocols for malicious and covert adversaries. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_1
Lindell, Y., Pinkas, B.: An efficient protocol for secure two-party computation in the presence of malicious adversaries. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 52–78. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_4
Lindell, Y., Pinkas, B.: Secure two-party computation via cut-and-choose oblivious transfer. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 329–346. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_20
Lindell, Y., Riva, B.: Cut-and-choose Yao-based secure computation in the online/offline and batch settings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 476–494. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_27
Lindell, Y., Riva, B.: Blazing fast 2PC in the offline/online setting with security for malicious adversaries. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, Denver, CO, USA, 12–16 October 2015, pp. 579–590. ACM Press (2015)
Malkhi, D., Nisan, N., Pinkas, B., Sella, Y.: Fairplay—a secure two-party computation system. In: USENIX Security 2004 (2004)
Naor, M., Pinkas, B., Sumner, R.: Privacy preserving auctions and mechanism design. In: 1st ACM Conference on Electronic Commerce (1999)
Nielsen, J., Schneider, T., Trifiletti, R.: Constant-round maliciously secure 2PC with function-independent preprocessing using LEGO. In: Network and Distributed System Security Symposium (NDSS) (2017)
Nielsen, J.B., Nordholt, P.S., Orlandi, C., Burra, S.S.: A new approach to practical active-secure two-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 681–700. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_40
Nielsen, J.B., Orlandi, C.: LEGO for two-party secure computation. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 368–386. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_22
Nielsen, J.B., Orlandi, C.: Cross and clean: amortized garbled circuits with constant overhead. In: Hirt, M., Smith, A.D. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 582–603. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_22
Pinkas, B., Schneider, T., Smart, N.P., Williams, S.C.: Secure two-party computation is practical. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 250–267. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_15
Rindal, P., Rosulek, M.: Faster malicious 2-party secure computation with online/offline dual execution. In: USENIX Security 2016 (2016)
Shelat, A., Shen, C.H.: Two-output secure computation with malicious adversaries. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 386–405. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_22
Shelat, A., Shen, C.H.: Fast two-party secure computation with minimal assumptions. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, Berlin, Germany, 4–8 November 2013, pp. 523–534. ACM Press (2013)
Wang, X., Malozemoff, A.J., Katz, J.: Faster secure two-party computation in the single-execution setting. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part II. LNCS, vol. 10212, pp. 399–424. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_14
Wang, X., Ranellucci, S., Katz, J.: Authenticated garbling and efficient maliciously secure two-party computation. In: ACM CCS 2017, pp. 21–37. ACM Press (2017)
Wang, X., Ranellucci, S., Katz, J.: Global-scale secure multiparty computation. In: ACM CCS 2017, pp. 39–56. ACM Press (2017)
Yao, A.C.C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, Toronto, Ontario, Canada, 27–29 October 1986, pp. 162–167. IEEE Computer Society Press (1986)
Zahur, S., Rosulek, M., Evans, D.: Two halves make a whole - Reducing Data Transfer in Garbled Circuits Using Half Gates. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 220–250. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_8
Zhu, R., Huang, Y.: JIMU: faster LEGO-based secure computation using additive homomorphic hashes. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part II. LNCS, vol. 10625, pp. 529–572. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_19
Acknowledgments
This material is based on work supported by NSF awards #1111599, #1563722, #1564088, and #1617197. Portions of this work were also supported by DARPA and SPAWAR under contract N66001-15-C-4065. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes not withstanding any copyright notation thereon. The views, opinions, and/or findings expressed are those of the authors and should not be interpreted as representing the official views or policies of the Department of Defense or the U.S. Government.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Katz, J., Ranellucci, S., Rosulek, M., Wang, X. (2018). Optimizing Authenticated Garbling for Faster Secure Two-Party Computation. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10993. Springer, Cham. https://doi.org/10.1007/978-3-319-96878-0_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-96878-0_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96877-3
Online ISBN: 978-3-319-96878-0
eBook Packages: Computer ScienceComputer Science (R0)



 . We refer to the value
. We refer to the value  as the mask on wire w.
as the mask on wire w.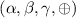 , generate a random authenticated share
, generate a random authenticated share 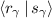 whose value
whose value 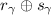 is the XOR of the masks on the input wires
is the XOR of the masks on the input wires 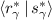 such that
such that 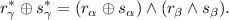

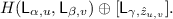 These require
These require  in each row of a garbled table. The evaluator decrypts one of the rows and checks the appropriate tag. These encrypted tags contribute
in each row of a garbled table. The evaluator decrypts one of the rows and checks the appropriate tag. These encrypted tags contribute 
 hybrid model
hybrid model .
.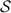 plays the role of
plays the role of 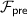 and records all values that
and records all values that 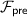 sends to two parties.
sends to two parties. receives all values that
receives all values that 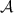 sends.
sends. acts as an honest
acts as an honest 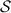 receives
receives  in the previous steps.
in the previous steps. picks random bits for all
picks random bits for all 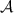 .
.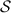 acts as an honest
acts as an honest  aborts; otherwise
aborts; otherwise  computes the input x of
computes the input x of  . from the output of
. from the output of 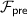 and the values
and the values 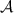 sent.
sent. 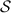 then sends x to
then sends x to  playing the role of an honest
playing the role of an honest 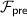 .
.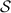 receives
receives 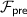 . If an honest
. If an honest  sends
sends  in
in  uses
uses  sends back. Then in step 6,
sends back. Then in step 6, 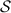 sends random bits instead of the value for
sends random bits instead of the value for 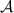 in
in  plays the role of
plays the role of 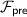 and records all values sent to both parties.
and records all values sent to both parties.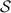 acts as an honest
acts as an honest 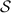 receives
receives 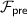 in the previous steps.
in the previous steps. acts as an honest
acts as an honest 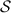 acts as an honest
acts as an honest  abort.
abort. sends y computed in step 3 to
sends y computed in step 3 to  then computes
then computes  then acts as an honest
then acts as an honest  . If an honest
. If an honest 
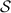 outputs whatever
outputs whatever 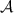 outputs.
outputs. acts as an honest
acts as an honest 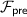 .
. receives
receives 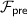 . If an honest
. If an honest  acts as an honest
acts as an honest  sends x computed in step 3 to
sends x computed in step 3 to  then computes
then computes  then acts as an honest
then acts as an honest  . If an honest
. If an honest 
 outputs.
outputs. in
in 
 for computing a leaky AND triple.
for computing a leaky AND triple.
 interacts with
interacts with  and obtains
and obtains  .
.  also gets
also gets 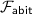 .
. 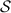 randomly picks
randomly picks 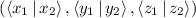 in a way that makes it consistent with
in a way that makes it consistent with  now randomly picks d and computes
now randomly picks d and computes 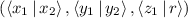 from both parties,
from both parties,  locally emulates all messages sent by each party, namely
locally emulates all messages sent by each party, namely  plays the role of
plays the role of 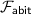 and sends out
and sends out 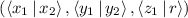 as defined above.
as defined above.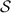 acts as an honest
acts as an honest 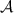 .
.  computes
computes 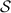 randomly picks a
randomly picks a  .
. acts as an honest
acts as an honest  computes
computes 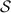 plays the role of
plays the role of 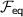 and obtain
and obtain  computes
computes 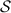 sends
sends  as the selective failure attack query. If
as the selective failure attack query. If  abort,
abort,  plays the role of
plays the role of  and aborts. If the value d in the protocol equals to r defined in step 0a,
and aborts. If the value d in the protocol equals to r defined in step 0a,  returns 0; otherwise
returns 0; otherwise  returns 1.
returns 1. sends
sends  as the selective failure query. If
as the selective failure query. If  returns
returns 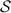 sends 0 to
sends 0 to  as the output of
as the output of 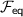 .
.
 instantiating
instantiating  in the
in the  -hybrid model.
-hybrid model.