Keywords

1 Introduction

There are thousands of jobs, which could be sent to cloud data centers at the same time. In some cases, the lack of available clusters and servers for performing these jobs is inevitable. To resolve this issue, the jobs are formed a queue to wait for processing in succession. In this way, a large number of studies that have proposed queuing models to optimize service waiting time for incoming jobs, energy consumption for data centers, and improve the quality of service (QoS) [1]. However, because jobs have different sizes and arrival times, the waiting time in the queue is also different and often not optimal.

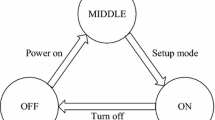
Most studies that developed two-state models like [1, 2] also exploited infinite queues. Because almost all providers offer computational resources based on capacity of their data centers, hence proposing models of finite job queues is essential. Nevertheless, the number of studies that dealt with the feature is quite small. We built an ON/OFF/MIDDLE/c/K model applying to a single finite-capacity queue in the work [4] for cloud data center management problem. In another aspect, although jobs abandonment has been considered in research [3] before, with the three-state approach, there are no related studies, which have addressed this problem. Hence, based on the motivation, this work continues to develop the three-state model proposed in our previous works [4] with consideration of occurring jobs abandonment when they already wait for ON servers in a long time. With this direction, our target is to reduce the mean waiting time for incoming jobs. In order to solve the job abandonment problem, we have to reduce waiting time of jobs inside the system. In this paper, we inherit the three-state model ON/OFF/MIDDLE/c/K proposed in our previous work [4] to develop a new three-state model, which operates under job abandonment phenomenon with a finite queue. In this way, the new model is called Ab(ON/OFF/MIDDLE/c/K).

The paper is organized as follows. In Sect. 2, we build a mathematical model for Ab(ON/OFF/MIDDLE/c/K). Also in this section, we propose control mechanism for the model. Section 3 dedicates to presenting our experiments with simulation dataset. The paper concludes in Sect. 4.

2 Designing Mathematical Model and Control Algorithm

2.1 Three-State Servers and Job Abandonment Phenomenon

In this research, we go further by examining the job abandonment condition with the three-state model presented in [4]. In order to build a theoretical model, jobs also are assumed to arrive at the system according to a Poisson distribution and the needed time to finish a job (service time) is an exponentially distributed random variable X with rate \(\mu = \frac{1}{E[X]}\). Under abandonment condition, if a job comes to a full queue, it will be blocked. However, if a job in queue already has been waiting for an ON server for a long time that exceeds a certain threshold, the job will abandon. We assume that a job abandons from the queue with an exponential distribution having expectation: \(\frac{1}{\theta }\). If the system has i ON servers and j jobs, then the abandonment rate is \((j-i)\theta \) and the number of servers in SETUP process is \(min(j-i, c-i)\). Because the power supply for the turning process of servers (from OFF to MIDDLE) is assumed as a constant variable (\(t_{OFF\rightarrow MIDDLE}\)), we can model the system states transition for our proposed Ab(ON/OFF/MIDDLE/c/K) by a Markov chain. In which, (i, j) is a state pair, where i and j are the number of ON servers, and jobs in the system (including jobs in the queue and jobs being served) respectively.

2.2 Ab(ON/OFF/MIDDLE/c/K) Model

We inherit lemmas proved in [5], and Lemma 2 demonstrated in our previous work [4], then we improve and prove Lemma 1 in this document with job abandonment condition to build our Theorem 1 below.

Lemma 1

In the Ab(ON/OFF/MIDDLE/c/K) model with job abandonment, at time t, system is in state (i, j) with \(j > i\). At time \(t + h\), probability of the system moves to a new state \((i_1,j_1)\) (\(i\ne i_1\) or \(j \ne j_1\)) is:

$$\begin{aligned} P((i,j) \rightarrow ({i_1},{j_1})) = {\left\{ \begin{array}{ll} \min (j - i,c - i)\alpha h + o(h) &{}where\;{i_1} = i + 1\;and\;j = {j_1}\\ \lambda h + o(h) &{}where\;{i_1} = i\;and\;{j_1} = j + 1\\ (i\mu + (j-i)\theta )h + o(h)\quad &{}where\;{i_1} = i\;and\;{j_1} = j - 1\\ o(h) &{}in\;other\;cases \end{array}\right. } \end{aligned}$$
(1)

Proof

When \(j>i\), queue has \(j-i\) jobs. Four event types can happen at time \((t, t+h)\), including a job arrives, a job is completed, a job leaves queue, and a server is switched from SETUP to ON. As assumptions presented above, jobs arrive according to a Poisson distribution with rate \(\lambda \), this leads to the inter-arrival time (i.e. time period between two incoming jobs) being independent and conforming to an exponentially distributed random variable with expectation \(\lambda ^{-1}\). Otherwise, the time of execution, SETUP and abandonment processes are also considered as exponentially distributed with expectations \(\mu ^{-1}\), \(\alpha ^{-1}\) and \(\theta ^{-1}\) respectively.

In this way, the required time to switch from an event to the next one is the minimum of the following four random variables: inter-arrival time, i execution time of i running servers, min(\(c-i\), \(j-i\)) SETUP time of min(\(c-i\), \(j-i\)) servers, which are switching to ON state and \(j-i\) abandonment time of \(j-i\) jobs in the queue. Consequently, time from t until the next event has an exponential distribution with expectation \((\lambda +min(c-i,j-i)\alpha +i\mu +(j-i)\theta )^{-1}\), and probability that an event will occur in \((t,t+h)\) is:

$$\begin{aligned} 1-e^{(\lambda +min(c-i,j-i)\alpha +i\mu +(j-i)\theta )} = (\lambda +min(c-i,j-i)\alpha +i\mu +(j-i)\theta )h+o(h) \end{aligned}$$

According to Lemma 2 defined in [4], when an event occurs, probability of a server switched to ON state is:

$$\begin{aligned} \frac{{\min (c - i,j - i)\alpha }}{{\lambda + \min (j - i,c - i)\alpha + i\mu + (j-i)\theta }} \end{aligned}$$

In addition, because the time length required for an event occurrence and event types are independent, probability of transition occurrence \((i,j)\rightarrow (i+1,j)\) is:

$$\begin{aligned} \begin{aligned} P((i,j) \rightarrow (i+1,j))&= \frac{{\min (c - i,j - i)\alpha }}{{\lambda + \min (j - i,c - i)\alpha + i\mu + (j-i)\theta }} \\&\quad \times ((\lambda +min(c-i,j-i)\alpha +i\mu +(j-i)\theta )h+o(h)) \\&=min(c-i,j-i)\alpha h+o(h) \end{aligned} \end{aligned}$$

Similarly, we also have:

$$\begin{aligned} \begin{aligned} P((i,j) \rightarrow (i,j+1))&= \frac{{\lambda }}{{\lambda + \min (j - i,c - i)\alpha + i\mu + (j-i)\theta }} \\&\quad \times ((\lambda +min(c-i,j-i)\alpha +i\mu +(j-i)\theta )h+o(h))\\&=\lambda h+o(h) \end{aligned} \end{aligned}$$

and:

$$\begin{aligned} \begin{aligned} P((i,j) \rightarrow (i,j-1))&= \frac{{i\mu +(j-i)\theta }}{{\lambda + \min (j - i,c - i)\alpha i\mu + (j-i)\theta }} \\&\quad \times ((\lambda +min(c-i,j-i)\alpha +i\mu +(j-i)\theta )ho(h))\\&=(i\mu +(j-i)\theta ) h+o(h) \end{aligned} \end{aligned}$$

Probability of more than one event will occur in time \((t,t+h)\) is o(h) with \(h\rightarrow 0\). The probability thus follows \(P((i,j)\rightarrow (i_{1},j_{1}))\) in others cases.

Theorem 1

In the Ab(ON/OFF/MIDDLE/c/K) model, expectation of the server number, which is switched from MIDDLE to ON state in time t is given by:

$$\begin{aligned} E[M] \approx at\sum \limits _{j > i} {{\pi _{i,j}}\min (c - i,j - i)} \end{aligned}$$
(2)

Proof

Let \(K_h\) is the number of servers that are switched to ON state in period of time h. Therefore \(K_h > 0\) when the \((i,j) \rightarrow ({i_1},j)\) \((i_1 >i)\) event occurs. Based on Lemma 1, \(O(K_h>1)=o(h)\), and the total probability formula:

$$ P({K_h} = 1) = \sum \limits _{j> i} {{\pi _{i,j}}P((i,j) \rightarrow ({i_1},j))} = \sum \limits _{j > i} {{\pi _{i,j}}(\min (c - i,j - i)\alpha h + o(h))} $$
$$ \approx \sum \limits _{j > i} {{\pi _{i,j}}(\min (c - i,j - i))} $$

We have:

$$ E[{K_h}] \approx ah\sum \limits _{j > i} {{\pi _{i,j}}(\min (c - i,j - i))} $$

Dividing t into small enough time period h, assuming \(K_h^{(z)}\) is the number of servers switched to ON state in time period z. We also have:

$$ E[M] = E[\sum \limits _z {K_h^{(z)}} ] \approx ah\sum \limits _{j > i} {{\pi _{i,j}}(\min (c - i,j - i))} \frac{t}{h} $$
$$ = at\sum \limits _{j > i} {{\pi _{i,j}}(\min (c - i,j - i))} $$

2.3 Control Algorithm

Theorem 1 puts forward a formula for calculating expectation of the server number switched from MIDDLE to ON successfully. The requirement for our strategy is that the number of servers switched from OFF to MIDDLE state must equal the expectation of server number switched from MIDDLE to ON state in any time period. For this reason, the average number of servers that must be switched to MIDDLE state is calculated by formula 2.

$$\begin{aligned} \tau = \frac{t}{{E[M]}} = \frac{1}{{a\sum \limits _{j > i} {{\pi _{i,j}}(\min (c - i,j - i))} }} \end{aligned}$$
(3)
figure a

In Algorithm 1, the switching process of servers from OFF to ON is divided into two periods. Firstly, an OFF server is periodically switched to MIDDLE state after a period of time \(\tau \). Secondly, using Ab(ON/OFF/MIDDLE/c/K) strategy, MIDDLE servers are turned into ON based on the number of jobs in queue.

3 Experiment and Evaluation

3.1 Experimental Setup

For our experiments, CloudSim is used to simulate cloud environment with a data center, servers, and a finite job queue. We set the needed time to turn a server from OFF to MIDDLE state \({t_{OFF\rightarrow MIDDLE}}\) = 400(s), SETUP mode time with \(\alpha \) = 0.02, the number of servers in system c = 200, and queue length K = 200. \(\lambda \) is increased from 1 to 10 to assess the impact of arrival job rate on our model. While \(\lambda \) values are changed, the traffic intensity \(\rho = \frac{\lambda }{{c\mu }}\) also are altered from 0.1 to 1. We also set the job service time \(\mu \) = 0.05 and vary \(\theta \) from 0.001 to 0.02.

3.2 Ab(ON/OFF/MIDDLE/c/K) Evaluations

For the first test, Fig. 1 expresses the gained time period values. There are two important observations here: while \(\lambda \) has a tremendous impact on values of \(\tau \), the impacts of \(\theta \) on \(\tau \) are quite small. Hence, the differences of charts with diverse \(\theta \) values are very small. While \(\lambda \) increases from 1 to 8, \(\tau \) decreases from about 9.5 to 3.7. However, it raises slightly when \(\lambda \) exceeds 8. The phenomenon can be explained as follows: when \(\lambda \) is small, there are not many jobs that arrive at the data center. So the system just needs to keep a small number of MIDDLE servers. When \(\lambda \) augments, more jobs come into our data center, therefore, the system has to turn servers from OFF to MIDDLE more quickly. \(\tau \) thus gradually decreases in inverse proportion \(\lambda \). However, when \(\lambda \) exceeds 8, traffic intensity \(\rho \) tends to 1, almost servers are in ON state, and \(\tau \) increases as shown in the Fig. 1.

Fig. 1.
figure 1

Time period

Full size image
Fig. 2.
figure 2

Mean job waiting time

Full size image
Fig. 3.
figure 3

Abandonment proportion

Full size image
Fig. 4.
figure 4

Block proportion

Full size image

To compare Ab(ON/OFF/MIDDLE/c/K) and Ab(ON/OFF/c/K), we measure three metrics, including: mean waiting time, abandonment and block proportion. The achieved results are shown by Figs. 2, 3, and 4 respectively. In Fig. 2, it is easy to see that when \(\lambda \) is in range (1, 6), the mean job waiting time of Ab(ON/OFF/MIDDLE/c/K) model is significantly smaller than Ab(ON/OFF/c/K). However, there is no big difference between two models when \(\lambda \) is in range of (7, 10). This could be explained as follows. While arrival rate is high (\(\lambda \) > 6), almost all servers are in ON state, consequently the number of MIDDLE and SETUP servers is small. In this case, our proposed control algorithm effectiveness is insignificant. On the other hand, as presented before, because \(\lambda \) is large, ON server quantity also is large, the mean job waiting time thus decreases and the number of leaving jobs also is small. Through this experiment, we demonstrate that our proposed model operates more effectively than the two-state model. Figure 3 shows abandonment proportion of both model with diverse values of \(\lambda \) and \(\theta \). The Ab(ON/OFF/MIDDLE/c/K) model thus obtains better outcomes as compared with Ab(ON/OFF/c/K) when \(\lambda \) is in range (1, 6). However, when \(\lambda \) in range (6, 10), almost all servers in this time are in ON state, so there is no big difference between two models. Like the mean waiting time results above, the job abandonment proportion decreases when \(\lambda \) increases. This happens because while \(\lambda \) augments, the mean waiting time decreases, hence jobs in queue have to wait for processing in a shorter time. This leads to the abandonment probability of a single job reduces, and the job abandonment proportion decreases. The block proportion results of both models with different values of \(\lambda \) and \(\theta \) are described by Fig. 4. It can be seen that Ab(ON/OFF/MIDDLE/c/K) has smaller job block proportion as compared with Ab(ON/OFF/c/K). The reason for this issue is that with \(\lambda \) augments, traffic intensity tends to 1, so system thus also tends to reach overload point. As a result, there is a large number of jobs, which is blocked during system operation.

4 Conclusion and Future Work

In this paper, we developed a new management strategy for cloud data center under job abandonment phenomenon called Ab(ON/OFF/MIDDLE/c/K), which reduces the mean job waiting time inside the cloud system. We tested and evaluated Ab(ON/OFF/MIDDLE/c/K) by CloudSim in the simulated cloud environment. Achieved results show that our new model works well and brings good performance as compared with the two-state server model under the job abandonment phenomenon. In the near future, we will continue to evaluate our model in the aspect of energy consumption.