Abstract
We present the first lattice-based group signature scheme whose cryptographic artifacts are of size small enough to be usable in practice: for a group of \(2^{25}\) users, signatures take 910 kB and public keys are 501 kB. Our scheme builds upon two recently proposed lattice-based primitives: the verifiable encryption scheme by Lyubashevsky and Neven (Eurocrypt 2017) and the signature scheme by Boschini, Camenisch, and Neven (IACR ePrint 2017). To achieve such short signatures and keys, we first re-define verifiable encryption to allow one to encrypt a function of the witness, rather than the full witness. This definition enables more efficient realizations of verifiable encryption and is of independent interest. Second, to minimize the size of the signatures and public keys of our group signature scheme, we revisit the proof of knowledge of a signature and the proofs in the verifiable encryption scheme provided in the respective papers.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Lattice-based cryptography has made substantial advances and now includes public-key encryption schemes [30, 31] and digital signature schemes [14, 15, 27] that are essentially as practical as those based on traditional number-theoretic assumptions: all keys and outputs are less than 1 kB for 128 bits of security. Somewhat more complex primitives such as identity-based encryption [15, 19] can be implemented with keys and ciphertexts being around 4 kB, and the best blind signature scheme [35] has artifacts of around 100 kB. For group signatures [13], however, the lattice-based schemes known are much less efficient than their traditional counterparts, despite the attention they have recently received.
In a group signature scheme, the group manager provides distinct secret keys to each user, who is then able to sign messages anonymously on behalf of the group. While anyone can check that a message was signed by a group member, only the opener is able to recover the identity of the originator of a signature. Group signatures are particularly useful in scenarios where remote devices need to be authenticated as valid devices, but privacy imposes that individual devices can only be identified by a designated authority. Examples include government-issued electronic identity (eID) cards, where each issued smart card creates identity claims as signed statements about its attributes, without needing to fully identify its owner [6], or remote anonymous attestation of computing platforms, where devices prove which software they execute [9].
A typical approach to construct a group signature scheme is to use a signature scheme, an encryption scheme, and a non-interactive zero-knowledge proof of knowledge (NIZK PoK) [1, 5, 12] as follows. The group public key consists of the group manager’s signature public key and the opener’s encryption public key. A user’s secret key is a signature by the group manager on the identity of the user. To sign a message, the user encrypts her identity under the opener’s public key and creates a NIZK PoK of a signature on the encrypted value.
The main obstacle in achieving an efficient scheme with this approach is the efficiency of the NIZK PoK and the choice of signature and encryption schemes that allow for an efficient NIZK PoK. In this paper, we build a dynamic group signature scheme by combining the recent signature scheme with protocols by Boschini et al. [8] and the recent (verifiable) encryption scheme by Lyubashevsky and Neven [29]. Both these schemes already come with NIZK proofs of knowledge of a signature and of a plaintext, but their straightforward combination results in a group signature scheme that is not practical due to its large signature size.
Our Techniques and Results. Boschini et al. [8] presented a (relaxed) signature scheme allowing for efficient zero-knowledge proofs of knowledge of a signature on a hidden message, where a signature on a polynomial with small coefficients \(\mathbf {m}\) is a vector \(\mathbf {S}\) of small-coefficient polynomials (or “short” vector) such that \([\mathbf {A}|\mathbf {B}|\mathbf {C}+\mathbf {m}\mathbf {G}|\mathbf {1}]\mathbf {S}=\mathbf {u}\), where the public key contains row vectors \(\mathbf {A},\mathbf {B},\mathbf {C},\mathbf {G}\) and a polynomial \(\mathbf {u}\). To prove knowledge of a signature on a hidden message, the prover first generates a commitment \(\mathbf {F} = \mathbf {b}^{-1} (\mathbf {C}+\mathbf {m}\mathbf {G}+\mathbf {E})\) to \(\mathbf {m}\), where \(\mathbf {b}\) is a random small-coefficient polynomial and \(\mathbf {E}\) is an error vector. The commitment \(\mathbf {F}\) can be plugged into the verification equation by computing a short vector \(\mathbf {S}'\) such that \([\mathbf {A}|\mathbf {B}|\mathbf {F}|\mathbf {1}]\mathbf {S}'=\mathbf {u}\). The prover can then use Lyubashevsky’s Fiat-Shamir with aborts technique [27] to prove knowledge of

The relaxed verifiable encryption scheme of Lyubashevsky and Neven [29] can encrypt a witness \(\mathbf {x}\) to a relation \(\mathbf {M}\mathbf {x} = \mathbf {y}\) so that decryption is guaranteed to yield \((\bar{\mathbf {x}},\bar{\mathbf {c}})\) such that \(\mathbf {M}\bar{\mathbf {x}}= \bar{\mathbf {c}}\mathbf {y}\). The most straightforward way to build a group signature scheme would be to combine it with the above building blocks, letting a user’s signing key be given by a signature  by the group manager on the user’s identity
by the group manager on the user’s identity  , and letting a group signature be a non-interactive proof of relations (I) and (II), combined with a verifiable encryption to allow the opener to recover the user’s identity
, and letting a group signature be a non-interactive proof of relations (I) and (II), combined with a verifiable encryption to allow the opener to recover the user’s identity  .
.
The problem with this approach is that the Lyubashevsky-Neven verifiable encryption scheme encrypts the full witness  , rather than just the witness
, rather than just the witness  , resulting in a very long signature size. In this paper, we define a variant of relaxed verifiable encryption that encrypts only part of the witness, resulting in a much shorter signature size. In this way, given \(\mathbf {F}\) as before, it is possible to encrypt the message \(\mathbf {m}\) and still prove that it was used to construct \(\mathbf {F}\), without having to also encrypt \(\mathbf {S}\), \(\mathbf {b}\), and \(\mathbf {E}\). Moreover, we prove relations (I) and (II) in two separate proofs, resulting in better parameters.
, resulting in a very long signature size. In this paper, we define a variant of relaxed verifiable encryption that encrypts only part of the witness, resulting in a much shorter signature size. In this way, given \(\mathbf {F}\) as before, it is possible to encrypt the message \(\mathbf {m}\) and still prove that it was used to construct \(\mathbf {F}\), without having to also encrypt \(\mathbf {S}\), \(\mathbf {b}\), and \(\mathbf {E}\). Moreover, we prove relations (I) and (II) in two separate proofs, resulting in better parameters.
Our group signature scheme satisfies anonymity and traceability as defined by Bellare et al. [4] in the random-oracle model. Analogously to the non-lattice-based world, where schemes under weak assumptions do exist [3, 4] but truly practical schemes typically require stronger assumptions [1, 7], we also prove our scheme secure under relatively strong assumptions. Namely, we follow the approach by Boschini et al. [8] and use two interactive assumptions that can be interpreted in two different ways. One can either believe the interactive assumptions as stated, in which case we obtain a tight security reduction and the most efficient parameters for our scheme, resulting in signatures of 910 kB for a group of \(2^{25}\) users and 80 bits of security. Alternatively, one can see our assumptions as being implied by the standard Ring-SIS and Ring-LWE assumptions through a complexity leveraging argument. To compensate for the loose reduction, the parameters increase, resulting in signatures of 1.72 MB.
Related Work. The early lattice-based group signature schemes [10, 20] have signature sizes that are linear in the number of group members and are therefore mainly proofs of concepts, unsuitable for any practical application. Later schemes [21, 25, 34] are asymptotically more efficient with signature sizes being logarithmic in the number of users.
Making use of the advances in lattice-based signature schemes, a number of group signature schemes were proposed following the general construction approach we have outlined earlier [21, 23,24,25,26, 37]. These schemes use as proof of knowledge protocols either an adaptation of Stern’s protocol [36] or the “single-bit-challenge” version of the lattice-based Fiat-Shamir protocol by Lyubashevsky [27]. As these proofs have soundness error 2/3 and 1/2, respectively, they need to be repeated sufficiently many times in parallel, resulting in group signature schemes that can hardly be considered practical. None of these scheme give concrete parameters, providing asymptotic efficiency analyses instead. The only exception is the scheme by Libert et al. [23] which is the most efficient scheme prior to ours, with signatures over 60 MB and public keys of 4.9 MB for a group size of only \(2^{10}\) users for 80 bits of security – still much less efficient than ours.
2 Prerequisites
We denote vectors and matrices with upper-case letters. Column vectors are denoted as \(V=\begin{bmatrix} v_1&;&\ldots&;&v_n\end{bmatrix}\) and row vectors as \(V=\begin{bmatrix} v_1&\ldots&v_n\end{bmatrix}\). Sampling and element x from a distribution \(\mathcal {D}\) will be denoted as  . If x is sampled from a uniform over a set A, we will abuse the notation and write
. If x is sampled from a uniform over a set A, we will abuse the notation and write  . With \(x\leftarrow a\) we will denote that x is assigned the value a. When necessary, we will denote the uniform distribution over a set S as \(U({S})\).
. With \(x\leftarrow a\) we will denote that x is assigned the value a. When necessary, we will denote the uniform distribution over a set S as \(U({S})\).
2.1 Polynomial Rings
Consider the polynomial ring \(\mathcal {R}_{q}=\mathbb {Z}_q/\langle \mathbf {x}^n+1\rangle \) for a prime \(q\equiv 5\text { mod }8\). Elements in the ring are polynomials of degree at most \(n-1\) with coefficients in \(\left[ -(q-1)/2,(q-1)/2\right] \) and operations between ring elements are done modulo q. Let \(\deg (\mathbf {a})\) be the degree of the polynomial \(\mathbf {a}\). For an element \(\mathbf {a}=\sum _{i=0}^{n-1}a_i\mathbf {x}^i\) in \(\mathcal {R}_{q}\), the standard norms are computed as \(\Vert \mathbf {a} \Vert _1=\sum _i|a_i|\), \(\Vert \mathbf {a} \Vert =\sqrt{\sum _ia_i^2}\) and \(\Vert \mathbf {a} \Vert _\infty =\max |a_i|\). For any K|n, we can construct a subring \(\mathcal {R}_{q}^{(K)}\) of \(\mathcal {R}_{q}\) as the subset of elements \(\mathbf {a}\in \mathcal {R}_{q}\) such that \(\mathbf {a}=\sum _{i=0}^{K-1}a_i\mathbf {x}^{in/K}\). For integer p, \(\mathcal {R}_{p}\) (resp., \(\mathcal {R}_{p}^{(K)}\)) is the subset of \(\mathcal {R}_{q}\) (resp., \(\mathcal {R}_{q}^{(K)}\)) that contains polynomials with coefficients in \([-(p-1)/2,(p-1)/2]\). Lemma 1 shows that the ring \(\mathcal {R}_{q}\) has a large set of invertible elements that are easy to identify.
Lemma 1
([29, Lemma 2.2]). Let \(\mathcal {R}_{q}=\mathbb {Z}_q[\mathbf {x}]/\langle \mathbf {x}^n+1\rangle \) where \(n>1\) is a power of 2 and q is a prime congruent to \(5\text { mod }8\). This ring has exactly \(2q^{n/2}-1\) elements without an inverse. Moreover, every non-zero polynomial \(\mathbf {a}\) in \(\mathcal {R}_{q}\) with \(\Vert \mathbf {a} \Vert _\infty <\sqrt{q/2}\) has an inverse.
There are some easy bounds on the norm of the product of polynomials.
Lemma 2
For \(\mathbf {a},\mathbf {b}\in \mathcal {R}_{q}\) it holds: \(\Vert \mathbf {a}\mathbf {b} \Vert _\infty \le \min \left\{ \Vert \mathbf {a} \Vert _\infty \Vert \mathbf {b} \Vert _1,(q-1)/2\right\} \). Moreover, let \(\mathbf {a},~\mathbf {b}\in \mathcal {R}_{q}\) be such that \(n\Vert \mathbf {a} \Vert _{\infty }\cdot \Vert \mathbf {b} \Vert _{\infty }\le (q-1)/2\). Then we have that \(\Vert \mathbf {a}\mathbf {b} \Vert \le \Vert \mathbf {a} \Vert \Vert \mathbf {b} \Vert \sqrt{n}\) and \(\Vert \mathbf {a}\mathbf {b} \Vert _{\infty }\le \Vert \mathbf {a} \Vert _{\infty }\Vert \mathbf {b} \Vert _{\infty }n\le \frac{q-1}{2}\).
2.2 Lattices
An integer lattice is an additive subgroup of \(\mathbb {Z}^n\). Every lattice \(\varLambda \) is generated by a basis \(\mathbf {B}=\{\mathbf {b}_1,\ldots ,\mathbf {b}_k\}\in \mathbb {Z}^{n\times m}\), where m is called dimension of the lattice. Such lattice is denoted by \(\varLambda =\mathcal {L}(\mathbf {B})\). If \(k=n\) and the vectors in the basis are linearly independent the lattice is a full-rank lattice. The Gram-Schmidt orthogonalization of a full-rank basis \(\mathbf {B}\) is denoted by \(\tilde{\mathbf {B}}=\{\tilde{\mathbf {b}}_1,\ldots \tilde{\mathbf {b}}_n\}\). Let \(\tilde{\lambda }(\mathcal {L}(\mathbf {B}))=\min _{\mathbf {B}'\text {s.t.}\mathcal {L}(\mathbf {B}')=\mathcal {L}(\mathbf {B})}\Vert \tilde{\mathbf {B}}' \Vert \). For a matrix \(\mathbf {A}\in \mathbb {Z}^{n\times m}\), \(\varLambda ^{\bot }\) is the lattice: \(\varLambda ^{\bot }=\mathcal {L}^{\bot }(\mathbf {A})=\{\mathbf {x}\in \mathbb {Z}^m\,|\,\mathbf {A}\mathbf {x}=\mathbf {0}\text { mod }q\}\subseteq \mathbb {Z}^{m}\). We define the discrete Gaussian distribution centered in \(\mathbf {c}\) with standard deviation \(\sigma \) on a full-rank lattice \(\varLambda \) as \(\mathcal {D}^{}_{\varLambda ,\mathbf {c},\sigma }(\mathbf {v})=e^{-\frac{\pi \Vert \mathbf {v}-\mathbf {c} \Vert ^2}{\sigma ^2}}/ \sum _{\mathbf {u}\in \varLambda }e^{-\frac{\pi \Vert \mathbf {u}-\mathbf {c} \Vert ^2}{\sigma ^2}}\) for all \(\mathbf {v}\in \varLambda \), and 0 on all the other points in the space. Let \(\mathcal {D}^{\bot }_{\mathbf {A},\mathbf {u},\sigma }\) be the distribution of the vectors \(\mathbf {s}\) such that \(\mathbf {s}\sim \mathcal {D}^{}_{\mathbb {Z}^n,\mathbf {0},\sigma }\) conditioned on \(\mathbf {A}\mathbf {s}=\mathbf {u}\text { mod }q\).
Lemma 3
(cf. [2, Lemma 1.5], [27, Lemma 4.4]). Let \(\mathbf {A}\in \mathbb {Z}^{n\times m}\) with \(2^{11}< m\) and \(\mathbf {u}\in \mathbb {Z}^n_q\). For \(\sigma \ge \tilde{\lambda }(\mathcal {L}^\perp (\mathbf {A}))\) it holds:
 .
.
In particular, the inequalities hold also when  .
.
2.3 Lattices over Rings
Lattices over the polynomial ring \(\mathcal {R}_{q}\) can be defined similarly to lattices over \(\mathbb {Z}_q\). Indeed, given \(\mathbf {A}\in \mathcal {R}_{q}^{1\times m}\) we can construct m-dimensional lattice \(\mathcal {L}^{\bot }(\mathbf {A})\) as \(\varLambda ^{\bot }=\mathcal {L}^{\bot }(\mathbf {A})=\{\mathbf {V}\in \left( \mathbb {Z}[\mathbf {x}]/\langle \mathbf {x}^n+1\rangle \right) ^m\,|\, \mathbf {A}\mathbf {V}=\mathbf {0}\text { mod }q\}\subseteq \mathcal {R}_{q}^m\). Consider the obvious embedding that maps a polynomial to the vector of its coefficients. Then \(\varLambda ^{\bot }\) can be also seen as a nm-dimensional integer lattice over \(\mathbb {Z}\). With a slight abuse of notation, we will write  to indicate that \(\mathbf {y}\) was sampled from \(\mathcal {D}^{}_{\mathbb {Z}^n,\mathbf {u},\sigma }\) and then mapped to \(\mathcal {R}_{q}\). Similarly, we omit the \(\mathbf {0}\) and write
to indicate that \(\mathbf {y}\) was sampled from \(\mathcal {D}^{}_{\mathbb {Z}^n,\mathbf {u},\sigma }\) and then mapped to \(\mathcal {R}_{q}\). Similarly, we omit the \(\mathbf {0}\) and write  to mean that a vector \(\mathbf {y}\) is generated according to \(\mathcal {D}^{}_{\mathbb {Z}^{kn},\mathbf {0},\sigma }\) and then gets interpreted as k polynomials \(\mathbf {y}_i\).
to mean that a vector \(\mathbf {y}\) is generated according to \(\mathcal {D}^{}_{\mathbb {Z}^{kn},\mathbf {0},\sigma }\) and then gets interpreted as k polynomials \(\mathbf {y}_i\).
We recall some results about sampling an element from a Gaussian distribution over a lattice given some trapdoor.
Theorem 1
(adapted from [32]). Let \(\mathbf {A}\) be a vector in \(\mathcal {R}_{q}^{1\times \ell }\) and \(\mathbf {X}\) be a matrix in \(\mathcal {R}_{q}^{\ell \times m}\). Also define the gadget matrix \(\mathbf {G}=\begin{bmatrix} 1&\lceil q^{1/m}\rceil&\ldots&\lceil q^{(m-1)/m}\rceil \end{bmatrix}\). Then for any invertible \(\mathbf {m}\in \mathcal {R}_{q}\), there is an algorithm that can sample from the distribution  for any
for any  for any
for any  .
.
Lemma 4
Suppose \(\mathbf {U}\in \mathcal {R}_{q}^{1\times k}\) and \(\mathbf {V}\in \mathcal {R}_{q}^{1\times m}\) are polynomial vectors, and \(\mathbf {B}_U,\mathbf {B}_{(U,V)}\) are bases of \(\varLambda ^{\bot }(\mathbf {U})\) and \(\varLambda ^{\bot }(\begin{bmatrix} \mathbf {U}&\mathbf {V} \end{bmatrix})\) respectively such that \(\Vert {\tilde{\mathbf {B}}_U}\Vert \), \(\Vert {\tilde{\mathbf {B}}_{(U,V)}}\Vert < \sigma \sqrt{\pi /\ln (2n+4)}\). Then, there exists an algorithm \(\mathsf {SampleD}(\mathbf {U},\mathbf {V},\mathbf {B},\mathbf {u},\sigma )\), where \(\mathbf {B}\) is either \(\mathbf {B}_U\) or \(\mathbf {B}_{(U,V)}\), that can efficiently sample from the distribution  for any
for any  .
.
2.4 Hardness Assumptions
We recall two well-studied lattice problems over rings: Ring-SIS and Ring-LWE.
Definition 1
(Ring-SIS\(_{m,q,\beta }\) problem). The Ring-SIS\(_{m,q,\beta }\) problem is given a vector \(\mathbf {A}\in \mathcal {R}_{q}^{1\times (m-1)}\) to find a vector \(\mathbf {S}\in \mathcal {R}_{q}^m\) such that \(\begin{bmatrix} \mathbf {A}&\mathbf {1}\end{bmatrix}\mathbf {S}=\mathbf {0}\) and \(\Vert \mathbf {S} \Vert \le \beta \).
Definition 2
The Ring-LWE\(_{D}\) distribution outputs pairs \((\mathbf {a},\mathbf {b})\in \mathcal {R}_{q}\times \mathcal {R}_{q}\) such that \(\mathbf {b}=\mathbf {a}\mathbf {s}+\mathbf {e}\) for a uniformly random \(\mathbf {a}\) from \(\mathcal {R}_{q}\) and \(\mathbf {s},\mathbf {e}\) sampled from distribution D. The Ring-LWE\(_{k,D}\) decisional problem on ring \(\mathcal {R}_{q}\) with distribution D is to distinguish whether k pairs \((\mathbf {a}_1,\mathbf {b}_1),\ldots ,(\mathbf {a}_k,\mathbf {b}_k)\) were sampled from the Ring-LWE\(_{D}\) distribution or from the uniform distribution over \(\mathcal {R}_{q}^2\).
There is a polynomial-time reduction from solving the shortest vector problem over rings to Ring-SIS [28, Theorem 5.1] and a polynomial-time quantum reduction from solving the shortest vector problem over rings to Ring-LWE with Gaussian error distribution (cf. [30]). The root Hermite factor \(\delta \) introduced by Gama and Nguyen [18] is used to estimate the hardness of the lattice problems for given parameters in the security reductions.
Boschini et al. [8] introduce new hardness assumptions to be able to prove their schemes secure with or without complexity leveraging. The idea is to state the assumptions in two forms, selective and adaptive. The schemes are proved secure assuming the adaptive variants of the assumptions. Then, a reduction from adaptive to selective is proved using complexity leveraging, and Ring-SIS and Ring-LWE are reduced to the selective version. Hence, allowing the use of complexity leveraging it is possible to base the security of the schemes on Ring-SIS and Ring-LWE, otherwise security is guaranteed under the adaptive version of the new hardness assumptions (cf. Assumptions 1 and 3).
Assumption 1
Consider the following game between an adversary \(\mathsf {A}\) and a challenger for fixed \(m \in \mathbb {N}\) and distribution D:
-
1.
The challenger outputs a uniformly random
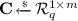 to \(\mathsf {A}\).
to \(\mathsf {A}\). -
2.
\(\mathsf {A}\) sends back \(\mathbf {m}\in \mathcal {U}\).
-
3.
The challenger picks a uniformly random bit
 . If \(b=1\), it samples an error vector
. If \(b=1\), it samples an error vector 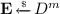 and
and 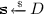 , and sends \(\mathbf {F} = (\mathbf {C}+\mathbf {m}\mathbf {G}-\mathbf {E})\mathbf {s}^{-1}\) to \(\mathsf {A}\). Otherwise, it sends a uniform
, and sends \(\mathbf {F} = (\mathbf {C}+\mathbf {m}\mathbf {G}-\mathbf {E})\mathbf {s}^{-1}\) to \(\mathsf {A}\). Otherwise, it sends a uniform 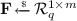 to \(\mathsf {A}\).
to \(\mathsf {A}\). -
4.
\(\mathsf {A}\) sends a bit \(b'\) to the challenger.
The advantage of \(\mathsf {A}\) in winning the game is \(\left| \mathsf {Pr}(b=b')-\frac{1}{2}\right| \). The assumption states that no PPT \(\mathsf {A}\) can win the previous game with non-negligible advantage.
Assumption 2
(Selective variant of Assumption 1). Consider the game of Assumption 1, but with steps 1 and 2 switched, meaning, \(\mathsf {A}\) outputs \(\mathbf {m} \in \mathcal {U}\) before being given \(\mathbf {C}\). The assumption states that no PPT adversary can win this previous game with non-negligible advantage.
Boschini et al. proved that Assumption 2 is at least as hard as Ring-LWE with m samples and distribution D. It is possible to reduce Assumption 2 to 1 with a complexity leveraging argument by guessing the value of \(\mathbf {m} \in \mathcal {U}\).
Assumption 3
Let \(\bar{\varSigma }= \{(\mathbf {c}_1,\mathbf {S},\mathbf {c}_2)\in \bar{\mathcal {C}}\times \mathcal {R}_{q}^{3+2m}\times \mathcal {R}_{q}:\;\Vert \mathbf {S} \Vert \le N'~\wedge ~\Vert \mathbf {c}_2 \Vert \le C'\}\) for some fixed parameters. Consider the following game between an adversary \(\mathsf {A}\) and a challenger for fixed \(m \in \mathbb {N}\) and distribution D:
-
1.
The challenger chooses
 , and
, and  . It sets \(\mathbf {A}=[\mathbf {a}|\mathbf {1}]\) and \(\mathbf {B}=\mathbf {A}\mathbf {X}+\mathbf {G}\), where \(\mathbf {G} = \begin{bmatrix} 1&\lceil q^{1/m}\rceil&\ldots&\lceil q^{(m-1)/m}\rceil \end{bmatrix}\).
. It sets \(\mathbf {A}=[\mathbf {a}|\mathbf {1}]\) and \(\mathbf {B}=\mathbf {A}\mathbf {X}+\mathbf {G}\), where \(\mathbf {G} = \begin{bmatrix} 1&\lceil q^{1/m}\rceil&\ldots&\lceil q^{(m-1)/m}\rceil \end{bmatrix}\). -
2.
The challenger runs \(\mathsf {A}\) on input \(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C}&\mathbf {1} \end{bmatrix}\), giving it access to a random oracle \(\mathcal {H}: \{0,1\}^* \rightarrow \mathcal {R}_{q}\) and an oracle \(\mathcal {O}_{S}\) that on input \(\mathbf {m}\in \mathcal {U}\) and a string \(\alpha \in \{0,1\}^*\) outputs a small vector \(\begin{bmatrix} \mathbf {S}&;&\mathbf {0}\end{bmatrix}\) in the coset \(\mathcal {L}^\bot (\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C}+\mathbf {m}\mathbf {G}&\mathbf {1} \end{bmatrix})+\mathcal {H}(\alpha )\) such that \(\Vert \mathbf {S} \Vert \le N_S\).
-
3.
Algorithm \(\mathsf {A}\) outputs \(\bar{\mathbf {m}} \in \bar{\mathcal {U}}\), \(\bar{\alpha }\in \{0,1\}^*\), \(\bar{\mathbf {c}}_1 \in \bar{\mathcal {C}}\), a ring element \(\bar{\mathbf {c}}_2\) and a vector \(\bar{\mathbf {S}}\). Algorithm \(\mathsf {A}\) wins the game if \((\bar{\mathbf {c}}_1,\bar{\mathbf {S}},\bar{\mathbf {c}}_2)\in \bar{\varSigma }\), \(\bar{\mathbf {m}}\in \bar{\mathcal {U}}\), such that \(\mathbf {S}\) is a short vector of the coset \(\mathcal {L}^\bot (\begin{bmatrix} \mathbf {A}&\mathbf {B}&\bar{\mathbf {C}}&\mathbf {1}\end{bmatrix})+\mathbf {c}_2\mathcal {H}(\bar{\alpha }))\) where \(\bar{\mathbf {C}}=\bar{\mathbf {c}}_1\mathbf {C}-\bar{\mathbf {m}}\mathbf {G}\), and \((\bar{\mathbf {m}}\bar{\mathbf {c}}_1^{-1},\bar{\alpha })\) was not queried to the \(\mathcal {O}_{S}\) oracle.
The assumption states that no PPT algorithm \(\mathsf {A}\) can win the game with non-negligible probability.
Assumption 4
(Selective variant of Assumption 3). Consider the game of Assumption 3, but where step 1 is preceded with a step where \(\mathsf {A}\), on input only the security parameter \(\lambda \), outputs the message \(\bar{\mathbf {m}} \in \bar{\mathcal {U}}\), and in step 3 outputs the remaining items \(\bar{\alpha }\), \(\bar{\mathbf {c}}_1, \bar{\mathbf {c}}_2 \in \bar{\mathcal {C}}\), and \(\bar{\mathbf {S}}\). The assumption states that no PPT adversary can win this previous game with non-negligible advantage.
Theorem 2
(Hardness of Assumption 4). Let \(\mathsf {A}\) be a probabilistic algorithm that breaks Assumption 4 in time t with probability \(\epsilon _A\). Then there exists a probabilistic algorithm \(\mathsf {B}\) that either breaks Ring-LWE\(_{m,\mathcal {D}^{}_{\sigma }}\) in time t with probability \(\epsilon _A\) or Ring-SIS\(_{3+m,q,\beta _s}\) in time t with probability \(\epsilon _B\ge (\epsilon _A-\epsilon _{\mathrm {LWE}})/(2\cdot |\bar{\mathcal {C}}|)\), where \(\beta _\mathrm {s}=N'^2+\frac{\sigma _t^2}{\pi }n^2(\sqrt{2}+\sqrt{m}+\log {n})^2(2\sqrt{2^{K_c}})^2N'^2+\frac{\sigma ^2}{\pi }n(1+\sqrt{2}+\log {n})^2(C'^2+(1.05\sigma _t\sqrt{n})^2)\), \(\epsilon _{\mathrm {LWE}}\) is the probability of breaking the Ring-LWE problem over \(\mathcal {R}_{q}\) in time t, in the Random Oracle Model.
The bound \(\beta _\mathrm {s}\) is different from the original result, as we choose larger message and challenge spaces. From complexity leveraging (guessing \(\bar{\mathbf {m}}\) in \(\bar{\mathcal {U}}\) and \(\bar{c}_1\) in \(\bar{\mathcal {C}}\)) it follows that breaking Assumption 4 implies breaking Assumption 3.
2.5 Group Signature
A group signature is a set of algorithms \((\mathsf {GPGen},\mathsf {GKGen},\mathsf {UKGen},\mathsf {OKGen},\mathsf {GSign},\mathsf {GVerify},\mathsf {GOpen})\) run by a group manager, an opener and users. The group signature parameters \( gpar \) are generated via \(\mathsf {GPGen}(1^\lambda )\) (where \(\lambda \) is the security parameter). The group manager and the opener generate their keys running \(( gpk , gsk )\leftarrow \mathsf {GKGen}( gpar )\) and \(( opk , osk )\leftarrow \mathsf {OKGen}( gpk )\) respectively. If a user wants to join, she sends her identity to the group manager and obtains back her user secret key \( usk \leftarrow \mathsf {UKGen}( gsk , id )\). The user can sign a message \(M\) on behalf of the group using her secret key with the algorithm \(\mathsf {GSign}( usk , gpk , opk ,M)\). A signature \( sig \) on a message \(M\) can be verified with the algorithm \(\{1,0\}\leftarrow \mathsf {GVerify}(M, sig , gpk , opk )\). Finally, the opener can recover the identity of the group member that signed a message \(M\) running \( id \leftarrow \mathsf {GOpen}(M, sig , osk )\). We require the scheme to be correct (honestly generated signatures satisfy verification and can be opened to the identity of the signer), traceable (the group manager should be able to link every signature to the user who produced it) and anonymous (signatures produced by different users should be indistinguishable).
2.6 One-Time Signature
A One-Time Signature (OTS) scheme for message set \(\mathcal {M}\) is a triple \((\mathsf {OTSGen},\mathsf {OTSSign},\mathsf {OTSVf})\), where \(( sk , vk )\leftarrow \mathsf {OTSGen}(1^\lambda )\) is the key generation algorithm, \( ots \leftarrow \mathsf {OTSSign}( sk , msg )\) is the signing algorithm and \(0/1\leftarrow \mathsf {OTSVf}( vk , msg , ots )\) is the verification algorithm. Correctness requires that for all security parameters \(\lambda \in \mathbb {N}\) the verification of a honestly generated signature always outputs 1. An OTS is unforgeable if, given \( sk \), \( vk \), no adversary can come up with a signature on a message \( msg '\) w.r.t. \( vk \) after seeing a signature on \( msg \) generated using \( sk \). In particular, the Lamport signature [22] is quantum-secure, thus it can be used with the relaxed \(\varSigma \)-protocol.
2.7 Relaxed ZK Proofs
Given two NP-languages \( L \subseteq \bar{ L }\) defined by the relations \( R \subseteq \bar{ R }\) respectively, a relaxed \(\varSigma \)-protocol for \( L ,\bar{ L }\) is a three-rounds two-party protocol between PPT algorithms \((\mathcal {P},\mathcal {V})\) that satisfies standard completeness and zero-knowledge, but where extraction is only guaranteed to output a witness \(w\) such that \((x,w)\in \bar{ R }\). A protocol can be made non-interactive using Fiat-Shamir transform [17]. Simulation-soundness of the transform can be ensured (cf. [16]) by a property called “quasi-unique responses”: it should be impossible for an adversary to create two valid transcripts that differ only in the responses. Applying the Fiat-Shamir transform to a relaxed \(\varSigma \)-protocol with quasi-unique responses results in a relaxed NIZK proof, i.e., a non-interactive protocol that satisfies classical completeness, unbounded non-interactive zero-knowledge and the following relaxed definition of simulation soundness:
Definition 3
(Relaxed unbounded simulation soundness). There exists a PPT simulator \(\mathsf{S}\) such that for all PPT adversaries \(\mathsf {A}\),

is negligible, where \(Q\) is the set of tuples \((x,\pi )\) where \(\mathsf {A}\) made a query \(\mathsf{S}_2(x)\) and obtained response \(\pi \).
It is also possible to obtain relaxed unbounded simulation soundness using an OTS scheme with the Fiat-Shamir transform. A formal description and full proof of the construction can be found in the work by Boschini et al. [8].
To instantiate such protocols over lattices, consider the languages \(( L ,\bar{ L })\) associated with the following relations:

where \(0<N\le \bar{N}_2\), \(0<\bar{N}_\infty \) and, if the set of the challenges used in the protocol is \(\mathcal {C}\), the set of relaxed challenges is \(\bar{\mathcal {C}}=\{\mathbf {c}-\mathbf {c}'~:~\mathbf {c},\mathbf {c}'\in \mathcal {C}\}\). Finding a witness \((\mathbf {S},\mathbf {c})\) for an element \((\mathbf {A},\mathbf {U})\) of the language \(\bar{ L }\) is hard under the computational assumption that Ring-SIS\(_{\bar{N}}\) is hard. In the relaxed \(\varSigma \)-protocol for \( L ,\bar{ L }\), the prover \(\mathcal {P}\) samples a masking vector  and sends \(\mathbf {T}=\mathbf {A}\mathbf {Y}\) to the verifier \(\mathcal {V}\). Next, \(\mathcal {V}\) samples a challenge \(\mathbf {c}\in \mathcal {C}\) and sends it back to \(\mathcal {P}\). The prover constructs \(\mathbf {Z}=\mathbf {Y}+\mathbf {c}\mathbf {S}\) and, depending on rejection sampling (see [27, Theorem 4.6]), either aborts or sends it to \(\mathcal {V}\). The verifier accepts if \(\mathbf {A}\mathbf {Z}-\mathbf {c}\mathbf {U}=\mathbf {T}\) and \(\Vert \mathbf {Z} \Vert \le 1.05\sigma \sqrt{mn}=:N_2\), \(\Vert \mathbf {Z} \Vert _\infty \le 8\sigma =:N_\infty \). The zero-knowledge property is guaranteed by rejection sampling. A standard deviation \(\sigma =12T\), where T is a bound on the norm of \(\mathbf {c}\mathbf {S}\) obtained from N, guarantees that the prover outputs something with probability greater than \((1--2^{100})/e\) (cf. [27, Theorem 4.6]). Setting \(\bar{N}_2=2N_2=2.1\sigma \sqrt{mn}\) and \(\bar{N}_\infty =2N_\infty =16\sigma \) allows to prove that this is a relaxed \(\varSigma \)-protocol.
and sends \(\mathbf {T}=\mathbf {A}\mathbf {Y}\) to the verifier \(\mathcal {V}\). Next, \(\mathcal {V}\) samples a challenge \(\mathbf {c}\in \mathcal {C}\) and sends it back to \(\mathcal {P}\). The prover constructs \(\mathbf {Z}=\mathbf {Y}+\mathbf {c}\mathbf {S}\) and, depending on rejection sampling (see [27, Theorem 4.6]), either aborts or sends it to \(\mathcal {V}\). The verifier accepts if \(\mathbf {A}\mathbf {Z}-\mathbf {c}\mathbf {U}=\mathbf {T}\) and \(\Vert \mathbf {Z} \Vert \le 1.05\sigma \sqrt{mn}=:N_2\), \(\Vert \mathbf {Z} \Vert _\infty \le 8\sigma =:N_\infty \). The zero-knowledge property is guaranteed by rejection sampling. A standard deviation \(\sigma =12T\), where T is a bound on the norm of \(\mathbf {c}\mathbf {S}\) obtained from N, guarantees that the prover outputs something with probability greater than \((1--2^{100})/e\) (cf. [27, Theorem 4.6]). Setting \(\bar{N}_2=2N_2=2.1\sigma \sqrt{mn}\) and \(\bar{N}_\infty =2N_\infty =16\sigma \) allows to prove that this is a relaxed \(\varSigma \)-protocol.
The proof-system we introduced can be adapted to prove that a component \(\mathbf {s}_i\) of \(\mathbf {S}\) is in a subring \(\mathcal {R}_{q}^{(2^{K_m})}\) by using as challenge space \(\mathcal {C}=\mathcal {R}_{3}^{(2^{K_c})}\), that is a subset of \(\mathcal {R}_{q}^{(2^{K_m})}\) when \(K_m\ge K_c\) and sampling the i-th element of the “masking” vector \(\mathbf {Y}\) from \(\mathcal {R}_{q}^{(2^{K_m})}\). Hence the output vector \(\mathbf {Z} = \mathbf {S}\mathbf {c} + \mathbf {Y}\) is such that \(\mathbf {z}_i\in \mathcal {R}_{q}^{(2^{K_m})}\). The verifier has to check also this latter condition before accepting.
2.8 Relaxed Signatures
Boschini et at. [8] introduced a new lattice-based relaxed signature scheme, i.e., a signature \((\mathsf {SParGen},\mathsf {SKeyGen},\mathsf {Sign},\mathsf {SVerify})\) where the verification algorithm is relaxed to accept signature on messages coming from a set \(\bar{\mathcal {M}}\) larger than the set \(\mathcal {M}\) of signed messages. The signature is proved unforgeable under a relaxed notion of unforgeability under chosen-message attacks that includes as a forgery a signature on a message in \(\bar{\mathcal {M}}\) that is the image of a message in \(\mathcal {M}\) through some function \(f\) that was not signed by the signing oracle. The relaxation in the definition is necessary in order to combine the signature with the relaxed \(\varSigma \)-protocol (see Sect. 2.7).
Given that we reduce the unforgeability of the group signature directly to the hardness of Assumption 1, we do not discuss security of the signature here. We only remark that we use a different set of messages, namely \(\mathcal {U}=\mathcal {R}_{3}^{(16)}\), while the original lattice instantiation signs messages composed by a small polynomial and a bit-string. When using it in the group signature, the small polynomial \(\mathbf {m}\in \mathcal {U}\) encodes a user’s identity, but there is no need for the bit string. Therefore, we substitute the output of the hash of the bit-string with a constant polynomial \(\mathbf {u}\) chosen uniformly at random in \(\mathcal {R}_{q}\) during the key generation and sign only messages in \(\mathcal {M}=\mathcal {U}\). The modified scheme is trivially still unforgeable under Assumption 3 in the Random Oracle Model.
Parameters Generation. The parameters \( spar \) are generated by \(\mathsf {SParGen}(1^\lambda )\) and include \((n,q,m,\sigma _t,\sigma ,r,N,N',C',\mathbf {C})\) where: n is a power of 2, q is a prime, \(q\equiv 5\text { mod }8\), m determines the gadget vector \(\mathbf {G}\) in Theorem 1, \(\sigma _t\) is standard deviation of the distribution of the trapdoor, \(\sigma =q^{1/m}\frac{\sigma _t}{\sqrt{\pi }}\sqrt{n}\cdot (\sqrt{2}+\sqrt{m}+\log (n))\) is the standard deviation of the Gaussian from which signatures are sampled, r bounds the norm of the polynomial part of the messages in \(\bar{\mathcal {U}}=\mathcal {R}_{r}^{(16)}\), \(N=1.05\sigma \sqrt{n(2m+2)}\) bounds the norm of a signature output by \(\mathsf {Sign}\), \(N'>N\) and \(C'\ge 1\) define the set of valid signatures \(\bar{\varSigma }\), and \(\mathbf {C}\) is uniformly random matrix in \(\mathcal {R}_{q}^{1\times m}\).
Key generation. The signer selects a uniformly random matrix \(\mathbf {A}=\begin{bmatrix} \mathbf {a}&\mathbf {1} \end{bmatrix}\) in \(\mathcal {R}_{q}^{1\times 2}\) and an element  as verification key and a matrix with small coefficients
as verification key and a matrix with small coefficients  as secret signing key. The public verification key is the vector \(\mathbf {V} = \begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C} \end{bmatrix} = \begin{bmatrix} \mathbf {A}&\mathbf {AX}+\mathbf {G}&\mathbf {C} \end{bmatrix} \in \mathcal {R}_{q}^{1\times (2+2m)}\).
as secret signing key. The public verification key is the vector \(\mathbf {V} = \begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C} \end{bmatrix} = \begin{bmatrix} \mathbf {A}&\mathbf {AX}+\mathbf {G}&\mathbf {C} \end{bmatrix} \in \mathcal {R}_{q}^{1\times (2+2m)}\).
Signing. If \(M= \mathbf {m} \notin \mathcal {M}\) abort. Otherwise, the signer computes \(\mathbf {S}\leftarrow \mathsf {SampleD}(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C}+\mathbf {m}\mathbf {G} \end{bmatrix},\mathbf {u},\sigma )\) (see Lemma 4) and outputs a signature \( sig = (\mathbf {1},\begin{bmatrix} \mathbf {S}&;&\mathbf {0} \end{bmatrix},\mathbf {1})\). The entry \((\mathbf {m}, sig )\) is stored so that if a signature on \(\mathbf {m}\) is queried twice, the algorithm outputs always \( sig \).
Verification. Verification of a signature \( sig = (\mathbf {c}_1,\mathbf {S},\mathbf {c}_2)\) on message \(M= \mathbf {m}\) returns 1 if \(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {c}_1\mathbf {C}+\mathbf {m}\mathbf {G}&\mathbf {1} \end{bmatrix} \mathbf {S} = \mathbf {c}_2\mathbf {u}\), if the message \(M\in \bar{\mathcal {M}}\), and if the signature \( sig \in \bar{\varSigma }= \{(\mathbf {c}_1,\mathbf {S},\mathbf {c}_2)\in \bar{\mathcal {C}}\times \mathcal {R}_{q}^{3+2m}\times \mathcal {R}_{q}:\;\Vert \mathbf {S} \Vert \le N'~\wedge ~\Vert \mathbf {c}_2 \Vert \le C'\}\). Otherwise, it returns 0.
The relaxed signature scheme is \(\text {f-uf-cma}\) secure w.r.t. the message relaxation function \(f(\mathbf {m})=\{(\mathbf {m}\mathbf {c}) \;:\; \mathbf {c}\in \bar{\mathcal {C}}\}\).
Theorem 3
An algorithm \(\mathsf {A}\) that breaks the \(\text {f-uf-cma}\) unforgeability of the relaxed signature scheme in time t and probability \(\epsilon _A\) can break the Assumption 3 in time t with probability \(\epsilon _A\) in the Random Oracle Model.
To prove knowledge of a signature on a message \(\mathbf {m}\) without revealing \(\mathbf {m}\), Boschini et al. combine the relaxed signature, a relaxed commitment and the relaxed \(\varSigma \)-protocol, where the commitment is used to hide the part of the verification key of the signature that depends on \(\mathbf {m}\). Let \(\mathbf {S} = \begin{bmatrix} \mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {S}_3&;&\mathbf {1} \end{bmatrix}\) be a signature on \(\mathbf {m}\) w.r.t. the public key \( spk = \begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C} \end{bmatrix}\). To hide the part of the verification equation of the signature that depends on \(\mathbf {m}\), Boschini et al. present the following trick. First, construct \(\mathbf {F}=\mathbf {b}^{-1}(\mathbf {C}+\mathbf {m}\mathbf {G}+\mathbf {E})\) choosing random  and
and  . Assuming Assumption 1 is hard or using complexity leveraging and assuming the hardness of Ring-LWE (cf. Sect. 2.4), we have that \(\mathbf {F}\) hides \(\mathbf {m}\)Footnote 1 then, set \(\mathbf {S}_\mathrm {s}\) to be \(\mathbf {S}_{\mathrm {s}}=\begin{bmatrix}\mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {b}\mathbf {S}_3&;&-\mathbf {ES}_3\end{bmatrix}\). It is easy to see that \(\mathbf {s}_\mathrm {s}\) satisfies \(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {F}&\mathbf {1}\end{bmatrix}\mathbf {S}_\mathrm {s}=\mathbf {u}\).
. Assuming Assumption 1 is hard or using complexity leveraging and assuming the hardness of Ring-LWE (cf. Sect. 2.4), we have that \(\mathbf {F}\) hides \(\mathbf {m}\)Footnote 1 then, set \(\mathbf {S}_\mathrm {s}\) to be \(\mathbf {S}_{\mathrm {s}}=\begin{bmatrix}\mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {b}\mathbf {S}_3&;&-\mathbf {ES}_3\end{bmatrix}\). It is easy to see that \(\mathbf {s}_\mathrm {s}\) satisfies \(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {F}&\mathbf {1}\end{bmatrix}\mathbf {S}_\mathrm {s}=\mathbf {u}\).
3 Relaxed Partial Verifiable Encryption
Lyubashevsky and Neven [29] defined a relaxed verifiable encryption as a scheme to encrypt a witness \(w\) of \(x\in L \) such that decryption of a valid ciphertext is guaranteed to yield a witness \(\bar{w}\) in the relaxed language such that \((x, \bar{w}) \in \bar{ R }\).
The straightforward combination with the relaxed signature and commitment scheme of Boschini et al. [8] does not yield a particularly efficient group signature scheme, however, because the Lyubashevsky-Neven verifiable encryption scheme encrypts and recovers the full witness. A group signature typically consists of a verifiable encryption of the user’s identity together with a proof that the user knows a valid signature on the encrypted identity by the group manager. The verifiable encryption as defined by Lyubashevsky and Neven would therefore encrypt both the user’s identity and the signature on it, which unnecessarily blows up the size of the verifiable ciphertext. Even when using a commitment to the user’s identity to separate the proof of knowledge of the signature from the verifiable encryption, the ciphertext will encrypt the user’s identity as well as the opening information to the commitment.
We therefore introduce a variant of the Lyubashevsky-Neven relaxed verifiable encryption scheme called relaxed partial verifiable encryption that, rather than decrypting the full witness \(\bar{w}\), recovers only a function of that witness \(g(\bar{w})\) while proving knowledge of the full witness \(\bar{w}\). When constructing a group signature case, we will use a function \(g\) that outputs just the user’s identity.
3.1 Definition of Relaxed Partial Verifiable Encryption
Our general definition of relaxed partial verifiable encryption are inspired by the definition of relaxed verifiable encryption by Lyubashevsky and Neven [29] and of verifiable encryption by Camenisch and Shoup [11]. Let \( L \) be a language with witness relation \( R \) and let \(\bar{ L }\supseteq L \) be a relaxed language with relaxed relation \(\bar{ R }\supseteq R \). Let \(\bar{ R }\subseteq \bar{ L }\times \bar{ W }\) and let \(g: \bar{ W }\rightarrow D \) be a function.
Given relations \( R \), \(\bar{ R }\) and function \(g\), a relaxed partial verifiable encryption scheme is composed by four algorithms \((\mathsf {EKeyGen},\mathsf {Enc},\mathsf {EVerify},\mathsf {Dec})\). The key generation algorithm \(\mathsf {EKeyGen}(1^\lambda )\) outputs a pair of keys \(( epk , esk )\). The encryption algorithm \(\mathsf {Enc}( epk ,x,w,\ell )\), where \((x,w) \in R \) and \(\ell \in \{0,1\}^*\) is an encryption label, returns a ciphertext \(t\) and a proof \(\pi = (\alpha ,\beta ,\gamma )\). Verification \(\mathsf {EVerify}( epk ,x,t,\pi ,\ell )\) returns 1 if \(\pi \) shows that \(t\) is a valid ciphertext w.r.t. \(x\) and \( epk \) with label \(\ell \), and returns 0 otherwise. Finally, the decryption algorithm \(\mathsf {Dec}( esk ,x,t,\pi ,\ell )\) returns a value \(M\) or a failure symbol \(\bot \).
-
Correctness. The scheme is correct if \(\mathsf {Pr}\left[ \mathsf {Dec}( esk ,x,\mathsf {Enc}( epk ,x,w,\ell ))=g(w)\right] =1\) for all keys \(( epk , esk )\leftarrow \mathsf {EKeyGen}(1^\lambda )\), all \((x,w)\in R \), and all \(\ell \in \{0,1\}^*\).
-
Completeness. The scheme satisfies completeness if \(\mathsf {Pr}[\mathsf {EVerify}( epk ,\mathsf {Enc}( epk ,x,w,\ell ),\ell )=1]=1\) for all keys \(( epk , esk )\leftarrow \mathsf {EKeyGen}(1^\lambda )\), all \((x,w)\in R \), and all \(\ell \in \{0,1\}^*\).
-
Special soundness. Special soundness implies that a valid proof \(\pi \) is a proof of knowledge of a valid witness \(\bar{w}\) for the relation \(\bar{ R }\) and that decryption of the ciphertext \(t\) returns \(g(\bar{w})\). More specifically, for all PPT adversaries \(\mathsf {A}\) there exists a PPT extractor \(\mathsf{E}\) such that the following probability is negligible:

-
Chosen-ciphertext simulatability. There exists a simulator \(\mathsf{S}\) that outputs ciphertexts indistinguishable from honestly generated ones, i.e., the following probability is negligible:

where \(\mathsf {A}\) cannot query its \(\mathsf {Dec}\) oracle on \((x,t_b,\pi _b,\ell )\).
Observe that our definition of Special Soundness hardwires the use of Fiat-Shamir in the general construction. It is possible to give a more general definition of Special Soundness adapting the definition of weak simulation extractability By Faust et al. [16], but such a definition would be beyond the scope of this paper.
3.2 Relaxed Partial Verifiable Encryption over Lattices
Let \( L \) and \(\bar{ L }\) be a language and its relaxed version defined w.r.t. the following relations

for some sets \(\mathcal {U}, \bar{\mathcal {U}}, \bar{\mathcal {C}}\subseteq \mathcal {R}_{q}\) and some integers \(\ell _1, \ell _2, N, \bar{N}>0\).
We will construct a relaxed partial verifiable encryption scheme for relations \( R _\mathrm {ve}\) and \(\bar{ R }_\mathrm {ve}\) and function \(g((\bar{\mathbf {m}},\bar{\mathbf {S}},\bar{\mathbf {c}})) = \bar{\mathbf {m}}/\bar{\mathbf {c}}\text { mod }q\). Our scheme is a modified version of the “multi-shot” chosen-ciphertext secure verifiable encryption scheme of Lyubashevsky-Neven. The multi-shot scheme involves multiple parallel repetitions of the proof with sub-exponential challenge set sizes, and decryption takes strictly sub exponential time (as opposed to expected polynomial time for the one-shot scheme).
Rather than producing one big proof of knowledge of the terms in relation \( R _\mathrm {ve}\), we split it into two proofs, one for each term. The first proof only contains the ciphertext equations and is repeated multiple times with a sub-exponential challenge set to enable efficient decryption. The second includes the relation equation as well as the ciphertext, proving that the encrypted plaintext is derived from a valid witness. The latter proof uses an exponential-size challenge set, so that it doesn’t need to be repeated. Let p and q be two public primes with \(p>2\).
Key Generation. The recipient generates two key pairs for Ring-LWE encryption [30], but discards the secret key of the second pair. It samples  and
and  , and computes \(\mathbf {t}_1=\mathbf {a}\mathbf {s}_1+\mathbf {d}_1 \text { mod }q\) and \(\mathbf {t}_2=\mathbf {a}\mathbf {s}_2+\mathbf {d}_2 \text { mod }q\). The public key is \( epk =(p,q,\mathbf {a},\mathbf {t}_1,\mathbf {t}_2)\), the secret key is \( esk =\mathbf {s}_1\).
, and computes \(\mathbf {t}_1=\mathbf {a}\mathbf {s}_1+\mathbf {d}_1 \text { mod }q\) and \(\mathbf {t}_2=\mathbf {a}\mathbf {s}_2+\mathbf {d}_2 \text { mod }q\). The public key is \( epk =(p,q,\mathbf {a},\mathbf {t}_1,\mathbf {t}_2)\), the secret key is \( esk =\mathbf {s}_1\).
Encryption. Given a witness \((\mathbf {m},\mathbf {S},\mathbf {1})\) for language member \((\mathbf {A}, \mathbf {U})\) in the relation \( R _\mathrm {ve}\), the algorithm \(\mathsf {Enc}\) uses the Naor-Yung technique [33] by encrypting \(\mathbf {m}\) twice using standard Ring-LWE encryption under public keys \(\mathbf {t}_1\) and \(\mathbf {t}_2\). More precisely, it samples  and sets \(\mathbf {v}_1 = p(\mathbf {a}\mathbf {r} + \mathbf {e}_1) \text { mod }q\), \(\mathbf {w}_1 = p(\mathbf {t}_1\mathbf {r} + \mathbf {f}_1) + \mathbf {m}\text { mod }q\), \(\mathbf {v}_2 = p(\mathbf {a}\mathbf {r} + \mathbf {e}_2) \text { mod }q\), and \(\mathbf {w}_2 = p(\mathbf {t}_2\mathbf {r} + \mathbf {f}_2) + \mathbf {m}\text { mod }q\).
and sets \(\mathbf {v}_1 = p(\mathbf {a}\mathbf {r} + \mathbf {e}_1) \text { mod }q\), \(\mathbf {w}_1 = p(\mathbf {t}_1\mathbf {r} + \mathbf {f}_1) + \mathbf {m}\text { mod }q\), \(\mathbf {v}_2 = p(\mathbf {a}\mathbf {r} + \mathbf {e}_2) \text { mod }q\), and \(\mathbf {w}_2 = p(\mathbf {t}_2\mathbf {r} + \mathbf {f}_2) + \mathbf {m}\text { mod }q\).
Then, letting \(\mathbf {A}_1\) be the first column of the matrix \(\mathbf {A} = \begin{bmatrix} \mathbf {A}_1&\mathbf {A}_2 \end{bmatrix}\) in relation \( R _\mathrm {ve}\), it constructs a NIZK proof \(\varPi _1\) using the scheme from Sect. 2.7 for the relation

whereby it uses the challenge set \(\mathcal {C}_1=\{\mathbf {c}\in \mathcal {R}_{3}~|~\Vert \mathbf {c} \Vert _1\le 32\}\).
To enable Lyubashevsky-Neven’s multi-shot decryption technique without having to repeat the above proof multiple times, the encryptor again uses the relaxed NIZK proof of Sect. 2.7 to construct a separate proof \(\varPi _2\) for the relation

whereby it includes \( epk , (\mathbf {A}, \mathbf {U}), (\mathbf {v}_1, \mathbf {w}_1, \mathbf {v}_2, \mathbf {w}_2), \varPi _1, \ell \) in the Fiat-Shamir hash. To obtain efficient decryption but keep the soundness error negligible, this proof is repeated \(l=11\) times with challenge set \(\mathcal {C}_2=\mathcal {R}_{3}^{(16)}\). The algorithm outputs ciphertext \((\mathbf {v}_1,\mathbf {w}_1, \mathbf {v}_2, \mathbf {w}_2)\) and proof \((\varPi _1,\varPi _2)\).
Verification. The verification algorithm \(\mathsf {EVerify}((p,q,\mathbf {a}, \mathbf {t}_1, \mathbf {t}_2), (\mathbf {A}, \mathbf {U}), (\mathbf {v}_1,\mathbf {w}_1, \mathbf {v}_2, \mathbf {w}_2,\varPi _1,\varPi _2), \ell )\) checks that \(\varPi _1\) and \(\varPi _2\) are valid relaxed NIZK proofs for the relations of Eqs. (1) and (2), including the correct arguments \( epk , (\mathbf {A}, \mathbf {U}),(\mathbf {v}_1, \mathbf {w}_1, \mathbf {v}_2, \mathbf {w}_2), \varPi _1, \ell \) in the Fiat-Shamir hash of \(\varPi _2\).
Decryption. The decryption algorithm \(\mathsf {Dec}(\mathbf {s}_1,(\mathbf {A},\mathbf {U}),(\mathbf {v}_1,\mathbf {w}_1,\mathbf {v}_2, \mathbf {w}_2),(\varPi _1,\) \(\varPi _2),\ell )\) first checks that the proofs are valid using the verification algorithm above, returning \(\bot \) if it is not valid. It then decrypts the cihpertext by applying the Lyubashevsky-Neven multi-shot decryption on proof \(\varPi _2 = (\mathbf {Y}^{(1)},\mathbf {c}^{(1)}, \mathbf {Z}^{(1)}, \ldots , \mathbf {Y}^{(l)},\mathbf {c}^{(l)},\mathbf {Z}^{(l)})\) by, for \(i=1,\ldots ,l\), going over all challenges \(\mathbf {c}' \in \mathcal {C}_2\) to try to decrypt \((\bar{\mathbf {c}}\mathbf {v}, \bar{\mathbf {c}}\mathbf {w}_1)\) as a Ring-LWE ciphertext, where \(\bar{\mathbf {c}}= \mathbf {c}^{(i)} - \mathbf {c}'\). It does so by computing \(\bar{\mathbf {m}}' = (\mathbf {w}_1 - \mathbf {v}_1 \mathbf {s}_1) \bar{\mathbf {c}}\text { mod }q\), checking that \(\Vert \bar{\mathbf {m}}'\Vert _\infty < q/2C\) where C is as defined in Lemma 5, and if so, compute \(\bar{\mathbf {m}}= \bar{\mathbf {m}}' \text { mod }p\) and return \(\bar{\mathbf {m}}/\bar{\mathbf {c}}\text { mod }q\); otherwise, it returns \(\bot \).
Decryption Runtime. Decryption terminates in time at most \(2^{26}\). Indeed, if the ciphertext is honestly generated the algorithm needs to guess the challenge only once. On the other hand, for a dishonestly generated ciphertext the probability that verification succeeds and still decryption fails is negligible. Indeed, if the adversary could answer only one challenge \(\mathbf {c}\), when making the random oracle queries the probability of hitting always  . Hence, a second challenge exists w.h.p. and decryption requires to guess a challenge
. Hence, a second challenge exists w.h.p. and decryption requires to guess a challenge  times.
times.
Remark that the decryption does not recover the full witness: the algorithm decrypts the ciphertext, but it does not recover the randomness used to generate it or the vector \(\mathbf {S}\). Moreover, differently from Lyubashevsky-Neven construction, in our case the relation  holds modulo q, while in the original scheme it has to hold modulo p. We show the correctness of the scheme using Lemma 5, which is a variant of a result by Lyubashevsky and Neven [29, Lemma 3.1]. In this lemma we show that, for some choice of the parameters, the decryption always return the same value
holds modulo q, while in the original scheme it has to hold modulo p. We show the correctness of the scheme using Lemma 5, which is a variant of a result by Lyubashevsky and Neven [29, Lemma 3.1]. In this lemma we show that, for some choice of the parameters, the decryption always return the same value  over the ring \(\mathcal {R}_{q}\). This is slightly different from the original decryption algorithm, as in the original scheme it was enough for decryption to return the same
over the ring \(\mathcal {R}_{q}\). This is slightly different from the original decryption algorithm, as in the original scheme it was enough for decryption to return the same  modulo p.
modulo p.
Lemma 5
Let  , and \(\mathbf {t}=\mathbf {a}\mathbf {s}+\mathbf {d}\) where
, and \(\mathbf {t}=\mathbf {a}\mathbf {s}+\mathbf {d}\) where  . If there exist \(\bar{\mathbf {r}}\), \(\bar{\mathbf {e}}\), \(\bar{\mathbf {f}}\), \(\bar{\mathbf {m}}\), \(\bar{\mathbf {c}}\) such that
. If there exist \(\bar{\mathbf {r}}\), \(\bar{\mathbf {e}}\), \(\bar{\mathbf {f}}\), \(\bar{\mathbf {m}}\), \(\bar{\mathbf {c}}\) such that

and \(\Vert p (\bar{\mathbf {r}}\mathbf {d} + \bar{\mathbf {f}}- \bar{\mathbf {e}}\mathbf {s}) + \bar{\mathbf {m}} \Vert _\infty < q / 2C\) and \(\Vert \bar{\mathbf {m}} \Vert _\infty < p / 2C\), where \(C = \max _{\bar{\mathbf {c}}\in \bar{\mathcal {C}}}\Vert \bar{\mathbf {c}} \Vert _1 = \max _{\bar{\mathbf {c}},\bar{\mathbf {c}}'\in \mathcal {C}}\Vert \bar{\mathbf {c}}-\bar{\mathbf {c}}' \Vert _1\), then
-
1.
\(\Vert (\mathbf {w} - \mathbf {v}\mathbf {s})\mathbf {c}'\text { mod }q \Vert _\infty < q/2C\) and \(\Vert (\mathbf {w} - \mathbf {v}\mathbf {s})\mathbf {c}'\text { mod }q\text { mod }p \Vert _\infty < p/2C\)
-
2.
for any \(\bar{\mathbf {c}}'\in \bar{\mathcal {C}}\) such that \(\Vert (\mathbf {w} - \mathbf {v}\mathbf {s})\mathbf {c}'\text { mod }q \Vert _\infty < q/2C\) and \(\Vert (\mathbf {w} - \mathbf {v}\mathbf {s})\mathbf {c}'\text { mod }q\text { mod }p \Vert _\infty < p/2C\) we have \((\mathbf {w} - \mathbf {v}\mathbf {s})\bar{\mathbf {c}}'\text { mod }q\text { mod }p/\bar{\mathbf {c}}' = \bar{\mathbf {m}}/\bar{\mathbf {c}}.\)
Proof
The proof is a simple verification of the claims and it is very similar to the proof of Lemma 3.1 in [29], hence we omit it.
Hence, for decryption to be correct, we must choose parameters that guarantee that the values decrypted from \(\varPi _2\) using \(\mathbf {s}_i\) for \(i=1,2\) satisfy \(\Vert p(\bar{\mathbf {r}}_i\mathbf {d}_i + \bar{\mathbf {f}}_i - \bar{\mathbf {e}}_i\mathbf {s}_i)+\bar{\mathbf {m}} \Vert _\infty <q/2C\) and \(\Vert \bar{\mathbf {m}}_i \Vert _\infty <p/2C\), i.e., p, q and n should be such that \(16\sigma _2(2np+p+1)<q/2C\) and \(16\sigma _2<p/2C\), where \(C\le 64\) as challenges come from \(\mathcal {R}_{3}^{(16)}\). We enforce this condition on both ciphertexts to guarantee decryption to work using either \(\mathbf {s}_1\) or \(\mathbf {s}_2\). This allows to prove CCA simulatability following the Naor-Young paradigm [33].
In the next lemma, we prove that with high probability the \(\bar{\mathbf {m}}/\bar{\mathbf {c}}\) returned by decryption is equal to the polynomial \(\bar{\mathbf {m}}'/\bar{\mathbf {c}}'\) returned from an extractor for \(\varPi _2\). The proof of this lemma consists only of a plain computation of the probability, and can be found in the full version of the paper.
Lemma 6
Let \(\bar{\mathbf {m}}\) and \(\bar{\mathbf {c}}\) be the output of the decryption and \(\bar{\mathbf {m}}',\bar{\mathbf {c}}'\) be the values extracted from \(\varPi _1\). Then with probability at least \(1-2^{-35928}\), over the choice of the opening key \(\mathbf {t}\), \(\bar{\mathbf {m}}/\bar{\mathbf {c}}=\bar{\mathbf {m}}'/\bar{\mathbf {c}}'\) (where parameters are set as in Table 1).
Finally, for the CCA simulatability the proofs that we use in the scheme need to be unbounded simulation soundness. Following the same reasoning used in Lyubashevsky and Neven, we prove that \(\varPi _2\) has quasi-unique responses, hence simulation soundness. Indeed, breaking quasi-uniqueness means finding \(\mathbf {z}\ne \mathbf {z}'\) with \(\ell _\infty \) norm less than \(8\sigma _2\) such that \(\mathbf {M}\mathbf {z}=\mathbf {M}\mathbf {z}'\text { mod }q\), where with \(\mathbf {M}\) we mean the matrix in 2. Thus, either there is a non-zero tuple \((\mathbf {y}_1, \mathbf {y}_2)\in \mathcal {R}_{q}\) with \(\ell _\infty \) norm less than \(16\sigma _2\) such that \(p(\mathbf {a}\mathbf {y}_1 + \mathbf {y}_2) = 0 \text { mod }q\) or \(p\mathbf {y}_1+\mathbf {y}_2 = 0 \text { mod }q\). Imposing \(p>16\sigma _2\) and \(16\sigma _2p + 16\sigma _2 < q\) implies that the second equality is not possible. Also, setting \((32\sigma _2)^2<q\), we can use a standard probabilistic argument to show that for all \(\mathbf {y}_1\), \(\mathbf {y}_2\) of \(\ell _\infty \) norm less than \(16\sigma _2\),
Therefore for almost all \(\mathbf {a}\), there will not be a short solution \((\mathbf {y}_1, \mathbf {y}_2)\) that satisfies \(\mathbf {a}\mathbf {y}_1 + p\mathbf {y}_2 = 0\). Observe that the same argument works for \(\varPi _1\). Hence imposing the same inequalities on \(\sigma _1\) yields simulation soundness also for \(\varPi _1\), thus for the protocol \((\varPi _1,\varPi _2)\).
Theorem 4
If Ring-LWE\(_{U({\mathcal {R}_{q}})}\) is hard and the relaxed NIZK proof system is unbounded non-interactive zero-knowledge and unbounded simulation soundness, the scheme \((\mathsf {EKeyGen},\mathsf {Enc},\mathsf {EVerify},\mathsf {Dec})\) is a relaxed partial verifiable encryption scheme w.r.t. the function \(g\).
4 Group Signature Scheme
The combination of Boschini et al.’s relaxed signature scheme [8] with our relaxed partial verifiable encryption scheme yields an efficient group signature with practical parameters (see Sect. 4.2). Although the building blocks are “relaxed” schemes, the resulting group signature enjoys non-relaxed traceability. Indeed, the correctness of the verifiable encryption guarantees that when opening a signature, the recovered identity is in the original set of group members id (and not in the relaxed one).
4.1 A Lattice-Based Group Signature
Let \(\mathcal {U}=\mathcal {R}_{3}^{(16)}\) be the set of possible user identities.
Parameters Generation. On input the security parameter \(\lambda \), the algorithm runs the parameter generator of the signature scheme \( par \leftarrow \mathsf {SParGen}(1^\lambda )\) and chooses integer p, q, n where p and q are prime and \(p<q\). It outputs \( gpar :=( par ,p,q,n)\).
Group Manager Key Generation. The group manager generates the keys \( gsk =\mathbf {X}\) and \( gpk =(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C}&\mathbf {1}\end{bmatrix},\mathbf {u})\) by running \(\mathsf {SKeyGen}\) and choosing a random ring element  .
.
Opener Key Generation. The opener runs the key generation algorithm of the verifiable encryption scheme \(\mathsf {EKeyGen}(1^\lambda )\) and returns the resulting key pair \(( opk = epk , osk = esk )\).
User Key Generation. The group manager generates a signing key user identity \( id = \mathbf {m} \in \mathcal {U}= \mathcal {R}_{3}^{(16)}\) by running \(\mathsf {Sign}( gsk , \mathbf {m})\) to yield \((\mathbf {1}, \begin{bmatrix} \mathbf {S}&;&\mathbf {0} \end{bmatrix}, \mathbf {1})\) as described in Sect. 2.8. Recall that \(\mathbf {S}\) is a short vector so that \(\begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {C} + \mathbf {m}\mathbf {G} \end{bmatrix} \mathbf {S} = \mathbf {u} \text { mod }q\). It then returns \( usk := \mathbf {S}\).
Signing Algorithm. The user first generates a key one-time signature key pair \(( sk , vk )\leftarrow \mathsf {OTSGen}(1^\lambda )\). The user then blinds her identity \(\mathbf {m}\) using the technique from Sect. 2.8 by choosing random  and
and  , and computing \(\mathbf {F}=\mathbf {b}^{-1}(\mathbf {C}+\mathbf {m}\mathbf {G}+\mathbf {E})\). If \(\mathbf {S} = \begin{bmatrix} \mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {S}_3 \end{bmatrix}\) with \(\mathbf {S}_1 \in \mathcal {R}_{q}^{2\times 1}\) and \(\mathbf {S}_2,\mathbf {S}_3 \in \mathcal {R}_{q}^{m \times 1}\), then we have that \( \begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {F}&\mathbf {1} \end{bmatrix} \begin{bmatrix} \mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {b} \mathbf {S}_3&;&- \mathbf {E} \mathbf {S}_3 \end{bmatrix} = \mathbf {u} \text { mod }q. \) The user can therefore create a relaxed NIZK proof \(\varPi _0\) for the relation
, and computing \(\mathbf {F}=\mathbf {b}^{-1}(\mathbf {C}+\mathbf {m}\mathbf {G}+\mathbf {E})\). If \(\mathbf {S} = \begin{bmatrix} \mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {S}_3 \end{bmatrix}\) with \(\mathbf {S}_1 \in \mathcal {R}_{q}^{2\times 1}\) and \(\mathbf {S}_2,\mathbf {S}_3 \in \mathcal {R}_{q}^{m \times 1}\), then we have that \( \begin{bmatrix} \mathbf {A}&\mathbf {B}&\mathbf {F}&\mathbf {1} \end{bmatrix} \begin{bmatrix} \mathbf {S}_1&;&\mathbf {S}_2&;&\mathbf {b} \mathbf {S}_3&;&- \mathbf {E} \mathbf {S}_3 \end{bmatrix} = \mathbf {u} \text { mod }q. \) The user can therefore create a relaxed NIZK proof \(\varPi _0\) for the relation

where she includes \( vk \) in the Fiat-Shamir hash. The parameters follow from rejection sampling (see Sect. 2.7): the noise vector is sampled from a Gaussian with standard deviation \(\sigma _0=12T_0\), where \(T_0\) is obtained from \(N_0\) as a bound on the norm of \(\mathbf {c}\mathbf {T}_0\) for \(\mathbf {c}\in \mathcal {C}_0\), and \(\bar{N}_0 = 2.1\sigma _0 \sqrt{n(3+2m)}\). The challenge space is set to \(\mathcal {C}_0=\{\mathbf {c}\in \mathcal {R}_{3}~:~\Vert \mathbf {c} \Vert _1\le 32\}\) so that the proof only needs to be repeated once, as indeed \(|\mathcal {C}_0|>2^{256}\).
Next, from the way \(\mathbf {F}\) was computed, we have that \(\begin{bmatrix} \mathbf {G}^\mathsf {T}&\mathbf {F}^\mathsf {T}&\mathbb {I}_{m} \end{bmatrix} \begin{bmatrix} \mathbf {m}&;&-\mathbf {b}&;&\mathbf {E}^\mathsf {T}\end{bmatrix} = -\mathbf {C}^\mathsf {T}\). Setting \(\mathbf {T}_\mathrm {ve}=\begin{bmatrix}-\mathbf {b}&;&\mathbf {E}^\mathsf {T}\end{bmatrix}\) the prover can therefore use the verifiable encryption scheme to encrypt a witness of the languages with relations

The user runs the encryption algorithm \(\mathsf {Enc}( opk ,x,w, vk )\) with language member \(x= (\begin{bmatrix} \mathbf {G}^\mathsf {T}&\mathbf {F}^\mathsf {T}&\mathbb {I}_{m} \end{bmatrix}, -\mathbf {C}^\mathsf {T})\), witness \(w= (\mathbf {m},\begin{bmatrix} -\mathbf {b}&;&\mathbf {E}^\mathsf {T}\end{bmatrix},\mathbf {1})\), and the verification key \( vk \) as the encryption label, to generate a ciphertext \(t= (\mathbf {v}_1, \mathbf {w}_1, \mathbf {v}_2, \mathbf {w}_2)\) and proof \(\pi = (\varPi _1, \varPi _2)\). The user then computes the one-time signature \( ots \leftarrow \mathsf {OTSSign}( sk , (\mathbf {A}, \mathbf {B}, \mathbf {F}, \mathbf {u}, \varPi _0, t, \pi , M))\) and returns the group signature \( sig = (\mathbf {F}, \varPi _0, t, \pi , vk , ots )\).
Verification Algorithm. The verifier checks the one-time signature by running \(\mathsf {OTSVf}( vk , (\mathbf {A}, \mathbf {B}, \mathbf {F}, \mathbf {u}, \varPi _0, t, \pi , M), ots )\), checks the NIZK proof \(\varPi _0\) in the group signature \( sig = (\mathbf {F}, \varPi _0, t, \pi )\), making sure that \( vk \) is included in the Fiat-Shamir hash, and checks the encryption proof by running \(\mathsf {EVerify}( opk ,x,t,\pi , vk )\) with \(x= (\begin{bmatrix} \mathbf {G}^\mathsf {T}&\mathbf {F}^\mathsf {T}&\mathbb {I}_{m} \end{bmatrix}, -\mathbf {C}^\mathsf {T})\) and with \( vk \) as the encryption label. If all tests succeed then he outputs 1, else he outputs 0.
Opening Algorithm. The opener first verifies the group signature by running the \(\mathsf {GVerify}\) algorithm above. If it is invalid, then the opener returns \(\bot \), else it decrypts \(\mathbf {m} \leftarrow \mathsf {Dec}( esk ,x,t,\pi , vk )\) with \(x\) as above and returns \( id = \mathbf {m}\).
To guarantee the correctness of the scheme, the norm bounds \(N_0\), \(N_\mathrm {ve}\) and \(\bar{N}_\mathrm {ve}\) should be chosen carefully. First, as observed in Sect. 2.8, a honest \(\mathbf {T}\) is generated as \(\mathbf {T}=\begin{bmatrix} \mathbf {S}_1&\mathbf {S}_2&\mathbf {b}\mathbf {S}_3&-\mathbf {E}\mathbf {S}_3 \end{bmatrix}\), where the vector \(\mathbf {S} = \begin{bmatrix} \mathbf {S}_1&\mathbf {S}_2&\mathbf {S}_3 \end{bmatrix}\in \mathcal {R}_{q}^{1\times (2+2m)}\) is sampled from a Gaussian with standard deviation \(\sigma \). Hence it each of its components has norm bounded by \(1.05\sigma \sqrt{n}\). Moreover, using the bounds in Lemma 2, it holds \(\Vert \mathbf {b}\mathbf {S}_3 \Vert \le 8\sigma n\sqrt{m}\) and \(\Vert -\mathbf {E}\mathbf {S}_3 \Vert \le \sqrt{\sum _{i=1}^m \Vert \mathbf {E}_i\mathbf {S}_{3,i} \Vert _2^2} \le 8\sigma n\sqrt{m}\). Hence we can set the bound \(N_0\) to be:
The value \(N_\mathrm {ve}\) in \( R _\mathrm {ve}\) bounds the norm of a vector of polynomials with coefficients in \(\{0,1\}\) one of which is in \(\mathcal {R}_{3}^{(16)}\), hence \(N_\mathrm {ve}:=\sqrt{256+n(m^2+1)}\). Finally, the parameter \(\bar{N}_\mathrm {ve}\) bounds the norm of what is returned extracting from the NIZK proof, hence it is computed from the standard deviation of the Gaussian distribution used in rejection sampling as explained in Sect. 2.7.
Theorem 5
(Traceability). Our group signature scheme is traceable in the random-oracle model if Assumption 3 holds and the relaxed partial verifiable encryption scheme of Sect. 3 satisfies special soundness.
Theorem 6
(CCA-Anonymity). Our group signature scheme is CCA-anonymous in the random-oracle model if Assumption 1 holds, if the NIZK proof is statistical zero-knowledge and if the relaxed partial verifiable encryption scheme of Sect. 3 is chosen-ciphertext simulatable.
As stated in Sect. 2.4, there are two ways to interpret Assumption 3 and Assumption 1, either as a quite strong interactive assumption, or as implied through a complexity leveraging argument by the Ring-LWE and the Ring-SIS assumptions, and by the Ring-LWE\(_{m,D}\) assumption, respectively.
4.2 Practical Parameters and Storage Requirement
In Table 1 we give a set of practical parameters for different security requirements and all guaranteeing \(\lambda =80\) bits of security against quantum adversaries. Following the approach in Boschini et al. [8], we give the possibility to choose whether to base the security of the scheme on complexity leveraging or not. All parameters are computed w.r.t. fixed \(n=2^{11}\), \(\sigma _t=4\) and p a prime such that \(\log p\le 2^{50}\). The second column contains the maximum value of the Hermite root factor computed for the Ring-SIS instance in Theorem 2. Given that not only Assumption 4, but also the hardness of finding a witness for an element of \( L \) in Sect. 2.7 is based on that, we decided to use it to have a hardness estimate even when relying only on the hardness of Assumption 3. The only difference with the other case (and the reason for which \(\delta _s\) is different) is that when assuming complexity leveraging we need to compensate also for the tightness loss of the reductions in Sect. 2.4, while in the other case it is only necessary to compensate for the tightness loss in the proofs of Theorems 5 and 6. We recall that the most efficient scheme prior to ours [23] has signatures over 60 MB and public keys of 4.9 MB for a group size of only \(2^{10}\) users for 80 bits of security. While they still have to deal with big lattices (dimensions: \(n=2^8\), \(m=2^{12}\)), their coefficients are smaller than ours (bounded by \(q=2^8\)), and this allow for more efficient computations.
Notes
- 1.
Boschini et al. proved that, for \(\mathcal {U}\subset \mathcal {R}_{3}^{(16)}\), this is actually a relaxed commitment scheme. We do not need the relaxed binding property, hence we can choose a larger set of messages (as long as it still guarantees the hiding property).
References
Ateniese, G., Camenisch, J., Joye, M., Tsudik, G.: A practical and provably secure coalition-resistant group signature scheme. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 255–270. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_16
Banaszczyk, W.: New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(1), 625–635 (1993)
Bellare, M., Micciancio, D., Warinschi, B.: Foundations of group signatures: formal definitions, simplified requirements, and a construction based on general assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 614–629. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_38
Bellare, M., Shi, H., Zhang, C.: Foundations of group signatures: the case of dynamic groups. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 136–153. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_11
Benhamouda, F., Camenisch, J., Krenn, S., Lyubashevsky, V., Neven, G.: Better zero-knowledge proofs for lattice encryption and their application to group signatures. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 551–572. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_29
Bichsel, P., Camenisch, J., Groß, T., Shoup, V.: Anonymous credentials on a standard Java card. In: ACM CCS (2009)
Boneh, D., Boyen, X., Goh, E.-J.: Hierarchical identity based encryption with constant size ciphertext. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 440–456. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_26
Boschini, C., Camenisch, J., Neven, G.: Relaxed lattice-based signatures with short zero-knowledge proofs. Cryptology ePrint Archive, Report 2017/1123 (2017)
Brickell, E.F., Camenisch, J., Chen, L.: Direct anonymous attestation. In: ACM CCS (2004)
Camenisch, J., Neven, G., Rückert, M.: Fully anonymous attribute tokens from lattices. In: Visconti, I., De Prisco, R. (eds.) SCN 2012. LNCS, vol. 7485, pp. 57–75. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32928-9_4
Camenisch, J., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_8
Chase, M., Lysyanskaya, A.: On signatures of knowledge. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 78–96. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_5
Chaum, D., van Heyst, E.: Group signatures. In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 257–265. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46416-6_22
Ducas, L., Durmus, A., Lepoint, T., Lyubashevsky, V.: Lattice signatures and bimodal Gaussians. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 40–56. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_3
Ducas, L., Lyubashevsky, V., Prest, T.: Efficient identity-based encryption over NTRU lattices. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 22–41. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_2
Faust, S., Kohlweiss, M., Marson, G.A., Venturi, D.: On the non-malleability of the Fiat-Shamir transform. In: Galbraith, S., Nandi, M. (eds.) INDOCRYPT 2012. LNCS, vol. 7668, pp. 60–79. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34931-7_5
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Gama, N., Nguyen, P.Q.: Predicting lattice reduction. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 31–51. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_3
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: ACM STOC (2008)
Gordon, S.D., Katz, J., Vaikuntanathan, V.: A group signature scheme from lattice assumptions. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 395–412. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_23
Laguillaumie, F., Langlois, A., Libert, B., Stehlé, D.: Lattice-based group signatures with logarithmic signature size. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 41–61. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_3
Lamport, L.: Constructing digital signatures from a one-way function. Technical report SRI-CSL-98, SRI International Computer Science Laboratory (1979)
Libert, B., Ling, S., Nguyen, K., Wang, H.: Zero-knowledge arguments for lattice-based accumulators: logarithmic-size ring signatures and group signatures without trapdoors. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 1–31. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_1
Libert, B., Mouhartem, F., Nguyen, K.: A lattice-based group signature scheme with message-dependent opening. In: Manulis, M., Sadeghi, A.-R., Schneider, S. (eds.) ACNS 2016. LNCS, vol. 9696, pp. 137–155. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39555-5_8
Ling, S., Nguyen, K., Wang, H.: Group signatures from lattices: simpler, tighter, shorter, ring-based. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 427–449. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_19
Ling, S., Nguyen, K., Wang, H., Xu, Y.: Lattice-based group signatures: achieving full dynamicity with ease. Cryptology ePrint Archive, Report 2017/353 (2017)
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Lyubashevsky, V., Micciancio, D.: Generalized compact knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_13
Lyubashevsky, V., Neven, G.: One-shot verifiable encryption from lattices. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 293–323. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_11
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Lyubashevsky, V., Peikert, C., Regev, O.: A toolkit for ring-LWE cryptography. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 35–54. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_3
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: ACM STOC (1990)
Nguyen, P.Q., Zhang, J., Zhang, Z.: Simpler efficient group signatures from lattices. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 401–426. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_18
Rückert, M.: Lattice-based blind signatures. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 413–430. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_24
Stern, J.: A new identification scheme based on syndrome decoding. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 13–21. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_2
Xagawa, K., Tanaka, K.: Zero-knowledge protocols for NTRU: application to identification and proof of plaintext knowledge. In: Pieprzyk, J., Zhang, F. (eds.) ProvSec 2009. LNCS, vol. 5848, pp. 198–213. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04642-1_17
Acknowledgements
The authors thank Vadim Lyubashevsky for many helpful discussions and the anonymous reviewers for the useful comments. This work was supported by the ERC under grant #321310 PERCY) and the SNF under grant #200021_157080 (Efficient Lattice-Based Cryptographic Protocols).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Boschini, C., Camenisch, J., Neven, G. (2018). Floppy-Sized Group Signatures from Lattices. In: Preneel, B., Vercauteren, F. (eds) Applied Cryptography and Network Security. ACNS 2018. Lecture Notes in Computer Science(), vol 10892. Springer, Cham. https://doi.org/10.1007/978-3-319-93387-0_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-93387-0_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93386-3
Online ISBN: 978-3-319-93387-0
eBook Packages: Computer ScienceComputer Science (R0)




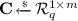 to
to  . If
. If 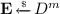 and
and 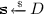 , and sends
, and sends 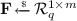 to
to  , and
, and  . It sets
. It sets 
