Abstract
In this paper we take a closer look at Penrose’s New Argument for the claim that the human mind cannot be mechanized and investigate whether the argument can be formalized in a sound and coherent way using a theory of truth and absolute provability. Our findings are negative; we can show that there will be no consistent theory that allows for a formalization of Penrose’s argument in a straightforward way. In a second step we consider Penrose’s overall strategy for arguing for his view and provide a reasonable theory of truth and absolute provability in which this strategy leads to a sound argument for the claim that the human mind cannot be mechanized. However, we argue that the argument is intuitively implausible since it relies on a pathological feature of the proposed theory.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In fact, assuming bivalence is not necessary to “derive” Gödel’s Disjunction. It suffices to argue that there are certain sentences that are either true or false but which are absolutely unprovable. Gödel (1995) argues convincingly that this situation also arises if non-classical mathematics is assumed.
- 2.
Mechanism can also be understood as the stronger thesis that the human mind functions like some particular algorithm, rather than that the human mind and some algorithm have the same outputs. We confine ourselves to the latter understanding and refer the reader to the Lindström (2001), Shapiro (2003, 2016) and Koellner (2016) for a discussion of this issue.
- 3.
- 4.
For remarks along these lines see, e.g., Shapiro (2003).
- 5.
- 6.
Ultimately, we are very skeptical whether anything interesting and coherent can be said on behalf of absolute provability but as indicated in the main text we bracket this worry for the purpose of this paper.
- 7.
See Shapiro (2003) for a very similar reconstruction of Penrose’s argument.
- 8.
Both assumption are plausible and frequently assumed in the literature. See, e.g., Koellner (2016) for discussion. A weaker arithmetical theory would do as well as long as it is sufficient for proving Gödel’s incompleteness theorems.
- 9.
Everything we say at this point would go through even if we do not assume a system to be closed under modus ponens. In this case we would need to distinguish throughout the argument between the system and what the system proves.
- 10.
Of course, there are logics in which modus ponens is not a sound rule of proof. But in such systems there will be alternative rules of proof and a similar problem will arise. Moreover, we would be surprised, if Penrose were to argue against modus ponens.
- 11.
Such a metalinguistic perspective is not unproblematic since it does not seem to be available to the anti-mechanist for he would need to step outside the system F, i.e. their “mind”, to assume it. At this point we ignore this problem but it is yet another reason why formulating Penrose’s New Argument in a rigorous way seems to require a truth predicate in the language (see below).
- 12.
Throughout the paper we take ∀xϕ to be short for ∀x(S e n t(x) → ϕ(x)) unless we explicitly mention the restriction of the quantifier. S e n t is a predicate representing the set of sentences of the language.
- 13.
The Gödel sentence G(F′) is a sentence for which, using the diagonal lemma, we can prove
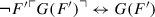 .
. - 14.
By the argument we obtain ¬∀x(Fx ↔ Kx) and by universal generalization in the metalanguage ∀F¬∀x(Fx ↔ Kx). This yields ¬∃F∀x(Fx ↔ Kx): there exists no recursively axiomatizable system F that coincides with the set of absolutely provable sentences.
- 15.
- 16.
- 17.
Introducing a hierarchy of typed absolute provability predicates would not be of any help here. Rather at each level we would face the problem anew and could never draw the desired conclusion. See Shapiro (2003) for remarks along these lines.
- 18.
The restriction has to be decidable only if we assume the schemata to be characteristic of the notion of absolute provability, that is, if they are assumed to be the axioms of the recursively axiomatizable system. Otherwise, the restriction could be recursively enumerable.
- 19.
See Line 1, 2, 3 and 5.
- 20.
Penrose (1996) explicitly agrees with this claim.
- 21.
It is possible to block this conclusion by restricting the principle (T K) to sentences of the language without the truth predicate. However, this would not really affect the argument: after all we would have sentences in which the truth predicate is applied to sentences which the knowledge predicate occurs. The knowledge predicate, in turn, may be applied to sentences in which the truth predicate occurs. So the truth predicate is applied to sentences in which it implicitly occurs. In order to maintain a coherent picture it should be possible to apply the truth predicate to sentences containing itself.
- 22.
See Koellner (2016, p. 184/185) for a clear expression of his skepticism.
- 23.
There is an interpretation of the resulting theory in the theory K F together with the completeness axiom. The interpretation would translate the absolute provability predicate as the truth predicate but hold the remaining vocabulary fixed. See Halbach (2011) for more on the truth theory K F and the completeness axiom.
- 24.
Notice that it is of no help to replace F′ by Σ, which is not closed under modus ponens, throughout the argument. To carry out the argument we need to show that whatever can be proved from Σ is true. To show this we need to assume the truth predicate to be closed under modus ponens.
- 25.
Actually, we only need to assume
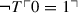 . However, this would not change the general situation. In particular Theorem 2 would still hold if (T
B) were replaced by
. However, this would not change the general situation. In particular Theorem 2 would still hold if (T
B) were replaced by 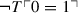 .
. - 26.
- 27.
In order to carry out Penrose’s reasoning we cannot restrict (T-I m p) to sentences of \(\mathbb {L_K}\). However, in the formulation of Theorem 3 we could use the restricted version of the principle as its proof should make clear.
- 28.
- 29.
We take it that any remotely plausible theory prevents the truth predicate from being entirely trivial. In other words it should rule out the truth of false arithmetical sentences, i.e.,
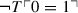 should be a theorem of F.
should be a theorem of F. - 30.
The discussion took place in the framework of epistemic arithmetic (Reinhardt 1986; Shapiro 1985) where paradoxical sentences can not be formed due to syntactic restrictions of the language. In Reinhardt (1985b) showed that “I am F”, suitably formalized, was consistent contra Lucas and Penrose. Reinhardt (1985a) establishes the inconsistency of I am F and I know that I am F. In a paper that somewhat completed this line of research Carlson (2000) showed that the so-called strong mechanistic thesis, that is, the proposition that I am F and I know that I am some recursively axiomatizable system was consistent. See, e.g., Koellner (2016) for discussion.
- 31.
See Shapiro (2003) for similar remarks.
- 32.
For an alternative presentation and a very different philosophical interpretation of the argument see Stern (2018).
- 33.
See Halbach (2011) for more details about K F C.
- 34.
So far the discussion has been entirely focused on classical logic. Since a very common reaction to the paradoxes is to give up classical logic it is a rather immediate thought to explore Penrose’s New Argument or, more generally, arguments for the first disjunct of GD assuming some non-classical logic.
- 35.
A similar, almost trivial argument shows that the first disjunct of GD can also not be obtained using the principles (T K), (T-I n), (T-I m p), and (N e c). A proof is left to the reader.
References
Benacerraf, P. 1967. God, the Devil, and Gödel. The Monist 51(1): 9–32.
Carlson, T.J. 2000. Knowledge, machines, and the consistency of Reinhard’s strong mechanistic thesis. Annals of Pure and Applied Logic 105: 51–82.
Chalmers, D.J. 1995. Mind, machines, and mathematics. A review of shadows of the mind by Roger Penrose. Psyche 2(9): 11–20.
Egré, P. 2005. The knower paradox in the light of provability interpretations of modal logic. Journal of Logic, Language and Information 14: 13–48.
Feferman, S. 2008. Axioms for determinateness and truth. Review of Symbolic Logic 1: 204–217.
Friedman, H., and M. Sheard. 1987. An axiomatic approach to self-referential truth. Annals of Pure and Applied Logic 33: 1–21.
Gödel, K. 1995. Some basic theorems on the foundations of mathematics and their implications. In Kurt Gödel: Collected works, vol. 3, ed. S. Feferman, J.W. Dawson Jr, W. Goldfarb, C. Parsons, and R.M. Solovay, 304–323. Oxford: Oxford University Press. Manuscript written in 1951.
Halbach, V. 2011. Axiomatic theories of truth. Cambridge: Cambridge University Press.
Koellner, P. 2016. Gödel’s disjunction. In Gödel’s disjunction. The scope and limits of mathematical knowledge, ed. L. Horsten, and P. Welch, 148–188. Oxford: Oxford University Press.
Leitgeb, H. 2009. On formal and informal provability. In New waves in philosophy of mathematics, ed. O. Linnebo, and O. Bueno, 263–299. Basingstoke/New York: Palgrave Macmillan.
Lindström, P. 2001. Penrose’s new argument. Journal of Philosophical Logic 30: 241–250.
Lindström, P. 2006. Remarks on Penrose’s “New Argument”. Journal of Philosophical Logic 35: 231–235.
Lucas, J.R. 1961. Minds, machines, and gödel. Philosophy 36: 112–127.
Montague, R. 1963. Syntactical treatments of modality, with corollaries on reflexion principles and finite axiomatizability. Acta Philosophica Fennica 16: 153–167.
Myhill, J. 1960. Some remarks on the notion of proof. The Journal of Philosophy 57: 461–471.
Penrose, R. 1989. The emperor’s new mind: Concerning computers, minds, and the laws of physics. Oxford: Oxford University Press.
Penrose, R. 1994. Shadows of the mind: In search for the missing science of consciousness. Oxford: Oxford University Press.
Penrose, R. 1996. Beyond the doubting of a shadow. Psyche 2(23): 89–129.
Reinhardt, W.N. 1985a. Absolute versions of incompleteness theorems. Nous 19: 317–346.
Reinhardt, W.N. 1985b. The consistency of a variant of church’s thesis with an axiomatic theory of an epistemic notation. In: Proceedings of the Fifth Latin American Symposium on Mathematical Logic held in Bogota, Revista Columbiana de Matematicas, ed. X. Caicedo, 177–200.
Reinhardt, W.N. 1986. Epistemic theories and the interpretation of gödel’s incompleteness theorems. The Journal of Philosophical Logic 15(4): 427–474.
Shapiro, S. 1985. Intensional mathematics. Amsterdam: North-Holland.
Shapiro, S. 2003. Mechanism, truth, and Penrose’s new argument. Journal of Philosophical Logic 32: 19–42.
Shapiro, S. 2016. Idealization, mechanism, and knowability. In Gödel’s disjunction. The scope and limits of mathematical knowledge, ed. L. Horsten, and P. Welch, 189–207. Oxford: Oxford University Press.
Stern, J. 2014a. Modality and axiomatic theories of truth I: Friedman-Sheard. The Review of Symbolic Logic 7(2): 273–298.
Stern, J. 2014b. Modality and axiomatic theories of truth II: Kripke-Feferman. The Review of Symbolic Logic 7(2): 299–318.
Stern, J. 2016. Toward predicate approaches to modality, trends in logic, vol. 44. Cham: Springer.
Stern, Johannes. 2018. Proving that the mind is not a machine? Thought. A Journal of Philosophy 7(2): 81–90.
Wang, H. 1996. A logical journey: From Gödel to philosophy. Cambridge: MIT Press.
Acknowledgements
This work was supported by the European Commission through a Marie Sklodowska Curie Individual Fellowship (TREPISTEME, Grant No. 703529). I wish to thank Catrin Campbell-Moore, Martin Fischer, Leon Horsten, Peter Koellner, Carlo Nicolai, and an anonymous referee for helpful comments on the content of this paper. Earlier versions of the paper were presented at the FSB Seminar in Bristol, the Fourth New College Logic Meeting, the University of Malaga and the Third Leuven-Bristol Workshop. I thank the audiences of these talks for their feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
In this appendix we show that the first disjunct of GD cannot be proved on the basis of the principles (T K), (T-I n), (T B), and (N e c).Footnote 34 We introduce some new terminology to state the result in a precise way. We write W e to denote the output of the Turing machine with index e. Using this terminology the first disjunct of GD can be formulated as
We will show that (∗) is not a consequence of the principles (T K), (T-I n), (T B), and (N e c).
Theorem 4
Let P A T K be the extension of PA in the language containing a truth and an absolute provability predicate ( \(\mathbb {L}_{\mathsf {PATK}}\) ). Then
Proof
The proof of Theorem 4 is an compactness argument: if we can prove (∗) in P A T K on the basis of (T K), (T-I n), (T B), and (N e c), then there must be a finite proof of (∗) in P A T K and, in particular, a proof with only finitely many applications of the rule (N e c). The argument we give shows that there cannot be such a proof of finite length for (∗). To this end we define a family of theories by recursion:

where C n denotes the operation that closes these sets of sentences under logical consequence. Σ n allows for proofs with n-many applications of the rule (N e c). Notice also that by construction Σ n+1 ⊆ Σ n+1. By our compactness argument it follows that if
then there must be a proof of (∗) in some Σ n for n ∈ ω. We now construct a suitable model M n for each Σ n with n ∈ ω such that
Let \(\mathsf {M}_0=(\mathbb {N}, \|T\|{ }_0,\|K\|{ }_0)\) with
Clearly, M 0⊧Σ 0 and M 0⊧∀x(P r PATK(x) ↔ Kx). But the theorems of P A T K are recursively enumerable and we thus know that M 0⊧∃e(W e(x) ↔ Kx). Now, for M n we define
It trivially follows that M n+1⊧Σ n+1 and \(\mathsf {M}_{n+1}\models \forall x(\mathsf {Pr}_{\varSigma _n}(x)\leftrightarrow Kx)\), which implies M n⊧∃e(W e(x) ↔ Kx). This concludes the proof of Theorem 4. There cannot be a proof establishing the first disjunct of GD on the basis of the principles (T K), (T-I n), (T B), and (N e c).
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Stern, J. (2018). Penrose’s New Argument and Paradox. In: Piazza, M., Pulcini, G. (eds) Truth, Existence and Explanation. Boston Studies in the Philosophy and History of Science, vol 334. Springer, Cham. https://doi.org/10.1007/978-3-319-93342-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-93342-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93341-2
Online ISBN: 978-3-319-93342-9
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


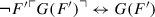 .
.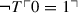 . However, this would not change the general situation. In particular Theorem
. However, this would not change the general situation. In particular Theorem 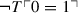 .
.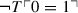 should be a theorem of F.
should be a theorem of F.