Keywords

1 Introduction and Definitions

The application of mathematical formulae and methods to solve geological problems started decades before the International Association for Mathematical Geosciences (IAMG) was founded. Initially, simple methods were used to compute derived parameters such as petrochemical mineral norms or grain size distributions and grain shapes. W. C. Krumbein in Chicago and A. B. Vistelius in the former Leningrad (now again St. Petersburg) were the first to introduce probability-based statistical methods into geoscientific applications. In the 1960s sophisticated mathematical methods were increasingly developed and applied simultaneously with the development of electronic data processing. Numerous monographs were published to introduce these new tools to geologists (Table 40.1). Step by step, a new sub-discipline—termed “mathematical geology”—was established. It was within this context that the IAMG was established as an association within the International Union of Geosciences at the International Geological Congress in Prague 1968.

Table 40.1 Early monographs of mathematical geology
Full size table

The majority of the methods introduced into the geosciences between the 1960s and 1980s were based on probability-statistical or heuristic models. Due to their high level of abstraction, these methods are equally applicable to the solution of analogous problems in other natural or social sciences provided the required data are available. Table 40.2 summarises some essential methods belonging to this group. For the purposes of this paper, these methods and models are classified as classical mathematical geology. (The term “geology” has recently been replaced by “geosciences” but the latter includes the former).

Table 40.2 Selected models of classical mathematical geology
Full size table

Classical mathematical geology applies mathematical methods and models, which comprise procedures that are not developed specifically for geosciences and which do not bear any direct relation to geological subjects or geological processes. They are extensively implemented in software packages such as Statistical Package for the Social Sciences (SPSS), and have been described in detail in the literature (e.g., Bühl 2016).

Over recent decades the development of mathematical geosciences has resulted in many new advanced models. These models have mostly been developed for specific geoscience applications such as basin modelling, groundwater flow models, contaminant transport models, heat flow models, and so they differ from the classical mathematical geology. This contribution does not cover these specific methods and models.

Classical mathematical geology models retain their applicability and practical advantages. They are helpful tools when other (specific) approaches are not available, when the development of a new model is disproportionately, when the geological problem does not require specific solutions or when limited questions are to be answered on the basis of few data. To date, this area of mathematical geology has not been replaced by later developments and it remains a useful component of the complete set of methodologies.

2 Hidden Errors and Case Study Examples

In the course of the past 50 years many correct, useful results have been generated by the application of classical mathematical geology. Whilst the application of classical mathematical geology does not necessarily result in incorrect or inaccurate solutions of geoscientific problems, it does have the potential to do so. Incorrect and frequently undetected errors can occur if the user is not sufficiently experienced with mathematical methods, with data processing problems or with the application of computer software. These problems occur mostly in geoscientific practice, especially when time and/or finance are restricted and the work is subject to pressure to produce positive results.

Spurious results or undetected errors result from apparently negligible inaccuracies such as unavailable or insufficient knowledge of data accuracy and precision, the uncritical use of values below the threshold of measurement, merging of different input data types, statistical parameter estimations without preliminary tests of the underlying type of frequency distribution, the restriction of correlation analyses to linear models, an unsuitable selection of non-supervised classification models and strategies, inclusion of non-informative attribute sets into the data file, missing information about the significance of statistical results, the acceptance of meaningless correlations, uncritical spatial or temporal extrapolation of trend-analytical results.

The application of classical mathematical geology methods and models requires frequent consideration of specific (mathematical) conditions such as the existence of a certain probability distribution, the independence of variables, a minimum number of observations, the proper treatment of missing values, a suitable choice of cluster model and strategy. Usually, long-term experience of the correct interpretation of results is necessary to avoid errors. All these fundamental conditions appear to be rarely included in training programmes and apparently insufficiently taught in courses. Commercial software is easy to handle but no signal alerts the user to the absence of essential pre-conditions and consequent occurrence of an inherent error in the results. Must computer-generated results be accepted as unbiased and reliable simply because they are produced by electronic equipment? Five selected cases derived from earlier projects will be used to demonstrate the problem in detail.

2.1 Bathymetric Map of the Azores

The archipelago of the Azores (Ilhas dos Açores) consists of nine islands and a reef area in the North Atlantic Ocean and is the result of partially active volcanoes. It covers an ocean surface between 31°30′ and 24°30′ W and 36°30′ and 40°00′ N (Fig. 40.1).

Fig. 40.1
figure 1

The Azores. Area of investigation

Full size image

The Azores are situated on the Azores plateau, an area of thickened oceanic crust due to submarine volcanism caused by a hot spot at the Azores triple junction. The NE-SW striking Mid-Atlantic Ridge crosses the plateau between the Graciosa Island and Terceira and continues over São Jorge and Pico. Along this tectonic element, the North American plate and the Eurasian Plate drift to the west and the east respectively. The Corvo and the Flores islands belong to the American plate. The NW-SE striking Terceira rift runs from the island Graciosa over the São Miguel island to the southeast. This is the tectonic line along which the African plate is subducting under the Eurasian plate. The volcanic and seismic activity started in the Miocene epoch and the formation of the islands continued during the Neogene period.

This entire part of the Atlantic Ocean is of great geological and economic interest and is the target of numerous geoscientific expeditions. The sea floor consists of basaltic rock and young volcanic glasses covered by abyssal clay and biogenous and clastic sediments (cf. Hübscher 2015). The close proximity to the crustal magmatic events causes the formation of important raw materials such as manganese nodules.

A fundamental component of marine survey expeditions is to make depth soundings of the locality. The depths measured in the early 1980s were interpolated by specialists at a computer centre to construct bathymetric contour lines. They used kriging interpolation, the results of which are shown in Fig. 40.2. These results do not reflect the expected predominant NW-SE striking structures described above and give a distorted representation of the main morphological structures. Investigation showed that a suitable mathematical model was applied but the wrong input data were used: geodetic coordinates were used but the minutes were recorded as decimal places. This error was not detected in the computer centre. The result obtained after correcting the data is shown in Fig. 40.3 in which the map more closely reflects the main morphological structures of the investigated area (OpenSeaMap 2016).

Fig. 40.2
figure 2

The Azores. Bathymetric contour lines based on inaccurate input data

Full size image
Fig. 40.3
figure 3

The Azores. Bathymetric contour lines based on corrected input data

Full size image

2.2 Granulometric Analysis of Coastal Sediments of the Southern Baltic Sea

The Bay of Greifswald (Greifswalder Bodden) in Germany occupies the south-central part of the Baltic Sea. Holocene sand, gravel and boulder cover late Pleistocene till and basin sand. The recent material originated from an active cliff and from an abrasion platform (for details, see Niedermeyer et al. 2011). The fine, medium- and coarse-grained sediments show a lithological differentiation more or less parallel to the erosional shore line. The grain size is specified using the European standard DIN EN ISO 14688-1 (2013).

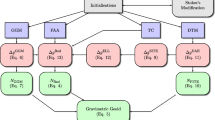
Knowledge of the characteristics of the sediment is important for designing measures to protect the coast and is necessary if the raw material is to be exploited for building purposes (cf. Börner 2011). One of the relevant parameters is the grain size. A principal component analysis was conducted to reduce the dimensions, or the number of manifest attributes, to a smaller number of latent components which largely explain the variance of the input data, and to avoid an undesirable multi-collinearity, i.e. to obtain a set of essential information (Fig. 40.4). A cluster (R) analysis should explain the relationships between the original grain size classes (Fig. 40.5). The result reflects only a trivial fact: the coastal sediments are mainly composed of silt and fine sand if they are not coarse-grained, and vice versa.

Fig. 40.4
figure 4

Baltic Sea. Clastic sediments of the south coast. Principal component analysis of grain size data

Full size image
Fig. 40.5
figure 5

Baltic Sea. Clastic sediments of the south coast. Cluster (R) analysis of grain size data

Full size image

The input information scaled in mass% was correctly recorded. However, the fact that the sum of all sieve fractions amounts to the constant sum of nearly 100% was ignored. This closed system means that mathematical results based on correlation among the attributes must be faulty. Chayes (1960a, b, 1971) and Vistelius and Sarmanov (1961) showed that the so-called percent correlation leads to unfeasible results. The modern approach to processing data that form a closed system was developed only later and therefore could not be applied (e.g., Pawlowsky-Glahn 2005; Pawlowsky-Glahn and Buccianti 2011).

2.3 Areal Distribution of Polycyclic Aromatics in an Abandoned Industrial Site

Until its abandonment an extensive industrial site in Germany was used for machine manufacture. During later assessment for redevelopment the site was investigated for possible ecological contamination. The disused, unsealed enterprise is located on near-surface Holocene sand and gravel. The consultants sampled and analysed twenty-five soil specimens and detected an appreciable concentration of polycyclic aromatic hydrocarbons (PAHs) at two locations. PAHs belong to a group of extremely carcinogenic substances. The 16 most important and persistent constituents are on the National Priority Pollutant List of the US-EPA. An occurrence of these hydrocarbons in subsoil typically requires appropriate remediation measures.

A map of the distribution of the pollutant within the site was constructed by means of kriging (Fig. 40.6) and an expensive soil excavation at well no. T20 over 75 m2 and at well no. T05 over 46 m2 was proposed. The application of this geostatistical model to create a contour map is a widely used technique in mathematical geosciences. Similar cases have been repeatedly observed. Less well-known is that the analysed attributes must be interpolable between adjacent points.

Fig. 40.6
figure 6

Contaminated industrial site. Contour map of the apparent distribution of polycyclic aromatics in subsoil

Full size image

PAHs include a wide spectrum of organic substances with relatively low solubility in water, e.g. naphthalene (32 mg l−1), acenaphthylene (3.4 mg l−1), acenaphthene (4 mg l−1), fluorine (1.8 mg l−1) and pyrene (0.134 mg l−1). Their solubility in water and tendency to migrate into aquifers rises if solvents such as mineral oil, halogenated organic compounds or phenols are present. PAHs will be generated during coking processes or coal-gas generation but they never occur as waste products of machine manufacturing. A study by a project controller showed that a gas generation facility had been operational on the site until 1898. Coal tar was an unprofitable by-product at that time and it was frequently deposited near the factory. Thus, PAH bearing waste was also deposited locally, at distinct locations. Originally included fluids are removed by natural weathering processes over decades. At present, the remaining solid PAH components are persistent and relatively immobile (Stupp and Püttmann 2001). A result of this man-made impact is a spatially limited, although not tolerable, area of contamination. Any extension of these spatially limited occurrences caused by mathematical interpolation methods is meaningless.

The groundwater flow direction must be included in the risk evaluation if contaminants in unconsolidated subsoil are water-soluble and if they are able to migrate. Contour maps generated by standard kriging cannot consider this factor and its application would also result in an incorrect result.

The resulting insolubility of the pollutants under natural conditions causes their inability to migrate. Due to this property of the contamination, it is not correct to interpolate the detected PAH concentration values between observed locations. An isoline map predicts an area-wide contamination whereas only local and isolated pollution actually occurs. Later, it was recommended that the survey data be presented in the form of a point map (Fig. 40.7) and to focus future remediation on the observed hot spots.

Fig. 40.7
figure 7

Contaminated industrial site. Hot spot map of polycyclic aromatics in subsoil

Full size image

A similar case study was discussed by Thiergärtner (1995).

2.4 Ore Grade Estimation in a Cassiterite Mine

Tin ore has been mined for centuries in Altenberg (Saxony, Germany). Monzo-, aplite- and albite-granite intruded during the Cisuralian epoch (Permian) into Precambrian paragneiss and were followed by acid, fluorine and silica rich overcritical auras. Feldspar was mainly altered to quartz; lithium bearing mica, topaz, fluorite, and ore minerals such as cassiterite, wolframite, and molybdenite crystallised in the form of small grains. For details, see Weinhold (2002).

Thirty samples were taken from an exploration gallery to calculate the mean grade of the deposit yield in the investigated direction. The range of the metal content was 0.07–4.22% tin. The arithmetic mean of all analysed sample values was computed “as usual” to be m arith  = 0.755% Sn. Inspection of the empirical histogram and the fitted normal distribution curve (Fig. 40.8) showed that the metal grade was extremely skewed to the right. A lognormal distribution was fitted to the input data (Fig. 40.9) and the arithmetic mean of the (decimal) logarithms of tin grade was calculated and the corresponding antilogarithm (m geom  = 0.512% Sn) was obtained. This value is less than the arithmetic mean. The geometric mean is a location parameter, such as the median or mode, and scarcely suitable to estimate the expected value of a population.

Fig. 40.8
figure 8

Tin grade. Arithmetical mean value estimation

Full size image
Fig. 40.9
figure 9

Tin grade. Lognormal mean value estimation

Full size image

Which estimator should be applied? The statistical “best” estimator Ê(mlg) of the expected value for lognormally distributed data is calculated using Eq. 40.1 developed by Aitchison and Brown (1957) and applied e.g. by Dowd (1984):

$$ {\hat{\text{E}}}\left( {{\text{m}}_{ \lg } } \right) = 10^{{{\text{mean }}\left( {{ \lg }\,{\text{X}}} \right)}} {\text{e}}^{\text{k}} \left( {1 - \frac{{{\text{k}}\left( {{\text{k}} - 1} \right)}}{n} + \cdots } \right) $$
(40.1)

where k = 2.65095 var (lg X) and n = number of observations.

This estimator is rather poorly known in geoscientific practice. The estimation results in m lg  = 0.765% Sn for the given example. Only this value can be applied to estimate the mean tin grade of the investigated gallery in an unbiased way. The true ore grades of samples in an operating underground mine can be used to estimate the mean grade of un-mined volumes of ground and this is one of the most important parameters in determining economic feasibility.

2.5 Classification of a Doleritic Sill Using Trace Elements

Tholeiitic basalt occurs in the Thuringian Forest (Germany) as Sakmarian doleritic sill (Lower Permian). It is intruded into a sandstone–siltstone formation. The contacts are metamorphosed. This sill was extensively described recently by Andreas and Voland (2010).

The matrix of the dolerite consists of pyroxene, plagioclase, olivine, alkali feldspar and some magnetite. The drill core was partitioned into seven sections by petrographical analysis (Table 40.3; Fig. 40.10a). Megascopic and mineralogical indications differ negligibly.

Table 40.3 Vertical sections of doleritic sill, Thuringian Forest
Full size table
Fig. 40.10
figure 10

Doleritic sill. Geochemical classification (for explanation see Table 40.3)

Full size image

The interesting question was to correlate this sequence with its chemical composition. Four trace elements were selected: cobalt and nickel which are fixed in the olivine mineral replacing magnesium, zircon as a constituent of feldspar or pyroxene, and copper which can occur in the form of microscopically small chalcopyrite crystals. These four chemical elements were analysed in 79 samples covering the whole sequence.

A hierarchical cluster analysis was carried out. It was based on z-scaled (normalized) input data to avoid an overestimation of attributes with large values, using the squared Euclidean distance measure and the Ward method. The cluster dendrogram shows clearly distinguishable classes and can be interpreted without difficulty. All resulting and interpretable classes have been assigned to the cross-section (Fig. 40.10b). Chemical symbols without brackets refer to high concentrations of an element in Fig. 40.10. Where medium concentrations occur they are enclosed in brackets and missing chemical symbols indicate low contents in the sample. The expressions High, Medium, and Low refer to the overall mean values. The figure shows first that the geochemical composition differs noticeably from the petrographical structure. The number of clearly distinguishable geochemical classes is low. Thick parts of the sill seem to be characterised by a similar micro-chemical composition. It is obvious that samples with lower depth (hanging-wall samples, marked by h) dominate the hanging-wall of the sill, and samples taken from the footwall (marked by ly) mainly occur at deeper levels. The middle section comprises samples that were collected at depths between 200 and 300 m (marked by m).

The results gave sufficient reason to review the methodological approach. First, it was noted that the depth was included as one of the input parameters and the parameter “depth” significantly influences the classification. Such procedures are not faulty in a mathematical sense but they accentuate the effect of neighbouring samples within a common class due to the similar value of the parameter “depth”. Within the drill core neighbouring samples have a higher chance of falling into this common class than do the more distant samples. This effect should be avoided if not explicitly requested by the researcher. The relatively long sections of the profile with little or no geochemical variation can be explained by this effect. Secondly, the critical test showed that the inclusion of both cobalt and nickel into the analysis caused an overestimation of the olivine component. The linear pairwise correlation coefficient (Pearson) between Co and Ni was calculated as r = +0.915. Cobalt is not significantly correlated with copper or zircon, and copper and zircon are uncorrelated, too. This result could be expected from the relationships of the geochemical bonds.

A repeated cluster analysis based on the attributes Ni, Cu and Zr resulted in classes which were drawn into the rock sequence as shown in Fig. 40.10c. The influence of the depth is eliminated and the double effect of the trace elements Co and Ni—reflecting the olivine content—is reduced to only one factor. Much more detail is visible; i.e. a clear vertical geochemical differentiation can be recognised. In addition, the resulting geochemical classification of the rock profile does not simply correspond to the mineralogical and petrographical structure and displays more essential details than the first result. Although the mathematical model was chosen correctly, an incorrect set of input data was applied to solve the problem.

3 Conclusion and Suggestions

Classical mathematical geology is the application of non-specific mathematical methods and models to solve geoscientific problems. Its proper application frequently results in useful solutions but its misapplication can generate spurious results that may not be recognised. These hidden errors are not caused by the algorithms but by insufficient knowledge of their application and deficient experience with their use. They are avoidable.

A significant proportion of the methodological contributions to classic mathematical geology are written in an academic environment. New developments are mainly published in journals specialising in mathematical geosciences. However, only in rare cases are they evaluated by engineers and geoscientists working in engineering practices, mining companies, environmental bureaus, governmental agencies or individual consultants.

As a conclusion the following suggestions are offered to developers of mathematical-geoscientific methods, models, algorithms and software and to all academic teachers in the field of mathematical geosciences:

  1. 1.

    Instructive tutorials on the applicability and modes of application should be developed, introduced and delivered. This problem can be solved best by experienced geoscientists who are experienced in the “traps” of applying mathematical geology.

  2. 2.

    Informative, methodologically sound case studies should be published in widely-used geoscientific and eco-scientific journals as a means of improving the “daily” application of mathematical geosciences in practice.

  3. 3.

    A more critical view of users is required when assessing outputs from computer-generated mathematical-geological methods and models. In particular, belief in the absolute correctness of such outputs should be discouraged.

  4. 4.

    University studies and post-graduate education in the correct application of mathematical-geological methods should be combined with the development of new application fields (application research).