Skip to main content
Springer Nature Link
Log in

Hodge Filtration and Operations in Higher Hochschild (Co)homology and Applications to Higher String Topology

  • Chapter
  • First Online:
Algebraic Topology

Part of the book series: Lecture Notes in Mathematics ((LNM,volume 2194))

Abstract

This paper is based on lectures given at the Vietnamese Institute for Advanced Studies in Mathematics and aims to present the theory of higher Hochschild (co)homology and its application to higher string topology. There is an emphasis on explicit combinatorial models provided by simplicial sets to describe derived structures carried or described by Higher Hochschild (co)homology functors. It contains detailed proofs of results stated in a previous note as well as some new results. One of the main result is a proof that string topology for higher spheres inherits a Hodge filtration compatible with an (homotopy) E n+1-algebra structure on the chains for d-connected Poincaré duality spaces. We also prove that the E n -centralizer of maps of commutative (dg-)algebras are equipped with a Hodge decomposition and a compatible structure of framed E n -algebras. We also study Hodge decompositions for suspensions and products by spheres, both as derived functors and combinatorially.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    Also called Brane topology [CV, GTZ3].

  2. 2.

    Also called n-disk-algebras or unoriented E n -algebras [AF, Gi4].

  3. 3.

    Though for instance [TW, GTZ] are also giving many details on it.

  4. 4.

    Also called chiral homology, an homology theory for n-dimensional framed manifold and E n -algebras.

  5. 5.

    In fact, this paper (and the concomitant lectures) were partially thought as an introduction to ideas and features of factorization homology in a special case of independent interest but which does not require as much higher homotopical background as the general theory.

  6. 6.

    Also called Pois 2-algebras in this paper.

  7. 7.

    Or unoriented in the terminology of [Gi4], or that of a d-disk algebra in the one of [AF].

  8. 8.

    Said otherwise it has an additional action of the orthogonal group O(d) for which the structure maps are equivariant.

  9. 9.

    That is the dg-structure on \(M \otimes \bigotimes _{i\in I_{+}\setminus \{+\}}A\) is the tensor product of the underlying dg-k-modules.

  10. 10.

    Here the commutativity is crucial.

  11. 11.

    Recall that we can consider normalized chains and cochains when applying Dold-Kan.

  12. 12.

    That is a commutative algebra object in the symmetric monoidal category of differential graded A-modules.

  13. 13.

    Meaning that the A-module structure is induced from the \({CH}_{X_{\bullet }}(A)\) one through the algebra map \(A \rightarrow {CH}_{X_{\bullet }}(A)\).

  14. 14.

    Said otherwise, the combinatorial definition of Hochschild chains has an natural derived enhancement.

  15. 15.

    Using the now standard terminology of calling homology an object of an ∞-derived category of complexes, not to be mistaken with their associated homology groups.

  16. 16.

    Which are actually k-modules.

  17. 17.

    For its standard monoidal structure given by tensoring over A.

  18. 18.

    Sometimes called E n -bimodules since for n = 1, they correspond to homotopy bimodules over an homotopy associative algebra.

  19. 19.

    And thus realizing R(D k −1).

  20. 20.

    That is π d (f k , ∗)(1) = k.

  21. 21.

    See Remark 1.3.21, this is the filtration induced by the simplicial degree.

  22. 22.

    See Definition 1.4.1.

  23. 23.

    See Definition 1.4.1, Remark 1.4.7.

  24. 24.

    In other words a functor from Mod CDGA to (γ, 0) − (Mod CDGA ).

  25. 25.

    In other words the quasi-isomorphism from \({CH}^{X_{\bullet }}(A,B) \otimes {CH}^{Y _{\bullet }}(A,B)\) to the chain complex associated to the diagonal cosimplicial space \(\big({CH}^{X_{n}}(A,B) \otimes {CH}^{Y _{n}}(A,B)\big)_{n\in \mathbb{N}}\).

  26. 26.

    By a diagonal sphere, we mean a component indexed by a tuple for which all the j i are the same. Which are precisely those on the diagonal cubes in Fig. 1.3.

  27. 27.

    That is continuous maps which are embeddings, which, restricted to each cube is obtained by a translation and an homothety in each of the nth direction of the cube I n.

  28. 28.

    In other words, \(\mathbf{CH}^{S^{d} }(-,-)\) is a functor CDGA(Mod CDGA ) → E n -Alg(k- Mod).

  29. 29.

    In particular of E n -algebra in cochain complexes.

  30. 30.

    Instead of rectangles parallel to the axes.

  31. 31.

    We follow the convention of [Gi4]; it is called framed in [SW].

  32. 32.

    A disk is open here.

  33. 33.

    Any A is quasi-isomorphic to a semi-free one of the form (Sym(V ), d) and by quasi-invariance of Hochschild chains it is enough to compute the left hand side of (1.93) for the later cdgas.

  34. 34.

    We recall that it means that f is quasi-isomorphic to H ∗(f): H ∗(Y ) → H ∗(X) in CDGA; in particular X and Y are formal.

  35. 35.

    It can also be deduced from the fact that Sym is a left adjoint hence commutes with colimits.

  36. 36.

    Note that Sym(V ) is endowed with the zero differential.

  37. 37.

    That is those not of the form ℓd + σ ℓ −1(1), …, ℓd + σ ℓ −1(d).

  38. 38.

    For the Lie algebroid \(\Omega ^{1}(R)[1 - n]\) deduced from the Lie algebra structure on R[1 − n].

References

  1. D. Ayala, J. Francis, Factorization homology of topological manifolds. J. Topol. 8(4), 1045–1084 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  2. G. Arone, V. Turchin, Graph-complexes computing the rational homotopy of high dimensional analogues of spaces of long knots. Ann. Inst. Fourier (Grenoble) 65(1), 1–62 (2015)

    Google Scholar 

  3. M. Atiyah, D. Tall, Group representations, λ-rings and the J-homomorphism. Topology 8, 253–297 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  4. A. Beilinson, V. Drinfeld, Chiral Algebras. American Mathematical Society Colloquium Publications, vol. 51 (American Mathematical Society, Providence, RI, 2004)

    Google Scholar 

  5. M. Bökstedt, W.C. Hsiang, I. Madsen, The cyclotomic trace and algebraic K-theory of spaces. Invent. Math. 111(3), 465–539 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  6. J. Block, A. Lazarev, André-Quillen cohomology and rational homotopy of function spaces. Adv. Math. 193(1), 18–39 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  7. P. Bressler, R. Nest, B. Tsygan, Riemann-Roch theorems via deformation quantization. I, II. Adv. Math. 167(1), 1–25, 26–73 (2002)

    Google Scholar 

  8. N. Bergeron, L. Wolfgang, The decomposition of Hochschild cohomology and Gerstenhaber operations. J. Pure Appl. Algebra 79, 109–129 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  9. K. Costello, Topological conformal field theories and gauge theories. Geom. Topol. 11, 1539–1579 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. K. Costello, Topological conformal field theories and Calabi-Yau categories. Adv. Math. 210(1), 165–214 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  11. A. Căldăraru, The Mukai pairing. II. The Hochschild-Kostant-Rosenberg isomorphism. Adv. Math. 194(1), 34–66 (2005)

    MATH  Google Scholar 

  12. A. Căldăraru, J. Tu, Curved A ∞ algebras and Landau-Ginzburg models. N. Y. J. Math. 19, 305–342 (2013)

    MathSciNet  MATH  Google Scholar 

  13. K. Costello, O. Gwilliam, Factorization algebras in perturbative quantum field theory. Online wiki available at http://math.northwestern.edu/~costello/factorization_public.html

  14. K.-T. Chen, Iterated integrals of differential forms and loop space homology. Ann. Math. (2) 97, 217–246 (1973)

    Google Scholar 

  15. R. Cohen, J. Jones, A homotopy theoretic realization of string topology. Math. Ann. 324(4), 773–798 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. F.R. Cohen, The homology of 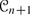-spaces, n ≥ 0, in The Homology of Iterated Loop Spaces. Lecture Notes in Mathematics, ed. by F.R.Cohen, T.J. Lada, J.P. May, vol. 533 (Springer, Berlin, 1976)

    Google Scholar 

  17. D. Calaque, T. Pantev, B. Toën, M. Vaquié, G. Vezzosi, Shifed Poisson structures. J. Topol. (to appear)

    Google Scholar 

  18. M. Chas, D. Sullivan, String topology. arXiv:math/9911159

    Google Scholar 

  19. R. Cohen, A. Voronov, Notes on string topology, in String Topology and Cyclic Homology. Advance Courses in Mathematics CRM Barcelona (Birkhäuser, Basel, 2006), pp. 1–95

    Google Scholar 

  20. D. Calaque, T. Willwacher, Triviality of the higher formality theorem. Preprint arXiv:1310.4605

    Google Scholar 

  21. V. Dolgushev, B. Paljug, Tamarkin’s construction is equivariant with respect to the action of the Grothendieck-Teichmueller group. J. Homotopy Relat. Struct. 11(3), 503–552 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  22. G. Dunn, Tensor product of operads and iterated loop spaces. J. Pure Appl. Algebra 50(3), 237–258 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  23. J. Francis, The tangent complex and Hochschild cohomology of E n -rings. Preprint AT/1104.0181

    Google Scholar 

  24. J. Francis, D. Gaitsgory, Chiral Koszul duality. Selecta Math. New Ser. 18, 27–87 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  25. B. Fresse, Théorie des opérades de Koszul et homologie des algèbres de Poisson. Ann. Math. Blaise Pascal 13(2), 237–312 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  26. B. Fresse, Iterated bar complexes of E-infinity algebras and homology theories. Algebr. Geom. Topol. 11(2), 747–838 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. B. Fresse, Modules over Operads and Functors. Lecture Notes in Mathematics, vol. 1967 (Springer, Berlin, 2009)

    Google Scholar 

  28. B. Fresse, Homotopy of Operads & Grothendieck-Teichmüller Groups. Mathematical Surveys and Monographs, vol. 217 (American Mathematical Society, Providence, 2017)

    Google Scholar 

  29. Y. Félix, J.-C. Thomas, Rational BV-algebra in string topology. Bull. Soc. Math. France 136(2), 311–327 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Y. Félix, J.-C. Thomas, M. Vigué, The Hochschild cohomology of a closed manifold. Publ. Math. Inst. Hautes Études Sci. 99, 235–252 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  31. M. Gerstenhaber, The cohomology structure of an associative ring. Ann. Math. 78(2), 267–288 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  32. G. Ginot, Homologie et modèle minimal des algèbres de Gerstenhaber. Ann. Math. Blaise Pascal 11(1), 95–127 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  33. G. Ginot, On the Hochschild and Harrison (co)homology of C ∞ -algebras and applications to string topology, in Deformation Spaces. Aspects of Mathematics, vol. E40 (Springer, Berlin, 2010), pp. 1–51

    Google Scholar 

  34. G. Ginot, Higher order Hochschild cohomology. C. R. Math. Acad. Sci. Paris 346(1–2), 5–10 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. G. Ginot, Notes on factorization algebras and factorization homology, 124 pp., in Mathematical Aspects of Field Theories. Springer, Mathematical Physics Studies, vol. 5, Part IV (Springer, Cham, 2015), pp. 429–552

    Google Scholar 

  36. G. Ginot, M. Robalo, Hochschild-Kostant-Rosenberg Theorem in derived geometry (in preparation)

    Google Scholar 

  37. P. Goerss, J. Jardine, Simplicial Homotopy Theory. Modern Birkhäuser Classics, 1st edn. (Birkhäuser, Basel, 2009)

    Google Scholar 

  38. T.G. Goodwillie, Cyclic homology, derivations, and the free loopspace. Topology 24(2), 187–215 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  39. M. Gerstenhaber, S. Schack, A Hodge-type decomposition for commutative algebra cohomology. J. Pure Appl. Algebra 48(3), 229–247 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  40. G. Ginot, T. Tradler, M. Zeinalian, A Chen model for mapping spaces and the surface product. Ann. Sc. de l’Éc. Norm. Sup., 4e série, t. 43, 811–881 (2010)

    Google Scholar 

  41. G. Ginot, T. Tradler, M. Zeinalian, Derived higher Hochschild homology, topological chiral homology and factorization algebras. Commun. Math. Phys. 326, 635–686 (2014)

    Article  MATH  Google Scholar 

  42. G. Ginot, T. Tradler, M. Zeinalian, Higher Hochschild cohomology of E ∞ -algebras, Brane topology and centralizers of E n -algebra maps (2015). Preprint

    Google Scholar 

  43. G. Ginot, S. Yalin, Deformation theory of bialgebras, higher Hochschild cohomology and formality, avec S. Yalin. Preprint arXiv:1606.01504

    Google Scholar 

  44. H. Hiller, λ-rings and algebraic K-theory. J. Pure Appl. Algebra 20(3), 241–266 (1981)

    Google Scholar 

  45. V. Hinich, Homological algebra of homotopy algebras. Commun. Algebra 25(10), 3291–3323 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  46. G. Horel, Higher Hochschild cohomology of the Lubin-Tate ring spectrum. Algebr. Geom. Topol. 15(6), 3215–3252 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  47. M. Kontsevich, Operads and motives in deformation quantization. Lett. Math. Phys. 48, 35–72 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  48. D. Kaledin, Motivic structures in non-commutative geometry, in Proceedings of the International Congress of Mathematicians. Volume II, vol. 461–496 (Hindustan Book Agency, New Delhi, 2010)

    Google Scholar 

  49. L. Katzarkov, M. Kontsevich, T. Pantev, Hodge theoretic aspects of mirror symmetry, in From Hodge Theory to Integrability and TQFT tt*-Geometry. Proceedings of Symposia in Pure Mathematics, vol. 78 (American Mathematical Society, Providence, RI, 2008), pp. 87–174

    Google Scholar 

  50. B. Knudsen, Higher enveloping algebras. arXiv:1605.01391

    Google Scholar 

  51. C. Kratzer, λ-structure en K-théorie algébrique. Comment. Math. Helv. 55(2), 233–254 (1980)

    Google Scholar 

  52. M. Kashiwara, P. Schapira, Deformation quantization modules. Astérisque 345, xii+147 pp. (2012)

    Google Scholar 

  53. M. Kontsevich, Y. Soibelman. Deformation Theory, Volume 1. Unpublished book draft. Available at www.math.ksu.edu/ soibel/Book-vol1.ps

  54. M. Kontsevich, Y. Soibelman, Notes on A ∞ -algebras, A ∞ -categories and non-commutative geometry, in Homological Mirror Symmetry. Lecture Notes in Physics, vol. 757 (Springer, Berlin, 2009), pp. 153–219

    Google Scholar 

  55. J.-L. Loday, Opérations sur l’homologie cyclique des algèbres commutatives. Invent. Math. 96(1), 205–230 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  56. J.-L. Loday, Cyclic Homology. Grundlehren der mathematischen Wissenschaften, vol. 301 (Springer, Berlin, 1992)

    Google Scholar 

  57. P. Lambrechts, D. Stanley, Poincaré duality and commutative differential graded algebras. Ann. Sci. Éc. Norm. Supér. (4) 41(4), 495–509 (2008)

    Google Scholar 

  58. J. Lurie, Higher Topos Theory. Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009), xviii+925 pp.

    Google Scholar 

  59. J. Lurie, On the classification of topological field theories. Preprint, arXiv:0905.0465v1

    Google Scholar 

  60. J. Lurie, Higher Algebra. Book, available at http://www.math.harvard.edu/~lurie/

  61. R. McCarthy, On operations for Hochschild homology. Commun. Algebra 21(8), 2947–2965 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  62. T. Pirashvili, Hodge Decomposition for higher order Hochschild homology. Ann. Sci. École Norm. Sup. (4) 33(2), 151–179 (2000)

    Google Scholar 

  63. T. Pantev, B. Toën, M. Vaquié, G. Vezzosi, Shifted symplectic structures. ubl. Math. Inst. Hautes Études Sci. 117, 271–328 (2013)

    Google Scholar 

  64. C. Rezk, A model for the homotopy theory of homotopy theory. Trans. Am. Math. Soc. 353(3), 937–1007 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  65. B. Richter, S. Ziegenhagen, A spectral sequence for the homology of a finite algebraic delooping. J. K-Theory 13(3), 563–599 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  66. D. Sullivan, Infinitesimal computations in topology. Inst. Hautes Études Sci. Publ. Math. 47, 269–331 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  67. P. Salvatore, N. Wahl, Framed discs operads and Batalin Vilkovisky algebras. Q. J. Math. 54(2), 213–231 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  68. D. Tamarkin, Deformation complex of a d-algebra is a (d+1)-algebra. preprint arXiv:math/0010072

    Google Scholar 

  69. T. Tradler, The Batalin-Vilkovisky algebra on Hochschild cohomology induced by infinity inner products. Ann. Inst. Fourier 58(7), 2351–2379 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  70. B. Toën, G. Vezzosi, Homotopical Algebraic Geometry II: Geometric Stacks and Applications. Memoirs of the American Mathematical Society, vol. 193(902) (American Mathematical Society, Providence, RI, 2008)

    Google Scholar 

  71. B. Toën, G. Vezzosi, Algèbres simpliciales S 1-équivariantes et théorie de de Rham. Compos. Math. 147(6), 1979–2000 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  72. B. Toën, G. Vezzosi, A note on Chern character, loop spaces and derived algebraic geometry, in Abel Symposium, Oslo, vol. 4 (2007), pp. 331–354

    MATH  Google Scholar 

  73. V. Turchin, T. Willwacher, Hochschild-Pirashvili homology on suspensions and representations of Out(F n ). arXiv:1507.08483

    Google Scholar 

  74. T. Tradler, M. Zeinalian, Infinity structure of Poincaré duality spaces. Algebr. Geom. Topol. 7, 233–260 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  75. M. Ungheretti, Free loop space and the cyclic bar construction. arXiv:1602.09035

    Google Scholar 

  76. M. Vigué-Poirrier, D. Burghelea, A model for cyclic homology and algebraic K-theory of 1-connected topological spaces. J. Differ. Geom. 22(2), 243–253 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  77. N. Wahl, Universal operations in Hochschild homology. J. Reine Angew. Math. 720, 81–127 (2016)

    MathSciNet  MATH  Google Scholar 

  78. C. Weibel, An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994)

    Google Scholar 

  79. C. Weibel, The Hodge filtration and cyclic homology. K-Theory 12(2), 145–164 (1997)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire Analyse, Géométrie et Applications, UMR 7539, Institut Galilée, Université Paris 13, 99 Avenue Jean Baptiste Clément, 93430, Villetaneuse, France

    Grégory Ginot

Authors
  1. Grégory Ginot
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Grégory Ginot .

Editor information

Editors and Affiliations

  1. Department of Mathematics, Vietnam National University, Hanoi, Vietnam

    H.V. Hưng Nguyễn

  2. LAGA, UMR 7539 CNRS Institut Galilée, Université Paris 13, Villetaneuse, France

    Lionel Schwartz

Rights and permissions

Reprints and permissions

Copyright information

© 2017 Springer International Publishing AG

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Ginot, G. (2017). Hodge Filtration and Operations in Higher Hochschild (Co)homology and Applications to Higher String Topology. In: Nguyễn, H., Schwartz, L. (eds) Algebraic Topology. Lecture Notes in Mathematics, vol 2194. Springer, Cham. https://doi.org/10.1007/978-3-319-69434-4_1

Download citation

Publish with us

Policies and ethics