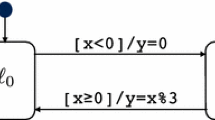Abstract
In this paper, it is shown how a complete input equivalence class testing strategy developed by the second author can be effectively used for infinite-state model checking of system models with infinite input domains but finitely many internal state values and finite output domains. This class of systems occurs frequently in the safety-critical domain, where controllers may input conceptually infinite analogue data, but make a finite number of control decisions based on inputs and current internal state. A variant of Kripke Structures is well-suited to provide a behavioural model for this system class. It is shown how the known construction of specific input equivalence classes can be used to abstract the infinite input domain of the reference model into finitely many classes. Then quick checks can be made on the implementation model showing that the implementation is not I/O-equivalent to the reference model if its abstraction to observable minimal finite state machines has a different number of states or a different input partitioning as the reference model. Only if these properties are consistent with the reference model, a detailed equivalence check between the abstracted models needs to be performed. The complete test suites obtained as a by-product of the checking procedure can be used to establish counter examples showing the non-conformity between implementation model and reference model. Using various sample models, it is shown that this approach outperforms model checkers that do not possess this equivalence class generation capability.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Motivation. Model checking of infinite-state systems is an important research field. Notable examples are Timed Automata, where physical time represents a model or meta variable with uncountable domain [3] and the more general Hybrid Systems, where also real-valued observables are taken into account [8]. Other approaches investigate model checking in presence of unbounded data structures, we cite here [6] as a representative of many results achieved in this area.
The close relationship between infinite state model checking and testing has been observed, for example, in [18], where a complete testing method for verifying real-time systems against Time Automata models has been presented.Footnote 1
In this paper, we show how results from model-based testing of reactive systems can inspire approaches to infinite-state model checking.
Main contribution. We present a new algorithm for checking I/O-equivalence of systems with infinite input domains, but finite domains for internal state variables and outputs. It applies to both deterministic and nondeterministic systems, whose behavioural semantics can be expressed by I/O-state transitions systems, a specific variant of Kripke Structures. The algorithm exploits a new method for calculating input equivalence classes, that has originally been developed for constructing complete test suites for systems of this type [10]. While an algorithm for calculating these classes for deterministic models has been published in [9], the algorithm presented in this paper can handle nondeterministic systems.
It is shown that for I/O-equivalence checking problems of reference and implementation models in this domain, the new algorithm clearly outperforms conventional model checkers, because the latter need to operate on an explicit discretisation of the input space, whereas the new algorithm presented here only needs to check a significantly smaller number of input equivalence classes. Moreover, the new method is very effective for constructing counter examples in case of failing equivalence checks, since these examples are simply given by failing test cases.
To our best knowledge, this approach to checking systems with infinite input domains is new: other authors using equivalence partition techniques of the input space used more general classes, at the cost of losing the completeness of the method [19].
Overview. The equivalence calculation method and the resulting model checking algorithm are described in Sect. 2. In Sect. 3, several model checking experiments are described, comparing the implementation of the method presented here against the well-established FDR3 model checker for the CSP process algebra. Section 4 presents the conclusions.
2 Method
In this section we describe how to calculate the input equivalence class partitioning of a given model described in Sect. 3 and how we use this input equivalence class partitioning to check two models for I/O-equivalence.
2.1 State Space Representation
Our approach is based on state transition systems (STS) described as triples \(\left( \mathcal {S}, \underline{s}, \mathcal {R}\right) \) where \(\mathcal {S}\) is the possibly infinite state space, \(\underline{s} \in \mathcal {S}\) is the initial state and \(\mathcal {R}\subseteq \mathcal {S}\times \mathcal {S}\) the transition relation. Furthermore, we assume that all states in \(\mathcal {S}\) are reachable from the initial state via the transition relation and require that the properties of I/O-state transition systems (IOSTS) apply which we specify as follows:
-
Every state \(s \in \mathcal {S}\) is a valuation function \(s : \mathcal {V} \rightarrow \mathcal {D}\), mapping variables v from a finite set of symbols \(v\in \mathcal {V}\) to their values s(v) in the domain \(\mathcal {D}\).
-
The set \(\mathcal {V}\) of variable symbols can be partitioned into disjoint sets of input variables, internal state variables, and output variables. Let \(I\subseteq \mathcal {V}\) be the set of input variables. Then \(D_I\) is the set of all input vectors which is the cross product of the domains of all input variables in I. From now on, the set of input variables is referred to as I, the set of internal state variables as M, and the set of output variables as O.
-
The state space of an IOSTS can be partitioned into two sets of states \(S_Q\) and \(S_T\) which are the sets of the so-called quiescent and transient states, respectively. Transient and quiescent states are characterised as follows.
$$\begin{aligned}&\forall (s_q, s) \in S_Q \times S_Q: (s_q, s) \in \mathcal {R} \Rightarrow s|_{M\cup O} = s_q|_{M\cup O}\end{aligned}$$(1)$$\begin{aligned}&\forall (s_t, s) \in S_T\times \mathcal {S}: (s_t, s) \in \mathcal {R} \Rightarrow s|_I = s_t|_I\end{aligned}$$(2)$$\begin{aligned}&\forall (s_q, s) \in S_Q\times S_T: (s_q, s) \in \mathcal {R} \Rightarrow \exists x \in I: s(x) \ne s_q(x) \end{aligned}$$(3)Here, \(s|_X, X \subseteq \mathcal {V}\) denotes the restriction of the valuation function s to the set of variables symbols \(v\in X\). Thus, no internal state or output variable may change over a transition from a quiescent state, no input variables may change over a transition from a transient state, and every transient state reached by a transition from a quiescent state needs to evaluate at least one input variable differently. If the latter were not the case, \(S_Q\) and \(S_T\) would not be disjoint.
-
The initial state is contained in \(S_Q\).
An IOSTS describes the behaviour of a state-based system. From the outside view, only input variables influence the state of the system and only output variables are observable. States in partition \(S_Q\) of the state space are stable states where the system waits for new inputs. States in partition \(S_T\) of the state space are transient states. A system performing some sort of calculation would wait in a quiescent state for the inputs to the calculation. If the inputs allow for the calculation to be performed, the internal state variables and output variables are modified in a sequence of transient states. The calculation is finished when a quiescent state is reached, allowing for the outputs to be observed. Inputs are changed by modifying the input variables. The possible modifications to the input variables are defined by the transition relation as follows: An input vector \({\varvec{c}}\) can be applied to the system if for the new state \(s' = s \oplus \{ {\varvec{x}} \mapsto {\varvec{c}} \}\) the condition \(\left( s, s'\right) \in \mathcal {R}\) holds. The set of all input vectors allowed in state s is defined as \(C(s) = \{{\varvec{c}} \in \mathcal {D}_I \mid \exists {\varvec{x}}: (s, s \oplus \{ {\varvec{x}} \mapsto {\varvec{c}}\}) \in \mathcal {R}\}\). If the condition \(\forall s \in S_Q: C(s) = \mathcal {D}_I\) holds for every state of \(S_Q\) of an IOSTS, that IOSTS is called completely specified. An IOSTS is free of livelocks if there is no reachable infinite sequence of transitions between transient states linked by the transition relation.
Let \(S = (\mathcal {S}, \underline{s}, \mathcal {R})\) be an IOSTS as defined above. Then, the partitioning of \(S_Q \subseteq \mathcal {S}\) induced by the equivalence relation \(s \sim _{MO} s' \iff \forall v_{mo} \in M \cup O: s(v_{mo}) = s'(v_{mo})\) with \(s, s' \in S_Q\) is called the MO partitioning. All states evaluating all internal state and output variables in the same way are members of the same partition. Here, such a partitioning is named \(\mathcal {A} = \mathcal {A}_0, \ldots , \mathcal {A}_n\) and it is finite, as the domains of all internal state and output variables are finite. Every member of \(\mathcal {A}\) is called a state class. The state class containing the initial state of the IOSTS under consideration is called \(\mathcal {A}_0\). For mapping a state to the corresponding state class, the shorthand \(MO : \mathcal {S} \rightarrow \mathcal {A}\) is introduced.
For any IOSTS free of livelocks, every quiescent state s of that IOSTS can be mapped to a set of quiescent states that are reachable by a finite, possibly empty sequence of only transient states for every input vector \({\varvec{c}} \in C(s)\). Let \(s/{\varvec{c}}\) be this mapping for state s and input vector \({\varvec{c}}\). The case where \((s \oplus \{ {\varvec{x}} \mapsto {\varvec{c}}\}) \in S_Q\) holds is trivial. If, however, \((s \oplus \{ {\varvec{x}} \mapsto {\varvec{c}}\}) \in S_T\) holds, the set of quiescent states the state s maps to under input vector \({\varvec{c}}\) can be determined by unrolling the transition relation. If, for any s and any \({\varvec{c}}\), \(|s/{\varvec{c}}| > 1\), the IOSTS is called nondeterministic.
2.2 Input Equivalence Class Partitioning
When checking a pair of livelock free IOSTS for I/O-equivalence, we may have to deal with a possibly infinite input domain. In our approach we partition the input domain into a finite number of input equivalence classes as presented by [10]. For every pair \(s_1,s_2\) of states in the same state class of the MO partitioning of an IOSTS, and for every input vector in every element \(\mathcal {I}_i\) of such an input equivalence class partitioning (IECP) \(\mathcal {I}\), the state classes of the reachable quiescent states are identical: \(\forall s_1,s_2 \in \mathcal {S} : \forall \mathcal {I}_i \in \mathcal {I} : \forall {\varvec{c}} \in \mathcal {I}_i : MO(s_1) = MO(s_2) \implies \{MO(s_1') | s_1' \in s_1/{\varvec{c}}\} = \{MO(s_2') | s_2' \in s_2/{\varvec{c}}\}\). To obtain such an IECP, first the input equivalence classes of every state class are calculated. An algorithm to do so is given in Sect. 2.2.1, taking nondeterminism into account. Given these IECPs for every state class, the final IECP is given as every non-empty intersection of input equivalence classes containing exactly one element from each of the calculated IECPs of every state class for which an algorithm is given in Sect. 2.2.2.
For illustration purposes, the approach is applied to the system described by the SysML state machine shown in Fig. 1. This model has one integer input variable x and one output variable m. Initially, the output m is 0, meaning that no alarm is active. If the input value x exceeds a threshold max, m is set to 2, triggering an alarm which will only be ceded after x is equal to or drops below another threshold max - delta. However, if the input value is equal to max, the behaviour of the described system is non-deterministic: either, the alarm is triggered and the system progresses as described before, or a state is entered where there is no full alarm but maybe a message is sent to a security company to check on the secured object (these possibilities are not shown in the model). For this state to be left into the idle state where there is no alarm, the input may simply drop by an arbitrary amount. However, if it rises further, a full alarm is triggered.
2.2.1 Input Equivalence Classes for State Classes
Let \(g_{i,j}\) be the condition on the input variables describing all input vectors for which there is a possibly empty sequence of only transient states terminated by a quiescent state for every state in state class \(\mathcal {A}_i\) ending in state class \(\mathcal {A}_j\): \(\forall {\varvec{c}} \in \mathcal {D}_I : {\varvec{c}} \,\models \, g_{i,j} \iff \forall s \in \mathcal {A}_i : \exists s' \in \mathcal {A}_j : s' \in s/{\varvec{c}}\). Furthermore, let G be the set of all such conditions for the MO partitioning of an IOSTS, where the set of satisfying input vectors is not empty, i.e. where there is at least one input vector allowing the transition from one state class into another. Finally, let \(G_i\) be a subset of G where \(g_{i,\ell } \in G_i \iff \forall s \in \mathcal {A}_i : \exists {\varvec{c}} \in \mathcal {D}_I : s/{\varvec{c}} \in \mathcal {A}_\ell \), that is, \(G_i\) contains all conditions applicable to transitions emanating from state class \(\mathcal {A}_i\). Then, for a given \(G_i\), Algorithm 1 calculates a set \(M_i\) of tuples of conditions:
Every tuple in \(M_i\) describes an input equivalence class for state class \(\mathcal {A}_i\).
Transferring this to our example, we first derive the state classes \(\mathcal {A}\). In the given model, every SysML state corresponds to a state class as every state maps to a separate state class in the MO partitioning. Thus, \(\mathcal {A}_0\) corresponds to S0. The other state class counterparts to the SysML states may be chosen arbitrarily. We chose \(\mathcal {A}_1\) to be equivalent to state S1 and \(\mathcal {A}_2\) to state S2. Then, the formulas in Fig. 2 are the elements of G.
For every state class, \(G_i\) is calculated, its elements are given by the \(i^{th}\) line of expressions in Fig. 2.

Algorithm 1 first calculates all satisfiable subsets of \(G_i\) for every state class \(\mathcal {A}_i\). As the IOSTS under consideration can be nondeterministic, there may be subsets with more than one member. The classes of a partitioning are disjoint, thus an IECP cannot contain overlapping elements, i.e. multiple classes containing the same input vector. Thus, for every satisfiable subset of \(G_i\) which is also a subset of another satisfiable subset of \(G_i\), the difference to all supersets is added as negated terms to form an input equivalence class if the resulting conjunction is satisfiable.
For \(G_0\) from our example, the sets
and
are tested for satisfiability. As neither \(g_{0,0} \wedge g_{0,1}\) nor \(g_{0,0} \wedge g_{0,2}\) is satisfiable, supersets of \(\{g_{0,0}, g_{0,1}\}\) and \(\{g_{0,0}, g_{0,2}\}\) do not have to be checked for satisfiability, as these will never be satisfiable either. The sets of expressions satisfiable under conjunction are the singleton sets and \(\{g_{0,1}, g_{0,2}\}\). The latter is introduced due to the non-determinism of the described system in the case of x == max. In this example, the satisfiable subset \(\{g_{0,2}\}\) of G cannot be an input equivalence class, since the set of input vectors described would not be disjoint from the set described by \(\{g_{0,1}, g_{0,2}\}\). However, \(g_{0,2} \wedge \lnot g_{0,1}\) is satisfiable, allowing \(\mathcal {A}_2\) to be reached deterministically by a set of input vectors which now represent one input equivalence class. As \(g_{0,1} \wedge \lnot g_{0,2}\) is not satisfiable, neither \(g_{0,1}\) nor \(g_{0,1} \wedge \lnot g_{0,2}\) represents an input equivalence class. Thus, the input equivalence classes of the system are given as follows:
In previous implementations, \(|p| + |n| = |G_i|\) held for every element \(m \in M_i\) as every element of \(G_i\) appeared in m in either identical or negated form. In contrast to this, our approach possibly results in smaller descriptions of input equivalence classes, where \(|p| + |n| \le |G_i|\), which has practical ramifications: for large sizes of \(|G_i|\), instantiating and solving the resulting input equivalence classes using an SMT solver shows significant speedups. Furthermore, our approach exploits the fact that  holds for arbitrary sets P of first order logic formulae and may thus show significant speedups in contrast to checking every subset of \(G_i\) for satisfiability.
holds for arbitrary sets P of first order logic formulae and may thus show significant speedups in contrast to checking every subset of \(G_i\) for satisfiability.
2.2.2 Input Equivalence Classes for IOSTS
Given the IECP for every state class, we can calculate the IECP over all state classes by calculating all non-empty intersections \(\phi \) of input equivalence classes containing exactly one input equivalence class from every state class. In other words, the IECP is a non-empty subset \(\mathcal {M}\) of \(M_0 \times \ldots \times M_{|\mathcal {A}|-1}\), where every element describes a set of first order logic expressions whose conjunction is satisfiable:
To calculate all \(\phi \) efficiently, Algorithm 2 is used. Similar to Algorithm 1, every satisfiable \(\phi \) has to be found. Otherwise, the partitioning would be incomplete, as parts of the input domain were not covered by the result. Again, parts of the search space \(M = M_0\times \ldots \times M_{|\mathcal {A}|-1}\) not containing a solution can be left out. If for a set P the fact could be established that the conjunction of its elements is not satisfiable, conjunctions with further expressions will not be satisfiable as well. The number of elements in M of which P is a subset is

assuming the elements of P were picked by ascending index of the elements of M. This number is maximal if |P| is as small and all \(M_i\) as large as possible, or if the following condition holds \(\forall 0 \le j< |P|: \forall |P| \le k < |\mathcal {A}|: |M_j| \le |M_k|\). To be able to ignore as large parts of the search space as possible, sorting the elements of M by cardinality, picking a P of size \(\ell \) out of the first \(\ell \) elements of M and checking it for satisfiability is beneficial. If P is satisfiable, then \(\ell \) should be increased and a new P picked until either \(\ell = |\mathcal {A}|\) or a conjunction of the elements of P is not satisfiable. In the former case, P describes an input equivalence class, in the latter a different P shall be picked. Algorithm 2 describes a possible implementation. In our example, first an order for the \(M_i\) is determined, beginning with the smallest set, which is \(M_2\). For each of its elements, every element of the next \(M_i\) in order, e.g. \(M_0\), is picked and the conjunction checked for satisfiability. If that is satisfiable, every conjunction with every element of \(M_1\) would be checked. This way, all IECP are found, which are listed in Fig. 3.
2.3 Checking for Input/Output Equivalence
Two IOSTS are I/O-equivalent, if they produce the same language of input/output traces. To check two IOSTS for I/O-equivalence, we first calculate the IECP for both. In [10] the authors show how to derive FSMs or, more precisely, transductors from these IECP which are I/O-equivalent iff the same holds for the corresponding IOSTS. In short, these transductors are constructed as follows: Let \(S_1, S_2\) be a pair of IOSTS to be checked for I/O-equivalence with a known bijective mapping for their input and output variables, i.e. for every input and output variable of \(S_1\) there is a corresponding variable in \(S_2\). Furthermore, let \(\mathcal {A}_{S_1}, \mathcal {A}_{S_2}\) be the MO partitionings and \(\mathcal {I}_{S_1}, \mathcal {I}_{S_2}\) be the IECPs for both IOSTS. Then, \(T_1 = (Q_1, \underline{q}_1, \varSigma _{I,1}, \varSigma _{O,1}, R_1), T_2 = (Q_2, \underline{q}_2, \varSigma _{I,2}, \varSigma _{O,2}, R_2)\) are the corresponding transductors, where every state in the state space \(Q_1\) has a corresponding state class in \(\mathcal {A}_{S_1}\), and every input symbol in the input alphabet \(\varSigma _{I,1}\) has a corresponding input space partition in \(\mathcal {I}_{S_1}\). The initial state \(\underline{q}_1 \in Q_1\) maps to the state class containing the initial state of \(S_1\). \(T_1\)’s output alphabet \(\varSigma _{O,1}\) results from the output vectors in the state classes \(\mathcal {A}_{S_1}\) where every distinct output vector is assigned an output symbol in \(\varSigma _{O,1}\). The transition relation \(R_1\) is constructed according to the transition relation of \(S_1\). \(T_2\) is constructed accordingly.
For a word composed of symbols from the input alphabet, each transductor produces a set of output traces. Only for non-deterministic IOSTS, this set may contain more than one trace. Every element of that set represents a possible response of the system for the applied input trace.
Minimising the transductor allows the input alphabet to be partitioned. Two input symbols \(x_1, x_2\) are equivalent and thus elements of the same partition element iff for every transition \((q, x_1, y, q') \in R_m\) there is a transition \((q, x_2, y, q') \in R_m\), where \(R_m\) is the transition relation of the minimised transductor. Merging all input space partitions corresponding to an element of a set of equivalent input symbols results in the coarsest IECP for the corresponding IOSTS.
After calculating the coarsest IECP using \(T_1\) and \(T_2\) described above, two further transductors \(\bar{T}_1, \bar{T}_2\) can be derived as described above, now using the coarsest IECPs to construct the input alphabets. These are I/O-equivalent, i.e. their languages are equal, iff \(S_1\) and \(S_2\) are I/O-equivalent. Using a test method which is complete regarding I/O-equivalence, a test suite can be calculated, consisting of a set of input words. \(\bar{T}_1\) and \(\bar{T}_2\) are I/O-equivalent if and only if they produce the same set of output words for every input word of the test suite. However, if for one input word the sets of output words differ, a counterexample has been found. The counterexample consists of the input word and the symmetric difference of the sets of output words produced by \(\bar{T}_1\) and \(\bar{T}_2\). Naturally, the shortest counterexample can be found effectively by executing the test suite sorted by the length of the input words in ascending order. As a prerequisite for the calculation and execution of a common test suite, a bijective mapping between the input symbols of \(\bar{T}_1\)’s and \(\bar{T}_2\)’s input alphabets has to be known. This requires that the input alphabets are of the same size and that for every input equivalence class partition of the coarsest IECP of \(S_1\) there is a congruent input equivalence class partition in the coarsest IECP of \(S_2\). If this is not the case, \(S_1\) and \(S_2\) are known to not be I/O-equivalent as shown in [16]. To calculate a common test suite nonetheless, the intersection of both coarsest IECPs can be used as the coarsest common IECP, allowing \(\bar{T}_1\) and \(\bar{T}_2\) to be constructed with the same IECP. This is necessary if a counterexample has to be calculated.
3 Case Study and Quantitative Evaluation
3.1 General Evaluation Approach
To evaluate the described approach, a case study involving models with varying complexity and state space size has been performed. Each model was represented as a SysML state machine [14]. Its behavioural semantics was specified by associating an IOSTS transition relation with the state machine, as described in [9]. Errors were injected into each model M by applying mutation operators, this resulted in mutant models \(M_1, M_2,\dots \). Each pair \((M,M_i)\) has been checked by means of the I/O-equivalence checking approach described in the previous section. Additionally, each model M and each mutant \(M_i\) has been represented using the CSP process algebra [17], so that the FDR3 model checker [7] could be used to check I/O-equivalence by means of CSP trace equivalence. For each equivalence check, the performance of our equivalence checker was compared to that of FDR3.
3.2 Models Used
For our case study, five models have been selected, two of these were already described in previous publications [11].
3.2.1 Airbag Controller
The most complex model used for our case study describes the behaviour of an airbag controller and is described in the following section as an example of the complexity our approach can handle. This model has two floating point inputs \(\text {s1}\) and \(\text {s2}\), describing the acceleration measured by the acceleration sensors the airbag controller is evaluating, and two Boolean output values, \(\text {fire}\) and \(\text {defect}\), which are set to true iff the airbag should be triggered or the sensors are regarded as defect, respectively. Furthermore, there is a Boolean input variable clk that toggles iff there is a new pair of input values to be processed.
If the system is not defect, and if the airbag has not been triggered, the controller waits for a new pair of input values. Such a pair will be checked for plausibility first. A difference of more than \(5\%\) is considered to be implausible. For a pair of plausible input values the following relation holds: \(\text {s1} \in \left[ \text {s2}\cdot 0.95, \text {s2}\cdot 1.05\right] \). An internal integer counter variable \(\text {plausibleCtr}\) is set to zero if this is not the case. Also, another internal integer counter variable \(\text {errCtr}\) is incremented. If afterwards the relation \(\text {errCtr} \ge 3\) holds, the system is regarded as defect, thus \(\text {defect}\) is set to true and the controller halts, otherwise, the next pair of input values is awaited. However, if the sensor values are plausible, \(\text {plausibleCtr}\) is incremented and the relation \(\text {plausibleCtr} \ge 3\) checked. If it holds, \(\text {errCnt}\) is reset to zero. In any case of plausible sensor values, the sensor values are compared to a threshold, in our model this is the floating point value 3.0. If one of the values does not exceed the threshold, another internal integer counter variable \(\text {crashCnt}\) is reset to zero, and the next pair of values awaited. However, if both exceed the threshold, \(\text {crashCnt}\) is incremented. If this counter equals 3 after the increment, this is considered as a trustworthy crash indication; thus the output \(\text {fire}\) is set to true, and the system halts. Figure 4 shows a SysML state machine describing this behaviour.
3.2.2 Further Models
Table 1 summarises the properties of all models used for the case study. Apart from the number of input variables, output variables and size of state space after applying our approach, it lists an approximation of the input domain size.
For SysML models, the size calculation \(|\mathcal{D}_I|\) of the input domain is based on the lower and upper bounds of each input variable type and the number of distinct representable values between these bounds. As CSP only admits data types based on integral numbers, all variables representing floating point numbers had to be approximated as integer variables using one of two methods:
-
1.
Two integers modelling one floating point number, where one models the integral part, and the other the fractional part.
-
2.
Scaling all floating point numbers in a model by the same factor sufficiently large to allow for discarding the fractional part.
Due to these changes, all models using floating point numbers show different input space sizes for SysML and CSP models. The size of the CSP model input space is denoted by \(|\mathcal {D}_{I,\text {CSP}}|\).
Model alarm1 is the simple alarm system used in the examples above, alarm2 is a more complex variant of alarm1. Model csm specifies a ceiling speed monitor for a train control system; it is described in [4]. Model turn_ind describes a turn indication controller for cars, taking left/right flashing and emergency flashing into account; it is a simplified version of the complete model described in [15].
3.2.3 Mutation Operators
For every model used in our case study – from now on called reference model – a set of mutated implementation models has been created. At least one implementation was chosen to be syntactically different, but semantically equivalent, and at least one mutation differed in its behaviour. To this end, we applied exactly one mutation operator out of a set of commonly used syntax mutation operators [1, 2, 13] to the SysML reference model, guaranteeing syntactically different implementations with the same input and output variables. Thirteen mutation operators described in Table 2 were selected and used for error injection into the reference models, as far as applicable.
3.2.4 CSP Models
The CSP models were manually created by translating SysML reference models and implementations into CSP, taking into account the discretisation of floating point input variables as described above.
3.3 Results
Every SysML reference model and each associated implementation were checked for I/O-equivalence using the method described in this paper. The test suites used to check the transductors for I/O-equivalence as described in Sect. 2 were calculated using the W-Method [5, 20]. The corresponding CSP reference and implementation models were checked for trace equivalence using the FDR3 model checker. Each check was limited to 40 GBytes of RAM and 2 h execution time (wallclock time).
Regarding the correctness of the checks, both our model checking method and the FDR3 tool detected the same I/O-equivalence violations, as was expected.
For the alarm1 model, the FDR3 tool was approximately 70 times slower than our checker and needed approximately 11 times more memory. These factors are calculated as the averages of all 10 checks performed for the alarm1 model and its 10 mutated implementations.
For the alarm2 model, the FDR3 tool was approximately 22 times slower and needed 7 times more memory. This value was calculated from 11 mutations checked against the reference model.
For all model pairs derived from the models csm, turn_ind and airbag, the CSP model checker was not able to complete the calculation within the resource limits set, while our checker completed these checks with durations from 27 s to 1217 s. The average checking time needed by our checker was 365 s.
All performance measurements described here included the time for abstracting the original model to its finite state machine and the time for creating a counter example in case of failures. A detailed tabular view documenting all checks and comparisons performed is given in [12].
4 Conclusion
We have presented a new algorithm for I/O-equivalence checking of models with infinite input domains but finite domains for internal state and outputs. The underlying method has been based on a new complete input equivalence class testing strategy previously developed by the second author and his research group.
Our approach clearly outperforms the FDR3 model checker. The cause is easy to understand, since FDR3 does not implement the equivalence class construction techniques that were available for our checker. As a consequence, FDR3 needed to explore the models by explicitly checking a very large number of input values instead of restricting the investigation to small numbers of input classes. This comparison shows that the input equivalence class construction method advocated in this paper can be a valuable extension to other model checking tools as well. Additionally, the results presented here are another example of the closeness between testing and model checking methods.
The algorithms needed for abstracting a nondeterministic I/O-state transition system to its finite state machine have exponential worst case complexity. Future work will focus on mitigating this problem by means of further distributing the algorithms involved on multiple threads and CPU cores.
Notes
- 1.
Recall that a test suite is called complete if it guarantees to accept every implementation conforming to a given reference model and to reject every non-conforming implementation, provided that its true behaviour is represented by a model from a well-defined fault domain.
References
Aichernig, B.K., Brandl, H., Jöbstl, E., Krenn, W.: Model-based mutation testing of hybrid systems. In: de Boer, F.S., Bonsangue, M.M., Hallerstede, S., Leuschel, M. (eds.) FMCO 2009. LNCS, vol. 6286, pp. 228–249. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17071-3_12
Aichernig, B.K., Lorber, F., Ničković, D.: Time for mutants — model-based mutation testing with timed automata. In: Veanes, M., Viganò, L. (eds.) TAP 2013. LNCS, vol. 7942, pp. 20–38. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38916-0_2
Alur, R., Madhusudan, P.: Decision problems for timed automata: a survey. In: Bernardo, M., Corradini, F. (eds.) SFM-RT 2004. LNCS, vol. 3185, pp. 1–24. Springer, Heidelberg (2004). doi:10.1007/978-3-540-30080-9_1
Braunstein, C., Haxthausen, A.E., Huang, W., Hübner, F., Peleska, J., Schulze, U., Vu Hong, L.: Complete model-based equivalence class testing for the ETCS ceiling speed monitor. In: Merz, S., Pang, J. (eds.) ICFEM 2014. LNCS, vol. 8829, pp. 380–395. Springer, Cham (2014). doi:10.1007/978-3-319-11737-9_25
Chow, T.S.: Testing software design modeled by finite-state machines. IEEE Trans. Softw. Eng. (SE) 4(3), 178–186 (1978)
Dingel, J., Filkorn, T.: Model checking for infinite state systems using data abstraction, assumption-commitment style reasoning and theorem proving. In: Wolper, P. (ed.) CAV 1995. LNCS, vol. 939, pp. 54–69. Springer, Heidelberg (1995). doi:10.1007/3-540-60045-0_40
Gibson-Robinson, T., Armstrong, P., Boulgakov, A., Roscoe, A.W.: FDR3: a parallel refinement checker for CSP. Int. J. Softw. Tools Technol. Transf. 18(2), 149–167 (2016). http://dx.doi.org/10.1007/s10009-015-0377-y
Henzinger, T.A., Ho, P., Wong-Toi, H.: HYTECH: a model checker for hybrid systems. STTT 1(1–2), 110–122 (1997). https://doi.org/10.1007/s100090050008
Huang, W., Peleska, J.: Complete model-based equivalence class testing. STTT 18(3), 265–283 (2016). http://dx.doi.org/10.1007/s10009-014-0356-8
Huang, W., Peleska, J.: Complete model-based equivalence class testing for nondeterministic systems. Form. Asp. Comput. 29(2), 335–364 (2017). http://dx.doi.org/10.1007/s00165-016-0402-2
Hübner, F., Huang, W., Peleska, J.: Experimental evaluation of a novel equivalence class partition testing strategy. In: Blanchette, J.C., Kosmatov, N. (eds.) TAP 2015. LNCS, vol. 9154, pp. 155–172. Springer, Cham (2015). doi:10.1007/978-3-319-21215-9_10
Krafczyk, N.: Äquivalenzprüfung für Zustandstransitionssysteme mittels Eingabeäquivalenzklassenpartitionierung. Master’s thesis, University of Bremen, November 2016
Krenn, W., Schlick, R., Tiran, S., Aichernig, B., Jobstl, E., Brandl, H.: MoMut: UML model-based mutation testing for UML. In: 2015 IEEE 8th International Conference on Software Testing, Verification and Validation (ICST), pp. 1–8. IEEE (2015)
Object Management Group: OMG Systems Modeling Language (OMG SysML), Version 1.4. Technical report, Object Management Group (2015). http://www.omg.org/spec/SysML/1.4
Peleska, J., et al.: A real-world benchmark model for testing concurrent real-time systems in the automotive domain. In: Wolff, B., Zaïdi, F. (eds.) ICTSS 2011. LNCS, vol. 7019, pp. 146–161. Springer, Heidelberg (2011). doi:10.1007/978-3-642-24580-0_11
Peleska, J., Huang, W.: Model-based testing strategies and their (in)dependence on syntactic model representations. In: Beek, M.H., Gnesi, S., Knapp, A. (eds.) FMICS/AVoCS -2016. LNCS, vol. 9933, pp. 3–21. Springer, Cham (2016). doi:10.1007/978-3-319-45943-1_1
Roscoe, A.W.: Understanding Concurrent Systems. Springer, London (2010). doi:10.1007/978-1-84882-258-0
Springintveld, J., Vaandrager, F., D’Argenio, P.: Testing timed automata. Theor. Comput. Sci. 254(1–2), 225–257 (2001)
Sulzmann, M., Zechner, A.: Model checking DSL-generated C source code. In: Donaldson, A., Parker, D. (eds.) SPIN 2012. LNCS, vol. 7385, pp. 241–247. Springer, Heidelberg (2012). doi:10.1007/978-3-642-31759-0_18
Vasilevskii, M.P.: Failure diagnosis of automata. Kibernetika (Transl.) 4, 98–108 (1973)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 IFIP International Federation for Information Processing
About this paper
Cite this paper
Krafczyk, N., Peleska, J. (2017). Effective Infinite-State Model Checking by Input Equivalence Class Partitioning. In: Yevtushenko, N., Cavalli, A., Yenigün, H. (eds) Testing Software and Systems. ICTSS 2017. Lecture Notes in Computer Science(), vol 10533. Springer, Cham. https://doi.org/10.1007/978-3-319-67549-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-67549-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-67548-0
Online ISBN: 978-3-319-67549-7
eBook Packages: Computer ScienceComputer Science (R0)