Approximate Matrix Inversion for Linear Pre-coders in Massive MIMO

Abstract

This work presents a high-throughput and low-latency matrix inversion design for linear pre-coders for massive multiple-input multiple-output (MIMO) systems. Because of the large number of base station (BS) antennas, as well as the multiple user terminals (UTs), served in a massive MIMO system, the channel matrix dimensions become large. Inversions of such large matrices using direct inversion methods, such as those used in linear pre-coders, would entail prohibitive complexity. To avoid such complexity, Neumann-series-based approximate inversion has been suggested for linear pre-coders in massive MIMO systems. However the performance, complexity and convergence speed of the Neumann series approach highly depends on the initial approximation of the inverse used as a starting point. In this work, we present a novel initial approximation for the Neumann series, which facilitates the parallel computation of the inverse and hence results in lower latency for inversion as well as better accuracy when compared to the previous approaches. A VLSI architecture of the proposed method is implemented for the inversion of a $16\times 16$ matrix in TSMC 65-nm technology. A throughput of 0.54 M to 15 M matrix inversion per second is achieved at a clock frequency of 460 MHz with a 117 K gate count.

1 Introduction

Multiple-input and multiple-output (MIMO) systems have been adopted in modern wireless communication standards such as IEEE 802.11n, 4G, 3GPP Long Term Evolution and WiMAX. Due to the ever-growing demand for higher data rates without further increasing the communication bandwidth, novel transmission technologies are still an urgent need [1, 3]. A potential technology for meeting this demand is large-scale multi-user MIMO, or ‘massive MIMO’, a form of multi-user multiple-antenna wireless technology which promises substantial improvements in spectral efficiency and energy efficiency [1, 3, 4, 10].

In massive MIMO systems, a base station (BS) is equipped with a large number of antennas (M), as compared to conventional MIMO systems, while serving a relatively low number (K) of user terminals (UTs). This disparity in number of service antennas to active user terminals helps in focusing energy into ever smaller regions of space to bring huge improvements in throughput and radiated energy efficiency. Other benefits of massive MIMO include extensive use of inexpensive low-power components, reduced latency, simplification of the MAC layer, and robustness against intentional jamming [2].

However, to enjoy the benefits of massive MIMO, an efficient linear pre-coding scheme at the transmitter side is of paramount importance. Pre-coding is a pre-processing technique that exploits channel state information (CSI) at the transmitter to match the transmission to the instantaneous channel conditions [13,14,15,16,17]. In particular, linear pre-coding is a simple and efficient method that can reduce the complexity of a MIMO receiver.

Linear pre-coding includes zero-forcing (ZF), matched filter (MF) and regularized zero forcing (RZF). It has been shown that when $M>>K$, the simplest linear pre-coders are optimal and thermal noise, interference and channel estimation errors vanish [3]. For such cases, simple linear pre-coders like ZF perform exceptionally well, and sum rates of up to 98% of the (optimal) dirty paper coding (DPC) are reported to have been achieved [4].

However, linear pre-coders like ZF and RZF involve channel inversion using the pseudo-inverse of the channel, which involves inverting a $K\times K$ gram matrix $Z\;(Z=GG^{H}\;for\;ZF\;and\;Z=(G^{H}G+\alpha I)\;for\;RZF)$, where K is the number of UTs and G is the propagation matrix. Exact matrix inversion methods, such as LU decomposition, Cholesky decomposition and QR decomposition, require cubic order complexity [7]. Hence exact inversion methods cannot be applied due to larger matrix dimensions in massive MIMO systems.

To reduce the matrix inversion complexity, the Neumann-series-based approximate inverse [8, 9] has been proposed for large matrices in massive MIMO systems. As the ratio of the number of antennas at the BS to the number of UTs, $\beta =M/K$, increases, Z becomes diagonally dominant [1]. Wu et al. [8] exploited this diagonal dominance property and suggested using the diagonal elements of matrix Z as an initial approximation (seed) for Neumann series expansion. This method is termed the diagonal Neumann series (DNS) in the rest of this chapter for easy reference.

However, for highly correlated channels or low $\beta$ values, matrix Z may not be very strongly diagonally dominant or perhaps not dominant at all. For such cases, using only the diagonal elements as a seed will result in slow convergence of the Neumann series. Since inversion accuracy is an important parameter, which defines the suppression of the multi-user interference (MUI) in the downlink [9], the DNS will require a greater number of Neumann series terms to achieve a certain accuracy.

For scenarios with low $\beta$ values or highly correlated channels, Prabhu et al. [9] proposed to include some off-diagonal elements in addition to the diagonal elements to form the initial approximation for the Neumann series. In particular, they used a tri-diagonal matrix as the seed. We call this method the tri-diagonal Neumann series (TNS) for easy reference. Using the tri-diagonal matrix as a seed in the Neumann series results in better convergence and superior performance as compared to the DNS [8].

For the approximate inverse calculation of either the DNS or TNS, the inverse of the seed matrix has to be calculated, and hence it should be easily invertible. However using the TNS as seed matrix results in an increase in complexity for calculating the inverse for the tri-diagonal matrix as compared to the DNS. Prabhu et al. [9] proposed to use a modified Gauss-elimination-based algorithm to obtain the inverse of the tri-diagonal matrix. However due to the sequential nature of the algorithm, the latency is proportional to K and cannot be reduced with parallel hardware. Thus it may not be desirable for a system that has a very low latency requirement.

In this work, we present a low-latency and high-throughput matrix inversion method, also based on the Neumann series. In particular we propose to use a new seed matrix [18], for which the inverse can be easily calculated in a parallel fashion with lower complexity, hence leading to lower latency and higher throughput.

2 System Model

For this work, we consider single-cell large-scale multi-user MIMO (MU-MIMO) with one BS and K UTs. The BS is equipped with M antennas and the UTs have a single antenna, such that M antennas at the BS communicate with K single-antenna UTs $(M>K>1)$. The system model considered in this work is in line with the corresponding system model described in [1].

The reverse link propagation matrix, G with a dimension of $M\times K$ is the product of the $M\times K$ matrix H, which accounts for the small-scale fading, and a $K\times K$ diagonal matrix $D_{\beta }^{1/2}$, which accounts for the large-scale fading [1]. Hence $G=HD_{\beta }^{1/2},$ where the $K^{th}$ column vector of H describes the small-scale fading between the $K^{th}$ UT and the M antennas, while the $K^{th}$ diagonal element of $D_{\beta }^{1/2}$ is the large-scale fading coefficient. For the forward link, the BS transmits an $M\times 1$ vector, x, through its M antennas and the K UTs collectively receive a $K\times 1$ vector:

$$\begin{aligned} y=\sqrt{\rho }G^{H}x+w, \end{aligned}$$

(1)

where w is the $K\times 1$ vector of the receiver noise whose components are independent and distributed as $CN\,(0,1)$. The total transmitted power is normalized to satisfy $E[x^{H}x]=1$. Hence, $\rho _{T}>0$ denotes the total downlink power.

2.1 Linear Pre-coding at the Transmitter

The $M\times 1$ transmitted signal vector x is given as $x=Ws$, where W is an $M\times K$ pre-coding matrix and s is a $K\times 1$ vector containing data symbols intended for K users. For MU-MIMO with large arrays of antennas at the BS, the columns of the propagation matrix are asymptotically orthogonal under favorable conditions [1], and

(2)

Due to this property, simple linear pre-coders, like MF, ZF and RZF, can be deployed on the transmitter side for close to optimal performance. The MF pre-coder, despite being simple, requires more BS antennas to achieve close to optimal performance [1]. Hence we focus on a ZF and RZF pre-coding scheme in our system model.

Zero Forcing (ZF) Pre-coding: The ZF pre-coding schemes [13] have been extensively studied on multiuser systems as ZF decouples the multiuser channel into independent single-user channels and has been shown to achieve a large proportion of dirty paper coding capacity [12].

The ZF [11] expression is given by

$$\begin{aligned} W_{ZF}=G(G^{H}G)^{-1}. \end{aligned}$$

(3)

Regularized Zero Forcing (RZF) Pre-coding: The regularized ZF pre-coder, as the name implies, introduces a regularization parameter in the channel inversion. One way to regularize an inverse is to add a multiple of the identity matrix before inversion, such as

$$\begin{aligned} W_{RZF}=G(G^{H}G+\alpha I)^{-1}. \end{aligned}$$

(4)

The amount of interference depends on $\alpha >0$. If $\alpha =0$, then it essentially becomes a ZF pre-coder(Eq. 3). The amount of interference increases with $\alpha$ , and the optimum value of $\alpha$ is given as [11]

$$\begin{aligned} \alpha =\frac{K}{\rho }\;where\;K\;is\;number\;of\;users\;and\;\rho \;is\;SNR. \end{aligned}$$

(5)

Both ZF and RZF pre-coding schemes involve inversion of a $K\times K$ gram matrix $Z\;(Z=GG^{H}\;for\;ZF\;and\;Z=(G^{H}G+\alpha I)\;for\;RZF)$, which is an expensive and critical operation. In the next section, we will present a low-latency approximate matrix inversion suitable for massive MIMO.

3 Approximate Matrix Inversion

An exact matrix inversion operation for a $K\times K$ gram matrix Z requires cubic order complexity [7]. Due to the increasing channel matrix size in massive MIMO systems, such direct inversion methods may not be a very efficient solution. To reduce the computational complexity, the Neumann series has been proposed as an alternative to exact inversion methods [8, 9].

If Z is very “close to” an invertible matrix X in the sense that

$$ lim_{n\rightarrow \infty }(I-X^{-1}Z)^{n}=0, $$

then Z is nonsingular and its inverse is given by [8]

$$\begin{aligned} Z^{-1}\;=\;\sum _{n=0\;}^{\infty }(I-X^{-1}Z)^{n}X^{-1}. \end{aligned}$$

(6)

And if the $L-1$ terms of the Neumann series are used for approximation, then Eq. 6 can be modified as

$$\begin{aligned} Z^{-1}\;=\;\sum _{n=0\;}^{L}(I-X^{-1}Z)^{n}X^{-1}. \end{aligned}$$

(7)

If the first two terms of the Neumann series are used $(L=1)$, and Eq. 7 becomes

$$\begin{aligned} Z^{-1}\;=\;X^{-1}+(I-X^{-1}Z)X^{-1}. \end{aligned}$$

(8)

Similarly, if the first four terms of the Neumann series are used $(L=3)$, Eq. 7 becomes

$$\begin{aligned} Z^{-1}\;=\;X^{-1}+(I-X^{-1}Z)X^{-1}+(I-X^{-1}Z)^{2}X^{-1}+(I-X^{-1}Z)^{3}X^{-1}. \end{aligned}$$

(9)

The matrix X, termed as the ‘seed’, is an initial approximation of $Z^{-1}$, which should be easily invertible for lower latency and higher throughput.

Diagonal Neumann Series. As mentioned, Wu et al. [8] suggested using the diagonal elements of matrix $Z\;$ as an initial approximation (seed) for Neumann series expansion, which we refer to as the DNS.

Inversion of a diagonal ‘seed’ matrix is very simple, and it requires only K inversion operations. Thus for $L=2$, the complexity of the inversion operation for a $K\times K$ gram matrix Z using Eq. 8 is $\mathcal {O}\;(K^{2})$ [8] as opposed to cubic order complexity $\mathcal {O}\;(K^{3})$ of the exact inversion methods [7].

Tri-Diagonal Neumann Series. For highly correlated channels or low $\beta$ values, using only the diagonal elements as a seed will result in slow convergence of the Neumann series. Hence more Neumann series terms will be required to achieve a certain accuracy, which will result in higher complexity as each additional term for a Neuman series involves computing power of the matrix $(I-X^{-1}Z)^{n}$ , as shown in Eq. 9.

As mentioned, Prabhu et al. [9] proposed that by including some off-diagonal elements with the diagonal elements as a seed, the convergence of the Neumann series could be improved. Hence they proposed using a tri-diagonal matrix as a seed, which we refer to as the TNS. This method results in better convergence and superior performance as compared to the DNS [8]. However the complexity of obtaining the inverse of the tri-diagonal seed matrix also increases as compared to the DNS.

4 Proposed Method

Here we propose a new seed matrix, which has similar performance to the TNS, but is much easier to invert, hence resulting in lower overall latency and resulting in higher throughput. In addition to the diagonal elements of Z, we also keep the first column to form the seed matrix for the Neumann series. The following shows an example of the seed matrix (X) of a $4\times 4$ gram matrix Z:

$$\begin{aligned} X=\left[ \begin{array}{cccc} Z_{00} &{} 0 &{} 0 &{} 0\\ Z_{10} &{} Z_{11} &{} 0 &{} 0\\ Z_{20} &{} 0 &{} Z_{22} &{} 0\\ Z_{30} &{} 0 &{} 0 &{} Z_{33} \end{array}\right] . \end{aligned}$$

(10)

The reason for using X as a seed matrix is that it is much easier to invert when compared to using a tri-diagonal matrix as a seed. The inverse of X can be obtained using the following procedure. X can be decomposed as $X=DA$ as follows:

$$\begin{aligned} X=\left[ \begin{array}{cccc} Z_{00} &{} 0 &{} 0 &{} 0\\ 0 &{} Z_{11} &{} 0 &{} 0\\ 0 &{} 0 &{} Z_{22} &{} 0\\ 0 &{} 0 &{} 0 &{} Z_{33} \end{array}\right] \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ Z_{10}Z_{11}^{-1} &{} 1 &{} 0 &{} 0\\ Z_{20}Z_{22}^{-1} &{} 0 &{} 1 &{} 0\\ Z_{30}Z_{33}^{-1} &{} 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$

(11)

Matrix D is a diagonal matrix of which the inverse is easy to obtain by simply calculating the reciprocal of the diagonal elements. Similarly, matrix A is called an atomic triangular matrix [7], of which the inverse can be obtained easily by the following:

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ a &{} 1 &{} 0 &{} 0\\ b &{} 0 &{} 1 &{} 0\\ c &{} 0 &{} 0 &{} 1 \end{array}\right] ^{-1}\,=\,\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ -a &{} 1 &{} 0 &{} 0\\ -b &{} 0 &{} 1 &{} 0\\ -c &{} 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$

(12)

Hence the inverse of the proposed seed matrix is calculated as $X^{-1}=A^{-1}D^{-1}$, and

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ -Z_{10}Z_{11}^{-1} &{} 1 &{} 0 &{} 0\\ -Z_{20}Z_{22}^{-1} &{} 0 &{} 1 &{} 0\\ -Z_{30}Z_{33}^{-1} &{} 0 &{} 0 &{} 1 \end{array}\right] \left[ \begin{array}{cccc} Z_{00}^{-1} &{} 0 &{} 0 &{} 0\\ 0 &{} Z_{11}^{-1} &{} 0 &{} 0\\ 0 &{} 0 &{} Z_{22}^{-1} &{} 0\\ 0 &{} 0 &{} 0 &{} Z_{33}^{-1} \end{array}\right] =\left[ \begin{array}{cccc} Z_{00}^{-1} &{} 0 &{} 0 &{} 0\\ -Z_{10}Z_{00}^{-1}Z_{11}^{-1} &{} Z_{11}^{-1} &{} 0 &{} 0\\ -Z_{20}Z_{00}^{-1}Z_{22}^{-1} &{} 0 &{} Z_{22}^{-1} &{} 0\\ -Z_{30}Z_{00}^{-1}Z_{33}^{-1} &{} 0 &{} 0 &{} Z_{33}^{-1} \end{array}\right] . \end{aligned}$$

(13)

From the above equation, it can be seen that $X^{-1}$ can be calculated in constant time as long as we have enough parallel hardware to calculate the reciprocal and the multiplication.

For the inversion of the tri-diagonal matrix, a modified Gaussian elimination method was proposed in [9]. The dependency of the Gaussian elimination algorithm makes it difficult to parallelize the computation, and hence the latency for computing the inverse of the tri-diagonal matrix is in the order of $O\;(K)$ [9], even when a large number of hardware resources are available.

Fig. 1.

Performance comparison $\beta =5$, number of UTs $(K=8)$, $L=1$

Fig. 2.

Performance comparison $\beta =5$, number of UTs $(K=8)$, $L=3$

Fig. 3.

Performance comparison $\beta =5$, number of UTs $(K=12)$, $L=1$

Fig. 4.

Performance comparison $\beta =5$, number of UTs $(K=12)$, $L=3$

Fig. 5.

Performance comparison $\beta =5$, number of UTs $(K=16)$, $L=1$

Fig. 6.

Performance comparision $\beta =5$, number of UTs $(K=16)$, $L=3$

Fig. 7.

Number of UTs $(K=8)$

Fig. 8.

Number of UTs $(K=12)$

Fig. 9.

Number of UTs $(K=16)$

5 Performance Analysis

We simulate an un-coded large-scale MU-MIMO downlink system, employing 4-QAM modulation and linear pre-coding at the transmitter side and MF detection at the receiver. For computing the inverse of the gram matrix Z, the Neumann series is employed with different seed matrices. Figures 1, 2, 3, 4, 5 and 6 compare the bit error rate (BER) performance of the Neumann-series-based inverse, using different seed matrices, with that using exact matrix inversion under the conditions of $\beta =5$ and with different numbers of UTs ($K=8$).

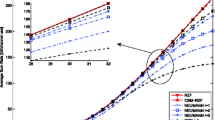
Figure 1 shows that for $K=8$, when only the first two terms of the Neumann series are included (i.e., $L=1$), the performance of the proposed seed matrix and TNS is much better than that of the DNS. Figure 1 (a) depicts the experimental results for ZF pre-coding and Fig. 1 (b) shows the result for RZF pre-coding at the transmitter.

Figure 2 shows that when we increase the number of Neumann series terms (i.e., when $L=3$), the BER performance of the proposed seed matrix and TNS becomes closer to that of the exact inversion, which shows that the proposed seed matrix and TNS require fewer Neumann series terms as compared to the DNS. The same BER performance trend can be observed for different numbers of UTs (K), as shown in Figs. 1, 2, 3, 4, 5 and 6.

For the experimental results presented in Figs. 1, 2, 3, 4, 5 and 6, a fixed value of $\beta =5$ is used. For evaluating the performance of the proposed scheme under different values of $\beta$, the proposed scheme is compared with the DNS [8] and TNS [9] methods by evaluating the SNR-loss compared to the exact inversion to achieve a BER of $10^{-3}$. The results are summarized in Figs. 7, 8 and 9, which show the performance comparisons for different numbers of UTs ($K=8,12\;and\;16$), different pre-coding methods (ZF and RZF) and different numbers of Neumann series terms (for $L=1$ and $L=3$), respectively.

Experimental results (Figs. 7, 8 and 9) show that for low values of $\beta$ $(\beta <10)$, the TNS and the proposed method give better performance than the DNS, whereas with higher values of $\beta$ (>10), the performance loss is almost zero. This means that using only the first two terms is sufficient for inverse calculation $(L=1)$. However for low $\beta$ values, a larger number of Neumann series terms is required to achieve a certain accuracy $(L=3)$.

In general, it can be deduced from the experimental results that using the proposed seed matrix gives a better performance than using the DNS, and is almost the same as using the TNS. However the complexity and latency of the proposed seed matrix is less than that of the TNS method.

Fig. 10.

proposed VLSI architecture (a) Block diagram of proposed inversion method (b) Seed multiplication unit $(X^{-1}Z)$ (c) Scheduling diagram for seed inversion $(X^{-1})$unit

6 Proposed Architecture

In this section, a VLSI architecture which performs the proposed matrix inversion with low latency and high throughput is presented. Figure 10(a) shows the top level block diagram of the architecture. After extracting the seed matrix (X) from the gram matrix Z, the seed is inverted in a seed inversion block. The inverted seed matrix $(X^{-1})$ is then multiplied with the gram matrix Z, to obtain the product $(X^{-1}Z)$, and a generic multiplication unit computes the powers of the product $(I_{K}-X^{-1}Z)^{n}$. For the best case scenarios with higher $\beta$ values, only the first two terms of the Neumann series are used for approximation, i.e., $Z^{-1}=X^{-1}+(I_{K}-X^{-1}Z)X^{-1}$. For this case, the generic matrix multiplication unit is not required and can be bypassed, resulting in much lower latency and higher throughput.

6.1 Seed Inversion Unit $(X^{-1})$

Fig. 10(b) shows the scheduling diagram of the seed inversion $(X^{-1})$ for a $4\times 4$ matrix, example presented in Sect. 4, using a single reciprocal unit and a multiplier. The overall latency for this inversion is , which is one third of the latency for inverting a tri-diagonal matrix (6K) using a modified Gaussian elimination algorithm [9]. For the reciprocal calculation $(Z_{ii}^{-1})$, a standard unrolled single Newton Raphson iteration, similar to that used in [8, 9], is employed. As discussed in the previous section, the latency of the proposed seed inversion can be further reduced by deploying a greater number of multipliers and reciprocal units, since there is no dependency, whereas the modified Gaussian elimination algorithm [9], due to the dependencies, may not be suitable for parallel implementation.

6.2 Seed Multiplication Unit $(X^{-1}Z)$

Figure 10 (c) shows a simple circuit that consists of two multipliers and one adder for the multiplication of $X^{-1}$and Z. $z_{ij}$ is multiplied by $x_{ii}$ and then added to the product of $z_{1j}$ and $x_{1i}$ to obtain the value of $y_{ij}$ $(Y=X^{-1}Z)$, where $z_{ij}$, $x_{ij}$, and $y_{ij}$ are the values of the elements at the $i^{th}$ row and the $j^{th}$ column of the matrices Z, $X^{-1}$, and Y, respectively. This multiplication unit has a latency of two cycles.

6.3 Generic Multiplication Unit $(I_{K}-X^{-1}Z)^{n}$

For lower values of $\beta$, more terms of the Neumann series are required for better accuracy of inversion. Hence we need to compute higher powers of the product $(I_{K}-X^{-1}A)^{n}$. Generic MAC (multiply and accumulate) banks are used to compute the higher powers of $(I_{K}-X^{-1}A)^{n}$. The matrix multiplication is of cubic order complexity, $O(K^{3})$, where K is the size of the matrix. As discussed in [9], parallel hardware can be used to speed up this calculation. Let $\alpha$ be a parallelization factor,. Then the total latency of the multiplication unit is reduced to $\frac{(L-1)K^{3}}{\alpha }$.

Table 1. Latency Comparision

7 Timing Analysis

Table 1 summarizes the latency comparison with the TNS [9] for high and low $\beta$ values under the same hardware complexity and $\alpha$ value (parallelization factor). For higher values of $\beta$ (e.g. $\beta$ > 10), using only the first two terms of the Neumann series is sufficient $(L=1)$, and hence the generic multiplication module can be bypassed and no matrix multiplications $(I_{K}-X^{-1}A)^{L-1}$ are required. Therefore the total latency for both the TNS and the proposed method is comprised of seed inversion latencies. It can be seen that the latency of the proposed seed matrix is three times smaller than that of the TNS. In fact, if more hardware is available, the latency reduction is even higher.

For lower values of $\beta$, more Neumann series terms are required, and $\frac{(L-1)K^{3}}{\alpha }$ cycles are added to the final latency. If $\alpha$ (parallelization factor) is small, the latency is dominated by that of the generic multiplication unit, and hence total latency for both the TNS and proposed method will be similar.

Table 2. ASIC implementation of matrix inversion

8 Implementation Results

The VLSI architecture for inverting a $16\times 16$ matrix using the proposed seed matrix was designed and synthesized in TSMC 65-nm technology. 16-bit internal precision is used for the datapath of the architecture. The implementation is compared with the architecture using direct matrix inversion [5, 6] and the TNS [9]. The comparison results are summarized in Table 2. It can be seen that the proposed architecture can sustain a maximum clock frequency of 448 MHz, with an area cost of 117 K gates.

For a MIMO system with $K=16,\;\beta =5,\;\alpha =10$ and $L=3$ the latencies for the proposed method and TNS are 850 cycles and 916 cycles, respectively. For such cases with lower values of $\beta$, as mentioned in Sect. 7, the latency is dominated by that of the generic multiplication unit. Due to overlapped scheduling, the latency for the seed inversion unit can be absorbed into the generic multiplication unit, and hence the generic multiplication unit is the main source of latency for both the TNS and proposed method at lower values of $\beta$. Therefore a throughput of 0.54M inversions per second is achieved for the proposed method operating at 448 MHz, while the TNS method operating at 420 MHz will have a throughput of 0.51M inversions per second.

Although it seems that for lower values of $\beta$, the TNS and proposed scheme have similar throughput and hardware efficiency. However we would like to mention that this is mainly due to lower values of the parellization factor $\alpha$ used in the generic multiplication unit, due to which the overall latency is dominated by that of the generic multiplication unit.

However if a higher paralleziation factor of $\alpha >100$ is used, the latency will be dominated by the seed multiplication unit instead of the generic multiplication unit. Since the proposed seed inversion has lower latency than the TNS, even for lower values of $\beta$, the proposed scheme will result in higher throughput than the TNS and better inversion accuracy than the DNS.

For MIMO systems with higher $\beta$ values, the generic multiplication unit can be bypassed, and the latency for the proposed method and TNS are reduced to 30 cycles and 96 cycles, respectively, resulting in a throughput of 15M and 4.37M inversions per second, respectively.

9 Conclusion

In this work, we have developed a low-latency and high-throughput matrix inversion method for the linear pre-coder in massive MIMO. The inversion method is based on Neumann series expansion, and a new seed matrix is used as an initial approximation for the Neumann series, which gives better performance, a lower complexity matrix inverse, and lower latency. Detailed latency and throughput analysis is presented for high and low values of $\beta$. A high-throughput VLSI architecture for inverting a $16\times 16$ matrix using the proposed method is also presented.