Abstract
Reducing latency overhead while maintaining critical security guarantees like forward secrecy has become a major design goal for key exchange (KE) protocols, both in academia and industry. Of particular interest in this regard are 0-RTT protocols, a class of KE protocols which allow a client to send cryptographically protected payload in zero round-trip time (0-RTT) along with the very first KE protocol message, thereby minimizing latency. Prominent examples are Google’s QUIC protocol and the upcoming TLS protocol version 1.3. Intrinsically, the main challenge in a 0-RTT key exchange is to achieve forward secrecy and security against replay attacks for the very first payload message sent in the protocol. According to cryptographic folklore, it is impossible to achieve forward secrecy for this message, because the session key used to protect it must depend on a non-ephemeral secret of the receiver. If this secret is later leaked to an attacker, it should intuitively be possible for the attacker to compute the session key by performing the same computations as the receiver in the actual session.
In this paper we show that this belief is actually false. We construct the first 0-RTT key exchange protocol which provides full forward secrecy for all transmitted payload messages and is automatically resilient to replay attacks. In our construction we leverage a puncturable key encapsulation scheme which permits each ciphertext to only be decrypted once. Fundamentally, this is achieved by evolving the secret key after each decryption operation, but without modifying the corresponding public key or relying on shared state.
Our construction can be seen as an application of the puncturable encryption idea of Green and Miers (S&P 2015). We provide a new generic and standard-model construction of this tool that can be instantiated with any selectively secure hierarchical identity-based key encapsulation scheme.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Authenticated key exchange and TLS. The Transport Layer Security (TLS) protocol is the most important cryptographic security mechanism on the Internet today, with TLS 1.2 being the most recent standardized version [16] and TLS 1.3 under development [40]. As one core functionality TLS provides an (authenticated) key exchange (AKE) which allows two remote parties to establish a shared cryptographic key over an insecure channel like the Internet. The study of provable security guarantees for AKE protocols was initiated by the seminal work of Bellare and Rogaway [4]; the huge body of work on cryptographic analyses of the TLS key exchange(s) includes [5, 17, 26, 28].
The Demand for low-latency key exchange. Classical AKE protocols like TLS incur a considerable latency overhead due to exchanging a relatively large number of protocol messages before the first actual (application) data messages can be transmitted under cryptographic protection. Latency is commonly measured in round-trip time (RTT), indicating the number of rounds/round trips messaging has to take before the first application data can be sent. Even very efficient examples of high-performance AKE protocols like HMQV [27] need at least two messages (i.e., 1-RTT) before either party can compute the session key.
0-RTT key exchange. Reducing the latency overhead of key exchange protocols to zero round-trip time (0-RTT) while maintaining reasonable security guarantees has become a major design goal both in academia [23, 29, 36, 44] and industry [38, 40].Footnote 1 In terms of practical designs, the two principal protocols are Google’s QUIC protocol [38] and the 0-RTT mode drafted for the upcoming TLS version 1.3 [40]. While the latter is still in development, QUIC is already implemented in recent versions of the Google Chrome and Opera web browsers, is currently used on Google’s web servers, and has been proposed as an IETF standard (July 2015).
As authentication and establishment of cryptographic keys in 0-RTT without prior knowledge is impossible, 0-RTT key-exchange protocols must leverage keying material obtained in some prior communication to establish 0-RTT keys. Consequently, one very common approach, employed in particular in QUIC, is based on the Diffie–Hellman key exchange and is essentially comprised of the following steps (see also Fig. 1):
-
1.
From prior communication (which may be a key exchange or some out-of-band communication), the client obtains a “medium-lived” (usually a couple of days) server configuration. This server configuration contains a Diffie–Hellman share \(g^s\) (with g being a generator of an algebraic group) for which the server knows s, and is signed under a public signing key certified for belonging to the server.
-
2.
In the 0-RTT key exchange, the client knowing \(g^s\) now picks a secret exponent x at random and sends the share \(g^x\) to the server. It also directly computes a preliminary, 0-RTT key \(K_1\) from the Diffie–Hellman value \(g^{xs}\). In immediate application, this key can be used to send cryptographically protected (0-RTT) application data along with the client’s key-exchange message.
-
3.
The server responds with a freshly chosen, ephemeral Diffie–Hellman share \(g^y\) which is used by both the server and the client to compute the actual session key \(K_2\) from \(g^{xy}\). All further communication throughout the session is subsequently protected under \(K_2\).
An alternative approach, pursued in the latest TLS 1.3 drafts, is to derive the 0-RTT key from a pre-shared symmetric key. Note that this requires storing secret key information on the client between sessions. In contrast, we consider 0-RTT key establishment protocols, which do not require secret information to be stored between sessions.
Issues with 0-RTT key exchange. As outlined, the 0-RTT key-exchange design elegantly allows clients to initiate a secure connection with zero latency overhead, addressing an important practical problem. Unfortunately, all protocols that follow this format—including QUIC and TLS 1.3 as well as academic approaches [23, 44]—face at least one of the following two very undesirable drawbacks.
Forward Secrecy. Recall that forward secrecy essentially demands that transmitted data remains secret even if an attacker learns the secret key of one communication partner. From contemporary insight, this is considered a standard and crucial security goal of modern key exchange protocols, as it addresses data protection in the presence of passive key compromises or mass surveillance. Observe that a 0-RTT key exchange of the form outlined above, however, cannot provide forward secrecy for the 0-RTT application data transmitted from the client to the server. As such data is protected under the key \(K_1\), derived from \(g^{xs}\), an attacker which eavesdrops on the communication and later compromises the server’s secret exponent s (possibly long after the session has finished) can easily compute \(K_1\) and thus decrypt the 0-RTT data sent. This drawback is clearly acknowledged in the design documents of QUIC and TLS 1.3 and one of the main reasons to upgrade to a second, forward-secret key \(K_2\). Notably, the lack of forward secrecy for TLS 1.3 0-RTT is true of both the original Diffie–Hellman-based and the latest pre-shared key (PSK) variants of the protocol, albeit under different assumptions on which key is learned by the attacker [29, 39, 40, 42].
In 2005, Krawczyk stated that it was not possible to obtain forward secrecy for implicitly-authenticated 2-message protocols in a public-key authentication context, if there was no pre-existing shared state [27]. Subsequent works referenced this idea prominently, but often dropped one or more of the original conditions [8, 11, 30]. Despite modeling changes and arguments to the contrary in relation to 1-round protocols [13, 15], and work on forward secrecy for non-interactive key-exchange (NIKE) protocols [37], the assumption that forward secrecy is fundamentally impossible under limited rounds has perpetuated. In particular, the QUIC crypto specification accepts an “upper bound on the forward security of the connection” for 0-RTT handshakes [31]. Likewise, this limitation is accepted as seemingly inherent in academic 0-RTT designs [23, 44], and early discussions around the development of TLS 1.3 go so far as to claim that forward secrecy “can’t be done in 0-RTT” [43].
Replay Attacks. In a replay attack, an attacker aims at making the receiver accept the same payload twice. Specifically, replay attacks in the example 0-RTT protocol given can take the form of replaying the client’s Diffie–Hellman share \(g^x\) or the 0-RTT data sent. Observe that, without further countermeasures, an adversary can simply replay (potentially multiple times) a recorded client message \(g^x\), making the server derive the same key \(K_1\) as in the original connection, and then replay the client’s 0-RTT data which the server can correctly decrypt and would therefore process. Depending on the application logic, such replays can lead to severe security issues. For example, an authenticated request (e.g., via login credentials or cookie tokens) might allow an adversary to replay client actions like online orders or financial transactions.
One potential countermeasure, implemented in QUIC, is essentially to store all seen client values \(g^x\) (in a certain time frame encoded in an additional nonce value) in order to detect and reject repeated requests with the same value and nonce.Footnote 2 Notably, this solution induces a substantial management overhead and arguably is acceptable only for certain server configurations. As such, the solution is not elegant, but effectively prevents the same key from being accepted twice by a server. We remark, though, that on a higher level applications may resend data under a later-derived key in common web scenarios, essentially rendering replay attacks on the application layer unavoidable in such cases [19, 41].
Low-latency key-exchange designs proposed thus far widely accepted the aforementioned drawbacks on forward secrecy and replay protection as inherent to the 0-RTT environment. This assumption paves the way for the following research question for the design of modern, low-latency authenticated key-exchange protocols: Can a key-exchange protocol establish a cryptographic key in 0-RTT while upholding strong forward-secrecy and replay protection guarantees?
Contributions. In this work we introduce the notion of forward-secret one-pass key exchange and a generic construction of such a protocol, resolving the aforementioned open problem. Notable features of this protocol are summarized as follows.
-
The protocol provides full forward secrecy, even for the first message transmitted from the client to the server, and is automatically resilient to replay attacks. We provide a rigorous security analysis for which we develop a novel key-exchange model (in the style of Bellare and Rogaway [4]) that captures the peculiarities of forward secrecy and replay protection in 0-RTT key exchange.
-
The protocol has the simplest message flow imaginable: the client encrypts a session key and sends it to the server. We do not need to distinguish between preliminary and final keys but only derive a single session key. The forward secrecy and replay security of the protocol stem from the fact that the long-term secret key of this scheme is evolved.
-
The construction and security proof are completely generic, based on any one-time signature scheme and any hierarchical identity-based key encapsulation scheme (HIBKEM) that needs to provide only a weak form of selective-ID security. This allows for flexible instantiation of the protocol with arbitrary cryptographic constructions of these primitives, adjusted with suitable deployment and efficiency parameters for a given application, and based on various hardness assumptions.
-
The construction and its security analysis are completely independent of a particular instantiation of building blocks, immediately yielding the first post-quantum secure 0-RTT key exchange protocol, via instantiation of the protocol with suitable lattice-based building blocks, such as the HIBE from [1] and the one-time signature from [34].
-
More generally, by instantiating the protocol with different HIBKEM schemes, one can easily obtain different “cipher suites”, with different security and performance characteristics. Replacement of a cipher suite is easy, as it does not require a new security analysis of the protocol. In contrast, several consecutive research papers were required to establish the security of only the most important basic cipher suites of TLS [26, 28, 32].
Our work is inspired by earlier work of Canetti, Halevi, and Katz [9] on forward-secure public-key encryption and Green and Miers [21] on forward-secret puncturable public-key encryption. The main novelties in this work are:
-
We make the conceptual observation that the tool of forward-secret puncturable public-key encryption can be leveraged to enable forward-secret 0-RTT AKE.
-
We carve out puncturable forward-secret key encapsulation as a versatile building block and build it in a generic fashion from any HIBKEM scheme, in the standard model, and from a wide range of assumptions. In contrast, the cunning, but involved construction by Green and Miers [21] blends the attribute-based encryption scheme of Ostrovsky, Sahai, and Waters [35] with forward-secret encryption [9]. It therefore relies on specific assumptions and, using the Fujisaki-Okamoto transform [20] to achieve CCA-security, relies on the random-oracle model.
-
We formalize 0-RTT key exchange security with forward secrecy. This is a non-trivial extension of previous models (particularly [24]) in that it needs to take evolving state, (semi-)synchronized time, and accordingly conditioned forward secrecy into account in the security experiment.
We consider the established concepts as valuable towards the understanding of forward-secret 0-RTT key exchange, its foundations, and its connection to, in particular, asynchronous messaging.
High-level protocol description. The basic outline of our protocol is the simplest one can imagine. We use a public-key key encapsulation mechanism (KEM)Footnote 3 to transport a random session key from the client to the server. That is, the server is in possession of a long-term key pair \(( pk , sk )\) for the KEM, and the client uses \( pk \) to encapsulate a key. This immediately yields a 0-RTT protocol, because we can send encrypted payload data along with the encapsulated key. However, of course, it does not yet provide forward secrecy or security against replay attacks.
The key idea to achieve these additional properties is not to modify the protocol, but to modify the way the server stores and processes its secret key. More precisely, we construct and use a special puncturable forward-secure KEM (PFS-KEM). Consider a server with long-term secret key \( sk \). When receiving an encapsulated session key in ciphertext \(c_1\), the server can use this scheme to proceed as follows.
-
1.
It decrypts \(c_1\) using \( sk \).
-
2.
The server then derives a new secret key \( sk _{\setminus c_1}\) from \( sk \), which is “punctured at position \(c_1\)”. This means that \( sk _{\setminus c_1}\) can be used to decrypt all ciphertexts except for \(c_1\).
-
3.
Finally, the server deletes \( sk \).
This process is executed repeatedly for all ciphertexts received by the server. That is, when the server receives a second ciphertext \(c_2\) from the same or a different client, it again “punctures” \( sk _{\setminus c_1 }\) to obtain a new secret key \( sk _{\setminus c_1,c_2 }\), which can be used to decrypt all ciphertexts except for \(c_1\) and \(c_2\). Note that this yields forward secrecy, because an attacker that obtains \( sk _{\setminus c_1,c_2 }\) will not be able to use this key to decrypt \(c_1\) or \(c_2\), and thus will not be able to learn the session key of previous sessions.
The drawback of using this approach naïvely is that the size of secret keys grows linearly with the number of sessions, which is of course impractical. For efficiency reasons, we therefore add an additional time component to the protocol, which requires only loosely synchronized clocks between client and server. Within each time slot, the size of the secret key grows linearly with the number of sessions. However, at the end of the time slot, the server is able to “purge” the key, which reduces its size back to a factor logarithmic in the number of time intervals. We stress that the loose time synchronization is included in our protocol’s design only for efficiency reasons, but is not needed to achieve the desired security goals.
A particularly beneficial aspect of this approach is that the server’s public key \( pk \) remains static over its entire lifetime (which would typically be 1–2 years in practice, but longer lifetimes are easily possible), because there is no QUIC-like server configuration that needs to be frequently updated at client-side. Thus, this yields a protocol without the need to frequently replace the server configuration \(g^s\) at the client.
The maximal size of punctured secret keys, and thus the storage requirement of the protocol, depends on the size of time slots. Longer time slots (several hours or possibly even a few days, depending on the number of connections during this time) require more storage, but only loosely synchronized clocks. Short time slots (a few minutes) require less storage, but more precisely synchronized clocks. These parameters can be chosen depending on the individual characteristics of a server and the services that it provides.
Related work. The idea of forward-secret encryption based on hierarchical identity-based encryption is due to Canetti, Halevi, and Katz [9]. Pointcheval and Sanders [37] studied forward secrecy for non-interactive key-exchange protocols based on multilinear maps. Both approaches however only provide coarse-grained forward secrecy with respect to time periods, whereas we aim at a fine-grained, immediate notion of forward secrecy in the setting of key exchange.
With a similar goal in mind, the previously mentioned work of Green and Miers [21] achieves forward secrecy in the context of asynchronous messaging.Footnote 4 Their construction blends the attribute-based encryption scheme of Ostrovsky, Sahai, and Waters [35] with the scheme of Canetti, Halevi, and Katz [9] or, alternatively, with the scheme of Boneh, Boyen, and Goh [7]. This makes their scheme relatively complex and bound to specific algebraic settings and complexity assumptions. Moreover, their scheme achieves only CPA security, and requires the random oracle model [3] and the Fujisaki-Okamoto transform [20] to achieve CCA security. In contrast, we describe a simple, natural and directly CCA-secure construction based on any hierarchical identity-based KEM (HIBKEM), which can be instantiated from any HIBKEM that only needs to provide weak selective-ID security.
The security of the QUIC protocol was formally analyzed by Fischlin and Günther [18] as well as Lychev et al. [33]. Krawczyk and Wee [29] described the OPTLS protocol as a foundation for TLS 1.3, including a 0-RTT mode. For TLS 1.3, Cremers et al. [14] conducted a tool-supported analysis of TLS 1.3 including a draft 0-RTT handshake mode, and Fischlin and Günther [19] analyzed the provable security of both Diffie–Hellman- and PSK-based 0-RTT handshake drafts. Foundational definitions and generic constructions of 0-RTT key exchange from other cryptographic primitives were given by Hale et al. [23]. All these works consider security models and constructions without forward secrecy of the first message. In a related, but different direction, Cohn-Gordon et al. [12] consider post-compromise security for key-exchange protocols that use key ratcheting, where the session key is frequently updated during the lifetime of a single session.
Outline of the paper. Section 2 introduces the necessary building blocks for our construction as well as puncturable forward-secret key encapsulation (PFSKEM), before we provide a generic PFSKEM construction from HIBE. We formalize forward-secret one-pass key exchange protocols (FSOPKE) in Sect. 3, together with a corresponding security model. In Sect. 4 we provide a generic construction of FSOPKE with server authentication from PFSKEM and prove its security in the FSOPKE model. In Sect. 5 we analyze the size of keys and messages for different deployment parameters.
2 Generic Construction of Puncturable Encryption
2.1 Building Blocks
Let us begin with recapping the definition and security of one-time signature schemes, as well as hierarchical identity-based key encapsulation schemes.
Definition 1
(One-Time Signatures). A one-time signature scheme \(\mathsf {OTSIG}\) consists of three probabilistic polynomial-time algorithms (\(\mathsf {OTSIG.KGen}\), \(\mathsf {OTSIG.Sign}\), \(\mathsf {OTSIG.Vfy}\)).
-
\(\mathsf {OTSIG.KGen}(1^\lambda )\) takes as input a security parameter \(\lambda \) and outputs a public key \( pk _{OT}\) and a secret key \( sk _{OT}\).
-
\(\mathsf {OTSIG.Sign}( sk _{OT},m)\) takes as input a secret key and a message \(m\in \{0,1\}^n\). Output is a signature \(\sigma \).
-
\(\mathsf {OTSIG.Vfy}( pk _{OT}, m, \sigma )\) input is a public key, a message \(m\in \{0,1\}^n\) and a signature \(\sigma \). If \(\sigma \) is a valid signature for m under \( pk _{OT}\), then the algorithm outputs 1, else 0.
Consider the following security experiment \(G_{\mathcal {A},\mathsf {OTSIG}}^{\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}}(\lambda )\) played between a challenger \(\mathcal {C}\) and an adversary \(\mathcal {A}\).
-
1.
The challenger \(\mathcal {C}\) computes \(( pk _{OT}, sk _{OT})\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {OTSIG.KGen}(1^\lambda )\) and runs \(\mathcal {A}\) with input \( pk _{OT}\).
-
2.
\(\mathcal {A}\) may query one arbitrary message m to the challenger. \(\mathcal {C}\) replies with \(\sigma \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {OTSIG.Sign}( sk _{OT},m)\).
-
3.
\(\mathcal {A}\) eventually outputs a message \(m^*\) and a signature \(\sigma ^*\). We denote the event that \(\mathsf {OTSIG.Vfy}( pk _{OT}, m^*, \sigma ^*)=1\) and \((m^*,\sigma ^*)\ne (m,\sigma )\) by
$$\begin{aligned} G_{\mathcal {A},\mathsf {OTSIG}}^{\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}}(\lambda ) = 1. \end{aligned}$$
Definition 2
(Security of One-Time Signatures). We define the advantage of an adversary \(\mathcal {A}\) in the game \(G_{\mathcal {A},\mathsf {OTSIG}}^{\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}}(\lambda )\) as
A one-time signature scheme \(\mathsf {OTSIG}\) is strongly secure against existential forgeries under adaptive chosen-message attacks (\(\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}\)), if \(\mathsf {Adv}_{\mathcal {A},\mathsf {OTSIG}}^{\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}}(\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \(\mathcal {A}\).
In our generic construction we use a hierarchical identity-based key encapsulation scheme (\(\mathsf {HIBKEM}\)) [6]. \(\mathsf {HIBKEM}\) schemes enable a user to encapsulate a symmetric key with the recipients identity. An identity at depth t in the hierarchical tree is represented by a vector \(\mathsf {ID}_{\vert t}=(I_1,\cdots , I_t)\). Ancestors of the identity \(\mathsf {ID}_{\vert t}\) are identities represented by vectors \(\mathsf {ID}_{\vert s}=(J_1,\cdots ,J_s)\) with \(1\le s<t\) and \(I_i=J_i\) for \(1\le i \le s\).
Definition 3
(HIBKEM [6]). A hierarchical identity-based key encapsulation scheme \(\mathsf {HIBKEM}\) consists of four probabilistic polynomial-time algorithms \((\mathsf {HIBKEM.KGen}, \mathsf {HIBKEM.Del}, \mathsf {HIBKEM.Enc}, \mathsf {HIBKEM.Dec})\).
-
\(\mathsf {HIBKEM.KGen}(1^\lambda )\) takes as input a security parameter \(\lambda \) and outputs an a public key \( pk \) and an initial secret key (or master key) msk, which we refer as the private key at depth 0. We assume that \( pk \) implicitly defines the identity space \(\mathcal {ID}\) and the key space \(\mathcal {K}\).
-
\(\mathsf {HIBKEM.Del}(\mathsf {ID}_{\vert t}, sk _{\mathsf {ID}'\vert s})\) takes as input an identity \(\mathsf {ID}_{\vert t}\) at depth t and the private key of an ancestor identity \(\mathsf {ID}'_{\vert s}\) at depth \(s<t\) or the master key msk. Output is a secret key \( sk _{\mathsf {ID}\vert t}\).
-
\(\mathsf {HIBKEM.Enc}( pk , \mathsf {ID})\) takes a input the public key \( pk \) and the target \(\mathsf {ID}\). The algorithm outputs a ciphertext \(\mathsf {CT}\) and a symmetric key \(\mathsf {K}\).
-
\(\mathsf {HIBKEM.Dec}( sk _{\mathsf {ID}}, \mathsf {CT})\) takes as input a secret key \(sk_{\mathsf {ID}}\) and a ciphertext \(\mathsf {CT}\). Output is a symmetric key \(\mathsf {K}\) or \(\bot \) if decryption fails.
Consider the following selective-ID CPA security experiment \(G_{\mathcal {A},\mathsf {HIBKEM}}^{\mathsf {IND{\text { -}}sID{\text { -}}CPA}}(\lambda )\) played between a challenger \(\mathcal {C}\) and an adversary \(\mathcal {A}\).
-
1.
\(\mathcal {A}\) outputs the target identity \(\mathsf {ID}^*\) on which it wants to be challenged.
-
2.
The challenger generates the system parameters and computes \(( pk , msk)\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {HIBKEM.KGen}(1^\lambda )\). \(\mathcal {C}\) generates \((\mathsf {K}_0,\mathsf {CT}^*)\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {HIBKEM.Enc}( pk , \mathsf {ID}^*)\) and \(K_1\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal {K}\). Then the challenger sends \((K_b, \mathsf {CT}^*, pk \)) to \(\mathcal {A}\) where \(b\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}\).
-
3.
\(\mathcal {A}\) may query an \(\mathsf {HIBKEM.Del}\) oracle. The \(\mathsf {HIBKEM.Del}\) oracle outputs the secret key of a requested identity \(\mathsf {ID}\). The only restriction is, that the attacker \(\mathcal {A}\) is not allowed to ask the \(\mathsf {HIBKEM.Del}\) oracle for the secret key of \(\mathsf {ID}^*\) or any ancestor identity of \(\mathsf {ID}^*\).
-
4.
Finally, \(\mathcal {A}\) eventually outputs a guess \(b'\). We denote the event that \(b=b'\) by
$$\begin{aligned} G_{\mathcal {A},\mathsf {HIBKEM}}^{\mathsf {IND{\text { -}}sID{\text { -}}CPA}}(\lambda ) = 1 \end{aligned}$$
Definition 4
(Security of HIBKEM). We define the advantage of an adversary \(\mathcal {A}\) in the selective-ID game \(G_{\mathcal {A},\mathsf {HIBKEM}}^{\mathsf {IND{\text { -}}sID{\text { -}}CPA}}(\lambda )\) as
A hierarchical identity-based key encapsulation scheme \(\mathsf {HIBKEM}\) is selective-ID CPA-secure (\(\mathsf {IND{\text { -}}sID{\text { -}}CPA}\)), if \(\mathsf {Adv}_{\mathcal {A},\mathsf {HIBKEM}}^{\mathsf {IND{\text { -}}sID{\text { -}}CPA}}(\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \(\mathcal {A}\).
2.2 Puncturable Forward-Secret Key Encapsulation
We now formally introduce the definition of a puncturable forward-secret key encapsulation (PFSKEM) scheme as well as its corresponding correctness definition and security notion.
Definition 5
(PFSKEM). A puncturable forward-secret key encapsulation scheme \(\mathsf {PFSKEM}\) consists of five probabilistic polynomial-time algorithms (\(\mathsf {PFSKEM.KGen}\), \(\mathsf {PFSKEM.Enc}\), \(\mathsf {PFSKEM.PnctCxt}\), \(\mathsf {PFSKEM.Dec}\), \(\mathsf {PFSKEM.PnctInt}\)).
-
\(\mathsf {PFSKEM.KGen}(1^\lambda )\) takes as input a security parameter \(\lambda \) and outputs a public key \( PK \) and an initial secret key \( SK \).
-
\(\mathsf {PFSKEM.Enc}( PK , \tau )\) takes as input a public key and a time period \(\tau \). Output is a ciphertext \(\mathsf {CT}\) and a symmetric key \(\mathsf {K}\).
-
\(\mathsf {PFSKEM.PnctCxt}( SK ,\tau ,\mathsf {CT})\) input is the current secret key \( SK \), a time period \(\tau \) and additionally a ciphertext \(\mathsf {CT}\). The algorithm outputs a new secret key \( SK '\).
-
\(\mathsf {PFSKEM.Dec}( SK , \tau , \mathsf {CT})\) takes as input a secret key \( SK \), time period \(\tau \) and a ciphertext \(\mathsf {CT}\). Output is a symmetric key \(\mathsf {K}\) or \(\bot \) if decapsulation fails.
-
\(\mathsf {PFSKEM.PnctInt}( SK ,\tau )\) takes as input a secret key \( SK \) and a time interval \(\tau \). Output is a secret key \( SK '\) for the next time interval \(\tau +1\).
Definition 6
(Correctness of PFSKEM). For all \(\lambda , n \in \mathbb {N}\), any \(( PK , SK ) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.KGen}(1^\lambda )\), any time period \(\tau ^*\), any \((\mathsf {K},\mathsf {CT}^*)\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.Enc}( PK , \tau ^*)\), and any (arbitrary interleaved) sequence \(i = 0, \dots , n-1\) of invocations of \( SK ' \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.PnctCxt}( SK , \tau , \mathsf {CT})\) for any \((\tau , \mathsf {CT}) \ne (\tau ^*, \mathsf {CT}^*)\) or \( SK ' \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.PnctInt}( SK , \tau )\) for any \(\tau \ne \tau ^*\) it holds that \(\mathsf {PFSKEM.Dec}( SK ', \tau ^*, \mathsf {CT}^*) = \mathsf {K}\).
Beyond the regular correctness definition above, we further define an extended variant of correctness which demands that decapsulation under a previously punctured out time-interval and ciphertext yields an error symbol \(\bot \).
Definition 7
(Extended Correctness of PFSKEM). For all \(\lambda , n \in \mathbb {N}\), any \(( PK , SK ) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.KGen}(1^\lambda )\), any time period \(\tau ^*\), any \((\mathsf {K},\mathsf {CT}^*)\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.Enc}( PK ,\tau ^*)\), and any (arbitrary interleaved) sequence \(i = 0, \dots , n-1\) of invocations of \( SK ' \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.PnctCxt}( SK , \tau _i, \mathsf {CT}_i)\) for any \((\tau _i, \mathsf {CT}_i)\) or \( SK ' \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.PnctInt}( SK ',\tau _i')\) for any \(\tau _i'\) it holds that if \((\tau _i, \mathsf {CT}_i) = (\tau ^*, \mathsf {CT}^*)\) or \(\tau _i' = \tau ^*\) for some \(i \in \{0,\dots ,n-1\}\), then \(\mathsf {PFSKEM.Dec}( SK ',\tau ^*,\mathsf {CT}^*) = \bot \).
The security of a \(\mathsf {PFSKEM}\) scheme is defined by the following selective-time CCA security experiment \(G_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}(\lambda )\) played between a challenger \(\mathcal {C}\) and an attacker \(\mathcal {A}\).
-
1.
In the beginning, \(\mathcal {A}\) outputs the target time \(\tau ^*\).
-
2.
The challenger \(\mathcal {C}\) generates a fresh key pair \(( PK , SK ) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.KGen}(1^\lambda )\). It computes \((\mathsf {CT}^*, \mathsf {K}_0^*) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.Enc}( PK , \tau ^*)\) and selects \(\mathsf {K}_1^* \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal {K}\). Additionally, it chooses a bit \(b\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}\) and then sends \(( PK ,\mathsf {CT}^*,\mathsf {K}_b^*)\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) can now ask a polynomial number of the following queries:
-
\(\mathtt {PFSKEM.Dec}(\tau , \mathsf {CT})\): The challenger computes \(\mathsf {K}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.Dec}( SK , \tau , \mathsf {CT})\) and returns \(\mathsf {K}\) to \(\mathcal {A}\).
-
\(\mathtt {PFSKEM.PnctCxt}(\tau , \mathsf {CT})\): The challenger runs \( SK \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.PnctCxt}( SK ,\tau ,\mathsf {CT})\) and returns symbol \(\top \).
-
\(\mathtt {PFSKEM.PnctInt}(\tau )\): The challenger runs \( SK \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {PFSKEM.PnctInt}( SK ,\tau )\) and returns symbol \(\top \).
-
\(\mathtt {PFSKEM.Corrupt}()\): The challenger aborts and outputs a random bit if \(\mathcal {A}\) has not queried \(\mathtt {PFSKEM.PnctCxt}(\tau ^*, \mathsf {CT}^*)\) or \(\mathtt {PFSKEM.PnctInt}(\tau ^*)\) before. Otherwise, the challenger returns the current secret key \( SK \) to \(\mathcal {A}\).
-
-
4.
\(\mathcal {A}\) eventually outputs a guess \(b'\). We denote the event that \(b=b'\) by
$$\begin{aligned} G_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}(\lambda ) = 1 \ . \end{aligned}$$
Definition 8
(Security of PFSKEM). We define the advantage of an adversary \(\mathcal {A}\) in the selective-time CCA game \(G_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}(\lambda )\) as
A puncturable forward-secret key encapsulation scheme \(\mathsf {PFSKEM}\) is selective-time CCA-secure (\(\mathsf {IND{\text { -}}sT{\text { -}}CCA}\)), if \(\mathsf {Adv}_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}(\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \(\mathcal {A}\).
2.3 A Generic PFSKEM Construction from HIBKEM
We have now set up the necessary building blocks for our generic PFSKEM construction. In this construction, we deploy a HIBKEM scheme over a binary hierarchy tree comprising time intervals in the upper part and identifiers within these intervals in the lower part. The latter identifiers are carefully crafted to be public keys of a one-time signature scheme, conveniently enabling our construction to achieve CCA security.
We start with a short description of the binary tree, where the root node has the label \(\epsilon \). The left child of a node under label n is labeled with \(n_0\) and the right child with \(n_1\). In a \(\mathsf {HIBKEM}\) scheme every identity \(\mathsf {ID}_i\) is represented by a node \(n_i\) of the hierarchy tree T and with \( sk _i\) we denote the secret key corresponding to node \(n_i\). The root node has the corresponding master secret key msk of the \(\mathsf {HIBKEM}\) scheme. To identify specific nodes in the tree we need the following functions.
-
\(\mathsf {Parent}(T, n)\). On input of a description of a tree T and a node n, this function outputs the label of the direct ancestor of n or \(\bot \) if it does not exists.
-
\(\mathsf {Sibling}(T, n)\). On input of a description of a tree T and a label of a node n this function outputs the other child \(n' \ne n\) of the node \(\mathsf {Parent}(T, n)\) or \(\bot \) if it does not exists.
On input of a description of a tree T, a set of secret keys and nodes \( SK = \lbrace ( sk _1,n_1),\ldots ,( sk _u,n_u)\rbrace \) and a node n, the following algorithm computes a new set of secret keys and nodes \( SK '\). The secret keys in \( SK '\) can neither be used to derive the secret key of n nor of its descendants.
-
\(\mathsf {PunctureTree}(T, SK , n)\). Create an empty set \( SK '{:=}\{\}\). Then, for all tuples \(( sk _i,n_i)\) in \( SK \):
-
If \(n_i\) is neither an ancestor nor a descendant of n in the tree and if \(n_i\ne n\), then set \( SK '{:=} SK '\cup {( sk _i, n_i)}\) and \( SK {:=} SK \setminus \lbrace ( sk _i,n_i)\rbrace \).
If there is a remaining node \(n'\) with its secret key \( sk '\) in \( SK \) and if \(n'\) is an ancestor of n, then set \( ntmp {:=}n\), and while \(\mathsf {Parent}( ntmp )\ne \bot \):
-
if \(n'\) is an ancestor of \(\mathsf {Sibling}(ntmp)\) then \( SK '{:=} SK '\cup \lbrace \mathsf {HIBKEM.Del}(\mathsf {Sibling}( ntmp ), sk '), \mathsf {Sibling}(ntmp))\rbrace \)
-
\( ntmp {:=}\mathsf {Parent}( ntmp )\).
Output is the set of secret keys and nodes \( SK '\).
-
Illustrating the described algorithm, we provide an example in Fig. 2, with a tree where the nodes are labeled as described earlier. \( SK \) consists of the tuple \(\{(msk,\epsilon )\}\), where msk is the initial secret key of a \(\mathsf {HIBKEM}\). We would like to puncture the secret key SK for the input \(n_{01}\). In order to do so, we must delete all keys in \( SK \) that can be used to derive the secret keys for the nodes with label “01” or with the prefix “01”. For this, we run the algorithm \(\mathsf {PunctureTree}\) with input \((T, SK , 01)\). In Fig. 2 the gray nodes denote the labels for which we have to derive the secret keys within the new \(\mathsf {PFSKEM}\) secret key \(SK'\). The secret keys in \(SK'\) can only be used to generate secret keys for identities which are not ancestors or descendants of the punctured node “01”.
In the following, an identifier \(\mathsf {ID}=\tau \vert \vert pk _{OT}\) consisting of a time interval \(\tau \) and a one-time signature public key \( pk _{OT}\) is a leaf in a \(\mathsf {HIBKEM}\) tree T. The public key \( PK \) and the initial secret key SK of the \(\mathsf {PFSKEM}\) construction are, respectively, the public key \( pk \) and a pair consisting of the initial secret key of the \(\mathsf {HIBKEM}\) scheme with the label of the root node (\(msk,\epsilon \)).
To obtain a symmetric key at time \(\tau \), one can use the encapsulation algorithm of the \(\mathsf {HIBKEM}\) scheme with input \(( PK ,\tau \vert \vert pk _{OT})\). Correspondingly, the secret key \( SK \) of the \(\mathsf {PFSKEM}\) scheme can be punctured via the previously defined algorithm \(\mathsf {PunctureTree}(T, SK , n)\) by deleting the secret key for the identity \(\mathsf {ID}=\tau \vert \vert pk _{OT}\) in the \(\mathsf {HIBKEM}\) scheme including all secret keys of ancestors of \(\mathsf {ID}\). Particularly, this can be accomplished by using the previously defined algorithm \(\mathsf {PunctureTree}(T, SK , n)\). Decapsulation uses the secret key of the identity \(\mathsf {ID}=\tau \vert \vert pk _{OT}\) with a ciphertext \(\mathsf {CT}\) and outputs the symmetric key or \(\bot \) if the key is already deleted or the signature of the ciphertext is not valid.
The described generic construction is presented in Fig. 3.
As we establish next, our \(\mathsf {PFSKEM}\) construction is selective-time CCA-secure (according to Definition 8) if the underlying \(\mathsf {HIBKEM}\) scheme is \(\mathsf {IND{\text { -}}sID{\text { -}}CPA}\)-secure and the \(\mathsf {OTSIG}\) scheme is \(\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}\)-secure (cf. Definitions 4 and 2).
Theorem 1
For any efficient polynomial-time adversary \(\mathcal {A}\) in the \(\mathsf {IND{\text { -}}sT{\text { -}}CCA}\) game there exist efficient polynomial-time algorithms \(\mathcal {B}_{\mathsf {HIBKEM}}\) and \(\mathcal {B}_{\mathsf {OTSIG}}\) such that
Proof
An attacker \(\mathcal {A}\) on the \(\mathsf {PFSKEM}\) scheme outputs a target time period \(\tau ^*\) and can make the queries described in the security experiment for \(\mathsf {PFSKEM}\) schemes.
Let \((\mathsf {CT}^*_{\mathsf {PFSKEM}}, \mathsf {K}_b^*)=((\mathsf {CT}_{\mathsf {HIBKEM}}^*,\sigma ^*, pk _{OT}^*),\mathsf {K}_b^*)\) be the challenge we have to compute for the \(\mathsf {PFSKEM}\) attacker and let \(\mathsf {E}\) denote the event that the attacker \(\mathcal {A}\) never queries \(\mathtt {PFSKEM.Dec}(\tau ,\mathsf {CT}_{\mathsf {PFSKEM}} = (\mathsf {CT}_{\mathsf {HIBKEM}}, \sigma , pk _{OT}))\) where \((\mathsf {CT}_{\mathsf {HIBKEM}},\sigma ) \ne (\mathsf {CT}_{\mathsf {HIBKEM}}^*,\sigma ^*)\), \( pk _{OT}= pk _{OT}^*\), and \(\mathsf {OTSIG.Vfy}( pk _{OT},\mathsf {CT}_{\mathsf {HIBKEM}},\sigma )=1\) in the security game. The probability for \(\mathcal {A}\) to win the security game is
In case event \(\mathsf {\lnot E}\) occurs, \(\mathcal {A}\) asks for a decapsulation \(\mathtt {PFSKEM.Dec}(\tau , \mathsf {CT}_{\mathsf {PFSKEM}}=(\mathsf {CT}_\mathsf {HIBKEM}, \sigma , pk _{OT}))\) where \((\mathsf {CT}_{\mathsf {HIBKEM}},\sigma )\ne (\mathsf {CT}_{\mathsf {HIBKEM}}^*,\sigma ^*)\) with \( pk _{OT}= pk _{OT}^*\) and \(\mathsf {OTSIG.Vfy}( pk _{OT},\mathsf {CT}_{\mathsf {HIBKEM}},\sigma )=1\) in the security game. This means that \(\mathsf {CT}_{\mathsf {HIBKEM}} \ne \mathsf {CT}_{\mathsf {HIBKEM}}^*\) or \(\sigma \ne \sigma ^*\) (or both). Hence, \((\mathsf {CT}_{\mathsf {HIBKEM}}, \sigma )\) is a valid strong existential forgery under the \(\mathsf {OTSIG}\) scheme. Outputting this forgery, we can use \(\mathcal {A}\) to build an attacker \(\mathcal {B}_{\mathsf {OTSIG}}\) to break the \(\mathsf {sEUF{\text { -}}1{\text { -}}\mathsf {CMA}}\) security of \(\mathsf {OTSIG}\) whenever \(\mathcal {A}\) triggers event \(\mathsf {\lnot E}\). Therefore,
Next, we build an adversary \(\mathcal {B}_{\mathsf {HIBKEM}}\) against the \(\mathsf {IND\text {-}sID\text {-}CPA}\) security of the \(\mathsf {HIBKEM}\). \(\mathcal {B}_{\mathsf {HIBKEM}}\) generates a fresh key pair \(( pk _{OT}^*, sk _{OT}^*)\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf {OTSIG.KGen}(1^\lambda )\). Then, \(\mathcal {B}_{\mathsf {HIBKEM}}\) starts \(\mathcal {A}\) to obtain \(\tau ^*\), sends \(\mathsf {ID}=\tau ^*\vert \vert pk _{OT}^*\) to the \(\mathsf {HIBKEM}\) challenger and receives a challenge \((K_b, \mathsf {CT}^*_\mathsf {HIBKEM})\) with the public key \( pk _{\mathsf {HIBKEM}}\). \(\mathcal {B}_{\mathsf {HIBKEM}}\) sets \( PK = pk _{\mathsf {HIBKEM}}\) and computes the signature \(\sigma ^*\) for \(\mathsf {CT}^*_\mathsf {HIBKEM}\). \(\mathcal {B}_{\mathsf {HIBKEM}}\) continues to run \(\mathcal {A}\) with the challenge \((\mathsf {CT}^*_\mathsf {PFSKEM}=(\mathsf {CT}^*_\mathsf {HIBKEM},\sigma ^*, pk _{OT}^*),\mathsf {K}_b^*=K_b)\) and the public key \( PK \). \(\mathcal {B}_{\mathsf {HIBKEM}}\) provides answers to the queries defined in the selective-time CCA security experiment \(G_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}(\lambda )\) as follows:
-
\(\mathtt {PFSKEM.Dec}(\tau , \mathsf {CT}_{\mathsf {PFSKEM}}=(\mathsf {CT}_\mathsf {HIBKEM}, \sigma , pk _{OT}))\) with \(\tau \ne \tau ^*\): \(\mathcal {B}_{\mathsf {HIBKEM}}\) can query the \(\mathsf {HIBKEM}\) challenger for the secret key of identity \(\tau \vert \vert pk_{OT}\), because \(\tau \vert \vert pk_{OT}\) is not an ancestor identity of \(\tau ^*\vert \vert pk_{OT}^*\). With the secret key it is possible to decapsulate the key for \(\mathsf {CT}^*_\mathsf {HIBKEM}\).
-
\(\mathtt {PFSKEM.Dec}(\tau , \mathsf {CT}_{\mathsf {PFSKEM}}=(\mathsf {CT}_\mathsf {HIBKEM}, \sigma , pk _{OT}))\): \( \mathcal {B}_{\mathsf {HIBKEM}}\) can query the \(\mathsf {HIBKEM}\) challenger for the secret key of identity \(\tau ^*\vert \vert pk_{OT}\).
-
\(\mathtt {PFSKEM.Corrupt}\): If adversary \(\mathcal {A}\) did not call \(\mathtt {PFSKEM.PnctCxt}(\tau ^*, \mathsf {CT}^*)\) or \(\mathtt {PFSKEM.PnctInt}(\tau ^*)\) before, then \(\mathcal {B}_{\mathsf {HIBKEM}}\) aborts and outputs a random bit, else \(\mathcal {B}_{\mathsf {HIBKEM}}\) can query the \(\mathsf {HIBKEM}\) challenger for all secret keys of the requested identities and send them to \(\mathcal {A}\).
In the end \(\mathcal {A}\) outputs a guess \(b'\) and \(\mathcal {B}_{\mathsf {HIBKEM}}\) forwards \(b'\) to the \(\mathsf {HIBKEM}\) challenger as its own output. \(\mathcal {B}_{\mathsf {HIBKEM}}\) wins if \(\mathcal {A}\) outputs the right \(b'\). The security experiment can be simulated correctly if event \(\mathsf {E}\) occurs. Therefore we have
Putting the above bounds together, we obtain
which yields
\(\square \)
3 Forward-Secret One-Pass Key Exchange Protocols
3.1 Syntax
Protocols in a 0-RTT–like setting, where only one message is transmitted between two key exchange protocol partners, have been the object of previous design interest. In particular, a similar scenario was considered by Halevi and Krawczyk under the notion of one-pass key exchange [24]. Aiming for efficiency and optimal key management, we extend their setting by allowing shared state between several executions of the protocol and introduce a discretized notion of time.
Definition 9
(FSOPKE). A forward-secret one-pass key exchange (FSOPKE) protocol supporting \(\tau _{max}\) time periods and providing mutual or unilateral (server-only) authentication consists of the following four probabilistic algorithms.
-
\(\mathsf {FSOPKE}.\mathsf {KGen}(1^\lambda , r, \tau _{max}) \rightarrow ( pk , sk )\) . On input the security parameter \(1^\lambda \), a role \(r\in \{\mathsf {client}, \mathsf {server}\}\), and the maximum number of time periods \(\tau _{max}\in \mathbb {N}\), this algorithm outputs a public/secret key pair \(( pk , sk )\) for the specified role.
-
\(\mathsf {FSOPKE}.\mathsf {RunC}( sk , pk ) \rightarrow ( sk ', k, m)\) . On input a secret key \( sk \) and a public key \( pk \), this algorithm outputs a (potentially modified) secret key \( sk '\), a session key \(k \in \{0,1\}^* \cup \{\bot \}\), and a message \(m \in \{0,1\}^* \cup \{\bot \}\).
-
\(\mathsf {FSOPKE}.\mathsf {RunS}( sk , pk , m) \rightarrow ( sk ', k)\) . On input of a secret key \( sk \), a public key \( pk \), and a message \(m \in \{0,1\}^*\), this algorithm outputs a (potentially modified) secret key \( sk '\) and a session key \(k \in \{0,1\}^* \cup \{\bot \}\). For a unilateral authenticating protocol, \( pk = \bot \) indicates that the client is not authenticated.
-
\(\mathsf {FSOPKE}.\mathsf {TimeStep}( sk , r) \rightarrow sk '\) . On input a secret key \( sk \) and an according role \(r\in \{\mathsf {client}, \mathsf {server}\}\), this algorithm outputs a (potentially modified) secret key \( sk '\).
We say that a forward-secret one-pass key exchange protocol is correct if:
-
for all \(( pk _i, sk _i) \leftarrow \mathsf {FSOPKE}.\mathsf {KGen}(1^\lambda , \mathsf {client}, \tau _{max})\),
-
for all \(( pk _j, sk _j) \leftarrow \mathsf {FSOPKE}.\mathsf {KGen}(1^\lambda , \mathsf {server}, \tau _{max})\),
-
for any \(n \in \mathbb {N}\) with \(n < \tau _{max}\) and all
-
\( sk _i' \leftarrow \mathsf {FSOPKE}.\mathsf {TimeStep}^n( sk _i, \mathsf {client})\)
-
\( sk _j' \leftarrow \mathsf {FSOPKE}.\mathsf {TimeStep}^n( sk _j, \mathsf {server})\)
(where \(\mathsf {FSOPKE}.\mathsf {TimeStep}^n\) indicates n iterative applications of \(\mathsf {FSOPKE}.\mathsf {TimeStep}\)),
-
-
for all \(( sk _i'', k_i, m) \leftarrow \mathsf {FSOPKE}.\mathsf {RunC}( sk _i', pk _j)\),
-
and for all
-
\(( sk _j'', k_j) \leftarrow \mathsf {FSOPKE}.\mathsf {RunS}( sk _j', pk _i,m)\) (for mutual authentication)
-
resp. \(( sk _j'', k_j) \leftarrow \mathsf {FSOPKE}.\mathsf {RunS}( sk _j',\bot ,m)\) (for unilateral authentication),
-
it holds that \(k_i = k_j\).
A forward-secret one-pass key exchange protocol is used by a client and a server party as follows. First of all, both parties generate public/secret key pairs \(( pk , sk ) \leftarrow \mathsf {FSOPKE}.\mathsf {KGen}(1^\lambda ,r,\tau _{max})\) for their according role \(r= \mathsf {client}\) resp. \(r= \mathsf {server}\). To proceed in time (step-wise), they can invoke \(\mathsf {FSOPKE}.\mathsf {TimeStep}\) on their respective secret keys (up to \(\tau _{max}\, - 1\) times). Two parties holding secret keys in the same time frame then communicate by the client running \(\mathsf {FSOPKE}.\mathsf {RunC}\) on its secret key and the public key of its intended partner, obtaining the joint session key and a message; transmitting the latter to the server. The server then invokes \(\mathsf {FSOPKE}.\mathsf {RunS}\) on its secret key, the (intended) client’s public key (or \(\bot \) in case of unilateral authentication), and the obtained message, which outputs, by correctness, the same joint session key.
Note that this (0-RTT) session key is the only session key derived. Unlike in QUIC and TLS 1.3, we demand that this key immediately enjoys full forward secrecy and replay protection, making an upgrade to another key unnecessary. This demand is realized via the forthcoming security model in Sect. 3.2.
3.2 Security Model
We denote by \(\mathcal {I}= \mathcal {C}\,\mathbin {{\dot{\cup }}}\,\mathcal {S}\) the set of identities modeling both clients (\(\mathcal {C}\)) and servers (\(\mathcal {S}\)) in the system, each identity \(u \in \mathcal {I}\) being associated with a public/secret key pair \(( pk _u, sk _u)\). Here, the public-key part \( pk _u\) is generated once and fixed, whereas \( sk _u\) can be modified by (the sessions of) the according party over time. Each identity u moreover holds the local, current time in a variable denoted by \(\tau _u \in \mathbb {N}\), initialized to \(\tau _u \leftarrow 1\).
In our model, an adversary \(\mathcal {A}\) interacts with several sessions of multiple identities running a forward-secret one-pass key exchange protocol. We denote by \(\pi _u^i\) the i-th session of identity u and associate with each session the following internal state variables:
-
\(\mathsf {role}\in \{\mathsf {client}, \mathsf {server}\}\) indicates the role of the session. We demand that \(\mathsf {role}= \mathsf {client}\) resp. \(\mathsf {role}= \mathsf {server}\) if and only if \(u \in \mathcal {C}\) resp. \(u \in \mathcal {S}\).
-
\(\mathsf {id}\in \mathcal {I}\) indicates the owner of the session (e.g., u for a session \(\pi _u^i\)).
-
\(\mathsf {pid}\in \mathcal {I}\cup \{\bot \}\) indicates the intended communication partner, and is set exactly once. Setting \(\mathsf {pid}= \bot \) is possible if \(\mathsf {role}= \mathsf {server}\) to indicate the client is not authenticated. Initially, \(\mathsf {pid}= \bot \) can also be set (if \(\mathsf {role}= \mathsf {server}\)) to indicate that the client’s identity is to be learned within the protocol (i.e., post-specified).
-
\(\mathsf {trans}\in \{0,1\}^* \cup \{\bot \}\) records the (single) sent, resp. received, message.
-
\(\mathsf {time}\in \mathbb {N}\) records the time interval used when processing the sent, resp. received, message.
-
\(\mathsf {key}\in \{0,1\}^* \cup \{\bot \}\) is the session key derived in the session.
-
\(\mathsf {keystate}\in \{\mathsf {fresh}, \mathsf {revealed}\}\) indicates whether the session key has been revealed. Initially \(\mathsf {keystate}= \mathsf {fresh}\).
We write, e.g., \(\pi _u^i.\mathsf {key}\) when referring to state variables of a specific session.
Definition 10
(Partnered sessions). We say that two sessions \(\pi _u^i\) and \(\pi _v^j\) are partnered if
-
\(\pi _u^i.\mathsf {trans}= \pi _v^j.\mathsf {trans}\), i.e., they share the same transcript,
-
\(\pi _u^i.\mathsf {time}= \pi _v^j.\mathsf {time}\), i.e., they run in the same time interval,
-
\(\pi _u^i.\mathsf {role}= \mathsf {client}\wedge \pi _v^j.\mathsf {role}= \mathsf {server}\), i.e., they run in opposite roles,
-
\(\pi _u^i.\mathsf {pid}= \pi _v^i.\mathsf {id}\), i.e., the server session is owned by the client’s intended partner, and
-
\(\pi _u^i.\mathsf {id}= \pi _v^i.\mathsf {pid}\vee \pi _v^j.\mathsf {pid}= \bot \), i.e., the client session is owned by the server’s intended partner or the server considers its partner to be unauthenticated.
We assume the adversary \(\mathcal {A}\) controls the network, is responsible for transporting messages, and hence allowed to arbitrary modify, drop, or reorder messages. It interacts with the key exchange protocol and sessions via the following queries.
-
\(\mathsf {NewSession}(u, role, pid, m)\) . Initializes a new session of identity \(u \in \mathcal {I}\), taking role \(\mathsf {role}\in \{\mathsf {client}, \mathsf {server}\}\) and intended communication partner \(\mathsf {pid}\in \mathcal {I}\cup \{\bot \}\) (where \(\mathsf {pid}= \bot \) for a server session indicates an unauthenticated client partner). If \(\mathsf {role}\ne \mathsf {server}\), we require that \(m=\bot \).
If \(\mathsf {role}= \mathsf {client}\), invoke \(( sk _u, k, m) \leftarrow \mathsf {FSOPKE}.\mathsf {RunC}( sk _u, pk _{\mathsf {pid}})\), else invoke \(( sk _u, k) \leftarrow \mathsf {FSOPKE}.\mathsf {RunS}( sk _u, pk _{\mathsf {pid}},m)\), where \( pk _{\bot } = \bot \).
Register a new session \(\pi _u^i\) with \(\mathsf {role}= role\), \(\mathsf {id}= u\), \(\mathsf {pid}= pid\), \(\mathsf {trans}= m\), \(\mathsf {time}= \tau _u\), and \(\mathsf {key}= k\).
If \(\mathsf {role}= \mathsf {client}\), return m. If \(\mathsf {role}= \mathsf {server}\), return \(\bot \) if \(k = \bot \), and \(\top \) otherwise.
-
\(\mathsf {Reveal}(\pi _u^i)\) . Reveals the session key of a specific session, if derived.
If \(\pi _u^i.\mathsf {key}\ne \bot \), set \(\pi _u^i.\mathsf {keystate}\leftarrow \mathsf {revealed}\) and return \(\mathsf {key}\), else return \(\bot \).
-
\(\mathsf {Corrupt}(u)\) . Corrupts the long-term state of an identity \(u \in \mathcal {I}\). This query can be asked at most once per identity u and, from this point on, no further queries to (sessions of) u are allowed.
Let \(\mathsf {Corrupt}(u)\) be the \(\varsigma \)-th query issued by \(\mathcal {A}\); we set \(\varsigma ^{corr}_u \leftarrow \varsigma \), where \(\varsigma ^{corr}_u = \infty \) for uncorrupted identities. Likewise, we record the identity’s current time \(\tau _u\) at corruption and set \( \tau ^{corr}_u \leftarrow \tau _u\).
Return \( sk _u\).
-
\({\mathsf {Tick}}(u)\) . Forward the state of some identity \(u \in \mathcal {I}\) by one time step by invoking \( sk _u \leftarrow \mathsf {FSOPKE}.\mathsf {TimeStep}( sk _u)\). Record the new time as \(\tau _u \leftarrow \tau _u + 1\).
-
\(\mathsf {Test}(\pi _u^i)\) . Allows the adversary to challenge a derived session key and is asked exactly once. This oracle is given a secret bit \(b_{\mathsf {test}}\in \{0,1\}\) chosen at random in the security game.
If \(\pi _u^i.\mathsf {key}= \bot \), return \(\bot \).
Set \(\tau ^{t}\leftarrow \pi ^{t}.\mathsf {time}\). If \(b_{\mathsf {test}}= 0\), return \(\pi _u^i.\mathsf {key}\), else return a random key chosen according to the probability distribution specified by the protocol.
Definition 11
(Security for FSOPKE). Let \(\mathsf {FSOPKE}\) be a forward-secret one-pass key exchange protocol and \(\mathcal {A}\) a PPT adversary interacting with \(\mathsf {FSOPKE}\) via the queries defined above in the following game \(G_{\mathcal {A},\mathsf {FSOPKE}}^{\mathsf {FSOPKE{\text { -}}sec}}\):
-
The challenger generates keys and state for all parties \(u \in \mathcal {I}\) as \(( pk _u, sk _u) \leftarrow \mathsf {FSOPKE}.\mathsf {KGen}(1^\lambda )\) and chooses a random bit \(b_{\mathsf {test}}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}\).
-
The adversary \(\mathcal {A}\) receives \((u, pk _u)\) for all \(u \in \mathcal {I}\) and has access to the queries \(\mathsf {NewSession}\), \(\mathsf {Reveal}\), \(\mathsf {Corrupt}\), \({\mathsf {Tick}}\), and \(\mathsf {Test}\). Record for the \(\mathsf {Test}\) query, being the \(\varsigma ^{test}\)-th query, the tested session \(\pi ^{t}\).
-
Eventually, \(\mathcal {A}\) stops and outputs a guess \(b \in \{0,1\}\).
The challenger outputs 1 (denoted by \(G_{\mathcal {A},\mathsf {FSOPKE}}^{\mathsf {FSOPKE{\text { -}}sec}} = 1\)) and say the adversary wins if \(b = b_{\mathsf {test}}\) and the following conditions hold:
-
1.
\(\pi ^{t}.\mathsf {keystate}= \mathsf {fresh}\), i.e., \(\mathcal {A}\) has not issued a \(\mathsf {Reveal}\) query to the test session.
-
2.
\(\pi _v^j.\mathsf {keystate}= \mathsf {fresh}\) for any session \(\pi _v^j\) such that \(\pi _v^j\) and \(\pi ^{t}\) are partners, i.e., \(\mathcal {A}\) has not issued a \(\mathsf {Reveal}\) query to a session partnered with the test session.
-
3.
\(\varsigma ^{corr}_u > \varsigma ^{test}\) for \(u = \pi ^{t}.\mathsf {id}\), i.e., the owner of the test session has not been corrupted before the \(\mathsf {Test}\) query was issued.
-
4.
if \(\pi ^{t}.\mathsf {role}= \mathsf {client}\) and \(\varsigma ^{corr}_v \ne \infty \), for \(v = \pi ^{t}.\mathsf {pid}\), then one of the following must hold:
-
There exists a session \(\pi _v^j\) partnered with \(\pi ^{t}\), i.e., a session of the intended server partner processed the client session’s message in the intended time interval.
-
\(\tau ^{t}< \tau ^{corr}_v\), i.e., the intended partner was corrupted in a time interval after that of the tested session.
-
-
5.
if \(\pi ^{t}.\mathsf {role}= \mathsf {server}\) and \(\pi ^{t}.\mathsf {pid}\ne \bot \), then \(\varsigma ^{corr}_v > \varsigma ^{test}\) for \(v = \pi ^{t}.\mathsf {pid}\), i.e., the intended client partner of a tested server session has not been corrupted before the \(\mathsf {Test}\) query was issued.
-
6.
if \(\pi ^{t}.\mathsf {role}= \mathsf {server}\) and \(\pi ^{t}.\mathsf {pid}= \bot \), then there exists a session \(\pi _v^j\) partnered with \(\pi ^{t}\), i.e., when testing a server session without authenticated partner, there must exist an honest communication partner to the tested server session \(\pi ^{t}\).
Otherwise, the challenger outputs a random bit. We say that \(\mathsf {FSOPKE}\) is secure if the following advantage function is negligible in the security parameter:
Remark 1
Notably, our security model requires both forward secrecy and replay protection from a FSOPKE protocol. Furthermore, it captures unilateral authentication (of the server) and mutual authentication simultaneously.
As expected, we restrict \(\mathsf {Reveal}\) on both partner sessions involved in the test session (conditions 1 and 2). However, our notion of partnering in Definition 10 lends more power to an adversary than is typically provided. Partnering is defined not only with respect to the session transcripts, partner IDs, and roles, but also with respect to time. Consequently, if the two sessions are not operating within the same time interval, \(\mathsf {Reveal}\) queries are, in fact, permitted on the intended partner session to the test session – even if all other aspects of partnering are fulfilled (condition 2).
To ensure replay protection, the adversary is allowed to test and reveal matching sessions of the same role; we only forbid testing and revealing two matching sessions of opposite roles (via the partnering condition). This explicitly allows for replaying of a client’s message to two server sessions (i.e., spawning two server sessions on input of the same client message m) and revealing one server session while testing the other session. Hence, our model requires that secure protocols prevent replays.
For forward secrecy, corruption of the tested identity is allowed after the \(\mathsf {Test}\) query was issued (condition 3). This applies to both clients (if the client identity exists) and servers.
Server corruption under a tested client session in the 0-RTT setting necessitates special considerations (condition 4). First we consider the scenario that the intended partner server session processes messages in the same time interval as the test query, i.e. \(\tau ^{t}\). In this case a tested client’s message must have been processed by the intended partner server session before the server is corruptedFootnote 5 to exclude the following trivial attack: observe that an adversary spawning a new client session (with some \(\mathsf {pid}= v\), outputting a message m) which it subsequently tests, may obtain the secret key \( sk _v\) of the (server) identity v through a \(\mathsf {Corrupt}(v)\) query such that, by correctness of the FSOPKE protocol, it can process message m and derive the correct session key. In this manner, an adversary would always be trivially able to win the key secrecy game. Hence, condition 4 (first item) encodes the strongest possible forward secrecy guarantees in such a scenario: whenever a client’s message has been processed by the server, the corresponding session key becomes forward-secret w.r.t. compromises of the server’s long-term secret.
Alternatively, we consider the scenario where the intended partner server session processes messages in a time interval after that used in the tested session, i.e. \(\tau ^{t}< \tau ^{corr}_v\). If the server session’s time interval is ahead of that of the tested client session then different session keys are computed. Yet this implies that there are no immediate forward secrecy guarantees should the client’s clock be ahead of the server’s time interval, since the server’s clock can be moved forward after corruption of the server. Thus, condition 4 (second item) gives an additional forward secrecy guarantee: the tested session key is forward-secret w.r.t. compromises of the server’s long-term secret for any future time interval.
As with corruption of the test session identity (condition 3), if a server session is tested such that a partnered client identity is defined, corruption of the partnered client is restricted until after the test query has been made (condition 5). We do guarantee security if the client is corrupted immediately after it has issued the test session message, but before the server has processed it, due to potential authentication by the client. Should the message be signed, for example, such corruption would allow an adversary to tamper with the message. Thus, for compromises of the client’s long-term secret, we demand forward secrecy immediately after the server establishes the session key.
For the case of unilateral authentication, we must naturally restrict \(\mathsf {Test}\) queries on the server side to cases where an honest partnered client exists (condition 6), as otherwise the adversary can take the role of the client and hence trivially learns the key.
Finally, all security guarantees are required to be provided independent of the time stepping mechanism, making the latter a functional property of a FSOPKE scheme which does not affect the scheme’s security. For example, a scheme could liberally allow session key establishment even if the states of both of the involved sessions are off by a number of time steps. While this is beyond the requirements for a correct scheme, key secrecy still requires that such session keys are secure.
In our model, we do not consider randomness or session-state reveal queries [10, 30], but note that it could be augmented with such queries.
4 Constructions
For the construction of a forward-secret 0-RTT key exchange protocol we now first focus on the more common case where only the server authenticates. Our construction builds on puncturable forward-secure key encapsulation and leverages some synchronization of time between parties in the system. Later, we discuss how to adapt this construction to scenarios where relying on time synchronization is not an option.
4.1 Construction Based on Synchronized Time
We construct a forward-secret one-pass key exchange protocol in a generic way from any puncturable forward-secure key encapsulation scheme. For our construction, we assume that clients and servers hold some roughly synchronized time, but stress that we are concerned with time intervals rather than exact time and, hence, synchronization for example on the same day is sufficient for our scheme. Aiming at unilateral (server-only) authentication, clients do not hold long-term key material (i.e., we have \( pk = \bot \) for clients) and only (mis-)use their secret key to store the current time interval.
Definition 12
( \(\mathsf {FSOPKE_U}\) Construction). Let \(\mathsf {PFSKEM}\) be a puncturable forward-secure key encapsulation scheme. We construct a forward-secret one-pass key exchange protocol \(\mathsf {FSOPKE_U}\) with unilateral authentication as follows:
-
\(\mathsf {FSOPKE}.\mathsf {KGen}(1^\lambda , r, \tau _{max}) \rightarrow ( pk , sk )\) .
-
 Generate a public/secret key pair \(( PK , SK ) \leftarrow \mathsf {PFSKEM.KGen}(1^\lambda )\). Set \( pk \leftarrow ( PK , \tau _{max})\), \(\tau \leftarrow 1\), and \( sk \leftarrow ( SK , \tau , \tau _{max})\), and output \(( pk , sk )\).
Generate a public/secret key pair \(( PK , SK ) \leftarrow \mathsf {PFSKEM.KGen}(1^\lambda )\). Set \( pk \leftarrow ( PK , \tau _{max})\), \(\tau \leftarrow 1\), and \( sk \leftarrow ( SK , \tau , \tau _{max})\), and output \(( pk , sk )\). -
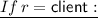 Set \( pk \leftarrow \bot \), \(\tau \leftarrow 1\), and \( sk \leftarrow (\tau )\), and output \(( pk , sk )\).
Set \( pk \leftarrow \bot \), \(\tau \leftarrow 1\), and \( sk \leftarrow (\tau )\), and output \(( pk , sk )\).
-
\(\mathsf {FSOPKE}.\mathsf {RunC}( sk , pk ) \rightarrow ( sk ', k, m)\) . Parse \( sk = (\tau )\) and \( pk = ( PK , \tau _{max})\). If \(\tau > \tau _{max}\), then abort and output \(( sk ,\bot ,\bot )\).
Otherwise, compute \((\mathsf {CT}, \mathsf {K}) \leftarrow \mathsf {PFSKEM.Enc}( PK , \tau )\), set \(k \leftarrow \mathsf {K}\) and \(m \leftarrow \mathsf {CT}\), and output \(( sk , k, m)\).
-
\(\mathsf {FSOPKE}.\mathsf {RunS}( sk , pk = \bot , m) \rightarrow ( sk ', k)\) . Parse \( sk = ( SK ,\tau ,\tau _{max})\). If \( SK = \bot \) or \(\tau > \tau _{max}\), then abort and output \(( sk , \bot )\).
Compute \(\mathsf {K}\leftarrow \mathsf {PFSKEM.Dec}( SK , \tau , m)\). If \(\mathsf {K}= \bot \), then abort and output \(( sk , \bot )\).
Otherwise, issue \( SK ' \leftarrow \mathsf {PFSKEM.PnctCxt}( SK ,\tau ,m)\). Let \( sk \leftarrow ( SK ', \tau , \tau _{max})\), set \(k \leftarrow \mathsf {K}\), and output \(( sk , k)\).
-
\(\mathsf {FSOPKE}.\mathsf {TimeStep}( sk , r) \rightarrow sk '\) .
-
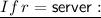 Parse \( sk = ( SK ,\tau ,\tau _{max})\). If \(\tau \ge \tau _{max}\), then set \( sk \leftarrow (\bot , \tau + 1, \tau _{max})\), and output \( sk \). Otherwise, let \( SK ' \leftarrow \mathsf {PFSKEM.PnctInt}( SK , \tau )\), set \( sk \leftarrow ( SK ', \tau + 1, \tau _{max})\), and output \( sk \).
Parse \( sk = ( SK ,\tau ,\tau _{max})\). If \(\tau \ge \tau _{max}\), then set \( sk \leftarrow (\bot , \tau + 1, \tau _{max})\), and output \( sk \). Otherwise, let \( SK ' \leftarrow \mathsf {PFSKEM.PnctInt}( SK , \tau )\), set \( sk \leftarrow ( SK ', \tau + 1, \tau _{max})\), and output \( sk \). -
 Parse \( sk = (\tau )\), set \( sk \leftarrow (\tau + 1)\), and output \( sk \).
Parse \( sk = (\tau )\), set \( sk \leftarrow (\tau + 1)\), and output \( sk \).
Correctness follows from the correctness of the underlying \(\mathsf {PFSKEM}\) scheme; the details are omitted here due to space limitations.
Security Analysis. We now investigate the security of our construction and show that it is a secure forward-secret one-pass key exchange protocol with unilateral authentication.
Theorem 2
The \(\mathsf {FSOPKE_U}\) construction from Definition 12 is a secure \(\mathsf {FSOPKE}\) protocol (with unilateral authentication). Formally, for any efficient adversary \(\mathcal {A}\) in the \(\mathsf {FSOPKE{\text { -}}sec}\) game there exists an efficient algorithm \(\mathcal {B}\) such that
where \(n_\mathcal {I}= |\mathcal {I}|\) is the maximum number of identities, \({\hat{\tau }}_{max}\) is the maximum time interval for any session, and \(n_s\) is the maximum number of sessions.
Proof
Let \(\mathcal {A}\) be an adversary against the security of \(\mathsf {FSOPKE_U}\). We proceed in a sequence of games, bounding the introduced difference in \(\mathcal {A}\)’s advantage for each step. By \(\mathsf {Adv}_{i}\) we denote \(\mathcal {A}\)’s advantage in one of the i-th game.
Game 0. This is the original security experiment, with adversarial advantage \(\mathsf {Adv}_{0}=\mathsf {Adv}_{\mathcal {A},\mathsf {FSOPKE_U}}^{\mathsf {FSOPKE{\text { -}}sec}}(\lambda )\).
Game 1. Here we let the challenger upfront guess a server identity \(s^*\in \mathcal {I}\), associated with public/secret key pair \(( pk ^*, sk ^*)\), and let it abort the game if this is not the identity involved in the test session. I.e., if a server session is tested (i.e., \(\pi ^{t}.\mathsf {role}= \mathsf {server}\)) this is the session owner \(s^*= \pi ^{t}.\mathsf {id}\), while, if a client session is tested (\(\pi ^{t}.\mathsf {role}= \mathsf {client}\)) it is the intended partner (\(s^*= \pi ^{t}.\mathsf {pid}\)). Let \(n_\mathcal {I}=|\mathcal {I}|\). Then
Game 2. Now the \(\mathcal {A}\) guesses the time interval \(\tau ^*= \pi ^{t}.\mathsf {time}\) in which the tested session ran, and aborts if the guess is incorrect. Letting \({\hat{\tau }}_{max}\) denote the maximum value \(\pi .\mathsf {time}\) for any session \(\pi \), it follows that
Game 3. Continuing from Game 2 the challenger aborts if it does not correctly guess the involved client session \(\pi ^{t}_c\) (i.e., \(\pi ^{t}_c.\mathsf {role}= \mathsf {client}\)) for which one of the following two conditions holds:
-
either \(\pi ^{t}_c = \pi ^{t}\), i.e., \(\pi ^{t}_c\) is the tested session, or
-
\(\pi ^{t}_c\) is partnered with the tested (server) session \(\pi ^{t}\).
For the second case, observe that if a server is tested, by condition 6 of the \(\mathsf {FSOPKE{\text { -}}sec}\) security game in Definition 11, there must exist such a partnered client session \(\pi ^{t}_c\) with \(\pi ^{t}_c.\mathsf {pid}= \pi ^{t}.\mathsf {id}\) in order for \(\mathcal {A}\) to win.
Denoting \(n_s\) as the total number of sessions, we have
Furthermore, observe that by Definition 7, if a server session is tested, session \(\pi ^{t}\) must actually be the first accepting session owned by \(s^*\) that is partnered with \(\pi ^{t}_c\) in order for \(\mathcal {A}\) to win. Recall that the first such accepting session, by correctness, derives a key \(\mathsf {K}\ne \bot \) as \(\mathsf {K}\leftarrow \mathsf {PFSKEM.Dec}( SK ^*,\tau ^*,m)\) (where \(m = \pi ^{t}.\mathsf {trans}\)) and hence invokes \( SK ^* \leftarrow \mathsf {PFSKEM.PnctCxt}( SK ^*,\tau ^*,m)\). Any later such accepting session would hence, by Definition 7, derive \(\mathsf {K}= \bot \) through \(\mathsf {K}\leftarrow \mathsf {PFSKEM.Dec}( SK ^*,\tau ^*,m)\), so an adversary would be given \(\bot \) as the response to its \(\mathsf {Test}\) query and cannot win.
Game 4. In this game hop, we replace the key \(\mathsf {k^*}\) derived in the tested session \(\pi ^{t}\) by one chosen uniformly at random from the output space of \(\mathsf {PFSKEM.Dec}\). We show that any adversary that distinguishes the change from Game 3 to Game 4 with non-negligible advantage can be turned into an algorithm \(\mathcal {B}\) which wins in \(G_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}\) with the same advantage.
In this reduction, \(\mathcal {B}\) first outputs the time interval \(\tau ^*\) guessed in Game 2 as the time interval it wants to be challenged on in \(G_{\mathcal {A},\mathsf {PFSKEM}}^{\mathsf {IND{\text { -}}sT{\text { -}}CCA}}\). It then obtains a challenge public key \( PK ^*\), which it associates with the server identity \(s^*\) within the \( pk ^*= ( PK ^*, \tau _{max})\) guessed in Game 1. For all other identities \(u \in \mathcal {I}\setminus \{s^*\}\), algorithm \(\mathcal {B}\) generates appropriate public/secret key pairs on its own following \(\mathsf {FSOPKE}.\mathsf {KGen}\). In particular, it generates \(\mathsf {PFSKEM}\) keys for all other server identities \(s \in \mathcal {S}\setminus \{s^*\}\). Furthermore, \(\mathcal {B}\) obtains a challenge ciphertext \(\mathsf {CT}^*\) and key \(\mathsf {K}^*\), with \(\mathsf {K}^*\) either being the real key encapsulated in \(\mathsf {CT}^*\) or and independently chosen random one.
Our goal is now to have algorithm \(\mathcal {B}\) (correctly) simulate the security game for \(\mathcal {A}\) in such a way that, if \(\mathsf {K}^*\) is the real key, it perfectly simulates Game 3, whereas if \(\mathsf {K}^*\) is a randomly chosen key, it perfectly simulates Game 4. To this extent, algorithm \(\mathcal {B}\) uses its oracles \(\mathtt {KGen}()\), \(\mathtt {PFSKEM.Dec}()\), \(\mathtt {PFSKEM.PnctInt}()\), and \(\mathtt {PFSKEM.PnctCxt}()\) given in the selective ID, selective time CCA security game in Definition 8 as follows, answering the queries of \(\mathcal {A}\) in the key exchange game:
-
\(\mathsf {NewSession}(u, role, pid, m)\) . We distinguish the following cases:
-
For all client sessions \(\pi _u^i\) (\(u \in \mathcal {C}\)) except for the client session \(\pi ^{t}_c\) guessed in Game 3, \(\mathcal {B}\) simulates \(\mathsf {NewSession}\) queries as specified in the security game.
-
For the guessed client session \(\pi ^{t}_c\), \(\mathcal {B}\) does not invoke \(\mathsf {PFSKEM.Enc}\) but uses its challenge key \(\mathsf {K}^*\) as the session key k and the challenge ciphertext \(\mathsf {CT}^*\) as the output message m. Observe that, through Games 1–3, we ensure that \(\pi ^{t}_c\) uses time interval \(\tau ^*\) and public key \( pk ^*\) (and hence the challenge \(\mathsf {PFSKEM}\) public key \( PK ^*\)) of server \(s^*\).
-
For all server sessions \(\pi _s^i\) not owned by the server identity \(s^*\) guessed in Game 1 (i.e., \(s \in \mathcal {S}\setminus \{s^*\}\)), \(\mathcal {B}\) simulates \(\mathsf {NewSession}\) queries as specified, using the according (self-generated) secret key \( sk _s\).
-
For all server sessions \(\pi _{s^*}^i\) owned by \(s^*\) and not partnered with the guessed client session \(\pi ^{t}_c\), \(\mathcal {B}\) uses its oracles \(\mathtt {PFSKEM.Dec}\) and \(\mathtt {PFSKEM.PnctCxt}\) from the selective ID, selective time CCA game to simulate the operations for the \(\mathsf {NewSession}\) query. Note that, as \(\pi _{s^*}^i\) is not partnered with \(\pi ^{t}_c\) (though having opposite roles and \(\pi ^{t}_c.\mathsf {pid}= s^*\)), we have \((\pi ^{t}_c.\mathsf {time},\pi ^{t}_c.\mathsf {trans}) = (\tau ^*,\mathsf {CT}^*) \ne (\pi _{s^*}^i.\mathsf {time},\pi _{s^*}^i.\mathsf {trans})\) and are hence allowed to call the \(\mathtt {PFSKEM.Dec}\) oracle on this input.
-
For the first server session \(\pi ^{t}_{s^*}\) owned by \(s^*\) which is partnered with the guessed client session \(\pi ^{t}_c\), \(\mathcal {B}\) sets the session key to be the challenge key \(k \leftarrow \mathsf {K}^*\) and invokes \(\mathtt {PFSKEM.PnctCxt}(\tau ^*, \mathsf {CT}^*)\).
Note that partnering in particular implies \(\pi ^{t}_{s^*}\) holds the same time as \(\pi ^{t}_c\) and obtains the message of \(\pi ^{t}_c\), i.e., \(\pi ^{t}_c.\mathsf {time}= \tau ^*= \pi ^{t}_{s^*}.\mathsf {time}\) and \(\pi ^{t}_c.\mathsf {trans}= m = \pi ^{t}_{s^*}.\mathsf {trans}\). Furthermore, \(\mathtt {PFSKEM.PnctCxt}\) was not invoked before on \((\tau ^*, \mathsf {CT}^*)\). Hence, by correctness, \(\pi ^{t}_{s^*}\) establishes the same session key \(\mathsf {K}^*\) as \(\pi ^{t}_c\).
-
For any further server session \(\pi _{s^*}^i\) partnered with \(\pi ^{t}_c\), \(\mathcal {B}\) sets \(k \leftarrow \bot \). By Definition 7, we know that any such session would obtain \(\bot \leftarrow \mathsf {PFSKEM.Dec}( SK ,\tau ^*,\mathsf {CT}^*)\), as \(\mathtt {PFSKEM.PnctCxt}\) has been called before on \((\tau ^*,\mathsf {CT}^*)\).
-
\(\mathsf {Reveal}(\pi _u^i)\) . First, observe that any winning adversary \(\mathcal {A}\) cannot call \(\mathsf {Reveal}\) on the sessions \(\pi ^{t}_c\) and \(\pi ^{t}_{s^*}\) by conditions 1 and 2 of the security model, as one of them is the tested session and the other, if it exists, is partnered with the tested session.
For all other sessions, \(\mathcal {B}\) holds the correct key from simulation of the \(\mathsf {NewSession}\) queries above, and can therefore respond to according \(\mathsf {Reveal}\) queries as specified.
-
\(\mathsf {Corrupt}(u)\) . For the server identity \(s^*\) involved in the tested session \(\pi ^{t}\), \(\mathcal {B}\) invokes its \(\mathtt {PFSKEM.Corrupt}\) oracle to obtain the \(\mathsf {PFSKEM}\) secret key \( SK ^*\), which it returns within \( sk ^*= ( SK ^*,\tau _{s^*},\tau _{max})\). Observe, that if \(\mathcal {A}\) calls \(\mathsf {Corrupt}(s^*)\) without losing, we are ensured that \(\mathcal {B}\) has called \(\mathtt {PFSKEM.PnctCxt}(\tau ^*,\mathsf {CT}^*)\) and/or \(\mathtt {PFSKEM.PnctInt}(\tau ^*)\) before \(\mathsf {Corrupt}(s^*)\), and hence also does not lose in the selective-time CCA security game:
-
If \(\pi ^{t}= \pi ^{t}_{s^*}\) is a server session (owned by \(s^*\)), condition 3 of the security model ensures that \(s^*\) can only be corrupted after \(\pi ^{t}\) has accepted. In the process of \(\pi ^{t}\) accepting (with \(\pi ^{t}.\mathsf {time}= \tau ^*\) and \(\pi ^{t}.\mathsf {trans}= \mathsf {CT}^*\)), \(\mathcal {B}\) must have invoked \(\mathtt {PFSKEM.PnctCxt}(\tau ^*,\mathsf {CT}^*)\), and therefore before corruption of \(s^*\).
-
If \(\pi ^{t}= \pi ^{t}_c\) is a client session, condition 4 of the security model ensures that either there exists a partnered server session (\(\pi ^{t}_{s^*}\)) that processed \(\mathsf {CT}^*\) in the time interval \(\tau ^*\) or that \(s^*\) gets corrupted in a time interval \(\tau ^{corr}_{s^*} > \pi ^{t}.\mathsf {time}= \tau ^*\). Hence, \(\mathcal {B}\) must have invoked \(\mathtt {PFSKEM.PnctCxt}(\tau ^*,\mathsf {CT}^*)\) or \(\mathtt {PFSKEM.PnctInt}(\tau ^*)\), respectively, before corruption of \(s^*\).Footnote 6
-
For any other (client or server) identity \(u \ne s^*\), \(\mathcal {B}\) maintains the corresponding secret key \( sk _u\) and can therefore respond to according \(\mathsf {Corrupt}\) queries as specified.
-
\({\mathsf {Tick}}(u)\) . Algorithm \(\mathcal {B}\) conducts the time stepping procedures as specified, using its oracle \(\mathtt {PFSKEM.PnctInt}\) on the (unknown) secret key \( SK ^*\) corresponding to the \(\mathsf {PFSKEM}\) challenge public key \( PK ^*\).
-
\(\mathsf {Test}(\pi ^{t})\) . Observe that the tested session \(\pi ^{t}\) must be either the client session \(\pi ^{t}_c\) guessed in Game 3 or the (first) server session \(\pi ^{t}_{s^*}\) owned by \(s^*\) partnered with \(\pi ^{t}_c\). Algorithm \(\mathcal {B}\), in both cases, simply outputs \(\pi ^{t}.\mathsf {key}= \mathsf {K}^*\) as the response of the \(\mathsf {Test}\) query.
When \(\mathcal {A}\) stops and outputs a guess \(b \in \{0,1\}\), \(\mathcal {B}\) stops as well and outputs b as its own guess.
Observe that algorithm \(\mathcal {B}\) correctly answers all queries of \(\mathcal {A}\) and, in the case that \(\mathsf {K}^*\) is the real key encapsulated in \(\mathsf {CT}^*\), perfectly simulates Game 3, while it perfectly simulates Game 4 if \(\mathsf {K}^*\) is chosen independently at random. Algorithm \(\mathcal {B}\) moreover obeys all restrictions in the selective ID, selective time CCA security game of Definition 8 if \(\mathcal {A}\) adheres to the conditions in the \(\mathsf {FSOPKE}\) security game.
As \(\mathcal {B}\) inherits the output of \(\mathcal {A}\), a difference between \(\mathcal {A}\)’s advantage in Game 3 and its advantage in Game 4 corresponds to the probability difference of \(\mathcal {B}\) outputting 1 in the two cases of the selective ID, selective time CCA security experiment. Thus,
As in Game 4 the session key \(\mathsf {k^*}\) in the tested session is always chosen uniformly at random the response to the \(\mathsf {Test}\) query is independent of the challenge bit b and hence \(\mathcal {A}\) cannot predict b better than by guessing, i.e., \(\mathsf {Adv}_{4} \le 0\). Combining the advantage bounds in Games 1–4 yields the overall bound. \(\square \)
4.2 Variant Without Synchronized Time
For those environments where more relaxed requirements for time synchronization are preferable, we outline a variant of our forward-secret 0-RTT key exchange construction above that does not rely on synchronized time. For this variant, we essentially combine the \(\mathsf {FSOPKE_U}\) construction from Definition 12, restricted to a single time interval, with the concept of server configurations used in recent key exchange protocol designs, namely Google’s QUIC protocol [31] and TLS 1.3 with Diffie–Hellman-based 0-RTT mode [39]. A server configuration here essentially is a publicly accessible string that contains a semi-static public key, signed with the long-term signing key of the corresponding party. Utilizing this string, a forward-secret 0-RTT key exchange protocol variant without time synchronization then works as follows.
For each time interval (e.g., a set number of days or weeks), servers generate a \(\mathsf {PFSKEM}\) key pair (i.e., with \(\tau _{max}= 1\)), which they sign and publish within a server configuration. Clients can then retrieve and use the currently offered public key for the server to establish connections within this time interval.
We stress that, while introducing a slightly higher communication overhead, this variant offers the same security properties as the time-synchronized one. In particular recall that, due to puncturing, compromising the semi-static secret key for some time interval does not endanger the forward secrecy of priorly established connections within the same time interval. Indeed, the choice of how often to publish new server configurations (i.e., how long the conceptual time intervals are) is a purely functional one, based on the performance trade-off between storage and computation overhead for \(\mathsf {PFSKEM}\) keys covering a shorter or longer interval (and hence more or fewer connections).
5 Analysis
We analyze our protocol for security levels \(\lambda \in \{80, 128, 256\}\). We instantiate our scheme based on the DDH-based HIBE scheme from [6] and the discrete log-based one-time signature scheme from [22, Sect. 5.4]. We consider groups with asymmetric bilinear map \( e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T \) where groups are of order p such that \(p = 2^{2 \lambda }\) for the given security parameter \(\lambda \). Thus, an element of \({\mathbb {Z}}_p\) can be represented by \(2\lambda \) bits. We assume a setting based on Barreto-Naehrig curves [2], where elements of \(\mathbb {G}_1\) can be represented by \(2\lambda \) bits, while elements of \(\mathbb {G}_2\) have size \(4 \lambda \) bits. In this setting, we can instantiate our PFS-KEM (and thus our FSOPKE) as follows.
-
A ciphertext consist of three elements of \(\mathbb {G}_1\) (from the HIBE of [6]) plus three \(\mathbb {G}_1\)-elements for \( pk _{OT}\), plus two \({\mathbb {Z}}_p\)-elements for \(\sigma \). Thus, ciphertexts have size \(6 \times |\mathbb {G}_1| + 2 \times |{\mathbb {Z}}_p| = 16 \lambda \) bits.
-
A public key contains \(2 \lambda +35\) elements of \(\mathbb {G}_2\), which amounts to \(8\lambda ^2 +140\lambda \) bits.
-
A punctured secret key contains \(R + S\) user secret keys of the HIBKEM, each consisting of \(3 \times |\mathbb {G}_2| = 12\lambda \) bits. Here \(R = | pk _{OT}| + |\tau |\) denotes the bit-length of “HIBKEM-identities”, and S denotes the number of sessions per time slot. Assuming a setting with \(2^{32}\) time slots (which should be sufficient for any conceivable practical application, even with very short time slots), and that a collision-resistant hash function with range \(\{0,1\}^{2\lambda }\) is used to compute a short representation of \( pk _{OT}\) inside the HIBKEM, we have \(R = 2\lambda + 32\). Thus, the size of the secret key as a function of S is \((S+2\lambda +32) \cdot 12\lambda \) bits.
For different values \(S \in \{2^{10}, 2^{16}, 2^{20}\}\) of sessions per time slot, and security parameters \(\lambda \in \{80, 128, 256\}\), we obtain the sizes of public keys and messages and the upper bounds on the size of secret keys displayed in Fig. 4.
Notes
- 1.
Beyond the pure cryptographic protocol, round trips may also be induced by lower-layer transport protocols. For example, the TCP protocol requires 1-RTT for its own handshake before a higher-level cryptographic key exchange can start. Here we focus on the overhead round-trip time caused by the cryptographic components of the key-exchange protocol.
- 2.
In case of Google this approach amounts to a few gigabytes of data to be held in shared state between multiple server instances.
- 3.
This is essentially a public-key encryption scheme which can only be used to transport random keys, but not to transport payload messages.
- 4.
Observe that asynchronous messaging and 0-RTT key exchange are conceptually relatively close. In both settings, a data protection key is to be established while only unilateral communication is possible. While different, e.g., in constraints for latency and storage overhead, this in particular implies that our construction can also be employed in the setting of asynchronous messaging.
- 5.
Recall that the adversary cannot spawn or interact with sessions of a party anymore after corrupting it.
- 6.
Recall that \(\pi ^{t}_{s^*}\) must have accepted before \(s^*\) is corrupted, as afterwards no further queries to sessions owned by \(s^*\) are allowed.
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_28
Barreto, P.S.L.M., Naehrig, M.: Pairing-friendly elliptic curves of prime order. In: Preneel, B., Tavares, S. (eds.) SAC 2005. LNCS, vol. 3897, pp. 319–331. Springer, Heidelberg (2006). doi:10.1007/11693383_22
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, , Fairfax, Virginia, USA, pp. 62–73. ACM Press, 3–5 November 1993
Bellare, M., Rogaway, P.: Entity authentication and key distribution. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 232–249. Springer, Heidelberg (1994). doi:10.1007/3-540-48329-2_21
Bhargavan, K., Fournet, C., Kohlweiss, M., Pironti, A., Strub, P.-Y., Zanella-Béguelin, S.: Proving the TLS handshake secure (as it is). In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 235–255. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_14
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_23
Boneh, D., Boyen, X., Goh, E.-J.: Hierarchical identity based encryption with constant size ciphertext. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 440–456. Springer, Heidelberg (2005). doi:10.1007/11426639_26
Boyd, C., Cliff, Y., Gonzalez Nieto, J., Paterson, K.G.: Efficient one-round key exchange in the standard model. In: Mu, Y., Susilo, W., Seberry, J. (eds.) ACISP 2008. LNCS, vol. 5107, pp. 69–83. Springer, Heidelberg (2008). doi:10.1007/978-3-540-70500-0_6
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 255–271. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_16
Canetti, R., Krawczyk, H.: Analysis of key-exchange protocols and their use for building secure channels. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 453–474. Springer, Heidelberg (2001). doi:10.1007/3-540-44987-6_28
Chow, S.S.M., Choo, K.-K.R.: Strongly-secure identity-based key agreement and anonymous extension. In: Garay, J.A., Lenstra, A.K., Mambo, M., Peralta, R. (eds.) ISC 2007. LNCS, vol. 4779, pp. 203–220. Springer, Heidelberg (2007). doi:10.1007/978-3-540-75496-1_14
Cohn-Gordon, K., Cremers, C., Garratt, L.: On post-compromise security. In: IEEE 29th Computer Security Foundations Symposium, CSF 2016, pp. 164–178 (2016)
Cremers, C., Feltz, M.: One-round strongly secure key exchange with perfect forward secrecy and deniability. Cryptology ePrint Archive, Report 2011/300 (2011). http://eprint.iacr.org/2011/300
Cremers, C., Horvat, M., Scott, S., van der Merwe, T.: Automated analysis, verification of TLS 1.3: 0-RTT, resumption and delayed authentication. In: IEEE Symposium on Security and Privacy, San Jose, CA, USA, pp. 470–485. IEEE Computer Society Press, 22–26 May 2016
Cremers, C., Feltz, M.: Beyond eCK: perfect forward secrecy under actor compromise and ephemeral-key reveal. In: Foresti, S., Yung, M., Martinelli, F. (eds.) ESORICS 2012. LNCS, vol. 7459, pp. 734–751. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33167-1_42
Dierks, T., Rescorla, E.: The Transport Layer Security (TLS) Protocol Version 1.2. RFC 5246 (Proposed Standard), Updated by RFCs 5746, 5878, 6176, August 2008
Dowling, B., Fischlin, M., Günther, F., Stebila, D.: A cryptographic analysis of the TLS 1.3 handshake protocol candidates. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, Denver, CO, USA, pp. 1197–1210. ACM Press, 12–16 October 2015
Fischlin, M., Günther, F.: Multi-stage key exchange and the case of Google’s QUIC protocol. In: Ahn, G.-J., Yung, M., Li, N. (eds.) ACM CCS 2014, Scottsdale, AZ, USA, pp. 1193–1204. ACM Press, 3–7 November 2014
Fischlin, M., Günther, F.: Replay attacks on zero round-trip time: the case of the TLS 1.3 handshake candidates. In: 2017 IEEE European Symposium on Security and Privacy. IEEE, April 2017
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 537–554. Springer, Heidelberg (1999). doi:10.1007/3-540-48405-1_34
Green, M.D., Miers, I.: Forward secure asynchronous messaging from puncturable encryption. In: IEEE S&P 2015 [25], pp. 305–320 (2015)
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). doi:10.1007/11935230_29
Hale, B., Jager, T., Lauer, S., Schwenk, J.: Simple security definitions for and constructions of 0-RTT key exchange. Cryptology ePrint Archive, Report 2015/1214 (2015). http://eprint.iacr.org/2015/1214
Halevi, S., Krawczyk, H.: One-pass HMQV and asymmetric key-wrapping. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 317–334. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19379-8_20
IEEE Symposium on Security and Privacy, San Jose, CA, USA. IEEE Computer Society Press, 17–21 May 2015
Jager, T., Kohlar, F., Schäge, S., Schwenk, J.: On the security of TLS-DHE in the standard model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 273–293. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_17
Krawczyk, H.: HMQV: a high-performance secure Diffie-Hellman protocol. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 546–566. Springer, Heidelberg (2005). doi:10.1007/11535218_33
Krawczyk, H., Paterson, K.G., Wee, H.: On the security of the TLS protocol: a systematic analysis. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 429–448. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_24
Krawczyk, H., Wee, H.: The OPTLS protocol and TLS 1.3. In: 2016 IEEE European Symposium on Security and Privacy, pp. 81–96. IEEE, March 2016
LaMacchia, B., Lauter, K., Mityagin, A.: Stronger security of authenticated key exchange. In: Susilo, W., Liu, J.K., Mu, Y. (eds.) ProvSec 2007. LNCS, vol. 4784, pp. 1–16. Springer, Heidelberg (2007). doi:10.1007/978-3-540-75670-5_1
Langley, A., Chang, W.-T.: QUIC Crypto. https://docs.google.com/document/d/1g5nIXAIkN_Y-7XJW5K45IblHd_L2f5LTaDUDwvZ5L6g/. Accessed May 2016, Revision 26 May 2016
Li, Y., Schäge, S., Yang, Z., Kohlar, F., Schwenk, J.: On the security of the pre-shared key ciphersuites of TLS. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 669–684. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_38
Lychev, R., Jero, S., Boldyreva, A., Nita-Rotaru, C.: How secure and quick is QUIC? Provable security and performance analyses. In: IEEE S&P 2015 [25], pp. 214–231 (2015)
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_43
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Ning, P., De Capitani di Vimercati, S., Syverson, P.F. (eds.) ACM CCS 2007, Alexandria, Virginia, USA, pp. 195–203. ACM Press, 28–31 October 2007
Petullo, W.M., Zhang, X., Solworth, J.A., Bernstein, D.J., Lange, T.: MinimaLT: minimal-latency networking through better security. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, Berlin, Germany, pp. 425–438. ACM Press, 4–8 November 2013
Pointcheval, D., Sanders, O.: Forward secure non-interactive key exchange. In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 21–39. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10879-7_2
QUIC, a multiplexed stream transport over UDP. https://www.chromium.org/quic
Rescorla, E.: The Transport Layer Security (TLS) Protocol Version 1.3 - draft-ietf-tls-tls13-12. https://tools.ietf.org/html/draft-ietf-tls-tls13-12. Accessed March 2016
Rescorla, E.: The Transport Layer Security (TLS) Protocol Version 1.3 - draft-ietf-tls-tls13-18. https://tools.ietf.org/html/draft-ietf-tls-tls13-18. Accessed October 2016
Rescorla, E.: 0-RTT and Anti-Replay (IETF TLS working group mailing list). IETF Mail Archive, https://mailarchive.ietf.org/arch/msg/tls/gDzOxgKQADVfItfC4NyW3ylr7yc. Accessed March 2015
Rescorla, E.: [TLS] Do we actually need semi-static DHE-based 0-RTT? IETF Mail Archive, https://mailarchive.ietf.org/arch/msg/tls/c43zNQH9vGeHVnXhAb_D3cpIAIw. Accessed February 2016
Williams, N.: [TLS] 0-RTT security considerations (was OPTLS). IETF Mail Archive, https://mailarchive.ietf.org/arch/msg/tls/OZwGgVhySbVhU36BMX1elQ9x0GE. Accessed November 2014
Wu, D.J., Taly, A., Shankar, A., Boneh, D.: Privacy, discovery, and authentication for the internet of things. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 301–319. Springer, Heidelberg (2016). doi:10.1007/978-3-319-45741-3_16
Acknowledgments
We thank the anonymous reviewers for valuable comments. This work has been co-funded by the DFG as part of project S4 within the CRC 1119 CROSSING and by DFG grant JA 2445/1-2.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Günther, F., Hale, B., Jager, T., Lauer, S. (2017). 0-RTT Key Exchange with Full Forward Secrecy. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10212. Springer, Cham. https://doi.org/10.1007/978-3-319-56617-7_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-56617-7_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56616-0
Online ISBN: 978-3-319-56617-7
eBook Packages: Computer ScienceComputer Science (R0)





 Generate a public/secret key pair
Generate a public/secret key pair 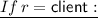 Set
Set 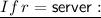 Parse
Parse  Parse
Parse 
