Abstract
Functional encryption (FE) enables fine-grained control of sensitive data by allowing users to only compute certain functions for which they have a key. The vast majority of work in FE has focused on deterministic functions, but for several applications such as privacy-aware auditing, differentially-private data release, proxy re-encryption, and more, the functionality of interest is more naturally captured by a randomized function. Recently, Goyal et al. (TCC 2015) initiated a formal study of FE for randomized functionalities with security against malicious encrypters, and gave a selectively secure construction from indistinguishability obfuscation. To date, this is the only construction of FE for randomized functionalities in the public-key setting. This stands in stark contrast to FE for deterministic functions which has been realized from a variety of assumptions.
Our key contribution in this work is a generic transformation that converts any general-purpose, public-key FE scheme for deterministic functionalities into one that supports randomized functionalities. Our transformation uses the underlying FE scheme in a black-box way and can be instantiated using very standard number-theoretic assumptions (for instance, the DDH and RSA assumptions suffice). When applied to existing FE constructions, we obtain several adaptively-secure, public-key functional encryption schemes for randomized functionalities with security against malicious encrypters from many different assumptions such as concrete assumptions on multilinear maps, indistinguishability obfuscation, and in the bounded-collusion setting, the existence of public-key encryption, together with standard number-theoretic assumptions.
Additionally, we introduce a new, stronger definition for malicious security as the existing one falls short of capturing an important class of correlation attacks. In realizing this definition, our compiler combines ideas from disparate domains like related-key security for pseudorandom functions and deterministic encryption in a novel way. We believe that our techniques could be useful in expanding the scope of new variants of functional encryption (e.g., multi-input, hierarchical, and others) to support randomized functionalities.
S. Agrawal—Part of this work was done when the author was a graduate student at the University of Illinois, Urbana-Champaign, supported by NSF CNS 12-28856 and the Andrew & Shana Laursen fellowship.
D.J. Wu—This work was supported in part by NSF, DARPA, the Simons foundation, a grant from ONR, and an NSF Graduate Research Fellowship. Opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of DARPA.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Traditionally, encryption schemes have provided an all-or-nothing approach to data access: a user who holds the secret key can completely recover the message from a ciphertext while a user who does not hold the secret key learns nothing at all from the ciphertext. In the last fifteen years, numerous paradigms, such as identity-based encryption [31, 45, 85], attribute-based encryption [24, 66, 84], predicate encryption [37, 71, 75, 78], and more have been introduced to enable more fine-grained access control on encrypted data. More recently, the cryptographic community has worked to unify these different paradigms under the general umbrella of functional encryption (FE) [35, 79, 83].
At a high level, an FE scheme enables delegation of decryption keys that allow users to learn specific functions of the data, and nothing else. More precisely, given a ciphertext for a message x and a secret key for a function f, one can only learn the value f(x). In the last few years, numerous works have explored different security notions [3, 4, 7, 16, 23, 35, 79] as well as constructions from a wide range of assumptions [8, 10, 50, 55, 62, 64, 86]. Until very recently, the vast majority of work in functional encryption has focused on deterministic functionalities, i.e., on schemes that issue keys for deterministic functions only. However, there are many scenarios where the functionality of interest is more naturally captured by a randomized function. The first two examples below are adapted from those of Goyal et al. [65].
Privacy-aware auditing. Suppose a government agency is tasked with monitoring various financial institutions to ensure that their day-to-day activity is compliant with federal regulations. The financial institutions do not want to give complete access of their confidential data to any external auditor. Partial access is insufficient if the financial institution is able to (adversarially) choose which part of its database to expose. An ideal solution should allow the institutions to encrypt their database before providing access. Next, the government agency can give the external auditors a key that allows them to sample a small number of randomly chosen records from each database.
Constructing an encryption scheme that supports this kind of sampling functionality is non-trivial for several reasons. If an auditor obtains two independent keys from the government agency, applying them to the same encrypted database should nonetheless generate two independent samples from it. On the flip side, if the same key is applied to two distinct databases, the auditor should obtain an independent sample from each.
Another source of difficulty that arises in this setting is that the encryption is performed locally by the financial institution. Thus, if malicious institutions are able to construct “bad” ciphertexts such that the auditor obtains correlated or non-uniform samples from the encrypted databases, then they can completely compromise the integrity of the audit. Hence, any encryption scheme we design for privacy-aware auditing must also protect against malicious encrypters.
Differential privacy. Suppose a consortium of hospitals, in an effort to promote medical research, would like to provide restricted access to their patient records to approved scientists. In particular, they want to release information in a differentially-private manner to protect the privacy of their patients. The functionality of interest in this case is the evaluation of some differentially-private mechanism, which is always a randomized function. Thus, the scheme used to encrypt patient data should also support issuing keys for randomized functions. These keys would be managed by the consortium.
Proxy re-encryption. In a proxy re-encryption system, a proxy is able to transform a ciphertext encrypted under Alice’s public key into one encrypted under Bob’s public key [13]. Such a capability is very useful if, for example, Alice wants to forward her encrypted emails to her secretary Bob while she is away on vacation [27]. We refer to [13] for other applications of this primitive.
Proxy re-encryption can be constructed very naturally from a functional encryption scheme that supports randomized functionalities. For instance, in the above example, Alice would generate a master public/secret key-pair for an FE scheme that supports randomized functionalities. When users send mail to Alice, they would encrypt under her master public key. Then, when Alice goes on vacation, she can delegate her email to Bob by simply giving her mail server a re-encryption key that re-encrypts emails for Alice under Bob’s public key. Since standard semantically-secure encryption is necessarily randomized, this re-encryption functionality is a randomized functionality. In fact, in this scenario, Alice can delegate an arbitrary decryption capability to other parties. For instance, she can issue a key that only re-encrypts emails tagged with “work” to Bob. Using our solution, the re-encryption function does not require interaction with Bob or knowledge of any of Bob’s secrets.
Randomized functional encryption. Motivated by these applications, Alwen et al. [8] and Goyal et al. [65] were the first to formally study the problem of FE for randomized functionalities. In such an FE scheme, a secret key for a randomized function f and an encryption of a message x should reveal a single sample from the output distribution of f(x). Moreover, given a collection of secret keys \(\mathsf {sk} _{f_1}, \ldots , \mathsf {sk} _{f_n}\) for functions \(f_1, \ldots , f_n\), and ciphertexts \(\mathsf {ct} _{x_1}, \ldots , \mathsf {ct} _{x_n}\) corresponding to messages \(x_1, \ldots , x_n\), where neither the functions nor the messages need to be distinct, each secret key \(\mathsf {sk} _{f_i}\) and ciphertext \(\mathsf {ct} _{x_j}\) should reveal an independent draw from the output distribution of \(f_i(x_j)\), and nothing more.
In supporting randomized functionalities, handling malicious encrypters is a central issue: a malicious encrypter may construct a ciphertext for a message x such that when decrypted with a key for f, the resulting distribution differs significantly from that of f(x). For instance, in the auditing application discussed earlier, a malicious bank could manipulate the randomness used to sample records in its database, thereby compromising the integrity of the audit. We refer to [65] for a more thorough discussion on the importance of handling malicious encrypters.
1.1 Our Contributions
To date, the only known construction of public-key FE for randomized functionalities secure against malicious encrypters is due to Goyal et al. [65] and relies on indistinguishability obfuscation (\(i\mathcal {O}\)) [15, 55] together with one-way functions. However, \(i\mathcal {O}\) is not a particularly appealing assumption since the security of existing \(i\mathcal {O}\) constructions either rely on an exponential number of assumptions [11, 14, 40, 80, 87], or on a polynomial set of assumptions but with an exponential loss in the security reduction [58, 59]. This shortcoming may even be inherent, as suggested by [57]. Moreover, numerous recent attacks on multilinear maps (the underlying primitive on which all candidate constructions \(i\mathcal {O}\) are based) [38, 42,43,44, 46, 47, 69, 77] have reduced the community’s confidence in the security of existing constructions of \(i\mathcal {O}\).
On the other hand, functional encryption for deterministic functions (with different levels of security and efficiency) can be realized from a variety of assumptions such as the existence of public-key encryption [63, 83], learning with errors [62], indistinguishability obfuscation [55, 86], multilinear maps [56], and more. Thus, there is a very large gap between the assumptions needed to build FE schemes for deterministic functionalities and those needed for randomized functionalities. Hence, it is important to ask:
Does extending public-key FE to support the richer class of randomized functions require strong additional assumptions such as \(i\mathcal {O}\)?
If there was a general transformation that we could apply to any FE scheme for deterministic functions, and obtain one that supported randomized functions, then we could leverage the extensive work on FE for the former to build FE for the latter with various capabilities and security guarantees. In this paper, we achieve exactly this. We bridge the gap between FE schemes for deterministic and randomized functionalities by showing that any general-purpose, simulation-secure FE scheme for deterministic functionalities can be extended to support randomized functionalities with security against malicious encrypters. Our generic transformation applies to any general-purpose, simulation-secure FE scheme with perfect correctness and only requires fairly mild additional assumptions (e.g., the decisional Diffie-Hellman (DDH) [29] and the RSA [30, 82] assumptions suffice). Moreover, our transformation is tight in the sense that it preserves the security of the underlying FE scheme. Because our transformation relies only on simple additional assumptions, future work in constructing general-purpose FE can primarily focus on handling deterministic functions rather than devising specialized constructions to support randomized functions. We now give an informal statement of our main theorem:
Theorem 1.1
(Main theorem, informal). Under standard number-theoretic assumptions, given any general-purpose, public-key functional encryption scheme for deterministic functions, there exists a general-purpose, public-key functional encryption scheme for randomized functions secure against malicious encrypters.
In this work, we focus on simulation-based notions of security for FE. As shown by several works [35, 79], game-based formulations of security are inadequate if the function family under consideration has some computational hiding properties. Moreover, as noted by Goyal et al. [65, Remark 2.8], the natural notion of indistinguishability-based security in the randomized setting can potentially introduce circularities in the definition and render it vacuous. Additionally, there are generic ways to boost the security of FE for deterministic functionalities from a game-based notion to a simulation-based notion [50].
We do note though that these generic indistinguishability-to-simulation boosting techniques sometimes incur a loss in expressiveness (due to the lower bounds associated with simulation-based security for FE [5, 7, 35, 79]). For instance, while it is possible to construct a general-purpose FE scheme secure against adversaries that makes an arbitrary (polynomial) number of secret key queries under an indistinguishability-based notion of security, an analogous construction is impossible under a simulation-based notion of security. We leave as an important open problem the development of a generic transformation like the one in Theorem 1.1 that applies to (public-key) FE schemes which satisfy indistinguishability-based notions of security and which does not incur the loss in expressiveness associated with first boosting to a simulation-based notion of security. Such a transformation is known in the secret-key setting [73], though it does not provide security against malicious encrypters.
Concrete instantiations. Instantiating Theorem 1.1 with existing FE schemes such as [55, 56, 64] and applying transformations like [10, 26, 50, 51] to boost correctness and/or security, we obtain several new public-key FE schemes for randomized functionalities with adaptive simulation-based security against malicious encrypters. For example, if we start with
-
the GVW scheme [63], we obtain a scheme secure under bounded collusions assuming the existence of semantically-secure public-key encryption and low-depth pseudorandom generators.
-
the GGHZ scheme [56], we obtain a scheme with best-possible simulation security relying on the polynomial hardness of concrete assumptions on composite-order multilinear maps [36, 48, 49].
-
the GGHRSW scheme [55], we obtain a scheme with best-possible simulation security from indistinguishability obfuscation and one-way functions.
The second and third schemes above should be contrasted with the one given by Goyal et al. [65], which achieves selective security assuming the existence of \(i\mathcal {O}\). We describe these instantiations in greater detail in Sect. 5.
Security definition. We also propose a strong simulation-based definition for security against malicious encrypters, strengthening the one given by Goyal et al. [65]. We first give a brief overview of their definition in Sect. 1.2 and then show why it does not capture an important class of correlation attacks. We also discuss the subtleties involved in extending their definition.
Our techniques. At a very high level, we must balance between two conflicting goals in order to achieve our strengthened security definition. On the one hand, the encryption and key-generation algorithms must be randomized to ensure that the decryption operation induces the correct output distribution, or even more fundamentally, that the scheme is semantically-secure. On the other hand, a malicious encrypter could exploit its freedom to choose the randomness when constructing ciphertexts in order to induce correlations when multiple ciphertexts or keys are operated upon. We overcome this barrier by employing ideas from disparate domains like related-key security for pseudorandom functions and deterministic encryption in a novel way. We discuss our transformation and the tools involved in more detail in Sect. 1.3.
We believe that our techniques could be used to extend the capability of new variants of functional encryption like multi-input FE [32, 61], hierarchical or delegatable FE [9, 39], and others so that they can support randomized functionalities with security against malicious encrypters as well.
Other related work. Recently, Komargodski et al. [73] studied the same question of extending standard FE to FE for randomized functionalities, but restricted to the private-key setting. They show that starting from any “function-private” secret-key FE scheme for deterministic functionalities, a secret-key FE scheme for randomized functionalities can be constructed (though without robustness against malicious encrypters). However, as we discuss below, it seems challenging to extend their techniques to work in the public-key setting:
-
The types of function-privacy that are achievable in the public-key setting are much more limited (primarily because the adversary can encrypt messages of its own and decrypt them in order to learn something about the underlying function keys). For instance, in the case of identity-based and subspace-membership encryption schemes, function privacy is only possible if we assume the function keys are drawn from certain high-entropy distributions [33, 34].
-
An adversary has limited control over ciphertexts in the private-key setting. For instance, since it cannot construct new ciphertexts by itself, it can only maul honestly-generated ciphertexts. In such a setting, attacks can often be prevented using zero-knowledge techniques.
Concurrent with [65], Alwen et al. [8] also explored the connections between FE for deterministic functionalities and FE for randomized functionalities. Their construction focused only on the simpler case of handling honest encrypters and moreover, they worked under an indistinguishability-based notion of security that has certain circularity problems (see the discussion in [65, Remark 2.8]) which might render it vacuous.
1.2 Security Against Malicious Encrypters
Simulation security. Informally, simulation security for FE schemes supporting randomized functionalities states that the output of any efficient adversary with a secret key for a randomized function f and an encryption of a message x can be simulated given only f(x; r), where the randomness r used to evaluate f is independently and uniformly sampled. Goyal et al. [65] extend this notion to include security against malicious encrypters by further requiring that the output of any efficient adversary holding a secret key for a function g and a (possibly dishonestly-generated) ciphertext \(\hat{\mathsf {ct}}\) should be simulatable given only \(g(\hat{x}; r)\), where \(\hat{x}\) is a message that is information-theoretically fixed by \(\hat{\mathsf {ct}}\), and the randomness r is uniform and unknown to the adversary. This captures the notion that a malicious encrypter is unable to influence the randomness used to evaluate the function during decryption.
More formally, in the simulation-based definitions of security [35, 79], an adversary tries to distinguish its interactions in a real world where ciphertexts and secret keys are generated according to the specifications of the FE scheme from its interactions in an ideal world where they are constructed by a simulator given only a minimal amount of information. To model security against malicious encrypters, Goyal et al. give the adversary access to a decryption oracle in the security game (similar to the formulation of IND-CCA2 security [81]) that takes as input a single ciphertext \(\mathsf {ct} \) along with a function f. In the real world, the challenger first extracts a secret key \(\mathsf {sk} _f\) for f and then outputs the decryption of \(\mathsf {ct} \) with \(\mathsf {sk} _f\). In the ideal world, the challenger invokes the simulator on \(\mathsf {ct} \). The simulator then outputs a value x (or a special symbol \(\bot \)), at which point the challenger replies to the adversary with an independently uniform value drawn from the distribution f(x) (or \(\bot \)).
Limitations of the existing definition. While the definition in [65] captures security against dishonest encrypters when dealing with deterministic functionalities, it does not fully capture the desired security goals in the randomized setting. Notably, the security definition only considers one ciphertext. However, when extending functional encryption to randomized functionalities, we are also interested in the joint distribution of multiple ciphertexts and secret keys. Thus, while it is the case that in any scheme satisfying the security definition in [65], the adversary cannot produce any single ciphertext that decrypts improperly, a malicious encrypter could still produce a collection of ciphertexts such that when the same key is used for decryption, the outputs are correlated. In the auditing application discussed before, it is imperative to prevent this type of attack, for otherwise, the integrity of the audit can be compromised.
Strengthening the definition. A natural way to strengthen Goyal et al.’s definition is to allow the decryption oracle to take in a set of (polynomially-many) ciphertexts along with a function f. In the real world, the challenger extracts a single key \(\mathsf {sk} _f\) for f and applies the decryption algorithm with \(\mathsf {sk} _f\) to each ciphertext. In the ideal world, the simulator is given the set of ciphertexts and is allowed to query the evaluation oracle \(\mathcal {O}_f\) once for each ciphertext submitted. On each query x, the oracle responds with a fresh evaluation of f(x). This direct extension, however, is too strong, and not achievable by any existing scheme. Suppose that an adversary could efficiently find two ciphertexts \(\mathsf {ct} _1 \ne \mathsf {ct} _2\) such that for all secret keys \(\mathsf {sk} \), \(\mathsf {Decrypt} (\mathsf {sk}, \mathsf {ct} _1) = \mathsf {Decrypt} (\mathsf {sk}, \mathsf {ct} _2)\), then it can easily distinguish the real and ideal distributions. When queried with \((f, (\mathsf {ct} _1, \mathsf {ct} _2))\), the decryption oracle always replies with two identical values in the real world irrespective of what f is. In the ideal world, however, it replies with two independent values since fresh randomness is used to evaluate f every time.
While we might want to preclude this type of behavior with our security definition, it is also one that arises naturally. For example, in both Goyal et al.’s and our construction, ciphertexts have the form \((\mathsf {ct} ', \pi )\) where \(\mathsf {ct} '\) is the ciphertext component that is actually combined with the decryption key and \(\pi \) is a proof of the well-formedness of \(\mathsf {ct} '\). Decryption proceeds only if the proof verifies. Since the proofs are randomized, an adversary can construct a valid ciphertext component \(\mathsf {ct} '\) and two distinct proofs \(\pi _1, \pi _2\) and submit the pair of ciphertexts \((\mathsf {ct} ', \pi _1)\) and \((\mathsf {ct} ', \pi _2)\) to the decryption oracle. Since \(\pi _1\) and \(\pi _2\) do not participate in the decryption process after verification, these two ciphertexts are effectively identical from the perspective of the decryption function. However, as noted above, an adversary that can construct such ciphertexts can trivially distinguish between the real and ideal worlds.
Intuitively, if the adversary submitted the same ciphertext multiple times in a decryption query, it does not make sense for the decryption oracle to respond with independently distributed outputs in the ideal experiment. The expected behavior is that the decryption oracle responds with the same value on all identical ciphertexts. In our setting, we allow for this behavior by considering a generalization of “ciphertext equivalence.” In particular, when the adversary submits a decryption query, the decryption oracle in the ideal experiment responds consistently on all equivalent ciphertexts that appear in the query. Formally, we capture this by introducing an efficiently-checkable equivalence relation on the ciphertext space of the FE scheme. For example, if the ciphertexts have the form \((\mathsf {ct} ', \pi )\), one valid equivalence relation on ciphertexts is equality of the \(\mathsf {ct} '\) components. To respond to a decryption query, the challenger first groups the ciphertexts according to their equivalence class, and responds consistently for all ciphertexts belonging to the same class. Thus, without loss of generality, it suffices to just consider adversaries whose decryption queries contain at most one representative from each equivalence class. We provide a more thorough discussion of our strengthened definition in Sect. 3.
As far as we understand, the Goyal et al. construction remains secure under our strengthened notion of security against malicious encrypters, but it was only shown to be selectively secure assuming the existence of \(i\mathcal {O}\) (and one-way functions).Footnote 1 Our transformation, on the other hand, provides a generic way of building adaptively-secure schemes from both \(i\mathcal {O}\) as well as plausibly weaker assumptions such as those on composite-order multilinear maps (Sect. 5). Finally, we note that not all schemes satisfying the Goyal et al. security notion satisfy our strengthened definition. In fact, a simplified version of our transformation yields a scheme secure under their original definition, but not our new definition (Remark 4.2).
Further strengthening the security definition. An important assumption that underlies all existing definitions of FE security against malicious encrypters is that the adversary cannot craft its “malicious” ciphertexts with (partial) knowledge of the secret key that will be used for decryption. More formally, in the security model, when the adversary submits a query to the decryption oracle, the secret key used for decryption is honestly generated and hidden from the adversary. An interesting problem is to formulate stronger notions of randomized FE where the adversary cannot induce correlations within ciphertexts even if it has some (limited) information about the function keys that will be used during decryption. At the same time, we stress that our existing notions already suffice for all of the applications we describe at the beginning of Sect. 1.
1.3 Overview of Our Generic Transformation
Our primary contribution in this work is giving a generic transformation from any simulation-secure general-purpose (public-key) FE schemeFootnote 2 for deterministic functionalities to a corresponding simulation-secure (public-key) FE scheme for randomized functionalities. In this section, we provide a brief overview of our generic transformation. The complete construction is given in Sect. 4.
Derandomization. Our starting point is the generic transformation of Alwen et al. [8] who use a pseudorandom function (PRF) to “derandomize” functionalities. In their construction, an encryption of a message x consists of an FE encryption of the pair (x, k) where k is a uniformly chosen PRF key. A secret key for a randomized functionality f is constructed by first choosing a random point t in the domain of the PRF and then extracting an FE secret key for the derandomized functionality \(g_t(x, k) = f(x ; \mathsf {PRF} (k, t))\), that is, the evaluation of f using randomness derived from the PRF. Evidently, this construction is not robust against malicious encrypters, since by reusing the same PRF key when constructing the ciphertexts, a malicious encrypter can induce correlations in the function evaluations. In fact, since the PRF key is fully under the control of the encrypter (who needs not sample it from the honest distribution), it is no longer possible to invoke PRF security to argue that \(\mathsf {PRF} (k, t)\) looks like a random string.
Secret sharing the PRF key. In our transformation, we start with the same derandomization approach. Since allowing the encrypter full control over the PRF key is problematic, we instead secret share the PRF key across the ciphertext and the decryption key. Suppose the key-space \(\mathcal {K}\) of the PRF forms a group under an operation \(\diamond \). As before, an encryption of a message x corresponds to an FE encryption of the pair (x, k), but now k is just a single share of the PRF key. To issue a key for f, another random key-share \(k'\) is chosen from \(\mathcal {K}\). The key \(\mathsf {sk} _f\) is then an FE key for the derandomized functionality \(f(x ; \mathsf {PRF} (k \diamond k', x))\). In this scheme, a malicious encrypter is able to influence the PRF key, but does not have full control. However, because the malicious encrypter can induce correlated PRF keys in the decryption queries, the usual notion of PRF security no longer suffices. Instead, we require the stronger property that the outputs of the PRF appear indistinguishable from random even if the adversary observes PRF outputs under related keys. Security against related-key attacks (RKA-security) for PRFs has been well-studied [1, 2, 18, 19, 22, 25, 72, 74] in the last few years, and for our particular application, a variant of the Naor-Reingold PRF is related-key secure for the class of group-induced transformations [18].
Applying deterministic encryption. By secret-sharing the PRF key and using a PRF secure against related-key attacks, we obtain robustness against malicious encrypters that only requests the decryption of unique (x, k) pairs (in this case, either k or x is unique, so by related-key security, the output of the PRF appears uniformly random). However, a malicious encrypter can encrypt the same pair (x, k) multiple times, using freshly generated randomness for the base FE scheme each time. Since each of these ciphertexts encrypt the same underlying value, in the real world, the adversary receives the same value from the decryption oracle. In the ideal world, the adversary receives independent draws from the distribution f(x). This problem arises because the adversary is able to choose additional randomness when constructing the ciphertexts that does not affect the output of the decryption algorithm. As such, it can construct ciphertexts that induce correlations in the outputs of the decryption process.
To protect against the adversary that encrypts the same (x, k) pair, we note that in the honest-encrypter setting, the messages that are encrypted have high entropy (since the key-share is sampled uniformly at random). Thus, instead of having the adversary choose its randomness for each encryption arbitrarily, we instead force the adversary to derive the randomness from the message. This is similar to what has been done when constructing deterministic public-key encryption [17, 20, 41, 54] and other primitives where it is important to restrict the adversary’s freedom when constructing ciphertexts [21]. Specifically, we sample a one-way permutation h on the key-space of the PRF, set the key-share in the ciphertext to h(k) where k is uniform over \(\mathcal {K}\), and then derive the randomness used in the encryption using a hard-core function \(\mathsf {hc}\) of h.Footnote 3 In addition, we require the adversary to include a non-interactive zero-knowledge (NIZK) argument that each ciphertext is properly constructed. In this way, we guarantee that for each pair (x, k), there is exactly a single ciphertext that is valid. By our admissibility requirement, the adversary is required to submit distinct ciphertexts (since matching ciphertexts belong to the same equivalence class). Thus, the underlying messages encrypted by each ciphertext in a decryption query necessarily differ in either the key-share or the message component. Security then follows by RKA-security.
2 Preliminaries
For \(n \ge 1\), we write [n] to denote the set of integers \(\left\{ 1, \ldots , n \right\} \). For bit-strings \(a, b \in \{0,1\} ^*\), we write \(a \Vert b\) to denote the concatenation of a and b. For a finite set S, we write \(x \xleftarrow {\textsc {r}}S\) to denote that x is sampled uniformly from S. We denote the evaluation of a randomized function f on input x with randomness r by f(x; r). We write \(\mathsf {Funs}[\mathcal {X}, \mathcal {Y}]\) to denote the set of all functions mapping from a domain \(\mathcal {X}\) to a range \(\mathcal {Y}\). We use \(\lambda \) to denote the security parameter. We say a function \(f(\lambda )\) is negligible in \(\lambda \), denoted by \(\mathsf {negl} (\lambda )\), if \(f(\lambda ) = o(1/\lambda ^c)\) for all \(c \in \mathbb {N}\). We say an algorithm is efficient if it runs in probabilistic polynomial time in the length of its input. We use \(\mathsf {poly}(\lambda )\) (or just \(\mathsf {poly}\)) to denote a quantity whose value is bounded by some polynomial in \(\lambda \).
We now formally define the tools we need to build FE schemes for randomized functionalities with security against malicious encrypters. In the full version of this paper [6], we also review the standard definitions of non-interactive zero-knowledge (NIZK) arguments of knowledge [28, 53, 67, 68] and one-way permutations [60].
2.1 RKA-Secure PRFs
We begin by reviewing the notion of related-key security [1, 2, 18, 19, 22, 25, 72, 74] for PRFs.
Definition 2.1
(RKA-Secure PRF [18, 22]). Let \(\mathcal {K}= \left\{ \mathcal {K}_\lambda \right\} _{\lambda \in \mathbb {N}}\), \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\), and \(\mathcal {Y}_\lambda = \left\{ \mathcal {Y}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be ensembles where \(\mathcal {K}_\lambda \), \(\mathcal {X}_\lambda \), and \(\mathcal {Y}_\lambda \) are finite sets and represent the key-space, domain, and range, respectively. Let \(F: \mathcal {K}_\lambda \times \mathcal {X}_\lambda \rightarrow \mathcal {Y}_\lambda \) be an efficiently computable family of pseudorandom functions. Let \(\varPhi \subseteq \mathsf {Funs}[\mathcal {K}_\lambda , \mathcal {K}_\lambda ]\) be a family of key derivation functions. We say that F is \(\varPhi \)-RKA secure if for all efficient, non-uniform adversaries \(\mathcal {A}\),

where the oracle \(\mathcal {O}(k, \cdot , \cdot )\) outputs \(F(\phi (k), x)\) on input \((\phi , x) \in \varPhi \times \mathcal {X}_\lambda \).
Definition 2.2
(Group Induced Classes [18, 76]). If the key space \(\mathcal {K}\) forms a group under an operation \(\diamond \), then the group-induced class \(\varPhi _\diamond \) is the class of functions \(\varPhi _\diamond = \left\{ \phi _b : a \in \mathcal {K}\mapsto a \diamond b \mid b \in \mathcal {K} \right\} \).
2.2 Functional Encryption
The notion of functional encryption was first formalized by Boneh et al. [35] and O’Neill [79]. The work of Boneh et al. begins with a natural indistinguishability-based notion of security. They then describe some example scenarios where these game-based definitions of security are inadequate (in the sense that a trivially insecure FE scheme can be proven secure under the standard game-based definition). To address these limitations, Boneh et al. defined a stronger simulation-based notion of security, which has subsequently been the subject of intense study [7, 50, 62, 63, 65]. In this work, we focus on this stronger security notion.
Let \(\mathcal {X}= \{ \mathcal {X}_\lambda \}_{\lambda \in \mathbb {N}}\) and \(\mathcal {Y}= \{\mathcal {Y}_{\lambda }\}_{\lambda \in \mathbb {N}}\) be ensembles where \(\mathcal {X}_{\lambda }\) and \(\mathcal {Y}_{\lambda }\) are finite sets and represent the input and output domains, respectively. Let \(\mathcal {F}= \{ \mathcal {F}_{\lambda }\}_{\lambda \in \mathbb {N}}\) be an ensemble where each \(\mathcal {F}_{\lambda }\) is a finite collection of (deterministic) functions from \(\mathcal {X}_\lambda \) to \(\mathcal {Y}_\lambda \). A functional encryption scheme \(\mathsf {FE}= (\mathsf {Setup}, \mathsf {Encrypt}, \mathsf {KeyGen}, \mathsf {Decrypt})\) for a (deterministic) family of functions \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) with domain \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\) and range \(\mathcal {Y}= \left\{ \mathcal {Y}_\lambda \right\} _{\lambda \in \mathbb {N}}\) is specified by the following four efficient algorithms:
-
Setup: \(\mathsf {Setup} (1^{\lambda })\) takes as input the security parameter \(\lambda \) and outputs a public key mpk and a master secret key \(\textsc {msk} \).
-
Encryption:
 takes as input the public key mpk and a message \(x \in \mathcal {X}_\lambda \), and outputs a ciphertext \(\mathsf {ct} \).
takes as input the public key mpk and a message \(x \in \mathcal {X}_\lambda \), and outputs a ciphertext \(\mathsf {ct} \). -
Key Generation: \(\mathsf {KeyGen} (\textsc {msk}, f)\) takes as input the master secret key \(\textsc {msk} \), a function \(f \in \mathcal {F}_\lambda \), and outputs a secret key \(\mathsf {sk} \).
-
Decryption:
 takes as input the public key mpk, a ciphertext \(\mathsf {ct} \), and a secret key \(\textsc {sk} \), and either outputs a string \(y \in \mathcal {Y}_\lambda \), or a special symbol \(\perp \). We can assume without loss of generality that this algorithm is deterministic.
takes as input the public key mpk, a ciphertext \(\mathsf {ct} \), and a secret key \(\textsc {sk} \), and either outputs a string \(y \in \mathcal {Y}_\lambda \), or a special symbol \(\perp \). We can assume without loss of generality that this algorithm is deterministic.
First, we state the correctness and security definitions for an FE scheme for deterministic functions.
Definition 2.3
(Perfect Correctness). A functional encryption scheme \(\mathsf {FE}= (\mathsf {Setup}, \mathsf {Encrypt}, \mathsf {KeyGen}, \mathsf {Decrypt})\) for a deterministic function family \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) with message space \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\) is perfectly correct if for all \(f \in \mathcal {F}_\lambda \), \(x \in \mathcal {X}_\lambda \),

Our simulation-based security definition is similar to the one in [7], except that we allow an adversary to submit a vector of messages in its challenge query (as opposed to a single message). Our definition is stronger than the one originally proposed by Boneh et al. [35] because we do not allow the simulator to rewind the adversary. On the other hand, it is weaker than [50, 63] since the simulator is allowed to program the public parameters and the responses to the pre-challenge secret key queries.
Definition 2.4
( \(\mathsf {SIM}\) -Security). An FE scheme \(\mathsf {FE}= (\mathsf {Setup}, \mathsf {Encrypt}, \mathsf {KeyGen}, \mathsf {Decrypt})\) for a deterministic function family \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in N}\) with message space \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\) is \(({q_1}, {q_c}, {q_2})\)-\(\mathsf {SIM}\) -secure if there exists an efficient simulator \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2, \mathcal {S}_3, \mathcal {S}_4)\) such that for all \(\mathsf {PPT} \) adversaries \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\), where \(\mathcal {A}_1\) makes at most \({q_1}\) oracle queries and \(\mathcal {A}_2\) makes at most \({q_2}\) oracle queries, the outputs of the following two experiments are computationally indistinguishable:

where \(\mathcal {O}_1(\textsc {msk}, \cdot )\) and \(\mathcal {O}_1'(\mathsf {st}', \cdot )\) are pre-challenge key-generation oracles, and \(\mathcal {O}_2(\textsc {msk}, \cdot )\) and \(\mathcal {O}_2'(\mathsf {st}', \cdot )\) are post-challenge ones. The oracles take a function \(f \in \mathcal {F}_\lambda \) as input and behave as follows:
-
Real experiment: Oracles \(\mathcal {O}_1(\textsc {msk},\cdot )\) and \(\mathcal {O}_2(\textsc {msk}, \cdot )\) both implement the key-generation function \(\mathsf {KeyGen} (\textsc {msk}, \cdot )\). The set \(\left\{ f \right\} \) is the (ordered) set of key queries made to \(\mathcal {O}_1(\textsc {msk}, \cdot )\) in the pre-challenge phase and to \(\mathcal {O}_2(\textsc {msk}, \cdot )\) in the post-challenge phase.
-
Ideal experiment: Oracles \(\mathcal {O}_1'(\mathsf {st}', \cdot )\) and \(\mathcal {O}_2'(\mathsf {st}', \cdot )\) are the simulator algorithms \(\mathcal {S}_2(\mathsf {st}', \cdot )\) and \(\mathcal {S}_4(\mathsf {st}', \cdot )\), respectively. On each invocation, the post-challenge simulator \(\mathcal {S}_4\) is also given oracle access to the ideal functionality \(\mathsf {KeyIdeal}(\mathbf {x},\cdot )\). The functionality \(\mathsf {KeyIdeal}\) accepts key queries \(f' \in \mathcal {F}_\lambda \) and returns \(f'(x_i)\) for every \(x_i\in \mathbf {x} \). Both algorithms \(\mathcal {S}_2\) and \(\mathcal {S}_4\) are stateful. In particular, after each invocation, they update their state \(\mathsf {st}'\), which is carried over to the next invocation. The (ordered) set \(\left\{ f' \right\} \) denotes the key queries made to \(\mathcal {O}_1'(\mathsf {st}', \cdot )\) in the pre-challenge phase, and the queries \(\mathcal {S}_4\) makes to \(\mathsf {KeyIdeal}\) in the post-challenge phase.
3 Functional Encryption for Randomized Functionalities
In a functional encryption scheme that supports randomized functionalities, the function class \(\mathcal {F}_\lambda \) is expanded to include randomized functions from the domain \(\mathcal {X}_\lambda \) to the range \(\mathcal {Y}_\lambda \). Thus, we now view the functions \(f \in \mathcal {F}_\lambda \) as taking as input a domain element \(x \in \mathcal {X}_\lambda \) and randomness \(r \in \mathcal {R}_\lambda \), where \(\mathcal {R}= \left\{ \mathcal {R}_\lambda \right\} _{\lambda \in \mathbb {N}}\) is the randomness space. As in the deterministic setting, the functional encryption scheme still consists of the same four algorithms, but the correctness and security requirements differ substantially.
For instance, in the randomized setting, whenever the decryption algorithm is invoked on a fresh encryption of a message x or a fresh key for a function f, we would expect that the resulting output is indistinguishable from evaluating f(x) with fresh randomness. Moreover, this property should hold regardless of the number of ciphertexts and keys one has. To capture this property, the correctness requirement for an FE scheme supporting randomized functions must consider multiple keys and ciphertexts. In contrast, in the deterministic setting, correctness for a single key-ciphertext pair implies correctness for multiple ciphertexts.
Definition 3.1
(Correctness). A functional encryption scheme \(\mathsf {rFE} = (\mathsf {Setup}, \mathsf {Encrypt}, \mathsf {KeyGen}, \mathsf {Decrypt})\) for a randomized function family \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) over a message space \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\) and a randomness space \(\mathcal {R}= \left\{ \mathcal {R}_\lambda \right\} _{\lambda \in \mathbb {N}}\) is correct if for every polynomial \(n=n(\lambda )\), every \(\mathbf {f} \in \mathcal {F}_\lambda ^{n}\) and every \(\mathbf {x} \in \mathcal {X}_\lambda ^{n}\), the following two distributions are computationally indistinguishable:
-
1.
Real: \(\left\{ \mathsf {Decrypt} \left( \textsc {mpk}, \mathsf {sk} _i, \mathsf {ct} _j\right) \right\} _{i,j \in [n]}\), where:
-
\((\textsc {mpk}, \textsc {msk}) \leftarrow \mathsf {Setup} (1^\lambda )\);
-
\(\mathsf {sk} _i \leftarrow \mathsf {KeyGen} (\textsc {msk}, f_i)\) for \(i \in [n]\);
-
\(\mathsf {ct} _j \leftarrow \mathsf {Encrypt} (\textsc {mpk}, x_j)\) for \(j \in [n]\).
-
-
2.
Ideal: \(\left\{ f_i\left( x_j;r_{i,j} \right) \right\} _{i, j \in [n]}\) where \(r_{i,j} \xleftarrow {\textsc {r}}\mathcal {R}_\lambda \).
As discussed in Sect. 1.2, formalizing and achieving security against malicious encrypters in the randomized setting is considerably harder than in the deterministic case. A decryption oracle that takes a single ciphertext along with a function f does not suffice in the randomized setting, since an adversary could still produce a collection of ciphertexts such that when the same key is used for decryption, the outputs are correlated. We could strengthen the security definition by allowing the adversary to query with multiple ciphertexts instead of just one, but as noted in Sect. 1.2, this direct extension is too strong. In order to obtain a realizable definition, we instead restrict the adversary to submit ciphertexts that do not behave in the same way. This is formally captured by defining an admissible equivalence relation on the space of ciphertexts.
Definition 3.2
(Admissible Relation on Ciphertext Space). Let \(\mathsf {rFE} = (\mathsf {Setup}, \mathsf {Encrypt}, \mathsf {KeyGen}, \mathsf {Decrypt})\) be an FE scheme for randomized functions with ciphertext space \(\mathcal {T}= \left\{ \mathcal {T}_\lambda \right\} _{\lambda \in \mathbb {N}}\). Let \(\sim \) be an equivalence relation on \(\mathcal {T}\). We say that \(\sim \) is admissible if \(\sim \) is efficiently checkable and for all \(\lambda \in \mathbb {N} \), all \((\textsc {mpk}, \textsc {msk})\) output by \(\mathsf {Setup} (1^\lambda )\), all secret keys \(\mathsf {sk} \) output by \(\mathsf {KeyGen} (\textsc {msk}, \cdot )\), and all ciphertexts \(\mathsf {ct} _1, \mathsf {ct} _2 \in \mathcal {T}_\lambda \), if \(\mathsf {ct} _1 \sim \mathsf {ct} _2\), then one of the following holds:
-
\(\mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \mathsf {ct} _1) =\ \perp \) or \(\mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \mathsf {ct} _2) =\ \perp \).
-
\(\mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \mathsf {ct} _1) = \mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \mathsf {ct} _2)\).
We remark here that there always exists an admissible equivalence relation on the ciphertext space, namely, the equality relation. Next, we define our strengthened requirement for security against malicious encrypters in the randomized setting. Like [65], we build on the usual simulation-based definition of security for functional encryption (Definition 2.4) by providing the adversary access to a decryption oracle. The definition we present here differs from that by Goyal et al. in two key respects. First, the adversary can submit multiple ciphertexts to the decryption oracle, and second, the adversary is allowed to choose its challenge messages adaptively (that is, after seeing the public parameters and making secret key queries).
Definition 3.3
( \(\mathsf {SIM}\) -security for \(\mathsf {rFE} \) ). Let \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a randomized function family over a domain \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\) and randomness space \(\mathcal {R}= \left\{ \mathcal {R}_\lambda \right\} _{\lambda \in \mathbb {N}}\). Let \(\mathsf {rFE} = (\mathsf {Setup}, \mathsf {Encrypt}, \mathsf {KeyGen}, \mathsf {Decrypt})\) be a randomized functional encryption scheme for \(\mathcal {F}\) with ciphertext space \(\mathcal {T}\). Then, we say that \(\mathsf {rFE} \) is \(({q_1}, {q_c}, {q_2})\)-\(\mathsf {SIM}\) -secure against malicious encrypters if there exists an admissible equivalence relation \(\sim \) associated with \(\mathcal {T}\) and there exists an efficient simulator \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2, \mathcal {S}_3, \mathcal {S}_4, \mathcal {S}_5)\) such that for all efficient adversaries \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\) where \(\mathcal {A}_1\) makes at most \({q_1}\) key-generation queries and \(\mathcal {A}_2\) makes at most \({q_2}\) key-generation queries, the outputs of the following experiments are computationally indistinguishable:Footnote 4

where the oracles \(\mathcal {O}_1(\textsc {msk}, \cdot )\), \(\mathcal {O}_1'(\mathsf {st}', \cdot )\), \(\mathcal {O}_2(\textsc {msk}, \cdot )\), and \(\mathcal {O}_2'(\mathsf {st}', \cdot )\) are the analogs of the key-generation oracles from Definition 2.4:
-
Real experiment: Oracles \(\mathcal {O}_1(\textsc {msk},\cdot )\) and \(\mathcal {O}_2(\textsc {msk}, \cdot )\) implement \(\mathsf {KeyGen} (\textsc {msk}, \cdot )\), and \(\left\{ f \right\} \) is the (ordered) set of key queries made to oracles \(\mathcal {O}_1(\textsc {msk}, \cdot )\) and \(\mathcal {O}_2(\textsc {msk}, \cdot )\).
-
Ideal experiment: Oracles \(\mathcal {O}_1'(\mathsf {st}', \cdot )\) and \(\mathcal {O}_2'(\mathsf {st}', \cdot )\) are the simulator algorithms \(\mathcal {S}_2(\mathsf {st}', \cdot )\) and \(\mathcal {S}_4(\mathsf {st}', \cdot )\), respectively. The simulator \(\mathcal {S}_4\) is given oracle access to \(\mathsf {KeyIdeal}(\mathbf {x},\cdot )\), which on input a function \(f' \in \mathcal {F}_\lambda \), outputs \(f'(x_i ; r_i)\) for every \(x_i\in \mathbf {x} \) and \(r_i \xleftarrow {\textsc {r}}\mathcal {R}_\lambda \). The (ordered) set \(\left\{ f' \right\} \) consists of the key queries made to \(\mathcal {O}_1'(\mathsf {st}', \cdot )\), and the queries \(\mathcal {S}_4\) makes to \(\mathsf {KeyIdeal}\).
Oracles \(\mathcal {O}_3(\textsc {msk}, \cdot , \cdot )\) and \(\mathcal {O}_3'(\mathsf {st}', \cdot , \cdot )\), are the decryption oracles that take inputs of the form (g, C) where \(g \in \mathcal {F}_\lambda \) and \(C = \left\{ \mathsf {ct} _i \right\} _{i \in [m]}\) is a collection of \(m = \mathsf {poly}(\lambda )\) ciphertexts. For queries made in the post-challenge phase, we additionally require that \(\mathsf {ct} _i^* \notin C\) for all \(i \in [{q_c}]\). Without loss of generality, we assume that for all \(i, j \in [m]\), if \(i \ne j\), then \(\mathsf {ct} _i \not \sim \mathsf {ct} _j\). In other words, the set C contains at most one representative from each equivalence class of ciphertexts.
-
Real experiment: On input (g, C), \(\mathcal {O}_3\) computes \(\mathsf {sk} _g \leftarrow \mathsf {KeyGen} (\textsc {msk}, g)\). For \(i \in [m]\), it sets \(y_i = \mathsf {Decrypt} (\mathsf {sk} _g, \mathsf {ct} _i)\) and replies with the ordered set \(\left\{ y_i \right\} _{i \in [m]}\). The (ordered) set \(\left\{ g \right\} \) denotes the functions that appear in the decryption queries of \(\mathcal {A}_2\) and \(\left\{ y \right\} \) denotes the set of responses of \(\mathcal {O}_3\).
-
Ideal experiment: On input \((g', C')\), \(\mathcal {O}_3'\) does the following:
-
1.
For each \(\mathsf {ct} _i' \in C'\), invoke the simulator algorithm \(\mathcal {S}_5(\mathsf {st}', \mathsf {ct} _i')\) to obtain a value \(x_i \in \mathcal {X}_\lambda \cup \left\{ \perp \right\} \). Note that \(\mathcal {S}_5\) is also stateful.
-
2.
For each \(i \in [m]\), if \(x_i = \ \perp \), then the oracle sets \(y_i' = \ \perp \). Otherwise, the oracle choose \(r_i \xleftarrow {\textsc {r}}\mathcal {R}_\lambda \) and sets \(y_i' = g'(x_i ; r_i)\).
-
3.
Output the ordered set of responses \(\left\{ y_i' \right\} _{i \in [m]}\).
The (ordered) set \(\left\{ g' \right\} \) denotes the functions that appear in the decryption queries of \(\mathcal {A}_2\) and \(\left\{ y' \right\} \) denotes the outputs of \(\mathcal {O}_3'\).
-
1.
Remark 3.4
Note that the above definition does not put any constraint on the equivalence relation used to prove security. Indeed, any equivalence relation—as long as it is admissible—suffices because if two ciphertexts \(\mathsf {ct} _1, \mathsf {ct} _2\) fall into the same equivalence class, they essentially behave identically (for all parameters output by \(\mathsf {Setup} \) and all keys \(\mathsf {sk} \) output by \(\mathsf {KeyGen} \), decrypting \(\mathsf {ct} _1, \mathsf {ct} _2\) with \(\mathsf {sk} \) must either give the same result, or one of the ciphertexts is invalid). Thus, by restricting an adversary to providing at most one ciphertext from each equivalence class in each decryption query, we are only preventing it from submitting ciphertexts which are effectively equivalent to the decryption oracle.
Remark 3.5
One could also consider an ideal model where the adversary is allowed to submit equivalent ciphertexts to the decryption oracle (at the cost of making the security game more cumbersome). In the extreme case where the adversary submits identical ciphertexts, it does not make sense for the decryption oracle to respond independently on each of them—rather, it should respond in a consistent way. In constructions of randomized FE that provide malicious security, there naturally arise ciphertexts that are not identical as bit-strings, but are identical from the perspective of the decryption function. In these cases, the expected behavior of the ideal functionality should again be to provide consistent, rather than independent, responses.
Consider now an adversary that submits a function f and a set C of ciphertexts to the decryption oracle, where some ciphertexts in C belong to the same equivalence class. To respond, the challenger can first group these ciphertexts by equivalence class. For each equivalence class \(C'\) of ciphertexts in C, the challenger invokes the simulator on \(C'\). On input the collection \(C'\), the simulator outputs a single value x and indicates which ciphertexts in \(C'\), if any, are valid. If \(C'\) contains at least one valid ciphertext, the challenger samples a value z from the output distribution of f(x). It then replies with the same value z on all ciphertexts marked valid by the simulator, and \(\bot \) on all ciphertexts marked invalid. (This is a natural generalization of how we would expect the decryption oracle to behave had the adversary submitted identical ciphertexts to it.)
4 Our Generic Transformation
Let \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a randomized function class over a domain \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\), randomness space \(\mathcal {R}= \left\{ \mathcal {R}_\lambda \right\} _{\lambda \in \mathbb {N}}\) and range \(\mathcal {Y}= \left\{ \mathcal {Y}_\lambda \right\} _{\lambda \in \mathbb {N}}\). We give the formal description of our functional encryption scheme for \(\mathcal {F}\) (based on any general-purpose FE scheme for deterministic functionalities) in Fig. 1. All the necessary cryptographic primitives are also shown in Fig. 1.
Generic construction of a functional encryption scheme for any family of randomized functions \(\mathcal {F}= \left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) over a domain \(\mathcal {X}= \left\{ \mathcal {X}_\lambda \right\} _{\lambda \in \mathbb {N}}\), randomness space \(\mathcal {R}= \left\{ \mathcal {R}_\lambda \right\} _{\lambda \in \mathbb {N}}\) and range \(\mathcal {Y}= \left\{ \mathcal {Y}_\lambda \right\} _{\lambda \in \mathbb {N}}\).
Theorem 4.1
If (1) \(\mathsf {NIZK} \) is a simulation-sound extractable non-interactive zero-knowledge argument, (2) \(\mathsf {PRF} \) is a \(\varPhi \)-RKA secure pseudorandom function where \(\varPhi \) is group-induced, (3) \(\mathsf {OWP}\) is a family of one-way permutations with hard-core function \(\mathsf {hc}\), and (4) \(\mathsf {FE}\) is a perfectly-correct \(({q_1}, {q_c}, {q_2})\)-\(\mathsf {SIM}\) secure functional encryption scheme for the derandomized class \(\mathcal {G}_\mathcal {F}\), then \(\mathsf {rFE} \) is \(({q_1}, {q_c}, {q_2})\)-\(\mathsf {SIM}\) secure against malicious encrypters for the class \(\mathcal {F}\) of randomized functions.
Before proceeding with the proof of Theorem 4.1, we remark that our strengthened definition of security against malicious encrypters (Definition 3.3) is indeed stronger than the original definition by Goyal et al. [65].
Remark 4.2
A simpler version of our generic transformation where we only secret share the RKA-secure PRF key used for derandomization and include a NIZK argument can be shown to satisfy the Goyal et al. [65] definition of security against malicious encrypters, but not our strengthened definition (Definition 3.3). In particular, if the randomness used in the base FE encryption is under the control of the adversary, a malicious encrypter can construct two fresh encryptions (under the base FE scheme) of the same (x, k) pair and submit them to the decryption oracle. In the real world, the outputs are identical (since the ciphertexts encrypt identical messages), but in the ideal world, the oracle replies with two independent outputs. This is an admissible query because if the underlying FE scheme is secure, one cannot efficiently decide whether two FE ciphertexts encrypt the same value without knowing any scheme parameters. But because each individual output is still properly distributed (by RKA-security of the PRF), security still holds in the Goyal et al. model.
We now proceed to give a proof of Theorem 4.1 in Sects. 4.1 and 4.2. In the full version [6], we also show that our transformed scheme is correct.
4.1 Proof of Theorem 4.1: Description of Simulator
To prove Theorem 4.1, and show that \(\mathsf {rFE} \) is secure in the sense of Definition 3.3, we first define an equivalence relation \(\sim \) over the ciphertext space \(\mathcal {T}= \left\{ \mathcal {T}_\lambda \right\} _{\lambda \in \mathbb {N}}\). Take two ciphertexts \(\mathsf {ct} _1, \mathsf {ct} _2 \in \mathcal {T}_\lambda \), and write \(\mathsf {ct} _1 = (\mathsf {ct} _1', \pi _1)\) and \(\mathsf {ct} _2 = (\mathsf {ct} _2', \pi _2)\). We say that \(\mathsf {ct} _1 \sim \mathsf {ct} _2\) if \(\mathsf {ct} _1' = \mathsf {ct} _2'\).
Certainly, \(\sim \) is an efficiently-checkable equivalence relation over \(\mathcal {T}_\lambda \). For the second admissibility condition, take any \((\textsc {mpk}, \textsc {msk})\) output by \(\mathsf {Setup} \) and any \(\mathsf {sk} \) output by \(\mathsf {KeyGen} (\textsc {msk}, \cdot )\). Suppose moreover that \(\mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \mathsf {ct} _1) \ne \ \perp \ \ne \mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \mathsf {ct} _2)\). Then, by definition of \(\mathsf {Decrypt} (\textsc {mpk}, \mathsf {sk}, \cdot )\),
where mpk’ is the master public key for the underlying FE scheme (included in mpk). The second equivalence follows since \(\mathsf {ct} _1' = \mathsf {ct} _2'\).
We now describe our ideal-world simulator \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2, \mathcal {S}_3, \mathcal {S}_4, \mathcal {S}_5)\). Let \(\mathcal {S}^{(\textsc {fe})}= (\mathcal {S}^{(\textsc {fe})}_1, \mathcal {S}^{(\textsc {fe})}_2, \mathcal {S}^{(\textsc {fe})}_3, \mathcal {S}^{(\textsc {fe})}_4)\) be the simulator for the underlying FE scheme for deterministic functionalities. Let \(\mathcal {S}^{(\textsc {nizk})}= (\mathcal {S}^{(\textsc {nizk})}_1, \mathcal {S}^{(\textsc {nizk})}_2)\) and \(\mathcal {E}^{(\textsc {nizk})}= (\mathcal {E}^{(\textsc {nizk})}_1, \mathcal {E}^{(\textsc {nizk})}_2)\) be the simulation and extraction algorithms, respectively, for the NIZK argument system.
Algorithm \(\mathcal {S}_1(1^\lambda )\) . \(\mathcal {S}_1\) simulates the setup procedure. On input a security parameter \(1^\lambda \), it operates as follows:
-
1.
Invoke \(\mathcal {S}^{(\textsc {fe})}_1(1^\lambda )\) to obtain a master public key mpk’ and some state \(\mathsf {st}^{(\textsc {fe})}\).
-
2.
Invoke \(\mathcal {E}^{(\textsc {nizk})}_1(1^\lambda )\) to obtain a \(\mathrm {CRS}\) \(\sigma \), a simulation trapdoor \(\tau \), and an extraction trapdoor \(\xi \).
-
3.
Sample a one-way permutation \(t \leftarrow \mathsf {OWP}.\mathsf {Setup} (1^\lambda )\) and define \(h_t(\cdot ) = \mathsf {OWP}.\mathsf {Eval}(t, \cdot )\).
-
4.
Set
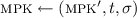 and
and  . Output \((\textsc {mpk}, \mathsf {st})\).
. Output \((\textsc {mpk}, \mathsf {st})\).
Algorithm \(\mathcal {S}_2(\mathsf {st}_0, f)\) . \(\mathcal {S}_2\) simulates the pre-challenge key-generation queries. On input a state \(\mathsf {st}_0 = (\mathsf {st}^{(\textsc {fe})}_0, \textsc {mpk}, \tau , \xi )\) and a function \(f \in \mathcal {F}_\lambda \), it operates as follows:
-
1.
Choose a random key \(k \xleftarrow {\textsc {r}}\mathcal {K}_\lambda \) and construct the derandomized function \(g_k^f\) as defined in Eq. (1).
-
2.
Invoke \(\mathcal {S}^{(\textsc {fe})}_2(\mathsf {st}^{(\textsc {fe})}_0, g_k^f)\) to obtain a key \(\mathsf {sk} \) and an updated state \(\mathsf {st}^{(\textsc {fe})}_1\).
-
3.
Output the key \(\mathsf {sk} \) and an updated state \(\mathsf {st}_1 = (\mathsf {st}^{(\textsc {fe})}_1, \textsc {mpk}, \tau , \xi )\).
Algorithm  . \(\mathcal {S}_3\) constructs the challenge ciphertexts. Let \(\mathbf {x} = (x_1, x_2, \ldots , x_{q_c})\) be the challenge messages the adversary outputs. On input a state
. \(\mathcal {S}_3\) constructs the challenge ciphertexts. Let \(\mathbf {x} = (x_1, x_2, \ldots , x_{q_c})\) be the challenge messages the adversary outputs. On input a state  , where
, where  , and a collection of function evaluations \(\left\{ y_{ij} \right\} _{i \in [{q_c}], j \in [{q_1}]}\), \(\mathcal {S}_3\) operates as follows:
, and a collection of function evaluations \(\left\{ y_{ij} \right\} _{i \in [{q_c}], j \in [{q_1}]}\), \(\mathcal {S}_3\) operates as follows:
-
1.
Invoke \(\mathcal {S}^{(\textsc {fe})}_3(\mathsf {st}^{(\textsc {fe})}_0, \left\{ y_{ij} \right\} _{i \in [{q_c}], j \in [{q_1}]})\) to obtain a set of ciphertexts \(\left\{ \mathsf {ct} _i' \right\} _{i \in [{q_c}]}\) and an updated state \(\mathsf {st}^{(\textsc {fe})}_1\).
-
2.
For \(i \in [{q_c}]\), let \(s_i\) be the statement
$$\begin{aligned} \exists x, k : \mathsf {ct} _i' = \mathsf {FE}.\mathsf {Encrypt} (\textsc {mpk} ', (x, h_t(k)); \mathsf {hc}(k)). \end{aligned}$$(3)Using the trapdoor \(\tau \) in \(\mathsf {st}_0\), simulate an argument \(\pi _i \leftarrow \mathcal {S}^{(\textsc {nizk})}_2(\sigma , \tau , s_i)\), and set \(\mathsf {ct} _i^* = (\mathsf {ct} _i', \pi _i)\).
-
3.
Output the challenge ciphertexts \(\left\{ \mathsf {ct} _i^* \right\} _{i \in [{q_c}]}\) and the updated state \(\mathsf {st}_1 = (\mathsf {st}^{(\textsc {fe})}_1, \textsc {mpk}, \tau , \xi )\).
Algorithm \(\mathcal {S}_4(\mathsf {st}_0, f)\) . \(\mathcal {S}_4\) simulates the post-challenge key-generation queries with help from the ideal functionality \(\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\). On input a state \(\mathsf {st}_0 = (\mathsf {st}^{(\textsc {fe})}_0, \textsc {mpk}, \tau , \xi )\) and a function \(f \in \mathcal {F}_\lambda \), it operates as follows:
-
1.
Choose a random key \(k \xleftarrow {\textsc {r}}\mathcal {K}\), and construct the derandomized function \(g_k^f\) as defined in Eq. (1).
-
2.
Invoke \(\mathcal {S}^{(\textsc {fe})}_4(\mathsf {st}^{(\textsc {fe})}_0, g_k^f)\). Here, \(\mathcal {S}_4\) also simulates the \(\mathsf {FE}.\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\) oracle for \(\mathcal {S}^{(\textsc {fe})}_4\). Specifically, when \(\mathcal {S}^{(\textsc {fe})}_4\) makes a query of the form \(g_{k'}^{f'}\) to \(\mathsf {FE}.\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\), \(\mathcal {S}_4\) queries its own oracle \(\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\) on \(f'\) to obtain values \(z_i\) for each \(i \in [{q_c}]\).Footnote 5 It replies to \(\mathcal {S}^{(\textsc {fe})}_4\) with the value \(z_i\) for all \(i \in [{q_c}]\). Let \(\mathsf {sk} \) and \(\mathsf {st}^{(\textsc {fe})}_1\) be the output of \(\mathcal {S}^{(\textsc {fe})}_4\).
-
3.
Output the key \(\mathsf {sk} \) and an updated state \(\mathsf {st}_1 = (\mathsf {st}^{(\textsc {fe})}_1, \textsc {mpk}, \tau , \xi )\).
Algorithm \(\mathcal {S}_5(\mathsf {st}, \mathsf {ct})\). \(\mathcal {S}_5\) handles the decryption queries. On input a state \(\mathsf {st}= (\mathsf {st}^{(\textsc {fe})}, \textsc {mpk}, \tau , \xi )\) and a ciphertext \(\mathsf {ct} \), it proceeds as follows:Footnote 6
-
1.
Parse mpk as
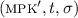 and \(\mathsf {ct} \) as \((\mathsf {ct} ', \pi )\). Let s be the statement $$\begin{aligned} \exists x, k : \mathsf {ct} = \mathsf {FE}.\mathsf {Encrypt} (\textsc {mpk} ', (x, h_t(k)); \mathsf {hc}(k)). \end{aligned}$$
and \(\mathsf {ct} \) as \((\mathsf {ct} ', \pi )\). Let s be the statement $$\begin{aligned} \exists x, k : \mathsf {ct} = \mathsf {FE}.\mathsf {Encrypt} (\textsc {mpk} ', (x, h_t(k)); \mathsf {hc}(k)). \end{aligned}$$If \(\mathsf {NIZK}.\mathsf {Verify} (\sigma , s, \pi ) = 0\), then stop and output \(\perp \).
-
2.
Otherwise, invoke the extractor \(\mathcal {E}^{(\textsc {nizk})}_2(\sigma , \xi , s, \pi )\) using the extraction trapdoor \(\xi \) to obtain a witness \((x, k) \in \mathcal {X}_\lambda \times \mathcal {K}_\lambda \). Output x and state \(\mathsf {st}\).
4.2 Proof of Theorem 4.1: Hybrid Argument
To prove security, we proceed via a series of hybrid experiments between an adversary \(\mathcal {A}\) and a challenger. Each experiment consists of the following phases:
-
1.
Setup phase. The challenger begins by generating the public parameters of the \(\mathsf {rFE} \) scheme, and sends those to the adversary \(\mathcal {A}\).
-
2.
Pre-challenge queries. In this phase of the experiment, \(\mathcal {A}\) can issue key-generation queries of the form \(f \in \mathcal {F}_\lambda \) and decryption queries of the form \((f, C) \in \mathcal {F}_\lambda \times \mathcal {T}_\lambda ^m\) to the challenger. For all decryption queries (f, C), we require that for any \(\mathsf {ct} _i, \mathsf {ct} _j \in C\), \(\mathsf {ct} _i \not \sim \mathsf {ct} _j\) if \(i \ne j\). In other words, each set of ciphertexts C can contain at most one representative from each equivalence class.
-
3.
Challenge phase. The adversary \(\mathcal {A}\) submits a vector of messages \(\mathbf {x} \in \mathcal {X}_\lambda ^{q_c}\) to the challenger, who replies with ciphertexts \(\left\{ \mathsf {ct} ^*_i \right\} _{i \in [{q_c}]}\).
-
4.
Post-challenge queries. In this phase, \(\mathcal {A}\) is again allowed to issue key-generation and decryption queries, with a further restriction that no decryption query can contain any of the challenge ciphertexts (i.e., for any query (f, C), \(\mathsf {ct} _i^* \notin C\) for all \(i \in [q_c]\)).
-
5.
Output. At the end of the experiment, \(\mathcal {A}\) outputs a bit \(b \in \{0,1\} \).
We now describe our sequence of hybrid experiments. Note that in defining a new hybrid, we only describe the phases that differ from the previous one. If one or more of the above phases are omitted, the reader should assume that they are exactly the same as in the previous hybrid.
 In this experiment, the challenger responds to \(\mathcal {A}\) according to the specification of the real experiment \(\mathsf {Real}_\mathcal {A}^\mathsf {rFE} \).
In this experiment, the challenger responds to \(\mathcal {A}\) according to the specification of the real experiment \(\mathsf {Real}_\mathcal {A}^\mathsf {rFE} \).
-
Setup phase. The challenger samples \((\textsc {mpk}, \textsc {msk}) \leftarrow \mathsf {Setup} (1^\lambda )\) and sends mpk to \(\mathcal {A}\).
-
Pre-challenge queries. The challenger responds to each query as follows:
-
Key-generation queries. On a key-generation query \(f \in \mathcal {F}_\lambda \), the challenger responds with \(\mathsf {KeyGen} (\textsc {msk}, f)\).
-
Decryption queries. On a decryption query \((f, C) \in \mathcal {F}_\lambda \times \mathcal {T}_\lambda ^m\), the challenger samples \(\mathsf {sk} \leftarrow \mathsf {KeyGen} (\textsc {msk}, f)\). For each \(\mathsf {ct} _i \in C\), the challenger sets \(y_i = \mathsf {Decrypt} (\mathsf {sk}, \mathsf {ct} _i)\), and sends \(\left\{ y_i \right\} _{i \in [m]}\) to the adversary.
-
-
Challenge phase. When the challenger receives a vector \(\mathbf {x} \in \mathcal {X}_\lambda ^{q_c}\), it sets \(\mathsf {ct} _i^* = \mathsf {Encrypt} (\textsc {mpk}, x_i)\) for each \(i \in [{q_c}]\) and replies to \(\mathcal {A}\) with \(\left\{ \mathsf {ct} _i^* \right\} _{i \in [{q_c}]}\).
-
Post-challenge queries. This is identical to the pre-challenge phase.
 This is the same as \(\mathsf {Hyb}_0\), except the challenger simulates the \(\mathrm {CRS}\) in the setup phase and the arguments in the challenge ciphertexts in the challenge phase. Let \(\mathcal {S}^{(\textsc {nizk})}= (\mathcal {S}^{(\textsc {nizk})}_1, \mathcal {S}^{(\textsc {nizk})}_2)\) be the simulator for \(\mathsf {NIZK} \). Note that we omit the description of the pre- and post-challenge phases in the description below because they are identical to those phases in \(\mathsf {Hyb}_0\).
This is the same as \(\mathsf {Hyb}_0\), except the challenger simulates the \(\mathrm {CRS}\) in the setup phase and the arguments in the challenge ciphertexts in the challenge phase. Let \(\mathcal {S}^{(\textsc {nizk})}= (\mathcal {S}^{(\textsc {nizk})}_1, \mathcal {S}^{(\textsc {nizk})}_2)\) be the simulator for \(\mathsf {NIZK} \). Note that we omit the description of the pre- and post-challenge phases in the description below because they are identical to those phases in \(\mathsf {Hyb}_0\).
-
Setup phase. The challenger generates the public parameters as in \(\mathsf {Hyb}_0\), except it uses \(\mathcal {S}^{(\textsc {nizk})}_1\) to generate the \(\mathrm {CRS}\). Specifically, it does the following:
-
1.
Sample
 .
. -
2.
Run \(\mathcal {S}^{(\textsc {nizk})}_1(1^\lambda )\) to obtain a \(\mathrm {CRS}\) \(\sigma \) and a simulation trapdoor \(\tau \).
-
3.
Sample a one-way permutation \(t \leftarrow \mathsf {OWP}.\mathsf {Setup} (1^\lambda )\), and define \(h_t(\cdot ) = \mathsf {OWP}.\mathsf {Eval}(t, \cdot )\).
-
4.
Set
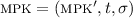 and send mpk to \(\mathcal {A}\).
and send mpk to \(\mathcal {A}\).
-
1.
-
Challenge phase. The challenger constructs the challenge ciphertexts as in \(\mathsf {Hyb}_0\), except it uses \(\mathcal {S}^{(\textsc {nizk})}_2\) to simulate the NIZK arguments. Let \(\mathbf {x} \in \mathcal {X}_\lambda ^{q_c}\) be the adversary’s challenge. For \(i \in [{q_c}]\), the challenger samples \(k_i^* \xleftarrow {\textsc {r}}\mathcal {K}_\lambda \) and sets
 . It invokes \(\mathcal {S}^{(\textsc {nizk})}_2(\sigma , \tau , s_i)\) to obtain a simulated argument \(\pi _i\), where \(s_i\) is the statement in Eq. (3). Finally, it sets \(\mathsf {ct} _i^* = (\mathsf {ct} _i', \pi _i)\) and sends \(\left\{ \mathsf {ct} _i^* \right\} _{i \in [{q_c}]}\) to \(\mathcal {A}\).
. It invokes \(\mathcal {S}^{(\textsc {nizk})}_2(\sigma , \tau , s_i)\) to obtain a simulated argument \(\pi _i\), where \(s_i\) is the statement in Eq. (3). Finally, it sets \(\mathsf {ct} _i^* = (\mathsf {ct} _i', \pi _i)\) and sends \(\left\{ \mathsf {ct} _i^* \right\} _{i \in [{q_c}]}\) to \(\mathcal {A}\).
 This is the same as \(\mathsf {Hyb}_1\), except the challenger uses uniformly sampled randomness when constructing the challenge ciphertexts.
This is the same as \(\mathsf {Hyb}_1\), except the challenger uses uniformly sampled randomness when constructing the challenge ciphertexts.
-
Challenge phase. Same as in \(\mathsf {Hyb}_1\), except that for every \(i \in [{q_c}]\), the challenger sets
 for a randomly chosen \(r_i \xleftarrow {\textsc {r}}\{0,1\} ^\rho \).
for a randomly chosen \(r_i \xleftarrow {\textsc {r}}\{0,1\} ^\rho \).
 This is the same as \(\mathsf {Hyb}_2\), except the challenger answers the decryption queries by first extracting the message-key pair (m, k) from the NIZK argument and then evaluating the derandomized function on it. Let \(\mathcal {E}^{(\textsc {nizk})}= (\mathcal {E}^{(\textsc {nizk})}_1, \mathcal {E}^{(\textsc {nizk})}_2)\) be the extraction algorithm for \(\mathsf {NIZK} \).
This is the same as \(\mathsf {Hyb}_2\), except the challenger answers the decryption queries by first extracting the message-key pair (m, k) from the NIZK argument and then evaluating the derandomized function on it. Let \(\mathcal {E}^{(\textsc {nizk})}= (\mathcal {E}^{(\textsc {nizk})}_1, \mathcal {E}^{(\textsc {nizk})}_2)\) be the extraction algorithm for \(\mathsf {NIZK} \).
-
Setup phase. Same as in \(\mathsf {Hyb}_2\) (or \(\mathsf {Hyb}_1\)), except the challenger runs \((\sigma , \tau , \xi ) \leftarrow \mathcal {E}^{(\textsc {nizk})}_1(1^\lambda )\) to obtain the \(\mathrm {CRS}\) \(\sigma \), the simulation trapdoor \(\tau \), and the extraction trapdoor \(\xi \).
-
Pre-challenge queries. The key-generation queries are handled as in \(\mathsf {Hyb}_2\), but the decryption queries are handled as follows.
-
Decryption queries. On input (f, C), where \(C = \left\{ \mathsf {ct} _i \right\} _{i \in [m]}\),
-
1.
Choose a random key \(k \xleftarrow {\textsc {r}}\mathcal {K}_\lambda \).
-
2.
For \(i \in [m]\), parse \(\mathsf {ct} _i\) as \((\mathsf {ct} _i', \pi _i)\), and let \(s_i\) be the statement in Eq. (3). If \(\mathsf {NIZK}.\mathsf {Verify} (\sigma , s_i, \pi _i) = 0\), set \(y_i = \ \perp \). Otherwise, invoke the extractor \(\mathcal {E}^{(\textsc {nizk})}_2(\sigma , \xi , s_i, \pi _i)\) to obtain a witness \((x_i, k_i)\), and set \(y_i = f(x_i ; \mathsf {PRF} (k \diamond h_t(k_i), x_i))\).
-
3.
Send the set \(\left\{ y_i \right\} _{i \in [m]}\) to \(\mathcal {A}\).
-
1.
-
-
Post-challenge queries. This is identical to the pre-challenge phase.
 This is the same as \(\mathsf {Hyb}_3\), except the challenger uses the simulator \(\mathcal {S}^{(\textsc {fe})}= (\mathcal {S}^{(\textsc {fe})}_1, \mathcal {S}^{(\textsc {fe})}_2, \mathcal {S}^{(\textsc {fe})}_3, \mathcal {S}^{(\textsc {fe})}_4)\) for the underlying FE scheme to respond to queries. Let \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2, \mathcal {S}_3, \mathcal {S}_4, \mathcal {S}_5)\) be the simulator described in Sect. 4.1.
This is the same as \(\mathsf {Hyb}_3\), except the challenger uses the simulator \(\mathcal {S}^{(\textsc {fe})}= (\mathcal {S}^{(\textsc {fe})}_1, \mathcal {S}^{(\textsc {fe})}_2, \mathcal {S}^{(\textsc {fe})}_3, \mathcal {S}^{(\textsc {fe})}_4)\) for the underlying FE scheme to respond to queries. Let \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2, \mathcal {S}_3, \mathcal {S}_4, \mathcal {S}_5)\) be the simulator described in Sect. 4.1.
-
Setup phase. Same as in \(\mathsf {Hyb}_3\), except the challenger invokes the base FE simulator \(\mathcal {S}^{(\textsc {fe})}_1\) to construct mpk. The resulting setup algorithm corresponds to the simulation algorithm \(\mathcal {S}_1\). Hence, we can alternately say that the challenger runs \(\mathcal {S}_1(1^\lambda )\) to obtain
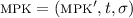 and \(\mathsf {st}= (\mathsf {st}^{(\textsc {fe})}, \textsc {mpk}, \tau , \xi )\), and sends mpk to \(\mathcal {A}\).
and \(\mathsf {st}= (\mathsf {st}^{(\textsc {fe})}, \textsc {mpk}, \tau , \xi )\), and sends mpk to \(\mathcal {A}\). -
Pre-challenge queries. The decryption queries are handled as described in \(\mathsf {Hyb}_3\), but key-generation queries are handled as follows.
-
Key-generation queries. On a key-generation query \(f \in \mathcal {F}_\lambda \),
-
1.
Sample a key \(k \xleftarrow {\textsc {r}}\mathcal {K}_\lambda \). Let \(g_k^f\) be the derandomized function corresponding to f.
-
2.
Run \(\mathcal {S}^{(\textsc {fe})}_2(\mathsf {st}^{(\textsc {fe})}, g_k^f)\) to obtain a secret key \(\mathsf {sk} \) and an updated state.
-
3.
Update \(\mathsf {st}\) accordingly and send \(\mathsf {sk} \) to \(\mathcal {A}\).
Note that this is exactly how \(\mathcal {S}_2\) behaves when given f and \(\mathsf {st}\) as inputs.
-
1.
-
-
Challenge phase. The challenger constructs the challenge ciphertexts using the simulation algorithm \(\mathcal {S}_3\). Specifically, it does the following on receiving \(\mathbf {x} \in \mathcal {X}_\lambda ^{q_c}\):
-
1.
For each \(i \in [{q_c}]\), choose a key \(k_i^* \xleftarrow {\textsc {r}}\mathcal {K}_\lambda \).
-
2.
Let \(f_1, \ldots , f_{q_1}\in \mathcal {F}_\lambda \) be the pre-challenge key-generation queries made by \(\mathcal {A}\) and \(k_1, \ldots , k_{q_1}\in \mathcal {K}_\lambda \) be the keys chosen when responding to each query. For all \(i \in [{q_c}]\) and \(j \in [{q_1}]\), compute \(r_{ij} = \mathsf {PRF} (k_j \diamond h_t(k_i^*), x_i)\) and set \(y_{ij} = f_j(x_i ; r_{ij})\).
-
3.
Invoke the simulator algorithm \(\mathcal {S}_3(\mathsf {st}, \left\{ y_{ij} \right\} _{i \in [{q_c}], j \in [{q_1}]})\) to obtain a collection of ciphertexts \(\left\{ \mathsf {ct} _i^* \right\} _{i \in [{q_c}]}\) and an updated state \(\mathsf {st}\).
-
4.
Send \(\left\{ \mathsf {ct} _i^* \right\} _{i \in [{q_c}]}\) to \(\mathcal {A}\).
-
1.
-
Post-challenge queries. The decryption queries are handled as in the pre-challenge phase, but key-generation queries are handled differently as follows.
-
Key-generation queries. The first step stays the same: a key k is picked at random and \(g_k^f\) is defined. The challenger then invokes \(\mathcal {S}^{(\textsc {fe})}_4\) with inputs \(\mathsf {st}^{(\textsc {fe})}\) and \(g_k^f\), instead of \(\mathcal {S}^{(\textsc {fe})}_2\). In invoking \(\mathcal {S}^{(\textsc {fe})}_4\), it simulates the \(\mathsf {FE}.\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\) oracle as follows: on input a function of the form \(g^{f'}_{k'}\), it computes
 and replies with the set \(\left\{ y_i \right\} _{i \in [{q_c}]}\). The function key returned by \(\mathcal {S}^{(\textsc {fe})}_4\) is given to \(\mathcal {A}\), and \(\mathsf {st}\) is updated appropriately. This is the behavior of \(\mathcal {S}_4\).
and replies with the set \(\left\{ y_i \right\} _{i \in [{q_c}]}\). The function key returned by \(\mathcal {S}^{(\textsc {fe})}_4\) is given to \(\mathcal {A}\), and \(\mathsf {st}\) is updated appropriately. This is the behavior of \(\mathcal {S}_4\).
-
 This is the same as \(\mathsf {Hyb}_4\), except the outputs of \(\mathsf {PRF} \) are replaced by truly random strings. This matches the specification of the ideal experiment \(\mathsf {Ideal}_\mathcal {A}^\mathsf {rFE} \). We highlight below the differences from the previous hybrid.
This is the same as \(\mathsf {Hyb}_4\), except the outputs of \(\mathsf {PRF} \) are replaced by truly random strings. This matches the specification of the ideal experiment \(\mathsf {Ideal}_\mathcal {A}^\mathsf {rFE} \). We highlight below the differences from the previous hybrid.
-
Pre-challenge queries. While the key queries are handled as before, the decryption queries are handled as follows.
-
Decryption queries. Same as in \(\mathsf {Hyb}_4\), except the function f is evaluated using uniformly sampled randomness. In other words, on input f and \(C = \left\{ \mathsf {ct} _i \right\} _{i \in [m]}\), the challenger does the following:
-
1.
For every \(\mathsf {ct} _i \in C\), invoke the simulator algorithm \(\mathcal {S}_5(\mathsf {st}, \mathsf {ct} _i)\) to obtain a value \(x_i \in \mathcal {X}_\lambda \cup \left\{ \perp \right\} \) and an updated state \(\mathsf {st}\).
-
2.
If \(x_i = \ \perp \), set \(y_i\) to \(\perp \), else set it to \(f(x_i ; r_i)\), where \(r_i \xleftarrow {\textsc {r}}\mathcal {R}_\lambda \).
-
3.
Send the set of values \(\left\{ y_i \right\} _{i \in [m]}\) to \(\mathcal {A}\).
-
1.
-
-
Challenge phase. The challenge ciphertexts are constructed as in the ideal experiment. Specifically, instead of using \(\mathsf {PRF} \) to generate the randomness for evaluating \(y_{ij}\) in the first and second steps of the challenge phase, the challenger simply computes \(f_j(x_i ; r_{ij})\) for \(r_{ij} \xleftarrow {\textsc {r}}\mathcal {R}_\lambda \). The remaining two steps (third and fourth) stay the same.
-
Post-challenge queries. The decryption queries are handled as in the pre-challenge phase, but key queries are handled as follows:
-
Key-generation queries. Same as \(\mathsf {Hyb}_4\), except the oracle \(\mathsf {FE}.\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\) is implemented using uniformly sampled randomness as in the ideal experiment. Specifically, if \(\mathcal {S}^{(\textsc {fe})}_4\) makes a query to \(\mathsf {FE}.\mathsf {KeyIdeal}(\mathbf {x}, \cdot )\) with a derandomized function \(g_{k'}^{f'}\), the challenger chooses an \(r_i \xleftarrow {\textsc {r}}\mathcal {R}_\lambda \) for every \(i \in [{q_c}]\), and replies with \(\left\{ f'(x_i; r_i) \right\} _{i \in [{q_c}]}\).
-
In the full version [6], we complete the hybrid argument by showing that each consecutive pair of experiments are computationally indistinguishable. We also show in the full version that our transformed scheme is correct.
5 Instantiating and Applying the Transformation
In this section, we describe one way to instantiate the primitives (the NIZK argument system, the RKA-secure PRF, and the one-way permutation) needed to apply the generic transformation from Sect. 4, Theorem 4.1. Then, in Sect. 5.2, we show how to obtain new general-purpose functional encryption schemes for randomized functionalities with security against malicious encrypters from a wide range of assumptions by applying our transformation to existing functional encryption schemes.
5.1 Instantiating Primitives
All of the primitives required by our generic transformation can be built from standard number-theoretic assumptions, namely the decisional Diffie-Hellman (DDH) assumption [29], the hardness of discrete log in the multiplicative group \(\mathbb {Z}_p^*\) (for prime p), and the RSA assumption [30, 82]. The first two assumptions can be combined by assuming the DDH assumption holds in a prime-order subgroup of \(\mathbb {Z}_p^*\), such as the subgroup of quadratic residues of \(\mathbb {Z}_p^*\), where p is a safe prime (\(p = 2q + 1\), where q is also prime). We describe one such instantiation of our primitives from the DDH and RSA assumptions in the full version [6]. This yields the following corollary to Theorem 4.1:
Corollary 5.1
Assuming standard number-theoretic assumptions (that is, the DDH assumption in a prime-order subgroup of \(\mathbb {Z}_p^*\) and the RSA assumption), and that \(\mathsf {FE}\) is a perfectly-correct \(({q_1}, {q_c}, {q_2})\)-\(\mathsf {SIM}\) secure functional encryption scheme for the derandomized function class \(\mathcal {G}_\mathcal {F}\), then \(\mathsf {rFE} \) is \(({q_1}, {q_c}, {q_2})\)-\(\mathsf {SIM}\) secure against malicious encrypters for the class \(\mathcal {F}\) of randomized functions.
5.2 Applying the Transformation
In this section, we give three examples of how our generic transformation from Sect. 4 could be applied to existing functional encryption schemes to obtain schemes that support randomized functionalities. Our results show that functional encryption for randomized functionalities secure against malicious encrypters can be constructed from a wide range of assumptions such as public-key encryption, concrete assumptions over composite-order multilinear maps, or indistinguishability obfuscation, in conjunction with standard number-theoretic assumptions (Corollary 5.1). The examples we present here do not constitute an exhaustive list of the functional encryption schemes to which we could apply the transformation. For instance, the construction of single-key-secure, succinct FE from LWE by Goldwasser et al. [62] and the recent adaptively-secure construction from \(i\mathcal {O}\) by Waters [86] are also suitable candidates.
We note that the FE schemes for deterministic functions we consider below are secure (or can be made secure) under a slightly stronger notion of simulation security compared to Definition 2.4. Under the stronger notion (considered in [50, 63]), the simulator is not allowed to program the public-parameters (they are generated by the \(\mathsf {Setup} \) algorithm) or the pre-challenge key queries (they are generated using the \(\mathsf {KeyGen} \) algorithm). Hence, when our transformation is applied to these schemes, there is a small loss in security. We believe that this loss is inherent because the new schemes are secure under malleability attacks while the original schemes are not. In particular, the construction of Goyal et al. [65] also suffers from this limitation.
The GVW scheme. In [63], Gorbunov et al. give a construction of a general-purpose public-key FE scheme for a bounded number of secret key queries. More formally, they give both a \(({q_1}, 1, \mathsf {poly})\)- and a \(({q_1}, \mathsf {poly}, 0)\)-\(\mathsf {SIM}\) Footnote 7 secure FE scheme for any class of deterministic functions computable by polynomial-size circuits based on the existence of semantically-secure public-key encryption and pseudorandom generators (PRG) computable by low-degree circuits. These assumptions are implied by many concrete intractability assumptions such as factoring.
The GVW scheme can be made perfectly correct if we have the same guarantee from the two primitives it is based on: a semantically-secure public-key encryption scheme and a decomposable randomized encoding scheme [70]. There are many ways to get perfect correctness for the former, like ElGamal [52] or RSA [82]. For the latter, we can use Applebaum et al.’s construction [12, Theorem 4.14]. We can now apply our generic transformation (Corollary 5.1) to the GVW scheme to obtain the following corollary:
Corollary 5.2
Under standard number-theoretic assumptions, for any polynomial \({q_1}= {q_1}(\lambda )\), there exists a \(({q_1}, 1, \mathsf {poly})\)-\(\mathsf {SIM}\) and a \(({q_1}, \mathsf {poly}, 0)\)-\(\mathsf {SIM}\) secure FE scheme for any class of randomized functions computable by polynomial-size circuits with security against malicious encrypters.
In the full version [6], we describe how to apply our generic transformation from Sect. 4 to the GGHZ [56] and GGHRSW [55] functional encryption schemes to obtains FE schemes supporting randomized functionalities from concrete assumptions over multilinear maps and indistinguishability obfuscation, respectively. We thus obtain the following corollaries:
Corollary 5.3
Under standard number-theoretic assumptions, and the GGHZ complexity assumptions on composite-order multilinear maps [56, Section 2.3], for any polynomials \({q_1}= {q_1}(\lambda )\) and \({q_c}= {q_c}(\lambda )\), there exists a \(({q_1}, {q_c}, \mathsf {poly})\)-\(\mathsf {SIM}\) secure functional encryption for all polynomial-sized randomized functionalities with security against malicious encrypters.
Corollary 5.4
Under standard number-theoretic assumptions, and the existence of an indistinguishability obfuscator, for any polynomials \({q_1}= {q_1}(\lambda )\) and \({q_c}= {q_c}(\lambda )\), there exists a \(({q_1}, {q_c}, \mathsf {poly})\)-\(\mathsf {SIM}\) secure functional encryption for all polynomial-sized randomized functionalities with security against malicious encrypters.
Comparison with the GJKS scheme. We note that \(({q_1}, {q_c}, \mathsf {poly})\)-\(\mathsf {SIM}\) security matches the known lower bounds for simulation-based security in the standard model [7, 35]. We remark also that the FE schemes from Corollaries 5.3 and 5.4 provide stronger security than the original FE scheme for randomized functionalities by Goyal et al. [65]. Their construction was shown to be selectively rather than adaptively secure. Specifically, in their security model, the adversary must commit to its challenge messages before seeing the master public key. On the contrary, when we apply our generic transformation to both the GGHZ scheme from composite-order multilinear maps as well as the GGHSRW scheme from indistinguishability obfuscation, we obtain an adaptive-secure FE scheme where the adversary can not only see the master public key, but also make secret key queries prior to issuing the challenge query.
6 Open Questions
We conclude with a few interesting open questions for further study:
-
Can we construct an FE scheme for a more restrictive class of randomized functionalities (e.g., sampling from a database) without needing to go through our generic transformation? In other words, for simpler classes of randomized functionalities, can we construct a scheme that does not require a general-purpose FE scheme for deterministic functionalities?
-
Is it possible to generically convert a public-key FE scheme for deterministic functionalities into one that supports randomized functionalities without making any additional assumptions? Komargodski, Segev, and Yogev [73] show that this is possible in the secret-key setting.
Notes
- 1.
While there is a generic transformation from selectively-secure FE to adaptively-secure FE [10], it is described in the context of FE for deterministic functions. Though it is quite plausible that the transformation can be applied to FE schemes for randomized functions, a careful analysis is necessary to verify that it preserves security against malicious encrypters. In contrast, our generic transformation allows one to take advantage of the transformation in [10] “out-of-the-box” (i.e., apply it to existing selectively-secure FE schemes for deterministic functions) and directly transform adaptive-secure FE for deterministic functions to adaptively-secure FE for randomized functions.
- 2.
- 3.
In the deterministic encryption setting of Fuller et al. [54], the hard-core function must additionally be robust. This is necessary because \(\mathsf {hc}(x)\) is not guaranteed to hide the bits of x, which in the case of deterministic encryption, is the message itself (and precisely what needs to be hidden in a normal encryption scheme!). Our randomized FE scheme does not require that the bits of k remain hidden from the adversary. Rather, we only need that \(\mathsf {hc}(k)\) does not reveal any information about h(k) (the share of the PRF key used for derandomization). This property follows immediately from the definition of an ordinary hard-core function.
- 4.
In the specification of the experiments, the indices i always range over \([{q_c}]\) and the indices j always range over \([{q_1}]\).
- 5.
The underlying FE scheme is for the derandomized class \(\mathcal {G}_\mathcal {F}\), so the only permissible functions \(\mathcal {S}^{(\textsc {fe})}_4\) can issue to \(\mathsf {FE}.\mathsf {KeyIdeal}\) are of the form \(g_{k'}^{f'}\) for some \(k'\) and \(f'\).
- 6.
Recall that in the security definition (Definition 3.3), the decryption oracle accepts multiple ciphertexts, and invokes the simulator on each one individually. Thus, the simulator algorithm operates on a single ciphertext at a time.
- 7.
We write \(\mathsf {poly}\) to denotes that the quantity does not have to be a-priori bounded, and can be any polynomial in \(\lambda \).
References
Abdalla, M., Benhamouda, F., Passelègue, A.: An algebraic framework for pseudorandom functions and applications to related-key security. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 388–409. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_19
Abdalla, M., Benhamouda, F., Passelègue, A., Paterson, K.G.: Related-key security for pseudorandom functions beyond the linear barrier. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 77–94. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_5
Agrawal, S., Agrawal, S., Badrinarayanan, S., Kumarasubramanian, A., Prabhakaran, M., Sahai, A.: On the practical security of inner product functional encryption. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 777–798. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_35
Agrawal, S., Agrawal, S., Prabhakaran, M.: Cryptographic agents: towards a unified theory of computing on encrypted data. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 501–531. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_17
Agrawal, S., Koppula, V., Waters, B.: Impossibility of simulation secure functional encryption even with random oracles. Cryptology ePrint Archive, Report 2016/959 (2016). http://eprint.iacr.org/2016/959
Agrawal, S., Wu, D.J.: Functional encryption: Deterministic to randomized functions from simple assumptions. Cryptology ePrint Archive, Report 2016/482 (2016). http://eprint.iacr.org/2016/482
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_28
Alwen, J., Barbosa, M., Farshim, P., Gennaro, R., Gordon, S.D., Tessaro, S., Wilson, D.A.: On the relationship between functional encryption, obfuscation, and fully homomorphic encryption. In: IMA International Conference on Cryptography and Coding (2013)
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. Cryptology ePrint Archive, Report 2013/689 (2013). http://eprint.iacr.org/2013/689
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_32
Applebaum, B., Brakerski, Z.: Obfuscating circuits via composite-order graded encoding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 528–556. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_21
Applebaum, B., Ishai, Y., Kushilevitz, E.: Computationally private randomizing polynomials and their applications. Comput. Complex. 15(2), 115–162 (2006)
Ateniese, G., Fu, K., Green, M., Hohenberger, S.: Improved proxy re-encryption schemes with applications to secure distributed storage. ACM Trans. Inf. Syst. Secur. 9(1), 1–30 (2006). doi:10.1145/1127345.1127346
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_13
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Barbosa, M., Farshim, P.: On the semantic security of functional encryption schemes. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 143–161. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36362-7_10
Bellare, M., Boldyreva, A., O’Neill, A.: Deterministic and efficiently searchable encryption. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 535–552. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74143-5_30
Bellare, M., Cash, D.: Pseudorandom functions and permutations provably secure against related-key attacks. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 666–684. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_36
Bellare, M., Cash, D., Miller, R.: Cryptography secure against related-key attacks and tampering. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 486–503. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_26
Bellare, M., Fischlin, M., O’Neill, A., Ristenpart, T.: Deterministic encryption: definitional equivalences and constructions without random oracles. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 360–378. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_20
Bellare, M., Hoang, V.T.: Resisting randomness subversion: fast deterministic and hedged public-key encryption in the standard model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 627–656. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_21
Bellare, M., Kohno, T.: A theoretical treatment of related-key attacks: RKA-PRPs, RKA-PRFs, and applications. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 491–506. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_31
Bellare, M., O’Neill, A.: Semantically-secure functional encryption: possibility results, impossibility results and the quest for a general definition. In: Abdalla, M., Nita-Rotaru, C., Dahab, R. (eds.) CANS 2013. LNCS, vol. 8257, pp. 218–234. Springer, Cham (2013). doi:10.1007/978-3-319-02937-5_12
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: IEEE Symposium on Security and Privacy (2007)
Biham, E.: New types of cryptanalytic attacks using related keys. In: Helleseth, T. (ed.) EUROCRYPT 1993. LNCS, vol. 765, pp. 398–409. Springer, Heidelberg (1994). doi:10.1007/3-540-48285-7_34
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation: from approximate to exact. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 67–95. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_4
Blaze, M., Bleumer, G., Strauss, M.: Divertible protocols and atomic proxy cryptography. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 127–144. Springer, Heidelberg (1998). doi:10.1007/BFb0054122
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: ACM STOC (1988)
Boneh, D.: The decision Die-Hellman problem. In: Third Algorithmic Number Theory Symposium (ANTS), vol. 1423 (1998). Invited paper
Boneh, D.: Twenty years of attacks on the RSA cryptosystem. Not. Am. Math. Soc. 46(2), 203–213 (1999)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_13
Boneh, D., Lewi, K., Raykova, M., Sahai, A., Zhandry, M., Zimmerman, J.: Semantically secure order-revealing encryption: multi-input functional encryption without obfuscation. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 563–594. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_19
Boneh, D., Raghunathan, A., Segev, G.: Function-private identity-based encryption: hiding the function in functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 461–478. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_26
Boneh, D., Raghunathan, A., Segev, G.: Function-private subspace-membership encryption and its applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 255–275. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42033-7_14
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Boneh, D., Silverberg, A.: Applications of multilinear forms to cryptography. Cryptology ePrint Archive, Report 2002/080 (2002). http://eprint.iacr.org/2002/080
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_29
Boneh, D., Wu, D.J., Zimmerman, J.: Immunizing multilinear maps against zeroizing attacks. Cryptology ePrint Archive, Report 2014/930 (2014). http://eprint.iacr.org/2014/930
Brakerski, Z., Chandran, N., Goyal, V., Jain, A., Sahai, A., Segev, G.: Hierarchical functional encryption. In: ITCS (2017)
Brakerski, Z., Rothblum, G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 1–25. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_1
Brakerski, Z., Segev, G.: Better security for deterministic public-key encryption: the auxiliary-input setting. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 543–560. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22792-9_31
Cheon, J.H., Fouque, P.-A., Lee, C., Minaud, B., Ryu, H.: Cryptanalysis of the new CLT multilinear map over the integers. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 509–536. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_20
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_1
Cheon, J.H., Jeong, J., Lee, C.: An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low level encoding of zero. Cryptology ePrint Archive, Report 2016/139 (2016). http://eprint.iacr.org/2016/139
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). doi:10.1007/3-540-45325-3_32
Coron, J.-S., Gentry, C., Halevi, S., Lepoint, T., Maji, H.K., Miles, E., Raykova, M., Sahai, A., Tibouchi, M.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_12
Coron, J.-S., Lee, M.S., Lepoint, T., Tibouchi, M.: Cryptanalysis of GGH15 multilinear maps. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 607–628. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_21
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_26
Coron, J.-S., Lepoint, T., Tibouchi, M.: New multilinear maps over the integers. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 267–286. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_13
De Caro, A., Iovino, V., Jain, A., O’Neill, A., Paneth, O., Persiano, G.: On the achievability of simulation-based security for functional encryption. In: CRYPTO (2013)
Dwork, C., Naor, M., Reingold, O.: Immunizing encryption schemes from decryption errors. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 342–360. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24676-3_21
ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 31, 469–472 (1985)
Feige, U., Lapidot, D., Shamir, A.: Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract). In: FOCS (1990)
Fuller, B., O’Neill, A., Reyzin, L.: A unified approach to deterministic encryption: new constructions and a connection to computational entropy. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 582–599. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28914-9_33
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_18
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: ACM STOC (2013)
Gentry, C., Lewko, A., Waters, B.: Witness encryption from instance independent assumptions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 426–443. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_24
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: FOCS (2015)
Goldreich, O.: The Foundations of Cryptography. Basic Techniques, vol. 1. Cambridge University Press, Cambridge (2001)
Goldwasser, S., Gordon, S.D., Goyal, V., Jain, A., Katz, J., Liu, F.-H., Sahai, A., Shi, E., Zhou, H.-S.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_32
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: ACM STOC (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: ACM STOC (2013)
Goyal, V., Jain, A., Koppula, V., Sahai, A.: Functional encryption for randomized functionalities. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 325–351. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_13
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: ACM CCS (2006). Available as Cryptology ePrint Archive Report 2006/309
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). doi:10.1007/11935230_29
Groth, J., Ostrovsky, R., Sahai, A.: Perfect non-interactive zero knowledge for NP. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 339–358. Springer, Heidelberg (2006). doi:10.1007/11761679_21
Hu, Y., Jia, H.: Cryptanalysis of GGH map. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 537–565. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_21
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: A new representation with applications to round-efficient secure computation. In: FOCS (2000)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_9
Knudsen, L.R.: Cryptanalysis of LOKI 91. In: Seberry, J., Zheng, Y. (eds.) AUSCRYPT 1992. LNCS, vol. 718, pp. 196–208. Springer, Heidelberg (1993). doi:10.1007/3-540-57220-1_62
Goyal, V., Jain, A., Koppula, V., Sahai, A.: Functional encryption for randomized functionalities. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 325–351. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_13
Lewi, K., Montgomery, H., Raghunathan, A.: Improved constructions of PRFs secure against related-key attacks. In: Boureanu, I., Owesarski, P., Vaudenay, S. (eds.) ACNS 2014. LNCS, vol. 8479, pp. 44–61. Springer, Cham (2014). doi:10.1007/978-3-319-07536-5_4
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (Hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_4
Lucks, S.: Ciphers secure against related-key attacks. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 359–370. Springer, Heidelberg (2004). doi:10.1007/978-3-540-25937-4_23
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_22
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_11
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010). http://eprint.iacr.org/2010/556
Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation from semantically-secure multilinear encodings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 500–517. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_28
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). doi:10.1007/3-540-46766-1_35
Rivest, R.L., Shamir, A., Adleman, L.M.: A method for obtaining digital signature and public-key cryptosystems. Commun. Assoc. Comput. Mach. 21(2), 120–126 (1978)
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: ACM CCS (2010)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). doi:10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_5
Waters, B.: A punctured programming approach to adaptively secure functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 678–697. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_33
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_15
Acknowledgments
We thank Venkata Koppula for many helpful conversations and discussions related to this work. We also thank the anonymous reviewers for useful feedback on the presentation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Agrawal, S., Wu, D.J. (2017). Functional Encryption: Deterministic to Randomized Functions from Simple Assumptions. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10211. Springer, Cham. https://doi.org/10.1007/978-3-319-56614-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-56614-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56613-9
Online ISBN: 978-3-319-56614-6
eBook Packages: Computer ScienceComputer Science (R0)




 takes as input the public key
takes as input the public key  takes as input the public key
takes as input the public key 
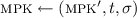 and
and  . Output
. Output 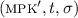 and
and  .
.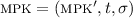 and send
and send  . It invokes
. It invokes  for a randomly chosen
for a randomly chosen 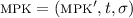 and
and  and replies with the set
and replies with the set