Abstract
The aim of the paper is to work towards a generalisation of coalgebraic logic enriched over a commutative quantale. Previous work has shown how to dualise the coalgebra type functor \(T:\varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat}\) in order to obtain the modal operators and axioms describing transitions of type T. Here we give a logical description of the dual of \(\varOmega \text {-}\mathsf {Cat}\).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Recently, following on work of Rutten [18] and Worrell [24], the interest in coalgebras enriched over posets or, more generally, enriched over a commutative quantale has attracted some attention. In particular, the question of a coalgebraic logic in this setting has been asked [2].
In the non-enriched situation we start with a functor \(T:\mathsf {Set}\rightarrow \mathsf {Set}\) and ask for a logic that allows us to completely describe T-coalgebras up to bisimilarity. More specifically, we would like to ensure strong expressivity in the sense that for any property \(p\subseteq X\) of any T-coalgebra \((X,\xi )\) there is a formula \(\phi \) such that p coincides with the semantics \([\![\phi ]\!]_{(X,\xi )}\) of \(\phi \) on \((X,\xi )\). Moreover, we would like to have completeness in the sense that if \([\![\phi ]\!]_{(X,\xi )}\subseteq [\![\phi ]\!]_{(X,\xi )}\) then \(\phi \le \psi \) in the initial algebra of formulas.
To achieve the above, the first step is to let \(LA=[T([A,2]),2]\) in

and to declare the initial L-algebra, if it exists, as the “Lindenbaum-algebra” of T. This terminology is justified in sofar as the adjoint transpose
of the iso \(L\rightarrow [T([-,2]),2]\) allows us to define the semantics \([\![]\!]_{(X,\xi )}\) wrt a coalgebra \((X,\xi )\) as the unique arrow from the initial L-algebra \(\iota : LI\mathop {\rightarrow }\limits ^{}I\) as in

But the reason why, at this stage, we cannot truly speak of \(\iota :LI\rightarrow I\) as a Lindenbaum algebra is that it lives in \(\mathsf {Set}^\mathrm {op}\) and is not (yet) an algebra over \(\mathsf {Set}\) with elements and operations in the usual sense.
The second step, then, consists in using the well-known fact that \([-,2]:\mathsf {Set}^\mathrm {op}\rightarrow \mathsf {Set}\) is monadic and, therefore, \(\mathsf {Set}^\mathrm {op}\) is equivalent to a category of algebras defined by operations and equations. In particular, we know that \(\mathsf {Set}^\mathrm {op}\) is equivalent to the category of complete atomic Boolean algebras, which now allows us to consider \((L,\iota )\) as the Lindenbaum algebra of infinitary T-logic.
The aim of the paper is to carry out these steps in the case where we replace \(\mathsf {Set}\) by the category \(\varOmega \text {-}\mathsf {Cat}\) of categories enriched over \(\varOmega \) for a commutative quantale \(\varOmega \). It is based on the \(\varOmega \)-generalisations of the downset monad \(\mathcal {D}\) and the upset monad \(\mathcal {U}\). We will define algebras for operations \(\varSigma _{\mathcal {D}\mathcal {U}}\) and equations \(E_{\mathcal {D}\mathcal {U}}\) and will argue via (3), Theorems 16, 22, and 49 that \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \)-algebras complete the table

Importantly, this includes an equation for generalised distributivity, Axiom (13), and will allow us to derive a logic for \(\varOmega \text {-}\mathsf {Cat}\) very much in the same way as we can say that Boolean logic is the logic of \(\mathsf {Set}\).
Related Work. The results in Sect. 3 generalize the results in [13] by Marmolejo, Rosebrugh, and Wood to arbitrary commutative quantales \(\varOmega \) but the proofs remain the same as they work in any 3-category where 3-cells form a poset. Theorem 16 is also a special case of a theorem of Stubbe [19].
Section 4 generalises the well-known dual adjunction

between preorders and completely distributive lattices to categories enriched over a commutative quantale. This is similar in spirit to the work in Hofmann [5], where a generalisation from preorders to topological spaces and to approach spaces can be found.
The category of distributive complete \(\varOmega \)-lattices of Lai and Zhang [9] coincides with what we denote \(\mathsf {CCD}\) in Definition 18. Compared to their work, we add the argument of how to obtain \(\mathsf {CCD}\) from the monad \([[-,\varOmega ],\varOmega ]\) and we show that the \(\mathsf {CCD}\) is isomorphic to the category of (ordinary, set-based) \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \)-algebras.
In Pu and Zhang [14] it is shown, amongst other things, that the category of anti-symmetric \(\mathsf {CCD}\)’s is monadic over \(\mathsf {Set}\), but the proof proceeds by Beck’s monadicity theorem whereas we give the operations and equations \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) explicitly.
The double powerset monad \(\mathcal {D}\mathcal {U}\) is investigated in detail, in the case \(\varOmega =\mathbbm {2}\), by Vickers in [20–23].
2 Preliminaries and Related Work
We are interested in categories enriched over commutative quantales [15].
Definition 1
By a quantale \(\varOmega =((\varOmega ,\le ), e,\otimes )\) we understand a complete lattice with a binary operation \( \otimes : \varOmega \times \varOmega \rightarrow \varOmega \) with unit e, such that \(\otimes \) preserves colimits in both arguments. We call a quantale commutative if the operation \(\otimes \) is commutative.
Since \(\otimes \) preserves joins, a commutative quantale \(\varOmega \) can be considered as a symmetric monoidal closed category and one can enrich over \(\varOmega \), see [7]. A category enriched over \(\varOmega \) is also called a \(\varOmega \)-category and the 2-category of \(\varOmega \)-categories, \(\varOmega \)-functors and \(\varOmega \)-natural transformations is denoted by \(\varOmega \text {-}\mathsf {Cat}\). The interpretation of such enriched categories as metric spaces is due to [10] and recalled in the following examples:
Example 2
-
1.
\(\varOmega =\mathbbm {2}= ((2, \le ), 1, \wedge ).\) Categories enriched over \(\mathbbm {2}\) are preorders and the corresponding functors are monotone maps. The closed structure is implication.
-
2.
\(\varOmega =(([0,\infty ],\ge _\mathbbm {R}),0,+)\), the non-negative reals with infinity and the opposite of the natural order. That the top element is 0 formalises the idea that the elements of \(\varOmega \) measure distance from ‘truth’. A \(\varOmega \)-category is called a generalised metric space. The corresponding functors are non-expansive maps. The closed structure is given by
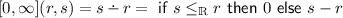
Examples inlcude:
-
(a)
\( [0,\infty ]\) itself.
-
(b)
The real numbers \((R,\le _\mathbb {R})\) with the metric given by \( R(a,b) = \textsf {\ if\ } a \le _\mathbb {R} b \textsf {\ then\ } 0 \textsf {\ else\ } a-b\)
-
(c)
Any metric space.
-
(a)
-
3.
\(\varOmega =(([0,1],\le _\mathbb {R}),1,\cdot )\) where \(x\cdot y\) is the usual multiplication. Then
$$\begin{aligned} x\Rightarrow y\ =\ \textsf {\ if\ } x\le y \textsf {\ then\ } 1 \textsf {\ else\ } \frac{y}{x} \end{aligned}$$The exponential map \(x\mapsto \mathsf {exp}(-x)\) induces an isomorphism from the \(\varOmega \) of the previous item, so that we can think of both representing two views of the same mathematics, one in terms of distances and the other in terms of truth-values.
-
4.
\(\varOmega =(([0,1],\ge _\mathbb {R}), 0, \max )\). This is example is in the same spirit as above, but this time \(\varOmega \)-categories are generalised ultrametric spaces [17]. The closed structure is given by
$$\begin{aligned}{}[0,1](x,y)= \textsf {\ if\ } x\ge _\mathbb {R} y \textsf {\ then\ } 0 \textsf {\ else\ } y \end{aligned}$$Examples include:
-
(a)
[0, 1] itself, as well as \([0,1]^\mathrm {op}\) with 1 and \(\min \).
-
(b)
Let \(A^\infty \) be the finite and infinite words over A. Define \(A^\infty (v,w)=0\) if v is a prefix of w and \(A^\infty (v,w)=2^{-n}\) otherwise where \(n\in \mathbbm {N}\) is the largest number such that \(v_n=w_n\) (where \(v_n\) is the prefix of v consisting of n letters from A).
-
(a)
Whenever we talk about limits or colimits in a \(\varOmega \)-category we understand a weighted limit or weighted colimit and we will use the same notations as in [7, Chapter 3].
Note that every \(\varOmega \)-category X is equipped with a preorder \(x\le y \Leftrightarrow X(x,y)\ge e\).
We call a \(\varOmega \)-category X anti-symmetric if \(x\le y\) and \(y\le x\) implies \(x=y\). In the examples above, this order coincides with the expected one. For example, in Example 2b the induced order on R is the natural one and in Example 3b it is the prefix order.
Proposition 3
-
1.
The order \(x\le y \Leftrightarrow \varOmega (x,y)\ge e\) is the order of \(\varOmega \).
-
2.
\([X,\varOmega ]\) is anti-symmetric for any \(\varOmega \)-category X.
-
3.
[X, Y] is anti-symmetric iff Y is anti-symmetric.
We already said that \(\varOmega \)-categories form a category \(\varOmega \text {-}\mathsf {Cat}\) of small \(\varOmega \)-categories. \(\varOmega \text {-}\mathsf {Cat}\) is \(\varOmega \text {-}\mathsf {Cat}\) enriched, with the distance between two \(\varOmega \)-functors \(f,g:A\rightarrow B\) given by \(\varOmega \text {-}\mathsf {Cat}(A,B)(f,g)=[A,B](f,g)=\bigwedge _{a\in A}B(fa,ga)\). Hence \(\varOmega \text {-}\mathsf {Cat}\) is an object of \((\varOmega \text {-}\mathsf {Cat})\textsf {\text {-}Cat}\). The category \((\varOmega \text {-}\mathsf {Cat})\textsf {\text {-}Cat}\) of \(\varOmega \text {-}\mathsf {Cat}\)-categories, \(\varOmega \text {-}\mathsf {Cat}\)-functors, and \(\varOmega \text {-}\mathsf {Cat}\)-natural transformations is a 3-category in which natural transformations \(\alpha ,\beta :F\rightarrow G:{\mathcal {A}}\rightarrow {\mathcal {B}}\) are pre-ordered since \((\varOmega \text {-}\mathsf {Cat})\textsf {\text {-}Cat}({\mathcal {A}},{\mathcal {B}})(F,G)\) is a \(\varOmega \)-category.
The reason to insist on pre-ordered natural transformations is that we can make use of the following notion due to [8] and reformulated by [12].
Definition 4
By a KZ-doctrine M on \(\varOmega \text {-}\mathsf {Cat}\) we understand a monad \((M,\eta ,\mu )\) such that we have the adjunctions \(M\eta \dashv \mu \dashv \eta M.\) Dually a co-KZ-doctrine is a monad where \(\eta M \dashv \mu \dashv M\eta \).
The following proposition is Kock’s definition of a KZ-doctrine simplified to the pre-ordered setting, see [8].
Proposition 5
\((M, \eta ,\mu )\) is a KZ-doctrine if and only if there exists a natural transformation \( \delta : M\eta \rightarrow \eta M\) and \(\mu \circ \eta M = \mu \circ M\eta = \mathrm {id}\). Dually \((M,\eta ,\mu )\) is a co-KZ-doctrine if there exists a natural transformation \(\lambda : \eta M \rightarrow M\eta \) and if \(\mu \circ \eta M = \mu \circ M\eta = \mathrm {id}.\)
If one has two monads for their composite to be again a monad one needs to have a distributive law between them, as in [1].
Definition 6
A distributive law between two monads \(\mathcal {D}\) and \(\mathcal {U}\) is a natural transformation \(r: \mathcal {U}\mathcal {D}\Rightarrow \mathcal {D}\mathcal {U}\) subject to the commutativity of

Definition 7
Let \(D=(D,\eta ,\mu )\) be a monad. By a D-algebra A we understand a pair \(A= (A,\alpha ),\) where A is category and \(\alpha : DA \rightarrow A\) is a functor such that

The next proposition is due to [8].
Proposition 8
Let \(M = (M,\eta ,\mu )\) be any KZ-doctrine, then \(A=(A,\alpha )\) is an M-algebra if and only if the structure map \(\alpha \) is a left adjoint of \(\eta _M\).
The following two propositions are stated in the case \(\varOmega =\mathbbm {2}\) in [13] and their proof transfers unchanged to our setting (because \(\varOmega \) is anti-symmetric).
Proposition 9
If at least one of the monads D or U is either a KZ or a co-KZ-doctrines then there is at most one distributive law \(r : UD \rightarrow DU.\)
Proposition 10
For monads D, U and a natural transformation \(r: UD \rightarrow DU\)
-
1.
if \((D,d,\mu )\) is KZ and \((U,u,\nu )\) is either KZ or co-KZ then \(r:UD \rightarrow DU\) is a distributive law if it satisfies \( r \circ Ud =dU\) and \(r \circ uD \le Du\);
-
2.
if \((U,u,\nu )\) is co-KZ and \((D,d,\mu )\) is either KZ or co-KZ then \(r:UD \rightarrow DU\) is a distributive law if it satisfies \(r \circ uD = Du\) and \(r \circ Ud \le dU.\)
3 Monads and algebras
\(\varOmega \) being a symmetric monoidal closed category, we have the contravariant adjunction where \( U = [-,\varOmega ] : \varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) is a left adjoint to \(D = [-,\varOmega ] : \varOmega \text {-}\mathsf {Cat}^\mathrm {op}\rightarrow \varOmega \text {-}\mathsf {Cat}.\) We want to study the algebras for the monad \(M = DU\) generated by it. For that we will prove that this monad is equivalent to the composite monad \(\mathcal {DU}\) where \(\mathcal {D},\mathcal {U}: \varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat}\) are the \(\varOmega \text {-}\mathsf {Cat}\) analogues of the downset and the upset monad as defined in Sect. 3.1. From there we will obtain two different sets of operations, one for each monad, and a distributive law between them. In the end we will give a categorical description for the category of algebras.
As \(\varOmega \) is symmetric monoidal closed, we have from [7, Chapter 1.5]
Proposition 11
\([-,\varOmega ]\,:\,\varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) is left adjoint to \([-,\varOmega ]\,:\,\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\rightarrow \varOmega \text {-}\mathsf {Cat}\).
As explained in the introduction, we want to consider \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) as the category of algebras of a ‘\(\varOmega \text {-}\mathsf {Cat}\)-logic’. Since \([-,\varOmega ]:\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\rightarrow \varOmega \text {-}\mathsf {Cat}\) need not be monadic itself, we are going to study instead its monadic closure. That is, we let \(M=DU\) and work with the category \(\varOmega \text {-}\mathsf {Cat}^M\) of algebras for the monad M. We show that there is an adjunction relating them to \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\), as in the following picture, which will guide us through this section.

3.1 Doctrines
The aim of this subsection is to describe two monads \(\mathcal {D},\mathcal {U}: \varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat}\) such that \(DU = \mathcal {D}\mathcal {U}\). Furthermore, \(\mathcal {D}\) will be a KZ-doctrine, and \(\mathcal {U}\) will be a co-KZ-doctrine, which in turn will help us to describe the distributive law relating them.
Recall that for any category X, one has two Yoneda embeddings \(dX : X \rightarrow [X^\mathrm {op},\varOmega ]\) given by \(x \mapsto X(-,x)\) and \(uX : X \rightarrow [X,\varOmega ]^\mathrm {op}\) given by \(x \mapsto X(x,-).\)
On objects, \(\mathcal {D}\) maps X to \([X^\mathrm {op},\varOmega ]\) and on arrows it constructs the left Kan extension along Yoneda, while \(\mathcal {U}\) maps an object X to \([X,\varOmega ]^\mathrm {op}\) and an arrow to the right Kan extension along Yoneda. Thus for any \(f :X \rightarrow Y\) in \(\varOmega \text {-}\mathsf {Cat}\), let \(\mathcal {D}f\) be defined as \(\mathrm {Lan}_{dX} dY \circ f = \mathrm {Lan}_{dX} Y(-,f)\) and \(\mathcal {U}f = \mathrm {Ran}_{dX} uY \circ f = \mathrm {Ran}_{dX} Y(f,-)\) as in

Writing down the formula for left and right Kan extensions, see [7, Chapter 4.2], we obtain for \(\varphi : X^\mathrm {op}\rightarrow V\) and \(\psi :X \rightarrow \varOmega \)
and
But considering that we calculate this end in \([Y,\varOmega ]^\mathrm {op}\), in \([Y,\varOmega ]\) it becomes
Because \(\mathcal {D}d\) and \(u\mathcal {U}\) are, respectively, left and right Kan extensions, their universal properties yield
Proposition 12
There exist natural transformations \( \lambda : \mathcal {D}d \rightarrow d\mathcal {D}\) and \(\delta : u \mathcal {U}\rightarrow \mathcal {U}u\).
We want \(\mathcal {D}\) to be a KZ-doctrine, so the multiplication \(\mu : \mathcal {D}\mathcal {D}\rightarrow \mathcal {D}\) has to be a left adjoint of \(d\mathcal {D}\). As \(d\mathcal {D}\) preserves all limits and the right Kan extension of \(\mathrm {id}_\mathcal {D}\) along \(d\mathcal {D}\) exists, using [7, Theorem 4.81], we know that the left adjoint of \(d\mathcal {D}\) exists and is expressed by \(Ran_{d\mathcal {D}}\, \mathrm {id}_\mathcal {D}\). Dually, the right adjoint of \(u\mathcal {U}\) exists and is expressed by \(Lan_{u\mathcal {U}}\,\mathrm {id}_\mathcal {U}\).

Furthermore as \(d\mathcal {D}\) and \(u\mathcal {U}\) are fully faithful, one has \(\mu \circ d\mathcal {D}= id_{\mathcal {D}}\) and \(\nu \circ u\mathcal {U}= id_{\mathcal {U}}.\) Following Proposition 5 to show that \(\mathcal {D}\) is a KZ-doctrine we just have to prove that \(\mu \circ \mathcal {D}d = \mathrm {id}\) as well. For that we know that \(\mu \) is a left adjoint so it preserves left Kan extensions, so \(\mu X \circ \mathcal {D}dX = \mu X \circ Lan_{dX} (d\mathcal {D}X \circ dX) = Lan_{dX} (\mu X \circ \mathcal {D}dX \circ dX ) = Lan_{dX} ( \mathrm {id}_{\mathcal {D}X} \circ d ) = Lan_{dX} dX = \mathrm {id}_{\mathcal {D}X} \)

Similarly, \(\nu \circ \mathcal {U}u =\mathrm {id}_\mathcal {U}\), so \(\mathcal {U}\) is a co-KZ-doctrine. Thus we have proved
Proposition 13
\((\mathcal {D},d,\mu )\) is a KZ-doctrine and \((\mathcal {U},u,\nu )\) is a co-KZ doctrine.
3.2 Distributive Laws and Equivalence of \(\mathcal {D}\mathcal {U}\) with \([[-,\varOmega ],\varOmega ]\)
In the previous section we constructed two monads, but in order for their composite to be a monad, one needs a distributive law between them.
Verifying that a natural transformation is indeed a distributive law may not be easy, but, thanks to [13], for KZ-doctrines, we just have to check the conditions of Proposition 10. To construct \(\mathcal {D}\) and \(\mathcal {U}\), we have used Kan extensions, thus it make sense that a distributive law between them is a Kan extension as well. Looking at the diamond above and as both \(u\mathcal {D}\) and \(\mathcal {U}d\) are fully faithful, a Kan extension along any of them would make that triangle commute, so intuitively, it should make no difference from which triangle one starts. So if one calculates all four Kan extensions one obtains
-
1.
\(r^r_{\mathcal {D}} = Ran_{u\mathcal {D}} \, \mathcal {D}u = \mathcal {U}\mathcal {D}(\mathcal {D}u,-) \)
-
2.
\(r^l_{\mathcal {U}} = Lan _{\mathcal {U}d} \, d\mathcal {U}= \mathcal {U}\mathcal {D}(\mathcal {U}d, - )\)
-
3.
\(r_\mathcal {D}^l = Lan_{u\mathcal {D}}\, \mathcal {D}u = \mathcal {U}\mathcal {D}(d\mathcal {D}\circ d,- ) *d\mathcal {U}\circ u \)
-
4.
\(r_\mathcal {U}^r = Ran_{\mathcal {U}d} d\mathcal {U}= \{\mathcal {U}\mathcal {D}(-, \mathcal {U}d), d\mathcal {U}\} \)
Now as for any X and any \(\varphi \in \mathcal {D}X\) and any \(\psi \in \mathcal {U}X\) one has \(\mathcal {D}uX (\varphi )(\psi ) = \mathcal {U}dX(\varphi )(\psi )\) it follows \(Ran_{u\mathcal {D}} \, \mathcal {D}u= Lan _{\mathcal {U}d} \,d\mathcal {U}.\)
Proposition 14
The natural transformation \(r = Ran_{u\mathcal {D}} \, \mathcal {D}u= Lan _{\mathcal {U}d} \,d\mathcal {U}: \mathcal {U}\mathcal {D}\rightarrow \mathcal {D}\mathcal {U}\) is a distributive law between \(\mathcal {D}\) and \(\mathcal {U}\).
In a similar way one has a distributive law \(l = Ran_{ \mathcal {D}u}\, u\mathcal {D}= Lan_{d\mathcal {U}}\, \mathcal {U}d: \mathcal {D}\mathcal {U}\rightarrow \mathcal {U}\mathcal {D},\) given by \(l = \mathcal {D}\mathcal {U}(-,\mathcal {D}u)\).
Proposition 15
With the notations from above we have \(l \dashv r\).
Next, we state that the monad \(\mathcal {D}\mathcal {U}\) is equivalent to the double dualisation monad DU, a result due to [13] and generalised in [19].
Theorem 16
For a commutative quantale \(\varOmega \), the composite monad \(\mathcal {D}\mathcal {U}\) is equivalent to the monad generated by the adjunction \([-,\varOmega ] \dashv [-,\varOmega ] : \varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat}^\mathrm {op}.\)
3.3 \(\mathsf {CCD}\): complete and completely distributive algebras
In this section we discuss the algebras of the two monads defined above. As \(\mathcal {D}\) is a KZ-doctrine, following [8], a \(\mathcal {D}\)-algebra A is a tuple \( A = (A,\alpha )\) such that \(\alpha : \mathcal {D}A \rightarrow A\) is a left adjoint to \(d_A\), and since \(\mathcal {U}\) is a co-KZ-doctrine a \(\mathcal {U}\)-algebra B is a tuple \(B = (B,\beta )\) such that \(\beta : \mathcal {U}B \rightarrow B\) is a right adjoint to \(u_B.\)
Proposition 17
The carrier A of a \(\mathcal {D}\)-algebra \(A= (A,\alpha _A) \) is co-complete, and the carrier C of an \(\mathcal {U}\)-algebra \(C = (C,\beta _C)\) is complete. Moreover, \(f: (A,\alpha _A) \rightarrow (B,\alpha _B)\) is \(\mathcal {D}\)-morphism if and only if f preserves all weighted colimits, and it is a \(\mathcal {U}\)-morphism if and only if it preserves all weighted limits.
The following transfers the notion of complete distributivity of [4] from \(\mathbbm {2}\) to a commutative quantale \(\varOmega \).
Definition 18
A \(\mathcal {D}\) algebra \((A,\alpha )\) is called \(\mathsf {ccd}\) if the structure map \(\alpha \) has a left adjoint. We denote with \(\mathsf {CCD}\) the subcategory of \(\mathcal {D}\)-alg such that the objects are \(\mathsf {ccd}\) and the arrows preserves weighted limits and colimits. Dually, a \(\mathcal {U}\)-algebra for which the structure map has a right adjoint is called \(^\mathrm {op}\mathsf {ccd}.\)
Example 19
In the case \(\varOmega =\mathbbm {2}\), a poset A equipped with a \(\mathcal {D}\)-algebra structure \(\alpha \) is a join semi-lattice. Moreover, A is \(\mathsf {ccd}\) in the sense of the definition above iff it is completely distributive in the usual order-theoretic sense.
Definition 20
A \(\mathcal {D}\mathcal {U}\)-algebra is a \(\mathcal {U}\)-algebra \((A,\beta )\) which has a \(\mathcal {D}\)-structure \(\alpha : \mathcal {D}A \rightarrow A\) such that \(\alpha \) is a \(\mathcal {U}\)-homomorphism, i.e. the following diagram commutes.

For any two DU-algebras \((A,\alpha _A,\beta _A)\) and \((B,\alpha _B, \beta _B)\) a DU-morphism from A to B is a map \(f: A \rightarrow B\) such that it is simultaneously \(\mathcal {D}\) and \(\mathcal {U}\) morphism.
Lemma 21
The carrier A of a \(\mathsf {ccd}\)-algebra \((A,\alpha )\) is complete and cocomplete.
The following result is due to [13].
Theorem 22
\(\mathsf {\mathcal {DU}\text {-alg}}\cong \mathsf {CCD}\), and \(\mathcal {U}\mathcal {D}\text {-alg} \cong \ ^\mathrm {op}\mathsf {CCD}.\)
Whereas naturally occurring metric spaces, such as Euclidean spaces, are typically not \(\mathsf {ccd}\), the spaces of many-valued predicates over metric spaces are \(\mathsf {ccd}\):
Example 23
For any X in \(\varOmega \text {-}\mathsf {Cat}\),
-
1.
\(( \mathcal {D}X, \mu X)\) is \(\mathsf {ccd}\).
-
2.
\( ( \mathcal {U}X, \nu X)\) is \(^\mathrm {op}\mathsf {ccd}\).
4 The comparison functor \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\rightarrow \mathsf {\mathcal {DU}\text {-alg}}\)
Following [11], let the comparison functor \( K : \varOmega \text {-}\mathsf {Cat}^\mathrm {op}\rightarrow \mathsf {\mathcal {DU}\text {-alg}}\) be given by \(KX = (X, D\epsilon X)\), for the adjunction \(U \dashv D\). As \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) is cocomplete, K has a left adjoint. In order to describe it we first define the concept of atoms, also known as tiny or small projective objects, see [6] and [7, Chapter 5.5].
4.1 The Left Adjoint of the Comparison Functor
Definition 24
An atom in a category \(\mathcal{C}\) is an object C such that \(\mathcal{C}(C,-)\) preserves all colimits. \(\mathsf {At}(\mathcal{C})\) is the full subcategory of \(\mathcal{C}\) whose objects are atoms.
Before we continue let us give some example of atoms.
Example 25
-
1.
In posets atoms are known as completely prime elements. In a completely distributive lattice being an atom is equivalent to being completely join irreducible.
-
2.
The category \([0,\infty ]\) seen as a generalized metric space has only one atom 0.
-
3.
Let \([X^\mathrm {op},\varOmega ]\) be a functor category, then using Yoneda and the definition of a colimit in a functor category, see [7, Chapter 3.3], one has that any representable is an atom. Moreover, see [7, Chapter 5.5], one has that \([X^\mathrm {op},\varOmega ] \cong [\mathsf {At}(X)^\mathrm {op},\varOmega ].\) In general one has \( X \subseteq \mathsf {At}([X^\mathrm {op},\varOmega ])\).
We define a functor \(\mathsf {AT}:\mathsf {\mathcal {DU}\text {-alg}}\rightarrow \varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) on objects by \(\mathsf {AT}(A,\alpha ) = (\mathsf {At}(A))^\mathrm {op}.\) In order to define \(\mathsf {AT}\) on maps we need some additional lemmas.
First note that for any \(H : A \rightarrow B\) in \(\mathsf {\mathcal {DU}\text {-alg}}\), since A is complete and H preserves all limits, there exists a left adjoint \(L : B \rightarrow A\) in \(\varOmega \text {-}\mathsf {Cat}\).
Lemma 26
For all \(A,B \in \mathcal {A}\) and \(H : A \rightarrow B\) with left adjoint L, there exists \(f :\mathsf {At}(B) \rightarrow \mathsf {At}(A)\) such that \(L \circ i_B = i_A \circ f \), where \(i_A : \mathsf {At}(A) \rightarrow A\) and \(i_B : \mathsf {At}(B) \rightarrow B\) are the atom-inclusion maps.
We can now define \(\mathsf {AT}(H) = f^\mathrm {op}\) with f as in the lemma. This defines a functor because composition of adjoints is again an adjoint. We are ready to prove
Theorem 27
For any \(X \in \varOmega \text {-}\mathsf {Cat}\) and \(A \in \mathsf {\mathcal {DU}\text {-alg}}\), we have a natural isomorphism of categories \(\varOmega \text {-}\mathsf {Cat}(X^\mathrm {op},\mathsf {At}(A))^\mathrm {op}\,\cong \, \mathsf {\mathcal {DU}\text {-alg}}(A,[X,\varOmega ])\). Moreover this is isomorphism also an isomorphism of \(\varOmega \)-categories.
Proof
We sketch the construction of the isomorphism.
We have to define the functors
and show that they are inverse to each other. First define \(\phi _{XA}\) on objects. For all \(h : X^\mathrm {op}\rightarrow \mathsf {At}(A)\) let
Now define \( \psi _{XA}\) on objects. Let \(H : A \rightarrow [X,\varOmega ]\) and let \(L : [X,\varOmega ] \rightarrow A\) be its left adjoint, and also let \(uX : X^\mathrm {op}\rightarrow [X,\varOmega ]\), \(x \mapsto X(x,-)\) the Yoneda embedding.

Since \(L \circ uX(x)\) is an atom for all x in X, we let \(\psi _{XA}(H) = L \circ uX\). In order to define \(\phi _{XA}\) and \(\psi _{XA}\) on arrows, one uses the concept of conjugate natural transformation [11, Chapter 4.7].
Theorem 28
The functor \(\mathsf {AT}: \mathsf {\mathcal {DU}\text {-alg}}\rightarrow \varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) is a left adjoint to the functor \(K:\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\rightarrow \mathsf {\mathcal {DU}\text {-alg}}\).
Proof. Let \(X \in \varOmega \text {-}\mathsf {Cat}\) and \(A \in \mathsf {\mathcal {DU}\text {-alg}}\). We have to show that \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}(\mathsf {AT}(A),\) \(X) \cong \mathsf {\mathcal {DU}\text {-alg}}(A,KX)\) which is equivalent to \(\varOmega \text {-}\mathsf {Cat}(X,\mathsf {At}(A)^\mathrm {op}) \cong \mathsf {\mathcal {DU}\text {-alg}}(A,[X,\varOmega ])\), and as \(\varOmega \text {-}\mathsf {Cat}(X,\mathsf {At}(A)^\mathrm {op}) \cong \varOmega \text {-}\mathsf {Cat}(X^\mathrm {op},\mathsf {At}(A))^\mathrm {op}\), see [7, 2.28], we have to prove that there is a natural isomorphism between
which is Theorem 27.
After having constructed a left adjoint \(\mathsf {AT}\) of K, we next ask when \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) is a full reflective subcategory of \(\mathsf {\mathcal {DU}\text {-alg}}\), that is, we ask when K is fully faithful. We also want to characterise the image of K and describe the subcategories of \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) and \(\mathsf {\mathcal {DU}\text {-alg}}\) on which the adjunction restricts to an equivalence.
4.2 A Fully Faithfulness of the Comparison and Its Image
In the case of \(\varOmega = \mathbbm {2}\) the comparison K is fully faithful, but this is not true for all commutative quantales \(\varOmega \). In this subsection, we give necessary and sufficient conditions for K to be fully faithful and describe its image.
Using Proposition 3 we notice that K is faithful on \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}(X,Y)\) if and only if X is anti-symmetric. Indeed, if X is not anti-symmetric let \(g_1,g_2:Y \rightarrow X\) be two distinct equivalent maps. Then as \(\varOmega \) is we have that \(Kg_1 = Kg_2.\)
For K to be full we need that for any two categories \(X,Y \in \varOmega \text {-}\mathsf {Cat}\) and every map \(H : KX \rightarrow KY\) there exists a map \( h : Y \rightarrow X\) such that \( Kh = H\). Using the adjunction, we have \( K\circ \mathsf {AT}(H) = H\) so if one can make sure that \(\mathsf {At}(KX) \cong X\) and \(\mathsf {At}(KY) \cong Y\) then the functor K will be full. For that we need the following definition [6, 10].
Definition 29
We say that \(X \in \varOmega \text {-}\mathsf {Cat}\) is Cauchy complete if \(X \simeq \mathsf {At}([X,\varOmega ])^\mathrm {op}\). We denote by \(\varOmega \text {-}\mathsf {Cat_{cc}}\) the full subcategory of \(\varOmega \text {-}\mathsf {Cat}\) spanned by the antisymmetric Cauchy complete categories.
Remark 30
-
1.
Let \(\varOmega =[0,\infty ]\) and let Q and R be the rational and real numbers, respectively, with the usual Euclidean metric. Then the map in \(H : [Q,\varOmega ] \rightarrow [R,\varOmega ]\) given by \(H(f)(r)= \lim _n f(q_n)\) where \((q_n)\) is a Cauchy sequence with limit r, is in \(\mathsf {\mathcal {DU}\text {-alg}}\) and cannot be restricted to a map \(\mathsf {At}(H) : R \rightarrow Q\). So K is not full in general.
-
2.
Any poset is Cauchy complete, see [16].
-
3.
As shown in [10], a generalised metric space X is isomorphic to \(\mathsf {At}([X^\mathrm {op},\varOmega ])\) if it is Cauchy complete in the usual sense of metric spaces.
Theorem 31
The comparison functor for the adjunction \([-,\varOmega ]\dashv [-,\varOmega ] : \varOmega \text {-}\mathsf {Cat}\rightarrow \varOmega \text {-}\mathsf {Cat_{cc}}^\mathrm {op}\) is full and faithful.
This result is conceptually important to us. When we started out from the basic picture (3), we were guided by the example \(\varOmega =\mathbbm {2}\), in which \(\varOmega \text {-}\mathsf {Cat_{cc}}=\varOmega \text {-}\mathsf {Cat}\). Therefore we could as well have chosen \(\varOmega \text {-}\mathsf {Cat_{cc}}^\mathrm {op}\) instead of \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) in (3). From this point of view, the theorem confirms that we are free to consider K in (3) to by fully faithful.
To characterise the image of K, we use the description of full reflective subcategories by orthogonality, see [3, Chapter 5.4]. First we need again some definitions.
Definition 32
A functor \(F : A \rightarrow C\) is called dense if \( c = C(F-,c) *F\) for all \(c \in C\).
For more equivalent descriptions of dense functors see [7, Chapter 5].
Definition 33
A category A is called atomic if the atom-inclusion functor \(i_A: \mathsf {At}(A) \rightarrow A\) is dense.
Let us give some example of atomic categories.
Example 34
-
1.
Any finite distributive lattice is atomic.
-
2.
Any presheaf category is atomic as every functor is a colimit of representables.
-
3.
The category \([0,\infty ]\) is atomic if seen as a generalised metric space but not if seen as a poset.
We will need the following property of dense functors.
Lemma 35
If A is cocomplete and the atom-inclusion functor \(i_A : \mathsf {At}(A) \rightarrow A\) is dense then \(A \cong [\mathsf {At}(A)^\mathrm {op},\varOmega ]\).
Proof
Let \(A \in \mathcal {A}\) such that \(i : \mathsf {At}(A) \rightarrow A\) is dense. According to [7, Theorem 5.1] if i is dense then \(\tilde{i} : A \rightarrow [\mathsf {At}(A)^\mathrm {op},\varOmega ],\) defined by \(\tilde{i}a = A(i-,a)\), is fully faithful. So we just have to show that it is essentially surjective. Let \(H : \mathsf {At}(A)^\mathrm {op}\rightarrow \varOmega \), as A is cocomplete \(H *i \) exists, then \(\tilde{i} (H *i) \cong H *\tilde{i}i \cong H *d{\mathsf {At}(A)} \cong H\) thus \(\tilde{i}\) is essentially surjective and so \(A \cong [\mathsf {At}(A)^\mathrm {op},\varOmega ]\).
Theorem 36
An algebra A in \(\mathsf {\mathcal {DU}\text {-alg}}\) is isomorphic to an algebra in the image of K if and only if it is atomic.
Proof
We shall use orthogonality [3, Chapter 5.4]. First let us take X in \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) and show that it is atomic. Let us denote by \(\theta : \mathrm {id}\rightarrow K\mathsf {AT}\) the unit of the adjunction \(\mathsf {AT}\dashv K\). From orthogonality we obtain that for every \(B \in \mathsf {\mathcal {DU}\text {-alg}}\) and any \(f : B \rightarrow X\) we have a unique factorisation through \(\theta _B\), so let us take \(B = X\) and \(f = \mathrm {id}_X\). There exists \( g : [\mathsf {At}^\mathrm {op}(X),\varOmega ] \rightarrow X\) such that g preserves limits and colimits and such that \( g \circ \theta _X = \mathrm {id}_X\). Thus, for every \(x \in X\) one has
Now \(\theta _X(x) = X(-,x): \mathsf {At}^\mathrm {op}(X) \rightarrow \varOmega \) and as every presheaf is a colimit of representables one has
Thus one also has
So, in conclusion, X is atomic as \(i_X : \mathsf {At}(X) \rightarrow X\) is dense. The converse follows from Lemma 35 because \(X \cong [\mathsf {At}^\mathrm {op}(X),\varOmega ]= \mathcal {D}( \mathsf {At}(X)) \) which is \(\mathsf {ccd}\).
Remark 37
In the case \(\varOmega =\mathbbm {2}\), we have \(^\mathrm {op}\mathsf {CCD}=\mathsf {CCD}\) (since the dual of a completely distributive lattice is a completely distributive lattice). But this is not true for general \(\varOmega \). Using results from [4] and reproving them for the enriched case we can show that the categories of \(\mathcal {D}\mathcal {U}\)-algebras and \(\mathcal {U}\mathcal {D}\)-algebras are isomorphic if \(\varOmega \cong \varOmega ^\mathrm {op}\) in \(\varOmega \text {-}\mathsf {Cat}\).
5 Algebras for Operations and Equations
We will show that the categories of algebras for the monads \(\mathcal {D},\mathcal {U},\) and \(\mathcal {D}\mathcal {U}\) are isomorphic to categories of algebras given by operations and equations over \(\mathsf {Set}\).
5.1 Syntactic \(\mathcal {D}\)-algebras and \(\mathcal {U}\)-algebras
Definition 38
By a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra we understand a set A together with a family of unary operations \((v\star \_)_{v \in \varOmega } : A \rightarrow A\) indexed by \(\varOmega \), and a family of operations \( \bigsqcup _K : A ^K \rightarrow A \), where K ranges over all sets, satisfying the following 7 axioms. Dually the notions of a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra is given by a set B together with a family of unary operations \((v\rhd \_)_{v \in \varOmega } : B \rightarrow B\) and for each set K an operation  satisfying the following 7 axioms.
satisfying the following 7 axioms.
-
1.

-
2.
For all \(a \in A\), \(b \in B\) and \(v,w \in \varOmega \)

-
3.
For all \(v \in \varOmega \) and \(a_k \in [K,A]\), \(b_k \in [K,B]\)

-
4.
For all \(a \in A\), \(b \in B\) and \(v_k \in [K,\varOmega ]\)

-
5.
For a set K and function \(J : K \rightarrow \mathsf {Set}\) let us denote with \(\bar{J} = \coprod _{k \in K} Jk\). For each \(k \in K\) let \(a_{k}: J(k)\rightarrow A\) and let \(a:\bar{J}\rightarrow A\) be the map induced by the coproduct. For each \(k \in K\) let \(b_{k}: J(k)\rightarrow B\) and let \(b:\bar{J}\rightarrow B\) be the map induced by the coproduct.

-
6.
Let \(\varDelta \) be the diagonal functor then for any set K and for all \(a \in A\) and \(b \in B\) we have

-
7.
For any two sets J, K and any bijective function \(f:J \rightarrow K\) one has

Before we continue let us fix some notations and give some examples. If the set K is 2 then we put \(\bigsqcup _K = \sqcup \) and  and use infix notation. For any set K by an element \(a_K \) of \(A^K\) we understand any function \( a_K : K \rightarrow A\). If K is finite \(a_K\) can be represented as a tuple \( a_K= (a_1,a_2,...,a_k)\) where \(k = | K |.\)
and use infix notation. For any set K by an element \(a_K \) of \(A^K\) we understand any function \( a_K : K \rightarrow A\). If K is finite \(a_K\) can be represented as a tuple \( a_K= (a_1,a_2,...,a_k)\) where \(k = | K |.\)
Example 39
-
1.
For any quantale \(\varOmega \), the \(\varOmega \)-category \(\varOmega \) is a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra, with \(\bigsqcup \) given by \(\bigvee \) and \(v \star - \) given by \(v \otimes - .\) The fact that this satisfies all the axioms is trivial. In a similar way \(\varOmega \) is also a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra with
 given by \(\bigwedge \) and \(v \rhd - \) given by \( \varOmega (v,-).\)
given by \(\bigwedge \) and \(v \rhd - \) given by \( \varOmega (v,-).\)
-
2.
Any cocomplete \(\varOmega \)-category A is a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra. For any \(v \in \varOmega \) and \(a \in A\) we define \(v \star a \) as the colimit of a weighted by v. And for every set K and any \(a_K \in A^K\) we define \(\bigsqcup _K a_K\) as the colimit of \(a_K\) weighted by constant \(\varOmega \)-functor \(e_K :K \rightarrow \varOmega \) given by \(e_K(k) = e \) for all \(k \in K\). That is equivalent to saying that \(\bigsqcup _K\) is a coend.
-
3.
Any complete \(\varOmega \)-category A is a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)–algebra
-
4.
For any quantale \(\varOmega \) and any \(\varOmega \)-category X the functor category \([X,\varOmega ]\) is a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra and the functor category \([X,\varOmega ]^\mathrm {op}\) is a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra. If \(\varOmega \cong \varOmega ^\mathrm {op}\) then any functor category is both a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \) and a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra.
As any \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra A has a preorder structure on it, given by \(a \le b \Leftrightarrow a \sqcup b = b\). We now show that A also carries a \(\varOmega \)-category structure.
Proposition 40
Any \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra A has a \(\varOmega \)-category structure given by
for all \(a,b \in A.\) Also any \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra B has a \(\varOmega \)-category structure given by
for all \(b,b' \in B.\)
One could ask why we do not define A(a, b) as that \(v \in \varOmega \) such that \( v \star a = b \), and the answer is because \( \star \) is not injective in general. For example, take \( \varOmega = [0,\infty ]\) and note that \( w\star \infty = \infty \) for all \( w \in \varOmega \), thus there is no unique \( w \in \varOmega \) to define \([0,\infty ](\infty ,\infty ) .\)
Example 41
Let us look at \(\varOmega =(( [0,\infty ]\ge ), 0 , + )\). Define \(v \star a = v + a\) and \(\bigsqcup _K (v_1,...,v_k) = \inf _{\mathbb {R}} (v_1,..v_k)\), thus \(\varOmega \) is a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra. Let us check that the \(\varOmega \)-category structure given by Proposition 40 is the usual one. Let \(a,b \in [0,\infty ]\), then one has
Now obviously  . Also let us note that \( \bigwedge \{v \in \varOmega \mid v \ge _\mathbb {R} b - a \} = \infty \).
. Also let us note that \( \bigwedge \{v \in \varOmega \mid v \ge _\mathbb {R} b - a \} = \infty \).
One has two equivalent definitions of a semi-lattice, one using operations and equations, and one saying that a semi-lattice is a complete/cocomplete poset. The \(\varOmega \text {-}\mathsf {Cat}\) analogue is as follows.
Theorem 42
Let A be a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra and B a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra.
-
1.
For any \(v \in \varOmega \) and \(a,b \in A\) we have \(A(v \star a, b) = \varOmega (v, A(a,b))\). Thus \(v\star a\) is the colimit of a weighted by v.
-
2.
The operation \(\bigsqcup _K \) is a coend, in the sense that for any set K one has \(A(\bigsqcup _K a_k, b) = \int _{k\in K} A(a_k,b)\).
-
3.
For any \(v \in \varOmega \) and \(a,b \in B\) we have \(B(a, v \rhd b) = \varOmega (v, A(a,b))\). Thus \(v\rhd b\) is the limit of b weighted by v.
-
4.
The operation
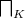 is an end, in the sense that for any set K one has
is an end, in the sense that for any set K one has  .
.
Thus any \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra is co-complete as a \(\varOmega \)-category, and any \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra is complete as a \(\varOmega \)-category.
Definition 43
If \((A, (v \star ^A\_)_{v \in \varOmega }, \bigsqcup ^A_K )\) and \((B,(v \star ^B\_)_{v\in \varOmega }, \bigsqcup ^B_K )\) are \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebras, a map \(f: A \rightarrow B\) is a morphism if f preserves all operations, that is if the following diagrams commute.

Theorem 44
The category \( \langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-alg of \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebras and their morphisms is isomorphic to the category of \(\mathcal {D}\)-algebras, and the category of \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebras and their morphisms is isomorphic to the category of \(\mathcal {U}\)-algebras.
5.2 Syntactic \(\mathcal {D}\mathcal {U}\)-algebras
In order to make the definition of a \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \)-algebra more readable we need some preliminary results. First let us recall the following known fact about lattices.
Lemma 45
Let \((A, (v \star -)_{(v\in \varOmega )}, (\bigsqcup _K)_K)\) be a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra and  be a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra. In particular A is a meet-semi lattice and join semi-lattice, so the order given by these is compatible if and only if we have the following two absorption axioms:
be a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra. In particular A is a meet-semi lattice and join semi-lattice, so the order given by these is compatible if and only if we have the following two absorption axioms:
-
1.
\( a\sqcap ( a \sqcup b) = a \) for all \(a,b \in A \)
-
2.
\( a\sqcup ( a \sqcap b) = a\) for all \(a,b \in A \)
Proposition 46
Let A be simultaneously a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \) and a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra, which satisfies the absorbtion rules defined in the previous lemma, then the \(\varOmega \)-category structures given by A being a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra and a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra are compatible, that is for all \(a,b \in A\) we have \(\bigvee \{ v \in \varOmega \mid v \star a \le _\sqcup b\} = \bigvee \{ v \in \varOmega \mid a \le _\sqcap v \rhd b \}\)
Now we can formulate the following definition.
Definition 47
By a \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \)-algebra we understand, a set A together with two unary family of operations \((v \star -)_{(v\in \varOmega )} : A \rightarrow A\) and \((v \rhd -)_{(v\in \varOmega )} : A \rightarrow A\), and for each set K two K-arity operations \(\bigsqcup _K : A^K \rightarrow A\) and  , such that \((A, (v \star -)_{(v\in \varOmega )}, (\bigsqcup _K)_K)\) is a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra and
, such that \((A, (v \star -)_{(v\in \varOmega )}, (\bigsqcup _K)_K)\) is a \(\langle \varSigma _\mathcal {D}, E_\mathcal {D}\rangle \)-algebra and  is a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra satisfying the following equations:
is a \(\langle \varSigma _\mathcal {U}, E_\mathcal {U}\rangle \)-algebra satisfying the following equations:
-
1.
\( a\sqcap ( a \sqcup b) = a \) for all \(a,b \in A \)
-
2.
\( a\sqcup ( a \sqcap b) = a\) for all \(a,b \in A \)
-
3.
for any \(v \in \varOmega \) and any \(a,b \in A \) one has \( (v \star a) \le b \Leftrightarrow a \le (v \rhd b)\)
-
4.
for any set K and any functions \( \varphi : K \rightarrow \varOmega \) and \(G : K \times A \rightarrow \varOmega \)
 (13)
(13)where \(\{\varphi ,{\downarrow } G(-,a)\}\) is a limit computed in \(\varOmega \) with \({\downarrow } G(k) : A^\mathrm {op}\rightarrow \varOmega \) given by \({\downarrow } G(k) = \mathrm {Lan}_i G = \int ^{b \in A} A(-,i(b)) \otimes G(k)(b)\) for \(i : | A | \rightarrow A^\mathrm {op}\) the object inclusion functor.
Remark 48
-
1.
As we will see below a \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \)-algebra A can be translated into a \(\mathcal {D}\mathcal {U}\)-algebras \((A,\alpha ,\beta )\). Under this translation, Axiom (13) becomes
$$\begin{aligned} \{\varphi ,\alpha \circ {\downarrow } G\} = \alpha (\{\varphi ,{\downarrow } G\}) \end{aligned}$$stating that \(\alpha \) preserves limits.
-
2.
In the case that \(\varphi \) and G are crisp, that is, they take values in \(\{\bot ,e\}\subseteq \varOmega \), we can identify K with the extension of \(\varphi \) and G(k) with subsets of A so that Axiom (13) becomes
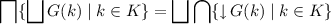
Note that this coincides with the specialisation of Axiom (13) to the case \(\varOmega =\mathbbm {2}\). It expresses that joins perserve meets. As observed in [4] this is equivalent (under the axiom of choice) to the usual distributive law using choice functions. Choice functions allow us to replace the intersection \(\bigcap \{{\downarrow }\, G(k)\mid k\in K\}\), which is a meet in \(\mathcal {D}A\), by a collection of meets in A. Moreover, in case that K and the G(k) are finite, the join \(\bigsqcup \bigcap \{{\downarrow }\, G(k)\mid k\in K\}\) can be replaced by a join indexed over finitely many choice functions, even if A is infinite. Under what circumstances the distributive law (13) can be restricted to a finite one is a question we do not pursue in this paper.
Now let us show that \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) algebras are indeed \(\mathcal {D}\mathcal {U}\)-algebras.
Theorem 49
The category of \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \)-algebras is isomorphic to the category of \(\mathcal {D}\mathcal {U}\)-algebras.
Proof
Let  be a \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) algebra. By Propositions 40 and 46, A has a \(\varOmega \)-category structure. Define \(\alpha : \mathcal {D}A \rightarrow A\) and \(\beta : \mathcal {U}A \rightarrow A,\) by \(\alpha (\varphi ) = \bigsqcup _{|A|} \varphi (a) \star a\) and
be a \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) algebra. By Propositions 40 and 46, A has a \(\varOmega \)-category structure. Define \(\alpha : \mathcal {D}A \rightarrow A\) and \(\beta : \mathcal {U}A \rightarrow A,\) by \(\alpha (\varphi ) = \bigsqcup _{|A|} \varphi (a) \star a\) and  . Using all axioms of Definition 38 and Theorem 42 one shows that \(\alpha \) is a \(\mathcal {D}\)-algebra and \(\beta \) is a \(\mathcal {U}\)-algebra. Moreover, A is complete and cocomplete. Axiom (13) implies that \(\alpha \) preserves all limits, hence has a left adjoint and thus is \(\mathsf {ccd}\). By Theorem 22, \((A,\alpha ,\beta )\) is a \(\mathcal {D}\mathcal {U}\)-algebra.
. Using all axioms of Definition 38 and Theorem 42 one shows that \(\alpha \) is a \(\mathcal {D}\)-algebra and \(\beta \) is a \(\mathcal {U}\)-algebra. Moreover, A is complete and cocomplete. Axiom (13) implies that \(\alpha \) preserves all limits, hence has a left adjoint and thus is \(\mathsf {ccd}\). By Theorem 22, \((A,\alpha ,\beta )\) is a \(\mathcal {D}\mathcal {U}\)-algebra.
For the converse, define \( \star , \) \(\rhd ,\) \(\bigsqcup ,\) and  as the respective (co)limits and show that \(\mathsf {ccd}\) implies Axiom (13).
as the respective (co)limits and show that \(\mathsf {ccd}\) implies Axiom (13).
5.3 \(\varOmega \text {-}\mathsf {Cat}\)-logic
For any (commutative) quantale \(\varOmega \), we have a propositional \(\varOmega \)-logic given by \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \). The language is given by

where p are atomic propositions; \(v\star -\) and \(v \rhd -\) are unary operations; \(\bigsqcup \) and  are K-ary operations for each set K. These operations satisfy the equations listed in Definitions 38 and 47.
are K-ary operations for each set K. These operations satisfy the equations listed in Definitions 38 and 47.
The semantics of these operations wrt a \(\varOmega \)-category X is as follows. If \(F_P\) is the free algebraFootnote 1 over atomic propositions \(p\in P\), then any interpretation of the atomic propositions as many-valued upsets \(X\rightarrow \varOmega \) induces a morphism \([\![-]\!]:F_P\rightarrow [X,\varOmega ]\), which is nothing but a many-valued relation (bimodule)
The values of \(\varOmega \) measure how well a state \(x\in X\) satisfies a specification \(\phi \in F_P\). We say “x satisfies \(\phi \) up to r” if \((x\Vdash \phi )=r\) and “x satisfies \(\phi \)” if r is top. The operations \(\bigsqcup \) and  are join and meet and we have
are join and meet and we have
Reasoning in the \(\varOmega \)-valued setting, we are interested in judgements
which are interpreted as \(F_P(\phi ,\psi ) \ge r\), the latter being equivalent to
for all \(\varOmega \)-categories X and all \(x\in X\).
Example 50
-
1.
In the case of \(\varOmega = \mathbbm {2}\) the operations \(\star \) and \(\rhd \) are redundant and we obtain the equational theory of complete and completely distributive lattices. \(\vdash _0\) is redundant and \(\phi \vdash _1\psi \) means \((x\Vdash \phi ) \Rightarrow (x\Vdash \psi )\) for all X and \(x\in X\).
-
2.
In the case of \(\varOmega = [0,\infty ]\), we write \(\inf \) for \(\bigsqcup \) and \(\sup \) for
 (note the reversal of the order to reflect that distance 0 is top and \(\infty \) is bottom). If x satsifies \(\phi \), then x satsifies \(v\star \phi \) up to v. If x satisfies \(\phi \) up to v, then x satisfies \(v\rhd \phi \). That \([X,\varOmega ]\) is atomic means that arbitrary predicates can be built from “singletons”, \(v\star -\) and \(\bigsqcup \). A judgement \(\phi \vdash _r\psi \) means \((x\Vdash \psi )-(x\Vdash \phi )\le _{\mathbb R} r\) for all X and \(x\in X\).
(note the reversal of the order to reflect that distance 0 is top and \(\infty \) is bottom). If x satsifies \(\phi \), then x satsifies \(v\star \phi \) up to v. If x satisfies \(\phi \) up to v, then x satisfies \(v\rhd \phi \). That \([X,\varOmega ]\) is atomic means that arbitrary predicates can be built from “singletons”, \(v\star -\) and \(\bigsqcup \). A judgement \(\phi \vdash _r\psi \) means \((x\Vdash \psi )-(x\Vdash \phi )\le _{\mathbb R} r\) for all X and \(x\in X\).
6 Conclusions
We have shown in Theorem 49 that for any commutative quantale \(\varOmega \) the category \(\varOmega \text {-}\mathsf {Cat}\) of \(\varOmega \)-categories, or, in other words, the category of \(\varOmega \)-valued generalised metric spaces, is isomorphic to a category of algebras for operations and equation in the usual sense, if we admit operations of infinite unbounded arity.
Moreover, due to the duality underlying our approach, these operations have a logical interpretation and the equations can be seen as logical axioms.
The value of Theorem 49 resides not only in its statement but even more so in how we proved it: We didn’t guess \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) and then proved the theorem, but we derived \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) in a systematic fashion from the functor \([-,\varOmega ]\). We started from the aim to derive the logic of \(\varOmega \)-valued predicates, that is, the logic given implicitely by the structure of the categories \([X,\varOmega ]\). To extract this logical structure, we considered \([X,\varOmega ]\) as algebras for the monad induced by \([-,\varOmega ]\). We then employed a result linking that monad to the ‘semi-lattice’ monads \(\mathcal {D}\) and \(\mathcal {U}\). The algebraic structure of these monads computes limits and colimits and an equational description of these was given as \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \).
It lies in the nature of this method that the logic \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) we derived from \(\varOmega \) is not purely syntactic but still depends on \(\varOmega \). The operations are infinitary and the laws contain side conditions depending on \(\varOmega \). We can think of \(\varOmega \) as an oracle that we need to consult in our reasoning. Restricting to particular, syntactically given \(\varOmega \) and then describing \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) fully syntactically, so that consulting the oracle can be replaced by asking an automated theorem prover, is a task of future research.
In future work, finitary versions of the \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) will be investigated. Extension with tensor and implication will also be of interest. These should be linked with the theory of MV-algebras. Properties of \(\langle \varSigma _\mathcal {DU}, E_\mathcal {DU}\rangle \) and their finitary versions should be linked with properties of \(\varOmega \). Moerover, it needs to be investigated how to integrate the propositional \(\varOmega \)-logics with the modalities arising from coalgebraic type functors.
Notes
- 1.
Here we make use of the fact that due to complete distributivity free algebras exist, even though the signature has operations of unbounded arity.
References
Beck, J.: Distributive laws. In: Eckmann, B. (ed.) Seminar on Triples and Categorical Homology Theory. Lecture Notes in Mathematics, vol. 80, pp. 119–140. Springer, Berlin (1969)
Bílková, M., Kurz, A., Petrisan, D., Velebil, J.: Relation lifting, with an application to the many-valued cover modality. Log. Methods Comput. Sci. 9(4) (2013)
Borceaux, F.: Handbook of Categorical Algebra 1, vol. 1. Cambridge University Press, Cambridge (1994)
Fawcett, B.W., Wood, R.J.: Constructive complete distributivity I. In: Mathematical Proceedings of the Cambridge Philosophical Society (1990)
Hofmann, D.: Duality for distributive space (2010). arXiv:1009.3892v1
Kelly, G.M., Schmitt, V.: Notes on enriched categories with colimits of some class. Theor. Appl. Categ. 14, 399–423 (2005)
Kelly, M.: Basic Concepts of Enriched Category Theory
Kock, A.: Monads for which structures are adjoint to units. J. Pure Appl. Algebra 104(1), 41–59 (1995)
Lai, H., Zhang, D.: Many-Valued Complete Distributivity (2006)
Lawvere, F.: Metric spaces, generalized logic and closed categories. Rendiconti del Seminario Matematico e Fisico di Milano, XLIII. Republished in Reprints in Theory Appl. Categ. (1973)
Mac Lane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics. Springer, New York (1971)
Marmolejo, F.: Doctrines whose structure forms a fully faithful adjoint string. Theor. Appl. Categ. 3, 24–44 (1997)
Marmolejo, F., Rosebrugh, R., Wood, R.J.: A basic distributive law. J. Pure Appl. Algebra 168(2), 209–226 (2002)
Pu, Q., Zhang, D.: Categories enriched over a quantaloid: algebras. Theor. Appl. Categ. 30, 751–774 (2015)
Rosenthal, K.I.: Quantales and Their Applications. Pitman Research Notes in Mathematics Series, vol. 234. Longman Scientific & Technical, Harlow (1990)
Rosolini, G.: A note on cauchy completeness for preorders
Rutten, J.J.M.M.: Elements of generalized ultrametric domain theory. Theoret. Comput. Sci. 170(1–2), 349–381 (1996)
Rutten, J.J.M.M.: Relators and metric bisimulations (extended abstract). In: CMCS 1998, vol. 11 (1998)
Stubbe, I.: The double power monad is the composite power monad. Technical report, LMPA, Université du Littoral-Côte d’Opale (2013)
Vickers, S.: The double powerlocale and exponentiation: a case study in geometric reasoning. Theor. Appl. Categ. 12, 372–422 (2004)
Vickers, S.: Localic completion of generalized metric spaces I. Theor. Appl. Categ. 14, 328–356 (2005)
Vickers, S.: Localic completion of generalized metric spaces II: powerlocales. J. Log. Anal. 1(11), 1–48 (2009)
Vickers, S., Townsend, C.: A universal characterization of the double powerlocale. Theoret. Comput. Sci. 316, 297–321 (2004)
Worrell, J.: Coinduction for recursive data types: partial order, metric spaces and omega-categories. In: CMCS 2000, vol. 33 of ENTCS (2000)
Acknowledgement
The second author acknowledges the influence of J. Velebil through a long-standing collaboration on enriched coalgebraic logic and his deep insights into the subject. In particular, our derscription of \(\varOmega \text {-}\mathsf {Cat}^\mathrm {op}\) by operations and equations confirms his suggestion that the propositional logic of \(\varOmega \text {-}\mathsf {Cat}\) should have operations corresponding the the categorical (co)limits of tensor and cotensor.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Babus, O., Kurz, A. (2016). On the Logic of Generalised Metric Spaces. In: Hasuo, I. (eds) Coalgebraic Methods in Computer Science. CMCS 2016. Lecture Notes in Computer Science(), vol 9608. Springer, Cham. https://doi.org/10.1007/978-3-319-40370-0_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-40370-0_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-40369-4
Online ISBN: 978-3-319-40370-0
eBook Packages: Computer ScienceComputer Science (R0)












 given by
given by 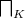 is an end, in the sense that for any set K one has
is an end, in the sense that for any set K one has  .
.
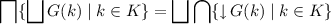
 (note the reversal of the order to reflect that distance 0 is top and
(note the reversal of the order to reflect that distance 0 is top and