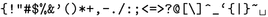Abstract
Cryptanalytic time-memory trade-offs (TMTO) are famous tools available in any security expert toolbox. They have been used to break ciphers such as A5/1, but their efficiency to crack passwords made them even more popular in the security community. While symmetric keys are generated randomly according to a uniform distribution, passwords chosen by users are in practice far from being random, as confirmed by recent leakage of databases. Unfortunately, the technique used to build TMTOs is not appropriate to deal with non-uniform distributions. In this paper, we introduce an efficient construction that consists in partitioning the search set into subsets of close densities, and a strategy to explore the TMTOs associated to the subsets based on an interleaved traversal. This approach results in a significant improvement compared to currently used TMTOs. We experimented our approach on a classical problem, namely cracking 7-character NTLM Hash passwords using an alphabet with 34 special characters. This resulted in speedups ranging from 16 to 76 (depending on the input distribution) over rainbow tables, which are considered as the most efficient variant of time-memory trade-offs.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Security experts are often facing the problem of guessing secret values such as passwords. Performing an exhaustive search in the set of possible secrets is an ad-hoc approach commonly used. In practice, the search time can usually be reduced (on average) by exploiting side information on the values to be guessed. For example, a password cracker checks the most commonly used passwords and their variants before launching an exhaustive search. This optimization is very effective, as described in [7, 15]. More generally, the distribution of the secrets can be exploited to reduce the average cryptanalysis time [14].
An alternative to an exhaustive search is the cryptanalytic time-memory trade-off (TMTO) technique, introduced by Hellman in 1980 [9]. It consists for an adversary in precalculating values that are then used to speed up the attack itself. The precalculation is quite expensive but they are done once, and the cryptanalysis time is significantly reduced if a large memory is used to store the precalculation. Nowadays, TMTOs are used by most password crackers, for example Ophcrack that is considered to be the most efficient password cracker, which implements a TMTO variant due to Oechslin [16] and known as the rainbow tables.
Unfortunately, TMTOs do not behave well with non-uniform distributions of secrets because TMTOs, by construction, uniformly explore the set of considered secrets. Duplicating secrets in the search set for instance artificially creates a non-uniform distribution but this approach does not make sense in practice due to the excessive waste of memory. Providing an efficient solution would be very impactful in practice, though, not only for cracking passwords, but also for solving any problem that can be reduced to a chosen plaintext attack. For example, anonymization techniques based on hashing email addresses or MAC addresses are vulnerable targets for non-uniform TMTOs.
This paper introduces a technique to make cryptanalytic time-memory trade-offs compliant with non-uniform distributions. More precisely, the approach consists in (i) dividing a set into subsets of close densities, and (ii) exploring the related time-memory trade-offs in an interleaved way (instead of sequentially) defined by a density-related metric. The technique significantly improves the cryptanalysis time when considering non-uniform distributions: we applied our technique to crack passwords and demonstrated that we are up to 76 times faster than state-of-the-art techniques [16] when considering real-life password distributions.
After an introduction to TMTOs in Sect. 2, we describe and analyze our technique in Sect. 3 and explain how to interleave the TMTOs in Sect. 4. Section 5 explains the memory allocation, and Sect. 6 provides experimental results.
2 Cryptanalytic Time-Memory Trade-Offs
2.1 Hellman Scheme
Hellman introduced in [9] a method to do an efficient cryptanalysis of a one-way function, the cryptanalytic time-memory trade-off (or TMTO). Given y, the goal is to discover x such that \(h(x) = y\), with \(h:A\rightarrow B\) a one-way function (such as a hash function or a block cipher). As its name suggests, it is a trade-off between two simple solutions, the exhaustive search and the lookup table. The exhaustive search consists in computing h over all possible input values in A, checking every time if the image corresponds to y. It requires no memory or precalculation, but on average |A| / 2 evaluations of h. The lookup table approach creates offline a huge table mapping all inputs in A with their image through h. During the online phase (when queried with an image), this approach requires no h evaluation and is very quick, but the precalculation cost is \(N = |A|\) evaluations of h, and more importantly the N mappings are saved in memory. Hellman’s method on the other hand, has an offline cost of O(N), and an online cost of \(O(N^2/M^2)\) for M units of memory.
2.2 Oechslin Scheme
There has been quite a few variants to Hellman’s method, but arguably the most significant improvement is the rainbow table, introduced by Oechslin in [16]. Rainbow tables are faster in practice than Hellman tables [12, 16], and are implemented in many popular tools, especially in the password-cracking scene (see e.g. Ophcrack [17], RainbowCrack [20]).
Rainbow tables are heavily inspired from Hellman tables and their behavior is similar. In the offline phase, a series of chains of hashes is built, by alternating \(h:A\rightarrow B\), the hash function to be inverted, and \(r_i:B\rightarrow A\), a reduction function. The goal of the reduction function is to output an arbitrary point in A in an efficient and deterministic way, and with outputs uniformly distributed in A (given inputs uniformly distributed in B). A typical reduction function set is:
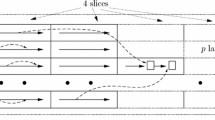
A different reduction function \(r_i\) is used at each iteration i (this is the major difference with Hellman tables where the same reduction function is used in a tableFootnote 1). Chains start with an arbitrary point in A. They are all of a given length t, and m chains are built this way. Of all the points in the chains, only the starting and ending points are saved. Figure 1 depicts the construction of a rainbow table.
Tables are said to be perfect [4, 16] or clean [2] when they contain no merges. A major advantage of rainbow tables over Hellman tables is that in rainbow tables, collisions only result in merges when they happened in the same column (whereas collisions always lead to merges in Hellman tables). In that case, merging chains result in duplicate ending points. It is therefore very easy to remove these chains and create clean tables. Clean tables have a maximal size (on average, only a given number of different ending points may be obtained by computing chains from all possible starting points), and have a bounded probability of success of about 86 %. In order to have a higher probability of success, several rainbow tables are computed, using a different reduction function set for each (a typical number is 4).
The online phase works as follows. Given an image y, the goal is to find x such that \(h(x) = y\). The first step is to compute \(r_{t-1}(y)\), and check whether it appears in the ending points list. If an ending point \(X_{j, t}\) matches \(r_{t-1}(y)\), a chain is rebuilt from \(X_{j, 1}\) up to \(X_{j, t-1}\), and \(h(X_{j, t-1})\) is compared to y. If they are equal, the search stops here and the preimage is \(x = X_{j, t-1}\). If they differ (this situation is called a false alarm and is due to the collisions created by the reduction functions), the search goes on to the next table, where \(r_{t-1}(y)\) is computed for that table. When all tables are searched in the last column, the next step is to compute \(r_{t-1}(h(r_{t-2}(y)))\) and to proceed to the next column. This procedure goes on until the answer is found, or until all t columns are searched through, in which case the search fails (as said previously, the number of tables can be adjusted to make this event extremely rare).
2.3 Related Works
There exists many variants of the original cryptanalytic time-memory trade-off introduced by Hellman [9], in particular the distinguished points [8, 11, 21] and the rainbow tables [16]. The choice on which variant to apply depends on the parameters (space size, memory, probability of success), and the applicability of their various optimizations (see [6, 12, 16] for discussions on their comparison). Lately however, rainbow tables have been shown [12] to be superior to the other trade-offs in most practical scenarios, and maximal tables have the best online performance (despite being slower to precompute). That being said, the interleaving technique discussed in this paper can be easily adapted to other variants or to non-maximal rainbow tables.
Maximal-Sized Rainbow Tables. This work focuses on clean maximal-sized rainbow tables. Clean rainbow tables have been analyzed extensively [4, 12]. Some earlier results on maximal-size rainbow tables from [4] that are relevant for the rest of the analysis are cited below for reference.
Result 1 . The probability of success of a set of \(\ell \) clean rainbow tables of maximal size is:
Result 2 . The average number of h evaluations during a search in column k (column 0 being the rightmost one) of a set of \(\ell \) clean rainbow tables of maximal size with chains of size t is:
with
Result 3 . The average number of h evaluations during the online phase of a set of \(\ell \) clean rainbow tables of maximal size with m chains of size t on a problem set of size N is:
Rainbow Table Improvements. Rainbow tables have had a few improvements of their own. Although they are not considered in this article, they are worth mentioning as they are independent and complementary to the interleaving technique.
Checkpoints, introduced by Avoine, Junod and Oechslin in [3] are additional data related to the chain that is stored alongside the starting points and the ending points. Their goal is to alleviate the overhead due to false alarms at the cost of a bit of extra memory.
Efficient storage is important in time-memory trade-offs, as more chains translates directly into faster online time. Techniques to store starting and ending points efficiently are discussed in [2].
Ending point truncation (as described for instance in [12]) is another effort to reduce memory usage. Truncating the ending points reduces storage required for chains, and thus more chains can be stored in the same amount of memory. A drawback is that it introduces additional false alarms and thus increases online cost somewhat, but a modest amount of truncation has been shown to be valuable.
Non-uniform Distribution. Working with non-uniform distribution is the core aspect of our work, and several approaches have been proposed [10, 13].
A possible means to favor some passwords over some others is to introduce a bias in the reduction functions [10]. However, the technique suffers from implementation issues and is not profitable in practice, as stated in [10].
Markov chains have been used to search through probable passwords instead of improbable ones [13, 15]. This is essentially the adaptation of dictionary attacks on time-memory trade-offs, as it allows to search for some passwords at the expense of not covering some others. Interleaving is different in that it aims at covering a given set, but searching through it in an efficient way, given its probability distribution. As detailed in Sect. 6, we used statistics on common passwords to guide the partitioning of the input set. One could alternatively use the technique described in [13] to determine the partitioning.
3 Interleaving
3.1 Description
The nature of rainbow tables dictates that each point of the input set is recovered using on average the same time. There is no bias in the coverage either: each point is covered a priori with the same probability. In order to work efficiently with a non-uniform input distribution, the technique introduced in this paper consists in (1) dividing the TMTO into several sub-TMTOs and (2) balancing the online search between the sub-TMTOs.
The TMTO is divided into several sub-TMTOs such that each subdivision of the input set is close to be uniform. For instance, if one wants to build a TMTO against passwords containing alphanumeric and special characters, two sub-TMTOs can be built on a partition of the input set: alphanumeric passwords on one side, and passwords containing special characters on the other side. As illustrated on Fig. 2, this makes sense because the first set (\(A_1\)) is considerably larger although most users choose their passwords in the second set (\(A_2\)). We say that the first set has a higher password density than the second one. This density disparity is not exploited in regular TMTOs while Sect. 5 demonstrates that a TMTO covering a high-density subset should be devoted a higher memory.
Formally, let the input set A be partitioned into n input subsetsFootnote 2 \([A]_b\) of size \(|[A]_b| = [N]_b\). Each subset has a probability \(p_b\) that the answer to the challenge in the online phase lies in \([A]_b\). The part of the trade-off dedicated to \([A]_b\) is named “sub-TMTO b”. The memory is divided and a slice \([M]_b = \rho _b M\) is allocated for each sub-TMTO b, where M is the total memory available for the trade-off. Each sub-TMTO b is built on \([A]_b\) using a memory of \([M]_b\), exactly in the same way than a regular TMTO.
In order to search through the sub-TMTOs, one naive approach could be to search through each of them one by one. However, this technique is very slow when the point to recover ends up being in one of the last sub-TMTOs. A more efficient approach consists in balancing the search between the sub-TMTOs: at every step of the online search, the balancer decides which sub-TMTO will be visited, as illustrated in Fig. 3 when 2 sub-TMTOs are considered. The search in a sub-TMTO is performed in the same way than in classical rainbow tables. The order of visits is chosen deterministically in a way that minimizes the average online time, as described in Sect. 4.
3.2 Analysis
Notations. In the analysis done in this article, the same number \(\ell \) of tables is used in each sub-TMTO. It is also possible to use a different number of tables per sub-TMTO, but this results in a different probability of success for each of them.
A step is defined as being a search in one column for the \(\ell \) tables of a given sub-TMTO. One could choose to define a step as being a search in a column for a single table of a given sub-TMTO, but doing so results in a negligible difference of performance at the cost of a more complicated analysis and implementation.
The notations used in this paper are presented in Table 1.
Online Phase
Probability of Success. The probability of success is the same in rainbow tables that use interleaving than in the undivided case, provided clean tables of maximal size are used.
Theorem 1
The probability of success of a set of interleaved clean rainbow tables of maximal size is:
Proof
The probability of success is
with \(P^*_i\) the probability of success of the sub-TMTO i. Since each sub-TMTO is a clean rainbow table of maximal size, we have that \(P^*_i \approx 1 - e^{-2\ell }\), as computed in Result 1. The results follows from \(\sum _{b=1}^n p_i = 1\).
Average Time. The average search time for interleaved rainbow tables is given in Theorem 2. An example of the average speedup realized is given in Sect. 6.
Theorem 2
The average number of hash operations required in the online phase of a set of interleaved clean rainbow tables of maximal size, given a set of n input subset sizes \(\{[N]_1, ..., [N]_n\}\), intrinsic probabilities \(\{p_1, ..., p_n\}\), numbers of chains \(\{[m]_1, ..., [m]_n\}\), and a vector \(V = (V_1, ..., V_{\hat{t}})\) representing the order of visits (i.e. \(V_k\) is the sub-TMTO chosen at step k) is:
with \(\hat{t} = \sum _{b=1}^n [t]_b\) the total maximum number of stepsFootnote 3, and \(S_k\) the number of steps for the sub-TMTO \(V_k\) after k steps in total, that is:
Proof
The formula is a relatively direct adaptation of the average time in the undivided case (Result 3) to the interleaved case. Let y be the given hash in the online phase, and \(x \in A\) be the the preimage of y. The average cryptanalysis time for a TMTO is:
\(V_k\) is the sub-TMTO chosen to visit at some step k. \(V_k\) has been visited \(S_k - 1\) times until step k. The probability \(\Pr (\text {search succeeds at step k})\) is therefore:
The first factor in (2) is simply \(\Pr (x \in [A]_{V_k})\) (the search may not succeed otherwise). Then, for the search to succeed at step k (or step \(S_k\) within the sub-TMTO \(V_k\)), it must have failed up to now. This is the third factor in (2). The expression \(\frac{[m]_{V_k}}{[N]_{V_k}}\) is the probability that x lies within any column of any table of the sub-TMTO \(V_k\), provided that \(x \in [A]_{V_k}\). The expression \(\left( 1 - \frac{[m]_{V_k}}{[N]_{V_k}}\right) ^{(S_k-1)\ell }\) is then just the probability that x is not in any of the \((S_k-1)\ell \) first columns visited, provided that \(x \in [A]_{V_k}\). Finally, the second factor in (2) expresses the probability that x lies within one of the \(\ell \) columns visited at this stepFootnote 4, provided that \(x \in [A]_{V_k}\) and that it has not been found up to now.
The value “cost up to step k” is the sum of the cost of each step up to the current one. For each step \(i \le k\), the sub-TMTO visited is \(V_i\) (and it is its \(S_i\)-th visit), and the associated cost is \([C_{S_i}]_{V_i}\) (see Result 2).
The probability \(\Pr (\text {search fails})\) is:
A failed search means that x is not in any of the \([t]_b\) columns of the sub-TMTO b where b is such that \(x \in [A]_b\). Since the subsets \([A]_i\) form a partition of A, the law of total probability gives (3). The factor \(\left( 1 - \frac{[m]_b}{[N]_b}\right) ^{[t]_b\ell }\) is the probability that x is not in any of the \([t]_b\) columns of the sub-TMTO b, given \(x \in [A]_b\).
Finally, the “cost of a complete search” is the sum of the cost of each step in all sub-TMTOs, that is \(\sum _{b=1}^n\sum _{s=1}^{[t]_b} \ell [C_s]_b\). This expression could also be written \(\sum _{k=1}^{\hat{t}} \ell [C_{S_k}]_{V_k}\), but the former expression is closer to its counterpart in Theorem 3 and also highlights that the cost of failure is independent of the order of visits V.
Note that Theorem 2 for interleaved rainbow tables is a generalization of Result 3 for classical rainbow tables. In particular, if \(n = 1\) and \(V = (1, 1, ..., 1)\) with \(|V| = t\), Theorem 2 gives the same equation as Result 3.
Worst-Case Time. A drawback of the interleaving is that it has in general a worse worst-case time than an undivided TMTO. The worst-case in interleaved rainbow tables corresponds to the second factor of the last term in (1), that is:
Note that it is independent of the subset probabilities and the order of visits.
Offline Phase. Precalculation of an interleaved TMTO consists in precalculation of each sub-TMTO independently. Precalculation of a clean rainbow table set of m chains requires to build \(m_1 = \alpha m\) chains, where \(\alpha \) is a factor depending on how close to tables of maximal size the implementer wants to get (typical numbers for \(\alpha \) are 20–50).
The precalculation cost is the same regardless of the order of visit (since this only regards the online phase), and asymptotically independent of the memory allocation for each sub-TMTO. In particular, it is the same as in the undivided case, as shown in Theorem 3.
Theorem 3
The number of hash operations required in the precalculation phase of a set of interleaved clean rainbow tables, given a set of n input subset sizes \(\{[N]_1, ..., [N]_n\}\), numbers of chains \(\{[m]_1, ..., [m]_n\}\), and given \(\alpha \), the overhead factor for clean tables, is:
Proof
The precalculation consists in computing, for each sub-TMTO b and for each of its \(\ell \) tables, \([m_1]_b = \alpha [m]_b\) chains of \([t_b]\) points.
By replacing the definition of \([t]_b\) for clean tables, we get
The approximation \(\left( \frac{2[N]_b}{[m]_b}-1\right) \approx \frac{2[N]_b}{[m]_b}\) is good because, typically, \([t]_b \gg 1\). For unusually small tables, the cost is slightly overestimated. The conclusion follows from \(\sum _{b=1}^n [N]_b = N\)
Storage. In this analysis, a naive storage consisting in storing both the starting and ending points on \(\lceil \log _2 N\rceil \) bits is used. This explains why the number of chains \([m]_b\) is given as \(\frac{[M]_b}{2\lceil \log _2 N\rceil }\) in Table 1.
Other options could be envisaged, such as storing the starting points on \(\lceil \log _2 [m_1]_b\rceil \) bits and the ending points on \(\lceil \log _2 [N]_b\rceil \) bits, or even better, using prefix-suffix decomposition or compressed delta encoding [2]. These storage techniques improve the memory efficiency and therefore implicitly the global efficiency of the trade-off. In fact, they are even more beneficial for interleaved sub-TMTOs than for an undivided TMTO, because sub-TMTOs operate on smaller subsets, and can therefore benefit from a more substantial reduction of the memory.
However, taking these into account makes both the analysis of interleaved sub-TMTOs and their comparison with an undivided TMTO quite a bit more complex. It is nevertheless strongly encouraged to take these storage improvements into consideration for practical implementations, and for figuring out the optimal memory allocation (as discussed in Sect. 5.2) for such practical implementations.
4 Order of Visit
4.1 Discussion
This section discusses the order of visit of the columns of the sub-TMTOs. Before every step during the search, a decision is made regarding in which sub-TMTO to search through during this step. This decision should be made easily and quickly, and the goal is to have an order of visit that minimizes the average search time.
What is suggested is that a metric is computed for each sub-TMTO b. This metric is defined as being the probability to find a solution in \([A]_b\) at the next step, divided by the average amount of work at the next step in sub-TMTO b (Definition 1).
Definition 1
The metric associated to the k-th step of sub-TMTO b is:
with x, an answer in the online phase.
The sub-TMTO that should be visited is the one with the highest metric. This metric is quantified for the rainbow scheme case in Sect. 4.2.
4.2 Analysis
It has been shown in [4] that the probability for the preimage to be in any column is m / N. This probability is thus independent of the column visited. Moreover, it may be seen from Result 2 that the cost is monotonically increasing towards the left columns in a rainbow table. This means that it is always preferable to visit the rightmost column that is not yet visited first. Therefore, the metric is only computed for each sub-TMTO rather than for each column, since the choice of the column is implicitly the rightmost oneFootnote 5.
Theorem 4
The metric associated to the k-th step of sub-TMTO b is:
Proof
The numerator in Definition 1 is the probability addressed in equation (2) in the proof of Theorem 2. The denominator, the expected work required at step k in sub-TMTO b is denoted \([C_k]_b\), and is computed as indicated in Result 2. Since the search is done in \(\ell \) tables, the total work done at this step on average is \(\ell [C_k]_b\).
The Lemma 1 provided below helps demonstrating Theorem 5.
Lemma 1
The metric \(\eta (b, k)\) from Theorem 4 is a decreasing function of k.
Proof
The numerator of \(\eta (b, k)\) is decreasing, because both \(\left( 1-\left( 1 - \frac{[m]_b}{[N]_b}\right) ^{\ell }\right) \) and \(p_b\) are constant, and because \(\left( 1 - \frac{[m]_b}{[N]_b}\right) ^{(k-1)\ell }\) is decreasing (since \(\frac{[m]_b}{[N]_b} > 0\)).
The denominator is an increasing function of k since the cost of a step is increasingly expensive towards the left of a rainbow table.
Theorem 5
The metric given in Theorem 4 is optimal, that is it minimizes T from Theorem 2 given a set of n input subset sizes \(\{[N]_1, ..., [N]_n\}\), intrinsic probabilities \(\{p_1, ..., p_n\}\) and numbers of chains \(\{[m]_1, ..., [m]_n\}\).
Proof
See Appendix A.
5 Input Set Partition and Memory Allocation
5.1 Input Set Partition
Dividing a set into subsets generates a time overhead for the online phase of the time-memory trade-off. Doing so is worth it if the gain outweighs this overhead. The ratio \(\frac{p_b}{[N]_b}\) represents the individual probability of occurrence for each point of the \([A]_b\) subset, and is intuitively a measure of the “density” of \([A]_b\). It makes sense to divide a set when it contains subsets of unbalanced densities. A TMTO covering a high-density subset should be devoted a higher memory and searched through more rapidly than usual, and vice versa. Once the considered set is partitioned into subsets, one may compute the expected online time given using Theorem 2.
5.2 Memory Allocation
Given a partition \(\{[N]_1, ..., [N]_n\}\) of the input set and their intrinsic probabilities \(\{p_1, ..., p_n\}\), a memory size must be assigned to each subset. Given \([N]_b\), we have \([M]_b = \rho _b M\). The expression T given in Theorem 2 is not simple enough to determine analytically an optimal memory allocation. Instead, the memory allocation can be done solving an optimization problem that consists in minimizing T by changing the variables \(\rho _1, ..., \rho _n\).
When the number of subsets n is small, the memory allocation can be found easily with a grid search. That is, T is evaluated at discretized values of the parameters \(\rho _1, ..., \rho _n\) (with \(\sum _{i=1}^n \rho _i = 1\)), and the point where T is minimal is kept as the selected memory allocation.
This technique however becomes quite costly when the number of subsets n is too large, or when the desired resolution of the discretization is too thin. Metaheuristic techniques of local search such as Hill Climbing [19] can be used instead to search for the optimal memory allocation more efficiently.
6 Results
In this section, the interleaving technique is illustrated on password cracking.
6.1 Statistics
In order to determine the password distribution, two publicly-available datasets have been considered: “RockYou” and “10 million combos”. The RockYou dataset originated from www.rockyou.com, a gaming website that lost 32.6 million unencrypted passwords in 2009. Among those passwords 14.3 million are unique. The 10 million combos was released by Mark Burnett in 2015. This 10 million passwords dataset contains passwords from various hack sources according to the author from which 5.18 million are unique. These datasets are for example used for wordlist attacks by the well-known password crackers Hashcat [1] and John the Ripper [18].
Tables 2 and 3 present some statistics on these datasets (the results are shown up to length of 7). Each cell of the two tables represents the per mille of passwords that have the length indicated on the left, and that correspond to the character set indicated on the top. More precisely: “Special” relates to passwords with at least a special characterFootnote 6,“Lower” to passwords containing only lowercase letters, “Upper” to passwords containing only uppercase letters, “Digit” to passwords containing only digits, “Alpha” to passwords containing only letters (at least one lowercase and one uppercase), “Alnum” to passwords containing letters and digits (at least one letter and one digit). Such statistics can then be used to feed the parameters for the interleaving technique.
6.2 RockYou
We decided to set A to the set of passwords of the special character set (96 characters) of length 7 or less, which corresponds to the same set covered in the “XP special” table of the Ophcrack software [17]. Likewise, we set the total memory to 8 GB, which is about the memory used for this table. With these settings, an undivided TMTO has an average cryptanalysis time of \(T = 6.27\times 10^9\) operations (obtained from Result 3).
We chose the following partition: \([A]_1\) is set to the passwords of length 7 (exactly) that contain at least one special character, and \([A]_2\) the rest of the passwords. This gives the following parameters for the RockYou dataset:
The probabilities are taken from Table 2, and are adjusted such that the sum of probabilities up to length 7 is 1.
Figure 4 represents T according to \(\rho _1\): the memory allocation is optimal when \(\rho _1 = 0.5957\), with \(T=3.81\times 10^8\) operations, which represents a speedup of about 16.45 with respect to the undivided caseFootnote 7.
Memory allocation for the RockYou database: the solid line represents the average number of operations as a function of the proportion \(\rho _1\) of the memory devoted to the first sub-TMTO. The cross mark is the optimal memory allocation, and the dashed line represents the cost of an undivided TMTO, about 16.45 times slower.
6.3 10 Million Combos
This second dataset presents comparable statistics to RockYou. Applying the same partitioning, we have:
This partitioning yields an even better result: \(T = 1.42 \times 10^{8}\) at the optimal memory division \(\rho _1 = 0.4695\), which represents a speedup of 44.29. This further improvement with respect to RockYou is due to \(p_1\) being even smaller in the case of the 10 million combos dataset, which results in a stronger disparity in the densities of \(A_1\) and \(A_2\).
In order to improve further the gain, one may partition A into more subsets. This was tried with three subsets: we sorted the cells of Table 3 in increasing order of density, and chose the partitioning that produced the best results (see Appendix B for details on the subsets chosen). These subsets correspond to:
The average time is of \(8.20 \times 10^{7}\), which represents a speedup of 76.48. The optimal memory decomposition was found using Hill Climbing [19]:
Partitioning into four subsets or more did not yield a better speedup in our experiments.
6.4 Discussion
Interleaving produces a gain over the classical method of 16.45, 44.29 and 76.48, respectively for RockYou with 2 subsets, 10 million combos with 2 subsets, and 10 million combos with 3 subsets. The gain thus strongly depends on the input distribution, and can be arbitrarily big. On the other hand, interleaving may not be profitable at all when the input distribution is close to uniform.
Increasing the number of subsets allows for a finer division of the input set, and is worthwhile when the resulting subsets have important differences of density. It has however an overhead, which means that in practice (at least for the distributions described in Sect. 6.1), the optimal size of the partitioning is relatively small.
Barkan, Biham and Shamir showed [5] that the cost of a search using a time-memory trade-offs is theoretically lower-bounded. With an appropriate input distribution, one could go below that bound using interleaving, which may seem to be in contradiction with the results of [5]. However, these results were provided in a context of uniform input distribution, so the bound is not violated since the assumptions are different.
7 Conclusion
This paper introduces a technique to magnify the efficiency of cryptanalytic time-memory trade-offs when the considered distribution of secrets is non-uniform. It consists – during the precalculation phase – in dividing the input set into smaller subsets of unbalanced densities and applying a time-memory trade-off on every subset. As importantly, the contribution also consists of a method to interleave – during the attack phase – the exploration of the time-memory trade-offs. For that, a metric to select at each step the time-memory trade-off to be explored is introduced, and a proof of optimality is provided.
Questions such as how the efficiency changes when a TMTO built on some distribution is applied to another distribution, or whether it is possible to find optimal memory division analytically remain to be explored.
The efficiency of the technique is practically demonstrated to crack 7-character passwords selected in a 96-character alphabet. Password length and alphabet size have been chosen in compliance with tools currently used by security experts to crack LM Hash passwords. The password distributions used to evaluate the efficiency of the technique come from recently leaked password databases of well-known websites. It has been shown that the time required to crack such passwords is divided by up 76 when the technique introduced in this paper is applied, compared to current methods. The efficiency can be even better when considering distributions with a higher standard deviation. As far as we know, this is the first time an improvement on time-memory trade-off divides by more than two the cracking time since Hellman’s seminal work.
Notes
- 1.
Multiple tables with different reduction functions are used in both Hellman and rainbow tables, although there are much more tables in typical settings for Hellman tables.
- 2.
For notations that already exist for rainbow tables, the convention adopted throughout the article to avoid confusion is to surround them with brackets, as summarized in Table 1.
- 3.
\(\hat{t}\) is used instead of t in order to avoid confusion with the number of columns of the undivided TMTO, which is a different number.
- 4.
Note that one would normally stop the search as soon as x is found rather than continuing with all \(\ell \) tables of this step. This results in a more complex formula for the average time, and a negligible difference numerically.
- 5.
Note that in rainbow tables with checkpoints [3], this is not entirely the case (columns where checkpoints are placed often have a slightly cheaper cost than the the column immediately to their right, for instance). Nevertheless, the search is performed from right to left as well in such tables (see [3]), and experiments show that the gain of reorganizing columns visit for taking this into account is extremely small.
- 6.
Here, a special character is one of
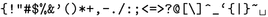
. These are the characters denoted as such in the “XP special” table of the Ophcrack software [17].
- 7.
For instance, in terms of time elapsed on a laptop capable of performing \(3\times 10^6\) SHA-1 operations per second, and on a memory of 8 GB, this corresponds to 34’50” (for the undivided case) reduced to 2’07” (for the interleaved case) on average.
References
Atom: The Hashcat password cracker (2014). http://hashcat.net/hashcat/
Avoine, G., Carpent, X.: Optimal storage for rainbow tables. In: Lee, H.-S., Han, D.-G. (eds.) ICISC 2013. LNCS, vol. 8565, pp. 144–157. Springer, Heidelberg (2014)
Avoine, G., Junod, P., Oechslin, P.: Time-memory trade-offs: false alarm detection using checkpoints. In: Maitra, S., Veni Madhavan, C.E., Venkatesan, R. (eds.) INDOCRYPT 2005. LNCS, vol. 3797, pp. 183–196. Springer, Heidelberg (2005)
Avoine, G., Junod, P., Oechslin, P.: Characterization and improvement of time-memory trade-off based on perfect tables. ACM Trans. Inf. Syst. Secur. TISSEC 11(4), 1–22 (2008)
Barkan, E., Biham, E., Shamir, A.: Rigorous Bounds on cryptanalytic time/memory tradeoffs. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 1–21. Springer, Heidelberg (2006)
Barkan, E.P.: Cryptanalysis of ciphers and protocols. Ph.D. thesis, Technion - Israel Institute of Technology, Haifa, Israel, March 2006
Bonneau, J.: The science of guessing: analyzing an anonymized corpus of 70 million passwords. In: IEEE Symposium on Security and Privacy - S&P 2012, San Francisco, CA, USA. IEEE Computer Society, May 2012
Denning, D.: Cryptography and Data Security, p. 100. Addison-Wesley, Boston (1982)
Hellman, M.: A cryptanalytic time-memory trade off. IEEE Trans. Inf. Theory IT 26(4), 401–406 (1980)
Hoch, Y.Z.: Security analysis of generic iterated hash functions. Ph.D. thesis, Weizmann Institute of Science, Rehovot, Israel, August 2009
Hong, J., Jeong, K.C., Kwon, E.Y., Lee, I.-S., Ma, D.: Variants of the distinguished point method for cryptanalytic time memory trade-offs. In: Chen, L., Mu, Y., Susilo, W. (eds.) ISPEC 2008. LNCS, vol. 4991, pp. 131–145. Springer, Heidelberg (2008)
Lee, G.W., Hong, J.: A comparison of perfect table cryptanalytic tradeoff algorithms. Cryptology ePrint Archive, report 2012/540 (2012)
Lestringant, P., Oechslin, P., Tissières, C.: Limites des tables rainbow et comment les dépasser en utilisant des méthodes probabilistes optimisées (in French). In: Symposium sur la sécurité des technologies de l’information et des communications - SSTIC, Rennes, France, June 2013
Massey, J.L.: Guessing and entropy. In: International Symposium on Information Theory - ISIT 1994, Trondheim, Norway, p. 204. IEEE, June 1994
Narayanan, A., Shmatikov, V.: Fast dictionary attacks on passwords using time-space tradeoff. In: ACM Conference on Computer and Communications Security - CCS 2005, Alexandria, VA, USA, pp. 364–372. ACM, November 2005
Oechslin, P.: Making a faster cryptanalytic time-memory trade-off. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 617–630. Springer, Heidelberg (2003)
Oechslin, P.: The ophcrack password cracker (2014). http://ophcrack.sourceforge.net/
Peslyak, A.: The John the Ripper password cracker (2014). http://www.openwall.com/john/
Russell, S.J., Norvig, P.: Artificial Intelligence: A Modern Approach, vol. 2. Pearson Education, Upper Saddle River (2003)
Shuanglei, Z.: The RainbowCrack project (2014). http://project-rainbowcrack.com/
Standaert, F.-X., Rouvroy, G., Quisquater, J.-J., Legat, J.-D.: A time-memory tradeoff using distinguished points: new analysis & FPGA results. In: Kaliski, B.S., Koç, C.K., Paar, C. (eds.) CHES 2002. LNCS, vol. 2523, pp. 593–609. Springer, Heidelberg (2002)
Acknowledgments
We thank the anonymous reviewers for their constructive comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proof of Theorem 5
For the sake of clarity, the following simplified notations are used in this proof:
Let V be a vector describing an arbitrary order of visit. Let \(V^*\) be a vector describing the order of visit dictated by the metric given in Theorem 4. V is thus an arbitrary permutation of \(V^*\). \(S_k\) (resp. \(S^*_k\)) is defined as in Theorem 2, that is how many times \(V_k\) (resp. \(V^*_k\)) has been visited up to step k included:
Additionally, let \(\sigma (b, k)\) be the position of the k-th apparition of the sub-TMTO b in V (and \(\sigma ^*(b, k)\) its \(V^*\) equivalent). In particular, the following identity binds these notations:
The goal is to minimize (1), that is:
Note that the second term of this expression is constant, regardless of the choice for V. Therefore, in order to prove the optimality of the metric and thus the optimality of the choice of \(V^*\), it suffices to show that \(G \ge G^*\), with:
and with V any permutation of \(V^*\). Equation 5 can be re-written such that sub-TMTOs are considered in consecutive order rather than considering them in the order of visit (this is a mere re-ordering of the terms in the sum):
and likewise for the sum in (6). It is now possible to factorize the difference \(G - G^*\) as such:
Some terms cancel each other out in the two sums of the bracketed factor in (7), i.e. terms that appear in both sums. Let \(\Delta ^+_{b, k}\) (resp. \(\Delta ^-_{b, k}\)) be the set of positions in V (resp. \(V^*\)) that only appear in the left (resp. right) sum. Formally,
This allows to rewrite the difference (7) as:
By construction, the following implication holds between \(\Delta ^+\) and \(\Delta ^-\):
Indeed, we have:
The first equivalence is the definition of \(\Delta ^+_{b, k}\), and the second comes from the fact that \(V_{\sigma (b, k)} = b\) and \(S_{\sigma (b, k)} = k\), by definition of V and S. Likewise,
The implication (9) comes from the equivalence between (10) and (11). As a particular case of (9), we have:
This means that for each negative term \(-f(b, k) g(V^*_j, S^*_j)\) in (8), there is also a positive counterpart \(f(V^*_j, S^*_j) g(b, k)\). This allows to rewrite the difference (8) as a simple sum of opposed crossed terms:
We have that \(\sigma ^*(b, k) > j = \sigma ^*(V^*_j, S^*_j)\), for all \(j \in \Delta ^-_{b, k}\), by definition of \(\Delta ^-_{b, k}\). Moreover, since the metric used to construct \(V^*\) is decreasing (see Lemma 1), we have that:
for all \(b, k, b', k'\) such that \(\sigma ^*(b, k) < \sigma ^*(b', k')\). Using this fact in (12) shows that each term of the sum is positive, and thus \(G \ge G^*\).
B Subsets of 10 Million Combos
The partition in three subsets that yields the best speedup on the 10 million combos dataset is depicted in Table 4.
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Avoine, G., Carpent, X., Lauradoux, C. (2015). Interleaving Cryptanalytic Time-Memory Trade-Offs on Non-uniform Distributions. In: Pernul, G., Y A Ryan, P., Weippl, E. (eds) Computer Security -- ESORICS 2015. ESORICS 2015. Lecture Notes in Computer Science(), vol 9326. Springer, Cham. https://doi.org/10.1007/978-3-319-24174-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-24174-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-24173-9
Online ISBN: 978-3-319-24174-6
eBook Packages: Computer ScienceComputer Science (R0)