Branching for General Relativists

Abstract

The chapter develops a theory of branching spatiotemporal histories that accommodates indeterminism and the insights of general relativity. A model of this theory can be viewed as a collection of overlapping histories, where histories are defined as maximal consistent subsets of the model’s base set. Subsequently, generalized (non-Hausdorff) manifolds are constructed on the theory’s models, and the manifold topology is introduced. The set of histories in a model turns out to be identical with the set of maximal subsets of the model’s base set with respect to being Hausdorff and downward closed (in the manifold topology). Further postulates ensure that the topology is connected, locally Euclidean, and satisfies the countable sub-cover condition.

1 Introduction

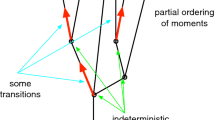
In 1992 Nuel Belnap put forward the branching space-times theory (BST1992) that offered a unified treatment of rudimentary relativistic spacetimes and indeterminism.¹ Building on earlier works on a more frugal theory of branching time (BT), BST1992 represents indeterminism by means of a collection of overlapping histories; in contrast to the linear histories of the former, however, histories are complex objects in BST1992. As a consequence, there are models of BST1992, in which histories are isomorphic to the Minkowski spacetime (see Placek and Belnap (2012)). BST1992 can be used to model quantum experiments with non-local correlations (Placek 2010). Furthermore, a branching reading can be given to the consistent histories formulation of quantum mechanics (see Müller (2007)).

This bright picture, however, has been marred by a tension between BST1992 and general relativity (GR). There are serious obstacles to accommodating GR in the branching framework, the most important of which, I believe, is a difference in spirit. The great perception of GR is that coordinalization works by patches: this theory permits the assignments of coordinates (elements of ${\mathbb {R}}^n$) to subsets (patches) of the totality of events, with the proviso that the patches cover the totality of events. Local coordinalization by patches is to be contrasted with a global coordinalization, as provided by a mapping of a whole spacetime on ${\mathbb {R}}^n$. Patches, if sufficiently small, have familiar and desirable properties. In essence, they look like subspaces of Minkowski spacetime,² which in turn permits a definition of a partial ordering on a patch. Typically these nice properties do not transform to a GR spacetime as a whole, however.

In contrast, BST1992 does not work in terms of local patches. This theory assumes a partial ordering on its base set, and defines history (aka BST spacetime) as a maximal upward directed subset of the base set. With some extra assumptions added, a BST1992 history can be mapped on ${\mathbb {R}}^n$. Even if one wants to do coordinalization in a piecemeal way, there is no structure in BST1992 that could play the role of patches.

Apart from this difference in spirit, there are technical issues as well: First, the ordering assumed in BST1992 is partial, whereas the natural ordering of a GR spacetime, defined in terms of geodesics, is not necessarily so: it allows for a failure of anti-symmetry. Second, the BST1992 criterion for historicity (or, belonging to one BST spacetime), i.e., being maximally upward directed, flies in the face of some well-studied GR spacetimes, like the Schwarzschild spacetime or the de Sitter cosmological model. The criterion rules out as well some intuitive, although non-physical, candidates for a spacetime since it implies that for two events $x$ and $y$ to belong to some one spacetime, there should be a “later witness”, that is, some $z$ such that $x \leqslant z$ and $y \leqslant z$. Consequently, an open square or an open half-plane ${\mathbb {R}}^- \times {\mathbb {R}}$, both with Minkowskian ordering, cannot be BST1992 spacetimes.³ A sought-for generalization of BST1992 should thus modify the criterion for historicity appropriately. (For a discussion as to how one can modify the BST1992 notion of history, see Müller (2013).)

The first attempt to overcome the tensions between GR and BST1992 is Müller (2011). The present chapter continues this work in a somewhat different way, by first generalizing BST1992 appropriately, then defining generalized manifolds on models of generalized BST and, finally, by producing tangent vector spaces.

Although the main aim of this chapter is to offer a GR-friendly generalization of BST1992, I begin by addressing an objection to BST1992. As John Norton once said, physical theories do not offer the kind of branching that BST1992 assumes.⁴ Indeed, the pattern of branching implied by the axioms of BST1992 is particular: If a maximal chain in a base set passes through a maximal element in the overlap of some two histories, then obviously the segment of the chain contained in the overlap has a maximum and, hence, a supremum. But if a maximal chain does not pass through a maximal element in the overlap, the chain’s segment contained in the overlap does not have a supremum, but rather two history-relative suprema. Instead of addressing the objection head-on, I argue that a slight modification of BST1992 axioms yields another pattern of branching, which appears to be better suited for a GR-friendly version of BST. In this discussion I introduce choice pairs, a valuable tool for the generalized BST, described in later sections.

The chapter is organized as follows. Section 2 puts forward a version of branching space-times that yields a different pattern of branching histories. Section 3 discusses how BST1992 should be generalized: its basic idea is that topological features of BST1992 should be preserved by the generalization. To this end, this section offers a summary of the topological properties of BST1992 models. Sections 4.1, 4.2, and 4.3 put forward a three-tiered construction of (1) generalized BST models, then (2) generalized manifolds built on these models, and finally, (3) vector spaces of tangent vectors. The next, Sect. 5, addresses some paradoxical issues concerning generalized manifold. Section 6 concludes the chapter with an overview of the chapter’s result.

2 BST with a New PCP

Let us recall the basic definitions of BST1992:

A model of BST1992 is a nonempty partial order ${\mathcal {W}} = \langle W, \leqslant \rangle$ that satisfies the axioms below, with histories in ${\mathcal {W}}$ defined as maximal upward directed subsets of $W$. The axioms are as follows:

• 1. ${\mathcal {W}}$ has no maximal elements;

• 2. $\leqslant$ is dense;

• 3. every lower bounded chain has an infimum in ${\mathcal {W}}$;

• 4. every upper bounded chain has a supremum in every history that contains it;

• 5. for a chain $C$ in ${\mathcal {W}}$: if $C \subseteq h/h'$, then there is a maximal element in $h\cap h'$ strictly below $C$ (such a maximal element is called a choice point for $h$ and $h'$; this axiom is called Prior Choice Principle—PCP).

We say that two histories, $h, h'$ are divided at $e$ if $e$ is a maximal element of the intersection $h \cap h'$. And we say that two histories, $h, h'$ are undivided at $e$ if $e\in h \cap h'$ but is not a maximal element of $h \cap h'$. Provably undividedness at $e$ is an equivalence relation on the set of histories containing $e$. The equivalence classes with respect to this relation are called “elementary possibilities open at $e$”.

A particular pattern of branching mentioned above (aka passive indeterminism or indeterminism without choice—see Placek and Belnap (2012)) is a consequence of PCP. To illustrate, consider a two-history model, with a single choice point $c$, and with histories identified with planes (i.e., ${\mathbb {R}}^2$), the ordering being Minkowskian. PCP then dictates, first, that the “wings” of the choice point $c$, that is, the set of events space-like related to $c$, are in the overlap of the two histories. Second, it prohibits points on the future light cone above $c$ to belong to the overlap; otherwise $c$ would not be maximal in the overlap, i.e., not a choice point.

Our idea is thus to replace PCP by a somewhat different principle, while keeping intact all the other axioms of BST1992.⁵ Our new principle postulates the existence of minimal pairs of a particular kind rather than maximal elements in the overlap of histories. As we will see, it enforces a different pattern of branching.

Pairs supreme, hot pairs, and choice pairs. In what follows, we assume tentatively the notion of BST1992 models, with PCP removed.

Definition 1

(pairs supreme) For $s, s' \in W$, we say that $\{ s, s'\}$ is a pair supreme for histories $h, h'$, to be written as $\{ s, s'\} \in \mathfrak {S}(h, h')$, iff $\exists C ( C \ne \emptyset \wedge C \subseteq h \cap h' \wedge s = \sup _{h}(C) \wedge s' = \sup _{h'}(C))$, where $C$ is an upper bounded chain in ${{\mathcal {W}}}$.

$\{ s, s'\}$ is a pair supreme simpliciter, to be written as $\{ s, s'\} \in \mathfrak {S}$, iff $\{ s, s'\} \in \mathfrak {S}(h, h')$ for some histories $h, h'$.

Note that the definition allows for a pair supreme $\{s, s'\}$ with identical elements, i.e., $s = s'$, as well as for a pair supreme with distinct elements. To capture the latter case, we define ‘hot pairs’:

Definition 2

(hot pair) For $s_1, s_2 \in W$, $\{ s_1, s_2\}$ is a hot pair for histories $h, h'$, to be written as $\{ s_1, s_2\} \in \mathfrak {H}(h_1, h_2)$, iff $\{ s_1, s_2\} \in \mathfrak {S}(h, h')$ and $s_1 \ne s_2$. And we say that $\{ s, s'\}$ is a hot pair simpliciter, to be written as $\{ s, s'\} \in \mathfrak {H}$, iff $\{ s, s'\} \in \mathfrak {H}(h, h')$ for some histories $h$ and $h'$.

Hot pairs decide between histories in the sense that an event above an element of a hot pair for two histories cannot belong to both these histories.

Fact 3.

If $\{ s_1, s_2\} \in \mathfrak {H}(h_1, h_2)$ and $s_i \leqslant e$ for some $i =1, 2$, then $e \not \in h_1\cap h_2$.

Proof   Obvious. Since histories are downward closed, $e \in h_1\cap h_2$ and $s_i \leqslant e$ imply $s_i \in h_1 \cap h_2$, which implies $s_1 = s_2$: a contradiction with $\{ s_1, s_2\}$ being a hot pair. $\square$

We next define an ordering of pairs supreme (simpliciter):

Definition 4

(ordering of pairs supreme) Let $s, t \in \mathfrak {S}$, where $s = \{ s_1, s_2\}$ and $t = \{ t_1, t_2\}$. We define $s \curlyeqprec t$ iff ${\exists }_{i, j \in \{ 1, 2\}}\,s_i \leqslant t_j \wedge s_{\tilde{\imath }}\leqslant t_{\tilde{\jmath }}$, where the tilde function means that ${\tilde{n}}= 1$ or $2$ iff $n = 2$ or $1$, resp. $s \prec t$ means that $s \curlyeqprec t$ but $s \ne t$.

We need to persuade ourselves that $\curlyeqprec$ is a partial ordering.

Fact 5.

$\curlyeqprec$ is a reflexive, anti-symmetric, and transitive relation on $\mathfrak S(h_1, h_2)$.

Proof   Let $s, t, u \in \mathfrak {S}$, where $s = \{ s_1, s_2\}$, $t = \{ t_1, t_2\}$, and $u = \{u_1, u_2\}$. It is immediate to see that $s \curlyeqprec s$ (reflexivity). To prove anti-symmetry, let $s \curlyeqprec t$ and $t \curlyeqprec s$, which entails $s_i \leqslant t_j \wedge s_{\tilde{\imath }}\leqslant t_{\tilde{\jmath }}$ and $t_m \leqslant s_n \wedge t_{\tilde{m}}\leqslant s_{\tilde{n}}$, for some $i, j, m, n \in \{1, 2\}$. If $j = m$, then $s_i \leqslant t_j \leqslant s_n$, and since $s_i \leqslant s_n$ implies $s_i = s_n$, we get $s_i = t_j$. We also have ${\tilde{\jmath }}= {\tilde{m}}$, which implies, by a similar argument, that $s_{\tilde{\imath }}= t_{\tilde{\jmath }}$. Putting the two together, we get $\{s_1, s_2 \} = \{t_1, t_2 \}$. If $j \ne m$, then ${\tilde{\jmath }}= m$, so $s_{\tilde{\imath }}\leqslant t_m \leqslant s_n$, hence $s_{\tilde{\imath }}= s_n$ and then $t_m = s_n$. But also $j = {\tilde{m}}$, so $s_i \leqslant t_{\tilde{m}}\leqslant s_{\tilde{n}}$, and hence $t_{\tilde{m}}= s_{\tilde{n}}$. Thus $\{s_1, s_2 \} = \{t_1, t_2 \}$.

Turning to transitivity, let $s \curlyeqprec t$, $t \curlyeqprec u$, and these relations be witnessed by $s_i \leqslant t_j \wedge s_{\tilde{\imath }}\leqslant t_{\tilde{\jmath }}$ and $t_m \leqslant u_n \wedge t_{\tilde{m}}\leqslant u_{\tilde{n}}$, for some $i, j, m, n \in \{1, 2\}$. If $j = m$ (and hence ${\tilde{\jmath }}= {\tilde{m}}$), it follows that $s_i \leqslant t_j \leqslant u_n$ and also $s_{\tilde{\imath }}\leqslant t_{\tilde{\jmath }}\leqslant u_{\tilde{n}}$, whence $s \curlyeqprec u$. And, if $j \ne m$ (and hence ${\tilde{\jmath }}= m$ and $j = {\tilde{m}}$), we get $s_{\tilde{\imath }}\leqslant t_{\tilde{\jmath }}\leqslant u_n$, and $s_i \leqslant t_{\tilde{\jmath }}\leqslant u_{\tilde{n}}$, so $s_{\tilde{\imath }}\leqslant u_n$ and $s_i \leqslant u_{\tilde{n}}$, whence $s \curlyeqprec u$. $\square$

We next use this ordering to define choice pairs for histories:

Definition 6

(choice pairs) For $s_1 s_2 \in W$, $\{ s_1, s_2\}$ is a choice pair for histories $h_1, h_2$, to be written as $\{ s_1, s_2\} \in \mathfrak {C}(h_1, h_2)$, iff $\{ s_1, s_2\}$ is a minimal element (wrt $\curlyeqprec$) in the set $\mathfrak {H}(h_1, h_2)$ of hot pairs for $h_1$ and $h_2$. We say that $\{s_1, s_2\}$ is a choice pair simpliciter iff there are histories $h_1, h_2$ such that $\{s_1, s_2\} \in \mathfrak {C}(h_1, h_2)$.

Having the required notions, we now introduce a substitute for the prior choice principle of BST1992, and we will refer to it by PCP$^*$:

Postulate 7

(PCP*). If $C$ is a chain in ${{\mathcal {W}}}$ and $C \subseteq h_1\setminus h_2$ for some histories $h_1, h_2$, then there is a choice pair $\{ s_1, s_2\} \in \mathfrak {C}(h_1, h_2)$ such that $s_1 \leqslant C$.⁶

PCP$^*$ postulates choice pairs, where the old PCP postulated choice points. Observe that in contrast to PCP, we need the weak ordering in $s_1 \leqslant C$ above. If $C$ is a one-element chain, i.e, $C = \{e\}$ for some $e \in W$, and $\{ e, e' \}$ is a choice pair for $h_1$ and $h_2$, there is clearly no choice pair for $h_1, h_2$ strictly below $\{e, e'\}$.

In the rest of this section we will work with a modified version of BST1992, which results from the definition of models of BST1992, with PCP replaced by PCP$^*$. We call this modified version: BST$^*$1992.

Let us next define in BST$^*$1992 the notions of dividedness and undividedness of histories:

Definition 8

(dividedness and undividedness) Let $\{ s, s'\}$ be a pair supreme (simpliciter). Then histories $h_1$ and $h_2$ divide at $\{ s, s'\}$, $h_1 \perp _{ss'} h_2$, iff $\{ s, s' \}$ is a choice pair for $h_1, h_2$, i.e., $\{ s, s' \} \in \mathfrak {C}(h_1, h_2)$.

Histories $h_1$ and $h_2$ are undivided at $\{ s, s'\}$, $h_1 \equiv _{ss'} h_2$ iff $s \in h_1 \cap h_2$ or $s' \in h_1 \cap h_2$ or $\{ s, s' \}$ is a hot pair for $h_1, h_2$, but not a choice pair for $h_1, h_2$.

The first line of the above definition decides a category of objects at which histories are divided or undivided: at pairs supreme simpliciter. Note an asymmetry, however: for two histories to be divided at a pair supreme, this pair supreme must be a choice pair for these histories. In contrast, two histories may be undivided at a pair supreme, which is not a pair supreme for these histories. Clearly, $\perp _{ss'}$ and $\perp _{s's}$ denote the same relation, and this is also true about $\equiv _{ss'}$ and $\equiv _{s's}$. To spell out the definition of $\equiv _{ss'}$, it says that two histories are undivided at a pair supreme $\{ s, s'\}$ in exactly three cases: (1) $\{ s, s'\}$ is not a pair supreme for these two histories, but one of its elements is shared by the two histories, or (2) $\{ s, s' \}$ is a pair supreme for these histories, but not a hot pair for these histories, or (3) it is a hot pair but not a maximal hot pair for the two histories. In case (2), a pair supreme is of the form $\{ s, s\}$, so $s \in h_1 \cap h_2$. Case (3) is interesting, as we will see it in a proof below. We prove that $\equiv _{ss'}$ is an equivalence relation on the set $H_{(s)} \cup H_{(s')}$ of histories containing $s$ or $s'$.

Fact 9.

$\equiv _{ss'}$ is a (1) reflexive, (2) symmetric, and (3) transitive relation on $H_{(s)} \cup H_{(s')}$.

Proof   (1) Pick an $h \in H_{(s)} \cup H_{(s')}$ and assume $s \in h$. (The case with $s' \in h$ is symmetrical). Clearly, $s \in h \cap h$, so $h \equiv _{ss'} h$.

(2) Let $h_1 \equiv _{ss'} h_2$. If $s$ or $s'$ belong to $h_1 \cap h_2$, we immediately get $h_2 \equiv _{ss'} h_1$. Suppose thus that $\{ s, s' \} \in \mathfrak {H}(h_1, h_2)$, but it is not a minimal element of $\mathfrak {H}(h_1, h_2)$. By the definitions of pairs supreme and hot pairs, $\{ s, s' \} \in \mathfrak {H}(h_1, h_2)$ iff $\{ s, s' \} \in \mathfrak {H}(h_2, h_1)$. Accordingly $\{ s, s' \} \in \mathfrak {H}(h_2, h_1)$, but it is not a minimal element of $\mathfrak {H}(h_2, h_1)$, and hence $h_2 \equiv _{ss'} h_1$.

(3) For transitivity, let ($\dagger$) $h_1 \equiv _{s_1s_2} h_2$ and ($\ddagger$) $h_2 \equiv _{s_1s_2} h_3$, and assume the convention that for $i=1, 2$, ${\tilde{\imath }}= 2, 1$, resp. The argument goes by cases, depending on which of the histories: $h_1, h_2, h_3$, $s_i$ belongs to ($i = 1, 2$):

(a) $s_i \in h_1 \cap h_3$. Then $h_1 \equiv _{s_1s_2} h_3$.

(b1) $s_i \in h_1 \setminus h_3$ and $s_i \in h_2$. Then by ($\ddagger$) $s_{{\tilde{\imath }}} \in h_3$ and $\{ s_1s_2\} \in \mathfrak {H}(h_2, h_3) \setminus \mathfrak {C}(h_2, h_3)$. It follows that $s_1\ne s_2$, so $\{ s_1s_2\} \in \mathfrak {H}(h_1, h_3)$. It also follows that there is $\{ x_1x_2\} \in \mathfrak {H}(h_2, h_3)$ such that $\{ x_1, x_2\} \prec \{ s_1, s_2\}$. Let $x_i < s_i$ and $x_{{\tilde{\imath }}} < s_{{\tilde{\imath }}}$ (case $x_i < s_{{\tilde{\imath }}}$ and $x_{\tilde{\imath }}< s_i$ is analogous). Since histories are downward closed, $x_i \in h_1$ and $x_{{\tilde{\imath }}} \in h_3$, and since $x_i \ne x_{{\tilde{\imath }}}$: $\{ x_1x_2\} \in \mathfrak {H}(h_1, h_3)$, so $\{ s_1s_2\} \in \mathfrak {H}(h_1, h_3) \setminus \mathfrak {C}(h_1, h_3)$, whence $h_1 \equiv _{s_1s_2} h_3$.

(b2) $s_i \in h_1 \setminus h_3$ and $s_i \not \in h_2$. By ($\ddagger$), $s_{{\tilde{\imath }}} \in h_2 \cap h_3$. Hence by ($\dagger$), $\{ s_1s_2\} \in \mathfrak {H}(h_1, h_2) \setminus \mathfrak {C}(h_1, h_2)$, so there is $\{ x_1x_2\} \in \mathfrak {H}(h_1, h_2)$ such that $\{ x_1, x_2\} \prec \{ s_1, s_2\}$. Let $x_i < s_i$ and $x_{{\tilde{\imath }}} < s_{{\tilde{\imath }}}$ (the case with $x_i < s_{{\tilde{\imath }}}$ and $x_{{\tilde{\imath }}} < s_i$ is analogous). Since histories being downward closed, $x_i \in h_1$ and $x_{{\tilde{\imath }}} \in h_3$, and since $x_i \ne x_{{\tilde{\imath }}}$, we get $\{ x_1x_2\} \in \mathfrak {H}(h_1, h_3)$, and hence $\{ s_1s_2\} \not \in \mathfrak {C}(h_1, h_3)$. But since $s_1 \ne s_2$, $\{s_1s_2\} \in \mathfrak {H}(h_1, h_3)$. Thus, $h_1 \equiv _{s_1s_2} h_3$.

(c) $s_i \in h_3 \setminus h_1$. As in cases (b1) and (b2) above.

(d) $s_i \not \in h_1 \cup h_3$. By ($\dagger$) $s_{\tilde{\imath }}\in h_1$ and by ($\ddagger$): $s_{\tilde{\imath }}\in h_3$, hence $h_1 \equiv _{s_1s_2} h_3$. $\square$

With the last result, we define elementary possibilities open at a pair supreme, which is analogous to a BST1992 notion of elementary possibilities open at a point event:

Definition 10

Let $\{s, s'\}$ be a pair supreme (simpliciter). Then the set $H_{ss'}$ of elementary possibilities open at $\{s, s'\}$ is defined as the set of equivalence classes on $H_{(s)} \cup H_{(s')}$ with respect to the relation $\equiv _{(s), (s')}$ of undividedness at $\{s, s'\}$.

We next argue that all the action lies at choice pairs, modally speaking:

Fact 11.

Only choice pairs have non-trivial sets of elementary open possibilities.

Proof   Let $\{s, s'\}$ be a pair supreme. If $s = s'$, i.e., $\{ s, s'\}$ is not a hot pair, then for any pair $h, h' \in H_{(s)} \cup H_{(s')}$, $s \in h\cap h'$, and hence $h \equiv _{ss'} h'$.

If $s \ne s'$, then $\{s, s'\}$ is a hot pair; let us assume it is not a choice pair, however. Then for some $h, h' \in H_{(s)} \cup H_{(s')}$, there is $\{x, x'\} \in \mathfrak {H}(h, h')$ such that ($\dagger$) $x < s, x' < s'$. Pick now arbitrary two histories $h_1, h_2 \in H_{(s)}\cup H_{(s')}$. If $h_1, h_2 \in H_{(s)}$ or $h_1, h_2 \in H_{(s')}$, we immediately obtain $h_1 \equiv _{ss'} h_2$. Suppose thus that $h_1 \in H_{(s)}\setminus H_{(s')}$ and $h_2 \in H_{(s')}\setminus H_{(s)}$ (the other case is analogous). Since histories are downward closed, ($\dagger$) implies $x \in h_1$ and $x' \in h_2$. And, because $x \ne x'$, $\{x, x'\} \in \mathfrak H(h_1, h_2)$, which together with ($\dagger$) entail $\{s, s' \} \in \mathfrak {H}(h_1, h_2) \setminus \mathfrak {C}(h_1, h_2)$. Whence $h_1 \equiv _{ss'} h_2$.

Finally, if $\{s, s'\}$ is a choice pair, there are histories $h, h' \in H_{(s)} \cup H_{(s')}$ such that $h \perp _{s s'} h'$; these two histories determine two elementary possibilities open at the pair. $\square$

Our next fact says that hot pairs abounds:

Fact 12.

Let ${\mathcal {W}}$ have two histories $h_1$ and $h_2$. Let also $t$ be a maximal chain in ${\mathcal {W}}$ such that $t' := t \cap h_1 \cap h_2 \ne \emptyset$ and $t \cap (h_1 \setminus h_2 ) \ne \emptyset$. Then (1) $t'$ is upper bounded and (2) $\sup _{h_1}(t') \ne \sup _{h_2}(t')$.

Proof   (1) We claim that any ($\dagger$) $e \in t'':= t \cap (h_1 \setminus h_2)$ upper bounds $t'$. Otherwise, since each element of $t'$ and $e$ are comparable, we would have $e < x$ for some $x \in t'$. Since $x \in h_1 \cap h_2$ and histories are downward closed, $e \in h_1 \cap h_2$, contradicting ($\dagger$).

(2) The above result implies, via the axiom of history-relative suprema, that $t'$ has history-relative suprema. Observe that $\sup _{h_1}(t') = \inf (t'')$. But $t'' \in h_1\setminus h_2$, so by PCP$^*$, there is (i) $\{s_1, s_2\} \in \mathfrak C (h_1, h_2)$ such that (ii) $s_i \leqslant t''$. Thus (iii) $s_i \leqslant \inf (t'') = \sup _{h_1}(t')$. Further, (ii) entails (iv) $s_i \in h_1$. Finally, it follows from (iii), (iv), and Fact 3 that $\sup _{h_1}(t') \not \in h_2$, and hence $\sup _{h_1}(t') \ne \sup _{h_2}(t')$. $\square$

Our last fact of this section says the following:

Fact 13.

(1) Every two histories of BST$^*$1992 overlap and (2) for every two histories, their overlap has no maximal element.

Proof   Ad. (1) For two histories $h, h'$, there must be a chain $C \subseteq h\setminus h'$. By PCP$^*$, there must be a choice pair $s, s'$ for these two histories. By the definition of choice pairs and pairs supreme, there is a chain $C^* \subseteq h\cap h'$. Ad. (2) This is an immediate consequence of Fact 12 (2). $\square$

The last two facts tell us that indeed the new version of BST1992 prescribes a different pattern of branching histories.

A still different pattern of branching is a consequence of a frugal branching framework I worked out with T. Kowalski (Kowalski and Placek 1999). This pattern consists in that every chain contained in the overlap of two histories has a maximum in the overlap. ⁷

The upshot of this section is that BST is versatile: if physics tells us how alternative possible courses of events are different, we can modify BST accordingly.

3 How to Generalize BST1992?

In Sect. 1 we argued for a generalization of BST1992 that would accommodate the insights of GR. But how should we do that? We will join a “happy coincidence” as works in different areas point to a similar idea of defining a GR spacetime as a maximal subset of a generalized manifold with respect to being Hausdorff (and perhaps having some additional property as well).

A topology ${\mathcal {T}}(X)$ is called ‘Hausdorff’ if for every two distinct $x, y \in X$ there are two non-overlapping open sets containing $x$ and $y$, respectively. Non-Hausdorff spacetimes were investigated in physics in the 1970s. Importantly, Hájíček (1971) proved the existence theorems for sub-manifolds maximal with respect to being Hausdorff and connected. Nevertheless, in later years a consensus emerged among physicists that a GR spacetime should be Hausdorff. This sentiment is embodied in the dramatic outcry of Penrose (1979, 595): “I must ...return firmly to sanity by repeating to myself three times: ‘spacetime is a Hausdorff differentiable manifold; spacetime is a Hausdorff ...’ ”. ⁸ For a survey of the consequences of allowing for non-Hausdorff spacetimes, see Earman (2008).

In a similar spirit, building on Hájíček’s results, Müller (2011) defines a history in his generalized BST as a subset of a base set maximal with respect to being Hausdorff and connected. Finally, there is the following result about a natural topology for BST1992, the so-called Bartha topology: given a natural assumption, a BST1992 history is a maximal Hausdorff and downward closed subset of a base set $W$ (see Fact 57).

Thus, our target is to define a candidate for a GR spacetime as a subset of a base set of a generalized BST model maximal with respect to being Hausdorff.

Our second desiderata says that our generalization should be “topologically conservative” with respect to BST1992, that is, the resulting models and histories in these models should have similar topological properties as models and histories of BST1992. What are then the topological facts about BST1992? BST1992 comes with a natural topology on the entire base set as well as with a natural topology on each history in the model. ⁹ Both kinds of the topologies are defined by the following condition, known as “the Bartha condition”:

Definition 14

(the diamond topology) Let ${\mathcal {W}} = \langle W, \leqslant \rangle$ be a BST1992 model and $X$ stand either for $W$, or for a history $h$ in ${\mathcal {W}}$.

$Z$ is an open subset of $X$, $Z \in {\mathcal {T}} (X)$, iff $Z= X$ or for every $e \in Z$ and for every maximal chain $t$ in $X$ containing $e$ there are $e_1, e_2 \in t$ such that $e_1 < e < e_2$ and $\{x \in W \mid e_1 \leqslant x \leqslant e_2\} \subseteq Z$.

Main topological facts about ${\mathcal {T}}(W)$ and ${\mathcal {T}}(h)$, where $h$ is a history in ${\mathcal {W}}$, are as follows:

• 1. ${\mathcal {T}}(h)$ is connected and (given some natural assumptions) Hausdorff ¹⁰;

• 2. ${\mathcal {T}}(h)$ is maximally Hausdorff in this sense: modulo some natural assumptions, the Bartha condition applied to any proper superset of $h$ yields a non-Hausdorff topology (see Fact 57).

• 3. for some history $h$, ${\mathcal {T}}(h)$ is locally Euclidean, and for some other history $h'$, ${\mathcal {T}}(h')$ is not locally Euclidean (see Fact 58).

• 4. ${\mathcal {T}}(W)$ is connected and non-Hausdorff (unless $W$ contains one history only) ¹¹;

• 5. $h \not \in {\mathcal {T}}(W)$ (unless $h = W$)—see Placek et al. (2013).

• 6. ${\mathcal {T}}(W)$ is not locally Euclidean (unless $W = h$ for some history $h$ and ${\mathcal {T}}(h)$ is locally Euclidean (see Fact 58)).

In what follows, we will construct a manifold topology on generalized BST, and, in an attempt to be conservative with respect to BST1992, we will see to it that the topology on a generalized history is Hausdorff, and moreover, maximally so. We will also secure that each generalized history is locally Euclidean. In contrast, we will initially allow that the topology on the whole model be not locally Euclidean and non-Hausdorff, and that a history is not open in this topology. In a sequel, we will face a dilemma, however. If we want to construct spaces of tangent vectors (which are needed for the GR equations to make sense), we need to impose a certain restriction on the generalized BST models. The restriction implies that a generalized BST model (as a whole) is locally Euclidean, and that generalized histories are open in the manifold topology. Thus, if we want to have tangent vectors spaces, our resulting construction is not conservative with respect to BST1992, after all.

4 Construction

Our construction proceeds in three steps: First, we will generalize BST1992, second we will construct a generalized differential manifold on a generalized BST model (at this stage we will equip BST models with a topology). Third, we will construct tangent vector spaces, needed for the formulation of GR equations. Our construction is not orthodox in the sense that, in contrast to GR, a base set for a (generalized) differential manifold has some structure: it is assumed to be pre-ordered (i.e., reflexive and transitive, but not necessarily anti-symmetric) and satisfy a few postulates.

4.1 BST Generalized

We take courage from the following theorem of GR.¹² For every event $p$ in an arbitrary GR spacetime there exists a convex normal neighborhood of $p$, that is, an open set $U$ with $p \in U$ such that for every $q, r \in U$ there is a unique geodesics connecting $q$ and $r$, and staying entirely in $U$. Since geodesics fall into three classes, of time-like, space-like, and null-like geodesics, the uniqueness of connectability means that the geodesics can be used to define a partial ordering $\leqslant$ on $U$: $q \leqslant r$ iff $q$ is connectible to $r$ by a future directed time-like or null-like geodesics. A sufficiently small convex normal set can be charted on an open subset of ${\mathbb {R}}^n$. In the spirit of this theorem, we will construct a manifold topology such that every element of a base set $W$ has an open neighborhood (“patch”), which is partially ordered. We further postulate that each patch is like a small BST1992 model. As a consequence, in contrast to GR patches, our patches may be modally inconsistent, i.e., containing objects that are not contained in a single spacetime. (So we really “take courage” from the above theorem, it is not a premise of our construction.) Without further ado, let us introduce some terminology and then turn to the definitions:

• 1. $MC(X)$ is the set of maximal chains in $X$, where $X$ is a non-empty pre-ordered set;

• 2. $MC(X; e) = \{t \in MC(X) \mid e \in t\}$;

• 3. $t^{< x} = \{z \in t\mid z <x \}$, where $t \in MC(X)$ and $x \in X$; $t^{< x}$ is the initial segment of $t$ below $x$ ($t^{\leqslant x}$, $t^{> x}$, and $t^{\geqslant x}$ are similarly defined).

Definition 15

(generalized BST model) Where $W \ne \emptyset$, $\curlyeqprec$ is a pre-order on $W$, and ${\mathcal {O}} \subseteq {\mathcal {P}}(W)$, a triple ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ is a generalized BST model (genBST model), iff for every $e \in W$ there is a set ${\mathcal {O}}_e \subseteq {\mathcal {O}}$ (of patches) around $e$ such that for every $O \in {\mathcal {O}}_e$:

• 1. $e \in O$;

• 2. $\langle O, \curlyeqprec _{\mid O}\rangle$ is a nonempty dense partial order satisfying the following:

  • (a) $\forall e' \!\in \! O \forall t \!\in \! MC(W; e') \exists x, \!y \!\in \! t\cap O \;(x\! \prec _{\mid O}\! e' \prec _{\mid O} \!y \;\wedge \; t^{\succ x}\cap t^{\prec y }\! \subseteq \! O)$;

  • (b) every lower bounded chain in $\langle O, \curlyeqprec _{\mid O}\rangle$ has an infimum in $O$;

  • (c) if a chain $C$ in $\langle O, \curlyeqprec _{\mid O}\rangle$ is upper bounded by $b \in O$, then $B:=\{x \in O\mid C \curlyeqprec _{\mid O} x \wedge x\curlyeqprec _{\mid O} b \}$ has a unique minimum,

  • (d) if $x, y \in O$ and $x \curlyeqprec z \curlyeqprec y$, then $z \in O$; and

• 3. $\bigcup _{e\in W} {\mathcal {O}}_e = {\mathcal {O}}$;

• 4. If $x, y \in O \cap O'$, where $O, O' \in \mathcal O$, then $x \curlyeqprec _{\mid O} y$ iff $x \curlyeqprec _{\mid O'} y$.¹³

Let us next put together some facts about patches:

Fact 16.

(about patches). Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model. Then:

(i) a subset of $O$, where $O \in {\mathcal {O}}$, does not necessarily belong to ${\mathcal {O}}$;

(ii) the union of $O, O' \in {\mathcal {O}}$ does not necessarily belong to ${\mathcal {O}}$, but

(ii) if $O\cap O' \ne \emptyset$, where $O, O' \in {\mathcal {O}}$, then $O\cap O' \in {\mathcal {O}}$.

Proof   (i) A subset of $O \in {\mathcal {O}}$ can fail to satisfy any of the conditions (2a)–(2d). (ii) The ordering $\curlyeqprec _{\mid O \cup O'}$ on the union of $O, O' \in {\mathcal {O}}$ may fail to be anti-symmetric; also (2d) can fail on $O\cup O'$. (iii) $\langle O\cap O', \curlyeqprec _{\mid O \cap O'}\rangle$ is a nonempty dense partial ordering because, by the assumption, $O\cap O' \ne \emptyset$ and each $\curlyeqprec _{\mid O }$ and $\curlyeqprec _{\mid O'}$ is a dense partial ordering. It is easy to check that $\langle O\cap O', \curlyeqprec _{\mid O \cap O'}\rangle$ satisfies (2a) and (2d). To argue for (2b), let $C$ be a chain in $\langle O\cap O', \curlyeqprec _{\mid O \cap O'}\rangle$, lower bounded by $b \in O \cap O'$. Then $C$ has $\inf _O(C)$ in $O$ and $\inf _{O'}(C)$ in $O'$. Since $b \curlyeqprec _{\mid O'} \inf _{O'}(C) \curlyeqprec _{\mid O'} C$ and $b \curlyeqprec _{\mid O} \inf _{O}(C) \curlyeqprec _{\mid O} C$, by Definition 15 (2d) $\inf _O(C) \in O\cap O'$ and $\inf _{O'}(C) \in O\cap O'$. By the definition of infimum, $\inf _O(C) \curlyeqprec _{\mid O'} \inf _{O'}(C)$ and $\inf _{O'} (C) \curlyeqprec _{\mid O} \inf _{O}(C)$. By Definition 15 (4) $\inf _O(C) = \inf _{O'}(C) := \inf _{O \cap O'}(C)$. To prove (2c), suppose there is a chain $C \subseteq O \cap O'$ upper bounded by $b \in O\cap O'$. Then, by Definition 15 (2d) and (4) $\{x \in O\mid C\curlyeqprec _{\mid O} x \wedge x \curlyeqprec _{\mid O} b\}$ and $\{x \in O'\mid C\curlyeqprec _{\mid O'} x \wedge x \curlyeqprec _{\mid O'} b\}$ are identical. Thus, a unique minimal element of one must be identical to a unique minimal element of the other, and must belong to $O \cap O'$. $\square$

Generalized BST models allow for causal loops in this sense: $x, y, z \in W$ with $x, y \in O$, $z \not \in O$, $y, z \in O'$, $x \not \in O'$ and $x, z \in O''$, $y \not \in O''$ and such that $x \curlyeqprec _{\mid O} y$, $y \curlyeqprec _{\mid O'} z$, and $z \curlyeqprec _{\mid O''} x$.

The idea of this chapter is that the Hausdorff property will decide whether a subset of $W$ is contained in a spacetime, or not. We do not have a topology yet, so an appeal to Hausdorffness remains on an intuitive level, to be justified later, when we define a topology. But, in spacetime theories, a bifurcating path, whose trunk has no maximal element indicates a failure of the Hausdorff property. Minimal elements of two upper arms of such a structure will be called “splitting pair”.

Definition 17

(splitting pairs) Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model and $O \in {\mathcal {O}}$. We say that $e, e' \in O$ form a splitting pair in $O$, $\{e, e'\} \in Y_O$, iff $e \ne e'$ and there is a chain $C$ in $\langle O, \curlyeqprec _{\mid O}\rangle$ and $b, b' \in O$ such that $C \curlyeqprec _{\mid O} b$, $C \curlyeqprec _{\mid O} b'$ and $e = \min \{x \in O\mid C \curlyeqprec _{\mid O} x \wedge x\curlyeqprec _{\mid O} b \}$ and $e' = \min \{x \in O\mid C \curlyeqprec _{\mid O} x \wedge x\curlyeqprec _{\mid O} b' \}$.

We then define the set $Y$ of splitting pairs of ${\mathcal {W}}$ as $Y := \bigcup _{O \in {\mathcal {O}}} Y_O$.

One may wonder how global pre-ordering $\curlyeqprec$ mesh with splitting pairs. Our postulates do not exclude the following situation:

(*) Events $e, e' \in O$ have a common upper bound with respect to $\curlyeqprec$, but are above a splitting pair $\{x, x'\} \in Y_O$ in the sense that $x \curlyeqprec _{\mid O} e$ and $x'\curlyeqprec _{\mid O} e'$.

We would like to prohibit (*): events separated by a splitting pair cannot be connected by causal curves to an event in their (common) future, as they do not have a common future. This intuition goes back to our reading of a splitting pair as a seed of modal inconsistency. Hence this condition:

Condition 18

(Hausdorff separation) If there is a pair $\{x, x' \} \in Y$, then $\lnot \exists z \in W\; (x \curlyeqprec z \wedge x' \curlyeqprec z)$.

Note the interplay between local and global notions: if $x$ and $x'$ are separated by a splitting pair in some patch $O$, then $x$ and $x'$ have no common upper bound, no matter how far we go along $\curlyeqprec$, possibly outside $O$. We next define consistency:

Definition 19

(consistency) $e, e'\in W$ are consistent iff there is no splitting pair $\{x, x'\} \in Y$ such that $x \curlyeqprec e$ and $x' \curlyeqprec e'$. $A \subseteq W$ is consistent iff  $\forall e, e' \in A:\; e \text { and } e'$ are consistent.

Definition 20

(inconsistency) $e, e'\in W$ are inconsistent iff there is a splitting pair $\{x , x'\} \in Y$ such $x\curlyeqprec e \wedge x' \curlyeqprec e'$.

We claim next that there are maximal consistent subsets of $W$.

Lemma 21

There is at least one maximal consistent subset of $W$.

Proof   The proof goes by the Zorn lemma. Observe first that for every $e\in W$, the singleton $\{e\}$ is a consistent set, since $x \curlyeqprec e$, $x' \curlyeqprec e$ and $\{x, x'\} \in Y$ contradict Condition 18. Consider then the set of consistent subsets of $W$, partially ordered by inclusion. To check if a premise of the Zorn lemma is satisfied, pick a chain $C= A_1, A_2, \ldots , A_\alpha , \ldots$ of consistent subsets of $W$. Let suppose $\bigcup C$ is not consistent. Then there must be $e, e' \in \bigcup C$ and $x, x'$ such that $\{x, x'\} \in Y$ and $x \curlyeqprec e$ and $x' \curlyeqprec e'$. Thus, for some $\beta , \beta '$: $e\in A_\beta$ and $e' \in A_{\beta '}$, where $A_\beta , A_{\beta '} \in C$. Since $A_\beta$ and $A_{\beta '}$ are comparable by $\subseteq$, for $\beta ^*= \max (\beta , \beta ')$ we have $e, e' \in A_{\beta ^*}$, and hence $A_{\beta ^*}$ is not consistent. Contradiction. $\square$

What are the properties of maximal consistent subsets of $W$? The fact below list some of them:

Fact 22.

(about maximal consistent subsets of $W$) Let $A, A'$ be maximally consistent subsets of $W$, where $W$ is a base set of a gen BST model. Then:

(1) A is downward closed.

(2) Let $e' \in A'\setminus A$. Then there is a “hot pair” $\{x, x'\}$ for $A$ and $A'$, i.e., there is a a chain $C \subseteq A \cap A'$, such that $x = \sup _A(C)$, $x' = sup_{A'}(C)$, $x \ne x'$, and $x' \curlyeqprec e'$.

(3) If $e, e', e^* \in W$ and $e \curlyeqprec e^*$ and $e' \curlyeqprec e^*$, then there is a maximally consistent subset $A^*$ of $W$ such that $e, e' , e^* \in A^*$.

Proof   (1) For a reductio, let us assume that $A$ is not downward closed, which means that there are some $e, e' \in W$ such that (i) $e \prec e'$, (ii) $e'\in A$, but (iii) $e\not \in A$. Since $A$ is a maximal consistent subset, (iii) implies that $e$ must be inconsistent with some $e^* \in A$, which means that there is a slitting pair $x, x^* \in W$ such that (iv) $x \curlyeqprec e$ and (v) $x^* \curlyeqprec e^*$. By (ii) $e'$ is consistent with $e^*$, which taken with (v) implies (vi) $\lnot (x\curlyeqprec e')$. But by (i) and (iv) we have $x \prec e'$, which contradicts (vi).

(2) Let $e'$, $A$, and $A'$ be as in the premise. Then $e'$ is inconsistent with some $e \in A$, from which it follows that there is $O \in {\mathcal {O}}$ and a splitting pair $\{x, x'\}\in Y_O$ such that $x \curlyeqprec e$ and $x' \curlyeqprec e'$. By item (1) of this Fact, $x \in A$ and $x' \in A'$. By Definition 17 of splitting pairs, $x \ne x'$ and there is a chain $C$ in $\langle O, \curlyeqprec _{\mid O}\rangle$ and $b, b' \in O$ such that $C \curlyeqprec _{\mid O} b$, $C \curlyeqprec _{\mid O} b'$ and ($\dagger$) $x = \min \{y \in O\mid C \curlyeqprec _{\mid O} y \wedge y\curlyeqprec _{\mid O} b \}$ and $x' = \min \{y \in O\mid C \curlyeqprec _{\mid O} y \wedge y\curlyeqprec _{\mid O} b' \}$. Item (1) of this Fact entails that $C \subseteq A$ and $C \subseteq A'$. To prove that $x = \sup _A(C)$ we argue as follows. Consider the set $U$ of upper bounds of $C$ in $A$. By condition (2a) of Definition 15, (i) for every upper bound $u \in U$ of $C$ there is $u' \in U \cap O$ such that $C \curlyeqprec _{\mid O} u'\curlyeqprec u$. (Just connect $C$ with $u$ by a maximal chain in $W$ and apply (2a).) We may thus restrict our attention to the set $U'$ of upper bounds of $C$ in $O\cap A$. Since $U'\subseteq A$, $U'$ is consistent, and hence there are no two upper-bound-relative minima of this kind: $z_1 = \min \{y \in O\mid C \curlyeqprec _{\mid O} y \wedge y\curlyeqprec _{\mid O} u_1 \}$ and $z_2 = \min \{y \in O\mid C \curlyeqprec _{\mid O} y \wedge y\curlyeqprec _{\mid O} u_2 \}$, where $u_1, u_2 \in U'$. Otherwise $z_1$ and $z_2$ would constitute a splitting pair below $u_1$ and $u_2$, respectively, yielding $u_1$ and $u_2$ inconsistent, which contradicts $u_1, u_2 \in A$. Thus, there is a unique minimum below (in the sense of $\curlyeqprec _{\mid O}$) all $u \in U'$, namely $x$, which, taken together with (i), proves that $x = sup_{A}(C)$. An argument that $x' = sup_{A'}(C)$ is analogous.

(3) By the Zorn lemma, there is a maximally consistent $A \subseteq W$ such that $e^* \in A$. By item (1) of this Fact, $e, e' \in A$. $\square$

Fact 22 points out to a striking resemblance between histories of BST1992 and maximal consistent subsets of $W$ of a generalized BST model. We take this resemblance to be a good enough justification for calling maximal consistent subsets of $W$ “generalized histories” (or g-histories, for short).

Definition 23

(g-histories) Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ be a generalized BST model. We say that $H$ is a generalized history (g-history) of ${\mathcal {W}}$ iff $H$ is a maximal consistent subset of $W.$ We denote the set of g-histories by $gHist$.

At this point one may wonder if g-histories extend to the future, as BST1992 histories do. Unfortunately, it is not excluded at this stage that a g-history has a maximal element. This situation will be ruled out, however, in the generalized BST models that admit a manifold structure—see Fact 23. A similar worry concerns PCP. We proved above that there is a hot pair for any two g-histories. A PCP-pair version, however, requires minimal hot pairs for any two histories; we do not know if the latter exist for g-histories.

As a next topic, let us ask what is an intersection of a g-history $H\subseteq W$ with a patch $O \in {\mathcal {O}}$? The answer is given by this fact:

Fact 24.

Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model, $H$ be a g-history of ${\mathcal {W}}$, and $O \in {\mathcal {O}}$. Then if $H \cap O \ne \emptyset$, $H \cap O$ is consistent and $\langle H \cap O, \curlyeqprec _{\mid H \cap O}\rangle$ is a nonempty partial order that satisfies conditions (2b)-(2d) of Definition 15.

Proof   It is left to the reader. $\square$

Note that if a model allows for maximal elements in the intersections of histories, $O \cap H$ does not satisfy clause (2a) of Definition 15, and hence $O \cap H$ is not a patch. This might be a motivation for banning such maximal elements.¹⁴ Observe also that every patch $O \in {\mathcal {O}}$ is divided between g-histories of ${\mathcal {W}}$, i.e $\forall x \in O\; \exists A\in gHist\; (x \in A)$. Of course, there might be an element of $O$ shared by a few g-histories; there might also be g-history $A$ and a patch $O$ such that $A \cap O = \emptyset$.

The final question for this section is: does generalized BST extend BST1992 or BST*1992 of Sect. 2, i.e., is genBST worth its name? Since BST1992 and BST$^*$1992 permit models with minimal elements, which generalized BST rules out, the latter does no generalize the former two, strictly speaking. Second, there is a discrepancy between histories of BST1992 and g-histories: the upper fork, extending indefinitely up and down, and with a maximal element in the trunk, is a two-history model of BST1992, but has only one g-history, as there is no splitting pair in it. Still, this fork is a model of generalized BST. Thus, we have the following, qualified, verdict concerning generalization (note that this result does not entail that histories and g-histories are to be identified):

Lemma 25

Let $\langle W, \leqslant \rangle$ have no minimal element and be a model of either BST1992 or BST*1992. Then $\langle W, \leqslant , \{W\}\rangle$ is a model of generalized BST.

Sketch of a proof Since a generalized BST model in question has only one patch, $W$ itself, the axioms of BST1992/BST*1992 immediately imply that $\langle W, \leqslant _{\mid W}\rangle$ is nonempty dense partial order. The axiom of no maximal elements together with the premise of this lemma, no minimal elements, imply clause (2a) of Definition 15. Axioms of infima and history-relative suprema imply clauses (2b) and (2c) of this definition. The remaining clauses, that is, (1), (2d), (3), and (4) are trivially satisfied. $\square$

4.2 Generalized Differential Manifolds and Matters Topological

The aim of this subsection is to set up a (generalized) differential manifold on the base set of a generalized BST model. This is the crux of the construction since, after all, GR spacetimes are differential manifolds of some kind. We do not imply that every generalized BST model can be equipped with the manifold structure—in the sequel we will consider only those that do.

This section generalizes an elegant construction of GR manifolds, due Geroch (1972) and Malament (2012), to modally inconsistent contexts. We will first define $n$-dimensional generalized charts on ${\mathcal {W}}$, in short $n$-g-charts, and say what it means that such charts are compatible.

Definition 26

($n$-g-chart) An $n$-g-chart on a generalized BST model ${\mathcal {W}}{=}\langle W, \curlyeqprec , {\mathcal {O}}\rangle$, is a pair $\langle O, \varphi \rangle$, where $O \in {\mathcal {O}}$ is a patch in ${\mathcal {W}}$ and $\varphi : O \rightarrow {\mathbb {R}}^n$ satisfies, for every $H \in gHist$:

If $O \cap H \ne \emptyset$, then

• 1. $\varphi _{\mid O \cap H}$ is injective (i.e., one-to-one),

• 2. $\varphi [O \cap H]$ is an open subset of ${\mathbb {R}}^n$ (in the standard topology on ${\mathbb {R}}^n$), and

• 3. $\forall e, e' \in O \cap H\; e \prec _{\mid O} e' \Leftrightarrow \varphi (e) <_M \varphi (e')$, where $<_M$ is a (strict) Minkowskian ordering.

The generalization consists in restricting the chart function to a modally consistent context, that is, to $O \cap H$. Furthermore, the orthodox approach has no analogue of (3).

Definition 27

(compatibility of $n$-g-charts) Two $n$-g-charts on an genBST model ${\mathcal {W}}$, $\langle O_1, \varphi _1\rangle$ and $\langle O_2, \varphi _2\rangle$, are called compatible iff for every $H \in gHist$ either $O_1 \cap O_2 \cap H = \emptyset$ or $O_1 \cap O_2 \cap H \ne \emptyset$ and these two conditions obtain:

(1) $\varphi _i[O_1 \cap O_2 \cap H]$ ($i=1, 2$) are open subsets of ${\mathbb {R}}^N$, and

(2) $\varphi _{2}\varphi _1^{-1}: \varphi _{1}[O_1 \cap O_2\cap H] \rightarrow {\mathbb {R}}^n$ and $\varphi _1\varphi _2^{-1}: \varphi _2[O_1 \cap O_2 \cap H] \rightarrow {\mathbb {R}}^n$ are both smooth.

A function from ${\mathbb {R}}^n$ to ${\mathbb {R}}^n$ is called smooth if it has a continuous derivative of any order. The generalization (with respect to the Geroch-Malament approach) consists in our appeal to histories and considering intersections $O_1 \cap O_2 \cap H$ rather than intersections $O_1 \cap O_2$.¹⁵

It is easy to see that compatibility is reflexive and symmetric; for an argument that it is not transitive, adapt an argument of Malament (2012) p. 2 appropriately. Following the Geroch-Malament definition of $n$-dimensional manifold, I define next a smooth $n$-dimensional generalized manifold, $n$-g-manifold for short.

Definition 28

(n-g-manifold) An $n$-g-manifold is a pair $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$, where ${\mathcal {W}} {=} \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ is a generalized BST model and ${\mathcal {C}}$ is a set of $n$-g-charts on ${\mathcal {W}}$ satisfying these conditions:

• (M1) Any two $n$-g-charts in ${\mathcal {C}}$ are compatible.

• (M2) For every $p \in W$ there is $\langle O, \varphi \rangle \in {\mathcal {C}}$ such that $p \in O$.

• (M3) ${\mathcal {C}}$ is maximal in the sense that every $n$-g-chart on ${\mathcal {W}}$ that is compatible with each $n$-g-chart in ${\mathcal {C}}$ belongs to ${\mathcal {C}}$.

The definition mimics Malament’s definition, but it drops the requirement of the Hausdorff property. That a maximal collection of $n$-g-charts (in the sense of (M3)) exists, can be proved by the Zorn lemma. This would leave open the question of what $n$-g-manifold s look like. This worry is addressed by the following lemma that gives a simple recipe of how to build $n$-g-manifold s: find first a collection $\mathcal C_0$ of $n$-g-charts on $W$ satisfying (M1) and (M2), and then add to it the set ${\mathcal {C}}_1$ of all $n$-g-charts on $W$ that are compatible with every $n$-g-chart in ${\mathcal {C}}_0$.

Lemma 29

Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ be a generalized BST model and ${\mathcal {C}}_0$ be a set of $n$-g-charts on ${\mathcal {W}}$ satisfying conditions (M1) and (M2). Let ${\mathcal {C}}_1$ be the set of all $n$-g-charts on ${\mathcal {W}}$ that are compatible with every $n$-g-chart in ${\mathcal {C}}_0$. Then $\langle {\mathcal {W}}, \mathcal C_0 \cup {\mathcal {C}}_1 \rangle$ is an $n$-g-manifold .

Proof   Since ${\mathcal {C}}_0$ satisfies (M2), so does ${\mathcal {C}}_0 \cup {\mathcal {C}}_1$. To verify (M1), we need to show that any $\langle O, \varphi \rangle , \langle O', \varphi '\rangle \in {\mathcal {C}}_1$ are compatible. Pick an arbitrary $H \in gHist$, and since $O \cap O' \cap H = \emptyset$ confirms compatibility of the two charts, assume $O \cap O' \cap H \ne \emptyset$.

We first show that $\varphi [O \cap O' \cap H]$ is open (an argument that $\varphi '[O \cap O' \cap H]$ is open is similar). Pick $p \in O \cap O' \cap H$, so $\varphi (p) \in \varphi [O \cap O' \cap H]$. By (M1) there is $\langle O^*, \varphi ^*\rangle \in {\mathcal {C}}_0$ such that $p \in O^*$, hence $p \in O\cap O' \cap O^* \cap H$ and $\varphi (p) \in \varphi [O\cap O' \cap O^* \cap H]$. Since $\langle O, \varphi \rangle$ is compatible with $\langle O^*, \varphi ^*\rangle$ and $\langle O', \varphi '\rangle$ is compatible with $\langle O^*, \varphi ^*\rangle$, $\varphi ^*[O \cap O^* \cap H]$ and $\varphi ^*[O' \cap O^* \cap H]$ are open. Accordingly, their intersection is open, and since $\varphi ^*$ restricted to $H$ is injective, $\varphi ^*[O^* \cap O \cap H] \cap \varphi ^*[ O^* \cap O' \cap H] = \varphi ^*[O^* \cap O \cap O' \cap H]$. Observe next that $\varphi [O^* \cap O \cap O' \cap H]$ is open because it is a pre-image of an open set $\varphi ^*[O^* \cap O \cap O' \cap H]$ under a continuous (because smooth) map $\varphi ^*\varphi ^{-1}: \varphi [O \cap O^* \cap H] \rightarrow {\mathbb {R}}^n$. Thus, for any $p \in O \cap O' \cap H$, there is an open set $\varphi [O^* \cap O \cap O' \cap H] \subseteq \varphi [O \cap O' \cap H]$ such that $\varphi (p) \in \varphi [O^* \cap O \cap O' \cap H]$. Thus, $\varphi [O \cap O' \cap H]$ is open.

Second, we verify that (i) $\varphi \varphi '^{-1}: \varphi '[O\cap O' \cap H] \rightarrow {\mathbb {R}}^n$ and (ii) $\varphi '\varphi ^{-1}: \varphi [O \cap O' \cap H] \rightarrow {\mathbb {R}}^n$ are smooth. To argue (i), note that for every $x \in \varphi '[O\cap O' \cap H]$, one can find $\langle O^*, \varphi ^*\rangle \in {\mathcal {C}}_0$ such that $\varphi '^{-1}(x) \in O^*$. Then we re-write (i) as the composition $\varphi \varphi ^{*\; -1}\circ \varphi ^*\varphi '^{-1}$ of two smooth maps, $\varphi ^*\varphi '^{-1}: \varphi '[O \cap O' \cap O^* \cap H] \rightarrow \varphi ^*[O \cap O' \cap O^* \cap H]$ and $\varphi \varphi ^{*\; -1}: \varphi ^*[O \cap O' \cap O^* \cap H] \rightarrow \varphi [O \cap O' \cap O^* \cap H]$. Because a composition of smooth maps is smooth and domains and counter-domains match, the conclusion follows. The argument for (ii) is analogous.

Finally, to prove (M3), note that since a chart not in $\mathcal C_1$ must be incompatible with some chart in ${\mathcal {C}}_0$, $\mathcal C_1 \cup {\mathcal {C}}_0$ is maximal. $\square$

Before we proceed to define topology on $W$ by using $n$-g-charts, we establish an auxiliary fact:

Fact 30.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} {=} \langle W, \curlyeqprec , \mathcal O\rangle$ and $\langle O, \varphi \rangle \in {\mathcal {C}}$. Then if $O' \in {\mathcal {O}}$ and $O' \subseteq O$, then $\langle O', \varphi _{\mid O'} \rangle \in {\mathcal {C}}$.

Proof   We need to show that, first, ($\dagger$) $\langle O', \varphi _{\mid O'}\rangle$ is an $n$-g-chart  and, second, that ($\ddagger$) it is compatible with every chart in ${\mathcal {C}}$. As for ($\dagger$), observe that a restriction of an injection is an injection. Note also that since $\varphi$ preserves the ordering on $O \cap H$, it preserves the ordering on $O' \cap H$, for any $H \in gHist$ such that $O' \cap H \ne \emptyset$. It remains to show that $\varphi [O' \cap H]$ is open, if $O' \cap H\ne \emptyset$. Let us pick an arbitrary $\tilde{e} \in \varphi [O' \cap H]$. Our aim is to find an open set in $\varphi [O' \cap H]$ containing $\tilde{e}$. Let us take a “vertical” maximal chain $\tilde{t} \in MC(\langle \varphi [O \cap H], <_M\rangle , \tilde{e})$ ¹⁶ and transform it into $t =\varphi ^{-1}(\tilde{t})$. Since $\varphi$ is injective and order preserving on $O\cap H$, $t$ is a maximal chain in $\langle O\cap H, \curlyeqprec _O\rangle$ and $\varphi ^{-1}(\tilde{e}) :=e \in t$. Recall that $O' \subseteq O$ is a patch as well, so by Definition 15 (2a), $t$ must extend up and down $e$ in $O'$, that is, there are $x, y \in t \cap O'$ such that $x \prec _{\mid O'} e \prec _{\mid O'} y$ and $t^{\succ _{\mid O'} x} \cap t^{\prec _{\mid O'} y} \subseteq O'$. Since $t \subseteq H$, $t^{\succ _{\mid O'} x}\cap t^{ \prec _{\mid O'} y} \subseteq O' \cap H$, moreover. Transforming $t^{\succ _{\mid O'} x}\cap t^{ \prec _{\mid O'} y}$ to ${\mathbb {R}}^n$, we find $\tilde{t}^{\;>_M \tilde{x}}\cap \tilde{t}^{ <_M \tilde{y}} = \varphi (t^{\succ _{\mid O'} x}\cap t^{ \prec _{\mid O'} y}) \subseteq \varphi [O'\cap H]$, with $\tilde{x} = \varphi (x)$, $\tilde{y} = \varphi (y)$ such that $\tilde{x}, \tilde{y} \in \tilde{t}$ and $\tilde{x} <_M \tilde{e} <_M \tilde{y}$. Thus, there is a nonempty $\tilde{x}', \tilde{y}' \in \tilde{t}$ such that $\tilde{x} <_M \tilde{x}' <_M \tilde{e} <_M \tilde{y}' <_M \tilde{y}$. Accordingly, $\tilde{x}', \tilde{y}' \in \varphi [O' \cap H]$ and moreover the “diamond” $d = \{\tilde{z} \in {\mathbb {R}}^n\mid \tilde{x} \leqslant _M \tilde{z} <_M \tilde{y}\}$ contained in $\varphi [O' \cap H]$ (because $z = \varphi ^{-1}(\tilde{z})$ is between $x$ and $y$ in $O' \cap H$, thanks to Definition 15 (2d) and histories being downward closed). By removing from $d$ its borders in ${\mathbb {R}}^n$, we construct the borderless diamond $b$ containing $\tilde{e}$ (because the diamond’s vertices $\tilde{x}$ and $\tilde{y}$ belong to the vertical chain $\tilde{t}$ passing through $\tilde{e}$). Clearly, $b \subseteq \varphi [O'\ \cap H]$ and is open, and hence we proved that $\langle O', \varphi _{\mid O'}\rangle$ is a chart.

To prove ($\ddagger$), i.e., compatibility of $\langle O', \varphi _{\mid O'}\rangle$ with any $\langle O^*, \psi ^*\rangle \in {\mathcal {C}}$, it is enough to consider only such $\langle O^*, \psi ^*\rangle$ and $H \in gHist$ that $O' \cap O^* \cap H \ne \emptyset$. As we just showed, $\varphi [ O' \cap H]$ is open. Since $\langle O, \varphi \rangle$ is compatible with $\langle O^*, \psi ^*\rangle$, $\varphi [O \cap O^* \cap H]$ is open. And $\varphi [O \cap O^* \cap H] \cap \varphi [O' \cap H] = \varphi [O' \cap O^* \cap H]$, because $\varphi _H$ is an injection. Thus, $\varphi [O' \cap O^* \cap H] = \varphi _{\mid O'}[O' \cap O^* \cap H]$ is open.

Finally, since $\langle O, \varphi \rangle$ and $\langle O^*, \psi ^*\rangle$ are compatible, $\psi ^*\varphi ^{-1}: \varphi [O \cap O^*\cap H] \rightarrow {\mathbb {R}}^n$ is smooth. And, as shown above, $\varphi _{\mid O'} [ O' \cap O^* \cap H]$ is open. Thus, by making the required restrictions, we see that $\psi ^*\varphi _{\mid O'}^{-1}: \varphi _{\mid O'}[ O' \cap O^*\cap H] \rightarrow \mathbb R^n$ is smooth. An argument that $\varphi _{\mid O'} \psi ^{* \; -1}: \psi ^*[ O' \cap O^*\cap H] \rightarrow {\mathbb {R}}^n$ is smooth is analogous. $\square$

Since the intersection of two patches is a patch (Fact 16), the fact above has an immediate corollary, which will be needed to define a topology:

Corollary 31

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold and $\mathcal W = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model. Then:

if $\langle O, \varphi \rangle , \langle O', \varphi '\rangle \in {\mathcal {C}}$ and $O \cap O' \ne \emptyset$, then $\langle O \cap O', \varphi _{\mid O \cap O'}\rangle$ and $\langle O \cap O', \varphi '_{\mid O \cap O'}\rangle$ belong to ${\mathcal {C}}$ as well.

Definition 32

(g-manifold topology) Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$. We say that $S \subseteq W$ is open in the g-manifold topology, $S \in {\mathcal {T}} (W)$, iff

$$ \forall p \!\in \! S \; \exists \;\langle O, \varphi \rangle \! \in \! {\mathcal {C}} \; (p \in O \wedge O \subseteq S). $$

We need to check that this definition indeed defines a topology on $W$.

Fact 33.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} {=} \langle W, \curlyeqprec , {\mathcal {O}} \rangle$. Then:

• (1) $\emptyset \in {\mathcal {T}} (W)$;

• (2) $W \in {\mathcal {T}} (W)$;

• (3) if $S, S' \in {\mathcal {T}}(W)$, then $S \cap S' \in {\mathcal {T}} (W)$ as well;

• (4) if $S_1, S_2, \ldots , S_\alpha , \ldots \in {\mathcal {T}} (W)$, then $\bigcup S_\sigma \in {\mathcal {T}} (W)$.

Proof   It is easy to see that (1) and (2) are true. To prove (3), let $p \in S \cap S'$; since $S$ and $S'$ are open, there are $\langle O, \varphi \rangle , \langle O', \varphi '\rangle \in {\mathcal {C}}$, such that $p \in O \wedge O \subseteq S$ and $p \in O' \wedge O' \subseteq S'$. Hence $O \cap O' \ne \emptyset$, so by Corollary 31, $\langle O\cap O', \varphi _{\mid O\cap O'}\rangle \in {\mathcal {C}}$. Since $p \in O\cap O'$ and $O \cap O' \subseteq S\cap S'$, $S \cap S'$ is open. To verify (4), let us pick $p \in \bigcup _\alpha S_\alpha$. Thus, for some $\beta$, $p \in S_\beta \in {\mathcal {T}} (W)$. Accordingly there is an $n$-g-chart$\langle O_\beta , \varphi _\beta \rangle$ such that $p \in O_\beta$ and $O_\beta \subseteq S_\beta \subseteq \bigcup _\alpha S_\alpha$. Thus, $\bigcup _\alpha S_\alpha \in {\mathcal {T}} (W)$.$\square$

We next observe the following fact about a base for this topology.

Fact 34.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$. Then the base for topology $T(W)$ is ${\mathcal {B}}_W := \{O \in {\mathcal {O}} \mid \langle O, \varphi \rangle \in {\mathcal {C}} \text { for some } \varphi : O \rightarrow {\mathbb {R}}^n\}$.

Proof   It is immediate to see that every element of $\mathbb B_W$ is open. From the definition, if $A \in {\mathcal {T}}(W)$, then $\forall p \!\in \! A \; \exists \;\langle O, \varphi \rangle \! \in \! {\mathcal {C}} \; (p \in O \wedge O \subseteq A)$, which implies that ${\mathcal {B}}_W$ is the basis of this topology. $\square$

By equipping a generalized BST model with a manifold topology, we impose some new properties on histories, not derivable in generalized BST alone.

Fact 35.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and $H$ be a g-history in ${\mathcal {W}}$. Then $H$ has no maximal elements.

Proof   Let $e$ be a maximal element of $H$. There is $\langle O, \varphi \rangle \in {\mathcal {C}}$ such that $e \in O$. Then $\varphi [O \cap H]$ is an open subset of ${\mathbb {R}}^n$. Since $\varphi _{\mid O \cap H}$ respects the ordering, $\varphi (e)$ is a maximal element in $\varphi [O \cap H]$. But then $\varphi [O \cap H]$ is not open, and hence $\langle O, \varphi \rangle \not \in {\mathcal {C}}$. Contradiction.$\square$

At this stage we do not know if g-histories are open, or whether they satisfy PCP. However, as a consequence of the fact above, we have that the openness of g-histories rules out PCP, point-like version:

Lemma 36

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and $H$ be a g-history in $\mathcal W$. Then:

$H \in {\mathcal {T}}(W)$ iff for every $H' \in gHist$ there is no maximal element in $H \cap H'$.

Proof   To the right: For reductio, let $H \in {\mathcal {T}}(W)$ and ($\dagger$) $e^*$ be a maximal element of $H \cap H'$ for some $H' \in gHist$. Thus, for every $e \in H$, and hence for $e^*$ as well, there is $\langle O, \varphi \rangle \in {\mathcal {C}}$ such that $e \in O$ and $O \subseteq H$. These last conditions imply that every maximal chain passing through $e^*$ should have some nonempty segment above $e^*$ contained in $O$, and hence in $H$. By the Fact above, however, $e^*$ is not a maximal element of $H'$. Moreover, it is a maximal element in $H\cap H'$. Hence some nonempty chains above $e^*$ are contained in $H'$ rather than $H$, no matter how short these chains are. Contradiction.

To the left: We need to show that for every $e \in H$ there is $O \in {\mathcal {T}}(W)$ such that $O \subseteq H$. Let us pick an arbitrary $e \in H$. By Definition 28 there is $\langle O', \varphi \rangle \in {\mathcal {C}}$ such that $e \in O'$. We claim that the sought-for $O = O' \cap H$. Observe that ($\ddagger$) if $O \in {\mathcal {O}}$, we would have by Fact 30 (since $O \subseteq O'$) that $O \in {\mathcal {T}}(W)$, as required. We thus need to prove that $O \in {\mathcal {O}}$, which amounts to checking if $O$ satisfies clause (2) of Definition 15.

First, since $e \in O'\cap H$ and $\langle O', \curlyeqprec _{\mid O'} \rangle$ is a nonempty dense partial order, $\langle O, \curlyeqprec _{\mid O} \rangle$ is a nonempty dense partial order as well.

Second, we need to prove that for every $e' \in O$ and every $t \!\in \! MC(W; e')$ there are $x, \!y \!\in \! t\cap O$ such that $x\! \prec _{\mid O}\! e' \prec _{\mid O} \!y$ and $t^{\succ x}\cap t^{\prec y }\! \subseteq \! O$. Since $e' \in O' \in {\mathcal {O}}$, there are $x', y' \in \! t\cap O'$ such that $x'\! \prec _{\mid O'}\! e' \prec _{\mid O'} \!y'$ and (i) $t^{\succ x'}\cap t^{\prec y' }\! \subseteq \! O'$. Since histories are downward closed and $e' \in H$, (ii) $t^{\succ x'}\cap t^{\curlyeqprec e' }\! \subseteq \! H$. There must also exist $y'' \in t$ such that (iii) $e'\! \prec _{\mid O'}\! y'' \prec _{\mid O'} \!y'$ and $y'' \in H$ (hence (iv) $t^{\succ e'}\cap t^{\prec y''}\! \subseteq \! H$). Otherwise, for every $z \in t$ such that $e' \prec z$ we would have $z \not \in H$. But since $z \in H'$ for some g-history, and hence $e' \in H'$, it would follow that $e'$ is a maximal element in $H \cap H'$, contradicting the Lemma’s premise. By (i), (ii), (iii), and (iv): $t^{\succ x'}\cap t^{\prec y''}\! \subseteq \! O'\cap H = O$.

Third, every lower bounded chain in $\langle O, \curlyeqprec _{\mid O}\rangle$ has an infimum in $O$ because it is lower bounded in $\langle O', \curlyeqprec _{\mid O'}\rangle$, so it has infimum in $O'$, and since histories are downward closed, this infimum is in $H$ as well.

Forth, by a similar argument, if a chain $C$ in $\langle O, \curlyeqprec _{\mid O}\rangle$ is upper bounded by $b \in O$, then $B:=\{x \in O_e\mid C \curlyeqprec _{\mid O} x \wedge x\curlyeqprec _{\mid O} b \}$ has a unique minimum. For, since $b \in H$, every $x\curlyeqprec _{\mid O'} b$ is in $H$ as well.

Finally, since histories are downward closed, if $x, y \in O$ and $x \curlyeqprec z \curlyeqprec y$, then $z \in O$.

These five observations prove that $O = O' \cap H \in {\mathcal {O}}$, and hence, by ($\ddagger$), $O \in {\mathcal {T}}(W)$. Moreover, $e \in O$ and $O \subseteq H$. As this is true for an arbitrary $e \in H$, we showed that $H \in {\mathcal {T}}(W)$. $\square$

4.2.1 The Hausdorff Property

Before we turn to a discussion of the Hausdorff property in the g-manifold topology defined above, it is helpful to establish an auxiliary fact:

Fact 37.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$. Then for any $S \in {\mathcal {T}}(W)$, if $p \in S$, then for any maximal chain $t \in MC(W; p)$, there are $x, y \in t$, $x \prec p \prec y$ such that $t^{ \succ x \wedge \prec y} \subseteq S$, where $t^{ \succ x \wedge \prec y} := \{z \in t \mid x\prec z \prec y\}$.

Proof   Let $p \in S \in \mathcal {T}(W)$ and let $t \in MC(W; p)$ be an arbitrary maximal chain. There is thus a patch $O \in {\mathcal {O}}$ such that $p \in O$ and $O \subseteq S$. By Definition 15 (2a), there must be $x, y \in t$, $x \prec p \prec y$ such that $t^{ \succ x \wedge \prec y} \subseteq O$. By Definition 15 (2d), for every $z \in t^{ \succ x \wedge \prec y}$, $z \in O$ and since $O \subseteq S$, it follows that $t^{ \succ x \wedge \prec y} \subseteq S$. $\square$

Theorem 38

(no Hausdorff property) Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ which has more than one g-history. Then the g-manifold topology on $W$ does not satisfy the Hausdorff property.

Proof   Since ${\mathcal {W}}$ has more than one g-history, there must be some inconsistent $e, e'\in W$, which is equivalent to the existence of a splitting pair $\{x , x'\}$ such that $x\curlyeqprec e \wedge x' \curlyeqprec e'$. This means that $x \ne x'$ and there is a patch $O \in {\mathcal {O}}$ and a chain $C$ in $\langle O, \curlyeqprec _{\mid O}\rangle$ and $b, b' \in O$ such that $C \curlyeqprec _{\mid O} b$, $C \curlyeqprec _{\mid O} b'$ and $x = \min \{z \in O\mid C \curlyeqprec _{\mid O} z \wedge z\curlyeqprec _{\mid O} b \}$ and $x' = \min \{z \in O\mid C \curlyeqprec _{\mid O} z \wedge z\curlyeqprec _{\mid O} b' \}$. Pick next arbitrary $U, U' \in {\mathcal {T}}(W)$ such that $x \in U$ and $x' \in U'$. Pick also $t \in MC(W;x)$ and $t' \in MC(W; x')$ such that $C \subseteq t\cap t'$ and $x \in t$ and $x' \in t'$. By Fact 37, there are $z \in t, z' \in t'$, $z \prec x$, $z' \prec x'$ such that $t^{ \succ z \wedge \prec x} \subseteq U$ and $t'^{ \succ z' \wedge \prec x'} \subseteq U'$. Accordingly, there is $z^* \in C$ such that $z \prec z^*$ and $z' \prec z^*$. It follows that $z^* \in t^{ \succ z \wedge \prec x} \subseteq U$ and $z^* \in t'^{ \succ z' \wedge \prec x'} \subseteq U'$, and hence $z^* \in U \cap U'$. Since $U$ and $U'$ are arbitrary, this proves that the Hausdorff property fails in the g-manifold topology on a model with more than one g-history.$\square$

Having established that the topology on a genBST model with more than one g-history is non-Hausdorff, let us now ask if g-histories are Hausdorff. More precisely, we ask if the subspace topology ${\mathcal {T}}_{\subseteq W}(H)$ has the Hausdorff property, where $H$ is a g-history and the ambient topology is ${\mathcal {T}}(W)$. To recall the concept of a subspace topology, given (ambient) topology ${\mathcal {T}}(W)$ and a nonempty subset $A\subseteq W$, the subspace topology on $A$ is ${\mathcal {T}}_{\subseteq W}(A) = \{ A \cap U \mid U \in {\mathcal {T}}(W)\}$. To proceed, we need an auxiliary fact and a definition, however.

Fact 39.

Let $e_1 \in O \in {\mathcal {O}}$ and $e_1, e_2 \in H \in gHist$ and suppose that $t^{\curlyeqprec e_2} \ne \emptyset$ and $t^{\curlyeqprec e_2} \curlyeqprec _{\mid O} e_1$ for some $t \in MC(W;e_1)$. Then $m \curlyeqprec e_2$, where $m = \min \{z \in O\mid t^{\curlyeqprec e_2} \curlyeqprec _{\mid O} z \wedge z \curlyeqprec _{\mid O} e_1\}$.

Proof   Clearly, $t^{\curlyeqprec e_2} \curlyeqprec e_2$. By Definition 15 (2c) there is $m' = \min \{z \in O\mid t^{\curlyeqprec e_2} \curlyeqprec _{\mid O} z \wedge z \curlyeqprec _{\mid O} e_2\}$. Clearly, $m' \curlyeqprec e_2$. By the same definition, there also exists $m = \min \{z \in O\mid t^{\curlyeqprec e_2} \curlyeqprec _{\mid O} z \wedge z \curlyeqprec _{\mid O} e_1\}$. If $m \ne m'$, then the two form a splitting pair and such that $m \curlyeqprec e_1$ and $m' \curlyeqprec e_2$, yielding $e_1$ and $e_2$ inconsistent, which contradicts $e_1, e_2\in H$. Thus, $m = m' \curlyeqprec e_2$. $\square$

Before the next definition, let us introduce some notation. For $e \in W$, we will write $(\succ _e) := \{ e' \in W \mid e \prec e'\}$. Also, for $\tilde{x} \in {\mathbb {R}}^n$, $flc(\tilde{x})$ denote the set of points in ${\mathbb {R}}^n$ lying on the brim of the future light-cone of $\tilde{x}$.

Definition 40

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$, $\langle O, \varphi \rangle \in {\mathcal {C}}$, and $x \in O$. We define:

$\bigtriangledown _O(x) := \bigcup _{H \in gHist}\{ \varphi ^{-1}[\varphi [O \cap H \cap (\succ _x)]\setminus flc(\varphi (x))] \mid O \cap H \ne \emptyset \}$

and .

Fact 41.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$, $\langle O, \varphi \rangle \in {\mathcal {C}}$, and $x \in O$. Then

(1) $\bigtriangledown _O(x) \in {\mathcal {O}}$ and (2) $\langle \bigtriangledown _O(x), \varphi _{\bigtriangledown _O(x)} \rangle \in {\mathcal {C}}$.

Moreover, if , then (3) and (4) .

Sketch of a proof The proof of (1) and (3) relies on the observation that the image of $\bigtriangledown _O(x) \cap H$ by $\varphi$ is the inside of the future light cone of $\varphi (x)$ and the image of is the outside of the future light cone of $\varphi (x)$, where both these images are open in the standard topology on ${\mathbb {R}}^n$. The argument then relies on noting that properties analogous to those required by Definition 15 (2) obtain in the latter topology, and then transforming these properties, by $\varphi _{\mid O \cap H}^{-1}$, to generalized BST. Then (2) and (4) follow by Fact 30. $\square$

Fact 42.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$, $e_1, e_2 \in H$, $H \in gHist$, and $e_1 \not \curlyeqprec e_2$. Then there is $O \in {\mathcal {O}}$ and $x \in O$ such that $e_1 \in \bigtriangledown _O(x)$ and $x \not \curlyeqprec e_2$, hence .

Proof   Pick n-g-chart $\langle O, \varphi \rangle \in {\mathcal {C}}$ such that $e_1 \in O$ so (i) $e_1 \in O \cap H$. Accordingly, $\emptyset \ne \varphi [O \cap H]$ and is open in ${\mathbb {R}}^n$, so there is a “vertical” maximal chain $\tilde{t} \subseteq \langle \varphi [O \cap H], <_M \rangle$ that contains $\tilde{e}_1 = \varphi (e_1)$ and extends (at least slightly) below and above $\tilde{e}_1$. Clearly, $t = \varphi ^{-1}_{\mid O\cap H}[\tilde{t}] \subseteq O\cap H$ and $e_1 \in t$. Consider next $t^{\curlyeqprec e_2}$. If it is empty, pick any $x \in t^{\curlyeqprec _{\mid O} e_1}$; then $x \curlyeqprec _{\mid O} e_1$ and $x \not \curlyeqprec e_2$.

But if $t^{\curlyeqprec e_2} \ne \emptyset$, then $t^{\curlyeqprec e_2}$ is upper bounded by $e_1$ (because $e_1 \in t$ and $e_1 \not \curlyeqprec e_2$), so by clause (2c) of Definition 15, there is $m = \min \{z\in O\mid t^{\curlyeqprec e_2} \curlyeqprec _{\mid O} z \wedge z \curlyeqprec _{\mid O} e_1 \}$, so $m \curlyeqprec e_1$. By Fact 39, $m \curlyeqprec e_2$, so $m \ne e_1$, and hence $m \prec e_1$. Pick now $x \in t$ such that $m \prec x \prec e_1$. It follows that $x \not \curlyeqprec e_2$, because otherwise $x \in t^{\curlyeqprec e_2}$, so $m$ would not be an upper bound of $t^{\curlyeqprec e_2}$. Thus, there is $x \in W$ such that (ii) $x \curlyeqprec _{\mid O} e_1$ and (iii) $x \not \curlyeqprec e_2$. Next, “verticality” of $\tilde{t}$ assures that $\tilde{e}_1 \not \in flc(\tilde{x})$, where $\tilde{x} = \varphi (x)$, and this result together with (i) and (ii) implies $e_1 \in \bigtriangledown _O(x)$. On the other hand, (iii) implies . $\square$

Theorem 43

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and $H \in gHist$ of ${\mathcal {W}}$. Then $\mathcal T_{\subseteq W}(H)$ is Hausdorff.

Proof   Let us take distinct $e_1, e_2 \in H$; either $e_1 \not \curlyeqprec e_2$, or $e_2 \not \curlyeqprec e_1$. Suppose the former is true (the latter is proved similarly). By Fact 42, there is $O_1 \in {\mathcal {O}}$ and $x \in O_1$ such that $e_1 \in \bigtriangledown _{O_1}(x)$ and . Pick next $O_2 \in {\mathcal {O}}$ such that $e_2 \in O_2$. Accordingly, , so by Fact 41, $\langle \bigtriangledown _{O_1}(x), \varphi _{\bigtriangledown _{O_1}(x)} \rangle \in {\mathcal {C}}$ and . It follows that $\bigtriangledown _{O_1}(x)$ and are open in the manifold topology, yet, by the construction, ($\dagger$) . Moreover, $e_1 \in H \cap \bigtriangledown _{O_1}(x) \in {\mathcal {T}}_{\subseteq W}(H)$ and , which together with ($\dagger$) show that ${\mathcal {T}}_{\subseteq W}(H)$ is Hausdorff. $\square$

The next topic of this section is maximality properties. It is a desirable goal that a g-history be not only Hausdorff, but maximally so. Similarly, it is desirable that every subset of base set $W$ maximal with respect to the Hausdorff property be identical to some g-history. The facts below do not fully achieve this goal, as they refer to maximality with respect to the joint property: the Hausdorff property plus being downward closed. This structure is similar to Müller’s (2011) maximality results, which refer to the conjunction: Hausdorff plus connectedness.

Let us begin with this observation:

Fact 44.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} =\! \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and ${\mathcal {T}}(W)$ be its manifold topology. There is a subset of $W$ that is maximal with respect to having the joint property of being Hausdorff and downward closed.

Proof   Left for the reader. Recall that a g-history is downward closed (Fact 22) and has the Hausdorff property (Theorem 43); then apply the Zorn lemma. $\square$

Fact 45.

Let $H$ be a g-history in a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on ${\mathcal {W}}$. Then $H$ is a maximal subset of $W$ with respect to being Hausdorff and downward closed.

Proof   The Fact claims that a subspace topology on any subset $A\subseteq W$ such that $H \subsetneq A$ is either not Hausdorff or $A$ is not downward closed. To prove it, we pick an arbitrary downward closed $A$ such that $A \supsetneq H$ and show that it does not have the Hausdorff property. Since $H$ is maximally consistent, there are $y' \in H$, $y \in A\setminus H$ such that $y, y'$ are not consistent. Accordingly, there is a splitting pair $\langle x, x' \rangle \in Y$ such that $x \curlyeqprec y$ and $x' \curlyeqprec y'$. Since g-histories are downward closed and $A$ is assumed to be downward closed, $x' \in H$ and $x \in A$, and hence $\{x, x'\} \subseteq A$. Accordingly, there is a chain $C \subseteq A$ (because $A$ is downward closed) that has two subsets of upper bounds, with $x$ and $x'$ being their respective minima. Then every open set $U\in \mathcal T_{\subseteq W}(A)$ with $x \in U$ contains some nonempty upper segment $C^{\succ z}$ of $C$, and similarly, every open set $U'\in {\mathcal {T}}_{\subseteq W}(A)$ with $x' \in U'$ contains some nonempty upper segment $C^{\succ z'}$ of $C$. Thus, every intersection of such $U$ and $U'$ contains some nonempty segment $C^{\succ z^*}$, $z^* = \max \{z, z'\}$, which shows that the subspace topology $T_{\subseteq W}(A)$ is not Hausdorff. $\square$

Note a striking similarity between the above fact and a property of BST1992 histories (see Fact 57). Next, we have a converse result:

Fact 46.

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} =\! \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and ${\mathcal {T}}(W)$ be its manifold topology. Then if $A$ is a maximal subset of $W$ with respect to being Hausdorff and downward closed, then $A \in gHist$.

Proof   Let us assume that $A$ is as in the premise and, as a reductio hypothesis, that $A$ is not a g-history. Accordingly, either (i) $A$ is not maximally consistent, i.e., $A \subsetneq H$ for some g-history $H$, or (ii) $A$ is not consistent. If (i), since $H$ has a joint property of being Hausdorff and downward closed, $A$ is not maximal with respect to this property, which contradicts the premise. Turning to (ii), there is a splitting pair $\{x, x'\}$ below some two elements of $A$, which is generated by some chain $C$. Since $A$ is assumed to be downward closed, $x, x' \in A$ and $C\subseteq A$. By an argument analogous to that in the last proof, ${\mathcal {T}}_{\subseteq W}(A)$ is not Hausdorff, which contradicts the Fact’s premise. $\square$

4.2.2 The Local Euclidean Property

Let us recall the concept of a locally Euclidean topological space. A topological space is called locally Euclidean if there is $n \in \mathbb N$ such that every element of the space has an open neighborhood homeomorphic to an open set of ${\mathbb {R}}^n$ (in the standard topology of reals). The (standard) definition of differential manifold requires its topology to be locally Euclidean. We should thus learn if our manifold topology ${\mathcal {T}}(W)$ and the subspace topologies ${\mathcal {T}}_{\subseteq W}(H)$, where $H$ is a g-history, are locally Euclidean.

Lemma 47

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$ and $H \in gHist$. Then the subspace topology ${\mathcal {T}}_{\subseteq W}(H)$ is locally Euclidean.

Proof   We need to show that every $e \in H$ has an open neighborhood $A \in {\mathcal {T}}_{\subseteq W}(H)$, $e \in A$ such that $A$ is homeomorphic to $B$, where $B$ is an open subset of ${\mathbb {R}}^n$. By Definition 28, there is $\langle O, \varphi \rangle \in {\mathcal {C}}$ such that $e \in O$ and $\varphi [O \cap H] = B$, where $B$ is an open subset of ${\mathbb {R}}^n$ and $\varphi _{\mid O \cap H}: O\cap H \rightarrow B$ is an injection. By Definition 32, $O \in {\mathcal {T}}(W)$, so $O \cap H \in {\mathcal {T}}_{\subseteq W} (H)$. Putting $A= O \cap H$, we need to show that $\varphi : A \rightarrow B$ is a homeomorphism.

First, consider an open set $B' \subseteq B$ and ask if $\varphi ^{-1}[B']$ is open? Take an arbitrary $e' \in \varphi ^{-1}[B']$; then $\tilde{e}' = \varphi (e') \in B'$. Since $B'$ is open, there is a borderless diamond $bd^{\tilde{x} \tilde{y}} \subseteq B'$ such that $\tilde{e}' \in bd^{\tilde{x} \tilde{y}}$. We put next $bd^{xy} : = \varphi ^{-1}[bd^{\tilde{x} \tilde{y}}]$. Clearly, $bd^{xy} \subseteq \varphi ^{-1}[B']\subseteq A$ and $x = \varphi ^{-1}(\tilde{x})$, and $y = \varphi ^{-1}(\tilde{y})$. Since $\varphi$ respects the ordering, $bd^{xy}$ is a borderless diamond in $\langle A, \curlyeqprec _{\mid O}\rangle$. We next define:

$$ z \in O' \text { iff } z \in O \wedge (z \in H \rightarrow z \in bd^{xy}) \wedge (z \not \in H \rightarrow \exists z' \in bd^{xy} \wedge z' \curlyeqprec _{\mid O} z) $$

It can be shown (but we leave the proof to the reader) that $O' \in {\mathcal {O}}$. Then, since $O' \subseteq O$, Fact 30 implies that $O' \in {\mathcal {T}}(W)$, from which we get $O' \cap H \in {\mathcal {T}}_{\subseteq W}(H)$. Since $O' \cap H = bd^{xy}$, it follows that $e' \in bd^{xy} \in \mathcal T_{\subseteq W}(H)$ and $bd^{xy} \subseteq \varphi ^{-1}[B']$. Since this is true about every $e' \in \varphi ^{-1}[B']$, we get that $\varphi ^{-1}[B'] \in \mathcal T_{\subseteq W}(H)$.

Second, pick an arbitrary set $A' \subseteq A$, $A' \in \mathcal T_{\subseteq W} (H)$ and ask if $\varphi [A']$ is open. The premise means that $A' = A'' \cap H$ for some $A'' \in {\mathcal {T}} (W)$. Accordingly, $A'' = \bigcup b_\alpha$, where $b_\alpha$ are elements of the base for $\mathcal T(W)$—see Fact 34. Thus, $\varphi [A'] = \varphi [\bigcup (b_\alpha \cap H) ]$ which is equal to $\bigcup \varphi [ (b_\alpha \cap H) ]$ (because $\varphi$ restricted to $A$ is injective). Since $b_\alpha$’s are domains of the chart maps (see the same Fact), $\varphi [ (b_\alpha \cap H)]$ are open subsets of ${\mathbb {R}}^n$, and hence $\bigcup \varphi [ (b_\alpha \cap H) ] = \varphi [A']$ is open as well. $\square$

Lemma 48

Let $\langle {\mathcal {W}}, {\mathcal {C}}\rangle$ be an $n$-g-manifold on a generalized BST model ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}} \rangle$. Then topology ${\mathcal {T}}(W)$ is not locally Euclidean, if there are g-histories $H^1, H^2$ in ${\mathcal {W}}$ whose intersection $H^1 \cap H^2$ has a maximal element.

Sketch of a proof    Let $e$ be a maximal element in $H^1 \cap H^2$ and assume, as a reductio hypothesis, that ${\mathcal {T}}(W)$ is locally Euclidean. Then there is some $b$—an element of the base for ${\mathcal {T}}(W)$ such that $e \in b$, and a homeomorphism $\psi : b \rightarrow B$, where $B$ is an open subset of ${\mathbb {R}}^m$. Clearly, $B\setminus \{\psi (e) \}$ is an open subset of ${\mathbb {R}}^m$, and hence (since $\psi$ is a homeomorphism), $b\setminus \{e \} \in {\mathcal {T}}(W)$. Again, since $\psi$ is a homeomorphism, it preserves a number of maximal connected components. $B\setminus \{\psi (e) \}$ has two maximal connected components if $m =1$ and one maximal connected component if $m > 1$ (see Munkres 2000, p.165). We have a contradiction since $b\setminus \{e \}$ has at least three maximal connected components ¹⁷: the trunk and two “rimless futures” $\bigtriangledown _b^1$ and $\bigtriangledown ^2_b$ of $e$, defined as follows (for $i =1,2$):

$$\begin{aligned} \bigtriangledown ^i_b = \bigcup _{H^* \in gHist}\{\psi ^{-1}[\psi [ \{z \in b\cap H^*\mid e \prec _{\mid b} z \}]\setminus flc(\psi (e)]\mid H^* \approx H^i\},\\ \text {where } H^* \approx H^i \text { iff } \exists e' \; (e' \in H^i \cap H^* \wedge e \prec _b e'), \end{aligned}$$

and $flc(\tilde{x})$ is the set of points in ${\mathbb {R}}^n$ that lie on the rim of the future light-cone of $\tilde{x}$.$\square$

Lemma 36 and the lemma above show the price that is to be paid for allowing that the intersection of two g-histories has a maximal element (or for assuming PCP, point-like version): g-histories are not open in the topology ${\mathcal {T}}(W)$ and this topology is not locally Euclidean.

4.2.3 Two Further Postulates

To ensure some desirable topological or differentiability properties in a manifold topology, we need two additional postulates:

Postulate 49

Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model. Then for every g-history $H$ of ${\mathcal {W}}$ there are no $O_1, O_2 \in {\mathcal {O}}$ such that $O_1 \cap H \ne \emptyset$, $O_2 \cap H \ne \emptyset$ and $(O_1 \cup O_2) \cap H = H$

Postulate 50

Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model. Then ${\mathcal {O}}$ contains a countable sub-cover ${\mathcal {O}}^*$ of $W$, i.e., $\mathcal O^* \subseteq {\mathcal {O}}$ and is countable, and $\forall e \in W \exists O \in {\mathcal {O}}^*\; e \in O$.

The first postulate ensures that our topologies ${\mathcal {T}}_{\subseteq W}(H)$ are connected. The second postulate is needed for the existence of affine connections.

4.3 Tangent Vectors

Although we have already constructed a generalized (non-Hausdorff) manifold, whose subsets maximal with respect to being Hausdorff and downward closed are very much like spacetimes of general relativity, we need to equip it with even more structure. GR equations are tensor equations, and tensors need vector spaces to operate. Accordingly, in GR one associates to each element $e$ of a manifold a vector space of vectors tangent at that point $e$. We thus need to add vector spaces to our generalized manifolds. That is, for each $e \in W$, where ${\mathcal {W}}$ is a generalized BST model that admits an $n$-g-manifold $\langle W, {\mathcal {C}}\rangle$ (and possibly satisfies Postulates 49 and 50), we will construct the space $V(e)$ of tangent vectors at $e$.

To recall the GR construction, one begins with the set $S(e): O \rightarrow {\mathbb {R}}$ of smooth maps, where $O$ is some open set containing $e$, or another. Since $O$ is generally not a subset of ${\mathbb {R}}^m$, the concept of smoothness needs an explanation:

A function $\alpha$ from an open set $O$ to ${\mathbb {R}}$ is said to be smooth iff for every chart $\langle O', \varphi \rangle \in {\mathcal {C}}$ such that $O \cap O' \ne \emptyset$, $\alpha \varphi ^{-1}: \mathbb R^n \rightarrow {\mathbb {R}}$ has derivatives of an arbitrary order and is continuous. Finally, a vector in $V(e)$ is defined as a map from $S(e)$ to ${\mathbb {R}}$ that satisfies some three conditions.¹⁸

A red light should already blink at this junction since, in the present framework, a chart function $\varphi$ is not necessarily injective, which makes $\varphi ^{-1}$ undefined. However, each chart function $\varphi$ of $\langle O, \varphi \rangle \in \mathbb C$ is injective if restricted to any g-history $H$ such that $H \cap O \ne \emptyset$. A natural remedy thus is to require that $O$ occurring in the definition of set $S(e)$ should be contained in a g-history.¹⁹ With this remedy, $V(e)$ will not depend on g-histories. Also, if $e$ and $e'$ belong to one g-history, the vector spaces $V(e)$ and $V(e')$ are to be connected in exactly the same way as in GR, that is, by the parallel transport. Finally, if $e$ and $e'$ do not share a g-history, no connection between $V(e)$ and $V(e')$ is postulated.

Unfortunately, the remedy is not going to work if the intersection of some two g-histories $H$ and $H'$ in ${\mathcal {W}}$ has a maximal element, say $m$. Each open set in ${\mathcal {T}}(W)$ containing $m$ must extend upward along every path passing through $m$, and hence must contain some elements of $H\setminus H'$ as well as some elements of $H' \setminus H$.

We thus are driven to outright prohibit maximal elements in intersections of g-histories by imposing the following postulate on generalized BST models:

Postulate 51

Let ${\mathcal {W}} = \langle W, \curlyeqprec , \mathcal O\rangle$ be a generalized BST model. Then:

$$ \forall e \in W \; \exists H \in gHist\; \exists O \in {\mathcal {O}}\; (e \in O \wedge O \subseteq H). $$

Postulate 51 has the following consequence:

Fact 52.

Let ${\mathcal {W}} = \langle W, \curlyeqprec , {\mathcal {O}}\rangle$ be a generalized BST model that satisfies Postulate 51. Then

(1) there are no two g-histories in ${\mathcal {W}}$ whose intersection has a maximal element;

(2) $\forall e \in W \; \exists O \in {\mathcal {T}}(W) \; \exists H \in gHist\; (e \in O \wedge O \subseteq H)$

Proof   A proof of (1) is immediate. As for (2), observe that for every $e \in W$ there is a chart ($\dagger$) $\langle O', \varphi \rangle \in {\mathcal {C}}$ such that $e \in O'$ (by Definition 28) and an $O'' \in {\mathcal {O}}$ such that $(e \in O'' \wedge O'' \subseteq H)$ (by Postulate 51). By Fact 34, ($\dagger$) implies $O' \in {\mathcal {O}}$, hence $O := O' \cap O'' \in {\mathcal {O}}$. Since $O \subseteq O'$, by ($\dagger$) Facts 30 and 34, $O \in \mathcal T(W)$. Moreover, $e \in O$ since $e \in O'$ and $e \in O''$ and $O \subseteq H$ since $O \subseteq O'' \subseteq H$. $\square$

Postulate 51 permits a sought-for modification of the construction of tangent vector spaces. The set $S(e)$ is now defined as a set of smooth maps from some $O\in {\mathcal {T}}(W)$ to ${\mathbb {R}}$, where $O$ is any open set containing $e$ and contained in some g-history. A vector in $V(e)$ is defined as before, as a map from $S(e)$ to ${\mathbb {R}}$ that satisfies the three conditions listed in the Footnote 18 above.

Postulate 51 comes at a price: generalized BST does not generalize BST1992 (though it generalizes BST*1992—in the sense of Lemma 25). Nevertheless, the bonuses outweigh the cost: The Postulate assures that there are tangent vector spaces (as required by GR), that g-histories are open in the topology ${\mathcal {T}}(W)$ (see Lemma 36), and that ${\mathcal {T}}(W)$ is locally Euclidean (see Lemma 48 and Postulate 51(1)).²⁰

5 Discussion

In this sections we address two issues that look troublesome for the generalized BST.

5.1 Hájíček-Müller Quasi-History

Following Hájíček (1971), Müller (2011) discusses an odd subset of a branching model. His tentative definition (which he amends accordingly) takes a history to be a subset of a base set that is maximal with respect to the joint property of being open, connected, and Hausdorff. The subset mentioned above satisfies this definition, but appears to be modally inconsistent (intuitively speaking). The branching model $M$ is the union of two $2$-dimensional Minkowski spacetimes $M_1$ and $M_2$, each with Minkowskian ordering, and pasted below and in the wings of the origin point $\bar{0} = \langle 0, 0\rangle$, so that the differences of the two Minkowskian spacetimes are the following:

$$ M_1 \setminus M_2 =J^+(\bar{0})\times \{1\}, \quad M_2 \setminus M_1 = J^+(\bar{0})\times \{2\}, $$

where $J^+(\bar{0}) = \{ \langle t, x \rangle \mid \bar{0} \leqslant _M \langle t, x \rangle \}$. That is, $M_1$ and $M_2$ share neither the point of origin nor its future light cone.

To construct the troublesome subset $A$ of $M_1 \cup M_2$, we subtract from the latter the “left” part of $J_1$ and the “right” part of $J_2$, that is,

$$ A := M \setminus (J_l \times \{1\} \cup J_r \times \{2\} ), $$

where $J_l\!:=\!\{ \langle t, x \rangle \in J^+(\bar{0})\mid x \leqslant _M 0\}$ and $J_r\!:=\!\{ \langle t, x \rangle \in J^+(\bar{0})\mid x \geqslant _M 0\}$. Note that $A$ contains no choice pairs, as the “doubled rim” (including $(\bar{0}, 1)$ and $(\bar{0}, 2)$) has been removed from $A$. For an argument that $A$ is Hausdorff as well as open and connected, see Müller (2011).

From the perspective of the present framework, $M$ with the usual ordering and a single patch, namely $M$ itself, is a model of genBST. However, $A$ turns out to be inconsistent, the witness being any pair $e_1, e_2 \in A$ such that $e_1 \in (J^+\setminus J_l)\times \{1\}$ and $e_2 \in (J^+\setminus J_r)\times \{2\}$. Clearly, $e_1$ is above $(\bar{0}, 1)$ and $e_2$ is above $(\bar{0}, 2)$, and $(\bar{0}, 1)$, $(\bar{0}, 1)$ constitute a splitting pair. Thus, $A$ is not a g-history (recall that g-history = maximal consistent subset of a base set). This diagnosis agrees with the verdict delivered by Müller’s (2011) final definition of histories, which additionally requires, for each subset $C \subseteq h$ of history $h$ that if $\partial C \ne \emptyset$, then $h \cap \partial C \ne \emptyset$ as well.

5.2 Borders in the Overlap

I have already warned against a branching model ${\mathcal {W}}$ that has more than one maximal upward directed subset (i.e., a BST1992 history) and in which every upper bounded chain has a supremum.²¹ Figuratively, in ${\mathcal {W}}$ the border of the overlap of two BST1992 histories is contained in the overlap. Since a model of this kind does not contain any splitting pair in the sense of Definition 17, from the perspective of the generalized BST ${\mathcal {W}}$ has a single g-history only, namely, the model itself. As we will now argue, this implies that no generalized manifold in the sense of Definition 28 can be constructed on ${\mathcal {W}}$. As a reductio hypothesis, let us assume that there is g-manifold constructed on ${\mathcal {W}}$. Since ${\mathcal {W}}$ has one g-history only, by Lemma 47 the manifold topology ${\mathcal {T}}(W)$ must be locally Euclidean. Since upper bounded chains in ${\mathcal {W}}$ are assumed to have suprema, any nonempty intersection $t \cap h_1 \cap h_2$ of a maximal chain in $\mathcal W$ and upward directed subsets $h_1, h_2$ of $\mathcal W$ has a maximal element $e'$. By an argument analogous to that given in the proof of Lemma 48, $e'$ does not have an open neighborhood homeomorphic to an open subset of ${\mathbb {R}}^n$ for any natural number $n$, which contradicts local Euclidicity.

The moral of this argument is that a generalized manifold cannot be constructed on a genBST model that has more than one maximal upper directed subset and in which every upper bounded chain has a supremum.

6 Conclusions

We have developed in this chapter a branching theory that captures the insights of general relativity. To pave the way towards this construction, in Sect. 2 we modified BST1992 by replacing its Prior Choice Principle (stated in terms of maximal points) with a pair-like version of this principle. As a consequence, the intersection of any two histories has no maximal element in the resulting theory (termed BST$^*$1992). The construction of the branching theory then proceeded in three stages. In Sect. 4.1 we defined generalized BST models, the underlying idea being that locally, that is, around any element of a base set, the model is similar to BST1992, although the base set is not necessarily partially ordered. Generalized histories are defined as maximally consistent subsets of a base set, where consistency is spelled out in terms of splitting points. In the second stage, in Sect. 4.2 we defined generalized non-Hausdorff manifolds on generalized BST models. The main result of this section is that a generalized history (aka spacetime) turns out to be a subset of a manifold’s base set that is maximal with respect to being Hausdorff and downward closed. And, vice versa, every subset of a manifold’s base set maximal with respect to being Hausdorff and downward closed is identical to some generalized history. Two postulates (49 and 50) of this section ensure that the manifold topology on a generalized history is connected and that it has a countable sub-cover. We can thus identify a generalized history with a single GR spacetime, and a generalized BST model with a bundle of GR spacetimes. In the third stage (Sect. 4.3), in order to define tangent vector spaces on a generalized history, we had to assume Postulate 51, which comes with significant consequences. First, it prohibits maximal elements in the intersections of generalized histories, making generalized histories similar to histories of BST$^*$1992 rather than to histories of BST1992. On a positive side, it implies that a generalized BST model is (as a whole) locally Euclidean and that a generalized history is open in the manifold topology. We wrapped up this chapter with a discussion (Sect. 5) of two potentially troublesome issues: we showed that the present framework delivers an intuitively adequate verdict concerning an odd structure discussed by Müller (2011) and we argued that generalized manifold cannot be constructed on the branching models advocated by Kowalski and Placek (1999).

Appendix Topological Facts About BST1992

Let ${\mathcal {W}} = \langle W, \leqslant \rangle$ be a BST1992 model. To simplify the proofs below, we introduce the concept of “diamond oriented by maximal chain $t$ with vertices $e_1$ and $e_2$”, to be written as $d^{\;e_1 e_2}_t$:

$$ d^{\;e_1 e_2}_t := \{y \in W\mid e_1 < e_2 \wedge e_1 \leqslant y \leqslant e_2\}, $$

where $t$ is a maximal chain in $W$ and $e_1, e_2 \in t$.

Fact 53.

The Bartha topology ${\mathcal {T}}(h)$ on a history $h$ in a BST1992 model is connected.

Proof   We need to show that the only subsets of history $h$ that are both closed and open, are $\emptyset$ and $h$ itself. To assume to the contrary is to assume that there are open nonempty subsets $A\subsetneq h$ and $B = h\setminus A$. Consider thus $x \in A$ and $y \in B$. Since histories are upward directed there is in $h$ an upper bound $z$ of $x$ and $y$, and either (i) $z\in A$, or to (ii) $z\in B$. If (i), we consider a maximal chain $t \in MC(h)$ such that $y, z \in t$. (If (ii), consider a maximal chain $t' \in MC(h)$ such that $x, z \in t'$.) By the BST axiom of infima and maximality of $t$, there is in $t$ an infimum $f = \inf {(t \cap A)}$. (Analogously, there is in $t'$ an infimum $f' = \inf {(t' \cap B)}$.) If $f \in A$, then there is no diamond containing $f$ and oriented by $t$ that is a subset of $A$, so $A$ is not open. But also, if $f \in B = h \setminus A$, then there is no diamond containing $f$, oriented by $t$, and a subset of $B$, so $B$ is not open. We similarly arrive at a contradiction if we ask whether $f'$ is in $A$, or not. $\square$

Fact 54.

The Bartha topology ${\mathcal {T}}(W)$ is connected.

Proof   Note that in the proof above, to show that ${\mathcal {T}}(h)$ is connected, we used a maximal chain $t\in MC(h)$ that intersects both $A$ and $h\setminus A$. Now, if we only know that there is at least one $t \in MC(W)$ that intersects $A \subseteq W$ and $B:= W \setminus A$, where each $A$ and $B$ is open and nonempty, we could use the same trick as above to prove that ${\mathcal {T}}(W)$ is connected. Thus, let us assume for an arbitrary pair of $A, B$ of the sort described above that ($\dagger$) $\forall t \in MC(W)\; t \subseteq A \vee t \subseteq B$. Let us then pick some $t \subseteq A$ nonempty $t \subseteq A$ (the case with $t \subseteq B$ proceeds analogously). Clearly, for some history $h$, $t \in MC(h)$. Suppose now that (i) there is some $x \in h\cap B$. Then we pick some $y \in t$, produce an upper bound $z$ of $x$ and $y$. If $z \in A$, there is a maximal chain containing $z$ and $x$, and if $z \in B$ there is a maximal chain containing $z$ and $y$, where each of these chains intersects $A$ and $B$—this contradicts ($\dagger$). Let us thus suppose that (ii) $h \cap B = \emptyset$, which entails $h \subseteq A$. Then, for any $x \in B$, we must have $x\not \in h$, but $x \in h'$ for some history $h'$. By PCP, there is a choice point $c$ such that $c < x$ and $h \perp _c h'$. It follows that any maximal chain containing $c$ and $x$ intersects with $A$ and $B$ since $x \in B$ and $c \in h \subseteq A$, which again contradicts ($\dagger$). $\square$

Fact 55.

For every $A \subseteq W$, the Bartha condition applied to $A$ yields topology ${\mathcal {T}}(A)$.

Proof   Rearrange Facts 8 and 9 of Placek et al. (2013) by replacing $h$ by $A$.$\square$

Our next fact appeals to continuous branching, which is defined as below:

Definition 56

(continuous branching surface) Histories $h$ and $h'$ branch along a continuous branching surface iff there is $x \in h\setminus h'$ such that for every chain $t \in h\cap h'$ upper bounded by $x$: $\sup _h{(t)} = \sup _{h'}{(t)}$.

Note that $x \in h \setminus h'$ entails (by PCP) that there is some $x' \in h\cap h'$ and below $x$, which in turn ensures that some chains containing $x$ pass through this intersection.

Fact 57.

Let $A$ be a proper superset of some history $h$ of $W$ ( i.e., $h \subsetneq A$). Let also $A$ be downward closed and there is no continuous branching surface for any two histories in $W$. Then ${\mathcal {T}}(A)$ does not satisfy the Hausdorff property.

Proof   Let (i) $h \subsetneq A$. Pick some $x \in A\setminus h$; hence $x \in h'$ for some $h' \in Hist$. Since $h$ and $h'$ do not branch along a continuous branching surface, there is a chain (ii) $t^*\subseteq h \cap h'$ such that (iii) $t^* < x$ and $\sup _h{(t^*)} \ne \sup _{h'}{(t^*)}$. By (iii) and downward closure of $A$, $\sup _h{(t^*)}, \sup _{h'}{(t^*)} \in A$. Consider then an arbitrary pair of open sets $O, O' \in \mathcal {T}(A)$ containing $s= \sup _h{(t^*)}$ and $s'= \sup _{h'}{(t^*)}$, respectively. This means that for every pair of maximal chains $t, t'$ such that $s \in t, s' \in t'$ and $y < s < z$, $y' < s' < z'$, there are oriented diamonds $d_t^{yz} \subseteq O$ and $d_{t'}^{y'z'} \subseteq O'$. Picking $t$ and $t'$ such that $t^* \subseteq t \cap t'$, we obtain that $\max \{y, y'\} \in d_t^{yz} \cap d_{t'}^{y'z'} \ne \emptyset$. Accordingly, any $O, O' \in \mathcal {T}(A)$ containing $s, s'$, respectively, must overlap.

Lemma 58

(1) There are BST histories such that ${\mathcal {T}}(h)$ is not locally Euclidean (in the Bartha topology).

(2) ${\mathcal {T}}(W)$ is not locally Euclidean (unless $W = h$ for some history $h$);

(3) There are BST models such that, for every history $h$ of such a model, ${\mathcal {T}}(h)$ is locally Euclidean (again, in the Bartha topology).

Proof   As an example for (1), consider a downward fork, with its upper arm having a minimal element —this a one-history BST model. For reductio, suppose there is homeomorphism $f$ between a neighborhood $u$ of the vertex $e$ and an open ball $b \subseteq \mathbb {R}^n$, for some $n \in \mathbb {N}$. Clearly, $b \setminus \{f(e)\}$ is open in standard topology on ${\mathbb {R}}^n$, so $u \setminus e$ must be open in the Bartha topology. However, $u \setminus \{e\}$ has three connected components (two lower arms and the top arm), whereas $b \setminus \{f(e)\}$ has two if $n =1$, or one (itself) if $n >1$. Thus, $f$ cannot be a homeomorphism.²²

As for (2), the above construction shows that any $W$ containing a choice point (that is, having more than one history) is not locally Euclidean;

For (3), take a history in a Minkowskian Branching Structure²³—it is locally (and globally) Euclidean since it is isomorphic to $\mathbb {R}^n$. $\square$