Machine Learning for Thermoacoustics

Abstract

This chapter demonstrates three promising ways to combine machine learning with physics-based modelling in order to model, forecast, and avoid thermoacoustic instability. The first method assimilates experimental data into candidate physics-based models and is demonstrated on a Rijke tube. This uses Bayesian inference to select the most likely model. This turns qualitatively-accurate models into quantitatively-accurate models that can extrapolate, which can be combined powerfully with automated design. The second method assimilates experimental data into level set numerical simulations of a premixed bunsen flame and a bluff-body stabilized flame. This uses either an Ensemble Kalman filter, which requires no prior simulation but is slow, or a Bayesian Neural Network Ensemble, which is fast but requires prior simulation. This method deduces the simulations’ parameters that best reproduce the data and quantifies their uncertainties. The third method recognises precursors of thermoacoustic instability from pressure measurements. It is demonstrated on a turbulent bunsen flame, an industrial fuel spray nozzle, and full scale aeroplane engines. With this method, Bayesian Neural Network Ensembles determine how far each system is from instability. The trained BayNNEs out-perform physics-based methods on a given system. This method will be useful for practical avoidance of thermoacoustic instability.

1 Introduction

At present there is no realistic alternative to combustion engines for long distance aircraft and rockets. These engines have unrivalled power to weight ratios and their fuels have unrivalled energy to weight ratios. If we continue to fly long distances or send rockets into space, we will continue to combust fuels in increasingly high-performance gas turbines and rockets. Despite decades of research and the development of sophisticated physics-based models, thermoacoustic instability in these engines remains difficult to predict and eliminate. The aim of this chapter is to introduce some promising avenues in which machine learning methods could be used to model, forecast, and avoid thermoacoustic instability.

1.1 The Physical Mechanism Driving Thermoacoustic Instability

The combustion chambers in aircraft and rocket engines have extraordinarily high power densities: from 100 MW/m$^3$ in aircraft gas turbines to 50 GW/m$^3$ in liquid-fuelled rocket engines (Culick 2006). They contain flames that are typically anchored by a recirculation zone (aircaft engines) or by fuel injector lips (rockets). Acoustic velocity fluctuations perturb the base of the flame, creating ripples that convect downstream and cause heat release rate fluctuations some time later, which in turn create acoustic fluctuations either directly or via entropy spots (Lieuwen 2012). If moments of higher (lower) heat release rate coincide sufficiently with moments of higher (lower) pressure around the flame, then more work is done by the heated gas during the expansion phase of the acoustic cycle than was done on it during the compression phase. If the work done by thermoacoustic driving exceeds the work dissipated through damping or acoustic radiation over a cycle, then the acoustic amplitude grows and the system is thermoacoustically unstable. This is also known as combustion instability. In high performance rocket and aircraft engines, the heat release rate is so high and the natural dissipation so low that these engines can become thermoacoustically unstable even if the thermodynamic efficiency of the cycle is as little as 0.1% (Huang and Yang 2009).

Thermoacoustic oscillations were first noticed over 200 years ago (Higgins 1802) and their physical mechanism was correctly identified nearly 150 years ago (Rayleigh 1878). They were recognized as a significant problem in rocket engines 80 years ago and have been investigated seriously for 70 years (Crocco and Cheng 1956). Nevertheless, they remain a problem for the design of gas turbine and rocket engines because engineers are rarely able to predict, at the design stage, whether a particular engine will suffer from them (Lieuwen and McManus 2003; Mongia et al. 2003). This chapter explains why thermoacoustic instability is so difficult to predict accurately and explores various data-driven approaches that could develop into alternatives or additions to current physics-based approaches.

1.2 The Extreme Sensitivity of Thermoacoustic Systems

Thermoacoustic instability is difficult to predict for two main reasons. Firstly, if the time lag between velocity fluctuations at the base of the flame and subsequent heat release rate fluctuations is similar to or greater than the acoustic period, which is usually the case, then the ratio of time lag to acoustic period strongly affects the efficiency of the thermoacoustic mechanism (Juniper and Sujith 2018). Secondly, this time lag often depends on factors that are difficult to simulate or model accurately, such as jet break-up, droplet evaporation, flame kinematics, and high Reynolds number combustion.

Rocket and aircraft engines are usually developed through component tests, sector tests, combustor tests, and full engine tests. The response of the flame to acoustic fluctuations, for example, might be measured in a well-characterized rig and then included in a model of the full engine. If, however, the flame’s behaviour were to change slightly when placed in the full engine then the model would contain unknown model error in a critical component. The model would remain qualitatively accurate but become quantitatively inaccurate and therefore misleading. Indeed, it is quite common for thermoacoustic instability to recur in the later stages of engine development, even though models compiled from component tests predicted it to be stable (Mongia et al. 2003).

Encouragingly, this sensitivity also explains why thermoacoustic oscillations can usually be suppressed by making small design changes (Mongia et al. 2003; Oefelein and Yang 1993; Dowling and Morgans 2005). The challenge, of course, is to devise these small design changes from a quantitatively-accurate model rather than by trial and error. Adjoint methods combined with gradient-based optimization provide an excellent mechanism for this (Juniper and Sujith 2018; Magri and Juniper 2013; Juniper 2018; Aguilar and Juniper 2020). They rely, however, on a quantitatively accurate model. This chapter explores how experimental or numerical data could be assimilated in order to create these quantitatively-accurate models from qualitatively-accurate physics-based models or from physics-agnostic models.

1.3 The Opportunity for Data-Driven Methods in Thermoacoustics

All models contain parameters that are tuned to fit data. These range from qualitatively-accurate physics-based models with $\mathcal {O}(10^1)$ parameters to Gaussian Process surrogate models with $\mathcal {O}(10^3)$ parameters, and to physics-agnostic neural networks with $\mathcal {O}(10^6)$ parameters. The challenge is to create models that are quantitatively accurate with quantified uncertainties and are sufficiently constrained to be informative.¹ To this end, all the approaches in this chapter take a Bayesian perspective and, where possible, employ rigorous statistical inference ² (MacKay 2003).

The first example is a canonical thermoacoustic system: the hot wire Rijke tube (Rijke 1859; Saito 1965). Although simple and cheap to operate, it is difficult to model accurately firstly because the heat release rate is small, meaning that many visco-thermal dissipation mechanisms are sufficiently large, in comparison, that they must be included in the model, and secondly because the heat release rate fluctuations at the wire cannot be measured directly. A hot wire Rijke tube is, however, easy to automate, meaning that millions of datapoints can be obtained cheaply and elements of the system can be moved easily (Rigas et al. 2016). Physics-based models of the Rijke tube can therefore be constructed sequentially, mirroring data assimilation from component tests, sector tests, combustor tests, and full engine tests in industry. The process (MacKay 2003; Juniper and Yoko 2022) is to:

• 1. choose various plausible physics-based models that could explain the data;

• 2. tune model parameters by assimilating data from experiments;

• 3. quantify the uncertainties in the parameters of each model;

• 4. calculate the marginal likelihood (also known as the evidence) for each model, and thereby penalise overly-complex models;

• 5. compare the models against each other and select the best model;

• 6. add the next component and assimilate more data, allowing the parameters describing the previous components to float within constrained priors.

The second example is the assimilation of DNS and/or experimental data into a simplified combustion model, the G-equation (Williams 1985) with around 4000 degrees of freedom (Hemchandra 2009). Two approaches are demonstrated. The first approach assimilates snapshots of the data sequentially with a Kalman filter (Evensen 2009), refining model parameters on the fly (Yu et al. 2020). The second approach assimilates 10 snapshots simultaneously with a Bayesian ensemble of Deep Neural Networks (BayNNE) (Pearce et al. 2020). This gives almost the same results as the Kalman filter but is around $10^6$ times faster. Both approaches assimilate data into physics-based models and obtain the expected values and uncertainties of the model parameters.

The third example is the assimilation of experimental data into physics-agnostic models. The models are trained to recognize how close a thermoacoustic system is to instability from the noise that it emits (Sengupta et al. 2021; Waxenegger-Wilfing et al. 2021; McCartney et al. 2022). As for the first two examples, a Bayesian approach is used so that the model can output its certainty about its prediction. This physics-agnostic approach is compared with model-based approaches quantified by the Hurst exponent (Nair et al. 2014), the permutation entropy (Kobayashi et al. 2017), and the autocorrelation decay (Lieuwen and Banaszuk 2005), which are based on a priori assumptions of how the noise signal will change as instability approaches.

Other examples of the application of Machine Learning to Thermoacoustics are in learning the nonlinear flame response with Neural Networks (Jaensch and Polifke 2017; Tathawadekar et al. 2021), identifying nonlinear flame describing functions (McCartney et al. 2020), modelling the flame impulse response from LES with a Gaussian Process surrogate model (Kulkarni et al. 2021), and the use of Gaussian Processes for Uncertainty Quantification (Guo et al. 2021a).

2 Physics-Based Bayesian Inference Applied to a Complete System

Physics-based Bayesian inference starts from a set of physics-based candidate models $\mathcal {H}_i$, each of which has a set of model parameters $\textbf{a}$. For thermoacoustic systems, typical model parameters would be physical dimensions, temperatures, reflection coefficients, and a flame transfer function. Data, $D$, arrive and, at the first level of inference, we find the parameters of each model that are most likely to explain the data (MacKay 2003, Sect. 2.6). For thermoacoustic systems, typical data would be temperatures, pressure fluctuations, or natural emission fluctuations. We start from the product rule of probability:

$$\begin{aligned} P(\textbf{a},D|\mathcal {H}_i) = P(\textbf{a}|D,\mathcal {H}_i) P(D|\mathcal {H}_i) = P(D|\textbf{a},\mathcal {H}_i) P(\textbf{a}|\mathcal {H}_i) \end{aligned}$$

(1)

where $P(\textbf{a}|\mathcal {H}_i)$ is our prior assumption about the probability of the parameters, $\textbf{a}$, given the model $\mathcal {H}_i$. Bayesian inference requires us to impose prior values for the model parameters and their uncertainties. This is appropriate because we usually know the model parameters approximately from previous experiments and will become increasingly certain about them as an experimental campaign progresses. The term $P(D|\textbf{a},\mathcal {H}_i)$ contains the data, $D$, which is fixed by the experiment, and the parameters, $\textbf{a}$, which we wish to obtain for model $\mathcal {H}_i$. For given $D$, the term $P(D|\textbf{a},\mathcal {H}_i)$ defines the likelihood of the parameters, $\textbf{a}$, of model $\mathcal {H}_i$ (MacKay 2003, p. 29). This likelihood does not have to sum to 1 because the proposed models $\mathcal {H}_i$ are not mutually exclusive or exhaustive. On the other hand, for a given model $\mathcal {H}_i$ and parameters, $\textbf{a}$, the term $P(D|\textbf{a},\mathcal {H}_i)$ defines the probability of the data, which does have to sum to 1. This distinction becomes important when incorporating measurement noise.

The term $P(D|\mathcal {H}_i)$ is the evidence for the model. This is the RHS of (1) integrated (also known as marginalized) over all parameter values:

$$\begin{aligned} P(D|\mathcal {H}_i) = \int _\textbf{a}P(D|\textbf{a},\mathcal {H}_i) P(\textbf{a}|\mathcal {H}_i) \; \text {d}\textbf{a}\end{aligned}$$

(2)

which is known as the marginal likelihood. At the first level of inference, this quantity has no significance because we simply find $\textbf{a}$ that maximizes $P(\textbf{a}|D,\mathcal {H}_i)$ for a given model $\mathcal {H}_i$. It is used in the second level of inference, in which we compare the marginal likelihoods of different candidate models.

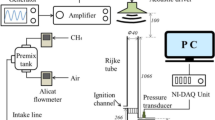
The experiments in this section are performed on a vertical Rijke tube containing an electric heater, which is moved through 19 different positions from the bottom end of the tube (Juniper and Yoko 2022; Garita et al. 2021; Garita 2021). The heater power is set to eight different values until the system reaches steady state. Then a loudspeaker at the base of the tube forces the system close to its resonant frequency and probe microphones measure the response throughout the tube. We assimilate the decay rates, $S_r$, frequencies, $S_i$, and relative pressures of the microphones, $(P_r,P_i)$ into a thermoacoustic network model.

2.1 Laplace’s Method

The most likely parameters, $\textbf{a}$, and their uncertainties can be found with sampling methods such as Markov Chain Monte Carlo (Metropolis et al. 1953; MacKay 2003) or Hamiltonian Monte Carlo. These sample the posterior probability distribution through a random walk. They can be applied to this thermoacoustic problem (Garita 2021) but are quite slow. The assimilation process can be accelerated greatly by assuming that all the probability distributions are Gaussian (MacKay 2003, Chap. 27). The prior probability distribution, which must integrate to 1, is then:

$$\begin{aligned} P(\textbf{a}|\mathcal {H}_i) = \frac{1}{\sqrt{(2\pi )^{N_a}|\textbf{C}_{aa}|}} \exp \left\{ - \frac{1}{2} (\textbf{a}- \textbf{a}_p)^T \textbf{C}_{aa} (\textbf{a}- \textbf{a}_p) \right\} \end{aligned}$$

(3)

where $N_a$ is the number of parameters, $\textbf{a}_p$ are their prior expected values and $\textbf{C}_{aa}$ is their prior covariance matrix. We assume that, for a given model $\mathcal {H}_i$ with parameters $\textbf{a}$, the measurements $D$ are normally-distributed around the model predictions $\mathcal {D}(\textbf{a})$:

$$\begin{aligned} P(D|\textbf{a},\mathcal {H}_i) = \frac{1}{\sqrt{(2\pi )^{N_D}|\textbf{C}_{DD}|}} \exp \left\{ - \frac{1}{2} (\mathcal {D}(\textbf{a}) - D)^T \textbf{C}_{DD} (\mathcal {D}(\textbf{a}) - D) \right\} \end{aligned}$$

(4)

where $N_D$ is the number of datapoints and $\textbf{C}_{DD}$ is a diagonal matrix containing the variance of each measurement. In this example, epistemic uncertainty such as model error and systematic measurement error is included within $\textbf{C}_{DD}$.

We define $\mathcal {J}$ to be the negative log of the RHS of (1):

$$\begin{aligned} \mathcal {J}= - \log \left\{ P(D| \textbf{a}, \mathcal {H}_i) P(\textbf{a}| \mathcal {H}_i) \right\} \end{aligned}$$

(5)

so that the most probable parameter values, $\textbf{a}_{mp}$, are found by minimizing $\mathcal {J}$ using an optimization algorithm. The RHS of (1) is the product of two Gaussians (3), (4), meaning that the posterior likelihood of the parameters, $P(\textbf{a}|D,\mathcal {H}_i)$, is a Gaussian centred around $\textbf{a}_{mp}$:

$$\begin{aligned} - \log \left\{ P(\textbf{a}|D,\mathcal {H}_i) \right\} = \frac{1}{2} (\textbf{a}- \textbf{a}_{{mp}})^T \; \textbf{A}\; (\textbf{a}- \textbf{a}_{{mp}}) + \text{ constant }\end{aligned}$$

(6)

where $\textbf{A}$ is the inverse of the posterior covariance matrix which, by inspection, is the Hessian of $\mathcal {J}$:

$$\begin{aligned} A_{ij} = \frac{\partial ^2 \mathcal {J}}{\partial a_i a_j} \end{aligned}$$

(7)

The posterior uncertainty in the parameters, $\textbf{A}^{-1}$, is therefore calculated cheaply. The integral (2), which can be prohibitively expensive to calculate without the Gaussian assumption, is now simply:

$$\begin{aligned} P(D|\mathcal {H}_i) = P(D|\textbf{a}_{{mp}},\mathcal {H}_i) P(\textbf{a}_{{mp}}|\mathcal {H}_i) \left( \det (\textbf{A}/2\pi ) \right) ^{-1/2} \end{aligned}$$

(8)

This integral allows us to rank different models, $\mathcal {H}_i$. By the product rule of probability $P(\mathcal {H}_i|D) P(D) = P(D|\mathcal {H}_i) P(\mathcal {H}_i)$. If the prior probability, $P(\mathcal {H}_i)$, is the same for each model then the models can be ranked by $P(D|\mathcal {H}_i)$. The fact that (8) is proportional to $\det (\textbf{A})^{-1/2}$ penalizes models for which $\det (\textbf{A})$ is large. This tends to favour models with fewer parameters (hence smaller $\textbf{A}$) even if they do not fit the data as well as models with more parameters. This does not, of course, prevent a model with many parameters from being the highest ranked, as long as the model fits the data well and the measurement uncertainty is small.

2.2 Accelerating Laplace’s Method with Adjoint Methods

If all probability distributions are assumed to be Gaussian then $\mathcal {J}$ is the sum of the squares of the discrepancies between the model predictions and the experimental measurements, weighted by our confidence in the experimental measurements, added to the sum of the squares of the discrepancies between the model parameters and their prior estimates, weighted by our confidence in the prior estimates:

$$\begin{aligned} \mathcal {J}= & {} - \log \left\{ P(D| \textbf{a}, \mathcal {H}_i) P(\textbf{a}| \mathcal {H}_i) \right\} \nonumber \\ \nonumber= & {} (\mathcal {S}_r(\textbf{a}) - S_r)^T C_{Sr}^{-1} (\mathcal {S}_r(\textbf{a}) - S_r) \ldots \\ \nonumber+ & {} (\mathcal {S}_i(\textbf{a}) - S_i)^T C_{Si}^{-1} (\mathcal {S}_i(\textbf{a}) - S_i) \ldots \\ \nonumber+ & {} (\mathcal {P}_r(\textbf{a}) - P_r)^T C_{Pr}^{-1} (\mathcal {P}_r(\textbf{a}) - P_r) \ldots \\ \nonumber+ & {} (\mathcal {P}_i(\textbf{a}) - P_i)^T C_{Pi}^{-1} (\mathcal {P}_i(\textbf{a}) - P_i) \ldots \\+ & {} (\textbf{a}- \textbf{a}_f)^T C_{aa}^{-1} (\textbf{a}- \textbf{a}_f) + \ldots \end{aligned}$$

(9)

By inspection, the Jacobian and Hessian of $\mathcal {J}$ contain $\partial \square / \partial a_i$ and $\partial ^2 \square / \partial a_i a_j$ respectively, where $\square$ refers to $\mathcal {S}_\star (\textbf{a})$ and $\mathcal {P}_\star (\textbf{a})$. These first and second derivatives can be found cheaply with first (Magri and Juniper 2013) and second (Tammisola et al. 2014; Magri et al. 2016) order adjoint methods. The remaining terms in $\mathcal {J}$ contain the normalizing factors in (3), (4). The derivatives w.r.t. the measurement uncertainties can also be calculated and one can then optimize to find the measurement noise that maximizes the posterior likelihood. In this example, the epistemic uncertainty is embedded within the measurement noise, so assimilating the measurement noise also assimilates the epistemic uncertainty.

Adjoint codes require a careful code structure and must avoid non-differentiable operators. The code used here consists of a low level thermoacoustic network model that contains floating parameters to quantify all possible local feedback mechanisms Juniper (2018). The gradients of $(\mathcal {S}_\star ,\mathcal {P}_\star )$ w.r.t. all possible feedback mechanisms are calculated. These mechanisms are then ascribed physical meaning by candidate models and the gradients w.r.t. each model’s parameters are extracted. The low level function is called by a mid-level function that calculates $\mathcal {J}$ and all its gradients. In turn this is called by a high level function that converges to $\textbf{a}_{{mp}}$ and then calculates the likelihoods and marginal likelihoods using Laplace’s method. A separate high level function performs Markov Chain Monte Carlo by calling the same mid-level and low-level functions. The code is available at Juniper (2022).

2.3 Applying Laplace’s Method to a Complete Thermoacoustic System

Matveev (2003) set out to create a quantitatively-accurate model of the hot wire Rijke tube by compiling quantitatively-accurate models of its components from the literature. Despite being tuned to be quantitatively correct at one heater position, this carefully-constructed model is only qualitatively correct at nearby heater positions (Matveev 2003, Figs. 5-5 to 5-8). This demonstrates the danger of relying on quantitative models from the literature: these models may have been quantitatively correct for the reported experiment, but they are probably only qualitatively correct for other experiments. The Bayesian inference demonstrated in this section uses qualitative models from the literature but, crucially, allows their parameters to float in order to match the new experiment at all operating points. As will be shown later, this creates a quantitatively-accurate model over the entire range studied and, if the model is physically-correct, it can extrapolate beyond the range studied.

Fig. 1

Expected values ($\pm 2$ standard deviations) of model predictions $\mathcal {D}(\textbf{a})$ verses experimentally measured values ($\pm 2$ standard deviations) $D$ of the growth rates and frequencies of the cold Rijke tube in four configurations: (i) empty tube; (ii) tube containing heater prongs; (iii) tube containing heater prongs and heater; (iv) tube containing heater prongs, heater, and thermocouples. Image adapted from Juniper and Yoko (2022)

Developing a quantitatively accurate model of the hot wire Rijke tube is challenging because the heat release rate is small and therefore the thermoacoustic driving mechanism is weak. For the experiment shown here, which is taken from Juniper and Yoko (2022), the thermoacoustic mechanism contributes around $\pm 10$ rad s$^{-1}$ to the growth rate and $\pm 100$ rad s$^{-1}$ to the frequency. For comparison, Fig. 1 shows the decay rate (negative growth rate) and frequency of acoustic oscillations in the cold Rijke tube (i) when empty, (ii) with the heater prongs in place, (iii) with the heater and prongs in place, and (iv) with the heater, prongs, and thermocouples in place. The growth rate and frequency drifts caused by these elements of the rig, even when the heater is off, are a similar size to the thermoacoustic effect and cannot be ignored in a quantitative model. These elements must be modelled but, even after reading the extensive literature on the Rijke tube such as Feldman (1968); Raun et al. (1993); Bisio and Rubatto (1999) and the references within them, it is not evident a priori which physical mechanisms must be included and which can be neglected. Instead, we propose several physics-based models, assimilate the data into those models using Laplace’s method combined with adjoint methods, and then select the model with the highest marginal likelihood because it is the one that is best supported by the experimental data. For example, Table 1 shows the best fit likelihood, $P(D|\textbf{a}_{MP},\mathcal {H}_i)$, and the marginal likelihood, $P(D|\mathcal {H}_i)$, for seven candidate models of the heater prongs. These models contain various combinations of the viscous boundary layer, the thermal boundary layer, and the blockage caused by the prongs, as described in the caption. The best data fit is achieved by model 4 but the highest marginal likelihood is achieved by model 6, which fits the data well with just two parameters. Model 6 contains the blockage caused by the prongs and the visco-thermal drag of the prong’s boundary layers, which is expressed as a real multiple of the visco-thermal drag of the tube’s boundary layers. It is re-assuring that the model with the highest marginal likelihood contains all the expected physics, but remains simple.

Table 1 log(Best Fit Likelihood) per datapoint and log(Marginal Likelihood) per datapoint for seven models of the heater prongs in the cold Rijke tube. The second column contains the number of parameters in each model. The third column describes how the viscous boundary layer on the prongs is modelled: it is the viscous dissipation in the tube’s boundary layer multiplied by a real number, a complex number, or zero. The fourth column is the equivalent for the thermal boundary layer. If the third and fourth columns are joined then the same factor is used for both the viscous and thermal boundary layers. The fifth column notes whether the blockage of the prongs is included in the model. Model 4 gives the best fit to the data but is not the most likely model. Model 6 is the most likely model (highest marginal likelihood) because it achieves a good data fit with just two model parameters. (Table adapted from Juniper and Yoko 2022)

This process is repeated for the heater itself and the thermocouples (Juniper and Yoko 2022) until a quantitatively-accurate model of the cold Rijke tube has been created. Figure 1 shows the model predictions and experimental measurements for the final model. This model is quantitatively accurate across the entire operating range with just a handful of parameters (Juniper and Yoko 2022). Using Laplace’s method, accelerated by first and second order adjoint methods, this data assimilation takes a few seconds on a laptop. Using MCMC takes around 1000 times longer on a workstation (Garita 2021). Although time-consuming, MCMC can be useful in order to confirm that the posterior likelihood distributions are close to Gaussian, which justifies the use of Laplace’s method.

Table 2 log(Best Fit Likelihood) per datapoint and log(Marginal Likelihood) per datapoint for nine models of the heater in the hot Rijke tube. Model parameters are denoted as k with a numerical index. $k_c$ are the model parameters from the cold experiments, which are fixed. The second column contains the number of parameters in each model. The third and fourth columns describe how the magnitude and phase of the fluctuating heat release rate are modelled. $Q_h$ is the heater power and $Q_{King}$ is adjusted for King’s law King (1914); Juniper and Yoko (2022). The fifth and sixth columns describe how the visco-thermal drag at the heater is modelled, where $\text{ i }s$ is the angular frequency and $\tau _L$ is Lighthill’s time delay Lighthill (1954). (Table adapted from Juniper and Yoko 2022)

The fluctuating heat release rate at the wire cannot be measured directly. Analytical relationships between velocity fluctuations and heat release rate fluctuations have been developed (King 1914; Lighthill 1954; Carrier 1955; Merk 1957) but subsequent numerical simulations (Witte and Polifke 2017) have shown that numerically-calculated relationships have a more intricate dependence on $\text{ Re }$ and $\text{ St }$ than can be derived analytically. Since the 1970s (Bayly 1986) therefore, researchers have tended to use CFD simulations or simple relations that are tuned to a particular operating point (Witte 2018, Table 1; Ghani et al. 2020).

Here we propose six candidate models for the heat release rate and two candidate models for how the thermo-viscous drag of the heater changes with the heater power. We then calculate the marginal likelihoods of these models, allowing the measurement noise to float in order to accommodate epistemic uncertainty such as systematic measurement error and model error. Table 2 shows the candidate models, their assimilated parameters, their log best fit likelihood (BFL) per datapoint, and their log marginal likelihood per datapoint. Model 8 has the highest Marginal Likelihood. In this model, the fluctuating heat release rate is proportional to the steady heat release rate; the time delay between velocity perturbations and subsequent heat release rate perturbations is the same for all configurations, and the thermo-viscous drag of the heater element is proportional to the heater power. There is, of course, no limit to the number of models that can be tested. The interested reader is encouraged to generate and test their own models using the code (Juniper 2022).

Figure 2 shows the experimental measurements verses the predictions of model 8 for the growth rates and frequencies when assimilating data from all 105 experiments. The agreement is excellent, particularly for the growth rate, which is more practically important than the frequency. Figure 3 is the same as Fig. 2 but is obtained by assimilating data from just 8 of the 105 experiments. The results are almost indistinguishable, which shows that, once a good physics-based model has been identified, very little data is required to tune its parameters. This model can then extrapolate to other operating points, even if they are far from those already examined. This is a desirable feature of any model and shows the advantage of assimilating data into physics-based models with a handful of parameters, rather than physics-agnostic models with many parameters, which would not be able to extrapolate.

Fig. 2

Expected values of model 8’s predictions $\mathcal {D}(\textbf{a})$ verses experimental measurements $D$ of the growth rates and frequencies of the hot Rijke tube, as a function of heater power and heater position. The model parameters are obtained by assimilating data from all 105 experimental configurations. The model is quantitatively-accurate over the entire operating range. (Image adapted from Juniper and Yoko 2022)

Fig. 3

As for Fig. 2 but when the model parameters are obtained by assimilating data from the eight circled configurations. This model is also quantitatively accurate over the entire operating range, showing that this model can extrapolate beyond the assimilated datapoints. (Image adapted from Juniper and Yoko 2022)

As a final comment, this assimilation of experimental data with rigorous Bayesian inference forces the experimentalist to design informative experiments. Firstly, without an excellent initial guess for the parameter values, it is almost impossible to assimilate all the parameters simultaneously. This encourages the experimentalist to assimilate the parameters sequentially with an experimental campaign in which some of the parameters take known values (usually zero) in some of the experiments. Secondly, this process reveals systematic measurement error that was previously unknown to the experimentalist. This epistemic error is revealed when the parameters shift to absorb the error and seem to uncover impossible physical behaviour.³ Once this systematic measurement error becomes known, the experimentalist is forced to remove it or avoid it with good experimental design.

3 Physics-Based Statistical Inference Applied to a Flame

The most influential element of any thermoacoustic system is the response of the flame to acoustic forcing. This is also the hardest element to model. In this section, experimental images of forced flames are assimilated into a physics-based model using the first level of inference described in Sect. 2. The physics-based model can then be used in thermoacoustic analysis for example (i) in nonlinear simulations, (ii) to create a nonlinear flame describing function (FDF), or (iii) to create a linear flame transfer function (FTF).

3.1 Assimilating Experimental Data with an Ensemble Kalman Filter

We take our model, $\mathcal {H}$, to be a partial differential equation (PDE) discretized onto a grid, with unknown parameters $\textbf{a}$. As before, we wish to infer the unknown parameters, $\textbf{a}$, by assimilating data, $D$, from an experiment. The model, which has state $\psi$, is marched forwards in time from some initial condition to produce a model prediction, $\mathcal {D}(\psi )$, that can be compared with the experimental measurements, $D$, over some time period $T$. In principle, it is possible to use the same method as in Sect. 2.1 to iterate to the values of $\textbf{a}$ that minimize an appropriate $\mathcal {J}$ for all the data simultaneously. This requires the model predictions, $\mathcal {D}(\psi )$, and their gradients w.r.t. all parameters, $a_i$, to be stored at all moments at which they are compared with the data $D$. This is not practical because it would require too much storage. This section describes an alternative approach that requires less storage.

We consider a level set model of a premixed laminar flame, taken from Yu et al. (2020). The state, $\psi$, is the flame position, and the parameters, $\textbf{a}$, are the flame aspect ratio $\beta$, the Markstein length L, the ratio, K, between the mean flow speed and the phase speed of perturbations down the flame, the amplitude, $\epsilon$, of velocity perturbations, and the parabolicity parameter, $\alpha$ of the base flow, where $U/\overline{U} = 1 + \alpha (1 - 2(r/R)^2)$. The parameters $\beta$, L, and $\alpha$ are inferred from an image of an unforced steady premixed bunsen flame. This flame is then forced at 200, 300, and 400 Hz, and the data, $D$, are experimental images taken at 2800 Hz. The state, $\psi$, is marched forward in time by the model, $\mathcal {H}$, with parameters $\textbf{a}$ to an assimilation step. At the assimilation step, the model prediction $\mathcal {D}(\psi )$ is compared with the data $D$, and the state $\psi$ and remaining parameters $\textbf{a}$ are both updated to statistically optimal estimates, as described in the next paragraph. The state, $\psi$, is then marched forward to the next assimilation step and the process is repeated until the parameters $\textbf{a}$ have converged.

If the evolution were linear or weakly nonlinear then a Kalman filter or extended Kalman filter would be appropriate. The evolution is highly nonlinear, however, with wrinkles and cusps forming at the flame. We therefore use an ensemble Kalman filter (EnKF) in which we generate an ensemble of N states $\psi _i$ from the model $\mathcal {H}$ with different parameter values $\textbf{a}_i$ (Evensen 2009). At each assimilation step, we append each parameter vector $\textbf{a}_i$ to its state vector $\psi _i$ to form an augmented state $\Psi _i$. The expected value $\bar{\Psi }$ and covariance $\textbf{C}_{\Psi \Psi }$ of the augmented state $\Psi$ are then derived from the ensemble:

$$\begin{aligned} \bar{\Psi }= & {} \frac{1}{N} \sum ^N \Psi _i \end{aligned}$$

(10)

$$\begin{aligned} \textbf{C}_{\Psi \Psi }= & {} \frac{1}{N-1} \sum ^N (\Psi _i - \bar{\Psi }) (\Psi _i - \bar{\Psi })^T \end{aligned}$$

(11)

The expected value $\bar{\Psi }$ becomes the prior expected value and replaces $\textbf{a}_p$ in (3). The covariance $\textbf{C}_{\Psi \Psi }$ becomes the prior expected covariance and replaces $\textbf{C}_{aa}$ in (3). The predicted flame position $\mathcal {D}({\bar{\psi }})$ is found from the expected state, $\bar{\psi }$. The discrepancy between the experimental flame position $D$ and the model prediction $\mathcal {D}(\psi )$ is then combined with an estimate of the measurement error $\textbf{C}_{DD}$ in (4). The posterior augmented state $\Psi _{mp}$ and its inverse covariance $\textbf{A}$ is calculated to be that which maximizes the RHS of (1), as in Sect. 2.1. The state $\psi$ and parameters $\textbf{a}$ are extracted from the expected value of the posterior augmented state. N states are created with this posterior expected value and covariance, and the process is repeated.

Fig. 4

Root-mean-square (RMS) discrepancy between experimental data, $D$, and model predictions, $\mathcal {D}$, for a conical bunsen flame forced at 200, 300 and 400 Hz (blue/orange/green, respectively). Data is assimilated from the experiments into the model (DA) between 10 and 15 periods. The snapshots shown in Fig. 5 are taken from the grey window. Image taken from Yu et al. (2020)

Figure 4 shows the RMS discrepancy between the experiments, $D$, and the expected value of the simulations, $\mathcal {D}(\psi )$, for flames forced at three different frequencies. The EnKF is switched on from time periods 10 to 15. The RMS discrepancy drops by more than one order of magnitude during this time, to a floor set by the model error. The largest drops in discrepancy occur when the EnKF is assimilating data just as a bubble of unburnt gases is pinching off from the flame. During these moments, which are relatively rare, the parameters converge rapidly towards their final values. This shows that relatively rare events contain more information than relatively common events, as is quantified, for example, through the Shannon information content of an event (MacKay 2003, Eq. (2.34)). After 5 time periods the EnKF is switched off and the tuned models evolve for a further 3 periods without assimilating data. Figure 5 shows the models’ expected values and uncertainties (yellow) and the experimental measurements (black) for one further period. This shows that the EnKF has successfully assimilated the model parameters from the experimental images and that simulations with these parameters remain accurate beyond the assimilation period.

The EnKF has the advantages that (i) no calculations are required before the assimilation process begins, (ii) it can assimilate any experimental flame that can be represented by the model $\mathcal {H}$. It has the disadvantages that (i) it cannot run in real time because the computational time of the simulations, $\mathcal {O}(10^1)$ seconds, exceeds the time between assimilation steps, $\mathcal {O}(10^{-3})$ seconds; (ii) if the ensemble starts far from the data, the ensemble tends to diverge rather than converge to the experimental results.

Fig. 5

Snapshots of log-normalized likelihood over one forcing period after combined state and parameter estimation for 200, 300 and 400 Hz (top/middle/bottom row, respectively). Highly likely positions of the flame surface are shown in yellow; less likely positions in green. The flame surface from experimental images is shown as black dots. Image taken from Yu et al. (2020)

3.2 Assimilating with a Bayesian Neural Network Ensemble

The two disadvantages of the EnKF can be overcome, while retaining uncertainty estimates, by assimilating data, $D$, with a Bayesian Neural Network ensemble (BayNNE) (Pearce et al. 2020; Gal 2016; Sengupta et al. 2020). Each Neural Network, $\mathcal {M}_i$, in the ensemble is a repeated composition of the function $f(\textbf{W}_i \textbf{x} + \textbf{b}_i)$ where f is a nonlinear function, $\textbf{x}$ are the inputs, $\textbf{W}_i$ is a matrix of weights, and $\textbf{b}_i$ is a vector of biases. Together $\textbf{W}_i$ and $\textbf{b}_i$ comprise the parameters $\theta _i$ of each neural network. The set of all parameters in the ensemble is denoted $\{\theta _i\}$. The posterior state, $\Psi (D,\{\theta _i\})$, contains the predicted parameters (e.g. $\beta , L, K, \epsilon$, $\alpha$) of the numerical simulation. The true targets, $\textbf{a}$, are the actual parameters of the simulations. The distribution of the prediction is assumed to be Gaussian: $P(\Psi |D,\{\theta _i\}) = \mathcal {N}(\bar{\Psi },C_{\Psi \Psi })$. Creating this prediction means learning the mean $\bar{\Psi }(D,\{\theta _i\})$ and the covariance $C_{\Psi \Psi }(D,\{\theta _i\})$ of the ensemble.

Each NN in the ensemble produces the expected value, $\boldsymbol{\mu }_i(D,\theta _i)$, and covariance, $\boldsymbol{\sigma }^2_i(D,\theta _i)$, of a Gaussian distribution by minimising the loss function:

$$\begin{aligned} \mathcal {J}_i= & {} ( \textbf{a}- \boldsymbol{\mu }_i)^T \Sigma _i^{-1} ( \textbf{a}- \boldsymbol{\mu }_i) + \log (| \Sigma _i^{-1} |) \end{aligned}$$

(12)

$$\begin{aligned}{} & {} + (\theta _i - \theta _{i,anc})^T \Sigma _{prior}^{-1} (\theta _i - \theta _{i,anc}) \end{aligned}$$

(13)

where

$$\begin{aligned} \Sigma _i^{-1} = \text{ diag } \big ( \boldsymbol{\sigma }^2_i \big ) \end{aligned}$$

(14)

and $\theta _{i,anc}$ are the initial weights and biases of the $i^{th}$ NN. These are sampled from the prior distribution $P(\theta ) = \mathcal {N}(\textbf{0},\Sigma _p)$, where $\Sigma _p= \text{ diag }(1/N_H)$, where $N_H$ is the number of units in each hidden layer. The above task is time-consuming but is performed just once.

The ensemble therefore contains a set of Gaussians, each with their own means, $\boldsymbol{\mu }_i$, and covariances, $\boldsymbol{\sigma }^2_i$. These are approximated by a single Gaussian with mean $\bar{\Psi }(D,\{\theta _i\})$ and covariance $C_{\Psi \Psi }(D,\{\theta _i\})$ using (Lakshminarayanan et al. 2017):

$$\begin{aligned} \bar{\Psi }(D,\{\theta _i\})= & {} \frac{1}{N} \sum _{i=1}^{N} \boldsymbol{\mu }_i(D,\theta _i) \end{aligned}$$

(15)

$$\begin{aligned} C_{\Psi \Psi }(D,\{\theta _i\})= & {} \text{ diag }\big ( \textbf{c}_{\Psi \Psi }(D,\{\theta _i\}) \big ) \end{aligned}$$

(16)

where N is the number of NNs in the ensemble and

$$\begin{aligned} \textbf{c}_{\Psi \Psi }(D,\{\theta _i\}) = \frac{1}{N} \sum _{i=1}^{N} \boldsymbol{\sigma }^2_i(D,\theta _i) + \frac{1}{N} \sum _{i=1}^{N} \boldsymbol{\mu }_i^2(D,\theta _i) - \left( \frac{1}{N} \sum _{i=1}^{N} \boldsymbol{\mu }_i(D,\theta _i) \right) ^2 \end{aligned}$$

(17)

The uncertainty of the ensemble therefore contains the average uncertainty of its members, combined with uncertainty arising from the distribution of the means of the ensemble members. If this uncertainty is large, the observed data is likely to have been outside the training data. This task is quick and is performed at each operating condition.

The BayNNE is trained on 8500 simulations of the level set solver used in Sect. 3.1. The parameters varied are the flame aspect ratio $\beta$, the Markstein length L, the ratio, K, between the mean flow speed and the phase speed of perturbations down the flame, the amplitude of velocity perturbations, $\epsilon$, the mean flow parabolicity, $\alpha$, and the Strouhal number, $\text{ St }$. The parameters are sampled using quasi-Monte Carlo in order to obtain good coverage of the parameter space within fixed ranges. For each simulation, 200 evenly-spaced snapshots of a forced periodic solution are stored. The data, $D$, used for training takes the form of 10 consecutive snapshots extracted from these images. The total library of data therefore consists of $8500 \times 200 = 1.7\times 10^6$ sets of data, $D$, each with known parameters $\textbf{a}$. The neural networks are trained to recognize the parameter values $\textbf{a}$ from the data $D$. Training takes around 12 hours per NN on an NVIDIA P100 GPU. Recognizing the parameter values takes $\mathcal {O}(10^{-3})$ seconds on an Intel Core i7 processor on a laptop, which is sufficiently fast to work in real time.

The top row of Fig. 6 shows 10 snapshots of a forced bunsen flame experiment alongside the automatically-detected flame edge. The bottom row shows the modelled flame edge and its variance, assimilated with the EnKF (left) and the BayNNE (right). The flame edge is shown in black. As expected, the expected values found with both assimilation methods are almost identical. The prediction is close to the experiments but, because of model error, the EnKF and the BayNNE both struggle to fit the most extreme pinch off event at 0.6T. The uncertainty in the BayNNE is greater than that of the EnKF because it assimilates just 10 flame images, while the EnKF has assimilated over 500 images by the time this sequence is generated. Alternative NN architectures, such as long-short term memory networks may be able to reduce this uncertainty.

Fig. 6

Top row: experimental images of one cycle of an acoustically forced conical Bunsen flame; the left half a shows the raw image while the right half b shows the detected edge. Bottom row: the flame edge and its uncertainty when assimilated into a G-equation model with an EnKF (c) and a BayNNE (d). With this model, propagation of perturbations down the flame is captured well but the pinch-off event is not. Image adapted from Croci et al. (2021)

The fact that the BayNNE assimilates just 10 snapshots is a disadvantage when the flame behaviour is periodic over many cycles, as in the previous example, but an advantage when the flame behaviour is intermittent, as in the next example. Intermittency is commonly observed in thermoacoustic systems, particularly when they are close to a subcritical bifurcation to instability (Juniper and Sujith 2018; Nair et al. 2014). Bursts of periodic behaviour are interspersed within moments of quasi-stochastic behaviour and, while these can be identified by eye and with recurrence plots (Juniper and Sujith 2018), they are not sufficiently regular to be assimilated with the EnKF.

In the next example, images of a bluff-body stabilized turbulent premixed flame Paxton et al. (2019, 2020) are recorded at 10 kHz using OH PLIF, and the flame edge is extracted and smoothed to remove the turbulent wrinkles. A BayNNE trained on 10 snapshots of G-equation simulations with 2400 combinations of parameters, $\textbf{a}$, then identifies the most likely parameters from 10 observed snapshots. In this example the model contains an extra parameter: the spatial growth rate, $\eta$, of perturbations,

Figure 7 shows the five assimilated parameters, ($K, \epsilon , \eta$, St, $\beta$) and their uncertainties during 430 timesteps of an experimental run imaged at 2.5 kHz. During this run, there are four to five oscillation cycles. The BayNNE successfully identifies the G-equation parameters that match the experimental results and, importantly, estimates their uncertainties. At four moments during the run, Fig. 7 shows snapshots of the experimental image (top left quadrant) alongside the expected value and uncertainty from the G-equation simulations. Because the G-equation simulation is physics-based, it can extrapolate beyond the window viewed in the experiments, as shown in the images. The distribution of fluctuating heat release rate, with its uncertainty, can be calculated from the model. This can then be expressed as a spatial distribution of the flame interaction index, n, and the flame time delay, $\tau$, as in Fig. 8, which can then be entered into a thermoacoustic network model or Helmholtz solver.

Fig. 7

Assimilated parameters $(K,\epsilon ,\eta ,\text{ St },\beta )$ of a G-equation model of a bluff-body-stabilized premixed flame during a sequence of 428 snapshots. The parameters are assimilated with a Bayesian Neural Network Ensemble (BayNNE), which also estimates the uncertainty in the assimilated values. The four flame images show (top-left of each frame) the detected flame edge from the experimental OH PLIF image and (remainder of each frame) the expected values and uncertainties in the G-equation model prediction. Image adapted from Croci et al. (2021)

Fig. 8

Spatial distribution of n and $\tau$ derived from the G-equation model of the bluff-body-stabilized premixed flame shown in Fig. 7

4 Identifying Precursors to Thermoacoustic Instability with BayNNEs

The noise from a thermoacoustically-stable turbulent combustor has broadband characteristics and is often assumed to be stochastic (Clavin et al. 1994; Burnley and Culick 2000). This assumption is a reasonable starting point for stochastic analysis (Clavin et al. 1994) but does not exploit the fact that combustion noise contains useful information about the system’s proximity to thermoacoustic instability (Juniper and Sujith 2018, Sect. 4). Analysis of this noise usually involves a statistical measure to detect transition away from stochastic behaviour. This can be a measure of departure from chaotic behaviour, using techniques for analysing dynamical systems (Gotoda et al. 2012; Sarkar et al. 2016; Murugesan and Sujith 2016), or the detection of precursors such as intermittency (Juniper and Sujith 2018; Nair et al. 2014; Scheffer et al. 2009).

These methods quantify the behaviour that a researcher thinks should be important, based on observation of similar systems. This approach is generally applicable but has the disadvantage that it will miss information that the researcher does not think is important, and cannot extract information that is peculiar to a particular engine. Given that this research is motivated by industrial applications in which several nominally-identical models of the same engine are deployed, it makes sense to extract as much information as possible from that particular engine model. In other words, we ask whether machine learning techniques can learn to recognize precursors on one set of engines and then identify precursors on another set of nominally-identical engines. Further we ask whether the machine learning approach is better than techniques that use a statistical measure. In this section, we examine a laboratory scale combustor to develop the method, then three aeroplane engine fuel injector nozzles in an intermediate pressure rig, and then 15 full scale commercial aeroplane engines.

4.1 Laboratory Combustor

In the first study we place a 1 kW turbulent premixed flame inside a steel tube with length 800 mm and diameter 80 mm (Sengupta et al. 2021). The system is run at 900 different operating conditions varying power, equivalence ratio, fuel composition, and the tube exit area. All operating points are thermoacoustically stable, but the thermoacoustic mechanism is active and some points are close to thermoacoutic instability.

For each operating point, the combustion noise is recorded at 10, 000 Hz. The system is then forced for 50 ms at 230 Hz, which is close to the natural frequency of the first longitudinal mode. The decay rate of the acoustic oscillations is extracted from the microphone signal. We then train a Bayesian Neural Network ensemble (BayNNE) to identify the decay rate from 300 ms clips of combustion noise before the acoustic excitation. The decay rate changes from negative to positive at the point of thermoacoustic instability, so is a good measure of the proximity to thermoacoustic instability. The BayNNE returns the uncertainty in its predictions, ensuring that the model does not make overconfident predictions from inputs that differ significantly from those on which it was trained. If the priors are specified correctly, this technique can work with smaller amounts of data and be more resistant to over-fitting (Pearce et al. 2020).

Before training, all the input variables are normalized in order to remove the amplitude information. The parameters $\textbf{a}_i$ of each ensemble member are initialized by drawing from a Gaussian prior distribution with zero mean and variance equal to $1/N_H$, where $N_H$ is the number of hidden nodes in the previous layer of the NN. This initialization means that the distribution of predictions made by the untrained prior neural network will be approximately zero-centred with unit variance. Each ensemble member is trained normally, but with a modified loss function that anchors the parameters to their initial values. This procedure approximates the true posterior distribution for wide neural networks (Pearce et al. 2020). We train on $80\%$ of the operating points, retain $20 \%$ for testing, and train ten different models using ten random test-train splits. This ensures the stability of our algorithm’s performance with respect to different train-test splits.

Fig. 9

a Decay timescale, $\pm 2$ standard deviations, predicted with a BayNNE, b Hurst exponent c autocorrelation decay, as functions of the measured decay timescale for thermoacousic oscillations of a turbulent premixed Bunsen flame in a tube. The BayNNE provides the most reliable indicator of proximity to thermoacoustic instability. This figure recreated is based on the data in Sengupta et al. (2021)

Figure 9a shows the decay timescale (the reciprocal of the decay rate) predicted by the BayNNE, compared with the decay timescale measured from the subsequent response to the pulse. The grey bars show the uncertainty outputted by the BayNNE. The decay timescales are predicted reasonably accurately. The grey uncertainty bars widen for the operating points closer to instability because there are only a few operating points close to instability; the decay timescale exceeds 0.3 s for just 13 operating points in the training set. This shows that the BayNNE can successfully predict how far the system is from instability while also indicating how confident it is in that prediction.

Figure 9b, c show the generalized Hurst exponent and the Autocorrelation decay of the combustion noise as functions of the measured decay timescale. As expected, the Hurst exponent drops and the autocorrelation decay increases as the decay timescale increases, showing that these measurements are working as precursors of combustion instability. They are not as accurate, however, as the BayNNE and contain no measure of uncertainty. It is clear therefore that, when trained on this specific combustor, the BayNNE out-performs the Hurst exponent and autocorrelation decay. This outcome would be reversed, of course, if the BayNNE were applied to a different combustor, without retraining.

We also trained the BayNNEs to recognize the equivalence ratio and burner power from 300 ms of combustion noise. The BayNNe could recognize the equivalence ratio with a rms error of $3.5\%$ and the power with a rms error of $2\%$. This shows that each operating condition has a unique acoustic signature that the BayNNE can learn. The experimentalist in the room can hear that all operating conditions sound slightly different, but cannot recognize the operating condition to the accuracy that the BayNNE can achieve.

4.2 Intermediate Pressure Industrial Fuel Spray Nozzle

The second study is on an industrial intermediate pressure combustion test rig, which is equipped with three pressure transducers, sampling at 50 kHz. Experiments are performed on three different fuel injectors over a range of operating points in order to identify operating points that are thermoaoustically unstable. The injectors are labelled $1a$, $1b$, and $2$. Injectors $1a$ and $1b$ are nominally identical. The operating points are identified by their air-fuel ratio (AFR) and their exit temperature ($T_{30}$). The threshold of thermoacoustic instability is defined as the operating points at which the acoustic amplitude exceeds $0.5\%$ of the static pressure. The black lines in Fig. 10 show this threshold in (AFR,$T_{30}$)–space. Despite being nominally identical, injectors $1a$ and $1b$ have instability thresholds at slightly different positions in (AFR,$T_{30}$)–space.

We normalize the ranges of AFR and $T_{30}$ to run from 0 to 1 and then train a BayNNE to recognize the Euclidian distance to the instability threshold, based on 500 ms of normalized pressure measurements. Stable points are assigned positive distances and unstable points are assigned negative distances. We compare the predictions from the BayNNE with those from the autocorrelation decay, the permutation entropy, and the Hurst exponent.

Fig. 10

The black line shows the thermoacoustic instability threshold as a function of air-fuel ratio (AFR) and exit temperature $T_{30}$  for three aeroplane engine fuel injectors in an intermediate pressure rig. The coloured lines show the distance to the black line. Injectors $1a$ and $1b$ are nominally identical

Fig. 11

a Hurst exponent, b autocorrelation decay, c permutation entropy calculated from the pressure signal of injector $1a$ in the intermediate pressure rig, as a function of the distance to the instability threshold in Fig. 10a. A positive (negative) distance indicates stable (unstable) thermoacoustic behaviour

Figure 11a–c show the Hurst exponent, the autocorrelation decay, and the permutation entropy for injector $1a$. The Hurst exponent reduces significantly as the system becomes unstable and this is a useful indicator of the instability threshold, albeit with significant unquantified uncertainty. The autocorrelation decay tends towards zero as the system becomes more unstable but, for this data, barely changes across the instability threshold and therefore does not provide a useful indicator for the threshold. The permutation entropy drops after the system has crossed the threshold from stable to unstable operation, meaning that it is not useful as a precursor in these experiments.

Fig. 12

Predicted distance to the instability threshold $\pm 2$ s.d. as a function of measured distance to instability threshold for a injector $1a$, b injector $1b$, c injector $2$ when the prediction is obtained from a BayNNE trained on injector $1a$. Injectors $1a$ and $1b$ are nominally identical

The BayNNE is trained on the training points of $1a$ and then applied to test points of $1a$, $1b$, and $2$. Figure 12a shows the distance from instability threshold predicted by the BayNNE compared with the true distance. Uncertainty bands of the BayNNE are shown in grey. The BayNNE provides a remarkably accurate prediction of the distance to instability from the pressure signal alone. Figure 12b shows the distance from the instability threshold predicted by the BayNNE trained on injector $1a$ when applied to the pressure data from the nominally identical injector $1b$. The BayNNE performs well when the system is unstable (distance less than 0) but performs less well, and assigns itself greater uncertainty, when the system is stable (distance greater than 0). As mentioned above, $1b$ is unstable over a different range of (AFR,/T30)–space than $1a$, and, despite this difference, the BayNNE has successfully identified the distance to instability on the new injector. The prediction is most inaccurate and uncertain, however, when the system is stable, which is the most useful scenario because it then acts as a precursor to instability. Figure 12c shows the distance from the instability threshold predicted by the BayNNE trained on $1a$ when applied to the pressure data from injector $2$. The BayNNE performs badly, particularly when the system is stable. This confirms that a BayNNE trained on one thermoacoustic system is a good indicator of thermoacoustic precursors on nominally-identical thermoacoustic systems, out-performing statistical measures, but is not useful for different systems. This is not surprising, given that the BayNNE is using all available information from the pressure signal of this particular system, while the statistical methods are quantifying general features in all systems.

4.3 Full Scale Aeroplane Engine

The third study is on 15 full scale prototype aeroplane engines operating at sea level (McCartney et al. 2022). The engines are equipped with two dynamic pressure sensors upstream of the combustor, sampling at 25 kHz. The compressor exit temperature, compressor exit pressure, fuel flow rate, primary/secondary fuel split, and core speed are sampled at 20 Hz. The core speed is increased (known as a ramp acceleration) such that the engines deliberately enter a thermoacoustically-unstable operating region. The instability threshold is defined by the point at which the peak to peak amplitude exceeds a certain value. Although the engines are nominally identical, the instability threshold is exceeded at a different core speed for each engine. Here, we investigate whether a BayNNE trained on the operating points and pressure signals from some of the engines can provide a useful warning of impending instability during a ramp acceleration in the other engines.

Previously we used BayNNEs to predict the decay rate of acoustic oscillations (Sect. 4.1) or the distance to instability in parameter space (Sect. 4.2). Now we consider a more practical quantity: the probability that the combustor will become thermoacoustically unstable within the next $\Delta t$ seconds during a ramp acceleration. We assume that this probability depends on the current operating point of the system, the future operating point, and the time it will take to reach the future operating point. In line with Sects. 4.1 and 4.2 we also assume that the current pressure signal contains useful information about how close the combustor is to thermoacoustic instability. We downsample the signal from a single sensor to 25 kHz, extract 4096 datapoints, which corresponds to around 160 ms, and then process it: (i) into a binary indication of whether the peak to peak pressure threshold has been exceeded; (ii) with de-trended fluctuation analysis (DFA) (Gotoda et al. 2012). The BayNNE is trained to learn the binary signal at time $\Delta t$ in the future, based on the operating conditions at time $\Delta t$ in the future and the pressure signal in the present. The future time, $\Delta t$, is varied from 100 ms to 1000 ms in steps of 100 ms. For comparison, a BayNNE is trained to learn the binary signal at time $\Delta t$ in the future, based on the operating conditions alone (i.e. without the pressure data).

There are three stages: tuning, training, and testing. In the tuning stage the number of hidden layers (2–10) and number of neurons in each layer (10–100) are optimized by performing a random search over these hyperparameters. For each combination, a BayNNE is trained on the training data and evaluated on the tuning data. We then select the hyperparameters and number of training epochs that perform best. In the testing stage, the BayNNE with optimal hyperparameters is applied to the testing data. This outputs the log likelihood of the BayNNE model, $\mathcal {M}$, given the data $D$. The different BayNNEs can then be ranked by the relative sizes of their log likelihoods. (The absolute value is not important.)

Fig. 13

The log likelihood of observing this data, given (i) the BayNNE trained on the operating point alone (OP) and (ii) the BayNNE trained on the operating point and DFA pressure signal (OP & DFA). For prediction horizons lower than 400 ms, inclusion of the pressure signal renders the model more likely and therefore more predictive. This figure is recreated based on the data in McCartney et al. (2022)

Figure 13 shows the log likelihoods of the BayNNE trained on the operating point (OP) alone and the BayNNE trained on the operating point and the DFA pressure signal (DFA). The OP BayNNE is the baseline against which to compare the DFA BayNNE. For future times below 400 ms, the tuned DFA BayNNE model fits the binary signal at that future time better than the tuned OP BayNNE model. In other words, the inclusion of pressure data gives smaller errors in the predicted probability that the threshold will be exceeded at that future time. For future times above 400 ms, the tuned DFA BayNNE model is marginally less likely than the OP BayNNE. This shows that the current pressure signal contains information that is useful up to 400 ms into the future, but no longer.

Fig. 14

Mean error in the predicted core-speed at which the engine will become thermoacoustically unstable as a function of time to instability onset as predicted by the BayNNE trained on the OP alone, and the BayNNE trained on the OP and the DFA pressure signal. This figure is recreated based on the data in McCartney et al. (2022)

Figure 14 shows the error in the predicted core speed at which the system becomes unstable. The OP BayNNE knows only the future operating point. The error in the predicted onset core speed arises from differences between the engines being tested. If all the engines were to behave identically, this error would be zero. The DFA BayNNE knows the future operating point and the current pressure signal. As expected from Fig. 13, the error in the predicted onset core speed drops around 400 ms before the instability starts. In other words, in this ramp acceleration, the pressure signal becomes informative around 400 ms before an instability starts but is not informative before then.

5 Conclusion

In the late 1990s, we were promised that the internet would change everything. Three decades later, very few internet-only companies have survived. The winners have been the companies who integrated the internet into what they did well already. If Machine Learning is to science what the internet was to business then the fields that thrive will be those that integrate machine learning into what they do well already. Fluid Dynamics in general, and Thermoacoustics in particular, is well placed to do this because the methods work well and the industrial motivation is strong.

Machine learning is successful because of its relentless focus on data, rather than on models, correlations, and assumptions that the research community has become used to. These models are not badly wrong, but they are rarely quantitatively accurate, and are therefore of limited use for design. It is particularly powerful to combine these physics-based models with one of the tools of probabilistic machine learning: Bayesian inference. By assimilating experimental or numerical data, we can turn qualitatively-accurate models into quantitatively accurate models, quantify their uncertainty, and rank the evidence for each model given the data. This should become standard practice at the intersection between low order models and experiments (numerical or physical). The days of sketching a line by eye through a cloud of points on a 2D plot should be over. This should be replaced by rigorous Bayesian inference, with all subjectivity well-defined, and in as many dimensions as required.

For low order models, assimilation with Laplace’s method combined with first and second order adjoints of those models is fast and powerful. For models with more than a few hundred degrees of freedom, this method becomes cumbersome. Nevertheless, it is still possible to assimilate data into larger physics-based models and to estimate the uncertainty in their parameters using iterative methods such as the Ensemble Kalman Filter, or parameter recognition with Bayesian Neural Network Ensembles. This is a powerful way to combine the practical aspects of Machine Learning with the attractive aspects of physics-based models. It is demonstrated here for a simple level set solver but, with enough simulations, could be extended to CFD.

Sometimes, however, we must accept that we do not recognise or cannot model the influential physical mechanisms in a system we are observing. In these circumstances, physics-agnostic neural networks are an ideal tool because they can learn to recognise features that humans will miss. Perhaps the most striking conclusion of the experiment reported in Sect. 4.1 is that every operating point had a different sound and that a Neural Network could recognise the operating point just from that sound. A human may suspect this but would be unable to remember them all. This is an interesting feature for aircraft engines because fleets contains thousands of nominally-identical but slightly different engines. The signs of impending thermoacoustic instability can therefore be learned from the sound on a handful of engines and applied confidently to the others. This gives a way to avoid thermoacoustic instability, even if it has been impossible to design it out.

For thermoacoustics, this chapter shows some promising ways to combine 30 years of machine learning with 200 years of physics-based learning. If we continue to fly long distance or send rockets into space, we will need to continue to avoid thermoacoustic instability. With novel research methods and continual industrial motivation, the field of thermoacoustics looks set to be interesting for many decades to come.