Abstract
We put forth a template for constructing statistical ZAPs for NP. Our template compiles NIZKs for NP in the hidden-bit model (which exist unconditionally) into statistical ZAPs using a new notion of interactive hidden-bit generator (\(\mathsf {IHBG}\)), which adapts the notion of hidden-bit generator to the plain model by building upon the recent notion of statistically-hiding extractable commitments. We provide a construction of \(\mathsf {IHBG}\) from the explicit hardness of the decision Diffie-Hellman assumption (where explicit refers to requiring an explicit upper bound on the advantage of any polynomial-time adversary against the assumption) and the existence of statistical ZAPs for a specific simple language, building upon the recent construction of dual-mode hidden-bit generator from (Libert et al., EUROCRYPT 2020). We provide two instantiations of the underlying simple ZAP:
- Using the recent statistical ZAP for the Diffie-Hellman language of (Couteau and Hartmann, CRYPTO 2020), we obtain statistical ZAPs for NP assuming (the explicit hardness of) DDH in \(\mathbb {G}_1\) and kernel-DH in \(\mathbb {G}_2\) (a search assumption which is weaker than DDH), where \((\mathbb {G}_1,\mathbb {G}_2)\) are groups equipped with an asymmetric pairing. This improves over the recent work of (Lombardi et al., EUROCRYPT 2020) which achieved a relaxed variant of statistical ZAP for NP, under a stronger assumption.
- Using the recent work of (Couteau et al., EUROCRYPT 2020), we obtain statistical ZAPs for NP assuming the explicit hardness of DDH, together with the assumption that no efficient adversary can break the key-dependent message one-wayness of ElGamal with respect to efficient functions over groups of size \({2^\uplambda }\) with probability better than \({\mathsf {poly} (\uplambda )/2^{(c + o(1)) \cdot \uplambda }}\), denoted \({2^{-c\uplambda }}\)-\(\mathsf {OW\text {-}KDM}\), for a constant \(c = 1/2\), in pairing-free groups. Note that the latter is a search discrete-log-style falsifiable assumption, incomparable to DDH (in particular, it is not known to imply public-key encryption).
Similar content being viewed by others
1 Introduction
Zero-knowledge proof systems, introduced in [GMR89], are a fundamental cryptographic primitive, allowing a prover to convince a verifier of the veracity of a statement, while not divulging anything beyond whether the statement is true. Zero-knowledge proofs have countless applications. However, they suffer from strong lower bounds on the number of rounds of interactions required in their execution: they require at least three rounds of interactions [GO94]. Therefore, the dream result of proofs that consists of a single message from the prover to the verifier (NIZKs [BFM88]) can only be achieved when assuming a trusted setup. Due to the importance of round-efficient zero-knowledge proofs, a large effort has been devoted to the construction of such proofs; yet, this trusted setup is often undesirable.
Witness-indistinguishability (WI) [FS90] is a natural relaxation of zero-knowledge, and is one of the most widely used privacy notions in proof systems. It provides the following guarantee: if there exist two witnesses \((w_0,w_1)\) for a statement \(x\in \mathscr {L}\), the verifier should not be able to distinguish an honest prover using \(w_0\) from an honest prover using \(w_1\). Witness-indistinguishable proofs can replace zero-knowledge proofs in many of their applications. At the same time, their round complexity is not subject to any known lower bounds.
ZAPs. The work of Dwork and Naor [DN00] introduced (and constructed) ZAPs, which are two-message public-coin WI proof systems. These proof systems have several advantages: being public-coin, they are publicly verifiable (the validity of the proof can be verified solely by looking at the transcript). Furthermore, the first flow, which is just a uniformly random string, is inherently reusable for an arbitrary (polynomial) number of proofs on possibly different statements. ZAPs have proven to be important cryptographic primitives. By now, we have constructions of ZAPs from many standard assumptions, including trapdoor permutations (which is implied by factoring) [DN00], the decision linear assumption (DLIN) in bilinear maps [GOS06a], the (quasi-polynomial hardness of the) learning with error assumption [LVW19, GJJM20, BFJ+20], and also from more complex notions, such as indistinguishability obfuscation [BP15].
Statistical ZAP Arguments. ZAPs were initially defined to satisfy unbounded soundness, and computational WI [DN00]. Statistical ZAP arguments provide the converse properties: computational soundness, and witness-indistinguishability against unbounded attackers. Unlike their computational WI counterpart, statistical ZAP arguments enjoy a very appealing property, that of everlasting security. Namely, soundness is an online security notion: as long as the prover cannot break soundness at the time where it produces the proof, security is guaranteed, even if the assumption it is based upon is later broken. On the other hand, WI and zero-knowledge should hold not only during the proof generation, but must continuously keep on holding in the future: compromising the assumptions underlying the WI property of proofs generated in the past at any point in the future would be sufficient to break privacy. Hence, targeting statistical privacy avoids being forced to assume the nonexistence of unforeseen cryptanalytic advances in the future.
Intriguingly, statistical ZAPs have proven much harder to construct than their computationally WI counterparts. In fact, for almost two decades after their introduction and until very recently, no construction of statistical ZAP argument was known, under any assumption. The situation changed very recently, with the construction of statistical ZAP arguments under the quasi-polynomial hardness of LWE, in two concurrent and independent works [GJJM20, BFJ+20]. Still, these results leave open the question of whether statistical ZAPs can be based on any of the other cryptographic assumptions that computational ZAPs can be based on, such as factoring or pairing-based assumptions.
The very recent work of [LVW20] comes very close to improving this state of affairs: they construct, from the quasi-polynomial hardness of the decision linear assumption in bilinear groups, ZAPs with private randomness. This primitive is essentially as versatile as a standard ZAP: while the verifier uses private coins, the proof remains publicly verifiable, and the first flow remains reusable. Yet, it still falls short of constructing true statistical ZAPs from pairing-based assumptions.
1.1 Our Result
In this work, we develop a new approach for constructing statistical ZAPs. At a high-level, our approach works by bootstrapping statistical ZAPs for simple languages to statistical ZAPs for NP, using a new primitive called interactive hidden-bits generator (IHBG), a plain-model variant of hidden-bits generators, which have been recently introduced in [CH19, QRW19, KNYY19, LPWW20] for constructing NIZKs for NP from different assumptions. We provide two instantiations of our framework (in groups with or without pairings in the publicly verifiable setting), and obtain:
-
Statistical ZAPs in pairing groups. A statistical ZAP argument for NP, assuming the explicit hardnessFootnote 1 of the \(\textsf {DDH} \) assumption in \(\mathbb {G}_1\) and of the kernel Diffie-Hellman assumption in \(\mathbb {G}_2\), where \((\mathbb {G}_1,\mathbb {G}_2)\) are groups equipped with an asymmetric pairing. The kernel Diffie-Hellman assumption is a standard search assumption in bilinear groups [MRV15, KW15], which is implied by (and is qualitatively weaker than) the \(\textsf {DDH} \) assumption. This improves over [LVW20], both in terms of assumption (we rely on a qualitatively weaker assumption, since [LVW20] requires \(\textsf {DDH} \) both in \(\mathbb {G}_1\) and \(\mathbb {G}_2\)) and of the primitive constructed (we achieve a true statistical ZAP argument, while [LVW20] achieves a relaxed variant).
-
Statistical ZAPs in pairing-free groups. A statistical ZAP argument from NP, assuming explicit hardness of the \(\textsf {DDH} \) assumption in a pairing-free group \(\mathbb {G}\) with \(\log |\mathbb {G}| \approx \lambda ^{1/2}\), and the assumption that no polynomial-time adversary can break the \(\mathsf {OW\text {-}KDM} \) security of ElGamal with respect to efficient functions with success probability significantly better than \(2^{-\lambda /2}\), denoted as \({2^{-\uplambda /2}-\mathsf {OW\text {-}KDM}}\) security. Note that the best-known attack against such \(\mathsf {OW\text {-}KDM} \) security of ElGamal succeeds with probability \(\mathsf {poly} (\lambda )\cdot 2^{-\lambda }\). While non-standard, this is a falsifiable search assumption, and there is an exponential gap between the required security margin and the best known attack. Under the same KDM assumption, but assuming only the standard polynomial hardness of \(\textsf {DDH} \), we also obtain statistical NIZKs (\(\mathsf {NISZKs}\)) for NP in the common reference string (CRS) model (settling for computational NIZKs, we can further relax \(\textsf {DDH} \) to computational Diffie-Hellman). This builds upon and improves over the recent work of [CKU20] which constructed computational NIZK arguments in the CRS model, under CDH and a stronger assumption: the \(2^{-3\lambda /4}\)-\(\mathsf {OW\text {-}KDM} \)-hardness of ElGamal.
In all the above, the (decisional or kernel) Diffie-Hellman assumption can be replaced by any of its standard generalizations, namely the decisional \(k\text {-}\mathsf {Lin} \) [HK07] and kernel \(k\text {-}\mathsf {Lin} \) assumptions, or even more generally any assumption from the family of the (decisional or kernel) matrix Diffie-Hellman assumptions [EHK+13, MRV15].
Relation to [JZ21]. In a breakthrough work (very recently accepted at Eurocrypt’21), Jain and Zhengzhong have solved the long-standing open problem of basing NIZKs on a well-studied assumption in pairing-free groups (the subexponential hardness of DDH). Furthermore, their work also achieves a statistical ZAP under the same assumption. We clarify the relation of our work to theirs.
The results presented in our work have been obtained concurrently and independently of those presented in [JZ21]. However, we were made aware of the existence and content of [JZ21] while it was submitted to Eurocrypt (through private communication), and before we had completed the write-up of our paper. The techniques developed in our work are unrelated to those in [JZ21], and our results are complementary:
-
We show that explicit hardness of DDH (or superpolynomial hardness of DDH, for any arbitrarily small superpolynomial function) gives statistical ZAPs in the pairing setting, and two-round statistical WI arguments in the pairing-free setting. In contrast, [JZ21] relies on the subexponential hardness of DDH (but does not need pairings to achieve public verifiability).
-
In the pairing-free setting, we also rely on an exponential search discrete-log-style hardness assumption, which is incomparable to subexponential DDH (albeit the latter is of course more standard). In particular, our assumption is falsifiable, holds in the generic group model, and is not known to imply public-key encryption.
Still, although our results have been achieved concurrently and independently of theirs, we cannot (and do not) claim to achieve the first construction of a statistical ZAP from standard group-based assumptions, since their construction precedes ours.
1.2 Our Techniques
At the heart of our results is a construction of a new cryptographic primitive, which we call an interactive hidden-bits generator (\(\mathsf {IHBG}\)). At a high level, an \(\mathsf {IHBG}\) adapts the notion of hidden-bits generator (defined in the CRS model) recently introduced and studied in [CH19, QRW19, KNYY19, LPWW20] to the plain model.
Dual-Mode Hidden-Bits Generators. More precisely, our starting point is the notion of a dual-mode hidden-bits generator (HBG) from [LPWW20]. In a dual-mode HBG, there are three algorithms: a CRS generation algorithm, a hidden-bits generator \(\mathsf {GenBits} \), and a verification algorithm \(\mathsf {VerifyBit} \). Given a CRS, the prover can, using \(\mathsf {GenBits} \), produce a short commitment c to a long, pseudorandom hidden-bit string \(\rho \), as well as openings \(\pi _i\) to all the bits \(\rho _i\) of \(\rho \). Then, \(\mathsf {VerifyBit} \) takes as input the CRS, a short commitment, a position i, a value \(\rho _i\), and an opening certificate \(\pi _i\), and returns 0 or 1 depending on whether the opening is accepted. A dual-mode HBG must satisfy three properties:
-
(Mode indistinguishability) the CRS can be generated in one of two modes, the hiding and the binding modes, which are computationally indistinguishable.
-
(Hiding) when the CRS is in hiding mode, the value \(\rho _i\) at all non-opened positions i is statistically hidden, even given c and openings \((\rho _j, \pi _j)\) at all other positions.
-
(Extractable) when the CRS is in binding mode, there exists an efficient extractor which can extract from c a string \(\rho \) such that no efficient prover can produce accepting openings for \(1-\rho _i\), for any position i.
As shown in [LPWW20], and following related transformations in [CH19, QRW19, KNYY19], a dual-mode HBG can be used to convert a NIZK for NP in the hidden-bits model (which exists unconditionally) into a dual-mode NIZK for NP in the CRS model (with statistical zero-knowledge when the HBG is used in hiding mode, and statistical soundness otherwise). These compilation techniques have their roots in the seminal works of Feige, Lapidot, and Shamir [FLS90] and of Dwork and Naor [DN00].
Interactive Hidden-Bits Generators. The statistical NIZKs by Libert et al. [LPWW20] crucially rely on the dual-mode feature of the HBG: the statistical binding property appears unavoidable to compile a NIZK in the hidden-bits model. Hence, obtaining statistical zero-knowledge is done by generating the CRS in hiding mode, but switching it to the binding mode when analyzing soundness. Of course, this standard technique is limited to the CRS model.
In an exciting recent work [KKS18], Kalai, Khurana, and Sahai, building upon previous results and ideas from [JKKR17, BGI+17, KS17], introduced an elegant and clever approach to partially emulate this “dual-mode feature” of the CRS model, but in the plain model. At a high level, they rely on statistically-hiding commitment schemes, which have the property that with some (negligible but not too small) probability, they will become binding and extractable; furthermore, this event cannot be detected by the committer. This in turn allows to obtain statistical privacy (e.g. statistical witness indistinguishability), while allowing to use the extractability properties to show soundness, at the cost of having to rely on assumptions which rule out even inverse-superpolynomial distinguishing advantages. This approach proved fruitful and led to a successful line of work [LVW19, GJJM20, BFJ+20] on building statistical ZAPs in the plain model.
Intuitively, our notion of interactive hidden-bits generator simply adapts this technique to the notion of dual-mode hidden-bits generator. That is, an \(\mathsf {IHBG}\) is a pair \((\mathsf {GenBits}, \mathsf {VerifyBit})\), similar to a dual-mode HBG, with the following core differences:
-
\(\mathsf {GenBits} \) takes as input a uniformly random string, which will correspond to the verifier message in the ZAP.
-
The non-opened values remain statistically hidden with overwhelming probability over the coins of \(\mathsf {VerifyBit} \), for any (possibly malicious) choice of the random string.
-
There exists a simulator which can produce simulated random coins (indistinguishable from true random coins) such that for any (possibly malicious) prover, with some not-too-small probability \(\mu \) (e.g. inverse-superpolynomial) over the coins of the simulator, the hidden bit string \(\rho \) can be extracted from c.
Defining \(\mathsf {IHBG}\) and Statistical ZAPs for NP. The above is of course very informal. Formally defining an interactive hidden-bits generator requires some care. In particular, we observe that the definition of extractability for statistically hiding extractable commitments in [LVW19, GJJM20, BFJ+20] do not suffice in our setting. At a high level, this is because these definition roughly say the following: the event that the commitments become extractable happens with probability \(\mu \), and whenever this event happens, the extracted value are guaranteed to be correct.
However, this will not hold in our setting: given a tuple \((c, \{i,\pi _i\}_i)\) of a commitment and set of openings from a possibly malicious prover, the hidden-bit string \(\rho \) recovered by the extractor is correct if \(\mathsf {VerifyBit} (c, i, 1-\rho _i, \pi _i) = \bot \) for all the opened positions i. Unfortunately, we can only guarantee that this will hold with overwhelming probability in our concrete construction, and not with probability 1. It turns out that, when building statistical ZAPs for NP, this is a crucial issue: in the soundness game of the ZAP construction from \(\mathsf {IHBG} \), the challenger will want extraction to succeed with probability \(\mu \) even when conditioning on other checks being successful. A guaranteed correctness of extraction (conditioned on extraction succeeding) would ensure that this is the case, but an overwhelming probability of correctness does not, since conditioning on other events could arbitrarily change this probability.
To work around this issue, we adopt an approach closer in spirit to the definition of [LVW20]. We define \(\mu \)-extractability as follows: an \(\mathsf {IHBG} \) is \(\mu \)-extractable if there exists an efficient simulator \(\textsf {SimCoin} \) and an efficient opener \(\mathsf {Open} \) such that, for any PPT adversary \(\mathcal {A}\) and any PPT distinguisher D, given simulated coins \((\widetilde{r}, \tau ) \leftarrow _{r}\textsf {SimCoin} \) (where \(\tau \) is an associated trapdoor for the opener), and a tuple \((c, S, \rho ^*_S, \{ \pi _i \} _s, \mathsf {st})\leftarrow _{r}\mathcal {A}(\widetilde{r})\) where c is a short commitment, S is a set of positions, \(\rho ^*_S\) are the values which \(\mathcal {A}\) opens the position to, the \(\pi _i\) are certificates of correct openings, and \(\mathsf {st} \) is an arbitrary state, and letting \(\rho \leftarrow \mathsf {Open} (\widetilde{r},c, \tau )\), the probability \(p_1\) that \(\mathsf {VerifyBit} (\widetilde{r}, c, i, 1-\rho _i, \pi _i)\) returns \(\bot \) for all \(i\in S\) and at the same time the distinguisher D, given \(\mathsf {st} \), outputs 1, should satisfy
where \(p_2\) is the probability of the same event without the check that the procedure \(\mathsf {VerifyBit} (\widetilde{r}, c, i, 1-\rho _i, \pi _i)\) returns \(\bot \) for all \(i\in S\). That is, \(\mu \)-extractability requires that for any other efficient conditions that we were verifying, the probability that these conditions are still verified and that simultaneously, extraction succeeded and produced a correct output, should not decrease by a factor more than \(\mu \) compared to the initial probability. This strong security notion is the key to capture the intuition that the extraction should succeed with probability \(\mu \) essentially independently of everything else.
Given this notion of \(\mu \)-extractable \(\mathsf {IHBG}\), we provide a natural construction of statistical ZAP for NP, which follows the standard template of using the \(\mathsf {IHBG}\) to compile an unconditional NIZK for NP in the hidden-bits model, and formally prove that the resulting construction is a ZAP.
Constructing IHBG. It remains to construct \(\mathsf {IHBG}\) with a statistical hiding property, satisfying the strong \(\mu \)-extractability notion defined above. The first natural idea is to rely on the construction of dual-mode HBG from [LPWW20], and to convert it into a plain model protocol by letting the verifier sample the CRS herself. However, this immediately runs into obstacles: nothing prevents the verifier from sampling the CRS in binding mode, breaking the statistical hiding property. To recover the statistical hiding property, we let the prover tweak the CRS sampled by the verifier in a way that simultaneously guarantee two things:
-
With overwhelming probability over the coins of the prover, the tweaked CRS will be in hiding mode, yet
-
The tweak comes from a superpolynomial-size set, and by successfully guessing the tweak in advance, a simulator can engineer the sampled CRS (in a way that is indistinguishable from sampling a CRS honestly) such that the tweaked CRS will be in binding mode.
To achieve these two features, we rely on an elegant linear-algebra trick. In order to explain the idea, we first recall the high-level template of the construction of dual-mode HBG described in [LPWW20]. Let m be the length of the hidden bit string. The LPWW construction works in a hard-discrete-log group \(\mathbb {G}\) of order p with generator g. It has the following structure:
-
The hiding CRS is \(g^\mathbf{A }\), where \(\mathbf{A} \) is a random full-rank matrix \(\mathbf{A} \in \mathbb {Z}_p^{(m+1)\times (m+1)}\).
-
The binding CRS is \(g^\mathbf{A }\), where \(\mathbf{A} \) is a random rank-1 matrix in \(\mathbb {Z}_p^{(m+1)\times (m+1)}\).
Under the DDH assumption, the two modes are indistinguishable. Let \(\mathbf {a}_0, \cdots , \mathbf {a}_m\) denote the columns of \(\mathbf{A} \). To provide a short commitment to a pseudorandom length-m hidden bit string, the prover picks a random length-\((m+1)\) vector \(\mathbf {y}\), and computes \(c = g^{\mathbf {y}^\top \cdot \mathbf {a}_0}\). Then, the i-th hidden bit is defined to be \(\rho _i = \mathsf {HB} (g^{\mathbf {y}^\top \cdot \mathbf {a}_i})\), where \(\mathsf {HB} (\cdot )\) is a hardcore bit function (e.g. a la Goldreich-Levin). Eventually, to prove correct opening of \(\rho _i\), given the commitment c and the CRS \(g^\mathbf{A }\), the prover reveals \(c _i = g^{\mathbf {y}^\top \cdot \mathbf {a}_i}\) and uses a NIZK to demonstrate the existence of a vector \(\mathbf {y}\) such that \(c = g^{\mathbf {y}^\top \cdot \mathbf {a}_0}\) and \(c _i = g^{\mathbf {y}^\top \cdot \mathbf {a}_i}\) (from now on, we will call this language the LPWW language, \(\mathscr {L}_\mathsf{LPWW} \)).
Observe that when the CRS is in binding mode, we have \(\mathbf {a}_i = v_i\cdot \mathbf {a}_0\) for some value \(v_i\) (since \(\mathbf{A} \) has rank 1), hence the above language becomes essentially a DDH language. Adapting existing statistical NIZKs for the DDH language suffices to guarantee extractability in binding mode. On the other hand, when the CRS is in hiding mode, where \(\mathbf{A} \) has full rank, any number of openings (of which there is at most m) \(g^{\mathbf {y}^\top \cdot \mathbf {a}_i}\) leak statistically no information about the unopened values (since \(\mathbf{A} \) is of dimension \((m+1)\times (m+1)\)). This is because for any possible choice of values for the unopened positions, there exists a unique vector \(\mathbf {y}\) that coincides with all the opened and unopened values when \(\mathbf{A} \) is full rank. Hence, this guarantees statistical hiding.
Now, the core idea to achieve statistical hiding and \(\mu \)-extractability in our construction (where \(\mu \) is some arbitrary fixed inverse-superpolynomial function) is to let the verifier sample and send \(g^\mathbf{A }\) herself, but to let the prover tweak this sample as follows: let \(\mathbf{I} _{m+1}\) denote the identity matrix in \(\mathbb {Z}_p^{(m+1)\times (m+1)}\). The prover picks a small exponent \(\alpha \) at random from a subset of \(\mathbb {Z}_p\) of size \(\approx 1/\mu \), e.g. by picking \(\alpha \) as a random integer smaller than \([1/\mu ]\), and using a natural encoding of integers in \(\{0, \cdots , p-1\}\) as elements of \(\mathbb {Z}_p\). Then, the prover defines the tweaked CRS \(g^\mathbf{A '}\) to be \(g^{\mathbf{A} - \alpha \cdot \mathbf{I}_{m+1}}\), and uses this tweaked CRS in the dual-mode HBG construction of [LPWW20].Footnote 2
To see why this tweak achieves exactly what we want, observe that the following holds:
-
First, we show that with overwhelming probability \(1 - (m+1)\mu \), the matrix \(\mathbf{A} '\) has full rank. Indeed, if \(\mathbf{A} '\) does not have full rank, it means that there is a nonzero vector \(\mathbf {u}\) in the kernel of \(\mathbf{A} '\). But then, \(\mathbf {u}\cdot \mathbf{A} ' = \mathbf{0} \) rewrites to \(\mathbf {u}\cdot \mathbf{A} = \alpha \cdot \mathbf {u}\) – in equivalent terms, this means that \(\alpha \) must be an eigenvalue of \(\mathbf{A} \). But since \(\mathbf{A} \) can have at most \(m+1\) eigenvalues and \(\alpha \) is randomly sampled from a set of size \(1/\mu \), then this event can happen with probability at most \((m+1)\mu \).
-
Second, we sketch why \(\mu \)-extractability holds. First, the simulator will guess a value \(\alpha '\), and set \(\mathbf{A} \leftarrow \mathbf{M} + \alpha '\cdot \mathbf{I} _{m+1}\), where \(\mathbf{M} \) is a rank-1 matrix. Observe that when the simulator guesses correctly, which happens with probability \(\mu \), it holds that \(g^\mathbf{A '}\) is a binding CRS. Furthermore, under the assumption that no PPT adversary can distinguish DDH tuples from random tuples with probability better than \({\mu \cdot \mathsf {negl}(\uplambda )}\), the replacement of truly random coins by simulated coins will not be detected. Hence, when further assuming that the ZAP for \(\mathscr {L}_\mathsf{LPWW} \) guarantees a bound \({\mu \cdot \mathsf {negl}(\uplambda )}\) on the probability that a malicious PPT prover breaks soundness, we can extract with probability almost \(\mu \) a correct hidden-bit string. In Sect. 3, we will formally prove that \(\mu \)-extractability holds with respect to an arbitrary PPT distinguisher D.
Summing up, the above provides a construction of \(\mathsf {IHBG}\) (which in turns implies statistical ZAPs for NP), assuming
-
the hardness of DDH with distinguishing advantage \({\mu \cdot \mathsf {negl}(\uplambda )}\) for any PPT adversary and for any negligible functions \(\mu \) and \(\mathsf {negl}\) (an assumption in-between standard polynomial time hardness and superpolynomial time hardness, which is called explicit hardness in [BFJ+20]), and
-
the existence of statistical ZAPs for \(\mathscr {L}_\mathsf{LPWW} \) with \({\mu \cdot \mathsf {negl}(\uplambda )}\)-soundness.
Instantiating the Statistical ZAPs for\(\mathscr {L}_{\mathbf {\mathsf{{LPWW}}}}\). Looking ahead, the formal analysis of our construction actually requires a slightly exotic notion of soundness: \(\mathscr {L}_\mathsf{LPWW} \) is formally not a language, but a parametrized family of languages, and (adaptive) soundness must hold for parameters sampled uniformly at random from a specific subset of language parameters (which are those that correspond to \(\mathbf{A} \) being of rank 1). We call a ZAP for the parameterized family of languages \(\mathscr {L}_\mathsf{LPWW}\) \(\mathsf {IHBG}\) -friendly when it satisfies this notion of soundness. We provide two instantiations for the underlying \(\mathsf {IHBG}\)-friendly statistical ZAP.
Using Pairings. First, we observe that the recent work of Couteau and Hartmann [CH20] provides a statistical ZAP for the DDH language, which extends directly to an \(\mathsf {IHBG}\)-friendly statistical ZAP for the \(\mathscr {L}_\mathsf{LPWW} \) language, under the standard kernel-DH assumption, in groups equipped with an asymmetric pairing. This leads to a statistical ZAP for NP under the explicit hardness of DDH in \(\mathbb {G}_1\), and the explicit hardness of kernel-DH in \(\mathbb {G}_2\), where \((\mathbb {G}_1, \mathbb {G}_2)\) are groups equipped with an asymmetric pairing.
Without Pairings. Secondly, we revisit the recent construction of statistical NIZKs for the DDH language in pairing-free groups by Couteau, Katsumata, and Ursu [CKU20]. Their construction relies on the assumption that no PPT algorithm can break the one-wayness of ElGamal against key-dependent message (\(\mathsf {OW\text {-}KDM}\)) attacks with respect to efficient functions (i.e., the assumption that no PPT adversary can recover m from an ElGamal encryption of m, even when m is some efficiently computable function of the ElGamal secret key) with probability better than \({2^{-3\uplambda /4 + o(\uplambda )}}\) (note that the best known PPT attack against this assumption, in appropriate groups, succeeds with probability \({2^{-\uplambda + o(\uplambda )}}\); furthermore, the restriction of KDM hardness to efficient functions of the secret key makes the assumption falsifiable “in spirit” – i.e., up to the negligible winning advantage). We denote this assumption the \({2^{-3\uplambda /4}}\)-\(\mathsf {OW\text {-}KDM} \) hardness of ElGamal. We adapt the CKU construction to the LPWW language. Along the way, we put forth a modification of their construction which significantly improves the underlying assumption: we only need to assume that no PPT adversary can break the \(\mathsf {OW\text {-}KDM} \) hardness of ElGamal with probability better than \({2^{-\uplambda /2 + o(\uplambda )}}\). This change directly improves the result of [CKU20]. With this instantiation, and observing that this statistical NIZK is also a statistical ZAP when the verifier can choose the CRS, we obtain a statistical ZAP for NP in pairing-free groups under the explicit hardness of DDH, and the \({2^{-\uplambda /2}}\)-\(\mathsf {OW\text {-}KDM} \) hardness of ElGamal (we note that the latter is incomparable to DDH: it is a search, discrete-logarithm-type assumption, which is not even known to imply public-key encryption).
1.3 A Direct Construction Using Pairings
Eventually, we point out that if one is willing to rely on a stronger assumption, one of our two instantiations (the pairing-based instantiation) can be obtained from our techniques in a much more direct (and simple-in-hindsight) way, without going through the hidden-bit model. Specifically, the core idea for our IHBG construction is to modify the CRS of a dual-mode NIZK using a simple tweak, sampled from a small set by the prover, which guarantees that with overwhelming probability a maliciously sampled CRS will be in hiding mode (but it will be in binding mode in the case when the verifier guesses the tweak).
A similar tweak can be applied directly to the dual-mode NIZK of Groth, Ostrovsky, and Sahai [GOS06b] instantiated with Groth-Sahai commitments [GS08]. Briefly, a Groth-Sahai commitment is of the form \((1,g^m)\cdot \mathbf{u}^r \cdot \mathbf{v}^s\), where \(\mathbf{u}, \mathbf{v}\) are two random vectors of length two, and \(\cdot \) denotes the coordinate-wise product (we write \(\mathbf{u}^r\) for \((u_1^r, u_2^r)\), where \(\mathbf{u} = (u_1,u_2)\)). When the vectors \((\mathbf{u},\mathbf{v})\) are random, the commitments are perfectly hiding; when \(\mathbf{v}\) is in the span of \(\mathbf{u}\), they become perfectly binding. A GOS proof for circuit satisfiability, given a circuit C and a witness w such that \(C(w) = 1\), works by committing to all bits of w, as well as to the bits on all wires during the evaluation of C(w). Then, the proof proceeds by showing that all commitments commit to bits, that all gate relations are satisfied (which reduces to proving that a linear combination of the committed input and output bits – homomorphically computed from the commitments – is itself a bit), and that the output commitment contains 1. All these proofs can be reduced to pairing-product equations, hence can be proven with a Groth-Sahai NIZK [GS08].
Now, letting the verifier choose the CRS \((\mathbf{u},\mathbf{v})\) themself, the prover can sample a small tweak \(z \leftarrow _{r}[1/\mu ]\), and set the CRS to be \((\mathbf{u}', \mathbf{v}') = (\mathbf{u}\cdot (1, g^z), \mathbf{v} \cdot (1, g^z))\). For any adversarial choice of \((\mathbf{u},\mathbf{v})\), \((\mathbf{u}',\mathbf{v}')\) will not be colinear except with negligible property; on the other hand, with probability \(\mu \), the verifier can guess the tweak z and cause \((\mathbf{u}', \mathbf{v}')\) to be in binding mode. To make the analysis work, we need to rely on the same notion of \(\mu \)-extractability which we defined previously. This direct approach leads to a statistical ZAP for \(\mathsf {NP}\) in groups \((\mathbb {G}_1,\mathbb {G}_2)\) equipped with an asymmetric pairing, assuming the explicit hardness of \(\textsf {DDH}\) in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\), a slightly stronger assumption compared to the one we obtain when going through the hidden-bit model. While simple in hindsight, this construction was apparently missed in previous works: the recent work of [LVW20] achieved, under the same assumption, a strictly weaker result (a ZAPR argument for \(\mathsf {NP}\)), using a considerably more involved and highly non-trivial construction.
2 Preliminaries
Due to page limitations, we provide the definitions of standard notations and cryptographic tools used throughout the paper in the full version of the paper [CKSU21].
2.1 Hardness Assumptions
Let \(\textsf {DHGen} \) be a deterministic algorithm that on input \({1^\uplambda }\) returns a description \(\mathcal {G}= (\mathbb {G}, p)\) where \(\mathbb {G}\) is a cyclic group of prime order p. Let \(\textsf {PGen} \) be a deterministic algorithm that on input \({1^\uplambda }\) returns a description \(\mathcal {PG}= (\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_{\mathsf {T}}, p)\) where \((\mathbb {G}_1,\mathbb {G}_2, \mathbb {G}_{\mathsf {T}})\) are cyclic groups of prime order p equipped with a bilinear pairing operation \(\bullet : \mathbb {G}_1\times \mathbb {G}_2 \mapsto \mathbb {G}_{\mathsf {T}}\). Below, we recall the definition of the decision Diffie-Hellman assumption in a cyclic group, as well as the definition of the kernel Diffie-Hellman assumption in a pairing group. Following [BFJ+20], we also consider the explicit hardness of the assumptions, where we say that an assumption has explicit \(\mu \)-hardness if \(\mu \) is an explicit bound on the advantage of any polynomial time adversary. Note that this notion of explicit hardness is stronger than standard polynomial hardness, but weaker than superpolynomial hardnessFootnote 3 for any superpolynomial factor.
Definition 1
(DDH Assumption). We say that the decisional Diffie-Hellman (\(\textsf {DDH}\)) assumption holds relative to \(\textsf {DHGen} \) if for all PPT adversaries \(\mathcal {A} \), it holds that \({\mathsf {Adv} ^\textsf {DDH} (\mathcal {A}) \le \mathsf {negl}(\uplambda )}\), where
Here, note that \({\mathcal {G}\leftarrow \textsf {DHGen} (1^\uplambda )}\) and \(\textsf {DHGen} \) outputs a fixed group \(\mathbb {G}\) per security parameter, and \(g \leftarrow _{r}\mathbb {G}\), \(\alpha , \beta , \gamma \leftarrow _{r}\mathbb {Z}_p\) are chosen uniformly. Furthermore, let \(\mu (\lambda )\) be an efficiently computable function. We say that the \(\mu \)-explicit hardness of the DDH assumption holds relative to \(\textsf {DHGen} \), if \({\mathsf {Adv} ^\textsf {DDH} (\mathcal {A}) \le \mu (\uplambda )}\) for all PPT adversaries \(\mathcal {A} \).
We now recall the definition of the kernel Diffie-Hellman assumption in a pairing group. The kernel DH assumption is a standard search assumption in bilinear groups, introduced in [MRV15] and used in several papers, e.g. [KW15]. In particular, kernel Diffie-Hellman in a group \(\mathbb {G}_2\) is implied by (and is qualitatively weaker than) the DDH assumption in the same group.
Definition 2
(Kernel DH Assumption). We say that the kernel Diffie-Hellman (\(\textsf {kerDH}\)) assumption holds relative to \(\textsf {PGen} \) if for all PPT adversaries \(\mathcal {A} \), it holds that \({\mathsf {Adv} ^\textsf {kerDH} (\mathcal {A}) \le \mathsf {negl}(\uplambda )}\), where
Furthermore, let \(\mu (\lambda )\) be an efficiently computable function. We say that the \(\mu \)-explicit hardness of the kernel DH assumption holds relative to \(\textsf {PGen} \), if \({\mathsf {Adv} ^\textsf {DDH} (\mathcal {A}) \le \mu (\uplambda )}\) for all PPT adversaries \(\mathcal {A} \).
To see why the above is implied by DDH in \(\mathbb {G}_2\), observe that on input \((g, g^\alpha , g^\beta , g^{\gamma })\), an adversary against DDH can run the kernel DH adversary on input \((g_1, g, g^\alpha )\), where \(g_1 \leftarrow _{r}\mathbb {G}_1\) and e is implicitly set as \(\alpha \). It then gets a vector \((g_1^u, g_1^v)\) in \(\mathbb {G}_1^2\) from the kernel DH adversary such that (u, v) is in the kernel of \((1,\alpha )\). Now, if \((g, g^\alpha , g^\beta , g^{\gamma })\) is a DDH tuple, then (u, v) is also in the kernel of \((g^\beta , g^{\gamma }) = (g, g^\alpha )^\beta \), and this can be checked efficiently given \((g_1^u, g_1^v)\) with the help of the pairing operation.
Remark 3
(Extensions to Matrix Diffie-Hellman.) For the sake of concreteness and simplicity, we state our results in this paper in terms of the DDH and kernel DH assumptions. However, all our results can be generalized to hold under the standard generalizations of the Diffie-Hellman assumption, namely the decisional \(k\text {-}\mathsf {Lin} \) [HK07] and kernel \(k\text {-}\mathsf {Lin} \) assumptions, or even more generally any assumption from the family of the (decisional or kernel) matrix Diffie-Hellman assumptions [EHK+13, MRV15].
One-Way KDM Security of ElGamal. The last hardness assumption we will use in this work states, in essence, that no PPT adversary can recover m given an ElGamal encryption of m, even when m might be an efficiently computable function of the ElGamal secret key, with probability significantly better than \({2^{-c\cdot \uplambda }}\) for some constant \(c < 1\) (where \({\uplambda }\) is the logarithm of the group size). Note that the best known attack against this falsifiable search assumption succeeds with probability \({\mathsf {poly} (\uplambda )/2^\uplambda }\). To formally introduce the assumption, we introduce a natural secret-key variant of ElGamal (which suffices for our construction and leads to a more conservative assumption compared to the public-key variant).
Definition 4
(Secret-Key ElGamal). Let \(\tilde{\mathbb {G}} = \{ \tilde{\mathbb {G}} _\lambda \} _{\lambda }\) be an ensemble of groups where each group \(\tilde{\mathbb {G}} _\lambda \) is of order q such that \(\lceil \log q \rceil \approx \lambda \). The natural (secret-key) variant of additive ElGamal with message space \(\mathbb {Z}_q\) consists of the following three PPT algorithms.
-
\(\mathsf {Setup} (1^\lambda ):\) The setup algorithm outputs a public-parameter \(\tilde{G} \leftarrow _{r}\tilde{\mathbb {G}} _\lambda \) and a secret key \(k \leftarrow _{r}\mathbb {Z}_q\).
-
\(\mathsf {Enc} _{\tilde{G}}(k, m):\) The encryption algorithm samples \(\tilde{R} \leftarrow _{r}\tilde{\mathbb {G}} \) and outputs a ciphertext \(\tilde{\mathbf {C}} = (\tilde{R}, \tilde{R} ^k \cdot \tilde{G} ^m)\).
-
\(\mathsf {HalfDec} (k, \tilde{\mathbf {C}}):\) The half decryption algorithm parses \(\tilde{\mathbf {C}} \) as \((\tilde{C} _0, \tilde{C} _1)\) and outputs \(\tilde{C} _1/\tilde{C} _0^k\).
Throughout the paper, we omit the subscript when the meaning is clear. Note that the scheme does not allow for full decryption, but only for decryption “up to discrete logarithm”: for every \((\tilde{G},k,m)\), it holds that \(\mathsf {HalfDec} (k, \mathsf {Enc} _{\tilde{G}}(k,m)) = \tilde{G} ^m\). One important property of the scheme is that it enjoys the notion of universality. Informally, the notion claims that the ciphertexts are not associated with a specific key, but rather, could have been an output of any key.
Definition 5
(Universality). For all \(\lambda \in \mathbb {N}\), \(\tilde{G} \in \tilde{\mathbb {G}} _\lambda \), and \(k^* \in \mathbb {Z}_q\), the ciphertexts of ElGamal satisfies
Definition 6
(OW-KDM Security). Let \(\mathcal {F} = \{ \mathcal {F}_\lambda \} _{\lambda \in \mathbb {N}}\) be an ensemble of sets of functions where each \(\mathcal {F}_\lambda = \{F_u\}_u\) is a family of (possibly randomized) efficiently-computable functions. We say that ElGamal satisfies (one-query) \(\delta \)-hard \(\mathsf {OW\text {-}KDM}\) security with respect to \(\mathcal {F}\) if for every \(F_u \in \mathcal {F}_\lambda \), superpolynomial function s, and every (non-uniform) PPT adversary \(\mathcal {A} \), it holds that

When ElGamal satisfies \(\delta \)-hard \(\mathsf {OW\text {-}KDM}\) security for \(\delta (\lambda ) = 2^{-(c + o(1))\cdot \lambda }\) for some constant \(c \in (0,1]\), we say it is \(2^{-c\lambda }\)-\(\mathsf {OW\text {-}KDM}\) secure or more simply, strong \(\mathsf {OW\text {-}KDM}\) secure.
The strong \(\mathsf {OW\text {-}KDM}\) security of ElGamal was introduced in [CCRR18]. However, this work considered an extreme variant of the notion with \(c=1\) (that is, \(2^{-\lambda }\)-\(\mathsf {OW\text {-}KDM}\)), and where security was required to hold with respect to all functions (even inefficient ones). The more conservative variant (with \(c < 1\) and a restriction to efficiently computable functions) was introduced in [CKU20], which used it (with constant \(c = 3/4\)) to build correlation-intractable hash functions. In this work, we will rely on an even more conservative variant with \(c = 1/2\).
2.2 ZAP
\(\textsf {ZAP}\) [DN00, DN07] is a public-coin two-move witness indistinguishable non-interactive argument. In this work, we focus on statistical \(\textsf {ZAPs}\) where witness indistinguishability holds unconditionally.
Definition 7
(ZAP). A \(\textsf {ZAP}\) system \(\varPi _\textsf {ZAP} \) for an \(\mathsf {NP}\) language \({\mathscr {L}= \{ \mathscr {L}_\uplambda \} _\uplambda }\) with corresponding relation \({\mathcal {R} = \{ \mathcal {R} _\uplambda \} _\uplambda }\) with public-coin length \({\ell (\uplambda )}\) is a tuple of PPT algorithms \((\mathsf {Prove},\mathsf {Verify})\) defined as follows.
-
\(\mathsf {Prove} ( r, x, w ) \rightarrow \mathbf {\pi }:\) The proving algorithm is given the public-coin \(r \in \{0 , 1\}^\ell \), a statement x, and a witness w, and outputs a proof \(\mathbf {\pi } \).
-
\(\mathsf {Verify} ( r, x, \mathbf {\pi }) \rightarrow \top \ \mathbf{or } \ \bot :\) The verification algorithm is given the public-coin \(r \in \{0 , 1\}^\ell \), a statement x, and a proof \(\mathbf {\pi } \), and outputs \(\top \) for acceptance or \(\bot \) for rejection.
We additionally require the following properties to hold.
Correctness: For any \({\uplambda \in \mathbb N}\), \(r \in \{0 , 1\}^\ell \) and \({(x, w) \in \mathcal {R} _\uplambda }\), we have \(\Pr [\mathsf {Verify} ( r, x, \mathsf {Prove} ( r, x, w)) = \top ] = 1.\)
(Non-Adaptive) Computational Soundness: For any \({\uplambda \in \mathbb N}\), PPT adversary \(\mathcal {A}\), and any statement \({x \not \in \mathscr {L}_\uplambda }\), we have
(Adaptive) Statistical Witness Indistinguishability: For any \({\uplambda \in \mathbb N}\) and unbounded adversary \(\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)\), we have
Remark 8
(On Adaptive Soundness). In this work, we construct a \(\textsf {ZAP}\) that is non-adaptive computationally sound and adaptive statistical witness indistinguishable. This security property is in alignment with all the recent \(\textsf {ZAPs}\) (or \(\textsf {ZAP}\) with private randomness) [GJJM20, BFJ+20, LVW20]. Constructing \(\textsf {ZAPs}\) satisfying adaptive soundness and statistical witness indistinguishability seems to be difficult, where the former stipulates that the adversary can choose the statement \(x \not \in \mathscr {L}\) after it sees the public-coin r. Although we do not have any formal proofs of nonexistence of such \(\textsf {ZAPs}\), we do have some evidence indicating the difficulty of obtaining them. In the context of \(\textsf {NIZKs}\) satisfying statistical zero-knowledge (NISZKs), Pass [Pas13] shows that there is no black-box reduction from the adaptive soundness of NISZK to a falsifiable assumption [Nao03, GW11].
2.3 NIZKs in the Hidden-Bits Model
We recall the notion of a \(\textsf {NIZK}\) in the hidden-bits model [FLS99].
Definition 9
A non-interactive proof system \(\varPi _\mathsf {HBM} \) in the hidden-bits model for an \(\mathsf {NP}\) language \({\mathscr {L}= \{ \mathscr {L}_\uplambda \} _\uplambda }\) with corresponding relation \({\mathcal {R} = \{ \mathcal {R} _\uplambda \} _\uplambda }\) with hidden-bits length \({m(\uplambda )}\) is a pair of PPT algorithms \((\mathsf {Prove}, \mathsf {Verify})\) defined as follows.
-
\(\mathsf {Prove} (\mathsf {hb},x,w) \rightarrow (I, \mathbf {\pi }):\) The proving algorithm is given a random bit string \(\mathsf {hb} \in \{0,1\} ^m\) and a statement x, and a witness w as inputs, and outputs a subset \(I\subseteq [m]\) together with a proof \(\mathbf {\pi } \).
-
\(\mathsf {Verify} (S, \mathsf {hb} _S, x, \mathbf {\pi }) \rightarrow \top \ \mathbf{or } \ \bot :\) The verification algorithm is given a subset \(S \subseteq [m]\), a string
 , a statement x and a proof \(\mathbf {\pi } \) as inputs, and outputs \(\top \) for acceptance or \(\bot \) for rejection.
, a statement x and a proof \(\mathbf {\pi } \) as inputs, and outputs \(\top \) for acceptance or \(\bot \) for rejection.
We additionally require the following properties to hold.
Correctness. For any \({\uplambda \in \mathbb N}\), \({(x, w) \in \mathcal {R} _\uplambda }\), any \(\mathsf {hb} \in \{0,1\} ^m\), and for \((I,\mathbf {\pi })\leftarrow _{r}\mathsf {Prove} (\mathsf {hb},x,w)\), we have \(\mathsf {Verify} (x, \mathsf {hb} _S, x, \mathbf {\pi }) = \top \).
Statistical \(\varepsilon \)-Soundness. For any \({\uplambda \in \mathbb N}\) and (possibly unbounded) adversary \(\mathcal {A} \), we have
Perfect Zero-Knowledge. For any \({\uplambda \in \mathbb N}\) and any (possibly unbounded) stateful adversary \(\mathcal {A} \), there exists a PPTFootnote 4 zero-knowledge simulator \(\mathsf {Sim} \) such that for every \({(x, w)\in \mathcal {R} _\uplambda }\), the distributions \(\{ (S, \mathsf {hb} _S, \mathbf {\pi }):\mathsf {hb} \leftarrow _{r}\{0,1\} ^m, (S,\mathbf {\pi }) \leftarrow _{r}\mathsf {Prove} (\mathsf {hb},x,w)\}\) and \(\{\mathsf {Sim} _\textsf {zk} (x)\}\) are perfectly indistinguishable.
We use the following result regarding the existence of \(\textsf {NIZKs}\) in the hidden-bits model [FLS90].
Theorem 10
( \(\textsf {NIZK}\) for all of \(\mathsf {NP}\) in the hidden-bits model). Let \(k= k(\lambda )\) be any positive integer-valued function. Then, unconditionally, there exists a non-interactive proof system \(\varPi _\mathsf {HBM} \) for any \(\mathsf {NP}\) language \({\mathscr {L}= \{ \mathscr {L}_\uplambda \} _\uplambda }\) in the hidden-bits model that uses \(\mathsf {hb} = k \cdot \mathsf {poly} (\lambda )\) hidden-bits with soundness error \(\epsilon \le 2^{- k \cdot \lambda }\), where \(\mathsf {poly} \) is a polynomial function related to the \(\mathsf {NP} \) language \(\mathscr {L}\).
2.4 Correlation-Intractable Hash Functions
Finally, we recall the definition of correlation-intractable hash functions (CIH). We also require a CIH to be programmable, which roughly means for any input-output pair (x, y), we can efficiently find a key k such that \(H(k, x) = y\). Due to page limitations, the formal definition is provided in the full version.
Definition 11
(Correlation Intractable Hash Function). A collection \(\mathcal {H} = \{H_\lambda : K_\lambda \times I_\lambda \mapsto O_\lambda \}_{\lambda }\) of (efficient) keyed hash functions is a \(\mathcal {R}\)-correlation intractable hash (CIH) family, with respect to a parameterized relation ensemble \({\mathcal {R} = \{\mathcal {R} _\lambda \}_\uplambda = \{ \{ \mathcal {R} _{\lambda , t} \subseteq I_\lambda \times O_\lambda \} _{t \in T_\uplambda } \}_\uplambda }\), if for every (non-uniform) PPT adversary \(\mathcal {A} \) and \({t \in T_\uplambda }\), it holds that

Furthermore, let \(\mu (\lambda )\) be an efficiently computable function. We say that the collection \(\mathcal {H} \) satisfies \((\mu ,\mathcal {R})\)-correlation intractability if the above probability is bounded by  for all PPT adversaries \(\mathcal {A}\).
for all PPT adversaries \(\mathcal {A}\).
3 Interactive Hidden-Bits Generating Protocol and \(\textsf {ZAPs}\) for \(\mathsf {NP}\)
In this section, we formally define an interactive hidden-bits generating (\(\mathsf {IHBG}\)) protocol. Our definition builds on the definition of a (dual-mode) hidden-bits generator from [QRW19, LPWW20] (and the similar notion of (designated-verifier) PRG [DN00, DN07, CH19]). The main difference is that we allow a two-round interaction between the hidden-bits generator and the verifier, while removing the common reference string. Below, we define a public-coin flavor of an \(\mathsf {IHBG}\) protocol to allow for public verifiability and reusability of the message from the verifier.
3.1 Definition
We formalize the notion of an interactive hidden-bits generating (\(\mathsf {IHBG}\)) protocol.
Definition 12
(Interactive Hidden-Bits Generating Protocol). Let \({s(\uplambda )}\) and \({m(\uplambda )}\) be positive valued polynomials. An interactive hidden-bits generating (\(\mathsf {IHBG}\)) protocol \(\varPi _\mathsf {IHBG} \) with public-coin length \({\ell (\uplambda )}\) is a tuple of efficient algorithms \((\mathsf {GenBits}, \mathsf {VerifyBit})\) defined as follows.
-
\({\mathsf {GenBits} (1^\uplambda , m, r) \rightarrow (\sigma , \rho , \{ \pi _i \} _{i \in [m]} ):}\) The hidden-bits generator algorithm is given the security parameter \({1^\uplambda }\) (in unary), a length m, a public-coin \(r \in \{0 , 1\}^\ell \) and outputs a commitment \(\sigma \in \{0 , 1\}^s\), a string \(\rho \in \{0 , 1\}^m\), and a set of proofs \( \{ \pi _i \} _{i \in m} \).
-
\(\mathsf {VerifyBit} (r, \sigma , i, \rho _i, \pi _i) \rightarrow \top \ \mathbf{or } \ \bot \): The verification algorithm is given a public-coin \(r \in \{0 , 1\}^\ell \), a commitment \(\sigma \in \{0 , 1\}^s\), a bit \(\rho _i \in \{0 , 1\}\), and a proof \(\pi _i\), and outputs \(\top \) for acceptance or \(\bot \) for rejection.
We additionally require the following properties to hold. Below, we assume that the security parameter is provided to all algorithms, and omit it for simplicity.
Correctness: For any \({\uplambda \in \mathbb {N}}\), \(j \in [m]\), and \(r \in \{0 , 1\}^\ell \), we have
Succinctness: The commitment length s only depends on the security parameter, i.e., \({s(\uplambda ) = \mathsf {poly} (\uplambda )}\), and in particular, does not depend on the length m of the generated bits.
\(\mu \)-Extractability: There exists a PPT public-coin simulator \(\textsf {SimCoin} \) and a deterministic polynomial-time open algorithm \(\mathsf {Open} \) such that for all polynomial m, the following two conditions hold. For an intuitive explanation for \(\mu \)-successful extraction, we refer the readers to the technical overview in Sect. 1.2.
-
(Public-Coin Indistinguishability) for any PPT adversary \(\mathcal {A}\), we have

-
(\(\mu \)-Successful Extraction) for any PPT adversary \(\mathcal {A}\) and any PPT distinguisher D, we have

Statistical Hiding: For all polynomial m, public-coin \(r \in \{0 , 1\}^\ell \), and all unbounded adversaries \(\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1) \), there exists a (possibly unbounded) simulator \(\mathsf {Sim} \) such that
3.2 ZAPs for \(\mathsf {NP}\) from Interactive Hidden-Bits Generating Protocols
Here, we construct a \(\textsf {ZAP}\) for \(\mathsf {NP}\) based on an \(\mathsf {IHBG}\) protocol and a \(\textsf {NIZK}\) in the hidden-bits model, where the latter exists unconditionally.
Building Block. Let \(\mathscr {L}\) be an \(\mathsf {NP}\) language and \(\mathcal {R}\) be its corresponding relation.Footnote 5 We construct a \(\textsf {ZAP}\) for \(\mathscr {L}\) based on the following building blocks.
-
\(\varPi _\mathsf {IHBG} = (\mathsf {GenBits}, \mathsf {VerifyBit})\) is an interactive hidden-bits generating protocol. We assume it has public-coin length \({\ell (\uplambda )}\), commitment length \({s(\uplambda )}\), and output length \({m(\uplambda )}\) (i.e., \(\rho \in \{0 , 1\}^m\)). We further assume it satisfies \({\mu (\uplambda )}\)-extractability.
-
\(\varPi _\mathsf {HBM} = (\mathsf {HBM}.\mathsf {Prove}, \mathsf {HBM}.\mathsf {Verify})\) is a \(\textsf {NIZK}\) in the hidden-bits model for \(\mathscr {L}\). We assume the hidden-bits length is \({m(\uplambda )}\) and it is statistically \(\varepsilon _\mathsf {HBM} \)-sound, where \({\varepsilon _\mathsf {HBM} = 2^{-s(\uplambda )} \cdot \mu (\uplambda ) \cdot \mathsf {negl}(\uplambda )}\).Footnote 6
Construction. The construction of a \(\textsf {ZAP}\) for \(\mathscr {L}\) with public-coin length \({\ell '(\uplambda ) = \ell (\uplambda ) + m(\uplambda )}\), denoted as \(\varPi _\textsf {ZAP} \), is described as follows.
-
\(\textsf {ZAP}.\mathsf {Prove} ( r', x, w):\) On input a public-coin \(r' \in \{0 , 1\}^{\ell '}\), a statement x and a witness w, parse it as \((r, \varDelta ) \leftarrow r'\) such that \(r \in \{0 , 1\}^\ell \) and \(\varDelta \in \{0 , 1\}^m\). Then run \({( \sigma , \rho , \{ \pi _{\mathsf {IHBG}, i} \} _{i \in [m]} ) \leftarrow _{r}\mathsf {GenBits} ( 1^\uplambda , m, r )}\) and compute an \(\mathsf {HBM}\) proof \((S, \mathbf {\pi } _\mathsf {HBM}) \leftarrow _{r}\mathsf {HBM}.\mathsf {Prove} ( \mathsf {hb}, x, w )\), where \(\mathsf {hb}:= \rho \oplus \varDelta \). Finally, output \(\mathbf {\pi } _\textsf {ZAP} = (\sigma , S, \rho _S, \{ \pi _{\mathsf {IHBG}, i} \} _{i \in S}, \mathbf {\pi } _\mathsf {HBM})\).
-
\(\textsf {ZAP}.\mathsf {Verify} ( r', x, \mathbf {\pi } _\textsf {ZAP}):\) On input a public-coin \(r' \in \{0 , 1\}^{\ell '}\), a statement x and a proof \(\mathbf {\pi } _\textsf {ZAP} \), parse it as \((r, \varDelta ) \leftarrow r'\) such that \(r \in \{0 , 1\}^\ell \) and \(\varDelta \in \{0 , 1\}^m\), and \((\sigma , S, \rho _S, \{ \pi _{\mathsf {IHBG}, i} \} _{i \in S}, \mathbf {\pi } _\mathsf {HBM}) \leftarrow \mathbf {\pi } _\textsf {ZAP} \). Then, output \(\top \) if \( \mathsf {HBM}.\mathsf {Verify} ( S, \rho _S \oplus \varDelta _S, x, \mathbf {\pi } _\mathsf {HBM}) = \top \) and \(\mathsf {VerifyBit} ( r, \sigma , i, \rho _i, \pi _{\mathsf {IHBG}, i} ) = \top \) for all \(i \in S\). Otherwise, output \(\bot \).
3.3 Security
Correctness of our \(\textsf {ZAP}\) follows from a routine check. Below, we show our \(\textsf {ZAP}\) satisfies non-adaptive computational soundness and adaptive statistical witness indistinguishability in Theorems 14 and 13. Since the proof of witness indistinguishability is similar to those in [LPWW20], we provide the details in the full version of this paper [CKSU21].
Theorem 13
(Statistical Witness Indistinguishability). If \(\varPi _\mathsf {IHBG} \) is statistically hiding and \(\varPi _\mathsf {HBM} \) has perfect zero-knowledge, then \(\varPi _\textsf {ZAP} \) is adaptive statistical witness indistinguishability.
Theorem 14
(Soundness). If \(\varPi _\mathsf {IHBG} \) is \(\mu \)-extractable and \(\varPi _\mathsf {HBM} \) has statistical \(\varepsilon _\mathsf {HBM} \)-soundness, where \({\varepsilon _\mathsf {HBM} = 2^{-s(\uplambda )} \cdot \mu (\uplambda )\cdot \mathsf {negl}(\uplambda )}\), then \(\varPi _\textsf {ZAP} \) has non-adaptive computational soundness.
Proof
Assume there exists a statement \(x \not \in \mathscr {L}\) and a PPT adversary \(\mathcal {A}\) against the non-adaptive computational soundness of \(\varPi _\textsf {ZAP} \) with advantage \(\varepsilon \). Below, we consider the following sequence of games between \(\mathcal {A}\) and a challenger and denote \(\mathsf {E} _i\) as the event that the challenger outputs 1.
-
\(\mathsf {Game} _1\): This is the real soundness game that proceeds as follows: The challenger first samples a public-coin \(r' \leftarrow _{r}\{0 , 1\}^{\ell '}\) and sends it to \(\mathcal {A}\). \(\mathcal {A}\) then outputs a proof \(\mathbf {\pi } ^*_\textsf {ZAP} \) and sends it to the challenger. The challenger outputs 1 if \(\textsf {ZAP}.\mathsf {Verify} ( r', x, \mathbf {\pi } ^*_\textsf {ZAP}) = \top \), and outputs 0 otherwise. By definition \(\Pr [\mathsf {E} _1] = \varepsilon \).
-
\(\mathsf {Game} _2\): This game is identical to the previous game except that the public-coin \(r' \in \{0 , 1\}^{\ell '}\) is sampled differently. Let \(\textsf {SimCoin} \) be the PPT public-coin simulator of the \(\mathsf {IHBG}\) protocol \(\varPi _\mathsf {IHBG} \). Then, in this game, the challenger first runs \((\widetilde{r}, \tau ) \leftarrow _{r}\textsf {SimCoin} (m)\) and samples \(\varDelta \leftarrow _{r}\{0 , 1\}^m\), where \(\widetilde{r} \in \{0 , 1\}^\ell \), and outputs the simulated public-coin \(\widetilde{r} ' := (\widetilde{r}, \varDelta ) \in \{0 , 1\}^{\ell '}\). The rest is defined the same as in the previous game.
-
\(\mathsf {Game} _3\): This game is identical to the previous game except that the challenger checks an additional condition regarding \(\mathbf {\pi } ^*_\textsf {ZAP} \) output by \(\mathcal {A}\). Let \(\mathsf {Open} \) be the efficient deterministic open algorithm of the \(\mathsf {IHBG}\) protocol \(\varPi _\mathsf {IHBG} \). Then, in this game, when \(\mathcal {A}\) outputs \(\mathbf {\pi } ^*_\textsf {ZAP} \), the challenger first parses
$$\begin{aligned} (\sigma ^*, S^*, \rho ^*_{S^*}, \{ \pi ^*_{\mathsf {IHBG}, i} \} _{i \in S^*}, \mathbf {\pi } ^*_\mathsf {HBM}) \leftarrow \mathbf {\pi } ^*_\textsf {ZAP} \end{aligned}$$and runs \(\rho \leftarrow \mathsf {Open} ( \widetilde{r}, \sigma ^*, \tau )\). It then outputs 1 if \(\textsf {ZAP}.\mathsf {Verify} ( r', x, \mathbf {\pi } ^*_\textsf {ZAP}) = \top \), \(\rho \in \{0 , 1\}^m\), and \(\rho ^*_{S^*} = \rho _{S^*}\), and 0 otherwise.
The following Lemmas 15 to 16 establish \({\Pr [\mathsf {E} _1] = \varepsilon \le \mathsf {negl}(\uplambda )}\), thus completing the proof.
Lemma 15
If \(\varPi _\mathsf {IHBG} \) is \(\mu \)-extractable for all PPT adversary, then we have  , hence \({\Pr [\mathsf {E} _2] \ge \varepsilon - \mathsf {negl}(\uplambda )}\).
, hence \({\Pr [\mathsf {E} _2] \ge \varepsilon - \mathsf {negl}(\uplambda )}\).
Proof
The only difference between the two games is how the public-coin is generated. Let us consider the following adversary \(\mathcal {B}\) against the public-coin indistinguishability of \(\varPi _\mathsf {IHBG} \): \(\mathcal {B}\) receives \(r \in \{0 , 1\}^\ell \) from its challenger and samples \(\varDelta \leftarrow _{r}\{0 , 1\}^m\). It then invokes \(\mathcal {A}\) on input \(r' = (r, \varDelta )\), and outputs 1 if the proof \(\mathbf {\pi } _\textsf {ZAP} \) output by \(\mathcal {A}\) satisfies \(\textsf {ZAP}.\mathsf {Verify} ( r', x, \mathbf {\pi } ^*_\textsf {ZAP}) = \top \), and 0 otherwise. Since \(\mathcal {B}\) perfectly simulates \(\mathsf {Game} _1\) (resp. \(\mathsf {Game} _2\)) when \(r \leftarrow _{r}\{0 , 1\}^\ell \) (resp. \((r, \tau ) \leftarrow _{r}\textsf {SimCoin} (m)\)), we have  .
.
Lemma 16
If \(\varPi _\mathsf {IHBG} \) is \(\mu \)-extractable for all PPT adversary, then we have \({\Pr [\mathsf {E} _3] \ge \mu (\uplambda )\cdot (\Pr [\mathsf {E} _2]-\mathsf {negl}(\uplambda ))}\).
Proof
This follows from the \(\mu \)-successful extractability of \(\varPi _\mathsf {IHBG} \). Let us consider the following adversary \(\mathcal {B}\) and distinguisher \(\mathcal {D} \) against the \(\mu \)-successful extractability: \(\mathcal {B}\) on input m and \(\widetilde{r} \) invokes \(\mathcal {A}\) and simulates the challenger in \(\mathsf {Game} _2\). When \(\mathcal {A}\) outputs a forgery \(\mathbf {\pi } ^*_\textsf {ZAP} = (\sigma ^*, S^*, \rho ^*_{S^*}, \{ \pi ^*_{\mathsf {IHBG}, i} \} _{i \in S^*}, \mathbf {\pi } ^*_\mathsf {HBM})\), \(\mathcal {B}\) outputs \((\sigma ^*, S^*, \rho ^*_{S^*}, \{ \pi ^*_{\mathsf {IHBG}, i} \} _{i \in S^*}, \mathsf {st})\), where \(\mathsf {st} = (\widetilde{r}, \mathbf {\pi } ^*_\textsf {ZAP})\); \(\mathcal {D} \) on input \(\mathsf {st} \), checks if \(\textsf {ZAP}.\mathsf {Verify} (\widetilde{r}, x,\mathbf {\pi } ^*_\textsf {ZAP}) = \top \), and outputs 1 if so and outputs 0 otherwise. Observe that the probability \(\mathcal {D} \) outputs 1 is the same as the probability that event \(\mathsf {E} _2\) occurs. Below, we relate the probability that event \(\mathsf {E} _3\) occurs with the left hand side equation of \(\mu \)-successful extractability.
The only difference between \(\mathsf {Game} _2\) and \(\mathsf {Game} _3\) is the check that \(\rho \in \{0 , 1\}^m\) and \(\rho ^*_{S^*} = \rho _{S^*}\). Now, consider a variant \(\mathsf {Game} '_3\) of \(\mathsf {Game} _3\) where, instead of checking \(\rho ^*_{S^*} = \rho _{S^*}\), the challenger checks that for all \(i \in S^*\), it holds that
Let \(\mathsf {E} '_3\) be the event that the challenger outputs 1 in this variant. Observe that if event \(\mathsf {E} '_3\) occurs then so does event \(\mathsf {E} _3\). Indeed, whenever the challenger outputs 1 in \(\mathsf {E} '_3\), it holds in particular that
The latter implies that it can never hold, for any \(i \in S^*\), that \(\rho ^*_i = 1-\rho _i\); hence, since we check \(\rho \in \{0 , 1\}^m\) in both events, whenever \(\mathsf {E} '_3\) happens, it further holds that \(\rho ^*_{S^*} = \rho _{S^*}\) and \(\mathsf {E} _3\) therefore holds as well. In other terms,
Therefore, by applying the \(\mu \)-successful extractability of \(\varPi _\mathsf {IHBG} \) with respect to \(\mathcal {B}\) and \(\mathcal {D} \), since the only difference between \(\mathsf {Game} _2\) and \(\mathsf {Game} '_3\) is the check that \(\rho \in \{0 , 1\}^m\) and \(\mathsf {VerifyBit} (\widetilde{r},\sigma ^*, i, 1-\rho _i, \pi ^*_{\mathsf {IHBG}, i}) = \bot \), we get
which concludes the proof of Lemma 16.
Lemma 17
If \(\varPi _\mathsf {HBM} \) is statistical \(\varepsilon _\mathsf {HBM} \)-sound, then we have \({\Pr [\mathsf {E} _3] \le \mu (\uplambda )}\)\({\cdot \mathsf {negl}(\uplambda )}\).
Proof
Let \((\sigma ^*, S^*, \rho ^*_{S^*}, \{ \pi ^*_{\mathsf {IHBG}, i} \} _{i \in S^*}, \mathbf {\pi } ^*_\mathsf {HBM}) \leftarrow \mathbf {\pi } ^*_\textsf {ZAP} \) be \(\mathcal {A}\)’s output. When the challenger outputs 1 (i.e., event \(\mathsf {E} _3\) occurs), we have \(\rho ^*_{S^*} = \rho _{S^*}\), where \(\rho \leftarrow \mathsf {Open} ( \widetilde{r}, \sigma ^*, \tau )\), and \( \mathsf {HBM}.\mathsf {Verify} ( S^*, \rho ^*_{S^*} \oplus \varDelta _{S^*}, x, \mathbf {\pi } ^*_\mathsf {HBM}) = \top \). For an any \(S^* \subseteq [m]\) and \(\rho _{S^*}\), if \(\varDelta \leftarrow _{r}\{0 , 1\}^m\) is sampled uniformly at random, then \(\rho _{S^*} \oplus \varDelta _{S^*}\) is distributed uniformly random. Then, by soundness of \(\varPi _\mathsf {HBM} \), for a fixed \(\rho _{S^*}\) we have
where the probability is taken over the randomness of \(\varDelta \), \(\mathcal {A}\), and the challenger, conditioned on \(\mathcal {A}\) outputting \(\rho ^*_{S^*}\) that is consistent with \(\rho _{S^*}\). Here, we do not include the condition \(x \not \in \mathscr {L}\) in the above equation since we consider non-adaptive soundness for \(\varPi _\textsf {ZAP} \).
If we fix an arbitrary \((\widetilde{r}, \tau )\), then for any commitment \(\sigma \in \{0 , 1\}^s\) the output of \(\rho \leftarrow \mathsf {Open} ( \widetilde{r}, \sigma , \tau )\) is uniquely defined since \(\mathsf {Open} \) is deterministic. Let us denote the unique \(\rho \) as \(\rho ^\sigma \). Then, taking a union bound over all possible commitments \(\sigma \in \{0 , 1\}^s\), we have

Thus, we conclude \({\Pr [\mathsf {E} _3] \le \mu (\uplambda )\cdot \mathsf {negl}(\uplambda )}\).
Putting everything together, this gives \({\mu (\uplambda )\cdot (\varepsilon -\mathsf {negl}(\uplambda )) \le \mu (\uplambda )\cdot \mathsf {negl}(\uplambda )}\), which implies \({\varepsilon \le \mathsf {negl}(\uplambda )}\). This concludes the proof.
4 The LPWW Language \(\mathscr {L}_\mathsf{LPWW} \)
To instantiate the generic construction of statistical ZAP for NP given in Sect. 3, we will construct an \(\mathsf {IHBG}\) which builds upon the dual-mode hidden-bit generator of Libert, Passelègue, Wee, and Wu [LPWW20]. In this section, we first recall the specific parameterized language considered by [LPWW20] (denoted as the LPWW language \(\mathscr {L}_\mathsf{LPWW} \)). We then introduce some tools related to this parameterized language: a specific type of statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\), which we call \(\mathsf {IHBG} \)-friendly statistical ZAP, and a \(\varSigma \)-protocol for \(\mathscr {L}_\mathsf{LPWW}\).
4.1 Definition
Formally, we denote by \({\mathscr {L}_\mathsf{LPWW}:= \{ \mathscr {L}_{\mathsf{LPWW}, \uplambda } \} _\uplambda }\) the following family of parametrized languages: let \(\mathbb {G}\) be a cyclic group of prime order p. We implicitly fix a vector length \(d \in \mathbb {N}\) and a generator \(g \in \mathbb {G}\) for each security parameter \({\uplambda }\).Footnote 7 Let a set of parameter space \({\varLambda _\uplambda }\) be \((\mathbb {G}^d \backslash \{ \mathbf{1} \} )^2\), where \(\mathbf{1} := g^{\mathbf{0}}\) for \(\mathbf{0} \in \mathbb {Z}_p^{d}\). Then, for any parameter \({{\mathsf {par}} = (g^{\mathbf {v}}, g^{\mathbf {w}}) \in \varLambda _\uplambda }\), we define \({\mathscr {L}_{\mathsf{LPWW}, \uplambda } = \{\mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \}_{{\mathsf {par}} \in \varLambda _\uplambda }}\) such that \(\mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \) is the following parametrized language:
Let \(\mathsf {Col} (\mathbb {G}^d) \subset \varLambda _\uplambda \) denote the set of elements of the form \((g^{\mathbf {v}}, g^{\alpha \cdot \mathbf {v}})\) for some \(\mathbf {v}\ne \mathbf{0}\) and \(\alpha \in \mathbb {Z}^*_p\), that is, the exponents form colinear vectors over \((\mathbb {Z}_p)^d\). Observe that for any \({\mathsf {par}} \in \mathsf {Col} (\mathbb {G}^d)\), \(\mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \) is a non-trivial Diffie-Hellman-style language (hence, \(\mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \) is a sparse subset of \({\varLambda _\uplambda }\)); however, for any \({{\mathsf {par}} \in \varLambda _\uplambda \backslash \mathsf {Col} (\mathbb {G}^d)}\), \(\mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \) is actually equal to \(\mathbb {G}^2\) (hence, \(\mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \) is a trivial language). Below, we may omit the security parameter and use the shorthand \(\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\) when the meaning is clear.
4.2 \(\mathsf {IHBG}\)-Friendly Statistical ZAPs for the LPWW Language \(\mathscr {L}_\mathsf{LPWW} \)
Looking ahead, our construction of \(\mathsf {IHBG}\) in Sect. 5 will rely at its core on an adaptively secure statistical ZAP for the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\). More precisely, the statistical ZAP which we will use in our construction satisfies a variant of the standard notion of adaptive computational soundness (which we defined for a single language in Sect. 2): we require adaptive computational soundness to hold with respect to parameters \({\mathsf {par}} \) sampled uniformly from \(\mathsf {Col} (\mathbb {G}^d) \subset \varLambda \) (recall that \(\mathsf {Col} (\mathbb {G}^d)\) is the subset of parameters such that \(\mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \) is nontrivial). In contrast, adaptive statistical witness indistinguishability must hold even for adversarially chosen parameters \({\mathsf {par}} \in \varLambda \) (hence, in a sense, WI is doubly-adaptive: with respect to the statement, and with respect to the language parameters). We call a statistical ZAP with these properties an \(\mathsf {IHBG}\) -friendly statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\). We provide a formal definition below.
Definition. We formally introduce the notion of \(\mathsf {IHBG}\)-friendly statistical ZAP for the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} \).
Definition 18
( \(\mathsf {IHBG}\) -Friendly Statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\) ). Let \({\varLambda _\uplambda = (\mathbb {G}^d \backslash \{ \mathbf{1} \} )^2}\) be the parameter space for any \({\uplambda \in \mathbb N}\) and consider the family of parameterized \(\mathsf {NP}\) languages \({\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_{\mathsf{LPWW}, \uplambda } \} _\uplambda = \{ \{ \mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda _\uplambda } \} _\uplambda }\), with associated witness relation \({\mathcal {R} _\mathsf{LPWW} = \{ \mathcal {R}_{\mathsf{LPWW}, \uplambda } \} _\uplambda = \{ \{ \mathcal {R}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda _\uplambda } \} _\uplambda }\). Then, an \(\mathsf {IHBG} \)-friendly \(\textsf {ZAP}\) system \(\varPi _\textsf {ZAP} \) for \(\mathscr {L}_\mathsf{LPWW} \) with with public-coin length \({\ell (\uplambda )}\) is a tuple of PPT algorithms \((\mathsf {Prove},\mathsf {Verify})\) defined as follows.
-
\(\mathsf {Prove} ({\mathsf {par}}, r, x, w ) \rightarrow \mathbf {\pi }:\) The proving algorithm is given the parameters \({{\mathsf {par}} \in \varLambda _\uplambda }\), the public-coin \(r \in \{0 , 1\}^\ell \), a statement x, and a witness w, and outputs a proof \(\mathbf {\pi } \).
-
\(\mathsf {Verify} ({\mathsf {par}}, r, x, \mathbf {\pi }) \rightarrow \top \ \mathbf{or } \ \bot :\) The verification algorithm is given the parameters \({{\mathsf {par}} \in \varLambda _\uplambda }\), the public-coin \(r \in \{0 , 1\}^\ell \), a statement x, and a proof \(\mathbf {\pi } \), and outputs \(\top \) for acceptance or \(\bot \) for rejection.
We additionally require the following properties to hold.
Correctness: For any \({\uplambda \in \mathbb N}\), \(r \in \{0 , 1\}^\ell \), \({{\mathsf {par}} \in \varLambda _\uplambda }\), and \((x, w) \in \mathcal {R}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \), we have
(Adaptive) Computational \(\varepsilon _\mathsf {sound} \)-Soundness w.r.t. Colinear Parameters: For any \({\uplambda \in \mathbb N}\) and PPT adversary \(\mathcal {A}\), we have
(Doubly-Adaptive) Statistical Witness Indistinguishability: For any \({\uplambda \in \mathbb N}\) and unbounded adversary \(\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)\), we have
Building \(\mathsf {IHBG}\) -Friendly Statistical ZAPs for \(\mathscr {L}_\mathsf{LPWW}\) . In Sect. 6, we will provide two constructions of an \(\mathsf {IHBG}\)-friendly statistical ZAPs for \(\mathscr {L}_\mathsf{LPWW}\), one in pairing groups (Theorem 25), and one in pairing-free groups (Theorem 28). Both constructions are obtained by compiling the \(\varSigma \)-protocol for \(\mathscr {L}_\mathsf{LPWW}\) described in Sect. 4.3 into an \(\mathsf {IHBG}\)-friendly statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\). Below, we give an overview of the main lemmas regarding our two constructions whose proofs are provided in Sect. 6.
Pairing-Based Construction. The pairing-based construction builds upon the Couteau-Hartmann compiler from [CH20], which relies on the hardness of the kernel Diffie-Hellman assumption in a group \(\mathbb {G}_2\) (more generally, it can be based on the kernel \(k\text {-}\mathsf {Lin} \) assumption in \(\mathbb {G}_2\) for any k), a standard search assumption (which is implied in particular by DDH in \(\mathbb {G}_2\)) introduced in [MRV15] and used in several works on pairing-based NIZKs, e.g. [KW15].
Lemma 19
Let \((\mathbb {G}_1, \mathbb {G}_2)\) be bilinear-map groups equipped with an asymmetric pairing (implicitly parameterized by the security parameter \({\uplambda }\)). There exists an \(\mathsf {IHBG}\)-friendly adaptive statistical ZAP for the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} \) over \(\mathbb {G}_1\) which satisfies adaptive computational \(\varepsilon _\mathsf {sound} \)-soundness w.r.t. colinear parameters, and doubly-adaptive statistical witness indistinguishability, assuming the explicit \(\varepsilon _\mathsf {sound} \)-hardness of the kernel Diffie-Hellman assumption in \(\mathbb {G}_2\).
Pairing-Free Construction. The pairing-free construction builds upon the compiler of [CKU20]. The work of [CKU20] build a correlation intractable hash function under the \({2^{-3\uplambda /4}}\)-\(\mathsf {OW\text {-}KDM}\) security of ElGamal, which suffices to compile the above \(\varSigma \)-protocol into a statistical ZAP. We refine their approach and achieve a similar result under a weaker assumption, by managing to reduce the constant 3/4 to 1/2, that is, rely on the \({2^{-\uplambda /2}}\)-\(\mathsf {OW\text {-}KDM}\) security of ElGamal. We note that the best known attack against this falsifiable search assumption succeeds with probability \({\mathsf {poly} (\uplambda )/2^\uplambda }\).
Lemma 20
Let \(\mathbb {G}\) be a group of order p such that \(\lambda \approx 2\lceil \log p\rceil ^2\). There exists an \(\mathsf {IHBG}\)-friendly adaptive statistical ZAP for the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} \) over \(\mathbb {G}\) which satisfies adaptive computational \(\varepsilon _\mathsf {sound} \)-soundness w.r.t. colinear parameters for any \(\varepsilon _\mathsf {sound} = 2^{-o(\lceil \log p\rceil ^2)}\), and doubly-adaptive statistical witness indistinguishability, assuming the \({2^{-\uplambda /2}}\)-\(\mathsf {OW\text {-}KDM}\) hardness of ElGamal over another group \(\tilde{\mathbb {G}} \) of size \({|\tilde{\mathbb {G}} | \approx 2^\uplambda }\).
4.3 \(\varSigma \)-protocols for the LPWW Language \(\mathscr {L}_\mathsf{LPWW}\)
To construct our \(\mathsf {IHBG}\)-friendly statistical ZAPs for \(\mathscr {L}_\mathsf{LPWW}\), we rely on a \(\varSigma \)-protocol for the family of parameterized language \(\mathscr {L}_\mathsf{LPWW}\). To this end, we need to first extend the standard definition of \(\varSigma \)-protocols for a single language to a family of parameterized languages. As the definition is a natural extension of the standard definition, we provide the detail in the full version of this paper [CKSU21].
We now provide a \(\varSigma \)-protocol for \(\mathscr {L}_\mathsf{LPWW}\) as follows. Fix some parameters \({\mathsf {par}} = (g^{\mathbf {v}}, g^{\mathbf {w}}) \in \varLambda = (\mathbb {G}^d \backslash \{ \mathbf{1} \} )^2\) (implicitly parameterized by the security parameter \({\uplambda }\)). To match with the notations which we will use later when building an \(\mathsf {IHBG}\), we denote the dimension d in \(\mathscr {L}_{\mathsf{LPWW}}^{\mathsf {par}} \) by \(m+1\). We consider a statement  and let \(\mathbf {y}\in \mathbb {Z}_p^{m + 1}\) be the prover witness (i.e., \(\mathbf {y}\) is any vector over \(\mathbb {Z}_p^{m+1}\) such that \(\mathbf {y}^\top \mathbf {v}= \hat{x}\) and \(\mathbf {y}^\top \mathbf {w}= \hat{y}\)). Let \(n \in \mathbb {N}\) be any positive integer. Then, a \(\varSigma \)-protocol for \(\mathscr {L}_{\mathsf{LPWW}} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\) is provided in Fig. 1. Correctness can be checked by routine calculation. Below, we prove prefect witness indistinguishability and adaptive soundness. Due to page limitation, the proof is provided in the full version of this paper [CKSU21].
and let \(\mathbf {y}\in \mathbb {Z}_p^{m + 1}\) be the prover witness (i.e., \(\mathbf {y}\) is any vector over \(\mathbb {Z}_p^{m+1}\) such that \(\mathbf {y}^\top \mathbf {v}= \hat{x}\) and \(\mathbf {y}^\top \mathbf {w}= \hat{y}\)). Let \(n \in \mathbb {N}\) be any positive integer. Then, a \(\varSigma \)-protocol for \(\mathscr {L}_{\mathsf{LPWW}} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\) is provided in Fig. 1. Correctness can be checked by routine calculation. Below, we prove prefect witness indistinguishability and adaptive soundness. Due to page limitation, the proof is provided in the full version of this paper [CKSU21].
Lemma 21
(Perfect Witness Indistinguishability). The \(\mathsf {IHBG}\)-friendly \(\varSigma \)-protocol for the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\) in Fig. 1 satisfies perfect witness indistinguishability.
Lemma 22
(Adaptive Soundness). The \(\mathsf {IHBG}\)-friendly \(\varSigma \)-protocol for the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\) in Fig. 1 satisfies adaptive \((\frac{1}{p-1})^{n-1}\)-soundness.
5 Interactive Hidden-Bits Generating Protocols from the Explicit Hardness of \(\textsf {DDH}\) and an \(\mathsf {IHBG}\)-Friendly Statistical \(\textsf {ZAPs}\) for \(\mathscr {L}_\mathsf{LPWW}\)
In this section, we construct an \(\mathsf {IHBG}\) protocol based on explicit \(\mu \)-hardness of the \(\textsf {DDH}\) assumption (over a pairing-free group, for a negligible function \(\mu \) arbitrarily close to an inverse polynomial function) and an \(\mathsf {IHBG}\)-friendly statistical \(\textsf {ZAP}\) for the language \(\mathscr {L}_\mathsf{LPWW} \), defined in Sect. 4, which is naturally induced from the (non-interactive) hidden-bits generator of Libert et al. [LPWW20].
5.1 Constructing the \(\mathsf {IHBG}\) Protocol
Building Block. Our construction is parametrized by \(\lambda \) and \(\mu (\lambda )\), and relies on the following building blocks:
-
\({\mathcal {H} = \{ \mathcal {H}_\uplambda \} _\uplambda = \{ \{ H: \mathbb {G}\mapsto \{0 , 1\} \} _H \} _\uplambda }\) is a family of universal hash functions with description size of at most \(O(\log _2 p)\) bits, where \(\mathbb {G}\) and p are implicitly parameterized by the security parameter.
-
\(\varPi _\textsf {ZAP} = (\textsf {ZAP}.\mathsf {Prove}, \textsf {ZAP}.\mathsf {Verify})\) is an \(\mathsf {IHBG}\)-friendly \(\textsf {ZAP}\) for the parametrized family of languages \({\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_{\mathsf{LPWW}, \uplambda } \} _\uplambda = \{ \{ \mathscr {L}_{\mathsf{LPWW}, \uplambda } ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda _\uplambda } \} _\uplambda }\) with public-coin length \({\ell '(\uplambda )}\), satisfying adaptive computational \(\epsilon _\mathsf {sound} \)-soundness w.r.t. colinear parameters for \({\epsilon _\mathsf {sound} = \frac{\mu (\lambda )}{m(\uplambda )}}\) and doubly-adaptive statistical witness indistinguishability. Here, we set the vector length parameter \({d(\uplambda )}\) in \(\mathscr {L}_{\mathsf{LPWW}, \uplambda }\) to \({m(\uplambda ) + 1}\), where \(n{m(\uplambda )}\) is the polynomial output bit length of the \(\mathsf {IHBG}\) protocol defined below.
Construction. The construction of an \(\mathsf {IHBG}\) protocol denoted as \(\varPi _\mathsf {IHBG} \) is described as follows. The commitment length is at most \(s(\lambda ) = \lceil \log _2 p\rceil +O(\log _2 p)\) where \({(\mathbb {G}, p) \leftarrow \textsf {DHGen} (1^\uplambda )}\) (note that \(\textsf {DHGen} \) guarantees in particular \({p>\uplambda ^{\omega (1)}}\), which is needed to use the uniformity property of H). The output bit length \({m(\uplambda )}\) is an arbitrary large enough fixed polynomial \(\mathsf {poly} (\uplambda )\), and the public-coin length \(\ell (\uplambda )\) is \(m \cdot \ell ' + (m + 2) \cdot \lceil \log _2 p \rceil \). We rely on one more parameter \(\nu (\uplambda )\) and require the parameters to satisfy the following conditions:
-
In order to prove statistical hiding, \(m(\uplambda )\cdot \mu (\uplambda )\) must be negligible; this holds by setting \(\mu (\uplambda )\) to be a negligible function.
-
For technical reasons in the hybrid games, we need a negligible gap between \(\nu \) and \(\mu \); that is, \(\nu (\uplambda )\) is a negligible function satisfying \(\mu (\uplambda ) = \nu (\uplambda ) \cdot \mathsf {negl}(\uplambda )\).
-
We also need \(1/\mu (\uplambda )\) (and hence \(1/\nu (\uplambda )\)) to be small compared to p (otherwise, assuming explicit \(\mu \)-hardness of \(\textsf {DDH}\) over \(\mathbb {G}\) does not make sense: a polynomial time attack with O(1/p) advantage against \(\textsf {DDH}\) trivially exists). In particular, \(\mu (\uplambda )\) can be set as an arbitrary close to an inverse polynomial, i.e., \(\uplambda ^{-\omega (1)}\). Here, since \(1/\nu (\lambda )\) is small compared to p, any element \(z \in [ 1/\nu (\uplambda ) ]\) can be seen as an element of \(\mathbb {Z}_p\).
We proceed with the description of the scheme. In the following we may omit the dependency on \(\uplambda \) for better readability when the context is clear.
-
\(\mathsf {GenBits} (1^\uplambda , m, r):\) On input the security parameter \(1^\uplambda \), bit length m, and a public-coin \(r \in \{0 , 1\}^\ell \), parse \(((r_{\textsf {ZAP}, i})_{i \in [m]}, g, g^{\mathbf {M}}) \leftarrow r\), where \(g \in \mathbb {G}\) and \(\mathbf {M}:= (\mathbf {v}| \mathbf {w}_1 | \ldots | \mathbf {w}_m) \in \mathbb {Z}_p^{(m+1)\times (m+1)}\).Footnote 8 Then sample \(z\leftarrow _{r}[ 1/\nu ]\), and compute \(g^{\mathbf {M}-z\cdot \mathbf {I}_{m+1}}\), where we denote \(\mathbf {M}' := \mathbf {M}- z\cdot \mathbf {I}_{m + 1} = ({\mathbf {v}'} |{\mathbf {w}'_1} | \cdots | {\mathbf {w}'_m}) \in \mathbb {Z}_p^{(m+1)\times (m+1)}\). Further sample a random hash function \(H \leftarrow _{r}\mathcal {H}\) and a uniformly random seed \(\mathbf {y}\leftarrow _{r}\mathbb {Z}_p^{m + 1}\), and compute a commitment \(g^s \leftarrow g^{\mathbf {y}^\top \mathbf {v}'}\), openings \(g^{u_i} \leftarrow g^{\mathbf {y}^\top \mathbf {w}'_i}\), and the hidden bits \(\rho _i \leftarrow H(g^{u_i})\) for all \(i \in [m]\). For each \(i \in [m]\), set the language parameter \({\mathsf {par}} _i := (g^{\mathbf {v}'}, g^{\mathbf {w}'_i})\), statement \(x_i := (g^s, g^{u_i})\), and witness \(w := \mathbf {y}\) for membership to the parametrized language \(\mathscr {L}_\mathsf{LPWW} ^{{\mathsf {par}} _i}\), and compute \(\mathbf {\pi } _{\textsf {ZAP}, i} \leftarrow _{r}\textsf {ZAP}.\mathsf {Prove} ({\mathsf {par}} _i, r_{\textsf {ZAP}, i}, x_i, w )\) and set \(\pi _i=(g^{u_i},\mathbf {\pi } _{\textsf {ZAP}, i})\). Finally, output the commitment \(\sigma := (H, g^s,z) \in \mathcal {H} \times \mathbb {G}\times [ 1/\nu ]\), string \(\rho := (\rho _i)_{i \in [m]} \in \{0 , 1\}^m\) and the set of proofs \( \{ \pi _i \} _{i \in [m]}\).
-
\(\mathsf {VerifyBit} ( r, \sigma , i, \rho _i, \pi _i ):\) Parse \(((r_{\textsf {ZAP}, i})_{i \in [m]}, g, g^{\mathbf {M}}) \leftarrow r\), \((H, g^s, z) \leftarrow \sigma \), \((g^{u_i},\mathbf {\pi } _{\textsf {ZAP}, i}) \leftarrow \pi _i\), and compute \(g^{\mathbf {M}'}\leftarrow g^{\mathbf {M}-z\mathbf {I}_{m+1}}\). Then, set the language parameter as \({\mathsf {par}} _i := (g^{\mathbf {v}'}, g^{\mathbf {w}'_i})\) and the statement as \(x_i := (g^s, g^{u_i})\). Check \(\rho _i = H(g^{u_i})\) and \(\textsf {ZAP}.\mathsf {Verify} ({\mathsf {par}} _i, r_{\textsf {ZAP}, i}, x_i, \mathbf {\pi } _{\textsf {ZAP}, i})=\top \). Output \(\top \) if both check passes and otherwise output \(\bot \).
Succinctness. The length of the commitment \(\sigma =(H,g^s,z)\) only depends on the security parameter, and in particular, independent of m. This is because \(g^s\) requires \(\lceil \log _2 p\rceil \) bits, z requires \(\lceil \log _2 (1/\nu (\lambda ))\rceil \le \lceil \log _2 p\rceil \) and the description of the universal hash function H requires at most \(O( \log _2 p)\) bits.
5.2 Security
Correctness of our \(\mathsf {IHBG}\) protocol can be verified by a routine check. Below, we show our \(\mathsf {IHBG}\) protocol satisfies extractability and statistical hiding in the following Theorems 23 and 24. Due to page limitations, the proof is provided in the full version of this paper [CKSU21], and we only give a proof sketch in the main body.
Theorem 23
(Extractability). Consider \(\mu (\lambda )\) an efficiently computable function, \(\varepsilon _\mathsf {sound} =\frac{\nu (\lambda )}{m(\uplambda )}\), and a negligible function \(\nu (\uplambda )\) such that \(\mu (\lambda )=\nu (\lambda )\cdot \mathsf {negl}(\lambda )\). If the \(\mathsf {IHBG}\)-friendly \(\textsf {ZAP}\) for \(\mathscr {L}_\mathsf{LPWW} \) is adaptively computational \(\varepsilon _\mathsf {sound} \)-sound w.r.t. colinear parameters and the DDH assumption is \(\mu \)-explicitly hard, then \(\mathsf {IHBG} \) satisfies \(\nu \)-extractability.
Proof Sketch. Recall that the hidden-bits generator receives \(g^{\mathbf {M}}\) and m first flows \((r_{\textsf {ZAP}, i})_{i \in [m]}\) of the underlying \(\textsf {ZAP} \). Verification is performed with respect to a matrix \(\mathbf {M}'\), which the verifier computes as \(g^{\mathbf {M}'}\leftarrow g^{\mathbf {M}-z\mathbf {I}_{m+1}}\) (where the value z is part of the commitment \(\sigma \) outputted by the hidden-bits generator). Intuitively, what this means is that a malicious hidden-bits generator can only influence \(g^{\mathbf {M}'}\) with its choice for z. In our proof, the \(\textsf {SimCoin} \) simulator will randomly pick \(\tilde{z}\) (its guess for z), generate a matrix \(\mathbf {M}''\) of rank 1 and compute \(g^{\mathbf {M}}:=g^{\mathbf {M}''+\tilde{z}\cdot \mathbf {I}_{m+1}}\).
Public-coin indistinguishability follows from polynomial DDH; when encoded in the exponent, rank 1 matrices are indistinguishable from full-rank ones.
When guessing z is successful (which happens with probability \(\nu \)), the matrix \(\mathbf {M}'\) will be equal to \(\mathbf {M}''\) (of rank 1), and the commitment uniquely determines the hidden-bits string \(\rho \) (moreover, we show that there exists an efficient, deterministic algorithm \(\mathsf {Open} \) which extracts \(\rho \)).
Extractability requires more work, because we need to remove the problematic extra checks that \(\mathsf {Open} \) succeeds and that \(\mathsf {VerifyBit} (\widetilde{r}, \sigma , i, 1-\rho _i, \pi _i) = \bot \) for all \(i\in S\). The probability we end up with should not be too far from our starting point (see extractability in Definition 12). In our hybrids, we first switch the real coins to simulated ones. Then, for simulated coins we know that the underlying \(\textsf {ZAP} \) satisfies soundness - so we can remove the checks \(\mathsf {VerifyBit} (\widetilde{r}, \sigma , i, 1-\rho _i, \pi _i) = \bot \) by relying on the soundness of the underlying \(\textsf {ZAP} \). The extra check that opening works is removed by a statistical argument. Finally, we revert back from simulated coins to real ones. Since all these steps are conditioned on our initial guess of z being correct, we require the explicit hardness of DDH and polynomial DDH does not suffice. For a formal proof, please see the full version of this paper [CKSU21].
Theorem 24
(Statistical Hiding). If the \(\mathsf {IHBG}\)-friendly \(\textsf {ZAP}\) for \(\mathscr {L}_\mathsf{LPWW} \) is doubly-adaptive statistically witness indistinguishable, the hash function family \(\mathcal {H}\) is universal, and \(\nu (\lambda )\) is negligible, then \(\varPi _\mathsf {IHBG} \) is statistically hiding.
6 \(\mathsf {IHBG}\)-Friendly Statistical ZAPs for \(\mathscr {L}_\mathsf{LPWW}\)
In this section, we provide two instantiations for the \(\mathsf {IHBG}\)-friendly statistical ZAP used in the construction of \(\mathsf {IHBG}\) from the previous section, one in pairing groups, and one in pairing-free groups. These constructions and their analysis constitute the proofs of Lemma 19 and Lemma 20.
6.1 First Construction: A Statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\) in Pairing Groups
For this construction, we employ the Couteau-Hartmann compiler from [CH20]. The high-level idea of the compiler is very simple: assume that the family of parametrized languages \(\mathscr {L}_\mathsf{LPWW} = \{ \mathscr {L}_\mathsf{LPWW} ^{\mathsf {par}} \} _{{\mathsf {par}} \in \varLambda }\) is defined over a group \(\mathbb {G}_1\), such that there exists another group \(\mathbb {G}_2\) and an asymmetric pairing from \(\mathbb {G}_1\times \mathbb {G}_2\) to a target group \(\mathbb {G}_{\mathsf {T}}\). Let \(g_2 \in \mathbb {G}_2\) be a generator of \(\mathbb {G}_2\). Then, the Couteau-Hartmann compiler converts a \(\varSigma \)-protocol with linear answer for the target language into a statistical ZAP by parsing the random message of the verifier as a pair \((g_2,g_2^e)\), where e is seen as some random verifier challenge for the \(\varSigma \)-protocol. The compiled ZAP is constructed by computing the first flow of the \(\varSigma \)-protocol normally, and the last flow (which is a linear function of the challenge e with coefficients known to the prover) “in the exponent of \(g_2\)” using \((g_2, g_2^e)\). The verification step is carried out using a pairing. Below, we adapt this compiler to the family of parameterized languages \(\mathscr {L}_\mathsf{LPWW}\) and prove its security.
Construction. Let \((\mathbb {G}_1,\mathbb {G}_2)\) be elliptic curves equipped with an asymmetric pairing \(\bullet : \mathbb {G}_1 \times \mathbb {G}_e \mapsto \mathbb {G}_{\mathsf {T}}\), where \(\mathbb {G}_1\) and \(\mathbb {G}_2\) both have prime order p. We extend the definition of \(\bullet \) to vectors in the conventional manner. Let \(g_1\) be a generator of \(\mathbb {G}_1\) and d be a vector length parameter. Let \({\mathsf {par}} = (\mathbf{g}, \mathbf{h}) \in \varLambda = (\mathbb {G}_1^d \backslash \{ \mathbf{1} \} )^2\) be the language parameters. We will rely on the \(\varSigma \)-protocol from Sect. 4.3 with repetition parameter \(n=1\). In particular, we do not require to rely on the adaptive soundness of the \(\varSigma \)-protocol (i.e., Lemma 22) to achieve adaptive soundness (looking ahead, higher value of n (i.e., adaptive soundness of the \(\varSigma \)-protocol) will only be useful in our pairing-free instantiation). The construction of a \(\textsf {ZAP}\) for \(\mathscr {L}_{\mathsf{LPWW}}\) over \(\mathbb {G}_1\) with public coin length \(\ell = 2\lceil \log |\mathbb {G}_2|\rceil \), denoted as \(\varPi _\textsf {ZAP} \), is described as follows.
-
\(\textsf {ZAP}.\mathsf {Prove} ({\mathsf {par}}, r',x,w):\) On input parameters \({\mathsf {par}} = (\mathbf{g}, \mathbf{h})\in \varLambda \), a public coin \(r \in \{0 , 1\}^{\ell }\), a statement
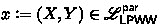 and a witness
and a witness 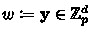 such that \((X,Y) = ((\mathbf{g}^\top )^\mathbf {y}, (\mathbf{h}^\top )^\mathbf {y})\), parse r as \((g_2, g_2^{e}) \in \mathbb {G}_2^2\) and proceed as follows:
such that \((X,Y) = ((\mathbf{g}^\top )^\mathbf {y}, (\mathbf{h}^\top )^\mathbf {y})\), parse r as \((g_2, g_2^{e}) \in \mathbb {G}_2^2\) and proceed as follows:
-
Pick \(\mathbf {z}\leftarrow _{r}\mathbb {Z}_p^d\) and set \((R, S) \leftarrow ((\mathbf{g}^\top )^{\mathbf {z}},(\mathbf{h}^\top )^{\mathbf {z}})\). Note that this corresponds to computing the first flow of the prover in the \(\varSigma \)-protocol from Sect. 4.3, with \(n = 1\).
-
Set \(g_2^{\mathbf {d}} \leftarrow (g_2^{e})^{\mathbf {y}}\cdot g_2^{\mathbf {z}}\). Note that this corresponds to computing the last flow of the prover in the \(\varSigma \)-protocol from Sect. 4.3, in the exponent domain of\(\mathbb {G}_2\).
-
Output \(\mathbf {\pi } _\textsf {ZAP} = (R,S, g_2^{\mathbf {d}})\).
-
\(\textsf {ZAP}.\mathsf {Verify} ({\mathsf {par}}, r,x,\mathbf {\pi } _\textsf {ZAP}):\) On input parameters \({\mathsf {par}} = (\mathbf{g}, \mathbf{h}) \in \varLambda \), a public coin \(r \in \{0 , 1\}^{\ell }\), a statement \(x = (X,Y)\), and a proof \(\mathbf {\pi } _\textsf {ZAP} \), parse \(\mathbf {\pi } _\textsf {ZAP} \) as \((R,S, g_2^{\mathbf {d}})\), and parse r as \((g_2, g_2^{e}) \in \mathbb {G}_2^2\). Check that \(\mathbf{g}^\top \bullet g_2^{\mathbf {d}} = (X \bullet g_2^{e}) \cdot (R \bullet g_2)\) and \(\mathbf{h}^\top \bullet g_2^{\mathbf {d}} = (Y \bullet g_2^{e}) \cdot (S \bullet g_2)\). Note that this corresponds to executing the verification procedure of the \(\varSigma \)-protocol from Sect. 4.3 (with \(n=1\)), but using the pairings to emulate the exponentiations of \((\mathbf{g}^\top , \mathbf{h}^\top )\) and (X, Y) (which are all over \(\mathbb {G}_1\)) by \(\mathbf {d}\) and e respectively, since the latter are now only known in the exponent of \(g_2\).
We prove Lemma 19. Namely, we show our \(\mathsf {IHBG}\)-friendly ZAP for \(\mathscr {L}_\mathsf{LPWW}\) satisfies doubly-adaptive perfect witness indistinguishability and adaptive computational \(\varepsilon _\mathsf {sound} \)-soundness w.r.t. colinear parameters. Due to page limitations, we provide them in the full version of this paper [CKSU21]. Plugging this \(\mathsf {IHBG}\)-friendly adaptive statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\) into the construction of \(\mathsf {IHBG}\) of Sect. 5 and combining it with the construction of statistical ZAP for \(\mathsf {NP}\) from any \(\mathsf {IHBG}\) from Sect. 3, we get our first main theorem:
Theorem 25
(Statistical ZAPs in Pairing Groups). Assume that the explicit \(\mu \)-hardness of the DDH assumption holds in a group \(\mathbb {G}_1\), and the explicit \((\mu /m)\)-hardness of the kernel Diffie-Hellman assumption holds in a group \(\mathbb {G}_2\), where \((\mathbb {G}_1,\mathbb {G}_2)\) are groups equipped with a bilinear pairing, m is the output length of the \(\mathsf {IHBG} \) protocol, and for any negligible function \(\mu \) (which can be arbitrarily close to an inverse polynomial function). Then there exists an adaptive statistically witness indistinguishable ZAP for \(\mathsf {NP}\) with non-adaptive computational soundness.
6.2 Second Construction: A Statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\) in Pairing-Free Groups
A Correlation-Intractable Hash Function for\(\mathcal {R}_{\mathbf {\mathsf{{LPWW}}}}\). Let \(\lambda \) be the security parameter. We consider a group \(\tilde{\mathbb {G}} \) of order \(q(\lambda )\) with \(\lceil \log q\rceil \approx \lambda \). Let \(\mathsf {Trunc}: \tilde{\mathbb {G}} \mapsto \{0,1\} ^{\lambda /2}\) be the function which, on input a group element \(\tilde{G} \in \tilde{\mathbb {G}} \), parses it as a \(\lceil \log q\rceil \)-bit string and returns the first \(\lambda /2\) bits of its input. We consider the following hash function \(\mathsf {H}: \tilde{\mathbb {G}} ^2 \times \mathbb {Z}_q \mapsto \{0,1\} ^{\lambda /2}\) based on secret key ElGamal:
-
Sampling the key: sample \((\tilde{G},k,m) \leftarrow _{r}\tilde{\mathbb {G}} \times \mathbb {Z}_q^2\) and set the hash key as \(\tilde{\mathbf {C}} \leftarrow _{r}\mathsf {Enc} _{\tilde{G}}(k,m)\). Note that the key distribution is exactly the uniform distribution over \(\tilde{\mathbb {G}} ^2\) due to universality (see Definition 5).
-
Evaluating \(\mathsf {H} (\tilde{\mathbf {C}},\cdot ):\) \(\mathsf {H} (\tilde{\mathbf {C}},x) = \mathsf {Trunc} (\mathsf {HalfDec} (x, \tilde{\mathbf {C}}))\).
Correlation-Intractability of\(\mathsf {H} \). Fix a parameter \(n\in \mathbb {N}\). Consider a group \(\mathbb {G}\) of order \(p(\lambda )\) with \(\lceil \log p\rceil \approx \lambda /2n\). Fix a parameter \(t \in \mathbb {Z}_p^*\) and define the set of parameters \(\varLambda ^t := \{ (g^\mathbf {v}, g^{t \cdot \mathbf {v}}) \} _{\mathbf {v}\in \mathbb {Z}_p^{m + 1} \backslash \{ \mathbf {0} \} } \subset \varLambda = (\mathbb {G}^d \backslash \{ \mathbf{1} \} )^2\) implicitly parameterized by the security parameter \(\uplambda \). Define \(\mathcal {R}^\mathsf{sparse}_\mathsf{LPWW} = \{ \mathcal {R}^\mathsf{sparse}_{\mathsf {LPWW}, \mathrm {t}} \} _{t \in \mathbb {Z}^*_p}\) to be the natural sparse relation associated to the \(\varSigma \)-protocol of Sect. 4.3 for the parametrized family of languages \(\mathscr {L}_\mathsf{LPWW} \), with repetition parameter n. That is,
where \(\alpha := \{ ( R_i, S_i ) \} _{i \in [n]}\), \(\beta := \{ e_i \} _{i \in [n]}\), and \(\gamma := \{ \mathbf {d}_i \} _{i \in [n]} \) in Fig. 1. Here, the above relation can also be described alternatively using the following (inefficient) randomized function:
Given this function, it is straightforward (albeit tedious) to check that the relation rewrites to
The following is the main contribution of this section. Due to page limitation, we provide the proof of the following theorem in the full version of this paper [CKSU21].
Theorem 26
Assume that ElGamal satisfies \(2^{-\lambda /2}\)-\(\mathsf {OW\text {-}KDM}\) security with respect to efficient functions. Let \(\mathcal {R}^\mathsf{sparse}_\mathsf{LPWW} = \{ \mathcal {R}^\mathsf{sparse}_\mathsf{LPWW, \uplambda } \} _{\uplambda } = \{ \{ \mathcal {R}^\mathsf{sparse}_{\mathsf {LPWW}, \uplambda , t} \} _{t \in \mathbb {Z}^*_p} \} _{\uplambda }\) be the family of parameterized sparse relation induced by \(\mathscr {L}_\mathsf{LPWW} \). Then the hash family \(\mathcal {H} = \{ \mathsf {H}: \tilde{\mathbb {G}} ^2 \times \mathbb {Z}_q \mapsto \{0,1\} ^{\lambda /2} \} _\lambda \) satisfies \((\varepsilon ,\mathcal {R}^\mathsf{sparse}_\mathsf{LPWW})\)-correlation intractability for every negligible function \(\varepsilon \) satisfying \(\varepsilon (\lambda ) = 2^{-o(\lambda )}\).
Remark 27
Theorem 26 should be compared to Theorem 24 from [CKU20]: in [CKU20], the authors restricted their attention to a \(\varSigma \)-protocol with only two parallel repetitions (the language we consider is also different, but this does not matter for the conclusion – both the DDH language from [CKU20] and the LPWW language could be used in their construction). As a consequence, they could only build a correlation-intractable hash function for their relation from the \(2^{-3\lambda /4}\)-\(\mathsf {OW\text {-}KDM} \) hardness of ElGamal. By considering the general case of n parallel repetitions, and adjusting n appropriately, we significantly strenghthen their conclusion and manage to rely on the \(2^{-\lambda /2}\)-\(\mathsf {OW\text {-}KDM} \) hardness of ElGamal. By Definition 6, this means that no PPT adversary has significantly better advantage than \(2^{-(1/2 + o(1))\cdot \uplambda }\), where the o(1) in the exponent can be made smaller than \(1/\lambda ^\varepsilon \) for any constant \(\varepsilon < 1\). Beyond this simple generalization, our analysis is essentially identical to that of [CKU20]; we provide it below for the sake of completeness.
\(\mathsf {IHBG}\) -Friendly Statistical ZAP for \(\mathscr {L}_\mathsf{LPWW} \) in Pairing-Free Groups. Equipped with the above correlation-intractable hash function, we are now ready to give our construction of our \(\mathsf {IHBG}\)-friendly statistical ZAP. We note that this construction will actually satisfy a stronger soundness notion than required for an \(\mathsf {IHBG}\)-friendly ZAP: adaptive computational soundness will hold for any parameters (an not just only for parameters sampled uniformly from \(\mathsf {Col} (\mathbb {G}^d)\)).Footnote 9 Let \(\mathbb {G}\) be a group of order p, and let \(\tilde{\mathbb {G}} \) be a group of order q such that \(\lceil \log q\rceil \approx \lambda \approx 2\lceil \log p\rceil ^2\). Let \(\varPi _\varSigma \) be the \(\varSigma \)-protocol for \(\mathscr {L}_{\mathsf{LPWW}}\), with repetition parameter \(n = \lceil \log p \rceil \). Let \(P_{1}\), \(P_{2}\) and V be the corresponding algorithms for the first and second move of the prover and the verifier, respectively. let \(\mathsf {H}: \tilde{\mathbb {G}} ^2 \times \mathbb {Z}_q \mapsto \{0,1\} ^{\lambda /2}\) be the correlation intractable hash function constructed above.
Construction. The construction of an \(\mathsf {IHBG}\)-friendly statistical \(\textsf {ZAP}\) for \(\mathscr {L}_{\mathsf{LPWW}}\) with public coin length \(\ell = 2\lceil \log q\rceil \), denoted as \(\varPi _\textsf {ZAP} \), is described as follows.
-
\(\textsf {ZAP}.\mathsf {Prove} ({\mathsf {par}},r,x,w):\) On input parameters \({\mathsf {par}} = (\mathbf{g}, \mathbf{h})\), a public coin \(r \in \{0 , 1\}^{\ell }\), a statement
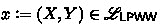 and a witness
and a witness  such that \((X,Y) = ((\mathbf{g}^\top )^\mathbf {y}, (\mathbf{h}^\top )^\mathbf {y})\), run \(\alpha \leftarrow _{r}P_{1}({\mathsf {par}}, x,w)\) and compute \(\beta = \mathsf {H} (r,\alpha )\), where r provides the description of the CIH hash \(\mathsf {H} \). Parse \(\beta \) as an element of \((\mathbb {Z}_p^{*})^{n}\), and further run \(\gamma \leftarrow _{r}P_{2}({\mathsf {par}},x,w,\alpha ,\beta )\). Finally, output \(\mathbf {\pi } _\textsf {ZAP} = (\alpha ,\gamma )\).
such that \((X,Y) = ((\mathbf{g}^\top )^\mathbf {y}, (\mathbf{h}^\top )^\mathbf {y})\), run \(\alpha \leftarrow _{r}P_{1}({\mathsf {par}}, x,w)\) and compute \(\beta = \mathsf {H} (r,\alpha )\), where r provides the description of the CIH hash \(\mathsf {H} \). Parse \(\beta \) as an element of \((\mathbb {Z}_p^{*})^{n}\), and further run \(\gamma \leftarrow _{r}P_{2}({\mathsf {par}},x,w,\alpha ,\beta )\). Finally, output \(\mathbf {\pi } _\textsf {ZAP} = (\alpha ,\gamma )\). -
\(\textsf {ZAP}.\mathsf {Verify} ({\mathsf {par}},r,x,\mathbf {\pi } _\textsf {ZAP}):\) On input parameters \({\mathsf {par}} = (\mathbf{g}, \mathbf{h})\), a public coin \(r \in \{0 , 1\}^{\ell }\), a statement x, and a proof \(\mathbf {\pi } _\textsf {ZAP} \), parse \(\mathbf {\pi } _\textsf {ZAP} \) as \((\alpha ,\gamma ) \leftarrow \mathbf {\pi } _\textsf {ZAP} \). Then, compute \(\beta = \mathsf {H} (r,\alpha )\) and output \(\top \) if \(V({\mathsf {par}}, x,\alpha ,\beta ,\gamma ) = \top \). Otherwise, output \(\bot \).
We prove Lemma 20. Namely, we show our \(\mathsf {IHBG}\)-friendly ZAP for \(\mathscr {L}_\mathsf{LPWW}\) satisfies doubly-adaptive perfect witness indistinguishability and adaptive computational \(\varepsilon _\mathsf {sound} \)-soundness w.r.t. colinear parameters. Due to page limitations, we provide them in the full version of this paper [CKSU21]. Plugging this \(\mathsf {IHBG}\)-friendly adaptive statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\) into the construction of \(\mathsf {IHBG}\) of Sect. 5 and combining it with the construction of statistical ZAP for \(\mathsf {NP}\) from any \(\mathsf {IHBG}\) from Sect. 3, we get our second main theorem:
Theorem 28
(Statistical ZAPs in Pairing-Free Groups). Assume that the explicit \(\mu \)-hardness of the DDH assumption holds in a group \(\mathbb {G}\) of order p for any negligible function \(\mu \) (which can be arbitrarily close to an inverse polynomial function), and that the \(2^{-\lambda /2}\)-\(\mathsf {OW\text {-}KDM}\) security of ElGamal holds over a group \(\tilde{\mathbb {G}} \) of order q such that \(\lceil \log q\rceil \approx \lambda \approx 2\lceil \log p\rceil ^2\). Then there exists an adaptive statistically witness indistinguishable ZAP for \(\mathsf {NP}\) with non-adaptive computational soundness.
Notes
- 1.
Explicit hardness in [BFJ+20] assumes that there exists an explicit bound \(\mu \) on the advantage of any polynomial time adversary against the assumption. In particular, this is a weaker requirement than superpolynomial hardness, for any arbitrarily small superpolynomial function. We note that previous works on statistical ZAPs using quasi-polynomial hardness [LVW19, GJJM20, BFJ+20, LVW20] can instead use explicit hardness.
- 2.
There is an obvious additional necessary change: when proving correctness of an opening, the statistical NIZK for \(\mathscr {L}_\mathsf{LPWW} \) is replaced by a statistical ZAP for \(\mathscr {L}_\mathsf{LPWW}\).
- 3.
We consider adversaries that run in superpolynomial time in case of superpolynomial hardness.
- 4.
Note that we can also relax the definition to allow for an unbounded zero-knowledge simulator.
- 5.
Although \(\mathscr {L}\) and \(\mathcal {R} \) are parameterized by the security parameter \({\uplambda }\), we omit them throughout the paper for better readability whenever the meaning is clear.
- 6.
Here, m can be set sufficiently large for both \(\varPi _\mathsf {IHBG} \) and \(\varPi _\mathsf {HBM} \) so that the existence of \(\varPi _\mathsf {HBM} \) is guaranteed unconditionally by Theorem 10.
- 7.
To be precise, \(g \in \mathbb {G}\) will be sampled for each security parameter \({\uplambda }\) and the family of parameterized language \(\mathscr {L}_{\mathsf{LPWW}, \uplambda } \) is defined with respect to such generator g. For better readability, we may make the random sampling of g implicit when the context is clear.
- 8.
Note the algorithm only has knowledge of the encodings \(g^{\mathbf {M}}\), and does not know the discrete logarithms \(\mathbf {M}\) themselves.
- 9.
We defined the weaker soundness notion since that was all we required to construct the \(\mathsf {IHBG}\) protocol, and moreover, it was what we could construct from the kernel DH assumption.
References
Badrinarayanan, S., Fernando, R., Jain, A., Khurana, D., Sahai, A.: Statistical ZAP Arguments. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 642–667. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_22
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112. ACM Press, May 1988
Badrinarayanan, S., Garg, S., Ishai, Y., Sahai, A., Wadia, A.: Two-message witness indistinguishability and secure computation in the plain model from new assumptions. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 275–303. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_10
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Canetti, R., Chen, Y., Reyzin, L., Rothblum, R.D.: Fiat-shamir and correlation intractability from strong KDM-secure encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 91–122. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_4
Couteau, G., Hofheinz, D.: Designated-verifier pseudorandom generators, and their applications. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 562–592. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_20
Couteau, G., Hartmann, D.: Shorter non-interactive zero-knowledge arguments and ZAPs for algebraic languages. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020. LNCS, vol. 12172, pp. 768–798. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_27
Couteau, G., Katsumata, S., Sadeghi, E., Ursu, B.: Statistical ZAPs from group-based assumptions. Cryptology ePrint Archive, Report 2021/688 (2021). https://ia.cr/2021/688
Couteau, G., Katsumata, S., Ursu, B.: Non-interactive zero-knowledge in pairing-free groups from weaker assumptions. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 442–471. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_15
Dwork, C., Naor, M.: Zaps and their applications. In: 41st FOCS, pp. 283–293. IEEE Computer Society Press, November 2000
Dwork, C., Naor, M.: Zaps and their applications. SIAM J. Comput. 36(6), 1513–1543 (2007)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Feige, U., Lapidot, D., Shamir, A.: Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract). In: 31st FOCS, pp. 308–317. IEEE Computer Society Press, October 1990
Feige, U., Lapidot, D., Shamir, A.: Multiple noninteractive zero knowledge proofs under general assumptions. SIAM J. Comput. 29(1), 1–28 (1999)
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: 22nd ACM STOC, pp. 416–426. ACM Press, May 1990
Goyal, V., Jain, A., Jin, Z., Malavolta, G.: Statistical zaps and new oblivious transfer protocols. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 668–699. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_23
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994). https://doi.org/10.1007/BF00195207
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_6
Groth, J., Ostrovsky, R., Sahai, A.: Perfect non-interactive zero knowledge for NP. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 339–358. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_21
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: 43rd ACM STOC, pp. 99–108. ACM Press, June 2011
Hofheinz, D., Kiltz, E.: Secure hybrid encryption from weakened key encapsulation. Cryptology ePrint Archive, Report 2007/288 (2007). https://eprint.iacr.org/2007/288
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Jain, A., Jin, Z.: Non-interactive zero knowledge from sub-exponential DDH. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12696, pp. 3–32. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77870-5_1
Kalai, Y.T., Khurana, D., Sahai, A.: Statistical witness indistinguishability (and more) in two messages. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 34–65. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_2
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T.: Designated verifier/prover and preprocessing NIZKs from Diffie-Hellman assumptions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 622–651. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_22
Khurana, D., Sahai, A.: How to achieve non-malleability in one or two rounds. In: 58th FOCS, pp. 564–575. IEEE Computer Society Press, October 2017
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_4
Libert, B., Passelègue, A., Wee, H., Wu, D.J.: New constructions of statistical NIZKs: dual-mode DV-NIZKs and more. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 410–441. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_14
Lombardi, A., Vaikuntanathan, V., Wichs, D.: 2-message publicly verifiable WI from (subexponential) LWE. Cryptology ePrint Archive, Report 2019/808 (2019). https://eprint.iacr.org/2019/808
Lombardi, A., Vaikuntanathan, V., Wichs, D.: Statistical ZAPR arguments from bilinear maps. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 620–641. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_21
Morillo, P., Ràfols, C., Villar, J.L.: Matrix computational assumptions in multilinear groups. Cryptology ePrint Archive, Report 2015/353 (2015). https://eprint.iacr.org/2015/353
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Pass, R.: Unprovable security of perfect NIZK and non-interactive non-malleable commitments. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 334–354. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_19
Quach, W., Rothblum, R.D., Wichs, D.: Reusable Designated-Verifier NIZKs for all NP from CDH. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 593–621. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_21
Acknowledgements
Geoffroy Couteau was supported by ANR SCENE. Shuichi Katsumata was supported by JST CREST Grant Number JPMJCR19F6. Bogdan Ursu was partly supported by ERC PREP-CRYPTO Grant 724307.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Couteau, G., Katsumata, S., Sadeghi, E., Ursu, B. (2021). Statistical ZAPs from Group-Based Assumptions. In: Nissim, K., Waters, B. (eds) Theory of Cryptography. TCC 2021. Lecture Notes in Computer Science(), vol 13042. Springer, Cham. https://doi.org/10.1007/978-3-030-90459-3_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-90459-3_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-90458-6
Online ISBN: 978-3-030-90459-3
eBook Packages: Computer ScienceComputer Science (R0)




 , a statement x and a proof
, a statement x and a proof 


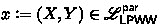 and a witness
and a witness 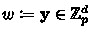 such that
such that 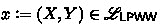 and a witness
and a witness  such that
such that 