Abstract
In a recent seminal work, Bitansky and Shmueli (STOC ’20) gave the first construction of a constant round zero-knowledge argument for \(\mathbf {NP}\) secure against quantum attacks. However, their construction has several drawbacks compared to the classical counterparts. Specifically, their construction only achieves computational soundness, requires strong assumptions of quantum hardness of learning with errors (QLWE assumption) and the existence of quantum fully homomorphic encryption (QFHE), and relies on non-black-box simulation.
In this paper, we resolve these issues at the cost of weakening the notion of zero-knowledge to what is called \(\epsilon \)-zero-knowledge. Concretely, we construct the following protocols:
– We construct a constant round interactive proof for \(\mathbf {NP}\) that satisfies statistical soundness and black-box \(\epsilon \)-zero-knowledge against quantum attacks assuming the existence of collapsing hash functions, which is a quantum counterpart of collision-resistant hash functions. Interestingly, this construction is just an adapted version of the classical protocol by Goldreich and Kahan (JoC ’96) though the proof of \(\epsilon \)-zero-knowledge property against quantum adversaries requires novel ideas.
– We construct a constant round interactive argument for \(\mathbf {NP}\) that satisfies computational soundness and black-box \(\epsilon \)-zero-knowledge against quantum attacks only assuming the existence of post-quantum one-way functions.
At the heart of our results is a new quantum rewinding technique that enables a simulator to extract a committed message of a malicious verifier while simulating verifier’s internal state in an appropriate sense.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Strictly speaking, Watrous’ assumption is a statistically binding and post-quantum computationally hiding commitment scheme, and he did not claim that this can be constructed under the existence of post-quantum OWFs. However, we can see that such a commitment scheme can be obtained by instantiating the construction of [Nao91, HILL99] with a post-quantum OWF.
- 2.
3-round suffices for achieving a constant soundness error, but super-constant times sequential repetitions are needed for achieving negligible soundness error (i.e., a cheating prover can let a verifier accept on a false statement only with a negligible probability). Negligible soundness error is a default requirement in this paper.
- 3.
- 4.
- 5.
In this paper, we use \(\varSigma \)-protocol to mean a parallel repetition version where soundness error is reduced to negligible.
- 6.
We note that this construction is based on an earlier work of [BCY91].
- 7.
This is also observed in [BS20].
- 8.
Strictly speaking, we need to use a slightly stronger variant of collapse-binding commitments which we call strong collapse-binding commitments. Such commitments can be constructed under the QLWE assumption or the existence of collapsing hash functions in more general. See Sect. 2.2 for more details.
- 9.
\(\mathbf {Aux}\) stores multiple qubits, but we denote by
 to mean
to mean 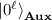 for the appropriate length \(\ell \) for notational simplicity.
for the appropriate length \(\ell \) for notational simplicity. - 10.
The protocol achieves full-fledged ZK if we allow the simulator to take non-uniform advice or assume a super-polynomial assumption.
- 11.
In [PS19], they do not explicitly claim ZK against quantum adversaries. However, since their security proof does not rely on rewinding, it immediately extends to post-quantum security if we assume the underlying assumption against quantum adversaries.
- 12.
Actually, their protocol is delayed-input, i.e., the first message generation does not use the statement either.
- 13.
A lossy function is defined similarly to a lossy trapdoor function [PW08] except that we do not require the existence of trapdoor.
- 14.
In other words, \(\mathcal {X}{\mathop {\approx }\limits ^{stat}}_{\delta }\mathcal {Y}\) means that there exists a negligible function \(\mathsf {negl}\) such that the trace distance between \(\rho _{X_i}\) and \(\rho _{Y_i}\) is at most \(\delta (\lambda ) + \mathsf {negl}(\lambda )\) for all \(\lambda \in \mathbb {N}\) and \(i\in I_\lambda \) where \(\rho _{X_i}\) and \(\rho _{Y_i}\) denote density matrices corresponding to \(X_{i}\) and \(Y_{i}\).
- 15.
We do not require special soundness, which is often a default requirement of \(\varSigma \)-protocol.
- 16.
Though \(\mathsf {Sim}_\mathsf {a}\) does not depend on \(\epsilon \), we include \(1^{\epsilon ^{-1}}\) in the input for notational uniformity.
- 17.
We note that we consider x to be hardwired into \(\mathcal {A}_{\mathtt {open},\lambda }\). We also note that though \(\mathcal {A}_{\mathtt {open},\lambda }\) does not take explicit randomness, it can generate randomness by say, applying Hadamard on its working register and then measuring it.
References
Alagic, G., Childs, A.M., Grilo, A.B., Hung, S.-H.: Non-interactive classical verification of quantum computation. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part III. LNCS, vol. 12552, pp. 153–180. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_6
Ananth, P., La Placa, R.L.: Secure quantum extraction protocols. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part III. LNCS, vol. 12552, pp. 123–152. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_5
Aharon, N., Regev, O.: Witness-preserving Amplification of QMA (lecture note) (2006). https://cims.nyu.edu/regev/teaching/quantum_fall_2005/ln/qma.pdf
Brassard, G., Crepeau, C.: Sorting out zero-knowledge. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 181–191. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_20
Brassard, G., Crépeau, C., Yung, M.: Constant-round perfect zero-knowledge computationally convincing protocols. Theor. Comput. Sci. 84(1), 23–52 (1991)
Broadbent, A., Grilo, A.B.: QMA-hardness of consistency of local density matrices with applications to quantum zero-knowledge. In: 61st FOCS, pp. 196–205 (2020)
Broadbent, A., Ji, Z., Song, F., Watrous, J.: Zero-knowledge proof systems for QMA. SIAM J. Comput. 49(2), 245–283 (2020)
Bitansky, N., Kalai, Y.T., Paneth, O.: Multi-collision resistance: a paradigm for keyless hash functions. In: 50th ACM STOC, pp. 671–684 (2018)
Bitansky, N., Khurana, D., Paneth, O.: Weak zero-knowledge beyond the black-box barrier. In: 51st ACM STOC, pp. 1091–1102 (2019)
Barak, B., Lindell, Y.: Strict polynomial-time in simulation and extraction. In: 34th ACM STOC, pp. 484–493 (2002)
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: 45th ACM STOC, pp. 575–584 (2013)
Blum, M.: How to prove a theorem so no one else can claim it. In: Proceedings of the International Congress of Mathematicians, pp. 1444–1451 (1986)
Bitansky, N., Paneth, O.: Point obfuscation and 3-round zero-knowledge. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 190–208. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_11
Brakerski, Z.: Quantum FHE (almost) as secure as classical. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 67–95. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_3
Bitansky, N., Shmueli, O.: Post-quantum zero knowledge in constant rounds. In: 52nd ACM STOC, pp. 269–279 (2020)
Brakerski, Z., Yuen, H.: Quantum Garbled Circuits. arXiv:2006.01085 (2020)
Chia, N.-H., Chung, K.-M., Liu, Q., Yamakawa, T.: On the Impossibility of Post-Quantum Black-Box Zero-Knowledge in Constant Rounds. arXiv:2103.11244 (2021)
Chia, N.-H., Chung, K.-M., Yamakawa, T.: Classical verification of quantum computations with efficient verifier. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part III. LNCS, vol. 12552, pp. 181–206. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_7
Chung, K.-M., Lui, E., Pass, R.: From weak to strong zero-knowledge and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 66–92. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_4
Coladangelo, A., Vidick, T., Zhang, T.: Non-interactive zero-knowledge arguments for QMA, with preprocessing. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 799–828. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_28
Damgård, I., Fehr, S., Salvail, L.: Zero-knowledge proofs and string commitments withstanding quantum attacks. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 254–272. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_16
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. J. ACM 50(6), 852–921 (2003)
Dwork, C., Naor, M., Sahai, A.: Concurrent zero-knowledge. J. ACM 51(6), 851–898 (2004)
Fleischhacker, N., Goyal, V., Jain, A.: On the existence of three round zero-knowledge proofs. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 3–33. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_1
Feige, U., Shamir, A.: Zero knowledge proofs of knowledge in two rounds. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 526–544. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_46
Goldreich, O., Kahan, A.: How to construct constant-round zero-knowledge proof systems for NP. J. Cryptol. 9(3), 167–190 (1996)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Goldreich, O., Micali, S., Wigderson, A.: Proofs that yield nothing but their validity for all languages in NP have zero-knowledge proof systems. J. ACM 38(3), 691–729 (1991)
Goldreich, O.: The Foundations of Cryptography - Volume 1: Basic Techniques. Cambridge University Press, Cambridge (2001)
Goldreich, O.: The Foundations of Cryptography - Volume 2: Basic Applications. Cambridge University Press, Cambridge (2004)
Graaf, J.V.D.: Towards a formal definition of security for quantum protocols. PhD thesis, University of Montreal, Montreal, Canada (1997)
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Kobayashi, H.: Non-interactive quantum perfect and statistical zero-knowledge. In: Ibaraki, T., Katoh, N., Ono, H. (eds.) ISAAC 2003. LNCS, vol. 2906, pp. 178–188. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-24587-2_20
Mahadev, U.: Classical homomorphic encryption for quantum circuits. In: 59th FOCS, pp. 332–338 (2018)
Mahadev, U.: Classical verification of quantum computations. In: 59th FOCS, pp. 259–267 (2018)
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991)
Nagaj, D., Wocjan, P., Zhang, Y.: Fast Amplification of QMA. arXiv:0904.1549 (2009)
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem: extended abstract. In: 41st ACM STOC, pp. 333–342 (2009)
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (plain) learning with errors. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 89–114. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_4
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: 40th ACM STOC, pp. 187–196 (2008)
Pass, R., Wee, H.: Black-box constructions of two-party protocols from one-way functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 403–418. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_24
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 34:1-34:40 (2009)
Shmueli, O.: Multi-theorem (Malicious) Designated-Verifier NIZK for QMA. arXiv:2007.12923 (2020)
Sahai, A., Vadhan, S.P.: A complete problem for statistical zero knowledge. J. ACM 50(2), 196–249 (2003)
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Unruh, D.: Collapse-binding quantum commitments without random oracles. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 166–195. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_6
Unruh, D.: Computationally binding quantum commitments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 497–527. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_18
Watrous, J.: Zero-knowledge against quantum attacks. SIAM J. Comput. 39(1), 25–58 (2009)
Zhandry, M.: Quantum lightning never strikes the same state twice. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 408–438. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_14
Acknowledgement
NHC’s research is support by the U.S. Department of Defense and NIST through the Hartree Postdoctoral Fellowship at QuICS and by NSF through IUCRC Planning Grant Indiana University: Center for Quantum Technologies (CQT) under award number 2052730. KMC’s research is partially supported by MOST, Taiwan, under Grant no. MOST 109-2223-E-001-001-MY3 and Executive Yuan Data Safety and Talent Cultivation Project (ASKPQ-109-DSTCP).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Chia, NH., Chung, KM., Yamakawa, T. (2021). A Black-Box Approach to Post-Quantum Zero-Knowledge in Constant Rounds. In: Malkin, T., Peikert, C. (eds) Advances in Cryptology – CRYPTO 2021. CRYPTO 2021. Lecture Notes in Computer Science(), vol 12825. Springer, Cham. https://doi.org/10.1007/978-3-030-84242-0_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-84242-0_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84241-3
Online ISBN: 978-3-030-84242-0
eBook Packages: Computer ScienceComputer Science (R0)


 to mean
to mean 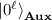 for the appropriate length
for the appropriate length 