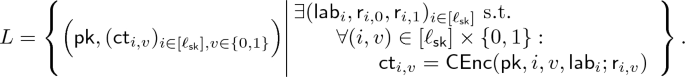Circular Security Is Complete for KDM Security

Abstract

Circular security is the most elementary form of key-dependent message (KDM) security, which allows us to securely encrypt only a copy of secret key bits. In this work, we show that circular security is complete for KDM security in the sense that an encryption scheme satisfying this security notion can be transformed into one satisfying KDM security with respect to all functions computable by a-priori bounded-size circuits (bounded-KDM security). This result holds in the presence of any number of keys and in any of secret-key/public-key and CPA/CCA settings. Such a completeness result was previously shown by Applebaum (EUROCRYPT 2011) for KDM security with respect to projection functions (projection-KDM security) that allows us to securely encrypt both a copy and a negation of secret key bits. Besides amplifying the strength of KDM security, our transformation in fact can start from an encryption scheme satisfying circular security against CPA attacks and results in one satisfying bounded-KDM security against CCA attacks. This result improves the recent result by Kitagawa and Matsuda (TCC 2019) showing a CPA-to-CCA transformation for KDM secure public-key encryption schemes.

1 Introduction

1.1 Background

Key-dependent message (KDM) security, introduced by Black, Rogaway, and Shrimpton [7], guarantees confidentiality of communication even if an adversary can get a ciphertext of secret keys. This notion was formulated in order to capture situations where there could be correlations between secret keys and messages to be encrypted. Although it seems that such situations only arise from bugs or errors, it turned out that they naturally occur in natural usage scenarios of encryption schemes such as hard-disc encryption [8], anonymous credentials [10], and formal methods [2]. Moreover, until today, a number of works have shown that KDM security is useful when constructing various cryptographic primitives including fully homomorphic encryption (FHE) [15], non-interactive zero-knowledge (NIZK) proofs/arguments [11, 12, 22, 25], homomorphic secret sharing [9], and chosen ciphertext secure encryption schemes and trapdoor functions [19, 23].

KDM security is defined with respect to a function family $\mathcal {F}$. Informally, a public-key encryption (PKE) scheme is said to be $\mathcal {F}\text {-}\text {KDM}^{(n)}$ secure if confidentiality of messages is protected even when an adversary can see a ciphertext of $f(\mathsf {sk}_1, \cdots , \mathsf {sk}_n)$ under the $s$-th public key for any $f \in \mathcal {F}$ and $s\in \{1, \cdots , n\}$, where $n$ denotes the number of keys. Also, KDM security is considered in both the chosen plaintext attack (CPA) and chosen ciphertext attack (CCA) settings.

Completeness of Projection-KDM Security. KDM security with respect to the family of projection functions (projection-KDM security) is one of the most widely studied notions. A projection function is an elementary function in which each output bit depends on at most a single bit of an input. Therefore, roughly speaking, projection-KDM security only guarantees that an encryption scheme can securely encrypt a copy and a negation of secret key bits.

Although this security notion looks somewhat weak at first glance, Applebaum [3] showed that it is complete for KDM security in the sense that we can construct an encryption scheme satisfying KDM security with respect to all functions computable by a-priori bounded-size circuits (bounded-KDM security) based on one satisfying projection-KDM security. The completeness of projection-KDM security in [3] has generality in the sense that it is insensitive to the exact setting of KDM security. More specifically, a projection-KDM secure encryption scheme can be transformed into a bounded-KDM secure one for any number of keys and in any of secret-key/public-key and CPA/CCA settings.

Moreover, recent works [22, 23, 25] also showed the power and usefulness of projection-KDM secure encryption schemes for achieving other security notions and constructing other primitives. Specifically, Kitagawa, Matsuda, and Tanaka [23] showed that projection-KDM secure PKE implies IND-CCA secure PKE, and Kitagawa and Matsuda [22] and Lombardi, Quach, Rothblum, Wichs, and Wu [25] independently showed that it implies a reusable designated-verifier NIZK argument system for any NP language.

Completeness of Circular Security? The focus in this work is on circular security, which is another elementary form of KDM security that has been widely studied from both the positive side [10, 11, 15, 19] and the negative side [1, 13, 17, 20, 24, 28]. Circular security is a weaker security notion compared to even projection-KDM security since circular security allows us to securely encrypt only a copy of secret key bits.¹ In this work, we clarify whether this most elementary form of KDM security is also complete in the above sense or not.

Let us explain the motivations for studying the completeness of circular security for KDM security. From the practical aspect, although it is an elementally form of KDM security, it is known to be sufficient for many practical applications of KDM security such as anonymous credentials, formal methods, and FHE listed above. Thus, studying circular security is expected to give us insights on these applications. From the theoretical aspect, it has impacts on the study of public-key cryptography since several recent works [22, 23, 25] showed that a projection-KDM secure encryption scheme is useful as a building block for constructing two important and central primitives of IND-CCA secure PKE and reusable designated-verifier NIZK argument systems, among which we will expand explanations on the former in the paragraph below. Furthermore, studying whether the ability to securely encrypt only a copy of secret key bits has a similar power to that to securely encrypt both a copy and a negation of secret key bits at the same time, is well-motivated from the viewpoint of “negation-complexity” of cryptographic primitives [16, 18]. For example, Goldreich and Izsak [16] showed that a one-way function can be computed by a monotone circuit and yet a pseudorandom generator cannot. It is interesting to investigate whether such a barrier exists in the context of KDM security.

Implications to the Study of CPA vs CCA. The question whether an IND-CCA secure PKE scheme can be constructed from an IND-CPA secure one has been standing as a major open question in cryptography. The completeness of circular security for KDM security also has a deep connection to this question: Hajiabadi and Kapron [19] tackled the above question, and they built an IND-CCA secure PKE scheme based on a PKE scheme satisfying circular security and a randomness re-usability property called reproducibility [6]. Also, Kitagawa et al. [23] showed that an IND-CCA secure PKE scheme can be constructed from a projection KDM secure PKE scheme.

The above two results surely made a progress on the study of CCA security versus CPA security by showing that an IND-CCA secure PKE scheme can be constructed from a PKE scheme satisfying only security notions against “CPA” (i.e. no decryption queries). Here, the above results are incomparable since the former result requires a structural property while the latter requires projection-KDM security that is stronger than circular security for the building block scheme. It is an open question whether we can construct an IND-CCA secure PKE scheme based on a PKE scheme satisfying only circular security without requiring any structural property for the building block scheme. We see that this question is solved affirmatively if we can prove the completeness of circular security for KDM security by combining it with the previous results [22, 23, 25].

1.2 Our Results

In this work, we show that circular security is complete in the sense that an encryption scheme satisfying this security notion can be transformed into a bounded-KDM secure one. In this work, unless stated otherwise, circular security indicates a security notion that guarantees that an encryption scheme can securely encrypt a copy of each of secret key bits separately. We show that this result has the same level of generality as the completeness of projection-KDM security shown by Applebaum [3]. Namely, we obtain the following theorem. Below, we denote circular security against CPA under $n$ key pairs as $\text {CIRC}^{(n)}$ security.

Theorem 1

(Informal). If there exists a $\text {CIRC}^{(n)}$ secure PKE (resp. SKE) scheme, then there exists a bounded-$\text {KDM}^{(n)}$-CCA secure PKE (resp. SKE) scheme for any number of keys $n$.

Note that the above theorem implies the completeness of circular security in both the CPA and CCA settings at the same time since we start with a scheme satisfying circular security against CPA and obtain a scheme satisfying bounded-KDM security against CCA. We obtain Theorem 1 in the following way.

How to Obtain Completeness in the Public-Key Setting. We first focus on the case where there is only a single key pair. In Sect. 4, as our main technical result, we show that an encryption primitive called targeted encryption (TE), formalized by Barak, Haitner, Hofheinz, and Ishai [5], can be constructed from the combination of a $\text {CIRC}^{(1)}$ secure SKE scheme and an IND-CPA secure PKE scheme. Since both of the building blocks are implied by $\text {CIRC}^{(1)}$ secure PKE, and a TE scheme in turn can be transformed into a bounded-$\text {KDM}^{(1)}$-CPA secure PKE scheme as shown by Barak et al. [5], this result implies that a $\text {CIRC}^{(1)}$ secure PKE scheme can be transformed into a bounded-$\text {KDM}^{(1)}$-CPA secure PKE scheme. Once we construct a bounded-$\text {KDM}^{(1)}$-CPA secure PKE scheme, by combining with the result by Kitagawa and Matsuda [22], we can transform it into a bounded-$\text {KDM}^{(1)}$-CCA secure PKE scheme, which is stated in Sect. 5.

We then turn our attention to the case where there are multiple key pairs. Similarly to the above, we can construct a bounded-$\text {KDM}^{(n)}$-CPA secure PKE scheme based on a $\text {CIRC}^{(n)}$ secure one for any $n$ through a primitive called augmented TE [5] that is an extension of TE. However, in the case of multiple key pairs, there is no transformation from a KDM-CPA secure PKE scheme to a KDM-CCA secure one regardless of the function family with respect to which we consider KDM security. Thus, in this case, we cannot easily carry the result in the CPA setting to that in the CCA setting.

To overcome the above problem, in Sect. 6, we first introduce a primitive that we call conformed TE (CTE). CTE is an extension of TE (with several similarities to augmented TE of Barak et al. [5]) that is conformed to the construction of a KDM-CCA secure PKE scheme in the presence of multiple key pairs. We then construct a CTE scheme based on a $\text {CIRC}^{(n)}$ secure SKE scheme and an IND-CPA secure PKE scheme. Finally, in Sect. 7, we construct a bounded-$\text {KDM}^{(n)}$-CCA secure PKE scheme from a CTE scheme, a garbling scheme, an IND-CCA secure PKE scheme, and a (reusable) DV-NIZK argument system. The last two components are implied by a circular secure PKE scheme from our result in the case of a single key pair and the results by Kitagawa and Matsuda [22] and Lombardi et al. [25]. This implies that circular security is complete in both the CPA and CCA settings even when there are multiple key pairs. Note that this result improves that of Kitagawa and Matsuda [22] in the following two aspects: Not only our construction can start from a circular secure PKE scheme, but also it works in the case of multiple key pairs.

How to Obtain Completeness in the Secret-Key Setting. From the result shown by Backes, Pfitzmann, and Scedrov [4], we can transform a bounded-$\text {KDM}^{(n)}$-CPA secure SKE scheme into a bounded-$\text {KDM}^{(n)}$-CCA secure one for any $n$. Thus, in the secret-key setting, all we have to do is to construct a bounded-$\text {KDM}^{(n)}$-CPA secure SKE scheme based on a $\text {CIRC}^{(n)}$ secure one. Similarly to the public-key setting, this is possible via the secret-key version of TE for the case of a single key pair and via the secret-key version of augmented TE for the case of multiple key pairs. These constructions are almost the same as the public-key counterparts, and thus we omit their formal descriptions in the paper. (In Sect. 2, this construction is outlined since we explain a technical overview of our results using the secret-key version of TE.)

Implications of Our Completeness Result. We obtain the following additional results: We show that the construction of the bounded-$\text {KDM}^{(1)}$-CPA secure PKE scheme mentioned above, is in fact a fully black-box construction [27] if we restrict the function family to projection functions. Thus, by combining this fact with the result by Kitagawa et al. [23], we obtain a fully black-box construction of an IND-CCA secure PKE scheme from a circular secure one.² Moreover, by simply combining Theorem 1 with the result independently achieved by Kitagawa and Matsuda [22] and Lombardi et al. [25], we see that a reusable DV-NIZK argument system can also be constructed from a circular secure PKE scheme.

1.3 Paper Organization

The rest of the paper is organized as follows: In Sect. 2, we give a technical overview of our results. In Sect. 3, we review definitions of cryptographic primitives. In Sect. 4, we present our construction of TE. In Sect. 5, we show several implications of our TE scheme, and in particular the completeness of circular security for the single-key setting. In Sect. 6, we introduce CTE and present its construction. Finally, in Sect. 7, we present the completeness of circular security in the multi-key setting using CTE.

2 Technical Overview

In this section, we provide a technical overview of our results. Our main technical contribution is to show that we can realize TE (and conformed TE) based only on a circular secure encryption scheme in a completely generic way. Thus, in this overview, we mainly focus on this part after briefly explaining how to construct a bounded-KDM secure scheme based on TE. For simplicity, we explain our ideas in this part by showing how to construct the secret-key version of a TE scheme based only on a $\text {CIRC}^{(1)}$ secure SKE scheme. In the following, for a natural number n, we let [n] denote the set $\{1, \dots , n\}$.

2.1 Secret-Key TE

We first introduce the secret-key version of TE [5]. A secret-key TE scheme consists of the three algorithms $\mathsf {TKG}$, $\mathsf {TEnc}$, and $\mathsf {TDec}$.³ Similarly to an ordinary SKE scheme, $\mathsf {TKG}$ is given a security parameter and outputs a secret key $\mathsf {sk}$. We let $\ell _{\mathsf {sk}}$ denote the secret key length. On the other hand, $\mathsf {TEnc}$ and $\mathsf {TDec}$ have a functionality of a somewhat special form. As we will soon see below, they are optimized for encrypting labels of garbled circuits [29]. In addition to the secret key $\mathsf {sk}$, $\mathsf {TEnc}$ is given an index $i \in [\ell _{\mathsf {sk}}]$ and a pair of messages $(X_0,X_1)$, and outputs a ciphertext as $\mathsf {ct}\leftarrow \mathsf {TEnc}(\mathsf {sk}, i, X_0, X_1)$. Correspondingly, given the secret key $\mathsf {sk}$, the index $i\in [\ell _{\mathsf {sk}}]$, and the ciphertext $\mathsf {ct}$, $\mathsf {TDec}$ outputs (only) $X_{\mathsf {sk}[i]}$, where $\mathsf {sk}[i]$ denotes the i-th bit of $\mathsf {sk}$. (Thus, it is similar to an oblivious transfer.) For TE, we consider two security notions: security against the receiver and security against outsiders. Security against the receiver ensures that $\mathsf {ct}$ hides the information of $X_{1\oplus \mathsf {sk}[i]}$ even against the receiver who holds $\mathsf {sk}$. Security against outsiders ensures that $\mathsf {ct}$ hides both $X_0$ and $X_1$ against adversaries who do not hold $\mathsf {sk}$.⁴

Bounded-$\text {KDM}^{(1)}$-CPA Security via TE. As shown by Barak et al. [5], we can construct a bounded-$\text {KDM}^{(1)}$-CPA secure SKE scheme based on a secret-key TE scheme by using garbled circuits.⁵ The construction is fairly simple. The secret key of the resulting SKE scheme is that of the underlying secret-key TE scheme itself. When encrypting a message $\mathsf {m}$, we first garble an $\ell _{\mathsf {sk}}$-bit-input constant function $\mathsf {C}_{\mathsf {m}}$ that outputs $\mathsf {m}$ for any input. This results in a single garbled circuit $\widetilde{\mathsf {C}}$ and $2 \ell _{\mathsf {sk}}$ labels $(\mathsf {lab}_{i,v})_{i \in [\ell _{\mathsf {sk}}],v \in \{0,1\}}$. Then, for every index $i \in [\ell _{\mathsf {sk}}]$, we encrypt the pair of labels $(\mathsf {lab}_{i,0},\mathsf {lab}_{i,1})$ under the index i into $\mathsf {ct}_i$ using $\mathsf {TEnc}$. The resulting ciphertext for the SKE scheme consists of $\widetilde{\mathsf {C}}$ and $(\mathsf {ct}_i)_{i\in [\ell _{\mathsf {sk}}]}$. When decrypting this ciphertext, we first obtain $(\mathsf {lab}_{i,\mathsf {sk}[i]})_{i\in [\ell _{\mathsf {sk}}]}$ from $(\mathsf {ct}_i)_{i\in [\ell _{\mathsf {sk}}]}$ by using $\mathsf {TDec}$ with $\mathsf {sk}$. Then, we evaluate the garbled circuit $\widetilde{\mathsf {C}}$ with these labels. This results in $\mathsf {m}$ from the correctness of the garbling scheme.

We can prove that the above construction is bounded-$\text {KDM}^{(1)}$-CPA secure. In a high level, we can generate a simulated encryption of $f(\mathsf {sk})$ without using $\mathsf {sk}$ itself that is indistinguishable from a real ciphertext based on the security against the receiver of the underlying secret-key TE scheme and the security of the underlying garbling scheme, where f is a function queried by an adversary as a KDM-encryption query. We then finish the security proof by relying on the security against outsiders of the secret-key TE scheme. For more details, see [5].

2.2 Secret-Key TE Based on Circular Secure SKE

Below, we explain how to construct a secret-key TE scheme based on a $\text {CIRC}^{(1)}$ secure SKE scheme. We first show that a secret-key TE scheme can be naturally realized from a projection-$\text {KDM}^{(1)}$ secure SKE scheme. We then show how to weaken the starting point to a $\text {CIRC}^{(1)}$ secure SKE scheme.

Secret-Key TE Based on Projection-KDM Secure SKE. Consider the following naive way to realize a secret-key TE scheme based on an SKE scheme $\mathsf {SKE}$. A secret key $\mathsf {sk}$ of $\mathsf {SKE}$ is used as that of the secret-key TE scheme. When encrypting $(X_0,X_1)$ under an index $i \in [\ell _{\mathsf {sk}}]$, we just encrypt $X_{\mathsf {sk}[i]}$ into $\mathsf {ct}$ by using the encryption algorithm $\mathsf {Enc}$ of $\mathsf {SKE}$ with the secret key $\mathsf {sk}$. We call this naive realization $\mathsf {Naive}$. $\mathsf {Naive}$ clearly satisfies security against the receiver since $\mathsf {ct}$ is independent of $X_{1 \oplus \mathsf {sk}[i]}$. However, it is not clear whether we can prove the security against outsiders of $\mathsf {Naive}$ if we only assume that $\mathsf {SKE}$ satisfies IND-CPA security. This is because the encrypted message $X_{\mathsf {sk}[i]}$ is dependent on the secret key $\mathsf {sk}$. On the other hand, we can prove the security against outsiders of $\mathsf {Naive}$ if $\mathsf {SKE}$ satisfies projection-$\text {KDM}^{(1)}$-CPA security which allows us to securely encrypt both a copy and a negation of $\mathsf {sk}[i]$.

To see this in detail, we suppose that $X_{\mathsf {sk}[i]}$ is encrypted by $\mathsf {SKE}$ in a bit-by-bit manner, and its length is $\mu$. We denote the j-th bit of $X_0$ (resp. $X_1$) by $X_0[j]$ (resp. $X_1[j]$). We can classify the indices in $[\mu ]$ into the following four types:

Type 1: $j \in [\mu ]$ such that $X_0[j]=X_1[j]=0$.

Type 2: $j \in [\mu ]$ such that $X_0[j]=X_1[j]=1$.

Type 3: $j \in [\mu ]$ such that $X_0[j]=0$ and $X_1[j]=1$.

Type 4: $j \in [\mu ]$ such that $X_0[j]=1$ and $X_1[j]=0$.

We have to generate the following ciphertexts of $\mathsf {SKE}$ for each type to encrypt $X_{\mathsf {sk}[i]}$:

• For j of Type 1, we have to generate $\mathsf {Enc}(\mathsf {sk},0)$ regardless of the value of $\mathsf {sk}[i]$.

• For j of Type 2, we have to generate $\mathsf {Enc}(\mathsf {sk},1)$ regardless of the value of $\mathsf {sk}[i]$.

• For j of Type 3, we have to generate $\mathsf {Enc}(\mathsf {sk}, \mathsf {sk}[i])$, that is, an encryption of a copy of $\mathsf {sk}[i]$.

• For j of Type 4, we have to generate $\mathsf {Enc}(\mathsf {sk},1\oplus \mathsf {sk}[i])$, that is, an encryption of a negation of $\mathsf {sk}[i]$.

Namely, when some bit of $X_0$ is 0 and the corresponding bit of $X_1$ is 1, we have to generate an encryption of a copy of $\mathsf {sk}[i]$. Similarly, when some bit of $X_0$ is 1 and the corresponding bit of $X_1$ is 0, we have to generate an encryption of a negation of $\mathsf {sk}[i]$. However, if $\mathsf {SKE}$ is projection-$\text {KDM}^{(1)}$-CPA secure, then $X_{\mathsf {sk}[i]}$ is hidden from outsiders. Since $X_{1\oplus \mathsf {sk}[i]}$ is completely hidden (even against the legitimate receiver), $\mathsf {Naive}$ satisfies security against outsiders based on the projection-$\text {KDM}^{(1)}$-CPA security of $\mathsf {SKE}$.

Replacing Projection-KDM-CPA Secure SKE with Circular Secure SKE. We now try to realize a secret-key TE scheme based on a circular secure ($\text {CIRC}^{(1)}$ secure) SKE scheme. Recall that $\text {CIRC}^{(1)}$ security allows us to securely encrypt only a copy of secret key bits. Thus, as the first attempt to avoid encrypting negations of secret key bits, we modify the above construction $\mathsf {Naive}$ into the following construction that we call $\mathsf {Naive}^*$.

In $\mathsf {Naive}^*$, when encrypting $(X_0,X_1)$ under an index $i \in [\ell _{\mathsf {sk}}]$, we basically encrypt $X_{\mathsf {sk}[i]}$ in a bit-by-bit manner in the same way as $\mathsf {Naive}$. However, for indices $j \in [\mu ]$ of Type 4, we replace the ciphertext of $\mathsf {SKE}$ with the special symbol $\mathtt {flip}$. When receiving the symbol $\mathtt {flip}$ instead of the j-th ciphertext, the receiver sets the value of $X_{\mathsf {sk}[i]}[j]$ as $1\oplus \mathsf {sk}[i]$. This is possible since the receiver has $\mathsf {sk}$ and knows the value of $\mathsf {sk}[i]$. Thus, if we modify the construction in this way, the receiver holding $\mathsf {sk}$ can obtain the entire bits of $X_{\mathsf {sk}[i]}$ similarly to $\mathsf {Naive}$.

In $\mathsf {Naive}^*$, we now need to generate encryptions of only a copy of $\mathsf {sk}[i]$ and not those of a negation of $\mathsf {sk}[i]$. However, we cannot prove that $\mathsf {Naive}^*$ satisfies the two security notions of TE (security against the receiver/outsiders) based on the $\text {CIRC}^{(1)}$ security of $\mathsf {SKE}$. For example, considering security against outsiders, $X_0$ and $X_1$ are partially leaked to outsiders because of the use of the symbol $\mathtt {flip}$. Concretely, outsiders can know that $X_0[j]=1$ and $X_1[j]=0$ for the indices j of Type 4. A similar problem lies in the argument on security against the receiver. Concretely, the receiver holding $\mathsf {sk}$ can know $X_{1\oplus \mathsf {sk}[i]}[j]$ for the indices j of Type 4 and either one of Type 1 or 2 depending on the value of $\mathsf {sk}[i]$. The reason why $X_{1\oplus \mathsf {sk}[i]}[j]$ for the indices j of Type 4 are leaked to the receiver is clear. The reason why those for the indices j of Type 1 or 2 are leaked to the receiver is as follows. For example, when $\mathsf {sk}[i]=0$, the receiver finds that the value of $X_{1\oplus \mathsf {sk}[i]}[j]$ is 1 for j of Type 2 from the fact that the decrypted message from the j-th ciphertext is 1 but the symbol $\mathtt {flip}$ was not sent for this j.

To summarize, if $\mathsf {SKE}$ is $\text {CIRC}^{(1)}$ secure, the following properties hold for $\mathsf {Naive}^*$: $X_0[j]$ and $X_1[j]$ for the indices j of Type 1, 2, and 3 are hidden but those for the indices j of Type 4 are leaked to outsiders. Also, $X_{1\oplus \mathsf {sk}[i]}[j]$ for the indices j of Type 3 and either one of Type 1 or 2 are hidden but the remaining parts are leaked to the receiver holding $\mathsf {sk}$.

Transforming into a Full-Fledged Secret-Key TE Scheme. A natural question here is whether the above $\mathsf {Naive}^*$ is useful or not. We show that by using a leakage-resilient SKE scheme $\mathsf {lrSKE}$, we can transform $\mathsf {Naive}^*$ into an ordinary secret-key TE scheme $\mathsf {sTE}$. As we will explain later, the type of leakage-resilience that $\mathsf {lrSKE}$ should satisfy is weak, and any IND-CPA secure SKE scheme can be transformed into one satisfying it. Thanks to this transformation, we can realize a secret-key TE scheme based only on a $\text {CIRC}^{(1)}$ secure SKE scheme.

The description of $\mathsf {sTE}$ is as follows. The secret key $\mathsf {sk}$ of $\mathsf {sTE}$ is that of $\mathsf {Naive}^*$ itself. When encrypting $(X_0,X_1)$ under the index $i \in [\ell _{\mathsf {sk}}]$, we first generate two keys $\mathsf {lrk}_0$ and $\mathsf {lrk}_1$ of $\mathsf {lrSKE}$. Then, we encrypt $X_0$ and $X_1$ into $\mathsf {lrct}_0$ and $\mathsf {lrct}_1$ by using $\mathsf {lrSKE}$ with the keys $\mathsf {lrk}_0$ and $\mathsf {lrk}_1$, respectively. Moreover, we encrypt $(\mathsf {lrk}_0,\mathsf {lrk}_1)$ into $\mathsf {ct}$ by using $\mathsf {Naive}^*$ with the key $\mathsf {sk}$. The resulting ciphertext of $\mathsf {sTE}$ is $(\mathsf {lrct}_0,\mathsf {lrct}_1,\mathsf {ct})$. When decrypting this ciphertext, we first obtain $\mathsf {lrk}_{\mathsf {sk}[i]}$ from $\mathsf {ct}$ by using $\mathsf {Naive}^*$ with the key $\mathsf {sk}$. We then obtain $X_{\mathsf {sk}[i]}$ by decrypting $\mathsf {ct}_{\mathsf {sk}[i]}$ using $\mathsf {lrSKE}$ with the key $\mathsf {lrk}_{\mathsf {sk}[i]}$.

We now argue that $\mathsf {sTE}$ satisfies (full-fledged) security against the receiver and that for outsiders. Without loss of generality, we assume that $\mathsf {lrk}_0$ and $\mathsf {lrk}_1$ are uniformly random n-bit strings. We define Type 1, 2, 3, and 4 for indices in $[n]$ as before using $\mathsf {lrk}_0$ and $\mathsf {lrk}_1$ instead of $X_0$ and $X_1$. Since $\mathsf {lrk}_0$ and $\mathsf {lrk}_1$ are chosen uniformly at random, these four types appear equally likely. In this case, $\mathsf {ct}$ hides expectedly a 1/2-fraction of bits of $\mathsf {lrk}_{1\oplus \mathsf {sk}[i]}$ against the receiver holding $\mathsf {sk}$. Also, $\mathsf {ct}$ hides expectedly a 3/4-fraction of bits of each of $\mathsf {lrk}_0$ and $\mathsf {lrk}_1$ against outsiders. Thus, if $\mathsf {lrSKE}$ is resilient against both forms of secret key leakage, $\mathsf {sTE}$ satisfies both security against the receiver and security against outsiders.

Fortunately, the leakage-resilience that $\mathsf {lrSKE}$ should satisfy in the above argument is weak. The amount of leakage is (expectedly) only a constant fraction. In addition, more importantly, which bits of the secret key are leaked is determined completely at random from the fact that Type 1, 2, 3, and 4 appear uniformly at random, out of the control of adversaries. Leakage-resilience against such secret key leakage is weak, and we can transform any IND-CPA secure SKE scheme into one satisfying it by using the leftover hash lemma [14, 21]. From this fact, $\mathsf {sTE}$ can be realized from a $\text {CIRC}^{(1)}$ secure SKE scheme.

2.3 Towards the Completeness in the Public-Key Setting

As we mentioned earlier, in the actual technical sections, we deal with the public-key setting. Namely, we prove Theorem 1 in the PKE setting. We finally explain how to prove it with the techniques explained so for.

Single-Key Setting. We first construct a (public-key) TE scheme based on a $\text {CIRC}^{(1)}$ secure SKE scheme and an IND-CPA secure PKE scheme both of which are implied by a $\text {CIRC}^{(1)}$ secure PKE scheme. This construction is almost the same as that of $\mathsf {sTE}$ above except that we use a leakage-resilient PKE scheme instead of a leakage-resilient SKE scheme. By combining this transformation with the previous results [5, 22], we can obtain Theorem 1 in the PKE setting for the number of key pairs $n=1$.

Multi-key Setting. We then move on to the case of multiple key pairs. As mentioned before, for achieving the completeness in this setting, we introduce an extended version of TE that we call conformed TE (CTE). CTE is conformed to construct $\text {KDM}^{(n)}$-CCA secure PKE schemes for $n> 1$. Roughly, CTE is TE that satisfies the following two additional properties.

• When generating a public/secret key pair, it additionally generates a trapdoor that enables us to recover both a “0-side” message $X_0$ and a “1-side” message $X_1$ from a ciphertext encrypting $(X_0, X_1)$. (Recall that in ordinary TE, the receiver can recover only one of them even having the secret key.)

• A CTE scheme has additional (untargeted and secret-key) encryption and decryption algorithms, and a ciphertext generated by the additional encryption algorithm is indistinguishable even under the existence of the above trapdoor and encryptions of a “key cycle” generated by the additional encryption algorithm. Encryptions of a key cycle are ciphertexts such that the s-th ciphertext is an encryption of the $(s \bmod n)+1$-th secret key under the s-th secret key when there are $n$ keys. We call this property special weak circular security.

We remark that a TE scheme satisfying only the second property is almost the same as augmented TE introduced by Barak et al. [5] to construct a bounded-$\text {KDM}^{(n)}$-CPA secure PKE scheme for $n> 1$. Roughly speaking, when constructing a KDM-CCA secure PKE scheme, the first property mainly plays its role to deal with decryption queries, and the second property plays its role to deal with multiple key pairs. For the details of the formalization of CTE as well as its relation to augmented TE, see Sect. 6.

We construct a CTE scheme based on a $\text {CIRC}^{(n)}$ secure SKE scheme and an IND-CPA secure PKE scheme. Basically, this construction is again an extension of $\mathsf {sTE}$ in which a leakage-resilient PKE scheme is used instead of a leakage-resilient SKE scheme. The trapdoor of the construction consists of secret keys of the leakage-resilient PKE scheme. Also, the special weak circular security of it is proved based on the $\text {CIRC}^{(n)}$ security of the underlying SKE scheme.

We finish the proof of Theorem 1 in the public-key setting for $n>1$ by constructing a bounded-$\text {KDM}^{(n)}$-CCA secure PKE scheme from the combination of the following four building blocks: (1) a CTE scheme, (2) an IND-CCA secure PKE scheme, (3) a garbling scheme for circuits, and (4) a reusable DV-NIZK argument system for NP languages. As we already explained, by Theorem 1 for $n=1$ and results by [22, 25], an IND-CCA secure PKE scheme and a reusable DV-NIZK argument system can be constructed from the combination of an IND-CPA secure PKE scheme and a $\text {CIRC}^{(1)}$ secure SKE scheme. Also, a garbling scheme for circuits can be constructed from a one-way function. Thus, all the building blocks can be based on the combination of an IND-CPA secure PKE scheme and a $\text {CIRC}^{(n)}$ secure SKE scheme. This completes the proof of Theorem 1 in the PKE setting for $n>1$.

Our construction of bounded-KDM-CCA secure PKE in the multi-key setting can be seen as combining the construction ideas from the two existing constructions: the construction of KDM-CPA secure PKE in the multi-key setting based on an augmented TE scheme by Barak et al. [5], and the construction of KDM-CCA secure PKE in the single key setting based on an IND-CPA secure PKE scheme and a projection-KDM secure SKE scheme by Kitagawa and Matsuda [22]. However, a simple combination of each of the techniques from [5, 22] as it is is not sufficient. We bridge the gap with the properties of the CTE scheme. For the details, see Sect. 7.

3 Preliminaries

In this section, we review the basic notation, and the definitions as well as existing results for cryptographic primitives treated in this paper.

3.1 Basic Notation and Notions

For $n \in \mathbb {N}$, we define $[n] := \{1, \dots , n\}$. For strings x and y, “|x|” denotes the bit-length of x, “x[i]” (with $i \in [|x|]$) denotes the i-th bit of x, and “$(x {\mathop {=}\limits ^{?}}y)$” is the operation that returns 1 if $x=y$ and 0 otherwise. For a discrete finite set S, “|S|” denotes its size, and “$x \xleftarrow {\mathsf {r}}S$” denotes choosing an element x uniformly at random from S. For a (probabilistic) algorithm $\mathsf {A}$, “$y \leftarrow \mathsf {A}(x)$” denotes assigning to y the output of $\mathcal {A}$ on input x, and if we need to specify a randomness r used in $\mathsf {A}$, we write “$y \leftarrow \mathsf {A}(x;r)$”. If furthermore $\mathcal {O}$ is a function or an algorithm, then “$\mathsf {A}^\mathcal {O}$” means that $\mathsf {A}$ has oracle access to $\mathcal {O}$. A function $\epsilon (\lambda ): \mathbb {N}\rightarrow [0,1]$ is said to be negligible if $\epsilon (\lambda ) = \lambda ^{-\omega (1)}$. We write $\epsilon (\lambda ) = \mathsf {negl}(\lambda )$ to mean $\epsilon$ being negligible. The character “$\lambda$” always denotes a security parameter. “PPT” stands for probabilistic polynomial time. For a distribution $\mathcal {X}$, the min-entropy of $\mathcal {X}$ is defined by $\mathbf {H}_{\infty }(\mathcal {X}) := - \log _2 (\max _{x} \Pr [\mathcal {X}= x])$. For distributions $\mathcal {X}$ and $\mathcal {Y}$ (forming a joint distribution), the average min-entropy of $\mathcal {X}$ given $\mathcal {Y}$ is defined by $\widetilde{\mathbf {H}}_{\infty }(\mathcal {X}|\mathcal {Y}) := - \log _2(\mathbf{E}_{y \leftarrow \mathcal {Y}} [ \max _{x} \Pr [\mathcal {X}= x | \mathcal {Y}= y]])$.

3.2 Public-Key and Secret-Key Encryption

Here, we recall the definitions for public-key and secret-key encryption schemes. We first introduce the definitions for PKE, and then briefly mention how to recover those for SKE.

Syntax of Public-Key Encryption. A PKE scheme $\mathsf {PKE}$ consists of the three PPT algorithms $(\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$:⁶

• $\mathsf {KG}$ is the key generation algorithm that takes $1^\lambda$ as input, and outputs a public/secret key pair $(\mathsf {pk}, \mathsf {sk})$.

• $\mathsf {Enc}$ is the encryption algorithm that takes a public key $\mathsf {pk}$ and a message $\mathsf {m}$ as input, and outputs a ciphertext $\mathsf {ct}$.

• $\mathsf {Dec}$ is the (deterministic) decryption algorithm that takes a public key $\mathsf {pk}$, a secret key $\mathsf {sk}$, and a ciphertext $\mathsf {ct}$ as input, and outputs a message $\mathsf {m}$ or the invalid symbol $\bot$.

A PKE scheme $\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$ is said to be correct if for all $\lambda \in \mathbb {N}$, $(\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {KG}(1^\lambda )$, and $\mathsf {m}$, we have $\mathsf {Dec}(\mathsf {pk}, \mathsf {sk}, \mathsf {Enc}(\mathsf {pk}, \mathsf {m})) = \mathsf {m}$.

We refer to a PKE scheme whose message space is 1-bit as a bit-PKE scheme.

Simple Key Generation. We say that a PKE scheme has simple key generation if its key generation algorithm $\mathsf {KG}$ first picks a secret key $\mathsf {sk}$ uniformly at random (from some prescribed secret key space) and then computes a public key $\mathsf {pk}$ from $\mathsf {sk}$. For PKE with simple key generation, we slightly abuse the notation and simply write $\mathsf {pk}\leftarrow \mathsf {KG}(\mathsf {sk})$ to denote this computation. Any IND-CPA/IND-CCA secure PKE scheme can be viewed as one with simple key generation by just regarding a randomness used in the key generation algorithm as $\mathsf {sk}$.

Weak Noisy-Leakage-Resilience. We will use a PKE scheme that satisfies weak noisy-leakage-resilience (against CPA), formalized by Naor and Segev [26]. In the weak “noisy” leakage setting, an adversary’s leakage function f must be chosen before seeing $\mathsf {pk}$, and must satisfy the condition that the average min-entropy of $\mathsf {sk}$ given $f(\mathsf {sk})$ is greater than a pre-determined lower bound.

Formally, for a PKE scheme $\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$, a polynomial $L = L(\lambda )$, and an adversary $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$, consider the experiment described in Fig. 1. In the experiment, $\mathcal {A}$ is required to be L-noisy-leakage-respecting, which requires that $L \ge \mathbf {H}_{\infty }(\mathsf {sk}) - \widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}|f(\mathsf {sk}), \mathsf {st})$ hold.

Definition 1

(Weak Noisy-Leakage-Resilience). Let $L = L(\lambda )$ be a polynomial. We say that a PKE scheme $\mathsf {PKE}$ is weakly L-noisy-leakage-resilient if for all PPT L-noisy-leakage-respecting adversaries $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$, we have $\mathsf {Adv}_{\mathsf {PKE}, \mathcal {A}, L}^{\mathsf {wlr}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {PKE}, \mathcal {A}, L}^{\mathsf {wlr}}(\lambda ) = 1] - 1/2| = \mathsf {negl}(\lambda )$.

Fig. 1.

The weak noisy-leakage-resilience experiment for PKE. In the experiment, it is required that $L \ge \mathbf {H}_{\infty }(\mathsf {sk}) - \widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}|f(\mathsf {sk}), \mathsf {st})$.

Any IND-CPA secure PKE scheme can be straightforwardly converted into a weakly noisy-leakage-resilient one by using the leftover hash lemma [14, 21]. In fact, Naor and Segev [26] showed this fact for the case of weak “bounded” leakage-resilience (where the output-length of a leakage function is bounded), and it is easy to see that their proof carries over to the case of weak noisy-leakage-resilience. Furthermore, this conversion is fully black-box and preserves the simple key generation property. (It works for SKE as well.) Since we will use this fact in Sect. 5, we state it formally, whose formal proof is given in the full version.

Lemma 1

Assume that there exists an IND-CPA secure PKE scheme with simple key generation whose secret key length is $\ell _{\mathsf {sk}}= \ell _{\mathsf {sk}}(\lambda )$. Then, for any polynomials $L = L(\lambda )$ and $\ell _{\mathsf {sk}}' = \ell _{\mathsf {sk}}'(\lambda )$ satisfying $\ell _{\mathsf {sk}}' - (L + \ell _{\mathsf {sk}}) = \omega (\log \lambda )$, there exists a weakly L-noisy-leakage-resilient PKE scheme with simple key generation whose secret key length is $\ell _{\mathsf {sk}}'$. Furthermore, the construction is fully black-box.⁷

For example, from an IND-CPA secure PKE scheme with simple key generation with secret key length $\ell _{\mathsf {sk}}$, for any constant $\beta \in [0, 1)$, we can construct a scheme whose secret key length is $\ell _{\mathsf {sk}}'$ and satisfies weak $(\beta \ell _{\mathsf {sk}}')$-noisy-leakage-resilience by setting the term $\omega (\log \lambda )$ simply as $\lambda$ and setting $\ell _{\mathsf {sk}}' := \frac{\ell _{\mathsf {sk}}+ \lambda }{1 - \beta }$.

KDM-CCA/CPA Security. We recall KDM-CCA/CPA security for PKE.

Definition 2

(KDM-CCA/CPA Security). Let $\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$ be a PKE scheme whose secret key length and message length are $\ell _{\mathsf {sk}}$ and $\mu$, respectively. Let $n= n(\lambda )$ be a polynomial, and $\mathcal {F}_{\mathsf {}}$ be a family of functions with domain $(\{0,1\}^{\ell _{\mathsf {sk}}})^n$ and range $\{0,1\}^{\mu }$. We say that $\mathsf {PKE}$ is KDM-CCA secure with respect to $\mathcal {F}_{\mathsf {}}$ in the $n$-key setting (${\mathcal {F}_{\mathsf {}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure) if for all PPT adversaries $\mathcal {A}$, we have $\mathsf {Adv}_{\mathsf {PKE}, \mathcal {F}_{\mathsf {}}, \mathcal {A}, n}^{\mathsf {kdmcca}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {PKE}, \mathcal {F}_{\mathsf {}}, \mathcal {A}, n}^{\mathsf {kdmcca}}(\lambda ) = 1] - 1/2| = \mathsf {negl}(\lambda )$, where the experiment $\mathsf {Expt}_{\mathsf {PKE}, \mathcal {F}_{\mathsf {}}, \mathcal {A}, n}^{\mathsf {kdmcca}}(\lambda )$ is described in Fig. 2.

KDM-CPA security with respect to $\mathcal {F}_{\mathsf {}}$ in the $n$-key setting (${\mathcal {F}_{\mathsf {}}}\text {-KDM}^{(n)}\text {-CPA}$ security) is defined analogously, except that $\mathcal {A}$ is disallowed to use $\mathcal {O}_{\mathsf {dec}}$.

Fig. 2.

The KDM-CCA experiment for PKE.

Function Families for KDM Security. In this paper, the function families for KDM security that we will specifically treat are as follows.

• $\mathcal {P}$ (Projection functions): A function is said to be a projection function if each of its output bits depends on at most a single bit of its input. We denote by $\mathcal {P}$ the family of projection functions.

• $\mathcal {B}_{\mathsf {size}}$ (Circuits of a-priori bounded size $\mathsf {size}$): We denote by $\mathcal {B}_{\mathsf {size}}$, where $\mathsf {size}= \mathsf {size}(\lambda )$ is a polynomial, the function family each of whose members can be described by a circuit of size $\mathsf {size}$.

Circular Security. In this paper, we also treat circular security (against CPA), which we consider for bit-encryption schemes. Although it is a special case of KDM security, it is convenient for us to introduce a separate definition in the form we use in this paper.

Definition 3

(Circular Security for Bit-PKE). Let $n= n(\lambda )$ be a polynomial. Let $\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$ be a bit-PKE scheme with the secret key length $\ell _{\mathsf {sk}}$. We say that $\mathsf {PKE}$ is circular secure in the $n$-key setting (CIRC$^{(n)}$ secure) if for all PPT adversaries $\mathcal {A}$, we have $\mathsf {Adv}_{\mathsf {PKE}, \mathcal {A}, n}^{\mathsf {circ}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {PKE}, \mathcal {A}, n}^{\mathsf {circ}}(\lambda ) = 1] - 1/2| = \mathsf {negl}(\lambda )$, where the experiment $\mathsf {Expt}_{\mathsf {PKE}, \mathcal {A}, n}^{\mathsf {circ}}(\lambda )$ is described in Fig. 3.

Our definition here follows the definition called “circular security with respect to indistinguishability of oracles” formalized by Rothblum [28], with a slight modification to the interface of the oracle: In addition to capturing the multi-key setting, the circular-encryption oracle $\mathcal {O}_{\mathsf {circ}}$ in our definition accepts the special commands “$\mathtt {zero}$” and “$\mathtt {one}$” (returning an encryption of 0 and that of 1, respectively, in the case $b=1$) to explicitly capture ordinary IND-CPA security. This is for convenience and clarity: A bit-encryption scheme satisfies our definition if and only if it simultaneously satisfies the original definition in [28] (without the augmentation of the oracle interface) and IND-CPA security.

Fig. 3.

The circular security experiment for bit-PKE.

Secret-Key Encryption. An SKE scheme $\mathsf {SKE}$ consists of the three PPT algorithms $(\mathsf {K}, \mathsf {E}, \mathsf {D})$:

• $\mathsf {K}$ is the key generation algorithm that takes $1^\lambda$ as input, and outputs a secret key $\mathsf {sk}$.

• $\mathsf {E}$ is the encryption algorithm that takes a secret key $\mathsf {sk}$ and a message $\mathsf {m}$ as input, and outputs a ciphertext $\mathsf {ct}$.

• $\mathsf {D}$ is the (deterministic) decryption algorithm that takes a secret key $\mathsf {sk}$ and a ciphertext $\mathsf {ct}$ as input, and outputs a message $\mathsf {m}$ or the invalid symbol $\bot$.

An SKE scheme $\mathsf {SKE}= (\mathsf {K}, \mathsf {E}, \mathsf {D})$ is said to be correct if for all $\lambda \in \mathbb {N}$, $\mathsf {sk}\leftarrow \mathsf {K}(1^\lambda )$ and $\mathsf {m}$, we have $\mathsf {D}(\mathsf {sk}, \mathsf {E}(\mathsf {sk}, \mathsf {m})) = \mathsf {m}$.

We refer to an SKE scheme whose message space is 1-bit as a bit-SKE scheme.

Weak noisy-leakage-resilience, KDM security, and circular security for (bit-)SKE are defined analogously to those defined for (bit-)PKE, with the following natural adaptions in the security experiments:

• All of $(\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {KG}(1^\lambda )$, $\mathsf {Enc}(\mathsf {pk}, \cdot )$, and $\mathsf {Dec}(\mathsf {pk}, \mathsf {sk}, \cdot )$ in the experiments for PKE are replaced with $\mathsf {sk}\leftarrow \mathsf {K}(1^\lambda )$, $\mathsf {E}(\mathsf {sk}, \cdot )$, and $\mathsf {D}(\mathsf {sk}, \cdot )$ in the experiments for SKE, respectively. We do the same treatment for those with the superscripts $s, \alpha \in [n]$.

• All the public keys $\mathsf {pk}$ and $\mathsf {pk}^s$ ($s\in [n]$) given as input to an adversary in the experiments for PKE are replaced with $1^\lambda$ in the experiments for SKE.

Results from [22, 23]. We recall the results on IND-CCA/KDM-CCA secure PKE from [22, 23], which we will use in Sect. 5.

Theorem 2

( [23]). If there exist an IND-CPA secure PKE scheme and a ${\mathcal {P}}\text {-KDM}^{(1)}\text {-CPA}$ secure SKE scheme, then there exists an IND-CCA secure PKE scheme. Furthermore, the construction is fully black-box.

Theorem 3

( [22]). If there exist an IND-CPA secure PKE scheme and a ${\mathcal {P}}\text {-KDM}^{(1)}\text {-CPA}$ secure SKE scheme, then for any polynomial $\mathsf {size}= \mathsf {size}(\lambda )$, there exists a ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(1)}\text {-}\mathrm{CCA}$ secure PKE scheme.

We note that [22] also showed a construction of a multi-key-KDM-CCA secure PKE scheme by additionally assuming (passive) RKA-KDM security with respect to projection functions for the underlying SKE scheme. We do not formally recall it here since it is not known if it follows from the multi-key version of ordinary $\mathcal {P}$-KDM security and our result in Sect. 7 improves it in terms of the strength of assumptions.

3.3 Targeted Encryption

Here, we recall targeted encryption (TE) [5]. A TE scheme $\mathsf {TE}$ consists of the three PPT algorithms $(\mathsf {TKG}, \mathsf {TEnc}, \mathsf {TDec})$:

• $\mathsf {TKG}$ is the key generation algorithm that takes $1^\lambda$ as input, and outputs a public/secret key pair $(\mathsf {pk}, \mathsf {sk})$, where $|\mathsf {sk}| =: \ell _{\mathsf {sk}}$.

• $\mathsf {TEnc}$ is the encryption algorithm that takes a public key $\mathsf {pk}$, an index $i \in [\ell _{\mathsf {sk}}]$, a bit $v \in \{0,1\}$, and a message $\mathsf {m}$ as input, and outputs a ciphertext $\mathsf {ct}$.

• $\mathsf {TDec}$ is the (deterministic) decryption algorithm that takes a public key $\mathsf {pk}$, a secret key $\mathsf {sk}\in \{0,1\}^{\ell _{\mathsf {sk}}}$, an index $i \in [\ell _{\mathsf {sk}}]$, and a ciphertext $\mathsf {ct}$ as input, and outputs a message $\mathsf {m}$ or the invalid symbol $\bot$.

As the correctness for a TE scheme, we require that for all $\lambda \in \mathbb {N}$, $(\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {TKG}(1^\lambda )$, $i \in [\ell _{\mathsf {sk}}]$, and $\mathsf {m}$, we have $\mathsf {TDec}(\mathsf {pk}, \mathsf {sk}, i, \mathsf {TEnc}(\mathsf {pk}, i, \mathsf {sk}[i], \mathsf {m})) = \mathsf {m}$.

Barak et al. [5] defined two kinds of security notions for TE: security against the receiver and security against outsiders. We recall them here.

Security Against the Receiver. As the name suggests, this is a security notion against a receiver who holds a secret key. More specifically, this security notion ensures that for every $i \in [\ell _{\mathsf {sk}}]$, if a message is encrypted under the position $(i, 1 \oplus \mathsf {sk}[i])$, its information does not leak to the receiver of the ciphertext who holds a secret key $\mathsf {sk}$. For convenience, we introduce the multi-challenge version of this security notion, which can be shown to be equivalent to the single-challenge version defined in [5] via a query-wise hybrid argument.

Formally, for a TE scheme $\mathsf {TE}= (\mathsf {TKG}, \mathsf {TEnc}, \mathsf {TDec})$ and an adversary $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$, consider the experiment $\mathsf {Expt}_{\mathsf {TE},\mathcal {A}}^{\mathsf {receiver}}(\lambda )$ described in Fig. 4 (left). We emphasize again that since this security is considered against a receiver, an adversary is given a secret key $\mathsf {sk}$ as input.⁸

Definition 4

(Security against the Receiver). We say that a TE scheme $\mathsf {TE}$ satisfies security against the receiver if for all PPT adversaries $\mathcal {A}$, we have $\mathsf {Adv}_{\mathsf {TE},\mathcal {A}}^{\mathsf {receiver}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {TE},\mathcal {A}}^{\mathsf {receiver}}(\lambda ) = 1] - 1/2| = \mathsf {negl}(\lambda )$.

Fig. 4.

The experiments for TE: Security against the receiver (left) and security against outsiders (right).

Security Against Outsiders. This security notion simply ensures that ciphertexts generated under any pair $(i, v) \in [\ell _{\mathsf {sk}}] \times \{0,1\}$ do not leak the information of encrypted messages. Again, we introduce the multi-challenge version for this security notion, which is equivalent to the single-challenge version formalized in [5].

Formally, for a TE scheme $\mathsf {TE}= (\mathsf {TKG}, \mathsf {TEnc}, \mathsf {TDec})$ and an adversary $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$, consider the experiment $\mathsf {Expt}_{\mathsf {TE},\mathcal {A}}^{\mathsf {outsider}}(\lambda )$ described in Fig. 4 (right).

Definition 5

(Security against Outsiders). We say that a TE scheme $\mathsf {TE}$ satisfies security against outsiders if for all PPT adversaries $\mathcal {A}$, we have $\mathsf {Adv}_{\mathsf {TE},\mathcal {A}}^{\mathsf {outsider}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {TE},\mathcal {A}}^{\mathsf {outsider}}(\lambda ) = 1] - 1/2| = \mathsf {negl}(\lambda )$.

Result from [5]. Barak et al.  [5] showed the following result, which we will use in Sect. 5.

Theorem 4

( [5]). If there exists a TE scheme satisfying security against the receiver and security against outsiders, then for any polynomial $\mathsf {size}=\mathsf {size}(\lambda )$, there exists a ${\mathcal {B}_{\mathsf {size}}}\text {-KDM}^{(1)}\text {-CPA}$ secure PKE scheme. Furthermore, there is a fully black-box construction of a ${\mathcal {P}}\text {-KDM}^{(1)}\text {-CPA}$ secure PKE scheme from a TE scheme satisfying the two security notions.

We remark that the result on the fully black-box construction can be extended to any function family such that a canonical description of a circuit computing any function in the family can be learned and reconstructed (with overwhelming probability) by just making polynomially many oracle queries to the function. (This is because in the security proof in [5], what is garbled is a function queried as a KDM-encryption query.) We only state it for $\mathcal {P}$-KDM security since it is sufficient for our purpose.

We also remark that [5] also showed that their construction achieves KDM-CPA security in the multi-key setting by additionally assuming that the underlying TE scheme is an augmented TE scheme satisfying circular security in the multi-key setting. We do not recall this result and the formal definition of augmented TE since we do not use them directly. In Sect. 6, we introduce conformed TE, which is also an extension of TE in a similar manner to augmented TE but has several differences. For the details, see the explanation there.

3.4 Additional Primitives

Here, we briefly recall the syntax of a DV-NIZK argument system and a garbling scheme used in Sect. 7. Due to the space limitation, we omit the formal security definitions in the proceedings version. See the full version for them.

Designated-Verifier Non-interactive Zero-Knowledge Arguments. Let L be an NP language associated with the corresponding NP relation R. A DV-NIZK argument system $\mathsf {DVNIZK}$ for L consists of the three PPT algorithms $(\mathsf {DVKG}, \mathsf {P}, \mathsf {V})$: $\mathsf {DVKG}$ is the key generation algorithm that takes $1^\lambda$ as input, and outputs a public proving key $\mathsf {pk}$ and a secret verification key $\mathsf {sk}$; $\mathsf {P}$ is the proving algorithm that takes a public proving key $\mathsf {pk}$, a statement x, and a witness w as input, and outputs a proof $\pi$; $\mathsf {V}$ is the (deterministic) verification algorithm that takes a secret verification key $\mathsf {sk}$, a statement x, and a proof $\pi$ as input, and outputs either $\mathsf {accept}$ or $\mathsf {reject}$.

For correctness, we require that for all $\lambda \in \mathbb {N}$, $(\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {DVKG}(1^\lambda )$, and $(x, w) \in R$, we have $\mathsf {V}(\mathsf {sk}, x, \mathsf {P}(\mathsf {pk}, x, w)) = \mathsf {accept}$.

We require that a DV-NIZK argument system satisfy (adaptive) soundness and (adaptive) zero-knowledge. As in [22, 25], we consider the reusable setting, where the security experiment for soundness (resp. zero-knowledge) allows an adversary to make multiple verification (resp. proving) queries. A DV-NIZK argument system satisfying these versions of soundness and zero-knowledge is called reusable. The formal definitions are given in the full version.

Garbling. Let $\mathcal {C}= \{\mathcal {C}_n\}_{n \in \mathbb {N}}$ be a family of circuits, where the input length of each member in $\mathcal {C}_n$ is n. A garbling scheme $\mathsf {GC}$ for $\mathcal {C}$ consists of the three PPT algorithms $(\mathsf {Garble}, \mathsf {Eval}, \mathsf {Sim})$: $\mathsf {Garble}$ is the garbling algorithm that takes as input $1^\lambda$ and (the description of) a circuit $\mathsf {C}\in \mathcal {C}_n$, where $n = n(\lambda )$ is a polynomial. Then, it outputs a garbled circuit $\widetilde{\mathsf {C}}$ and 2n labels $(\mathsf {lab}_{i,v})_{i \in [n],v \in \{0,1\}}$; $\mathsf {Eval}$ is the (deterministic) evaluation algorithm that takes a garbled circuit $\widetilde{\mathsf {C}}$ and n labels $(\mathsf {lab}_i)_{i \in [n]}$ as input, and outputs an evaluation result $\mathsf {y}$; $\mathsf {Sim}$ is the simulator algorithm that takes $1^\lambda$, the size parameter $\mathsf {size}$ (where $\mathsf {size}= \mathsf {size}(\lambda )$ is a polynomial), and a string $\mathsf {y}$ as input, and outputs a simulated garbled circuit $\widetilde{\mathsf {C}}$ and n simulated labels $(\mathsf {lab}_i)_{i \in [n]}$.

For correctness, we require that for all $\lambda , n \in \mathbb {N}$, $\mathsf {x}\in \{0,1\}^n$, and $\mathsf {C}\in \mathcal {C}_n$, the following two conditions hold: (1) $\mathsf {Eval}(\widetilde{\mathsf {C}}, (\mathsf {lab}_{i, \mathsf {x}[i]})_{i \in [n]}) = \mathsf {C}(\mathsf {x})$ holds for all $(\widetilde{\mathsf {C}}, (\mathsf {lab}_{i,v})_{i \in [n],v \in \{0,1\}})$ output by $\mathsf {Garble}(1^\lambda , \mathsf {C})$, and (2) $\mathsf {Eval}(\widetilde{\mathsf {C}}, (\mathsf {lab}_i)_{i \in [n]}) = \mathsf {C}(\mathsf {x})$ holds for all $(\widetilde{\mathsf {C}}, (\mathsf {lab}_i)_{i \in [n]})$ output by $\mathsf {Sim}(1^\lambda , |\mathsf {C}|, \mathsf {C}(\mathsf {x}))$, where $|\mathsf {C}|$ denotes the size of $\mathsf {C}$.

4 Targeted Encryption from Circular Security and Leakage-Resilience

In this section, as our main technical result, we show how to construct a TE scheme from the combination of a circular secure bit-SKE scheme (in the single-key setting) and a weakly noisy-leakage-resilient PKE scheme.

Construction. Our construction uses the following building blocks:

• Let $\mathsf {SKE}= (\mathsf {K}, \mathsf {E}, \mathsf {D})$ be a $\text {CIRC}^{(1)}$ secure bit-SKE scheme with the secret-key length $\ell _\mathsf {k}$ for some polynomial $\ell _\mathsf {k}= \ell _\mathsf {k}(\lambda )$. We assume that there exists a special symbol $\mathtt {flip}$ that is perfectly distinguishable from possible outputs of $\mathsf {E}$.

• Let $\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$ be a weakly L-noisy-leakage-resilient PKE scheme with simple key generation whose secret-key length is $\ell _{\mathsf {sk}}$ for some polynomial $\ell _{\mathsf {sk}}= \ell _{\mathsf {sk}}(\lambda )$. We assume $L = 0.6\ell _{\mathsf {sk}}$.

Using these building blocks, we construct a TE scheme $\mathsf {TE}= (\mathsf {TKG}, \mathsf {TEnc}, \mathsf {TDec})$, whose secret key length is $\ell _\mathsf {k}$, as described in Fig. 5.

Fig. 5.

The construction of a TE scheme $\mathsf {TE}$ from a circular secure bit-SKE scheme $\mathsf {SKE}$ and a weakly noisy-leakage-resilient PKE scheme $\mathsf {PKE}$.

Correctness. The correctness of $\mathsf {TE}$ follows from that of the building blocks $\mathsf {SKE}$ and $\mathsf {PKE}$. Specifically, since $\mathsf {TEnc}(\mathsf {PK}, i, \mathsf {SK}[i] = \mathsf {k}[i], \mathsf {m})$ just computes $\mathsf {Enc}({\mathsf {pk}}_{i,\mathsf {k}[i]}, \mathsf {m})$ and $\mathsf {TDec}(\mathsf {PK}, \mathsf {SK}, i, \mathsf {ct})$ computes $\mathsf {Dec}({\mathsf {pk}}_{i,\mathsf {k}[i]}, \mathsf {sk}', \mathsf {ct})$ in its last step, it suffices to see that $\mathsf {sk}'$ computed in $\mathsf {TDec}$ always equals to ${\mathsf {sk}}_{i,\mathsf {k}[i]}$ for any $i \in [\ell _\mathsf {k}]$. Indeed, for every $j \in [\ell _{\mathsf {sk}}]$, we have

• If $({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) = (1,0)$, then note that this case implies ${\mathsf {sk}}_{i,\mathsf {k}[i]}[j] = 1 \oplus \mathsf {k}[i]$. On the other hand, ${\mathsf {e}}_{i,j} = \mathtt {flip}$ holds by the design of $\mathsf {TKG}$. Hence, $\mathsf {TDec}$ sets $\mathsf {sk}'[j] \leftarrow 1 \oplus \mathsf {k}[i] = {\mathsf {sk}}_{i,\mathsf {k}[i]}[j]$.

• Otherwise (i.e. $({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) \ne (1,0)$), ${\mathsf {e}}_{i,j}$ is just an encryption of ${\mathsf {sk}}_{i,\mathsf {k}[i]}[j]$. Thus, $\mathsf {TDec}$ decrypts it as $\mathsf {sk}'[j] = \mathsf {D}(\mathsf {k}, {\mathsf {e}}_{i,j}) = {\mathsf {sk}}_{i,\mathsf {k}[i]}[j]$.

Hence, we have $\mathsf {sk}'[j] = {\mathsf {sk}}_{i,\mathsf {k}[i]}[j]$ for every $j \in [\ell _{\mathsf {sk}}]$, namely, $\mathsf {sk}' = {\mathsf {sk}}_{i,\mathsf {k}[i]}$ holds. Thus, $\mathsf {TE}$ satisfies correctness.

Security. We now show that $\mathsf {TE}$ satisfies the two security notions for TE.

Theorem 5

If $\mathsf {PKE}$ is weakly $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-resilient, then $\mathsf {TE}$ satisfies security against the receiver.

Proof of Theorem 5. Let $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$ be any PPT adversary that attacks the security against the receiver of $\mathsf {TE}$. We show that for $\mathcal {A}$, there exists a PPT $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-respecting adversary $\mathcal {B}_{\mathsf {}}$ such that $\mathsf {Adv}_{\mathsf {TE},\mathcal {A}}^{\mathsf {receiver}}(\lambda ) = \mathsf {Adv}_{\mathsf {PKE},\mathcal {B}_{\mathsf {}}, 0.6 \ell _{\mathsf {sk}}}^{\mathsf {wlr}}(\lambda )$, which implies the theorem. The description of $\mathcal {B}_{\mathsf {}} = (\mathcal {B}_{\mathsf {0}}, \mathcal {B}_{\mathsf {1}})$ is as follows.

• $\mathcal {B}_{\mathsf {0}}(1^\lambda )$: $\mathcal {B}_{\mathsf {0}}$ first runs $(i^*, \mathsf {st}) \leftarrow \mathcal {A}_0(1^\lambda )$. Next, $\mathcal {B}_{\mathsf {0}}$ computes $\mathsf {k}\leftarrow \mathsf {K}(1^\lambda )$, and picks ${\mathsf {sk}}_{i^*,\mathsf {k}[i^*]} \xleftarrow {\mathsf {r}}\{0,1\}^{\ell _{\mathsf {sk}}}$. Let $P := \{j \in [\ell _{\mathsf {sk}}] ~|~ {\mathsf {sk}}_{i^*,\mathsf {k}[i^*]}[j] = 1 \oplus \mathsf {k}[i^*]\}$ and $\ell := |P|$, and suppose P is $\{p_1,\dots , p_\ell \}$ such that $1 \le p_1< \dots < p_\ell \le \ell _{\mathsf {sk}}$. $\mathcal {B}_{\mathsf {0}}$ defines the leakage function $f_P: \{0,1\}^{\ell _{\mathsf {sk}}} \rightarrow \{0,1\}^{\ell }$ by

  $$ f_P(\mathsf {z}) := (\mathsf {z}[p_1], \dots , \mathsf {z}[p_\ell ]) \in \{0,1\}^\ell . $$

  Then, $\mathcal {B}_{\mathsf {0}}$ sets $\mathsf {st}_{\mathcal {B}_{\mathsf {}}}$ as all the information known to $\mathcal {B}_{\mathsf {0}}$, and terminates with output $(f_P, \mathsf {st}_{\mathcal {B}_{\mathsf {}}})$.

• $\mathcal {B}_{\mathsf {1}}^{\mathcal {O}_{\mathsf {Enc}}(\cdot , \cdot )}(\mathsf {pk}', f_P(\mathsf {sk}') = (\mathsf {sk}' [p_1 ], \dots , \mathsf {sk}' [p_{\ell } ]) \in \{0,1\}^{\ell }, \mathsf {st}_{\mathcal {B}_{\mathsf {}}})$: (where $(\mathsf {pk}', \mathsf {sk}')$ denotes the key pair generated in $\mathcal {B}_{\mathsf {}}$’s experiment) $\mathcal {B}_{\mathsf {1}}$ first computes ${\mathsf {pk}}_{i^*,\mathsf {k}[i^*]} \leftarrow \mathsf {KG}({\mathsf {sk}}_{i^*,\mathsf {k}[i^*]})$, and regards $\mathsf {pk}'$ as ${\mathsf {pk}}_{i^*,1 \oplus \mathsf {k}[i^*]}$ (correspondingly, implicitly regards $\mathsf {sk}'$ as ${\mathsf {sk}}_{i^*,1 \oplus \mathsf {k}[i^*]} \in \{0,1\}^{\ell _{\mathsf {sk}}}$). Then, for every $j \in [\ell _{\mathsf {sk}}]$, $\mathcal {B}_{\mathsf {1}}$ generates ${\mathsf {e}}_{i^*,j}$ by

  $$ {\mathsf {e}}_{i^*,j} \leftarrow {\left\{ \begin{array}{ll} \mathtt {flip}&{} \text {if}~j \in P \wedge \mathsf {sk}'[j] = \mathsf {k}[i^*]\\ \mathsf {E}(\mathsf {k}, {\mathsf {sk}}_{i^*,\mathsf {k}[i^*]}[j]) &{} \text {otherwise} \end{array}\right. }. $$

  Note that by the definition of P, we have ${\mathsf {sk}}_{i^*,\mathsf {k}[i^*]}[j] = 1 \oplus \mathsf {k}[i^*]$ if and only if $j \in P$. Furthermore, by the definition of the leakage function $f_P(\cdot )$, we have $\mathsf {sk}'[j] = {\mathsf {sk}}_{i^*,1 \oplus \mathsf {k}[i^*]}[j]$ for all $j \in P$. Hence, we have

  $$\begin{aligned} j \in P \wedge \mathsf {sk}'[j] = \mathsf {k}[i^*]&~~\Longleftrightarrow ~~ ({\mathsf {sk}}_{i^*,\mathsf {k}[i^*]}[j], {\mathsf {sk}}_{i^*,1 \oplus \mathsf {k}[i^*]}[j]) = (1 \oplus \mathsf {k}[i^*], \mathsf {k}[i^*])\\&~~\Longleftrightarrow ~~ ({\mathsf {sk}}_{i^*,0}[j], {\mathsf {sk}}_{i^*,1}[j]) = (1,0). \end{aligned}$$

  Hence, the generation of ${\mathsf {e}}_{i^*,j}$ is in fact exactly the same as in $\mathsf {Expt}_{\mathsf {TE},\mathcal {A}}^{\mathsf {receiver}}(\lambda )$. Then, $\mathcal {B}_{\mathsf {1}}$ generates the remaining components in $\mathsf {PK}= ({\mathsf {pk}}_{i,0}, {\mathsf {pk}}_{i,1}, {\mathsf {e}}_{i,1}, \dots , {\mathsf {e}}_{i,\ell _{\mathsf {sk}}})_{i \in [\ell _\mathsf {k}]}$ (i.e. the components for the positions $i \in [\ell _\mathsf {k}] \setminus \{i^*\}$) by itself exactly as $\mathsf {TKG}(1^\lambda )$ does. Now, $\mathcal {B}_{\mathsf {1}}$ runs $\mathcal {A}_1(\mathsf {PK}, \mathsf {SK}= \mathsf {k}, \mathsf {st})$. When $\mathcal {A}_1$ submits an encryption query $(\mathsf {m}_0, \mathsf {m}_1)$, $\mathcal {B}_{\mathsf {1}}$ just forwards it to its own encryption oracle $\mathcal {O}_{\mathsf {Enc}}(\cdot , \cdot )$, and returns whatever returned from the oracle to $\mathcal {A}_1$. When $\mathcal {A}_1$ terminates with output $b'$, $\mathcal {B}_{\mathsf {1}}$ terminates with output $b'$.

The above completes the description of $\mathcal {B}_{\mathsf {}}$. As mentioned above, $\mathcal {B}_{\mathsf {}}$ generates the key pair $(\mathsf {PK}, \mathsf {SK})$ with exactly the same distribution as that in the actual experiment for security against the receiver. Since $\mathcal {B}_{\mathsf {}}$ embeds its instance $\mathsf {pk}'$ to the position $(i^*, 1 \oplus \mathsf {k}[i^*])$, it is straightforward to see that $\mathcal {B}_{\mathsf {}}$ perfectly simulates the security experiment for $\mathcal {A}$ so that $\mathcal {A}$’s the challenge bit is that of $\mathcal {B}_{\mathsf {}}$’s, and thus $\mathcal {B}_{\mathsf {}}$’s advantage is exactly the same as that of $\mathcal {A}$’s.

It remains to confirm that $\mathcal {B}_{\mathsf {}}$ is a $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-respecting adversary, namely, $0.6 \ell _{\mathsf {sk}}\ge \mathbf {H}_{\infty }(\mathsf {sk}') - \widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}'| f_P(\mathsf {sk}'), \mathsf {st}_{\mathcal {B}_{\mathsf {}}}) = \ell _{\mathsf {sk}}- \widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}' | f_P(\mathsf {sk}'), \mathsf {st}_{\mathcal {B}_{\mathsf {}}})$ or equivalently $2^{-\widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}'|f_P(\mathsf {sk}'), \mathsf {st}_{\mathcal {B}_{\mathsf {}}})} \le 2^{- 0.4 \ell _{\mathsf {sk}}}$ holds. To see this, firstly note that $\mathsf {st}_{\mathcal {B}_{\mathsf {}}}$ output by $\mathcal {B}_{\mathsf {0}}$ is independent of the choice of $\mathsf {sk}'\xleftarrow {\mathsf {r}}\{0,1\}^{\ell _{\mathsf {sk}}}$, and thus we have $\widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}'|f_P(\mathsf {sk}'), \mathsf {st}_{\mathcal {B}_{\mathsf {}}}) = \widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}'|f_P(\mathsf {sk}'))$. Thus, it is sufficient to show $2^{-\widetilde{\mathbf {H}}_{\infty }(\mathsf {sk}'|f_P(\mathsf {sk}'))} \le 2^{- 0.4\ell _{\mathsf {sk}}}$. Next, notice that P is distributed uniformly over $2^{[\ell _{\mathsf {sk}}]}$ (i.e. all the subsets of $[\ell _{\mathsf {sk}}]$), since P is determined by the random choice of ${\mathsf {sk}}_{i^*,\mathsf {k}[i^*]} \xleftarrow {\mathsf {r}}\{0,1\}^{\ell _{\mathsf {sk}}}$. Thus, we have

where the equality (*) uses $\sum _{k = 0}^n \left( {\begin{array}{c}n\\ k\end{array}}\right) x^k = (1 + x)^n$, and the inequality (†) uses $\log _2 3 < 1.6$. Hence, $\mathcal {B}_{\mathsf {}}$ is $(0.6\ell _{\mathsf {sk}})$-noisy-leakage-respecting.       $\Box$ (Theorem 5)

Theorem 6

If $\mathsf {SKE}$ is $\text {CIRC}^{(1)}$ secure and $\mathsf {PKE}$ is $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-resilient, then $\mathsf {TE}$ satisfies security against outsiders.

Proof of Theorem 6. Let $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$ be any PPT adversary that attacks the security against outsiders of $\mathsf {TE}$. We show that there exist PPT adversaries $\mathcal {B}_{\mathsf {c}}$ and $\mathcal {B}_{\mathsf {w}}$ (where the latter is $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-respecting) satisfying

$$\begin{aligned} \mathsf {Adv}_{\mathsf {TE},\mathcal {A}}^{\mathsf {outsider}}(\lambda ) \le 2 \cdot \mathsf {Adv}_{\mathsf {SKE},\mathcal {B}_{\mathsf {c}},1}^{\mathsf {circ}}(\lambda ) + \mathsf {Adv}_{\mathsf {PKE},\mathcal {B}_{\mathsf {w}}, 0.6 \ell _{\mathsf {sk}}}^{\mathsf {wlr}}(\lambda ) , \end{aligned}$$

(1)

which implies the theorem.

To this end, we consider the following two games Game 1 and Game 2.

Game 1: This is the experiment for security against outsiders $\mathsf {Expt}_{\mathsf {TE},\mathcal {A}}^{\mathsf {outsider}}(\lambda )$.

Game 2: Same as Game 1, except that every invocation of $\mathsf {E}(\mathsf {k}, \cdot )$ during the generation of $\mathsf {PK}$ is replaced with $\mathsf {E}(\mathsf {k}, 0)$.

For $t \in \{1,2\}$, let $\mathtt {SUC}_{t}$ be the event that $\mathcal {A}$ succeeds in guessing the challenge bit (i.e. $b' = b$ occurs) in Game t. By the definitions of the games and events and the triangle inequality, we have

$$\begin{aligned} \mathsf {Adv}_{\mathsf {TE},\mathcal {A}}^{\mathsf {outsider}}(\lambda ) = 2 \cdot \Bigl |\Pr [\mathtt {SUC}_{1}] - \frac{1}{2} \Bigr | \le 2 \cdot \Bigl |\Pr [\mathtt {SUC}_{1}] - \Pr [\mathtt {SUC}_{2}] \Bigr | + 2 \cdot \Bigl | \Pr [\mathtt {SUC}_{2}] - \frac{1}{2} \Bigr |. \end{aligned}$$

(2)

In the following, we show how the terms appearing in Eq. 2 are bounded.

Lemma 2

There exists a PPT adversary $\mathcal {B}_{\mathsf {c}}$ such that $\mathsf {Adv}_{\mathsf {SKE},\mathcal {B}_{\mathsf {c}},1}^{\mathsf {circ}}(\lambda ) = |\Pr [\mathtt {SUC}_{1}] - \Pr [\mathtt {SUC}_{2}]|$.

Proof of Lemma 2. The description of $\mathcal {B}_{\mathsf {c}}$ is as follows. Below, $\mathsf {k}$ and $\beta$ denote the secret key and the challenge bit, respectively, chosen in $\mathcal {B}_{\mathsf {c}}$’s experiment. Furthermore, since there is only a single key in the experiment of $\mathcal {B}_{\mathsf {c}}$, we simplify the interface of the circular-encryption oracle $\mathcal {O}_{\mathsf {circ}}$ to take just $\mathtt {cmd}\in [\ell _\mathsf {k}] \cup \{\mathtt {zero}, \mathtt {one}\}$ as input.

$\mathcal {B}_{\mathsf {c}}^{\mathcal {O}_{\mathsf {circ}}(\cdot )}(1^\lambda )$: $\mathcal {B}_{\mathsf {c}}$ first runs $(i^*, v^*, \mathsf {st}) \leftarrow \mathcal {A}_0(1^\lambda )$. Next, for every $i \in [\ell _\mathsf {k}]$, $\mathcal {B}_{\mathsf {c}}$ does the following:

• 1. For both $v \in \{0,1\}$, pick ${\mathsf {sk}}_{i,v} \xleftarrow {\mathsf {r}}\{0,1\}^{\ell _{\mathsf {sk}}}$ and compute ${\mathsf {pk}}_{i,v} \leftarrow \mathsf {KG}({\mathsf {sk}}_{i,v})$.

• 2. For the positions $j \in [\ell _{\mathsf {sk}}]$ for which $({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) = (1,0)$ holds, set ${\mathsf {e}}_{i,j} \leftarrow \mathtt {flip}$.

• 3. For the remaining positions $j \in [\ell _{\mathsf {sk}}]$ with $({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) \ne (1,0)$, set

  $$ \mathtt {cmd}_j \leftarrow {\left\{ \begin{array}{ll} \mathtt {zero}&{} \text {if}~({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) = (0,0)\\ \mathtt {one}&{} \text {if}~({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) = (1,1)\\ i &{} \text {if}~({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) = (0,1) \end{array}\right. }, $$

  submit $\mathtt {cmd}_j$ to $\mathcal {B}_{\mathsf {c}}$’s oracle $\mathcal {O}_{\mathsf {circ}}(\cdot )$, and receive ${\mathsf {e}}_{i,j}$ as the answer from $\mathcal {O}_{\mathsf {circ}}$. Note that if $({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) = (0,1)$ then ${\mathsf {sk}}_{i,\mathsf {k}[i]}[j] = \mathsf {k}[i]$ holds, and the latter is trivially true for the cases $({\mathsf {sk}}_{i,0}[j], {\mathsf {sk}}_{i,1}[j]) \in \{(0,0), (1,1)\}$. Thus, $\mathcal {O}_{\mathsf {circ}}$ computes ${\mathsf {e}}_{i,j}$ as follows:

  $$ {\mathsf {e}}_{i,j} \leftarrow {\left\{ \begin{array}{ll} \mathsf {E}(\mathsf {k}, {\mathsf {sk}}_{i,\mathsf {k}[i]}[j]) &{} \text {if}~\beta = 1\\ \mathsf {E}(\mathsf {k}, 0) &{} \text {if}~\beta = 0 \end{array}\right. }. $$

  Therefore, if $\beta =1$ (resp. $\beta =0$), then ${\mathsf {e}}_{i,j}$ for every $j \in [\ell _{\mathsf {sk}}]$ is computed exactly as in Game 1 (resp. Game 2).

Then, $\mathcal {B}_{\mathsf {c}}$ sets $\mathsf {PK}\leftarrow ({\mathsf {pk}}_{i,0}, {\mathsf {pk}}_{i,1}, {\mathsf {e}}_{i,1}, \dots , {\mathsf {e}}_{i,\ell _{\mathsf {sk}}})_{i \in [\ell _\mathsf {k}]}$, picks $b \xleftarrow {\mathsf {r}}\{0,1\}$, and runs $\mathcal {A}_1(\mathsf {PK}, \mathsf {st})$.

$\mathcal {B}_{\mathsf {c}}$ answers encryption queries $(\mathsf {m}_0, \mathsf {m}_1)$ from $\mathcal {A}_1$ by returning $\mathsf {ct}\leftarrow \mathsf {Enc}({\mathsf {pk}}_{i^*,v^*}, \mathsf {m}_b)$ to $\mathcal {A}_1$.

When $\mathcal {A}_1$ terminates with output $b'$, $\mathcal {B}_{\mathsf {c}}$ terminates with output $\beta ' \leftarrow (b' {\mathop {=}\limits ^{?}}b)$.

The above completes the description of $\mathcal {B}_{\mathsf {c}}$. It is straightforward to see that if $\beta =1$ (resp. $\beta =0$), then $\mathcal {B}_{\mathsf {c}}$ simulates Game 1 (resp. Game 2) perfectly for $\mathcal {A}$. Since $\mathcal {B}_{\mathsf {c}}$ outputs $\beta ' = 1$ if and only if $\mathcal {A}$ succeeds in guessing the challenge bit (i.e. $b' = b$ occurs), we have

$$ \mathsf {Adv}_{\mathsf {SKE},\mathcal {B}_{\mathsf {c}},1}^{\mathsf {circ}}(\lambda ) = \Bigl |\Pr [\beta ' = 1|\beta = 1] - \Pr [\beta ' = 1 |\beta = 0] \Bigr | = \Bigl | \Pr [\mathtt {SUC}_{1}] - \Pr [\mathtt {SUC}_{2}] \Bigr |. $$

$\Box$ (Lemma 2)

Lemma 3

There exists a PPT $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-respecting adversary $\mathcal {B}_{\mathsf {w}}$ such that $\mathsf {Adv}_{\mathsf {PKE},\mathcal {B}_{\mathsf {w}}, 0.6\ell _{\mathsf {sk}}}^{\mathsf {wlr}}(\lambda ) = 2 \cdot |\Pr [\mathtt {SUC}_{2}] - 1/2]$.

Proof Sketch of Lemma 3. The reduction algorithm $\mathcal {B}_{\mathsf {w}}$ for the proof of this lemma proceeds very similarly to $\mathcal {B}_{\mathsf {}}$ used in the proof of Theorem 5, with the following differences:

• $\mathcal {B}_{\mathsf {w}}$ embeds its instance $\mathsf {pk}'$ into the position $(i^*, v^*)$ output by $\mathcal {A}_0$ (rather than $(i^*, 1 \oplus \mathsf {k}[i^*])$), which means that $(\mathsf {pk}', \mathsf {sk}')$ now corresponds to $({\mathsf {pk}}_{i^*,v^*}, {\mathsf {sk}}_{i^*,v^*})$; $\mathcal {B}_{\mathsf {w}}$ generates the key pair of the opposite position, namely $({\mathsf {pk}}_{i^*,1 \oplus v^*}, {\mathsf {sk}}_{i^*,1 \oplus v^*})$ by itself.

• $\mathcal {B}_{\mathsf {w}}$ defines the set P by $P := \{j \in [\ell _{\mathsf {sk}}]| {\mathsf {sk}}_{i^*,1 \oplus v^*}[j] = v^*\}$, and uses it to define the leakage function $f_P(\cdot )$ exactly $\mathcal {B}_{\mathsf {}}$ in the proof of Theorem 5 does. Note that since we have the correspondence $\mathsf {sk}' = {\mathsf {sk}}_{i^*,v^*}$, the leakage $f_P(\mathsf {sk}')$ is $({\mathsf {sk}}_{i^*,v^*}[j])_{j \in P}$.

• For every $j \in [\ell _{\mathsf {sk}}]$, $\mathcal {B}_{\mathsf {w}}$ generates ${\mathsf {e}}_{i^*,j}$ by

  $$ {\mathsf {e}}_{i^*,j} \leftarrow {\left\{ \begin{array}{ll} \mathtt {flip}&{} \text {if}~j \in P \wedge \mathsf {sk}'[j] = 1 \oplus v^*\\ \mathsf {E}(\mathsf {k}, 0) &{} \text {otherwise} \end{array}\right. }. $$

  Then, by the definition of P and the correspondence $\mathsf {sk}' = {\mathsf {sk}}_{i^*,v^*}$, we have

  $$\begin{aligned} j \in P \wedge \mathsf {sk}'[j] = 1 \oplus v^*&\Longleftrightarrow ({\mathsf {sk}}_{i^*,1 \oplus v^*}[j], {\mathsf {sk}}_{i^*,v^*}[j]) = (v^*, 1 \oplus v^*)\\&\Longleftrightarrow ({\mathsf {sk}}_{i^*,0}[j], {\mathsf {sk}}_{i^*,1}[j]) = (1,0). \end{aligned}$$

  Thus, ${\mathsf {e}}_{i^*,j}$ is generated exactly as in Game 2.

Then, it is straightforward to see that $\mathcal {B}_{\mathsf {w}}$ is $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-respecting and simulates Game 2 perfectly for $\mathcal {A}$, and its advantage in attacking the weak noisy-leakage-resilience of $\mathsf {PKE}$ is exactly $2 \cdot |\Pr [\mathtt {SUC}_{2}] - 1/2|$.      $\Box$ (Lemma 3)

Combining Lemmas 2 and 3 with Eq. 2, we can conclude that there exist PPT adversaries $\mathcal {B}_{\mathsf {c}}$ and $\mathcal {B}_{\mathsf {w}}$ satisfying Eq. 1.                                    $\Box$ (Theorem 6)

5 Implications of Our TE Scheme

In this section, we explain the implications of our TE scheme in Sect. 4.

Completeness of Circular Security for KDM Security in the Single-Key Setting. Note that our construction of TE is a fully black-box construction from the building blocks. Moreover, by appropriately setting parameters, we can construct a PKE scheme with simple key generation whose secret key length is $\ell _{\mathsf {sk}}$ and that satisfies weak $(0.6 \ell _{\mathsf {sk}})$-noisy-leakage-resilience, based on any IND-CPA secure PKE scheme via Lemma 1. Hence, the following theorem follows from the combination of Theorems 4, 5, and 6, and Lemma 1.

Theorem 7

If there exist an IND-CPA secure PKE scheme and a $\text {CIRC}^{(1)}$ secure bit-SKE scheme, then for any polynomial $\mathsf {size}= \mathsf {size}(\lambda )$, there exists a ${\mathcal {B}_{\mathsf {size}}}\text {-KDM}^{(1)}\text {-CPA}$ secure PKE scheme. Furthermore, there exists a fully black-box construction of a ${\mathcal {P}}\text {-KDM}^{(1)}\text {-CPA}$ secure PKE scheme from an IND-CPA secure PKE scheme and a $\text {CIRC}^{(1)}$ secure bit-SKE scheme.

Combining Theorem 7 with Theorem 3, we obtain the following completeness theorem for KDM security in the single-key setting. This improves the results of [3] and [22] in terms of assumptions.

Theorem 8

If there exists an IND-CPA secure PKE scheme and a $\text {CIRC}^{(1)}$ secure bit-SKE scheme, then for any polynomial $\mathsf {size}= \mathsf {size}(\lambda )$, there exists a ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(1)}\text {-}\mathrm{CCA}$ secure PKE scheme.

In Sect. 7, we will show that a similar completeness theorem for KDM security in the multi-key setting can be established. For the result, we will rely on the results on IND-CCA secure PKE and a reusable DV-NIZK argument system⁹ for NP languages stated below.

Additional Results on IND-CCA PKE and DV-NIZK. As stated in Theorem 7, a ${\mathcal {P}}\text {-KDM}^{(1)}\text {-CPA}$ secure PKE scheme can be constructed from an IND-CPA secure PKE and a $\text {CIRC}^{(1)}$ secure bit-SKE scheme in a fully black-box manner. Hence, combined with Theorem 2, we obtain the following result on IND-CCA secure PKE, which improves the results of [23] and [19] in terms of assumptions.

Theorem 9

There exists a fully black-box construction of an IND-CCA secure PKE scheme from an IND-CPA secure PKE scheme and a $\text {CIRC}^{(1)}$ secure bit-SKE scheme.

Finally, combining Theorem 7 with the results in [22, 25] that a reusable DV-NIZK argument system for all NP languages can be constructed from the combination of IND-CPA secure PKE and ${\mathcal {P}}\text {-KDM}^{(1)}\text {-CPA}$ secure SKE, we also obtain the following result that improves [22] and [25] in terms of assumptions.

Theorem 10

If there exists an IND-CPA secure PKE scheme and a $\text {CIRC}^{(1)}$ secure bit-SKE scheme, then there exists a reusable DV-NIZK argument system for all NP languages.

6 Conformed Targeted Encryption

In this section, we introduce an encryption primitive that we call conformed targeted encryption (CTE). This is an extension of an ordinary TE, and has some similar flavor to augmented TE formalized by Barak et al. [5]. Our definitional choice of CTE is made so that (1) it can be achieved from the combination of an IND-CPA secure PKE scheme and a circular secure bit-SKE scheme, and (2) it is sufficient as a building block for constructing a KDM-CCA secure PKE scheme in the multi-key setting.

In Sect. 6.1, we give the definitions for CTE and explain its difference with augmented TE formalized by Barak et al.. In Sect. 6.2, we show how our TE scheme presented in Sect. 4 can be extended to be a CTE scheme satisfying all the requirements.

6.1 Definitions

Syntax and Correctness. A conformed targeted encryption (CTE) scheme $\mathsf {TE}$ consists of the six algorithms $(\mathsf {CKG}, \mathsf {CEnc}, \mathsf {CDec}, \widehat{\mathsf {CDec}}, \mathsf {CSEnc}, \mathsf {CSDec})$:

• $\mathsf {CKG}$, $\mathsf {CEnc}$, and $\mathsf {CDec}$ are defined similarly to the key generation, encryption, and decryption algorithms of a TE scheme, respectively, except that in addition to a public/secret key pair $(\mathsf {pk}, \mathsf {sk})$, $\mathsf {CKG}$ also outputs a trapdoor $\mathsf {td}$. This process is written as $(\mathsf {pk}, \mathsf {sk}, \mathsf {td}) \leftarrow \mathsf {CKG}(1^\lambda )$.

• $\widehat{\mathsf {CDec}}$ is the trapdoor-decryption algorithm that takes $\mathsf {td}$, an index $i \in [\ell _{\mathsf {sk}}]$, a bit $v \in \{0,1\}$, and a ciphertext $\mathsf {ct}$ (supposedly generated by $\mathsf {CEnc}$) as input, and outputs a message $\mathsf {m}$.

• $\mathsf {CSEnc}$ and $\mathsf {CSDec}$ are the additional secret-key encryption and decryption algorithms, respectively, where they use a secret key $\mathsf {sk}$ generated by $\mathsf {CKG}$. We denote $\widetilde{\mathsf {ct}}$ to indicate that it is a ciphertext generated by $\mathsf {CSEnc}$.

As the correctness for a CTE scheme, we require that for all $\lambda \in \mathbb {N}$ and $(\mathsf {pk}, \mathsf {sk}, \mathsf {td}) \leftarrow \mathsf {CKG}(1^\lambda )$, the following conditions are satisfied:

• 1. $\mathsf {CDec}(\mathsf {pk}, \mathsf {sk}, i, \mathsf {CEnc}(\mathsf {pk}, i, \mathsf {sk}[i], \mathsf {m})) = \mathsf {m}$ holds for all $i \in [\ell _{\mathsf {sk}}]$ and $\mathsf {m}$.

• 2. $\widehat{\mathsf {CDec}}(\mathsf {td}, i, v, \mathsf {CEnc}(\mathsf {pk}, i, v, \mathsf {m})) = \mathsf {m}$ holds for all $(i, v) \in [\ell _{\mathsf {sk}}] \times \{0,1\}$ and $\mathsf {m}$.

• 3. $\mathsf {CDec}(\mathsf {pk}, \mathsf {sk}, i, \mathsf {ct}) = \widehat{\mathsf {CDec}}(\mathsf {td}, i, \mathsf {sk}[i], \mathsf {ct})$ holds for all $i \in [\ell _{\mathsf {sk}}]$ and $\mathsf {ct}$ (not necessarily in the support of $\mathsf {CEnc}$).

• 4. $\mathsf {CSDec}(\mathsf {sk}, \mathsf {CSEnc}(\mathsf {sk}, \mathsf {m})) = \mathsf {m}$ holds for all $\mathsf {m}$.

Note that the first condition of correctness ensures that $(\mathsf {CKG}, \mathsf {CEnc}, \mathsf {CDec})$ constitutes a TE scheme when $\mathsf {td}$ in the output of $\mathsf {CKG}$ is discarded. We also remark that the third condition of correctness is required to hold for all values of $\mathsf {ct}$ not necessarily in the support of $\mathsf {CEnc}$. Looking ahead, this property plays an important role in our construction of KDM-CCA secure PKE in Sect. 7.

Security Definitions for CTE. For a CTE scheme, we require two security notions: security against the receiver and special weak circular security (in the multi-key setting).¹⁰ The former is defined in exactly the same way as that for TE, except that we just discard and ignore the trapdoor $\mathsf {td}$ generated from $\mathsf {CKG}$. Thus, we omit its formal description.

The latter security notion, special weak circular security, requires that the additional secret-key encryption/decryption algorithms $(\mathsf {CSEnc}, \mathsf {CSDec})$ satisfy a weak form of circular security in the multi-key setting. Specifically, in the $n$-key setting, we require that messages encrypted by $\mathsf {CSEnc}$ be hidden even in the presence of public keys $\{\mathsf {pk}^{s}\}_{s\in [n]}$, trapdoors $\{\mathsf {td}^s\}_{s\in [n]}$, and encryptions of a “key cycle” $\{\mathsf {CSEnc}(\mathsf {sk}^s, \mathsf {sk}^{(s\bmod n) + 1})\}_{s\in [n]}$. We call it weak since except for giving $\{(\mathsf {pk}^s, \mathsf {td}^s)\}_{s\in [n]}$ to an adversary, our definition is the same as the definition of weak circular security formalized by Cash, Green, and Hohenberger [13].

Formally, let $n= n(\lambda )$ be a polynomial. For a CTE scheme $(\mathsf {CKG}, \mathsf {CEnc}, \mathsf {CDec}, \widehat{\mathsf {CDec}}, \mathsf {CSEnc}, \mathsf {CSDec})$, $n$, and an adversary $\mathcal {A}$, consider the experiment $\mathsf {Expt}_{\mathsf {CTE},\mathcal {A},n}^{\mathsf {sp-wcirc}}(\lambda )$ described in Fig. 6. Note that in the experiment, $\mathcal {O}_{\mathsf {\mathsf {CSEnc}}}$ is an ordinary (challenge) encryption oracle. Thus, except for the encryptions of a key cycle $\{\mathsf {CSEnc}(\mathsf {sk}^s, \mathsf {sk}^{(s\bmod n)+1})\}_{s\in [n]}$, $\mathcal {A}$ is not allowed to directly obtain encryptions of key-dependent messages.

Definition 6

(Special Weak Circular Security). Let $n= n(\lambda )$ be a polynomial. We say that a CTE scheme $\mathsf {CTE}$ satisfies special weak circular security in the $n$-key setting (special weak $\text {CIRC}^{(n)}$ security) if for all PPT adversaries $\mathcal {A}$, we have $\mathsf {Adv}_{\mathsf {CTE},\mathcal {A},n}^{\mathsf {sp-wcirc}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {CTE},\mathcal {A},n}^{\mathsf {sp-wcirc}}(\lambda ) = 1] - 1/2| = \mathsf {negl}(\lambda )$.

Fig. 6.

The experiment for defining special weak circular security for a CTE scheme.

Relation to Augmented TE. As mentioned earlier, Barak et al. [5] introduced the notion of augmented TE, and used it to construct a ${\mathcal {B}_{\mathsf {size}}}\text {-KDM}^{(n)}\text {-CPA}$-secure PKE scheme for any polynomials $n= n(\lambda )$ and $\mathsf {size}= \mathsf {size}(\lambda )$. An augmented TE scheme is a TE scheme with the additional public-key encryption/decryption algorithms, for which Barak et al. assumed circular security in the $n$-key setting. (Their definition requires that encryptions of a key cycle of length $n$ are indistinguishable from encryptions of some fixed messages.)

We observe that their security proof goes through even if (1) the additional encryption/decryption algorithms are of secret-key, and (2) we only require weak circular security in the $n$-key setting [13], which requires that IND-CPA security holds in the presence of encryptions of a key cycle of length $n$.

Our formalization for CTE is based on these observations, but CTE has an additional syntactical extension involving a trapdoor generated in the key generation algorithm, together with the additional correctness requirements. This plays an important role in the security proof for our ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure PKE scheme presented in Sect. 7. We also remark that we do not require CTE to satisfy security against outsiders, while it is necessary for augmented TE used in the construction of KDM-CPA secure PKE in [5]. Our construction of KDM-CCA secure PKE does not require security against outsiders for the underlying CTE scheme because of the other building blocks. (See Sect. 7.)

6.2 Construction

Let $n= n(\lambda )$ be a polynomial for which we would like our CTE scheme $\mathsf {CTE}$ to satisfy special weak $\text {CIRC}^{(n)}$ security. Let $\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$ and $\mathsf {SKE}= (\mathsf {K}, \mathsf {E}, \mathsf {D})$ be PKE and SKE schemes as in Sect. 4, respectively, where we now require $\mathsf {SKE}$ to be $\text {CIRC}^{(n)}$ secure.

Our construction of a CTE scheme $\mathsf {CTE}= (\mathsf {CKG}, \mathsf {CEnc}, \mathsf {CDec}, \widehat{\mathsf {CDec}}, \mathsf {CSEnc}, \mathsf {CSDec})$ based on $\mathsf {PKE}$ and $\mathsf {SKE}$, is a simple extension of our TE scheme $\mathsf {TE}= (\mathsf {TKG}, \mathsf {TEnc}, \mathsf {TDec})$ presented in Sect. 4. Specifically, each algorithm of $\mathsf {CTE}$ operates as follows:

• $\mathsf {CKG}$ computes a public/secret key pair $(\mathsf {PK}, \mathsf {SK})$ in exactly the same way as $\mathsf {TKG}$, and additionally outputs $\mathsf {td}:= ({\mathsf {pk}}_{i,v}, {\mathsf {sk}}_{i,v})_{i \in [\ell _\mathsf {k}], v \in \{0,1\}}$ as a trapdoor.

• $\mathsf {CEnc}$ and $\mathsf {CDec}$ are exactly $\mathsf {TEnc}$ and $\mathsf {TDec}$, respectively.

• $\widehat{\mathsf {CDec}}(\mathsf {td}, i, v, \mathsf {ct}) := \mathsf {Dec}({\mathsf {pk}}_{i,v}, {\mathsf {sk}}_{i,v}, \mathsf {ct})$.

• $\mathsf {CSEnc}$ and $\mathsf {CSDec}$ use $\mathsf {E}$ and $\mathsf {D}$ to encrypt/decrypt a message/ciphertext in a bit-wise fashion. More specifically, $\mathsf {CSEnc}(\mathsf {SK}= \mathsf {k}, \mathsf {m}\in \{0,1\}^\mu )$ outputs $\widetilde{\mathsf {ct}}= (\widetilde{\mathsf {ct}}_t)_{t \in [\mu ]}$, where $\widetilde{\mathsf {ct}}_t \leftarrow \mathsf {E}(\mathsf {k}, \mathsf {m}[t])$ for each $t \in [\mu ]$; $\mathsf {CDec}(\mathsf {SK}= \mathsf {k}, \widetilde{\mathsf {ct}}= (\widetilde{\mathsf {ct}}_t)_{t \in [\mu ]})$ computes $\mathsf {m}[t] \leftarrow \mathsf {D}(\mathsf {k}, \widetilde{\mathsf {ct}}_t)$ for each $t \in [\mu ]$, and outputs $\mathsf {m}$.

Correctness. The first condition of correctness is exactly the same as the correctness for TE. The third condition of correctness holds because $\mathsf {sk}'$ computed in $\mathsf {CDec}(\mathsf {PK}, \mathsf {SK}=\mathsf {k}, i, \cdot )$ is ${\mathsf {sk}}_{i,\mathsf {k}[i]}$ as we saw for the correctness of $\mathsf {TE}$. The second and fourth conditions of correctness are trivially satisfied because of the correctness of $\mathsf {PKE}$ and $\mathsf {SKE}$, respectively.

Security. The following theorems guarantee that $\mathsf {CTE}$ satisfies the two kinds of security notions for CTE. We omit the proof of Theorem 11 since it is exactly the same as that of Theorem 5.

Theorem 11

If $\mathsf {PKE}$ is weakly $(0.6\ell _{\mathsf {sk}})$-noisy-leakage-resilient, then $\mathsf {CTE}$ satisfies security against the receiver.

Theorem 12

Let $n= n(\lambda )$ be a polynomial. If $\mathsf {SKE}$ is $\text {CIRC}^{(n)}$ secure, then $\mathsf {CTE}$ satisfies special weak $\text {CIRC}^{(n)}$ security.

Proof Sketch of Theorem 12. This is straightforward to see by noting that $\mathsf {CSEnc}$ directly uses $\mathsf {E}$ to encrypt a given message in a bit-wise fashion, and the trapdoor $\mathsf {td}$ consists only of key pairs of the underlying PKE scheme $\mathsf {PKE}$ and thus is independent of a secret key $\mathsf {SK}= \mathsf {k}$.

More specifically, for $s\in [n]$, let $\mathsf {SK}^s= \mathsf {k}^s$ denote the $s$-th secret key. Then, consider a modified security experiment, which proceeds similarly to the experiment for the special weak $\text {CIRC}^{(n)}$ security of $\mathsf {CTE}$, except that for every $s\in [n]$, all invocations of $\mathsf {E}(\mathsf {k}^s, \cdot )$ (which include those during the execution of $\mathsf {EncCycle}((\mathsf {SK}^s= \mathsf {k}^s)_{s\in [n]})$, those during the execution of $(\mathsf {PK}^s, \mathsf {SK}^s= \mathsf {k}^s, \mathsf {td}^s) \leftarrow \mathsf {CKG}(1^\lambda )$, and those for encryption queries from an adversary) are replaced with $\mathsf {E}(\mathsf {k}^s, 0)$. Note that this modified experiment is independent of the challenge bit b, and thus any adversary has zero advantage. Furthermore, by the $\text {CIRC}^{(n)}$ security of $\mathsf {SKE}$, for any PPT adversary, its advantage in the original special weak $\text {CIRC}^{(n)}$ security experiment is negligibly close to that in the modified experiment. $\Box$ (Theorem 12)

7 KDM-CCA Security in the Multi-key Setting

In this section, we show the completeness of circular security in the multi-key setting. Specifically, we show the following theorem:

Theorem 13

Let $n= n(\lambda )$ be a polynomial. Assume that there exist an IND-CPA secure PKE scheme and a $\text {CIRC}^{(n)}$ secure bit-SKE scheme. Then, for any polynomial $\mathsf {size}= \mathsf {size}(\lambda )$, there exists a ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure PKE scheme.

Note that this result improves the result by Kitagawa and Matsuda [22] (recalled as Theorem 3) in terms of the strength of assumptions and the number of keys.

As explained earlier, we will show the above theorem by constructing a ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure PKE scheme from the building blocks that are all implied by an IND-CPA secure PKE scheme and a $\text {CIRC}^{(n)}$ secure bit-SKE scheme. Our construction can be seen as combining the construction ideas from the bounded-$\text {KDM}^{(n)}$-CPA secure PKE scheme from an augmented TE scheme by Barak et al. [5] and the bounded-$\text {KDM}^{(1)}$-CCA secure PKE scheme from an IND-CPA secure PKE scheme and a projection-$\text {KDM}^{(1)}$-CPA secure SKE scheme by Kitagawa and Matsuda [22]. The latter construction in fact uses an IND-CCA secure PKE scheme, a garbling scheme, and a reusable DV-NIZK argument system as additional building blocks, which are implied by the assumption used in [22]. Construction-wise, roughly speaking, our construction is obtained by replacing the underlying IND-CPA secure scheme of the Kitagawa-Matsuda construction with a CTE scheme.

Construction. To construct a ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure PKE scheme, we use the following building blocks all of which are implied by the combination of an IND-CPA secure PKE scheme and a $\text {CIRC}^{(n)}$ secure SKE scheme:

• Let $\mathsf {CTE}= (\mathsf {CKG}, \mathsf {CEnc}, \mathsf {CDec}, \widehat{\mathsf {CDec}}, \mathsf {CSEnc}, \mathsf {CSDec})$ be a CTE scheme whose secret key length is $\ell _{\mathsf {sk}}$. Let $\ell _{\widetilde{\mathsf {e}}}$ denote the length of a ciphertext when encrypting a message of length $\ell _{\mathsf {sk}}$ by using $\mathsf {CSEnc}$. We denote the randomness space of $\mathsf {CEnc}$ by $\mathcal {R}$.

• Let $\mathsf {PKE}_{\mathsf {cca}}= (\mathsf {KG}_{\mathsf {cca}}, \mathsf {Enc}_{\mathsf {cca}}, \mathsf {Dec}_{\mathsf {cca}})$ be an IND-CCA secure PKE scheme.

• Let $\mathsf {GC}= (\mathsf {Garble}, \mathsf {Eval}, \mathsf {Sim})$ be a garbling scheme for circuits.¹¹

• Let $\mathsf {DVNIZK}= (\mathsf {DVKG},\mathsf {P},\mathsf {V})$ be a reusable DV-NIZK argument system for the following NP language L:¹²

  

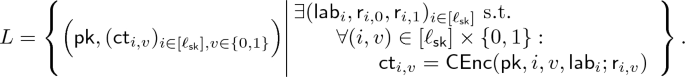
Let $\mu = \mu (\lambda )$ be a polynomial that denotes the length of messages to be encrypted by our constructed PKE scheme. Let $n= n(\lambda )$ and $\mathsf {size}= \mathsf {size}(\lambda ) \ge \max \{n\cdot \ell _{\mathsf {sk}}, \mu \}$ be polynomials for which we wish to achieve ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ security. Finally, let $\mathsf {pad}= O(n\cdot (|\mathsf {CSDec}| + \ell _{\widetilde{\mathsf {e}}}) + \mathsf {size}) \ge \mathsf {size}$ be the size parameter for the underlying garbling scheme (which is the size of a circuit that will be specified in the security proof), where $|\mathsf {CSDec}|$ denotes the size of the circuit computing $\mathsf {CSDec}$.

Using these ingredients, we construct our proposed PKE scheme $\mathsf {PKE}_{\mathsf {kdm}}= (\mathsf {KG}_{\mathsf {kdm}}, \mathsf {Enc}_{\mathsf {kdm}}, \mathsf {Dec}_{\mathsf {kdm}})$ whose message space is $\{0,1\}^{\mu }$ as described in Fig. 7.

Fig. 7.

The construction of a ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure PKE scheme $\mathsf {PKE}_{\mathsf {kdm}}$ from a CTE scheme $\mathsf {CTE}$, an IND-CCA secure PKE scheme $\mathsf {PKE}_{\mathsf {cca}}$, a garbling scheme for circuits $\mathsf {GC}$, and a reusable DV-NIZK argument system $\mathsf {DVNIZK}$. The notations like $(X_{i,v})_{i,v}$ and $(X_i)_i$ are abbreviations for $(X_{i,v})_{i \in [\ell _{\mathsf {sk}}],v \in \{0,1\}}$ and $(X_i)_{i \in [\ell _{\mathsf {sk}}]}$, respectively. $^{(\star )}$ If $\mathsf {CSDec}$, $\mathsf {CDec}$, or $\mathsf {Dec}_{\mathsf {cca}}$ returns $\bot$, then $\mathsf {Dec}_{\mathsf {kdm}}$ returns $\bot$ and terminate.

Correctness. The correctness of $\mathsf {PKE}_{\mathsf {kdm}}$ follows from that of the building blocks. Specifically, let $(\mathsf {PK}, \mathsf {SK}) = ((\mathsf {pk}, \mathsf {pk}_{\mathsf {cca}}, \mathsf {pk}_{\mathsf {dv}}, \widetilde{\mathsf {ct}}), \mathsf {sk})$ be a key pair output by $\mathsf {KG}_{\mathsf {kdm}}$, let $\mathsf {m}\in \{0,1\}^{\mu }$ be any message, and let $\mathsf {CT}\leftarrow \mathsf {Enc}_{\mathsf {kdm}}(\mathsf {PK}, \mathsf {m})$ be an honestly generated ciphertext. Due to the correctness of $\mathsf {CTE}$, $\mathsf {PKE}_{\mathsf {cca}}$, and $\mathsf {DVNIZK}$, each decryption/verification done in the execution of $\mathsf {Dec}_{\mathsf {kdm}}(\mathsf {PK}, \mathsf {SK}, \mathsf {CT})$ never fails, and just before the final step of $\mathsf {Dec}_{\mathsf {kdm}}$, the decryptor can recover a garbled circuit $\widetilde{\mathsf {Q}}$ and the labels $(\mathsf {lab}_i)_{i}$, which is generated as $(\widetilde{\mathsf {Q}}, (\mathsf {lab}_i)_{i}) \leftarrow \mathsf {Sim}(1^\lambda , \mathsf {pad}, \mathsf {m})$. Then, by the correctness of $\mathsf {GC}$, we have $\mathsf {Eval}(\widetilde{\mathsf {Q}}, (\mathsf {lab}_i)_{i}) = \mathsf {m}$.

Security. The following theorem guarantees the ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ security of $\mathsf {PKE}_{\mathsf {kdm}}$. Combined with Theorems 9, 10, 11, and 12, it implies Theorem 13.

Theorem 14

Let $n= n(\lambda )$, $\mu = \mu (\lambda )$, and $\mathsf {size}= \mathsf {size}(\lambda ) \ge \max \{n\cdot \ell _{\mathsf {sk}}, \mu \}$ be any polynomials. Also, let $\mathsf {pad}= O(n\cdot (|\mathsf {CSDec}| + \ell _{\widetilde{\mathsf {e}}}) + \mathsf {size}) \ge \mathsf {size}$ (which is the size of a circuit that will be specified in the proof), where $|\mathsf {CSDec}|$ denotes the size of the circuit computing $\mathsf {CSDec}$. Assume that $\mathsf {CTE}$ satisfies security against the receiver and special weak $\text {CIRC}^{(n)}$ security, $\mathsf {PKE}_{\mathsf {cca}}$ is IND-CCA secure, $\mathsf {GC}$ is a secure garbling scheme, and $\mathsf {DVNIZK}$ is a reusable DV-NIZK argument system (satisfying soundness and zero-knowledge) for the NP language L. Then, $\mathsf {PKE}_{\mathsf {kdm}}$ is ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ secure.

Overview of the Proof. Due to the space limitation, the formal proof is given in the full version. Here, we give an overview of the proof.

The proof uses a sequence of games argument. The first game is the original ${\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{KDM}^{(n)}\text {-}\mathrm{CCA}$ experiment regarding $\mathsf {PKE}_{\mathsf {kdm}}$. Let $\mathcal {A}$ be a PPT adversary, and for $s\in [n]$, let $(\mathsf {PK}^s = (\mathsf {pk}^s, \mathsf {pk}_{\mathsf {cca}}^s, \mathsf {pk}_{\mathsf {dv}}^s, \widetilde{\mathsf {ct}}^s), \mathsf {SK}^s= \mathsf {sk}^s)$ denote the s-th public/secret key pair.

We first invoke the zero-knowledge of $\mathsf {DVNIZK}$ to change the security game so that the simulator $\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2)$ is used to generate each $(\mathsf {pk}_{\mathsf {dv}}^s, \mathsf {sk}_{\mathsf {dv}}^s)$ at key generation, and generate $\pi$ in the response to KDM-encryption queries.

Next, we deal with the KDM-encryption queries $(\alpha , f_0, f_1)$, and make the behavior of the KDM-encryption oracle (essentially) independent of the secret keys $\{\mathsf {sk}^s\}_{s\in [n]}$. If there existed only a single key pair $(\mathsf {PK}, \mathsf {SK}= \mathsf {sk})$, then we could change the generation of the CTE-ciphertexts $(\mathsf {ct}_{i,v})_{i,v}$ in the KDM-encryption oracle so that we garble the KDM function $f_b$ by $(\widetilde{\mathsf {Q}}, (\mathsf {lab}_{i,v})_{i,v}) \leftarrow \mathsf {Garble}(1^\lambda , f_b)$ and then encrypt $\mathsf {lab}_{i,v}$ by $\mathsf {ct}_{i,v} \leftarrow \mathsf {CEnc}(\mathsf {pk}^s, i, v, \mathsf {lab}_{i,v})$ for every $(i, v) \in [\ell _{\mathsf {sk}}] \times \{0,1\}$. Since $\mathsf {Eval}(\widetilde{\mathsf {Q}}, (\mathsf {lab}_{i,\mathsf {sk}[i]})_{i \in [\ell _{\mathsf {sk}}]}) = f_b(\mathsf {sk})$, this can go unnoticed by $\mathcal {A}$ due to the security of $\mathsf {GC}$ and the security against the receiver of $\mathsf {CTE}$, and the behavior of the resulting KDM-encryption oracle becomes independent of the secret key $\mathsf {sk}$. However, we cannot take this rather simple approach in the multi-key setting, since the KDM-function $f_b$ here is a function that takes all keys $\{\mathsf {sk}^s\}_{s\in [n]}$ as input, while we need to garble a circuit that takes a single key $\mathsf {sk}^\alpha$ as input. Here, we rely on the clever technique of Barak et al. [5] to transform the KDM function $f_b$ to a circuit $\mathsf {Q}$ so that $\mathsf {Q}(\mathsf {sk}^\alpha ) = f_b((\mathsf {sk}^{s})_{s\in |n|})$ holds, by using encryptions of the key cycle $\{\widetilde{\mathsf {e}}^s= \mathsf {CSEnc}(\mathsf {sk}^s, \mathsf {sk}^{(s\bmod n) + 1})\}_{s\in [n]}$. Specifically, $\mathsf {Q}$ has $\alpha$, $f_b$, and $\{\widetilde{\mathsf {e}}^s\}_{s\in [n]}$ hardwired, and it on input $\mathsf {sk}^{\alpha }$ decrypts the encryptions of the key cycle one-by-one to recover all keys $\{\mathsf {sk}^s\}_{s\in [n]}$ and then outputs $f_b((\mathsf {sk}^s)_{s\in [n]})$. Then, we can garble $\mathsf {Q}$ instead of garbling $f_b$ directly, and the argument goes similarly to the above. This change necessitates that the subsequent games generate the encryptions of the key cycle.

Then, we deal with the decryption queries $(\alpha , \mathsf {CT})$, and make the behavior of the decryption oracle independent of the secret keys $\{\mathsf {sk}^s\}_{s\in [n]}$. To achieve this, notice that the only essential part that we need to use the secret key $\mathsf {sk}^\alpha$ in the decryption procedure is the step of executing $\mathsf {lab}_i \leftarrow \mathsf {CDec}(\mathsf {pk}^\alpha , \mathsf {sk}^\alpha , \mathsf {ct}_{i, \mathsf {sk}[i]})$ for every $i \in [\ell _{\mathsf {sk}}]$. To eliminate the dependency on $\mathsf {sk}^\alpha$ in this step, in the next game we replace the above step with $\mathsf {lab}_i \leftarrow \widehat{\mathsf {CDec}}(\mathsf {td}^\alpha , i,\mathsf {sk}^{\alpha }[i], \mathsf {ct}_{i, \mathsf {sk}^\alpha [i]})$ for every $i \in [\ell _{\mathsf {sk}}]$. This makes no change in the behavior of the decryption oracle due to the third condition of the correctness of $\mathsf {CTE}$. Next, we further change this step to always decrypt the “0-side” ciphertext $\mathsf {ct}_{i,0}$ as $\mathsf {lab}_i \leftarrow \widehat{\mathsf {CDec}}(\mathsf {td}^\alpha , i, 0, \mathsf {ct}_{i, 0})$ for every $i \in [\ell _{\mathsf {sk}}]$. Now the behavior of the decryption oracle becomes independent of the secret keys $\{\mathsf {sk}^s\}_{s\in [n]}$. The behavior of the decryption oracle could differ between the change only if $\widehat{\mathsf {CDec}}(\mathsf {td}^{\alpha }, i^*, 0, \mathsf {ct}_{i^*,0}) \ne \widehat{\mathsf {CDec}}(\mathsf {td}^{\alpha }, i^*, 1, \mathsf {ct}_{i^*, 1})$ holds for some $i^*\in [\ell _{\mathsf {sk}}]$ and yet the proof $\pi$ recovered from $\mathsf {CT}$ is valid. Let us call such a query a bad decryption query. If $\mathcal {A}$ does not make a bad decryption query, this change of the behavior of the decryption oracle cannot be noticed by $\mathcal {A}$. Similarly to [22], we bound the probability of a bad query occurring to be negligible using a deferred analysis technique and postpone to bound it in a later (in fact the final) game, together with the second correctness condition of $\mathsf {CTE}$. See the formal proof for this argument.

Now, since the behavior of the KDM-encryption and decryption oracles become independent of the secret keys $\{\mathsf {sk}^s\}_{s\in [n]}$, the remaining steps in which we use the secret keys are to generate $\{\widetilde{\mathsf {ct}}^s\}_{s\in [n]}$ in public keys, and to generate the encryptions of the key cycle $\{\widetilde{\mathsf {e}}^s\}_{s\in [n]}$. Then, we can rely on the special weak $\text {CIRC}^{(n)}$ security of $\mathsf {CTE}$ to ensure that $\widetilde{\mathsf {ct}}^{s}$ is indistinguishable from an encryption of a garbage that contains no information on $(\mathsf {sk}_{\mathsf {cca}}^s, \mathsf {sk}_{\mathsf {dv}}^s)$ in the presence of the trapdoors $\{\mathsf {td}^s\}_{s\in [n]}$ and the encryptions of the key cycle $\{\widetilde{\mathsf {e}}^s\}_{s\in [n]}$. Finally, we invoke the IND-CCA security of $\mathsf {PKE}_{\mathsf {cca}}$ to conclude that $\mathcal {A}$’s advantage in the final game is negligible.

For all the details, see the formal proof in the full version.