Abstract
We observe that all previously known lattice-based blind signature schemes contain subtle flaws in their security proofs (e.g., Rückert, ASIACRYPT ’08) or can be attacked (e.g., BLAZE by Alkadri et al., FC ’20). Motivated by this, we revisit the problem of constructing blind signatures from standard lattice assumptions.
We propose a new three-round lattice-based blind signature scheme whose security can be proved, in the random oracle model, from the standard SIS assumption. Our starting point is a modified version of the (insecure) BLAZE scheme, which itself is based Lyubashevsky’s three-round identification scheme combined with a new aborting technique to reduce the correctness error. Our proof builds upon and extends the recent modular framework for blind signatures of Hauck, Kiltz, and Loss (EUROCRYPT ’19). It also introduces several new techniques to overcome the additional challenges posed by the correctness error which is inherent to all lattice-based constructions.
While our construction is mostly of theoretical interest, we believe it to be an important stepping stone for future works in this area.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Blind Signatures. Blind signatures, first proposed by Chaum [18], are a fundamental cryptographic primitive with many applications such as eVoting [54], eCash [18], anonymous credentials [6, 8, 14,15,16, 19, 46], and, as of late, privacy preserving protocols in the context of blockchain protocols [61]. Informally, a blind signature scheme is an interactive protocol between a signer \(\mathsf {S} \) (holding a secret key \( sk \)) and a user \(\mathsf {U} \) (holding a public key \( pk \) and a message m) with the goal that \(\mathsf {U} \) obtains a signature \(\sigma \) on m. The protocol should satisfy correctness (i.e., \(\sigma \) can be verified using the public key \( pk \) of \(\mathsf {S} \) and m), unforgeability (i.e., only \(\mathsf {S} \) can issue signatures), and blindness (i.e., \(\mathsf {S} \) is not able to link \(\sigma \) to a particular execution of the protocol in which it was created). Blind signatures are among the most well-studied cryptographic primitives and it is well known how to construct blind signatures from general complexity assumptions [22, 23, 34]. However, achieving efficient constructions from standard assumptions is known to be a notoriously difficult task with only a handful of constructions being known. To make matters worse, even among these works, some have been pointed out to contain flawed security proofs [2, 56]. Effectively, this leaves only the original works due to Pointcheval and Stern [50,51,52,53] based on Schnorr [57] and Okomoto-Schnorr [44] signatures. Blind Signatures from Lattices. In this work, we revisit the problem of constructing blind signatures from standard lattice assumptions. This question was first addressed by Rückert [56], who gave a candidate construction based on Lyubashevsky’s identification scheme [38] from the SIS assumption. Unfortunately, as we will explain in Sect. 1.2, his security proof contains a subtle flaw. While the recent work of Hauck, Kiltz, and Loss [32] introduces a general framework to obtain blind signatures from (collision resistant) linear hash functions, their framework does not cover the setting of lattice assumptions. Informally, the reason for this is that in the context of lattice-based constructions, most known cryptographic primitives exhibit some form of noticeable correctness error. Indeed, this is also true for Lyubashevsky’s identification scheme/linear hash function implicitly used in [56]. This makes it impossible to apply the analysis of [32] directly, since it crucially relies on the fact that if both \(\mathsf {S} \) and \(\mathsf {U} \) behave honestly, \(\mathsf {U} \) always obtains a valid signature. Since [56] was published, more lattice-based constructions of blind signatures have been proposed. As we will discuss in detail below, all of these schemes either inherit the proof errors from [56] or introduce new ones. The main goal of our work is to give the first direct lattice-based blind signature scheme with a correct security proof.
1.1 Our Contributions
We construct a blind signature scheme from any linear hash functions [5, 32] with noticeable correctness error. We use the aborting technique introduced by Alkadri, El Bansarkhani, and Buchmann [4] to reduce the correctness error of the blind signature scheme. Instantiating our construction with Lyubashevsky’s linear hash function [38] we obtain a lattice-based blind signature scheme from the SIS assumption.
While our work offers the first correct proof for a lattice-based blind signature scheme, it comes with several severe drawbacks. First, we can only prove blindness in the weaker honest signer model [34] as compared to the malicious signer model [23]. We leave the construction of a scheme in the malicious signer setting as an open problem. Second, our construction comes with an exponential security loss in the reduction from the underlying hardness assumption (here, the SIS assumption). This is inherited from the proof technique of Pointcheval and Stern in the discrete logarithm setting [53]. This strongly restricts the number of signatures that can be issued per public key to a poly-logarithmic amount. Indeed, a sub-exponential attack due to Schnorr and Wagner [58, 60] resulting from the ROSFootnote 1 problem shows that for the Schnorr and Okamoto-Schnorr blind signature schemes, these parameters are optimal. Extending [32, 58], we are also able to relate the security of our blind signature to a Generalized ROS problem whose hardness is independent of the SIS problem. However, the sub-exponential attack of Schnorr and Wagner cannot be directly translated to the Generalized ROS problem due to the algebraic structure of our lattice-based instantiation (see Sect. 7). Therefore, an interesting open question is whether our “lattice” variant of the Generalized ROS problem can be solved in sub-exponential time. Nevertheless, we believe that our scheme makes an important first step toward future endeavors in this area by giving the first comprehensive and modular security proof for a blind signature scheme from lattice assumptions. While our scheme might not be practical by itself (our example instantiation has signatures sizes of roughly 36 MB),Footnote 2 it seems reasonable to apply similar ideas as in [49] to extend the number of allowed sessions per public key to a polynomial amount at not much overhead (but at the restriction of issuing signatures in a sequential fashion).
1.2 Problems with Existing Schemes
In the following we will first explain in detail the problems in the proof of Rückert’s lattice-based blind signature scheme and then sketch how these errors propagate to subsequent schemes. We also list some other lattice-based constructions which have been found to be incorrect.
Rückert’s Blind Signature Scheme. The key idea in the proof of Rückert’s lattice-based blind signature scheme [56] is to rewind the forger (with partially different random oracles) so as to obtain two distinct values \(\chi \) and \(\chi '\) satisfying \(\mathsf {F} (\chi )=\mathsf {F} (\chi ')\), i.e., a collision in the underlying linear hash function. (In the lattice setting, a collision in the hash function directly implies a non-trivial solution \(\chi -\chi '\) to the SIS problem.) To argue that \(\chi \ne \chi '\), [56] attempts to apply the general forking lemma of Bellare and Neven [9] to the forger and argues that witness indistinguishability alone is sufficient to ensure \(\chi \ne \chi '\). Here, [56] relies on Lemma 8 from Pointcheval and Stern’s proof [53], who followed a similar approach. However, Lemma 8 does not state that \(\chi \) and \(\chi '\) are distinct; only that (by witness indistinguishability of their scheme) there exist two distinct secret keys \( sk , sk '\), which can lead to identical transcripts. This is insufficient to ensure \(\chi \ne \chi '\) in the subsequent rewinding step. In fact, the Generalized ROS attack mentioned above works independently of the concrete secret key that is being used. Using this attack, it is always possible to force an outcome of \(\chi =\chi '\) if the number of signatures per public key becomes larger than polylogarithmic in the security parameter. The crucial argument toward proving \(\chi \ne \chi '\) only follows from Lemma 9 and the subsequent parts of Pointcheval and Stern’s proof and is completely missing from Rückert’s proof. It relies on a very subtle probabilistic method argument that only works in a (small) range of parameters for which the ROS problem remains information theoretically hard. Moreover, both Lemma 8 and 9 of [53] apply exclusively to the Okamoto-Schnorr scheme and cannot be transferred to other schemes directly. Adapting these lemmas to a setting with correctness error is one of the key novelties in our proof.
\(\mathsf {BLAZE}\) and \(\mathsf {BLAZE}^+\). \(\mathsf {BLAZE}\) by Alkadri, El Bansarkhani, and Buchmann [3] improves Rückert’s construction in the following two aspects. Firstly, \(\mathsf {BLAZE}\) applies Gaussian rejection sampling [39] instead of uniform [38]. Secondly, it introduces the concept of signed permutations which allows to get rid of rejection sampling on the unblinded challenge values. While \(\mathsf {BLAZE}\) introduces several interesting new concepts for constructing lattice-based blind signatures, its security analysis reuses the (incorrect) security arguments of Rückert at a crucial point in the reduction, and hence inherits its problems. Concretely, in the one-more unforgeability proof of [3, Theorem 3] it is missing the argument that the candidate solution for the inhomogeneous RSIS problem computed in Case 2 is non-trivial. Even worse and independent of the aforementioned problems with the proof, \(\mathsf {BLAZE}\) is not one-more unforgeable as we will sketch now. Consider a user \(\mathsf {U} \) interacting with the signer \(\mathsf {S} \) in the one-more unforgeability experiment. At the end of the protocol execution, an honest \(\mathsf {U} \) performs rejection sampling on some values \((\hat{z}_1, \hat{z}_2)\) contained in the signature. (Rejection sampling on \(\mathsf {U} \)’s side is used to ensure blindness.) If rejection sampling rejects, \(\mathsf {U} \) sends the random coins used for rejection sampling as a proof to \(\mathsf {S} \) which, upon successful verification, triggers a restart of the protocol. However, even in case rejection sampling rejects, the signature can still be valid and which case a dishonest \(\mathsf {U} \) can trigger a restart of the protocol while still learning a valid signature. Since by the restart of the protocol \(\mathsf {U} \) learns another valid signature, this observation can be turned into a simple one-more unforgeability attack. The aforementioned attack on \(\mathsf {BLAZE}\) actually disappears in the recently proposed \(\mathsf {BLAZE}^+\) protocol [4] because \(\mathsf {U} \) performs multiple rejection samplings in parallel and the probability that all of them reject becomes negligible. \(\mathsf {BLAZE}^+\) introduces a new technique of reducing correctness error by performing multiple rejection samplings in parallel in order to reduce the communication complexity. Unfortunately, the security analysis also reuses the (incorrect) security arguments of Rückert and hence inherits its problems.
Further Schemes. Three recent works [13, 37, 47] propose new lattice-based blind signatures, but they also rely on the same analysis as Rückert to argue that a collision can be found with non-negligible probability when rewinding (see above). Unfortunately, this implies that all of these schemes do not have a valid security proof. There has been a line of research on lattice-based blind signatures using preimage sampleable trapdoor functions [20, 28, 29, 62, 63]. As shown by [3], all these schemes are insecure. Concretely, they give attacks which either recover the secret key or solve the underlying lattice problem in at most two executions of the signing protocol.
1.3 Related Work
Three round blind signatures are not achievable in the standard model [25]. We circumvent their result by using (programmable) random oracles and therefore believe that our proof strategies cannot be easily extended to the standard model. Blind signatures are impossible to construct from one-way permutations [35], even in the random oracle model. We circumvent their result by relying on the stronger assumption of collision resistance. A large class of Schnorr-type blind signature schemes cannot be proved secure if the underlying identification scheme has a unique witness [7]. We circumvent their result by requiring our underlying hard problem to have multiple witnesses corresponding to each public key.
As already mentioned, round optimal blind signatures can be constructed from general complexity assumptions beyond one-way permutations [22, 23, 31, 34]. The impossibility results of [25] are circumvented by either relying on a CRS [23] or using complexity leveraging [22, 31]. We refer to [22] for a detailed discussion on the topic of constructing blind signatures from general assumptions.
Several works [2, 7, 12, 26, 30, 31, 45, 51, 53] show how to construct efficient blind signatures schemes from concrete assumptions in the setting of prime-order groups, in some cases relying on bilinear maps.
1.4 Organization
After establishing some preliminaries in Sect. 2, in Sect. 3 we will introduce the notion of linear hash functions \(\mathsf {LHF} \) with noticeable correctness error. In Sect. 4 we will define syntax and security of canonical (three-round) blind signature schemes. Figure 5 constructs a blind signature scheme \(\mathsf {BS} _{\eta }[\mathsf {LHF},\mathsf {H},\mathsf {G} ]\) from any linear hash function \(\mathsf {LHF} \) and two standard hash functions \(\mathsf {H} \) and \(\mathsf {G} \). This section also contains our main theorems about one-more unforgeability (Theorem 1) and blindness (Theorem 2). As a first step in the proof of Theorem 1, in Sect. 5 we will reduce the one-more unforgeability of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {H}, \mathsf {G} ]\) to one-more man-in-the-middle security of the underlying canonical identification scheme \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\) in the random oracle model. The proof of the one-more man-in-the-middle security of \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\) will be given in the full version [33]. In Sect. 6 we will provide an example instantiation of our framework based on the standard SIS assumption. Finally, Sect. 7 generalizes the ROS attack to our setting and proves that any attack on it also implies an attack on the one-more unforgeability of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {H}, \mathsf {G} ]\).
2 Preliminaries and Notation
Sets and Vectors. For \(n\in \mathbb {N}\), [n] denotes the set \(\{1,\dots ,n\}\). We use bold-faced, lower case letters \({\textit{\textbf{h}}}\) to denote a vector of elements and denote the length of \({\textit{\textbf{h}}}\) as \(|{\textit{\textbf{h}}}|\). For \(j\ge 1\), we write \({\textit{\textbf{h}}}_j\) to denote the j-th element of \({\textit{\textbf{h}}}\) and we write \({\textit{\textbf{h}}}_{[j]}\) to refer to the first j entries of \({\textit{\textbf{h}}}\), i.e., the elements \({\textit{\textbf{h}}}_1,...,{\textit{\textbf{h}}}_j\). We use boldface, upper case letters \(\mathbf {A}\) to denote matrices. We denote the i-th row of \(\mathbf {A}\) as \(\mathbf {A}_i\) and the j-th entry of \(\mathbf {A}_i\) as \(\mathbf {A}_{i,j}\). We let \(\varDelta (X,Y)\) indicate the statistical distance between two distributions X, Y.
Sampling from Sets. We write  to denote that the variable h is uniformly sampled from the finite set \(\mathcal {S}\). For \(1 \le j \le Q\) and \({\textit{\textbf{g}}} \in \mathcal {S}^{j-1}\), we write
to denote that the variable h is uniformly sampled from the finite set \(\mathcal {S}\). For \(1 \le j \le Q\) and \({\textit{\textbf{g}}} \in \mathcal {S}^{j-1}\), we write  to denote that the vector \({\varvec{h'}}\) is uniformly sampled from \(\mathcal {S}^{Q}\), conditioned on \({\varvec{h'}}_{[j-1]}= {\textit{\textbf{g}}}\). This sampling process can be implemented by copying vector \({\textit{\textbf{g}}}\) into the first \(j-1\) entries of \({\textit{\textbf{h}}}'\) and next sampling the remaining \(Q-j+1\) entries of \({\textit{\textbf{h}}}\), (i.e.,
to denote that the vector \({\varvec{h'}}\) is uniformly sampled from \(\mathcal {S}^{Q}\), conditioned on \({\varvec{h'}}_{[j-1]}= {\textit{\textbf{g}}}\). This sampling process can be implemented by copying vector \({\textit{\textbf{g}}}\) into the first \(j-1\) entries of \({\textit{\textbf{h}}}'\) and next sampling the remaining \(Q-j+1\) entries of \({\textit{\textbf{h}}}\), (i.e.,  ).
).
Algorithms. We use uppercase, serif-free letters \(\mathsf {A},\mathsf {B} \) to denote algorithms. Unless otherwise stated, algorithms are probabilistic and we write  to denote that \(\mathsf {A} \) returns \((y_1,\ldots )\) when run on input \((x_1,\ldots )\). We write \(\mathsf {A} ^\mathsf {B} \) to denote that \(\mathsf {A} \) has oracle access to \(\mathsf {B} \) during its execution. To make the randomness \(\omega \) of an algorithm \(\mathsf {A} \) on input x explicit, we write \(\mathsf {A} (x;\omega )\). Note that in this notation, \(\mathsf {A} \) is deterministic. For a randomised algorithm \(\mathsf {A} \), we use the notation \(y\in \mathsf {A} (x)\) to denote that y is a possible output of \(\mathsf {A} \) on input x.
to denote that \(\mathsf {A} \) returns \((y_1,\ldots )\) when run on input \((x_1,\ldots )\). We write \(\mathsf {A} ^\mathsf {B} \) to denote that \(\mathsf {A} \) has oracle access to \(\mathsf {B} \) during its execution. To make the randomness \(\omega \) of an algorithm \(\mathsf {A} \) on input x explicit, we write \(\mathsf {A} (x;\omega )\). Note that in this notation, \(\mathsf {A} \) is deterministic. For a randomised algorithm \(\mathsf {A} \), we use the notation \(y\in \mathsf {A} (x)\) to denote that y is a possible output of \(\mathsf {A} \) on input x.
Security Games. We use standard code-based security games [11]. A game \(\mathbf {G}\) is a probability experiment in which an adversary \(\mathsf {A} \) interacts with an implicit challenger that answers oracle queries issued by \(\mathsf {A} \). \(\mathbf {G}\) has one main procedure and an arbitrary amount of additional oracle procedures which describe how these oracle queries are answered. To distinguish game-related oracle procedures from algorithmic procedures more clearly, we denote the former using monospaced font, e.g., \(\mathtt {Oracle}\). We denote the (binary) output b of game \(\mathbf {G}\) between a challenger and an adversary \(\mathsf {A} \) as \(\mathbf {G}^\mathsf {A} \Rightarrow b\). \(\mathsf {A} \) is said to win \(\mathbf {G}\) if \(\mathbf {G}^\mathsf {A} \Rightarrow 1\). Unless otherwise stated, the randomness in the probability term \(\Pr [\mathbf {G}^\mathsf {A} \Rightarrow 1]\) is over all the random coins in game \(\mathbf {G}\).
Algebra. We let \(\oplus \) denote the bitwise XOR operation. A module is specified by two sets \(\mathcal {S} \) and \(\mathcal {M} \), where \(\mathcal {S} \) is a ring with multiplicative identity element \(1_\mathcal {S} \) and \(\langle \mathcal {M},+,0\rangle \) is an additive Abelian group and a mapping \(\cdot \) : \(\mathcal {S} \times \mathcal {M} \rightarrow \mathcal {M} \), s.t. for all \(r,s\in \mathcal {S} \) and \(x,y\in \mathcal {M} \) we have (i) \(r\cdot (x+y)=r\cdot x+r\cdot y\); (ii) \((r+s)\cdot x=r\cdot x+s\cdot x\); (iii) \((rs)\cdot x= r\cdot (s\cdot x)\); and (iv) \(1_S\cdot x=x\).
Security Notions. We formalize all security notions relative to some fixed parameters \( par \). This streamlines the exposition considerably. In doing so, we consider a non-uniform notion of security, as the RSIS problem is not hard for fixed \( par \), but only for \( par \) drawn (uniformly) at random in the security experiment. This is comparable to considerations as in [55]. However, we remark that using the splitting lemma our theorems can easily be made to work in a setting where \( par \) is indeed chosen at random along with the remaining (random) parts.
3 Linear Hash Functions
In this section we define linear hash function families with correctness error which are a generalization of linear (hash) function families with perfect correctness [5, 32].
Syntax. A linear hash function family \(\mathsf {LHF} \) is a tuple of algorithms \((\mathsf {PGen},\mathsf {F})\). On input the security parameter, the randomized algorithm \(\mathsf {PGen} \) returns some parameters \( par \), which implicitly define the sets
where \(\mathcal {S} \) is a set of scalars such that \(\mathcal {D} \) and \(\mathcal {R} \) are modules over \(\mathcal {S} \). The parameters \( par \) also define 9 filter sets
Throughout the paper, we will assume that \( par \) is fixed and implicitly given to all algorithms. For linear hash function families with perfect correctness [32], the filter sets are trivial, i.e., \(\mathcal {S}_{\mathsf {xxx}} =\mathcal {S} \) and \(\mathcal {D}_{\mathsf {yyy}} =\mathcal {D} \).
Algorithm \(\mathsf {F} ( par ,\cdot )\) implements a mapping from \(\mathcal {D} \) to \(\mathcal {R} \). To simplify our presentation, we will omit \( par \) from \(\mathsf {F} \)’s input from now on. \(\mathsf {F} (\cdot )\) is required to be a module homomorphism, meaning that for any \(x,y\in \mathcal {D} \) and \(s\in \mathcal {S} \):
We now define the technical conditions of torsion-freeness, regularity, enclosedness, and smoothness of \(\mathsf {LHF} \) that will be useful for proving correctness and security of blind signatures constructed from \(\mathsf {LHF} \).
Torsion-Freeness and Regularity. We say that \(\mathsf {LHF} \) has a torsion-free element from the kernel if for all \( par \) generated with \(\mathsf {PGen} \), there exist \(z^* \in \mathcal {D} \,{\setminus }\,\{0\}\) such that (i) \(\mathsf {F} (z^*)=0\); and (ii) for all \(c_1, c_2 \in \mathcal {S}_{c} \) satisfying \((c_1-c_2) \cdot z^* =0\) we have \(c_1-c_2=0\). Note that the existence of such an element implies that \(\mathsf {F} \) is a many-to-one mapping.
We call \(\mathsf {LHF} \) \((\varepsilon , Q')\)-regular, if for all \( par \) generated with \(\mathsf {PGen} \), there exist sets \(\mathcal {D}_{ sk } ',\mathcal {D}_{r} '\) and a torsion-free element from the kernel \(z^*\) s.t.
and where
and
Similar to the work of Hauck et al. [32], our proof of one-more unforgeability uses torsion-freeness and regularity to argue that a transcript of the scheme with a secret key \( sk \) can be preserved when switching to a different (valid) secret key \( sk ':= sk +z^*\), with high probability.
Enclosedness Error. We say that \(\mathsf {LHF} \) has enclosedness errors \((\delta _1,\delta _2,\delta _3)\) if for all \( par \in \mathsf {PGen} (1^\kappa ),\) \(c'\in \mathcal {S}_{c'},c\in \mathcal {S}_{c},s\in \mathcal {D}_{s}, sk \in \mathcal {D}_{ sk },\)

The enclosedness error of \(\mathsf {LHF} \) is directly linked to the correctness error of our schemes. Intuitively, the smaller this error, the easier it is to get a scheme which almost always works correctly.
Smoothness. We say that \(\mathsf {LHF} \) is smooth if the following conditions hold for all \( par \in \mathsf {PGen} (1^\kappa )\):
-
(S1)
For all \(s\in \mathcal {D}_{s} \) and \(s'\in \mathcal {D}_{s'} \), we have \(\left\Vert s'-s\right\Vert _{\infty }\in \mathcal {D}_{\alpha } \)
-
(S2)
For all \(s_1,s_2\in \mathcal {D}_{s} \) and random variables
 ,
,  we have that \(\hat{\alpha }+s_2\) and \(\alpha ^*+s_1\) are identically distributed.
we have that \(\hat{\alpha }+s_2\) and \(\alpha ^*+s_1\) are identically distributed. -
(S3)
For all \(s_1,s_2\in \mathcal {D}_{s} \) and random variables
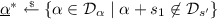 ,
, 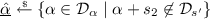 we have that \(\underline{\hat{\alpha }}+s_2\) and \(\underline{\alpha ^*}+s_1\) are identically distributed.
we have that \(\underline{\hat{\alpha }}+s_2\) and \(\underline{\alpha ^*}+s_1\) are identically distributed. -
(S4)
For all \(c'\in \mathcal {S}_{c'} \) and \(c\in \mathcal {S}_{c} \), we have \(\left\Vert c-c'\right\Vert _{\infty }\in \mathcal {S}_{\beta } \).
-
(S5)
For all \(c_1',c_2'\in \mathcal {S}_{c'} \) and random variables
 ,
,  we have that \(\hat{\beta }+c_2'\) and \(\beta ^*+c_1'\) are identically distributed.
we have that \(\hat{\beta }+c_2'\) and \(\beta ^*+c_1'\) are identically distributed. -
(S6)
For all \(c_1',c_2'\in \mathcal {S}_{c'} \) and random variables
 ,
, 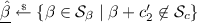 we have that \(\underline{\hat{\beta }}+c_2'\) and \(\underline{\beta ^*}+c_1'\) are identically distributed.
we have that \(\underline{\hat{\beta }}+c_2'\) and \(\underline{\beta ^*}+c_1'\) are identically distributed.
Smoothness of \(\mathsf {LHF} \) will be a crucial tool for proving blindness of our schemes. Intuitively, smoothness allows to ‘match’ any message/signature pair \((m_i,\sigma _i)\) that was generated via the \(i^{th}\) run of the scheme to the transcript \(T_j\) of any run \(j\in \{1,...,i,...\}\).
Collision Resistance. \(\mathsf {LHF} \) is \((\varepsilon ,t)\)-\(\mathbf {CR} \) relative to \( par \in \mathsf {PGen} (1^\kappa )\) if for all adversaries running in time at most t,

4 Canonical Blind Signature Schemes
In this section, we recall syntax and security of a special type of blind signature scheme, called canonical three-move blind signature scheme [32]. In Sect. 4.1, we first recall the syntax of such schemes and give the proper security definitions. Next, in Sect. 4.3, we give a generic construction that gives a canonical three-move blind signature scheme \(\mathsf {BS} [\mathsf {LHF} ]\) from any linear hash function family \(\mathsf {LHF} \).
4.1 Definitions
Definition 1
(Canonical Three-Move Blind Signature Scheme). A canonical three-move blind signature scheme \(\mathsf {BS} \) is a tuple of algorithms \(\mathsf {BS} =(\mathsf {PGen},\mathsf {KG},\mathsf {S},\mathsf {U},\mathsf {BSVer}).\)
-
The randomised parameter generation algorithm \(\mathsf {PGen} \) returns system parameters \( par \).
-
The randomised key generation algorithm \(\mathsf {KG} \) takes as input system parameters \( par \) and outputs a public key/secret key pair \(( pk , sk )\). We assume that \( pk \) defines a challenge set \(\mathcal {C}:=\mathcal {C} ( pk )\) and that \( pk \) is known to all parties.
-
The signer algorithm \(\mathsf {S} \) is split into two algorithms, i.e., \(\mathsf {S}:=(\mathsf {S} _1,\mathsf {S} _2)\), where:
-
The randomised algorithm \(\mathsf {S} _1\) takes as input the secret key \( sk \) and returns a commitment \(R \) and the signer’s state \( stS \).
-
The deterministic algorithm \(\mathsf {S} _2\) takes as input the signer’s state \( stS \), a secret key \( sk \), a commitment \(R \), and a challenge \(c \in \mathcal {C} \). It returns the response \(s \).
-
-
The user algorithm \(\mathsf {U} \) is split into two algorithms, i.e., \(\mathsf {U}:=(\mathsf {U} _1,\mathsf {U} _2)\), where:
-
The randomised algorithm \(\mathsf {U} _1\) takes as input the public key \( pk \), a commitment \(R \), and a message m. It returns the user’s state \( stU \) and a challenge \(c \in \mathcal {C} \).
-
The deterministic algorithm \(\mathsf {U} _2\) takes as input the public key \( pk \), a commitment \(R \), a challenge \(c\in \mathcal {C} \), a response \(s \), a message m, and the user’s state \( stU \). It returns a signature \(\sigma \) where, possibly, \(\sigma =\bot \).
-
-
The deterministic verification algorithm \(\mathsf {BSVer} \) takes as input the public key \( pk \), a signature \(\sigma \), and a message m. It outputs 1 (accept) or 0 (reject). We make the convention that \(\mathsf {BSVer} \) always outputs 0 on input a signature \(\sigma =\bot \).
We note that modeling \(\mathsf {S} _2\) and \(\mathsf {U} _2\) as deterministic algorithms is w.l.o.g. since randomness can be transmitted through the states.
Consider an interaction \((R,c,s,\sigma )\leftarrow \langle \mathsf {S} ( sk ),\mathsf {U} ( pk ,m)\rangle \) between signer \(\mathsf {S} \) and user \(\mathsf {U} \), as defined in Fig. 1. We say that \(\mathsf {BS} =(\mathsf {PGen},\mathsf {KG},\mathsf {S},\mathsf {U},\mathsf {BSVer})\) has correctness error \(\delta \), if for all messages \(m\in \{0,1\}^*, par \in \mathsf {PGen} (1^\kappa ), ( pk , sk )\in \mathsf {KG} ( par ),\)

Security Notions. Security of a Canonical Three-Move Blind Signature Scheme \(\mathsf {BS} \) is captured by two security notions: blindness and one-more unforgeability.
Intuitively, blindness ensures that a signer \(\mathsf {S} \) that issues signatures on two messages \(({\textit{\textbf{m}}}_0,{\textit{\textbf{m}}}_1)\) of its own choice to a user \(\mathsf {U},\) can not tell in what order it issues them. In particular, \(\mathsf {S} \) is given both resulting signatures \({\varvec{\sigma }}_0,{\varvec{\sigma }}_1\), and gets to keep the transcripts of both interactions with \(\mathsf {U} \). We remark that we consider for this work the weaker notion of blindness in the honest signer model [34] as compared to the malicious signer model [23]. The difference between these two models is that in the honest signer model, the adversary obtains the keys from the experiment, whereas in the malicious signer model, the adversary gets to choose its own keys. Also, our notion does not capture security of blind signatures under aborts, where \(\mathsf {S} \) or \(\mathsf {U} \) may stop the interactive signing protocol prematurely [17, 59]. The work of [24] proposes generic transformation to achieve such a stronger notion. We formalize the notion of blindness (for a canonical three-move blind signature scheme \(\mathsf {BS} \) and for parameters \( par \in \mathsf {PGen} \)) via game \(\mathbf {Blind} _{\mathsf {BS}, par }\) depicted in Fig. 2. In \(\mathbf {Blind} _{\mathsf {BS}, par }\), the game takes the role of the user and \(\mathsf {A} \) takes the role of the signer. First, the game selects a random bit b which determines the order of adversarially chosen messages in both transcripts. It then runs \(\mathsf {A} \) on a freshly generated key pair \(( pk , sk )\). \(\mathsf {A} \) is given access to the three oracles \(\mathtt {Init},\mathtt {U} _1\) and \( \mathtt {U} _2\). By convention, \(\mathsf {A} \) first has to query oracle \(\mathtt {Init} \). Subsequently, \(\mathsf {A} \) may open at most two sessions. For each of these two sessions, \(\mathsf {A} \) obtains corresponding transcripts \({\textit{\textbf{T}}}_1=({\textit{\textbf{R}}}_{1},{\textit{\textbf{c}}}_{1},{\textit{\textbf{s}}}_{1})\) and \({\textit{\textbf{T}}}_2=({\textit{\textbf{R}}}_{2},{\textit{\textbf{c}}}_{2},{\textit{\textbf{s}}}_{2})\). The game uses \({\textit{\textbf{m}}}_b\) and \({\textit{\textbf{m}}}_{1-b}\) to generate the transcripts \({\textit{\textbf{T}}}_1\) and \({\textit{\textbf{T}}}_2\), respectively. If \(\mathsf {A} \) honestly completes both sessions with the game, it obtains signatures \({\varvec{\sigma }}_b\) and \({\varvec{\sigma }}_{1-b}\) on messages \({\textit{\textbf{m}}}_b\) and \({\textit{\textbf{m}}}_{1-b}\). Note that \(\mathsf {A} \) obtains \({\varvec{\sigma }}_b\) and \({\varvec{\sigma }}_{1-b}\) by calling \(\mathtt {U} _2\) twice. More precisely, the first call to \(\mathtt {U} _2\) closes the first session and the second call closes the second session. Once both sessions are closed, the game checks if \(\mathsf {A} \) acted honestly in both of them and if so, returns the signatures \(({\varvec{\sigma }}_b,{\varvec{\sigma }}_{1-b})\). If instead \(\mathsf {A} \) has behaved dishonestly and, as a result, \({\varvec{\sigma }}_b=\bot \) or \({\varvec{\sigma }}_{1-b}=\bot \) at the time of closing the second session, \(\mathtt {U} _2\) returns \((\bot ,\bot )\). At the end of the experiment, \(\mathsf {A} \) has to guess the bit b. We define the advantage of adversary \(\mathsf {A} \) in \(\mathbf {Blind} _{\mathsf {BS}, par }\) as \(\mathbf {Adv}^{\mathbf {Blind}}_{\mathsf {BS}, par } (\mathsf {A}) := \left| \Pr [\mathbf {Blind} _{\mathsf {BS}, par }^{\mathsf {A}}\Rightarrow 1]-\frac{1}{2} \right| \).
Definition 2
(Perfect Blindness). Let \(\mathsf {BS} \) be a canonical three-move blind signature scheme. We say that \(\mathsf {BS} \) is perfectly blind relative to \( par \in \mathsf {PGen} (1^\kappa )\) if for all adversaries \(\mathsf {A} \), \(\mathbf {Adv}^{\mathbf {Blind}}_{\mathsf {BS}, par } (\mathsf {A}) =0\).
OMUF of Blind Signature Schemes. Intuitively, one-more unforgeability ensures that a user \(\mathsf {U} \) can not produce even a single signature more than it should be able to learn from its interactions with the signer \(\mathsf {S} \). Our notion does not cover the stronger notion of honest-user unforgeability but a generic transformation from [59] can be applied to achieve it. We formalize the notion of one-more unforgeability (for a canonical three-move blind signature scheme \(\mathsf {BS} \) and for all parameter \( par \in \mathsf {PGen} \)) via game \(\mathbf {OMUF} _{\mathsf {BS}, par }\) as depicted in Fig. 3. In \(\mathbf {OMUF} _{\mathsf {BS}, par }\), an adversary \(\mathsf {A} \) in the role of \(\mathsf {U} \) is run on input the public key of the signer \(\mathsf {S} \) and subsequently interacts with oracles that imitate the behaviour of \(\mathsf {S} \). A call to \(\mathtt {S} _1\) returns a new session identifier \( sid \) and sets flag \(\mathbf {sess}_ sid \) to \(\mathtt {open}\). A call to \(\mathtt {S} _2( sid , \cdot )\) with the same \( sid \) sets the flag \(\mathbf {sess}_{ sid }\) to \(\mathtt {closed}\). The closed sessions result in (at most) \(Q_{\mathsf {S}_2}\) transcripts \(({\textit{\textbf{R}}}_{k},{\textit{\textbf{c}}}_{k},{\textit{\textbf{s}}}_{k})\), where the challenges \({\textit{\textbf{c}}}_{k}\) are chosen by \(\mathsf {A} \). (The remaining (at most) \(Q_{\mathsf {S}_1}\) abandoned sessions are of the form \(({\textit{\textbf{R}}}_{k},\bot ,\bot )\) and hence do not contain a complete transcript.) \(\mathsf {A} \) wins the experiment, if it is able to produce \(\ell (\mathsf {A})\ge Q_{\mathsf {S}_2}(\mathsf {A})+1\) signatures (on distinct messages) after having closed \(Q_{\mathsf {S}_2}(\mathsf {A}) \le Q_{\mathsf {S}_2}\) signer sessions (from which it should be able to compute \(Q_{\mathsf {S}_2}(\mathsf {A})\) signatures). We define the advantage of adversary \(\mathsf {A} \) in \(\mathbf {OMUF} _{\mathsf {BS}, par }\) as \(\mathbf {Adv}^{\mathbf {OMUF}}_{\mathsf {BS}, par } (\mathsf {A}):=\Pr [\mathbf {OMUF} _{\mathsf {BS}, par }^{\mathsf {A}}\Rightarrow 1]\) and denote its running time as \(\mathbf {Time} ^{\mathbf {OMUF}}_{\mathsf {BS}, par }(\mathsf {A})\).
We remark that the definition of OMUF security is only meaningful for blind signature schemes with negligible correctness error: If the scheme has noticeable correctness error, then even an honest adversary would not be able to produce even \(\ell \) valid signatures after having interacted with \(\ell \) signing sessions. Thus an adversary may learn less than \(\ell \) signatures, but still has to come up with \(\ell +1\) signatures. This results in a significant weakening of the definition.
Definition 3
(One-More Unforgeability). Let \(\mathsf {BS} \) be a canonical three-move blind signature scheme. We say that \(\mathsf {BS} \) is \((\varepsilon , t, Q_{\mathsf {S}_1}, Q_{\mathsf {S}_2})\)-\(\mathbf {OMUF} \) relative to \( par \in \mathsf {PGen} \) if for all adversaries \(\mathsf {A} \) satisfying
we have \(\mathbf {Adv}^{\mathbf {OMUF}}_{\mathsf {BS}, par } (\mathsf {A}) \le \varepsilon \).
4.2 Hash Trees
In this section we define hash trees to build trees of commitments similarly as in [4]. The main advantage of this technique is that it significantly reduces the probability of abort in the signing protocol by performing a rejection sampling [38] multiple times and representing each trial as a leaf of the hash tree.
Let \(\mathsf {G} :\{0,1\}^*\mapsto \{0,1\}^{2\lambda }\) be a hash function. A hash tree \(\mathsf {HT} [\mathsf {G} ]\) associated to \(\mathsf {G} \) is the tuple of three deterministic algorithms \((\mathsf {HashTree},\mathsf {BuildAuth},\mathsf {RootCalc})\) from Fig. 4. Algorithm \(\mathsf {HashTree}\) takes as input a list of commitments \({\textit{\textbf{v}}}_{}\) and returns a sequence of nodes \(\mathsf {tree}\) spanning the tree and the root \(\mathsf {root}\) of the tree; Algorithm \(\mathsf {BuildAuth}\) takes as input a list of indices as well as a tree and outputs an authentication path \(\mathsf {auth}\); Algorithm \(\mathsf {RootCalc}\) takes as input a node and an authentication path \(\mathsf {auth}\) and returns the root \(\mathsf {root}\) of a hash tree.
Note that for all nodes \(({\textit{\textbf{v}}}_{1},\dots ,{\textit{\textbf{v}}}_{\ell })\) and for all indices \(m\in [\ell ]\), we have \(\mathsf {RootCalc}({\textit{\textbf{v}}}_{m},\mathsf {auth}) = \mathsf {root}\), where \((\mathsf {root},\mathsf {tree})\leftarrow \mathsf {HashTree}({\textit{\textbf{v}}}_{1},\dots ,{\textit{\textbf{v}}}_{\ell })\) and \(\mathsf {auth}\leftarrow \mathsf {BuildAuth}(m,\mathsf {tree})\).
4.3 Blind Signature Schemes from Linear Hash Function Families
Let \(\mathsf {LHF} \) be a linear hash function family and \(\mathsf {H} :\{0,1\}^* \rightarrow \mathcal {C} \), \(\mathsf {G} :\{0,1\}^* \rightarrow \{0,1\}^{2\lambda }\) be hash functions where \(\mathcal {C} = \mathcal {S} _{c'}\). Let \(\eta ,\nu ,\mu \in \mathbb {N}\) be repetition parameters. In the following we define mappings which convert a tuple of integers to an unique larger integer and vice versa. We define \(\mathsf {2Int}_{\eta ,\nu ,\mu }: [\eta ]\times [\nu ] \times [ \mu ] \rightarrow [\eta \nu \mu ]\) as the mapping \((i,j,k) \mapsto i+\eta \cdot ( j-1) + \eta \nu \cdot (k-1)\), such that \(\mathsf {2Int}_{\eta ,\nu ,\mu }(1,1,1)=1\) and \(\mathsf {2Int}_{\eta ,\nu ,\mu }(\eta ,\nu ,\mu ) = \eta \nu \mu \).
Figure 5 shows how to construct a canonical three-move blind signature scheme \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\), where the hashtree algorithms \(\mathsf {HT} [\mathsf {G} ]=(\mathsf {HashTree},\mathsf {BuildAuth},\mathsf {RootCalc})\) are defined in Fig. 4.
Construction of the canonical three-move blind signature scheme \(\mathsf {BS}:=\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H}]\) from a linear hash function family \(\mathsf {LHF} =(\mathsf {PGen},\mathsf {F})\), where \(\mathsf {BS}:=(\mathsf {PGen},\mathsf {KG},\mathsf {S} =(\mathsf {S} _1, \mathsf {S} _2), \mathsf {U} =(\mathsf {U} _1, \mathsf {U} _2),\mathsf {BSVer})\) and challenge set \(\mathcal {C}:=\mathcal {S} _{c'}\).
We begin by proving correctness of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\).
Lemma 1
(Correctness). Let \(\mathsf {LHF} \) be a linear hash function family, let \(\mathsf {G} :\{0,1\}^*\rightarrow \{0,1\}^{2\lambda }\) and \(\mathsf {H}:\{0,1\}^*\rightarrow \mathcal {C} \) be hash functions and \(\mathsf {HT} [\mathsf {G} ]\) be a hash tree and \(\mathsf {BS}:=\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ].\) If \(\mathsf {LHF} \) has enclosedness errors \((\delta _1,\delta _2,\delta _3)\) then \(\mathsf {BS} \) has correctness error \(\delta _1^{\mu }+\delta _2^{\eta }+\delta _3^{\nu }\).
Proof
Consider an execution of \(\mathsf {BS} \) defined in Fig. 5. From the definition of enclosedness errors \((\delta _1,\delta _2,\delta _3)\) it follows directly that the probability that during the execution lines 13, 31 and 43 abort are \(\delta _2^\eta \), \(\delta _1^\mu \) and \(\delta _3^\nu \), respectively.
We continue with a statement about OMUF security of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\). Its proof will be given in Sect. 5.
Theorem 1 (OMUF)
Let \(\mathsf {LHF} =(\mathsf {PGen},\mathsf {F})\) be a \((\varepsilon , \eta \nu \mu Q_{\mathsf {S}_1})\)-regular linear hash function family with a torsion-free element from the kernel, let \(\mathsf {G} :\{0,1\}^*\rightarrow \{0,1\}^{2\lambda }\) and \(\mathsf {H} :\{0,1\}^*\rightarrow \mathcal {C} \) be random oracles. If \(\mathsf {LHF} \) is \((\varepsilon ',t')\)-\(\mathbf {CR} \) relative to \( par \in \mathsf {PGen} (1^\kappa )\), then \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\) is \((\varepsilon , t, Q_{\mathsf {S}_1}, Q_{\mathsf {S}_2},Q_\mathsf {G}, Q_\mathsf {H} )\)-\(\mathbf {OMUF} \) relative to \( par \) in the random oracle model, where
\(Q_\mathsf {G} \) and \(Q_\mathsf {H} \) are the number of queries to random oracles \(\mathsf {G} \) and \(\mathsf {H} \).
Theorem 2 (Blindness)
Let \(\mathsf {LHF} =(\mathsf {PGen},\mathsf {F})\) be a smooth linear hash function family and let \(\mathsf {G} :\{0,1\}^*\rightarrow \{0,1\}^{2\lambda }\) and \(\mathsf {H}:\{0,1\}^*\rightarrow \mathcal {C} \) be random oracles. Then \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\) is perfectly blind relative to all \( par \in \mathsf {PGen} (1^\kappa )\).
Let \(\mathsf {BS}:=\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\). Intuitively the goal of an adversary in the \(\mathbf {Blind} _{\mathsf {BS}, par }\) experiment is as follows. The adversary interacts twice with the experiment and thus creates two transcripts. At the end of the interaction the adversary learns two message/signature pairs and tries to unblind which message/signature pair was created in which session. Intuitively to prevent the adversary from doing so, any combination of a transcript and a message/signature pair can be explained by some randomness (of the user) which (i) could have been used to create both the transcript and the message/signature pair and (ii) is indistinguishable from uniformly drawn randomness.
Proof
Fix two messages \({\textit{\textbf{m}}}_0,{\textit{\textbf{m}}}_1\) and let \(\mathsf {A} \) be an adversary in the \(\mathbf {Blind} _{\mathsf {BS}, par }\) experiment (cf. Fig. 2).
Given the output of an interaction  we define a transcript \(T:=({\textit{\textbf{R}}}_{1},\dots ,{\textit{\textbf{R}}}_{\eta },c,s)\). Consider \(\mathsf {A} \)’s view in an execution of \(\mathbf {Blind} _{\mathsf {BS}, par }\), which consists of the two transcripts \(({\textit{\textbf{T}}}_{1}, {\textit{\textbf{T}}}_{2})\) and the two signatures \(({\varvec{\sigma }}_{0}, {\varvec{\sigma }}_{1})\), where signature \({\varvec{\sigma }}_{b}\) corresponds to transcript \({\textit{\textbf{T}}}_{1}\), signature \({\varvec{\sigma }}_{1-b}\) corresponds to transcript \({\textit{\textbf{T}}}_{2}\), and b is the secret choice bit. Note that it is w.l.o.g. that \({\varvec{\sigma }}_{0},{\varvec{\sigma }}_{1}\ne \bot \). Now, the theorem is implied by the following two claims.
we define a transcript \(T:=({\textit{\textbf{R}}}_{1},\dots ,{\textit{\textbf{R}}}_{\eta },c,s)\). Consider \(\mathsf {A} \)’s view in an execution of \(\mathbf {Blind} _{\mathsf {BS}, par }\), which consists of the two transcripts \(({\textit{\textbf{T}}}_{1}, {\textit{\textbf{T}}}_{2})\) and the two signatures \(({\varvec{\sigma }}_{0}, {\varvec{\sigma }}_{1})\), where signature \({\varvec{\sigma }}_{b}\) corresponds to transcript \({\textit{\textbf{T}}}_{1}\), signature \({\varvec{\sigma }}_{1-b}\) corresponds to transcript \({\textit{\textbf{T}}}_{2}\), and b is the secret choice bit. Note that it is w.l.o.g. that \({\varvec{\sigma }}_{0},{\varvec{\sigma }}_{1}\ne \bot \). Now, the theorem is implied by the following two claims.
-
(B1)
For each of the four combinations \(({\textit{\textbf{T}}}_{ sid }, {\varvec{\sigma }}_{i})\), where \(( sid ,i) \in \{1,2\} \times \{0,1\}\), there exists randomness \({\textit{\textbf{ rndU }}}_{ sid ,i}:=({\varvec{\alpha }}_{ sid ,i,1}\dots ,{\varvec{\alpha }}_{ sid ,i,\nu },{\varvec{\beta }}_{ sid ,i,1},\dots ,{\varvec{\beta }}_{ sid ,i,\mu },{\varvec{\gamma }}_{ sid ,i})\) of the user algorithm which results in the tuple \(({\textit{\textbf{T}}}_{ sid }, {\varvec{\sigma }}_{i})\).
-
(B2)
The real randomness \(({\textit{\textbf{ rndU }}}_{1,b},{\textit{\textbf{ rndU }}}_{2,1-b})\) used in \(\mathbf {Blind} _{\mathsf {BS}, par }\) is identically distributed to the “fake” randomness \(({\textit{\textbf{ rndU }}}_{1,1-b},{\textit{\textbf{ rndU }}}_{2,b})\) .
To prove condition (B1) we argue as follows. Let \(\mathsf {2Int^{-1}}:[\eta \nu \mu ]\rightarrow [\eta ]\times [\nu ] \times [ \mu ]\) be the inverse of \(\mathsf {2Int}_{\eta ,\nu ,\mu }\), defined in Sect. 4.3. Let \(({\textit{\textbf{c}}}'_{i},{\textit{\textbf{s}}}'_{i},{\varvec{\mathsf {auth}}}_i)\leftarrow {\varvec{\sigma }}_{i}\). Let \(({\textit{\textbf{i}}}_{i},{\textit{\textbf{j}}}_{i},{\textit{\textbf{k}}}_{i})\leftarrow \mathsf {2Int^{-1}}({{\textit{\textbf{n}}}_{i}})\), where \(({{\textit{\textbf{n}}}_{i}},{\textit{\textbf{a}}}_{i,1},\dots ,{\textit{\textbf{a}}}_{i,h})\leftarrow \mathsf {auth}_i\). Define \({\varvec{\alpha }}_{ sid ,i,{\textit{\textbf{k}}}_{i}}:={\textit{\textbf{s}}}'_{{\textit{\textbf{k}}}_{i}}-{\textit{\textbf{s}}}_{ sid }\), \({\varvec{\beta }}_{ sid ,i,{\textit{\textbf{j}}}_{i}}:={\textit{\textbf{c}}}_{ sid }-{\textit{\textbf{c}}}'_{{\textit{\textbf{j}}}_{i}}\) and for all \(\ell \in [\nu ]\setminus \{{\textit{\textbf{k}}}_{i}\}\),  for all \(\ell \in [\mu ]\setminus \{{\textit{\textbf{j}}}_{i}\}\),
for all \(\ell \in [\mu ]\setminus \{{\textit{\textbf{j}}}_{i}\}\),  . Set \({\textit{\textbf{i}}}_{ sid }\in [\eta ]\) to be the smallest value s.t. \(\mathsf {F} ({\textit{\textbf{s}}}_{ sid }) = {\textit{\textbf{c}}}_{ sid }\cdot pk +{\textit{\textbf{R}}}_{ sid ,{\textit{\textbf{i}}}_{ sid }}.\) Define \({\varvec{\gamma }}_{ sid ,i}\leftarrow {\textit{\textbf{i}}}_{ sid }\oplus {\textit{\textbf{i}}}_{i}\). By smoothness conditions (S1) and (S4) it follows that \({\varvec{\alpha }}_{ sid ,i,{\textit{\textbf{k}}}_{i}}\in \mathcal {D}_{\alpha } \) and \({\varvec{\beta }}_{ sid ,i,{\textit{\textbf{j}}}_{i}}\in \mathcal {S}_{\beta } \). Clearly, for all \(\ell \in [\nu ]\setminus \{{\textit{\textbf{k}}}_{i}\}\), \({\varvec{\alpha }}_{ sid ,i,\ell }\in \mathcal {D}_{\alpha } \) for all \(\ell \in [\mu ]\setminus \{{\textit{\textbf{j}}}_{i}\}\), \({\varvec{\beta }}_{ sid ,i,\ell }\in \mathcal {S}_{\beta } \). Clearly, \({\varvec{\gamma }}_{ sid ,i}\in [\eta ]\). Let \({\textit{\textbf{R}}}'_{ sid ,i,{\textit{\textbf{i}}}_{i},{\textit{\textbf{j}}}_{i},{\textit{\textbf{k}}}_{i}}={\textit{\textbf{R}}}_{ sid ,{\textit{\textbf{i}}}_{i}}+{\varvec{\beta }}_{ sid ,i,{\textit{\textbf{j}}}_{j}}\cdot pk +\mathsf {F} ({\varvec{\alpha }}_{ sid ,i,{\textit{\textbf{k}}}_{i}})\). Let \({\varvec{\mathsf {root}}}_{ sid ,i}\leftarrow \mathsf {RootCalc}({\textit{\textbf{R}}}'_{ sid ,i,{\textit{\textbf{i}}}_{i},{\textit{\textbf{j}}}_{i},{\textit{\textbf{k}}}_{i}},\mathsf {auth}_i).\) To show that \({\textit{\textbf{c}}}'_{i}=\mathsf {H} ({\varvec{\mathsf {root}}}_{ sid ,i},{{\textit{\textbf{m}}}_{i}})\) we continue as follows. Since \({\textit{\textbf{T}}}_{ sid }\) is a valid transcript, we have \(\mathsf {F} ({\textit{\textbf{s}}}_{ sid }) = {\textit{\textbf{R}}}_{ sid ,{\textit{\textbf{i}}}_{i}} + {\textit{\textbf{c}}}_{ sid }\cdot pk \). Therefore,
. Set \({\textit{\textbf{i}}}_{ sid }\in [\eta ]\) to be the smallest value s.t. \(\mathsf {F} ({\textit{\textbf{s}}}_{ sid }) = {\textit{\textbf{c}}}_{ sid }\cdot pk +{\textit{\textbf{R}}}_{ sid ,{\textit{\textbf{i}}}_{ sid }}.\) Define \({\varvec{\gamma }}_{ sid ,i}\leftarrow {\textit{\textbf{i}}}_{ sid }\oplus {\textit{\textbf{i}}}_{i}\). By smoothness conditions (S1) and (S4) it follows that \({\varvec{\alpha }}_{ sid ,i,{\textit{\textbf{k}}}_{i}}\in \mathcal {D}_{\alpha } \) and \({\varvec{\beta }}_{ sid ,i,{\textit{\textbf{j}}}_{i}}\in \mathcal {S}_{\beta } \). Clearly, for all \(\ell \in [\nu ]\setminus \{{\textit{\textbf{k}}}_{i}\}\), \({\varvec{\alpha }}_{ sid ,i,\ell }\in \mathcal {D}_{\alpha } \) for all \(\ell \in [\mu ]\setminus \{{\textit{\textbf{j}}}_{i}\}\), \({\varvec{\beta }}_{ sid ,i,\ell }\in \mathcal {S}_{\beta } \). Clearly, \({\varvec{\gamma }}_{ sid ,i}\in [\eta ]\). Let \({\textit{\textbf{R}}}'_{ sid ,i,{\textit{\textbf{i}}}_{i},{\textit{\textbf{j}}}_{i},{\textit{\textbf{k}}}_{i}}={\textit{\textbf{R}}}_{ sid ,{\textit{\textbf{i}}}_{i}}+{\varvec{\beta }}_{ sid ,i,{\textit{\textbf{j}}}_{j}}\cdot pk +\mathsf {F} ({\varvec{\alpha }}_{ sid ,i,{\textit{\textbf{k}}}_{i}})\). Let \({\varvec{\mathsf {root}}}_{ sid ,i}\leftarrow \mathsf {RootCalc}({\textit{\textbf{R}}}'_{ sid ,i,{\textit{\textbf{i}}}_{i},{\textit{\textbf{j}}}_{i},{\textit{\textbf{k}}}_{i}},\mathsf {auth}_i).\) To show that \({\textit{\textbf{c}}}'_{i}=\mathsf {H} ({\varvec{\mathsf {root}}}_{ sid ,i},{{\textit{\textbf{m}}}_{i}})\) we continue as follows. Since \({\textit{\textbf{T}}}_{ sid }\) is a valid transcript, we have \(\mathsf {F} ({\textit{\textbf{s}}}_{ sid }) = {\textit{\textbf{R}}}_{ sid ,{\textit{\textbf{i}}}_{i}} + {\textit{\textbf{c}}}_{ sid }\cdot pk \). Therefore,
Since \({\varvec{\sigma }}_{i}\) is a valid signature we have \({\textit{\textbf{c}}}'_{i}= \mathsf {H} (\mathsf {RootCalc}(\mathsf {F} ({\textit{\textbf{s}}}'_{i}) - {\textit{\textbf{c}}}'_{i}\cdot pk ,{\varvec{\mathsf {auth}}}_i),{{\textit{\textbf{m}}}_{i}})=\mathsf {H} ({\varvec{\mathsf {root}}}_{ sid ,i},{{\textit{\textbf{m}}}_{i}})\).
To show condition (B2) we continue as follows. By smoothness condition (S2) if follows that \({\varvec{\alpha }}_{1,b,{\textit{\textbf{k}}}_{b}}\) and \({\varvec{\alpha }}_{2,1-b,{\textit{\textbf{k}}}_{1-b}}\) have the same distribution as \({\varvec{\alpha }}_{1,1-b,{\textit{\textbf{k}}}_{1-b}}\) and \({\varvec{\alpha }}_{2,b,{\textit{\textbf{k}}}_{b}}\). By smoothness condition (S5) it follows that \({\varvec{\beta }}_{1,b,{\textit{\textbf{j}}}_{b}}\) and \({\varvec{\beta }}_{2,1-b,{\textit{\textbf{j}}}_{1-b}}\) have the same distribution as \({\varvec{\beta }}_{1,1-b,{\textit{\textbf{j}}}_{1-b}}\) and \({\varvec{\beta }}_{2,b,{\textit{\textbf{j}}}_{b}}\). By smoothness condition (S3) for all \(\ell \in [\nu ]\,\setminus \,\{{\textit{\textbf{k}}}_{b},{\textit{\textbf{k}}}_{1-b}\}\), \({\varvec{\alpha }}_{1,b,\ell }\) and \({\varvec{\alpha }}_{1,1-b,\ell }\) have the same distribution as \({\varvec{\alpha }}_{2,b,\ell }\) and \({\varvec{\alpha }}_{2,1-b,\ell }\). By smoothness condition (S6) for all \(\ell \in [\mu ]\setminus \{{\textit{\textbf{j}}}_{b},{\textit{\textbf{j}}}_{1-b}\}\), \({\varvec{\beta }}_{1,b,\ell }\) and \({\varvec{\beta }}_{1,1-b,\ell }\) have the same distribution as \({\varvec{\beta }}_{2,b,\ell }\) and \({\varvec{\beta }}_{2,1-b,\ell }\). Clearly, all four \(\gamma _{1,0}\), \(\gamma _{1,1}\), \(\gamma _{2,0}\) and \(\gamma _{2,1}\) have the same distribution.
5 Proof of One-More Unforgeability
In this section, we will make a first step to the proof of Theorem 1, the one-more unforgeability of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {H}, \mathsf {G} ]\) defined in Fig. 5. To this end we first define canonical identification schemes and prove in Theorem 3 that one-more unforgeability of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {H}, \mathsf {G} ]\) is implied by one-more man-in-the-middle security of the underlying identification scheme \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\). Next, in Theorem 4 we will state that collision-resistance of \(\mathsf {LHF} \) implies one-more man-in-the-middle security of the canonical identification scheme \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\).
5.1 Canonical Identification Schemes
We recall syntax of canonical (three-move) identification schemes [1].
Definition 4
(Canonical Three-Move Identification Scheme). A canonical three-move identification scheme is a tuple of algorithms \(\mathsf {ID} =(\mathsf {\mathsf {PGen}}, \mathsf {\mathsf {KG}},\mathsf {P} =(\mathsf {P} _1,\mathsf {P} _2),\mathsf {IDVer})\).
-
The randomised parameter generation algorithm \(\mathsf {\mathsf {PGen}}\) returns system parameters \( par \).
-
The randomised key generation algorithm \(\mathsf {\mathsf {KG}} \) takes as input system parameters \( par \) and returns a public/secret key pair \(( pk , sk )\). We assume that \( pk \) implicitly defines a challenge space \(\mathcal {C}:=\mathcal {C} ( pk )\) and that \( pk \) is distributed (and hence known) to all parties.
-
The prover algorithm \(\mathsf {P} \) is split into two algorithms, i.e., \(\mathsf {P}:=(\mathsf {P} _1,\mathsf {P} _2)\), where:
-
The randomised algorithm \(\mathsf {P} _1\) takes as input a secret key \( sk \) and returns a commitment R and a state \( st \).
-
The deterministic algorithm \(\mathsf {P} _2\) takes as input a secret key \( sk \), a commitment R, a challenge \(c \), and a state \( st \). It returns a response \(s \).
-
-
The deterministic verification algorithm \(\mathsf {IDVer} \) takes as input a public key \( pk \), a commitment R, a challenge \(c \), and a response \(s \). It returns 1 (accept) or 0 (reject).
Figure 6 shows the interaction between algorithms \(\mathsf {P} _1,\mathsf {P} _2,\) and \(\mathsf {IDVer} \). Since we will use \(\mathsf {ID} \) only for the purpose of simplifying our main security statement, we refrain from giving the standard correctness definition.
We now recall One-More Man-in-the-Middle security for canonical identification schemes [32]. The One-More Man-in-the-Middle \((\mathbf {OMMIM})\) security experiment for an identification scheme \(\mathsf {ID} \) and an adversary \(\mathsf {A} \) is defined in Fig. 7. Adversary \(\mathsf {A} \) simultaneously plays against a prover (modeled through oracles \(\mathtt {P} _1\) and \(\mathtt {P} _2\)) and a verifier (modeled through oracles \({\mathtt {V}_1} \) and \({\mathtt {V}_2} \)). Session identifiers \( pSid \) and \( vSid \) are used to model an interaction with the prover and the verifier, respectively. A call to \(\mathtt {P} _1\) returns a new prover session identifier \( pSid \) and sets flag \(\mathbf {pSess}_ pSid \) to \(\mathtt {open}\). A call to \(\mathtt {P} _2( pSid , \cdot )\) with the same \( pSid \) sets the flag \(\mathbf {pSess}_{ pSid }\) to \(\mathtt {closed}\). Similarly, a call to \({\mathtt {V}_1} \) returns a new verifier session identifier \( vSid \) and sets flag \(\mathbf {vSess}_ vSid \) to \(\mathtt {open}\). A call to \({\mathtt {V}_2} ( vSid , \cdot )\) with the same \( vSid \) sets the flag \(\mathbf {vSess}_{ vSid }\) to \(\mathtt {closed}\). A closed verifier session \( vSid \) is successful if the oracle \({\mathtt {V}_2} ( vSid , \cdot )\) returns 1. Lines 04–07 define several internal random variables for later reference. Variable \(Q_{\mathsf {P}_2}(\mathsf {A})\) counts the number of closed prover sessions and \(Q_{\mathsf {P}_1}(\mathsf {A})\) counts the number of abandoned sessions (i.e., sessions that were opened but never closed). Most importantly, variable \(\ell (\mathsf {A})\) counts the number of successful verifier sessions and variable \(Q_{\mathsf {P}_2}(\mathsf {A})\) counts the number of closed sessions with the prover. Adversary \(\mathsf {A} \) wins the \(\mathbf {OMMIM} _{\mathsf {ID}, par }\) game, if \(\ell (\mathsf {A}) \ge Q_{\mathsf {P}_2}(\mathsf {A}) + 1\), i.e., if \(\mathsf {A} \) convinces the verifier in at least one more successful verifier sessions than there exist closed sessions with the prover. \(\mathsf {A} \)’s advantage in \(\mathbf {OMMIM} _{\mathsf {ID}, par }\) is defined as \(\mathbf {Adv}^{\mathbf {OMMIM}}_{{\mathsf {ID}, par }} (\mathsf {A}):=\Pr [\mathbf {OMMIM} ^\mathsf {A} _{{\mathsf {ID}, par }}\Rightarrow 1]\) and we denote its running time as \(\mathbf {Time} _{\mathsf {ID}, par }^\mathbf {OMMIM} (\mathsf {A})\).
Definition 5
(One-more man-in-the-middle security). We say that \(\mathsf {ID} \) is \((\varepsilon , t, Q_{\mathsf {V}}, Q_{\mathsf {P}_1}, Q_{\mathsf {P}_2})\)-\(\mathbf {OMMIM} \) relative to \( par \in \mathsf {PGen} (1^\kappa )\) if for all adversaries \(\mathsf {A} \) satisfying \(\mathbf {Time} _{\mathsf {ID}, par }^\mathbf {OMMIM} (\mathsf {A})\le t\), \(Q_{\mathsf {V}}(\mathsf {A}) \le Q_{\mathsf {V}}\), \(Q_{\mathsf {P}_2}(\mathsf {A}) \le Q_{\mathsf {P}_2}\), and \(Q_{\mathsf {P}_1}(\mathsf {A}) \le Q_{\mathsf {P}_1}\), we have \(\mathbf {Adv}^{\mathbf {OMMIM}}_{{\mathsf {ID}, par }} (\mathsf {A}) \le \varepsilon \).
We remark that security against impersonation under active and passive attacks [1] is a weaker notion than OMMIM security, whereas man-in-the-middle security [10] is stronger.
5.2 Identification Schemes from Linear Hash Function Families
Let \(\mathsf {LHF} \) be a linear hash function family and \(\eta '\) be a repetition parameter. Consider the canonical three-move blind signature scheme \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {H}, \mathsf {G} ] = (\mathsf {PGen},\mathsf {KG},\mathsf {S} =(\mathsf {S} _1, \mathsf {S} _2), \mathsf {U} =(\mathsf {U} _1, \mathsf {U} _2),\mathsf {BSVer})\) from Fig. 5. \(\mathsf {BS} \) directly implies a canonical identification scheme \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ] = (\mathsf {PGen},\mathsf {KG},\mathsf {P}, \mathsf {IDVer})\) with challenge set \(\mathcal {C}:=\mathcal {S} _{c'}\), where prover \(\mathsf {P} \) plays the role of the signer \(\mathsf {S} \), i.e., \(\mathsf {P} = (\mathsf {P} _1, \mathsf {P} _2):=(\mathsf {S} _1, \mathsf {S} _2)\) and algorithm \(\mathsf {IDVer} \) is defined as follows.

The identification scheme \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\) can be seen as the projection of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {H}, \mathsf {G} ]\) to the signer, i.e., all user algorithms (involving the techniques to achieve blindness) are removed. This makes it conceptually much simpler.
We will now show that OMUF security of \(\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ]\) is implied (in the ROM) by OMMIM security of \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\), where \(\eta ' = \eta \nu \mu \).
Theorem 3
Let \(\mathsf {LHF} \) be a linear hash function family, let \(\mathsf {G} :\{0,1\}^*\rightarrow \{0,1\}^{2\lambda }\) and \(\mathsf {H} :\{0,1\}^*\rightarrow \mathcal {C} \) be random oracles and let \(\mathsf {ID}:=\mathsf {ID} _{\eta '}[\mathsf {LHF} ], \mathsf {BS}:=\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ].\) If \(\mathsf {ID} \) is \((\varepsilon ', t', Q_{\mathsf {V}}, Q_{\mathsf {P}_1}, Q_{\mathsf {P}_2})\)-\(\mathbf {OMMIM} \) relative to \( par \in \mathsf {PGen} (1^\kappa )\) then \(\mathsf {BS} \) is \((\varepsilon , t,Q_{\mathsf {S}_1}, Q_{\mathsf {S}_2}, Q_\mathsf {G}, Q_\mathsf {H} )\)-\(\mathbf {OMUF} \) relative to \( par \) in the random oracle model, where
\(Q_\mathsf {G} \) and \(Q_\mathsf {H} \) are the number of queries to random oracles \(\mathsf {G} \) and \(\mathsf {H} \);
Proof
The technical proof of this theorem is comparable to the proof given in [32] and will be given in the full version [33].
We will now state that \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\) is OMMIM secure.
Theorem 4
Let \(\mathsf {LHF} \) be a \((\varepsilon , \eta ' Q_{\mathsf {P}_1})\)-regular linear hash function family with a torsion-free element from the kernel. If \(\mathsf {LHF} \) is \((\varepsilon ',t')\)-\(\mathbf {CR} \) relative to \( par \in \mathsf {PGen} (1^\kappa )\) then \(\mathsf {ID} _{\eta '}[\mathsf {LHF} ]\) is \((\varepsilon , t, Q_{\mathsf {V}}, Q_{\mathsf {P}_1},Q_{\mathsf {P}_2})\)-\(\mathbf {OMMIM} \) relative to \( par \), where
The technical proof of this theorem will be given in the full version [33].
6 Instantiation from Lattices
We now give a lattice-based example of a \(\mathsf {LHF} \) with noticeable correctness error which is derived from Lyubashevsky’s identification scheme [38] and has also been implicitly used in [56].
Notation. Let R and \(R_{q}\) denote the rings \(\mathbb {Z}[X]/\langle X^n+1\rangle \) and \(\mathbb {Z}_q[X]/\langle X^n+1\rangle \), for integer \(n=2^r\), where \(r\in \mathbb {Z}^+\) and q is an odd integer. Polynomials in \(R_{q}\) have degree at most \(n-1\) and coefficients in range \([-(q-1)/2,(q-1)/2]\). For such coefficients we abuse the notation mod to denote with \(x'=x\text { mod } q\), the unique element \(x'\) s.t. for any integer k: \(x' = x + kq\) and \(x'\in [-(q-1)/2,(q-1)/2]\). Bold lower-case letters denote elements in \(R_{q}\) and bold lower-case letters with a hat denote vectors of vectors with coefficients in ring \(R_{q}\). To measure the size of elements \(\mathbf {x}=x_0+x_1X^1+\dots +x_{n-1}X^{n-1}\) in ring \(R_{q}\) we define norm \(p_{\infty }\) as \(\left\Vert \mathbf {x}\right\Vert _{\infty } := \max \limits _{i}\left| x_i \mod q \right| \). In rings R and \(R_{q}\), \(\left\Vert x_i\right\Vert _{\infty }\) represents \(|x_i|\) and \(\left| x_i\text { mod }q \right| \), respectively. Similarly, for \(\mathbf {\hat{x}}=(\mathbf {x}_0,\dots ,\mathbf {x}_{k-1})\), we define norm \(p_{\infty }\) as \(\left\Vert \mathbf {\hat{x}}\right\Vert _{\infty } := \max \limits _{i}\left\Vert \mathbf {x}_i\right\Vert _{\infty }\). Further we define the \(p_1\) norm as \(\left\Vert \mathbf {x}\right\Vert _{1}:=\sum _{i}\left| \mathbf {x}_i \right| \) and \(p_2\) norm as \(\left\Vert \mathbf {x}\right\Vert _{2}:=(\sum _{i}\left| \mathbf {x}_i \right| ^2)^{1/2}\). It is not hard to see that for any two polynomials \(\mathbf {e},\mathbf {f}\in R_{q}\),
We now recall the \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d} \) problem over \(R_{q}\) [40, 48].
Definition 6
(\(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d} \)). We say that \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d} \) is \((\varepsilon ,t)\)-hard if for all adversaries \(\mathsf {A} \) running in time at most t, the probability that \(\mathsf {A} (\hat{{\textit{\textbf{a}}}})\) (where  ) outputs a non-zero \(\hat{{\textit{\textbf{z}}}}\in R_{q}^m\) s.t. \(\sum _{i=1}^{m}\mathbf {a}_i\cdot \mathbf {z}_i = 0\) and \(\left\Vert \hat{{\textit{\textbf{z}}}}\right\Vert _{\infty }\le d\), is bounded by \(\varepsilon \).
) outputs a non-zero \(\hat{{\textit{\textbf{z}}}}\in R_{q}^m\) s.t. \(\sum _{i=1}^{m}\mathbf {a}_i\cdot \mathbf {z}_i = 0\) and \(\left\Vert \hat{{\textit{\textbf{z}}}}\right\Vert _{\infty }\le d\), is bounded by \(\varepsilon \).
Similarly, \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d} \) is \((\varepsilon ,t)\)-hard relative to \(\hat{{\textit{\textbf{a}}}} \in R_{q}^m\) if for all adversaries \(\mathsf {A} \) running in time at most t, the probability that \(\mathsf {A} \) outputs a non-zero \(\hat{{\textit{\textbf{z}}}}\in R_{q}^m\) s.t. \(\sum _{i=1}^{m}\mathbf {a}_i\cdot \mathbf {z}_i = 0\) and \(\left\Vert \hat{{\textit{\textbf{z}}}}\right\Vert _{\infty }\le d\), is bounded by \(\varepsilon \).
Let us first estimate the concrete hardness of solving the \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d}\) problem for uniformly random \(\hat{{\textit{\textbf{a}}}}\) which is equivalent to finding a short vector in the related lattice
Gama and Nguyen [27] classified algorithms for finding short vectors in random lattices in terms of the root Hermite factor \(\delta \). Such algorithms compute a vector of length \(\delta ^n\) times the shortest vector of the lattice. Whereas \(\delta =1.01\) can be achieved, it is conjectured that a factor of \(\delta =1.007\) may not be achievable [21].
We use the following estimation from [38, Eqn. 3] to estimate the length of the shortest vector (in \(p_\infty \) norm) which can be efficiently found in lattice \(\mathbf {\Lambda }_q^{\bot }(\hat{{\textit{\textbf{a}}}})\) as
We make the following conjecture about \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d} \) with \(\delta =1.005\).
Conjecture 1
If \(d<\mathsf {sv}_{1.005}(n,q)\) then no efficient algorithm can solve \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d}\).
We note that security of our blind signature scheme depends on the hardness of \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,d} \) relative to fixed \(\hat{{\textit{\textbf{a}}}}\). However, as discussed in Sect. 2, our theorems can be easily re-written to work in a setting where  is chosen uniformly at random.
is chosen uniformly at random.
Linear Hash Function. We select the parameters according to Fig. 8. Firstly, variables q, n specify the ring \(R_{q}:=\mathbb {Z}_q[X]/\langle X^n+1\rangle \), where n is a power of two. Define the sets
where \(\mathcal {B}_{q}(w)\) is defined as
Note that the size of the challenge set \(\mathcal {C} = \mathcal {S} _{c'}\) is equal to \(3^{1024}\), hence \(1/|\mathcal {C}|\) is negligible.
For \(\hat{{\textit{\textbf{e}}}},\hat{{\textit{\textbf{f}}}}\in \mathcal {D} \) and \(\mathbf {g}\in \mathcal {S} \) we define addition \(\hat{{\textit{\textbf{e}}}}+\hat{{\textit{\textbf{f}}}}:=(\mathbf {e}_1+\mathbf {f}_1,\dots ,\mathbf {e}_m+\mathbf {f}_m)\), multiplication \(\mathbf {\hat{e}}\cdot \mathbf {\hat{f}}:=(\mathbf {e}_1\mathbf {f}_1,\dots ,\mathbf {e}_m\mathbf {f}_m)\), and scalar multiplication \(\mathbf {g} \cdot \hat{{\textit{\textbf{e}}}} = (\mathbf {g}\mathbf {e}_1,\dots ,\mathbf {g}\mathbf {e}_m).\) This makes \(\mathcal {R} \) and \(\mathcal {D} \) modules over \(\mathcal {S} \).
Algorithm \(\mathsf {PGen} (1^\kappa )\) returns a random element  . Algorithm \(\mathsf {F}:\mathcal {D} \mapsto \mathcal {R} \) is defined for any \(\hat{{\textit{\textbf{z}}}}\in \mathcal {D} \) as,
. Algorithm \(\mathsf {F}:\mathcal {D} \mapsto \mathcal {R} \) is defined for any \(\hat{{\textit{\textbf{z}}}}\in \mathcal {D} \) as,
Clearly, \(\mathsf {F} \) is a module homomorphism since for every \(\hat{{\textit{\textbf{y}}}},\hat{{\textit{\textbf{z}}}}\in \mathcal {D} \), \(\mathbf {c}\in \mathcal {R} \): \( \mathsf {F} (\hat{{\textit{\textbf{y}}}}+\hat{{\textit{\textbf{z}}}}) = \hat{{\textit{\textbf{a}}}}(\hat{{\textit{\textbf{y}}}}+\hat{{\textit{\textbf{z}}}}) = \hat{{\textit{\textbf{a}}}}\hat{{\textit{\textbf{y}}}} + \hat{{\textit{\textbf{a}}}}\hat{{\textit{\textbf{z}}}}= \mathsf {F} (\hat{{\textit{\textbf{y}}}}) + \mathsf {F} (\hat{{\textit{\textbf{z}}}}) \) and \( \mathsf {F} (\hat{{\textit{\textbf{y}}}}\mathbf {c}) = \hat{{\textit{\textbf{a}}}}(\mathbf {y}_1\mathbf {c},\dots ,\mathbf {y}_m\mathbf {c}) = \mathbf {a}_1\mathbf {y}_1\mathbf {c}+ \dots + \mathbf {a}_m\mathbf {y}_m\mathbf {c}= \mathsf {F} (\hat{{\textit{\textbf{y}}}})\mathbf {c}\).
For \(\mathsf {xxx}\in \{\beta ,c,c'\}\) and \(\mathsf {yyy}\in \{ sk ,r,s,s',\alpha \}\), the filter sets are defined as
To estimate the membership of sums and products of \(\hat{{\textit{\textbf{e}}}},\hat{{\textit{\textbf{f}}}}\in \mathcal {D} \) to specific subsets of \(\mathcal {D} \) we use the lemma proven by Rückert [56].
Lemma 2
Let \(k,d_a,d_b\) and \(\gamma \) be integers, s.t. \(d_b\ge \gamma knd_a\). Then, for all \(\hat{{\textit{\textbf{a}}}}\in \mathcal {B}_{q}^{k}(d_a)\),

Enclosedness Errors and Smoothness. First, we focus on calculating the enclosedness errors of \(\mathsf {LHF} \) based on parameters chosen in Fig. 8. Later on, we also show that \(\mathsf {LHF} \) is smooth.
Lemma 3
If \(d_\beta , d_r, d_\alpha , d_c, d_s, d_{s'}\) are defined as in Fig. 8 and \(\mathsf {LHF} \) is defined as above, then \(\mathsf {LHF} \) has enclosedness errors equal to:
Proof
The statement follows straightforwardly from Lemma 2 and the way we picked \(d_\beta , d_r, d_\alpha , d_c, d_s, d_{s'}\). \(\square \)
In Fig. 8 we select \(u=v=w\). Thus, we need choose appropriate \(\mu ,\eta ,\nu \) to make sure that correctness error of our blind signature is negligible. Indeed, we simply pick \(\mu = \eta = \nu \) such that
Then by Lemma 1, \(\mathsf {BS} [\mathsf {LHF} ]\) has correctness error at most \(3 \cdot 2^{-130} < 2^{-128}\).
Lemma 4
If \(d_s\) and \(d_c\) are defined as in Fig. 8, then \(\mathsf {LHF} \) is smooth.
Proof
In the following we prove smoothness conditions (S1) and (S2). Condition (S3) can be proven analogously to (S2). Conditions (S4), (S5) and (S6) can be proven analogously to (S1), (S2) and (S3), respectively.
Since \(d_\alpha =d_s+d_{s'}\), for all \(\hat{\mathbf {s}}\in \mathcal {D}_{s} \) and \(\hat{{\textit{\textbf{s}}}}'\in \mathcal {D}_{s'} \), \(\left\Vert \hat{{\textit{\textbf{s}}}}'-\hat{{\textit{\textbf{s}}}}\right\Vert _{\infty } \le d_{s'}+d_s=d_\alpha \) and therefore \(\hat{{\textit{\textbf{s}}}}'-\hat{{\textit{\textbf{s}}}}\in \mathcal {D}_{\alpha }.\) This proves smoothness condition (S1).
To prove (S2), we fix \(\hat{{\textit{\textbf{s}}}}_1, \hat{{\textit{\textbf{s}}}}_2 \in \mathcal {D}_{s} \) and define sets \(\mathcal {D}_{\alpha _1}:=\{\hat{{\varvec{\alpha }}}\in \mathcal {D}_{\alpha } \mid \hat{{\varvec{\alpha }}}+\hat{{\textit{\textbf{s}}}}_1\in \mathcal {D}_{s'} \}\) and \(\mathcal {D}_{\alpha _2}:=\{\hat{{\varvec{\alpha }}}\in \mathcal {D}_{\alpha } \mid \hat{{\varvec{\alpha }}}+\hat{{\textit{\textbf{s}}}}_2\in \mathcal {D}_{s'} \}\). Note that for all \(\hat{{\textit{\textbf{s}}}}_1,\hat{{\textit{\textbf{s}}}}_2\in \mathcal {D}_{s} \) and \(\hat{{\textit{\textbf{s}}}}'\in \mathcal {D}_{s'} \) there exist \(\hat{{\varvec{\alpha }}}_1\in \mathcal {D}_{\alpha _1} \) and \(\hat{{\varvec{\alpha }}}_2\in \mathcal {D}_{\alpha _2} \) s.t. \(\hat{{\varvec{\alpha }}}_1+\hat{{\textit{\textbf{s}}}}_1=\hat{{\textit{\textbf{s}}}}'\) and \(\hat{{\varvec{\alpha }}}_2+\hat{{\textit{\textbf{s}}}}_2=\hat{{\textit{\textbf{s}}}}'\). So, \(\left| \mathcal {D}_{\alpha _1} \right| =\left| \mathcal {D}_{\alpha _2} \right| = \left| \mathcal {D}_{s'} \right| \).
In the following, fix \(\hat{{\textit{\textbf{s}}}}_1,\hat{{\textit{\textbf{s}}}}_2\in \mathcal {D}_{s} \) and define the random variables  and
and  . To prove smoothness condition (S2), it remains to show that
. To prove smoothness condition (S2), it remains to show that
We have

To show that (5) amounts to zero, we argue as follows. If \(\bar{\hat{{\varvec{\alpha }}}} \not \in \mathcal {D}_{s'} \) then clearly

Now, suppose \(\bar{\hat{{\varvec{\alpha }}}}\in \mathcal {D}_{s'} \). Since \(\hat{{\varvec{\alpha }}}'\in \mathcal {D}_{\alpha _2} \) and random variable \(\hat{{\varvec{\alpha }}}'\) takes values in \(\mathcal {D}_{\alpha _2} \), the probability that random variable \(\hat{{\varvec{\alpha }}}'\) takes value \(\bar{\hat{{\varvec{\alpha }}}}\) is \(\frac{1}{\left| \mathcal {D}_{\alpha _2} \right| }=\frac{1}{\left| \mathcal {D}_{s'} \right| }\). So,  . Since \(\bar{\hat{{\varvec{\alpha }}}}\in \mathcal {D}_{\alpha _2} \), \(\bar{\hat{{\varvec{\alpha }}}}+\hat{{\textit{\textbf{s}}}}_2\in \mathcal {D}_{s'} \). Also \(\hat{{\varvec{\alpha }}}^*\in \mathcal {D}_{\alpha _1} \) implies \(\hat{{\varvec{\alpha }}}^*+\hat{{\textit{\textbf{s}}}}_1\in \mathcal {D}_{s'} \). So the probability that random variable \(\hat{{\varvec{\alpha }}}^*\) fulfills \(\hat{{\varvec{\alpha }}}^*+\hat{{\textit{\textbf{s}}}}_1=\bar{\hat{{\varvec{\alpha }}}}+\hat{{\textit{\textbf{s}}}}_2\) is \(\frac{1}{\left| \mathcal {D}_{\alpha _1} \right| }=\frac{1}{\left| \mathcal {D}_{s'} \right| }. \) Therefore,
. Since \(\bar{\hat{{\varvec{\alpha }}}}\in \mathcal {D}_{\alpha _2} \), \(\bar{\hat{{\varvec{\alpha }}}}+\hat{{\textit{\textbf{s}}}}_2\in \mathcal {D}_{s'} \). Also \(\hat{{\varvec{\alpha }}}^*\in \mathcal {D}_{\alpha _1} \) implies \(\hat{{\varvec{\alpha }}}^*+\hat{{\textit{\textbf{s}}}}_1\in \mathcal {D}_{s'} \). So the probability that random variable \(\hat{{\varvec{\alpha }}}^*\) fulfills \(\hat{{\varvec{\alpha }}}^*+\hat{{\textit{\textbf{s}}}}_1=\bar{\hat{{\varvec{\alpha }}}}+\hat{{\textit{\textbf{s}}}}_2\) is \(\frac{1}{\left| \mathcal {D}_{\alpha _1} \right| }=\frac{1}{\left| \mathcal {D}_{s'} \right| }. \) Therefore,  . This completes the proof.
. This completes the proof.
Torsion Free Elements from the Kernel. We first observe that we only need to find a non-zero \(\hat{\mathbf {z}}^*\) such that \(\mathsf {F} (\hat{\mathbf {z}}^*) = \mathbf {0}\). Indeed, if \(d_c\) is small enough then by selecting appropriate prime q we can apply the main result of Lyubashevsky and Seiler [41].
Lemma 5
( [41] Corollary 1.2). Let \(n\ge \iota > 1\) be powers of 2 and \(q\equiv 2\iota +1 \pmod {4\iota }\) be a prime. Then \(X^{n}+1\) factors into d irreducible polynomials \(X^{n/\iota }-r_j\) modulo q and any \(\mathbf {y}\in R_{q}\setminus \{\mathbf {0}\}\) that satisfies
is invertible in \(R_{q}\).
Hence, pick \(d_c < \frac{1}{2\sqrt{\iota }}\cdot q^{1/\iota }\). Then, for \(\mathbf {c}_1,\mathbf {c}_2 \in \mathcal {S}_{c} \), \((\mathbf {c}_1 - \mathbf {c}_2)\hat{\mathbf {z}}^* = \mathbf {0} \implies \mathbf {c}_1 = \mathbf {c}_2\) since otherwise \(\mathbf {c}_1 - \mathbf {c}_2\) is invertible and thus \(\hat{\mathbf {z}}^* = \mathbf {0}\). Therefore, \(\hat{\mathbf {z}}^*\) is a torsion-free element from the kernel.
Many papers investigate non-existence of a short vector in random module lattices e.g. [36, 43]. However, here we are interested in the existence. Concretely, we want to make sure there exists a \(\hat{\mathbf {z}}^*\) from the kernel with infinity norm at most \(\delta < q/2\). Consider the set of vectors \(B_\delta \subset R^m_{q}\) of polynomials with coefficients between 0 and \(\delta \). Clearly, for \(\hat{\mathbf {y}}_1,\hat{\mathbf {y}}_2 \in B_\delta \): \(\Vert \hat{\mathbf {y}}_1-\hat{\mathbf {y}}_2\Vert _\infty \le \delta < q/2\). If we select \(\delta \) such that \(|B_\delta |=(\delta +1)^{nm} > q^n\) then by the pigeonhole principle, there exist two distinct \(\hat{\mathbf {y}}_1, \hat{\mathbf {y}}_2 \in B_\delta \) such that \(\mathsf {F} (\hat{\mathbf {y}}_1) = \mathsf {F} (\hat{\mathbf {y}}_2)\). Hence, we can set \(\hat{\mathbf {z}}^* = \hat{\mathbf {y}}_1 - \hat{\mathbf {y}}_2\).
Collision Resistance. To estimate the hardness of finding collisions in \(\mathsf {LHF} \) we state the following simple lemma.
Lemma 6
If \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,2d}\) is \((\varepsilon ,t)\)-hard relative to \(\hat{{\textit{\textbf{a}}}} \in R_q^m\) then \(\mathsf {LHF} \) is \((\varepsilon ,t)\)-\(\mathbf {CR} \) relative to \( par \in \mathsf {PGen} \), where \( par \) contains all the values defined in Fig. 8 along with \(\hat{{\textit{\textbf{a}}}}\).
Proof
Adversary \(\mathsf {A} \) returns distinct values \(\hat{{\textit{\textbf{x}}}}_1,\hat{{\textit{\textbf{x}}}}_2\in \mathcal {D} \) after being called on parameters \( par \). Since \(\mathsf {F} (\hat{{\textit{\textbf{x}}}}_1)=\mathsf {F} (\hat{{\textit{\textbf{x}}}}_2)\) and since \(\mathsf {F} \) is a module homomorphism, \(\mathsf {F} (\hat{{\textit{\textbf{x}}}}_2-\hat{{\textit{\textbf{x}}}}_1) = \mathsf {F} (\hat{{\textit{\textbf{x}}}}_2) - \mathsf {F} (\hat{{\textit{\textbf{x}}}}_1) = 0\). Further, \(\left\Vert \hat{{\textit{\textbf{x}}}}_2-\hat{{\textit{\textbf{x}}}}_1\right\Vert _{\infty } \le 2d\). So \(\hat{{\textit{\textbf{x}}}}_2-\hat{{\textit{\textbf{x}}}}_1\) is a solution to the \(\mathsf {R}\hbox {-}\mathsf {SIS}_{q,n,m,2d}\) problem relative to \(\hat{{\textit{\textbf{a}}}}\).
As we described in the previous section, adversary \(\mathsf {A} \), which can win the OMUF game, manages to extract \(\hat{\mathbf {\chi }}_1, \hat{\mathbf {\chi }}_2\) so that \(\mathsf {F} (\hat{\mathbf {\chi }}_1 - \hat{\mathbf {\chi }}_2 ) = 0\). The norm of \(\hat{\mathbf {\chi }}_1\) (and similarly for \(\hat{\mathbf {\chi }}_2\)) can be simply bounded by:
Thus, we set \(d = 2d_{s'}\). With parameters defined in Fig. 8, \(d \approx 2^{233}\) and \(\frac{1}{2}\mathsf {sv}_{1.005}(n,q) \approx 2^{235}\). Therefore, we get \(\Vert \hat{\mathbf {\chi }}_1 - \hat{\mathbf {\chi }}_2\Vert _\infty< 2d < \mathsf {sv}_{1.005}(n,q)\).
Regularity. We now prove that by selecting sizes \(d_{ sk }\) and \(d_r\) as in Fig. 8, our \(\mathsf {LHF} \) is \((\epsilon ,Q')\)-regular where \(\varepsilon =2^{-128}\) and \(Q' = 7 \mu \eta \nu \). Note that we only allow seven signing queries due to a potential lattice variant of the ROS attack (see Sect. 7).
Lemma 7
Denote \(\varepsilon =2^{-128}\) and \(Q' = 7 \mu \eta \nu \). Then, for our selection of \(d_{ sk },d_r\), the \(\mathsf {LHF} \) is \((\epsilon ,Q')\)-regular, i.e.
where
and
Proof
Indeed, we first picked \(d_r\) so that
Simultaneously, we chose \(d_ sk \) which satisfies: \( |\mathcal {D}_{ sk } '|/|\mathcal {D}_{ sk } | \ge 1 - 2^{-131}\). Also, we check that \(d_{r} \ge vmn^2 d_ sk d_c\) for the enclosedness property. Then, Eq. (6) follows by the Bernoulli inequality.
Sizes. We pick prime \(q \approx 2^{1890}\) so that \(q \equiv 2\iota +1 \pmod {4\iota }\) where \(\iota =64\) and \(X^n+1\) splits into \(\iota \) irreducible polynomials modulo q. Hence, we can apply Lemma 5. Unfortunately, such a large prime modulus affects the signing time significantly. The signature consists of three parts: \(\hat{{\textit{\textbf{s}}}}', \mathbf {c}'\) and \(\mathsf {auth}\). The size for \(\hat{{\textit{\textbf{s}}}}'\) and \(\mathbf {c}'\) are respectively \(nm\log 2d_{s'}\) and \(n\log 2d_{c'}\). Also, \(\mathsf {auth}\) contains the index of the leaf (which can be represented with at most \(\log (\mu \eta \nu )\) bits) and \(\log (\mu \eta \nu )\) outputs of the hash function \(\mathsf {G}\). If we assume that \(\mathsf {G}:\{0,1\}^* \rightarrow \{0,1\}^{128}\) then \(\mathsf {auth}\) has at most \(\log (\mu \eta \nu ) + 128\cdot \log (\mu \eta \nu )\) bits. For parameters selected in Fig. 8, our signature has size around 36.03 MB. We observe that the main reason of obtaining such large signatures is the size for \(d_r\) and \(d_{ sk }\), which should satisfy the regularity property.
7 Generalized ROS Problem
The standard ROS (Random inhomogenities in an Overdetermined, Solvable system of linear equations) problem was first introduced by Schnorr [58] in the context of blind signatures. If one can solve the ROS problem then one is also able to break the security of the Schnorr as well as the Okamoto-Schnorr and Okamoto-Gouillou-Quisquarter blind signature schemes. Later works by Wagner and Minder and Sinclair [42, 60] proposed algorithms which solve the ROS problem in sub-exponential time. In this section, we discuss main challenges when translating the ROS problem to general linear hash function families with correctness error. To the best of our knowledge, none of previous works on lattice-based blind signatures (e.g. [3, 4, 56]) consider this issue.
We start by describing the Generalized ROS \((\mathbf {GROS})\) problem for linear hash function families with correctness error. For a linear hash function family \(\mathsf {LHF} \), \( par \in \mathsf {PGen} \) and a positive integer \(\ell \), let \(\mathcal {X}_\ell \) be the set
The game \(\ell \hbox {-}\mathbf {GROS}_{\mathsf {LHF}, par }\) is defined via Fig. 9. The advantage of adversary \(\mathsf {A} \) in \(\ell \hbox {-}\mathbf {GROS}_{\mathsf {LHF}, par }\) is defined as \(\mathbf {Adv}^{\ell \hbox {-}\mathbf {GROS}}_{\mathsf {LHF}, par } (\mathsf {A}):=\Pr [\ell \hbox {-}\mathbf {GROS}_{\mathsf {LHF}, par }^{\mathsf {A}}\Rightarrow 1]\) and its running time is denoted as \(\mathbf {Time} ^{\ell \hbox {-}\mathbf {GROS}}_{\mathsf {LHF}, par }(\mathsf {A})\).
Definition 7
(\(\ell \hbox {-}\mathbf {GROS}\) Hardness). Let \(\ell \in \mathbb {N},\ell >0\) and let \(\mathsf {LHF} \) be a linear function family and let \( par \in \mathsf {PGen} (1^\kappa )\). \(\ell \hbox {-}\mathbf {GROS}\) is said to be \((\varepsilon ,t,Q_\mathsf {H} )\)-hard in the random oracle model relative to \( par \) and \(\mathsf {LHF} \) if for all adversaries \(\mathsf {A} \) satisfying \(\mathbf {Time} ^{\ell \hbox {-}\mathbf {GROS}}_{\mathsf {LHF}, par }(\mathsf {A})\le t\) and making at most \(Q_\mathsf {H} \) queries to \(\mathsf {H} \), we have that \(\mathbf {Adv}^{\ell \hbox {-}\mathbf {GROS}}_{\mathsf {LHF}, par } (\mathsf {A})\le \varepsilon \).
The following theorem shows that an attack on \(\ell \hbox {-}\mathbf {GROS}_{\mathsf {LHF}, par }\) propagates to an attack against \(\mathbf {OMUF} _{\mathsf {BS} [\mathsf {LHF},\mathsf {G},\mathsf {H} ], par }\).
Theorem 5
Let \(\mathsf {LHF} \) be a linear hash function family with enclosedness error \((\delta _1,\delta _2,\delta _3)\), \(\mathsf {G} :\{0,1\}^*\rightarrow \{0,1\}^{2\lambda }\) and \(\mathsf {H} :\{0,1\}^*\rightarrow \mathcal {S} _{c'}\) be random oracles and let \(\mathsf {BS}:=\mathsf {BS} _{\eta ,\nu ,\mu }[\mathsf {LHF},\mathsf {G},\mathsf {H} ].\) If \(\mathsf {BS} \) is \((\varepsilon ,t,0,\ell ,Q_\mathsf {G},Q_\mathsf {H} )\)-\(\mathbf {OMUF} \) relative to \( par \) in the random oracle model then \(\ell \hbox {-}\mathbf {GROS}\) is \((\varepsilon /(1-\delta _2)^\ell ,t,Q_\mathsf {H} )\)-hard relative to \(\mathsf {LHF} \) and \( par \) in the random oracle model.
Proof (Sketch)
The proof is similar to one for perfect correctness [32, 58]. For readability, we assume that \(\mu =\nu =1\) since there is no need to blind challenges/signatures in this scenario (it can, however, be easily generalized to arbitrary \(\mu ,\nu \)). We now define an adversary \(\mathsf {B} \) in \(\mathbf {OMUF} _{\mathsf {BS}, par }\) that internally runs an adversary \(\mathsf {A} \) against \(\ell \hbox {-}\mathbf {GROS}_{\mathsf {LHF}, par }\) with random oracle \(\mathsf {H} '\).
-
It simultaneously opens \(\ell \) sessions with \(\mathtt {S} _1\), receiving commitments \({\textit{\textbf{R}}}_1,...,{\textit{\textbf{R}}}_\ell \). Let us denote \({\textit{\textbf{R}}}_i = ({\textit{\textbf{R}}}_{i,1},\ldots ,{\textit{\textbf{R}}}_{i,\eta })\) for \(i\in [\ell ]\).
-
Next, it executes \(\mathsf {A} ^{\mathsf {H} '}( par )\). When \(\mathsf {A} \) makes a fresh query \({\textit{\textbf{a}}}\) to \(\mathsf {H} '\), \(\mathsf {B} \) computes \({\textit{\textbf{R}}}'_{{\textit{\textbf{a}}},j}:=\sum ^\ell _{i=1}{\textit{\textbf{a}}}_i\cdot {\textit{\textbf{R}}}_{i,j}\) for all \(j\in [\eta ]\). It then computes \((\mathsf {root}_{\textit{\textbf{a}}},\mathsf {tree}_{{\textit{\textbf{a}}}})\leftarrow \mathsf {HashTree}({\textit{\textbf{R}}}'_{{\textit{\textbf{a}}},1},...,{\textit{\textbf{R}}}'_{{\textit{\textbf{a}}},\eta })\) and \(c'\leftarrow \mathsf {H} (\mathsf {root}_{\textit{\textbf{a}}},m_{\textit{\textbf{a}}})\), for a fresh message \(m_{\textit{\textbf{a}}}\), and then returns \(\mathsf {H} '({\textit{\textbf{a}}}):=c'\) as the answer. Clearly, \(c'\) is independent from commitments \({\textit{\textbf{R}}}_i\).
-
When \(\mathsf {A} \) terminates and returns \((\mathbf {A},{\textit{\textbf{c}}})\), \(\mathsf {B} \) sends the value \({\textit{\textbf{c}}}_i\) as the challenge value for the \(i^{th}\) session with \(\mathtt {S} _2\), where \(i\in [\ell ]\), and receives an answer \({\textit{\textbf{s}}}_i\). If \({\textit{\textbf{R}}}_{i,1} \ne \mathsf {F} ({\textit{\textbf{s}}}_i) - {\textit{\textbf{c}}}_i \cdot pk \) then \(\mathsf {B} \) aborts. Note that the probability that \(\mathsf {B} \) does not abort at all is at least \((1-\delta _2)^\ell \) by definition of the enclosedness error.
-
Next, for all \(j\in [\ell +1]\), \(\mathsf {B} \) computes \({\textit{\textbf{s}}}'_j:=\sum ^\ell _{i=1} {\textit{\textbf{A}}}_{j,i}\cdot {\textit{\textbf{s}}}_i\) and retrieves the values \(\mathsf {root}_{{\textit{\textbf{A}}}_j},\mathsf {tree}_{{\textit{\textbf{A}}}_j},m_{{\textit{\textbf{A}}}_j}\) used to compute \({{\textit{\textbf{A}}}_j}\) and computes \(c_j'\leftarrow \mathsf {H} (\mathsf {root}_{{\textit{\textbf{A}}}_j},m_{{\textit{\textbf{A}}}_j}),\mathsf {auth}_j\leftarrow \mathsf {BuildAuth}((0,1,1),\mathsf {tree})\). It sets \(\sigma _j:=(c_j',{\textit{\textbf{s}}}_j',\mathsf {auth}_j)\).
-
Finally, \(\mathsf {B} \) returns \(\ell +1\) message/signature pairs \((\sigma _1,m_{{\textit{\textbf{A}}}_1}),...,(\sigma _{\ell +1},m_{{\textit{\textbf{A}}}_{\ell +1}})\).
Correctness of the signatures follows because
Further, by (7) we have \({\textit{\textbf{s}}}_i'\in \mathcal {D}_{s'} \) for all \(i\in [\ell ]\). Correctness of the authentication path can easily be verified. \(\square \)
One observes that the attack only makes sense for small values of \(\ell \) due to the security loss of \((1-\delta _2)^\ell \). The reason is that we always force \(\mathtt {S} _2\) to accept the first rejection sampling, otherwise \(\mathsf {B} \) aborts. On interesting point about our attack is that it can be easily be modified to other lattice-based signatures (e.g. [56]) since the signer in such schemes usually outputs only one commitment per session instead of \(\eta \). The ROS problem in the standard setting is a special case where \(\mathcal {S} _{c'}=\mathcal {S} _{c} = \mathcal {S}\) are finite fields of size q and \(\mathcal {X}_\ell = \mathcal {S}^\ell \) [58]. In this setting Schnorr proves that the \(\ell \hbox {-}\mathbf {GROS}\) problem is solvable with probability at most \(\left( {\begin{array}{c}Q_H\\ \ell +1\end{array}}\right) /|\mathcal {S} _{c'}|<Q_H^{\ell +1}/q\). Wagner later proposed an algorithm \(\mathsf {A} \) in the \((\ell :=2^{2\sqrt{\log q}}-1,Q){\hbox {-}}\mathbf {GROS}^{\mathsf {A}}_{\mathsf {LHF}}\) experiment with running time \(O(2^{2\sqrt{\log q}})\) [60]. The two main reasons that Wagner’s algorithm [60] cannot be translated to the \(\ell \hbox {-}\mathbf {GROS}\) problem even with the lattice instantiation from Sect. 6 are the following. First, let us recall that in Sect. 6 we select \(\mathcal {S} : = R_q = \mathbb {Z}_q[X]/\langle X^n+1 \rangle \) to be a cyclotomic ring and \(\mathcal {S} _{c'}\) to be a set of short polynomials in \(R_q\). Therefore, we have \(\mathcal {S} _{c'} \subsetneq \mathcal {S} _{c} \subsetneq \mathcal {S}\) and \(\mathcal {S} _{c},\mathcal {S} _{c'}\) are not finite fields (or even rings). Secondly, compared to the work of Hauck et al. [32], the values \(s'\) in a signature have to lie in the set \(\mathcal {D}_{s'} \). This imposes a further restriction on the values in the matrix \(\mathbf {A}\) and the vector \({\textit{\textbf{c}}}\) returned by the \(\mathbf {GROS}\) adversary. We believe that the studying this variant of the \(\mathbf {GROS}\) problem further is an interesting problem for future work.
Notes
- 1.
ROS stands for Random inhomogenities in an Overdetermined, Solvable system of linear equations.
- 2.
It is not even clear how much better our scheme performs compared to generic constructions using non-interactive zero-knowledge proofs [23].
References
Abdalla, M., An, J.H., Bellare, M., Namprempre, C.: From identification to signatures via the Fiat-Shamir transform: minimizing assumptions for security and forward-security. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 418–433. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_28
Abe, M.: A secure three-move blind signature scheme for polynomially many signatures. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 136–151. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_9
Alkadri, N.A., Bansarkhani, R.E., Buchmann, J.: BLAZE: practical lattice-based blind signatures for privacy-preserving applications. In: Bonneau, J., Heninger, N. (eds.) FC 2020. LNCS, vol. 12059, pp. 484–502. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51280-4_26
Alkadri, N.A., Bansarkhani, R.E., Buchmann, J.: On lattice-based interactive protocols with aborts. Cryptology ePrint Archive, Report 2020/007 (2020). https://eprint.iacr.org/2020/007
Backendal, M., Bellare, M., Sorrell, J., Sun, J.: The Fiat-Shamir zoo: relating the security of different signature variants. In: Gruschka, N. (ed.) NordSec 2018. LNCS, vol. 11252, pp. 154–170. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03638-6_10
Baldimtsi, F., Lysyanskaya, A.: Anonymous credentials light. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 1087–1098. ACM Press, November 2013
Baldimtsi, F., Lysyanskaya, A.: On the security of one-witness blind signature schemes. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 82–99. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_5
Belenkiy, M., Camenisch, J., Chase, M., Kohlweiss, M., Lysyanskaya, A., Shacham, H.: Randomizable proofs and delegatable anonymous credentials. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 108–125. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_7
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 390–399. ACM Press, October/November 2006
Bellare, M., Palacio, A.: GQ and Schnorr identification schemes: proofs of security against impersonation under active and concurrent attacks. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 162–177. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_11
Bellare, M., Rogaway, P.: Code-based game-playing proofs and the security of triple encryption. Cryptology ePrint Archive, Report 2004/331 (2004). http://eprint.iacr.org/2004/331
Boldyreva, A.: Threshold signatures, multisignatures and blind signatures based on the gap-Diffie-Hellman-group signature scheme. In: Desmedt, Y.G. (ed.) PKC 2003. LNCS, vol. 2567, pp. 31–46. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36288-6_3
Bouaziz-Ermann, S., Canard, S., Eberhart, G., Kaim, G., Roux-Langlois, A., Traoré, J.: Lattice-based (partially) blind signature without restart. Cryptology ePrint Archive, Report 2020/260 (2020). https://eprint.iacr.org/2020/260
Brands, S.: Untraceable off-line cash in wallet with observers. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 302–318. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_26
Camenisch, J., Hohenberger, S., Lysyanskaya, A.: Compact e-cash. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 302–321. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_18
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Camenisch, J., Neven, G., Shelat, A.: Simulatable adaptive oblivious transfer. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 573–590. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_33
Chaum, D.: Blind signatures for untraceable payments. In: Chaum, D., Rivest, R.L., Sherman, A.T. (eds.) CRYPTO 1982, pp. 199–203. Plenum Press, New York (1982)
Chaum, D., Fiat, A., Naor, M.: Untraceable electronic cash. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 319–327. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_25
Chen, L., Cui, Y., Tang, X., Hu, D., Wan, X.: Hierarchical ID-based blind signature from lattices. In: Wang, Y., Cheung, Y., Guo, P., Wei, Y. (eds.) Seventh International Conference on Computational Intelligence and Security, CIS 2011, Sanya, Hainan, China, 3–4 December 2011, pp. 803–807. IEEE Computer Society (2011)
Chen, Y., Nguyen, P.Q.: BKZ 2.0: better lattice security estimates. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 1–20. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_1
Döttling, N., Fleischhacker, N., Krupp, J., Schröder, D.: Two-message, oblivious evaluation of cryptographic functionalities. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 619–648. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_22
Fischlin, M.: Round-optimal composable blind signatures in the common reference string model. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 60–77. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_4
Fischlin, M., Schröder, D.: Security of blind signatures under aborts. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 297–316. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_17
Fischlin, M., Schröder, D.: On the impossibility of three-move blind signature schemes. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 197–215. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_10
Fuchsbauer, G., Hanser, C., Slamanig, D.: Practical round-optimal blind signatures in the standard model. In: Gennaro, R., Robshaw, M.J.B. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 233–253. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_12
Gama, N., Nguyen, P.Q.: Predicting lattice reduction. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 31–51. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_3
Gao, W., Hu, Y., Wang, B., Xie, J.: Identity-based blind signature from lattices in standard model. In: Chen, K., Lin, D., Yung, M. (eds.) Inscrypt 2016. LNCS, vol. 10143, pp. 205–218. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-54705-3_13
Gao, W., Hu, Y., Wang, B., Xie, J., Liu, M.: Identity-based blind signature from lattices. Wuhan Univ. J. Nat. Sci. 22(4), 355–360 (2017). https://doi.org/10.1007/s11859-017-1258-x
Garg, S., Gupta, D.: Efficient round optimal blind signatures. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 477–495. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_27
Garg, S., Rao, V., Sahai, A., Schröder, D., Unruh, D.: Round optimal blind signatures. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 630–648. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_36
Hauck, E., Kiltz, E., Loss, J.: A modular treatment of blind signatures from identification schemes. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 345–375. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_12
Hauck, E., Kiltz, E., Loss, J., Nguyen, N.K.: Lattice-based blind signatures, revisited. Cryptology ePrint Archive, Report 2020 (2020). https://eprint.iacr.org/2020
Juels, A., Luby, M., Ostrovsky, R.: Security of blind digital signatures. In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 150–164. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052233
Katz, J., Schröder, D., Yerukhimovich, A.: Impossibility of blind signatures from one-way permutations. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 615–629. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_37
Langlois, A., Stehlé, D.: Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 75(3), 565–599 (2015)
Le, H.Q., Susilo, W., Khuc, T.X., Bui, M.K., Duong, D.H.: A blind signature from module latices. In: 2019 IEEE Conference on Dependable and Secure Computing (DSC), pp. 1–8. IEEE (2019)
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Lyubashevsky, V., Micciancio, D.: Generalized compact Knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006, Part II. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_13
Lyubashevsky, V., Seiler, G.: Short, invertible elements in partially splitting cyclotomic rings and applications to lattice-based zero-knowledge proofs. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 204–224. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_8
Minder, L., Sinclair, A.: The extended k-tree algorithm. In: Mathieu, C. (ed.) 20th SODA, pp. 586–595. ACM-SIAM, January 2009
Nguyen, N.K.: On the non-existence of short vectors in random module lattices. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part II. LNCS, vol. 11922, pp. 121–150. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34621-8_5
Okamoto, T.: Provably secure and practical identification schemes and corresponding signature schemes. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 31–53. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_3
Okamoto, T.: Efficient blind and partially blind signatures without random oracles. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 80–99. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_5
Okamoto, T., Ohta, K.: Universal electronic cash. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 324–337. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_27
Papachristoudis, D., Hristu-Varsakelis, D., Baldimtsi, F., Stephanides, G.: Leakage-resilient lattice-based partially blind signatures. Cryptology ePrint Archive, Report 2019/1452 (2019). https://eprint.iacr.org/2019/1452
Peikert, C., Rosen, A.: Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 145–166. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_8
Pointcheval, D.: Strengthened security for blind signatures. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 391–405. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054141
Pointcheval, D., Stern, J.: Provably secure blind signature schemes. In: Kim, K., Matsumoto, T. (eds.) ASIACRYPT 1996. LNCS, vol. 1163, pp. 252–265. Springer, Heidelberg (1996). https://doi.org/10.1007/BFb0034852
Pointcheval, D., Stern, J.: Security proofs for signature schemes. In: Maurer, U.M. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 387–398. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_33
Pointcheval, D., Stern, J.: New blind signatures equivalent to factorization (extended abstract). In: Graveman, R., Janson, P.A., Neuman, C., Gong, L. (eds.) ACM CCS 1997, pp. 92–99. ACM Press, April 1997
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000)
Rodriuguez-Henriquez, F., Ortiz-Arroyo, D., Garcia-Zamora, C.: Yet another improvement over the Mu-Varadharajan e-voting protocol. Comput. Stand. Interfaces 29(4), 471–480 (2007)
Rogaway, P.: Formalizing human ignorance. In: Nguyen, P.Q. (ed.) VIETCRYPT 2006. LNCS, vol. 4341, pp. 211–228. Springer, Heidelberg (2006). https://doi.org/10.1007/11958239_14
Rückert, M.: Lattice-based blind signatures. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 413–430. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_24
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991)
Schnorr, C.P.: Security of blind discrete log signatures against interactive attacks. In: Qing, S., Okamoto, T., Zhou, J. (eds.) ICICS 2001. LNCS, vol. 2229, pp. 1–12. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45600-7_1
Schröder, D., Unruh, D.: Security of blind signatures revisited. J. Cryptol. 30(2), 470–494 (2017)
Wagner, D.: A generalized birthday problem. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 288–304. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_19
Yi, X., Lam, K.-Y., Gollmann, D.: A new blind ECDSA scheme for bitcoin transaction anonymity. Cryptology ePrint Archive, Report 2018/660 (2018). https://eprint.iacr.org/2018/660
Zhang, L., Ma, Y.: A lattice-based identity-based proxy blind signature scheme in the standard model. Math. Probl. Eng. 2014 (2014)
Zhu, H., Tan, Y., Zhang, X., Zhu, L., Zhang, C., Zheng, J.: A round-optimal lattice-based blind signature scheme for cloud services. Future Gener. Comput. Syst. 73, 106–114 (2017)
Acknowledgments
We would like to thank Vadim Lyubashevsky for pointing out the flaw in BLAZE and Dominique Schröder for helping us with previous work on blind signatures. We are furthermore very grateful for the anonymous comments by the CRYPTO 2020 reviewers. Eduard Hauck was supported by DFG SPP 1736 Big Data. Eike Kiltz was supported by the BMBF iBlockchain project, the EU H2020 PROMETHEUS project 780701, DFG SPP 1736 Big Data, and the DFG Cluster of Excellence 2092 CASA. Ngoc Khanh Nguyen was supported by the SNSF ERC Transfer Grant CRETP2-166734 FELICITY. Julian Loss was supported by the financial assistance award 70NANB19H126 from U.S. Department of Commerce, National Institute of Standards and Technology.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Hauck, E., Kiltz, E., Loss, J., Nguyen, N.K. (2020). Lattice-Based Blind Signatures, Revisited. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12171. Springer, Cham. https://doi.org/10.1007/978-3-030-56880-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-56880-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56879-5
Online ISBN: 978-3-030-56880-1
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,  we have that
we have that 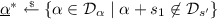 ,
, 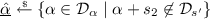 we have that
we have that  ,
,  we have that
we have that  ,
, 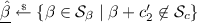 we have that
we have that 








