Testing the Significance of Interactions in Genetic Studies Using Interaction Information and Resampling Technique

Abstract

Interaction information is a model-free, non-parametric measure used for detection of interaction among variables. It frequently finds interactions which remain undetected by standard model-based methods. However in the previous studies application of interaction information was limited by lack of appropriate statistical tests. We study a challenging problem of testing the positiveness of interaction information which allows to confirm the statistical significance of the investigated interactions. It turns out that commonly used chi-squared test detects too many spurious interactions when the dependence between the variables (e.g. between two genetic markers) is strong. To overcome this problem we consider permutation test and also propose a novel HYBRID method that combines permutation and chi-squared tests and takes into account dependence between studied variables. We show in numerical experiments that, in contrast to chi-squared based test, the proposed method controls well the actual significance level and in many situations detects interactions which are undetected by standard methods. Moreover HYBRID method outperforms permutation test with respect to power and computational efficiency. The method is applied to find interactions among Single Nucleotide Polymorphisms as well as among gene expression levels of human immune cells.

1 Introduction

Detection of various types of interactions is one of the most important challenges in genetic studies. This is motivated by the fact that most human diseases are complex which means that they are typically caused by multiple factors, including gene-gene (G$\times$G) interactions and gene-environment (G$\times$E) interactions [1]. The analysis may include binary traits (case-control studies) as well as quantitative traits (e.g. blood pressure or patient survival times). The presence of gene-gene interactions has been shown in complex diseases such as breast cancer [2] or coronary heart disease [3]. The interactions are closely related to the concept of epistasis [4]. In biology, the epistasis is usually referred to as the modification, or most frequently, blocking of one allelic effect by another allele at a different locus [5]. In this work we focus on interactions of the second order, i.e. interactions between two variables in predicting the third variable, although higher order interactions may also contribute to many complex traits [6]. In our notation, $(X_1,X_2)$ denotes a pair of predictors, whereas Y stands for a response variable. We consider a general situation in which Y can be discrete (e.g. disease status) or quantitative (e.g. blood pressure or survival time), in the latter case Y is discretized.

There are many different concepts of measuring interactions, see e.g. [5]. Informally interaction arises when the simultaneous influence of variables $X_1$ and $X_2$ on Y is not additive. The classical approach to analyze interactions is to use ANOVA (in the case of quantitative Y) and logistic regression (in the case of binary Y) [7]. Recently entropy-based methods attracted a significant attention including interaction information (II) [8] which is a very promising measure having many desired properties. It is a non-parametric, model-free measure, which does not impose any particular assumptions on the data, unlike parametric measures of interactions based on e.g. linear or logistic regression. It is based on a very general measure of dependence - mutual information and thus it allows to detect interactions which remain undetected by standard methods based on parametric models, see e.g [9]. Finally, it can be applied to any types of variables, unlike e.g. logistic regression which is restricted to the case of binary response variable. Interaction information has been already used in genetic studies. For example, Moore et al. [10] use II for analysing gene-gene interactions associated with complex diseases. Recently, II was also used to verify existence of interactions between DNA methylation sites/gene expression profiles and gender/age in the context of glioma patients survival prediction [11]. II is applied as a main tool to detect interactions in packages: AMBIENCE [12] and BOOST [13]. Jakulin et al. [14] applied II to detect interactions between variables in classification task and studied how the interactions affect the performance of learning algorithms. Mielniczuk et al. [15] studied properties of II and its modifications in the context of finding interactions among Single Nucleotide Polymorphisms (SNPs). Mielniczuk and Teisseyre [9] have shown that, in context of gene-gene interaction detection, II is on the whole much more discriminative measure than the logistic regression, i.e. it finds certain types of interactions that remain undetected by logistic regression. Here, we provide evidences that II is also more powerful than ANOVA F test, when quantitative trait Y is considered. This is especially pronounced when a posteriori probability of Y given values of predictors is a non-linear function of Y.

Although II has attracted some attention, its application was hindered by lack of appropriate statistical tests. Here we study an important problem of testing positiveness of II. Positive value of II indicates that predictive interaction between $X_1$ and $X_2$ exists. The main contribution of the paper is a new test for positiveness of II which takes into account the fact that $X_1$ and $X_2$ may be dependent. This occurs frequently, e.g. in Genome Wide Associations Studies when dependence of SNPs in close proximity is due to crossing-over mechanism. The task is challenging as the distribution of II under the null hypothesis that its population value is zero is not known, except the special case when all three variables are mutually independent. In this case it turns out to be chi-squared distribution [16]. We show that indeed dependence matters in this context i.e. when association between $X_1$ and $X_2$ is strong the distribution of II can significantly deviate from chi-squared distribution. This means that in such cases a pertaining test based on chi-squared null distribution may not have an assumed level of significance, or equivalently, the calculated p-values may be misleading. In view of this we propose a hybrid method that combines two existing approaches: permutation test and chi-squared test. In brief, we use a chi-squared test when the dependence between the original variables is weak and the permutation test in the opposite case. The experiments show that the combined procedure, in contrast to the chi-squared test, allows to control actual significance level (type I error rate) and has a high power. At the same time it is less computationally expensive than standard permutation test.

2 Interaction Information

Variables denoted $X_1, X_2, Y$ take values $K_1, K_2, L$ respectively, and to simplify definitions are assumed to be discrete. Let $P(x_1,x_2):=P(X_1=x_1,X_2=x_2)$, $P(x_1):=P(X_1=x_1)$ and $P(x_2):=P(X_2=x_2)$ be joint and marginal probabilities, respectively. The independence between variables $X_1$ and $X_2$ will be denoted by $X_1\perp X_2$. $\chi ^2_k$ stands for the chi-squared distribution with k degrees of freedom will be denoted by and $\chi ^{2}_{k,1-\alpha }$ for the corresponding $1-\alpha$ quantile. Entropy of variable $X_1$, defined as $H(X_1):=-\sum _{x_1}P(x_1)\log P(x_1),$ is a basic measure of an uncertainty of the variable. Furthermore, conditional entropy, $H(X_1|X_2):=-\sum _{x_1,x_2}P(x_1,x_2)\log P(x_1|x_2)$, quantifies the uncertainty about $X_1$ when $X_2$ is given. Mutual information (MI) measures the amount of information obtained about one random variable, through the other random variable. It is defined as $I(X_1,X_2):=H(X_1)-H(X_1|X_2).$ MI is a popular non-negative measure of association and equals 0 only when if $X_1$ and $X_2$ are independent. MI can be also interpreted as the amount of uncertainty in one variable which is removed by knowing the other variable. In this context it is often called information gain. In addition define the conditional mutual information as $I(X_1,X_2|Y):=H(X_1|Y)-H(X_1|X_2,Y)=H(X_2|Y)-H(X_2|X_1,Y)$. It is equal zero if and only if $X_1$ and $X_2$ are conditionally independent given Y. For more properties of the basic measures above we refer to [17].

In this work the main object of our interest is interaction information (II) [8] that can be defined in two alternative ways. The first definition is

$$\begin{aligned} II(X_1,X_2,Y)=I((X_1,X_2),Y)-I(X_1,Y)-I(X_2,Y). \end{aligned}$$

(1)

Observe that $I(X_1,Y)$ and $I(X_2,Y)$ correspond to main effects. In practice we want to distinguish between situations when II is approximately 0 and when II is large, the latter indicating non-additive influence of both predictors on Y. In view of definition (1), interaction information can be interpreted as a part of mutual information between $(X_1,X_2)$ and Y which is solely due to interaction between $X_1$ and $X_2$ in predicting Y i.e. the part of $I((X_1,X_2),Y)$ which remains after subtraction of the main effect terms due to both predictors. Thus the definition of II corresponds to the intuitive meaning of interaction as a situation in which two variables affect a third one in a non-additive manner. Definition (1) also points out to important and challenging fact that existence of interactions is unrelated to existence of the main effects. Thus if SNPs with small main effects are not considered further, this does not necessarily mean that they do not contribute to the trait. The second definition states that

$$\begin{aligned} II(X_1,X_2,Y)=I(X_1,X_2|Y)-I(X_1,X_2). \end{aligned}$$

(2)

The equivalence of (1) and (2) follows from basic properties of MI (see e.g. [15]). Definition (2) indicates that II measures the influence of a variable Y on the amount of information shared between $X_1$ and $X_2$. In view of (1) and (2) we see that II is a valuable index which can be interpreted as a predictive interaction measure and at the same time as a measure of a deviation of conditional distributions from the unconditional one. This feature corresponds to two main approaches which are used to study interactions. The first one, which quantifies the remaining part of dependence after removing the main effects is exemplified by linear and logistic regression methods and testing significance of an interaction coefficient in such models [13]. The second one is based on measuring the difference of inter-loci associations between cases and controls [18].

Observe that II in contrast to the mutual information can be either positive or negative. In view of (2) positive value of II indicates that variable Y enhances the association between $X_1$ and $X_2$. In other words, the conditional dependence is stronger than the unconditional one. The negative value of II indicates that Y weakens or inhibits the dependence between $X_1$ and $X_2$. Alternatively, in view of (1), we can assert that positive interaction information means that information about Y contained in $(X_1,X_2)$ is larger than sum of individual informations $I(X_1,Y) +I(X_2,Y)$.

3 Testing the Positiveness of Interaction Information

The main goal of this paper is to propose a novel procedure for testing the positiveness of II. Such a procedure is useful to find pairs of variables $(X_1,X_2)$ that allow to jointly predict Y, even when the main effects are negligible and to confirm the statistical significance of the detected interaction. We state the following proposition which albeit simple, is instrumental for understanding the presented approach.

Proposition 1

If $Y\perp (X_1,X_2)$, then $II(X_1,X_2,Y)=0$.

Proof

The independence of $(X_1,X_2)$ and Y implies that $I((X_1,X_2),Y)=0$ and also $I(X_1,Y)=I(X_2,Y)=0$. Thus, the assertion follows directly from (1).

Note that although the converse to Proposition 1 is not true i.e. it is possible to have $II(X_1,X_2,Y)=0$ while $I((X_1,X_2),Y)>0$ ([19], p. 121) such examples require special constructions and are not typical. Moreover, it follows from (1) that when $X_1$ and $X_2$ are individually independent of Y and $II(X_1,X_2,Y)=0$ then pair $(X_1,X_2)$ is independent of Y. Whence, from the practical point of view hypotheses $II(X_1,X_2,Y)=0$ and $I((X_1,X_2),Y)=0$ are approximately equivalent.

Our principal aim is to test the null hypothesis:

$$\begin{aligned} \text {H}_0: II(X_1,X_2,Y)=0, \end{aligned}$$

(3)

against the alternative hypothesis corresponding to the positiveness of $II(X_1,X_2,Y)$:

$$\begin{aligned} \text {H}_1: II(X_1,X_2,Y)>0. \end{aligned}$$

(4)

In view of the above discussion we replace $H_0$ by:

$$ {\tilde{H}}_0: Y\perp (X_1,X_2), $$

The main operational reason for replacing $H_0$ by ${\tilde{H}}_0$ is that the distribution of a sample version of II under null hypothesis $H_0$ is unknown and determining it remains an open problem. We note that the sample versions of $I(X_1,X_2)$, $I(X_1,X_2|Y)$ and $II(X_1,X_2,Y)$ are simply obtained by replacing the true probabilities by estimated probabilities (i.e. fractions). They will be denoted by $\widehat{I}(X_1,X_2)$, $\widehat{I}(X_1,X_2|Y)$ and $\widehat{II}(X_1,X_2,Y)$, respectively. In contrast to $H_0$ scenario, it is possible to determine distribution of $\widehat{II}(X_1,X_2,Y)$ when ${\tilde{H}}_0$ is true using permutation based approach. We note that the latter allows to calculate the distribution of $\widehat{II}(X_1,X_2,Y)$ with arbitrary accuracy for any sample size n and for fixed sample distribution of Y and $(X_1,X_2)$ while chi-square approximation, even when it is valid, it is accurate only for large sample sizes. In this paper we combine these two approaches: permutation and based on asymptotic distribution. This yields a novel testing method which is computationally feasible (it is not as computationally intensive as permutation based test) and is more powerful than chi-squared test.

3.1 Chi-Squared Test IICHI

The distribution of $\widehat{II}(X_1,X_2,Y)$ under the null hypothesis (3) is not known. However, in a special case of (3) when all three variables are jointly independent and all probabilities $P(X_1=x_i,X_2=x_j,Y=y_k)$ are positive, Han [16] has shown that for a large sample size

$$\begin{aligned} 2n\widehat{II}(X_1,X_2,Y)\sim \chi ^2_{(K_1-1)(K_2-1)(L-1)}, \end{aligned}$$

(5)

approximately, where $K_1, K_2, L$ are the number of levels of $X_1$, $X_2$ and Y, respectively. Of course, joint independence of $(X_1,X_2,Y)$ is only a special case of ${\tilde{H}}_0$, which is in turn a special case of (3). Nonetheless the above approximation is informally used to test the positiveness of II under null hypothesis, see e.g. [12]. Thus for this method, we accept the null hypothesis (3) if $2n\widehat{II}(X_1,X_2,Y)<\chi ^{2}_{(K_1-1)(K_2-1)(L-1),1-\alpha }$, where $\alpha$ is a significance level. It turns out that if the dependence between $X_1$ and $X_2$ increases the distribution of $2n\widehat{II}(X_1,X_2,Y)$ deviates from $\chi ^2$ distribution. Thus the $\chi ^2$ test can be used to test the positiveness of $II(X_1,X_2,Y)$ only if there is a weak dependence between $X_1$ and $X_2$. It follows from our experiments that if the dependence between $X_1$ and $X_2$ is strong, then $\chi ^2$ test tends to reject the null hypothesis too often, i.e. its type I error rate may significantly exceed the prescribed level of significance $\alpha$.

3.2 Permutation Test IIPERM

The distribution of $2n\widehat{II}(X_1,X_2,Y)$ under the null hypothesis ${\tilde{H}}_0$ can be approximated using a permutation test. Although ${\tilde{H}}_0$ is a proper subset of (3), the Monte-Carlo approximation is used to test the positiveness of II under hypothesis (3). Observe that permuting the values of variable Y while keeping values of $(X_1,X_2)$ fixed we obtain the sample conforming the null distribution. An important advantage of permutation test is that while permuting the values of Y the dependence between $X_1$ and $X_2$ is preserved. We permute the values of variable Y and calculate $2n\widehat{II}(X_1,X_2,Y)$ using the resulting data. This step is repeated B times and allows to approximate the distribution of $2n\widehat{II}(X_1,X_2,Y)$ under the null hypothesis ${\tilde{H}}_0$.

Figure 1 shows the permutation distribution (for $B=10000$), $\chi ^2$ distribution and a true distribution of $2n\widehat{II}(X_1,X_2,Y)$, under the null hypothesis (3), for artificial data M0 (see Sect. 4.1), generated as follows. The pair $(X_1,X_2)$ is is drawn from distribution described in the Table 1, Y is generated independently from the standard Gaussian distribution and then discretized using the equal frequencies and 5 bins. The true distribution is approximated by calculating $2n\widehat{II}(X_1,X_2,Y)$ for 10000 data generation repetitions (this is possible only for artificially generated data). Since $X_1$ and $X_2$ take 3 possible values, we consider $\chi ^2$ distribution with $(3-1)\times (3-1)\times (5-1)=16$ degrees of freedom. In this experiment we control the dependence strength between $X_1$ and $X_2$ and analyse three cases: $I(X_1,X_2)=0$, $I(X_1,X_2)=0.27$ and $I(X_1,X_2)=0.71$. Thus in the first case $X_1$ and $X_2$ are independent whereas in the last case there is a strong dependence between $X_1$ and $X_2$. First observe that the lines corresponding to the permutation distribution and the true distribution are practically indistinguishable, which indicates that the permutation distribution approximates the true distribution very well. Secondly it is clearly seen that the $\chi ^2$ distribution deviates from the remaining ones when the dependence between $X_1$ and $X_2$ becomes large. Although this nicely illustrates (5) when complete independence occurs, it also underlines that $\chi ^2$ distribution is too crude when the dependence between $X_1$ and $X_2$ is strong. It is seen that the right tail of $\chi ^2$ distribution is thinner than the right tail of the true distribution and thus the uppermost quantiles of the true distribution are underestimated by the corresponding quantiles of $\chi ^2$ (Fig. 1). This is the reason why IICHI rejects the null hypothesis too often leading to many false positives. This problem is recognized for other scenarios of interaction detection (cf. [20]). The drawback of the permutation test is its computational cost. This becomes a serious problem when the procedure is applied for thousands of variables, as in the analysis of SNPs.

Fig. 1.

Probability density functions of chi-squared distribution, permutation distribution and true distribution of $2n\widehat{II}(X_1,X_2,Y)$ under the null hypothesis $(X_1,X_2)\perp Y$. Data is generated from model M0 described by Table 1, for $n=1000$.

3.3 Hybrid Test

To overcome the drawbacks of a $\chi ^2$ test (a significant deviation from the true distribution under the null hypothesis) and a permutation test (high computational cost) we propose a hybrid procedure that combines these two approaches. The procedure exploits the advantages of the both methods. It consists of two steps. We first verify whether the dependence between $X_1$ and $X_2$ exists. We use a test for a null hypothesis

$$\begin{aligned} \text {H}_0: I(X_1,X_2)=0, \end{aligned}$$

(6)

where the alternative hypothesis corresponds to the positiveness of MI:

$$\begin{aligned} \text {H}_1: I(X_1,X_2)>0. \end{aligned}$$

(7)

It is known (cf e.g. [21]) that under the null hypothesis (6), we approximately have:

$$ 2n\widehat{I}(X_1,X_2)\sim \chi ^{2}_{(K_1-1)(K_2-1)}, $$

for large sample sizes. If the null hypothesis (6) is not rejected, we apply chi-squared test for $II(X_1,X_2,Y)$ described in Sect. 3.1. Otherwise we use a permutation test described in Sect. 3.2. In the case of independence (or weak dependence) of $X_1$ and $X_2$ we do not perform, or perform rarely, the permutation test, which reduces the computation effort of the procedure. There are three input parameters. Parameter $\alpha$ is a nominal significance level of the test for interactions. Parameter $\alpha _0$ is a significance level of the initial test for independence between $X_1$ and $X_2$. The larger the value of $\alpha _0$ is, it is more likely to reject the null hypothesis (6) and thus it is also more likely to use the permutation test. Choosing the small value of $\alpha _0$ leads to more frequent use of the chi-squared test. This reduces the computational burden associated with the permutation test but can be misleading when chi-squared distribution deviates from the true distribution of $2n\widehat{II}(X_1,X_2,Y)$ under the null hypothesis (3). Parameter B corresponds to the number of loops in a permutation test. The larger the value of B, the more accurate is the approximation of the distribution of $2n\widehat{II}(X_1,X_2,Y)$ under the null hypothesis. On the other hand, choosing large B increases the computational burden. Algorithm for HYBRID method is given below.

4 Analysis of the Testing Procedures

In the following we analyse the type I error and the power of the three tests based on II. We present the results of selected experiments, extended results are included in the on-line supplement https://github.com/teisseyrep/Interactions. Although the methods based on II can be applied for any types of variables, in our experiments we focus on the common situation in Genome-Wide Association Studies when $X_1$ and $X_2$ are SNPs. For each SNP, there are three genotypes: the homozygous reference genotype (AA or BB), the heterozygous genotype (Aa or Bb respectively), and the homozygous variant genotype (aa or bb). Here A and a correspond to the alleles of the first SNP ($X_1$), whereas B and b to the alleles of the second SNP ($X_2$). Moreover we assume that Y is quantitative variable. Experiments for binary trait confirming the advantages of II over e.g. logistic regression are described in [9]. For the comparison we also use standard ANOVA test which is the state-of-the-art method for interaction detection, when Y is quantitative. In the experiments we compare the following methods: IICHI, IIPERM, HYBRID and as a baseline ANOVA.

4.1 Analysis of Type I Error Rate

In order to analyse the testing procedures, described in the previous sections, we first compare the type I errors rates, i.e. the probabilities of false rejection of the null hypothesis. We consider the following model (called M0) in which Y is independent from $(X_1,X_2)$. The distribution of $(X_1,X_2)$ is given in Table 1. Parameter $p_0\in [0,2/9]$ controls the dependence strength between $X_1$ and $X_2$. Probabilities of diagonal values (aa, bb), (Aa, Bb) and (AA, BB) are equal $1/9 +p_0$ and increase when $p_0$ increases. For $p_0$ in interval [0, 2/9] mutual information $I(X_1,X_2)$ ranges from 0 to 1.1. Value $I(X_1,X_2)=1.1$ is obtained for $p_0=2/9$ and corresponds to the extremal dependence when the probability is concentrated on the diagonal. Variable Y is generated from standard Gaussian distribution independently from $(X_1,X_2)$. To calculate $\widehat{II}(X_1,X_2,Y)$ we discretize Y using the equal frequencies and 5 bins. The type I error rate is approximated by generating data $L=10^5$ times, for each dataset we perform the tests and then calculate the fraction of simulations for which the null hypothesis is rejected. Number of repetitions in permutation test is $B=10^4$.

Figure 2 (left panel) shows how the type I error rate for model M0 depends on $I(X_1,X_2)$. For large $I(X_1,X_2)$ the type I error rate of chi-squared interaction test is significantly larger than the nominal level $\alpha =0.05$. For the other methods, the type I error rate oscillates around $\alpha$, even for a large $I(X_1,X_2)$. It is also worth noticing that starting from moderate dependence of $X_1$ and $X_2$ type I error rates of permutation and hybrid tests are almost undistinguishable. Figure 2 (right panel) shows how the type I error rate for model M0 depends on the sample size n in the case of moderate dependence between $X_1$ and $X_2$. For IICHI we observe significantly more false discoveries than for other methods. All methods other than IICHI control type I error rate well for $n\geqslant 300$ when the dependence of predictors is moderate or stronger ($I(X_1,X_2)\geqslant 0.15$). The above analysis confirms that for a strong dependence between variables, IICHI is not an appropriate test, while the IIPERM and HYBRID work as expected. The supplement contains results for different parameter settings.

4.2 Power Analysis

In the following we analyse the power of the discussed testing procedures. It follows from the previous section that method IICHI based on chi-squared distribution does not control the significance level, especially when the dependence between $X_1$ and $X_2$ is strong. Therefore to make a power comparison fair we do not take into account IICHI, which obviously has a largest power as it rejects the null hypothesis too often. For all other methods, IIPERM, HYBRID and ANOVA, which control probability of type I error satisfactorily for considered sample sizes, the distinction between them should be made based on their power and computational efficiency. We use a general framework in which a conditional distribution of $(X_1,X_2)$ given $Y=y$ is described by Table 1(b). This scenario corresponds to definition (2) of interaction information. Simulation models are designed in such a way to control the interaction strength as well as the dependence between $X_1$ and $X_2$ given Y. More precisely, function s(y) controls the value of $I(X_1,X_2|Y)$ and also the value of $II(X_1,X_2,Y)$. In addition we assume that $Y\in \{-1,0,1\}$ and $P(Y=-1)=P(Y=0)=P(Y=1)=1/3$. Here we present the result for typical simulation model called M1 in which function $s(y)=p$, when $y=-1$ or $y=1$ and $s(y)=0$, when $y=0$. Other models are described in Supplement. Power is measured as a fraction of simulations (out of $10^4$) for which the null hypothesis is rejected.

Fig. 2.

Type I error rate with respect to the mutual information and n for the simulation model M0, for $\alpha =0.05$ and $n=1000$.

Fig. 3.

Power with respect to the sample size n for a simulation model M1. $II(X_1,X_2,Y)= 0.1891, 0.0368, 0.0085$, for $p=0.2,0.1,0.05$, respectively.

Table 1. Distribution of ($X_1,X_2$) for simulation models M0 (a) and M1 (b).

Observe that the dependence between $X_1$ and $X_2$ varies for different values of Y. For example, setting $p\approx 2/9$ we obtain $I(X_1,X_2|Y=1)=I(X_1,X_2|Y=-1)\approx \log (3)$ and $I(X_1,X_2|Y=0)\approx 0$. Figure 3 shows how the power depends on the sample size n for different values of the parameter p. The larger the value of p, the larger the value of II. Observe that when II is large, it is more likely to reject the null hypothesis. When II is very small, all methods fail to detect interactions for considered sample sizes. The proposed HYBRID procedure is a winner. We should also note that HYBRID is considerably faster than IIPERM. Interestingly, ANOVA does not work for model M1 which is due to the incorrect specification of the linear regression model. For model M1, Y and a pair $(X_1,X_2)$ are non-linearly dependent. The above example shows that there are interesting dependence models in which interactions are detected by II whereas they are undetected by ANOVA. It should be also noted that HYBRID method outperforms IIPERM, which indicates that it is worthwhile to use chi-squared test when the dependence between $X_1$ and $X_2$ is weak and the permutation test otherwise. The results for other simulation models are presented in Supplement.

5 Real Data Analysis

5.1 Analysis of Pancreatic Cancer Data

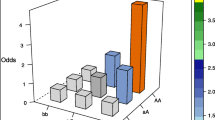
We carried out experiments on publicly available SNP dataset, related to pancreatic cancer [22]. Our aim was to detect interactions associated with the occurrence of cancer. Dataset consists of 230 observations (141 with cancer, 89 controls) and 1189 variables (genetic markers). Each variable takes three possible values (two homozygous variants and one heterozygous). For the considered data we evaluated all pairs of SNPs using the HYBRID procedure described in Sect. 3.3. There were 144158 pairs. We obtained 144158 SNP pairs for which II was computed and out of those 1494 were found significantly positive after Bonferroni correction. In HYBRID method, IICHI option was used for $83\%$ of pairs. In the following we present an analysis of the pair corresponding to the most significant interaction found between SNPs: rs209698, rs2258772. Figure 4 shows the results for this pair. The left hand side plot visualizes the unconditional joint distribution of two SNPs and the remaining two plots correspond to the conditional probabilities. In this case the dependence between SNPs is relatively weak- the mutual information $I(X_1,X_2)$ equals 0.02. On the other hand, the conditional dependence is much stronger which means that the conditional mutual information $I(X_1,X_2|Y)$ being an averaged mutual information of conditional distributions equals 0.14. So interaction information $II(X_1,X_2,Y)=0.14-0.02=0.12$ (values rounded to two decimal places). In this example, the main effects are very small. We have that $I(X_1,Y)=0$, $I(X_2,Y)=0.02$ and $I((X_1,X_2),Y)=0.14$, which yields $II=II(X_1,X_2,Y)=0.14-0.02-0=0.12$. It seems that the information about Y contained in $(X_1,X_2)$ is much larger than information contained in individual variables $X_1$ and $X_2$ and joint information about $(X_1,X_2)$ is found to be important in Y prediction. The presented results indicate three important issues: (1) the structure of dependence in subgroups (cases and controls) differs significantly; (2) the conditional dependencies are stronger than the unconditional one; (3) the presence of interaction between variables $X_1$ and $X_2$ in predicting Y. Namely, using certain combinations of values of $X_1$ and $X_2$ it is possible to predict Y (occurrence of disease) without error. Namely, knowing the values of SNPs in loci $X_1$ and $X_2$ it is possible to predict cancer presence (Y) accurately. Interestingly we realize that $X_1=AA$ and $X_2=BB$ implies $Y=cancer$. Similarly, $X_1=aa$ and $X_2=BB$ implies $Y=no{\ }cancer$. Such prediction is impossible based on an individual variable $X_1$ or $X_2$. Those detected loci could affect transcription factor binding affinity resulting in disregulation of a target gene expression.

Fig. 4.

Distributions of $(X_1,X_2)$. Left figure: joint probabilities for the pair $(X_1,X_2)=(rs209698,rs2258772)$. Middle figure: conditional probabilities given cancer. Right figure: conditional probabilities given no cancer. Mutual information $I(X_1,X_2)=0.0236$ and conditional mutual information $I(X_1,X_2|Y)= 0.1467$.

5.2 Analysis of Gene Expression Data of CD4+ T Cells

We also applied the proposed method to ImmVar dataset (1250 variables) concerning expression of 236 gene transcripts measured for five stimulation conditions of CD4+ T-cells as well as phenotypic characteristics of 348 doors: Caucasian (183), African-American (91) and Asian (74) ethnicities [23]. We focused on detection of gene-gene interactions that are associated with the specific ethnicity (Y variable). We detected interesting interactions using the HYBRID procedure: (i) Fatty Acid Desaturase 2 (FADS2) and Interferon Induced Transmembrane Protein 3 (IFITM3); (ii) IFITM3 and Steroid 5 Alpha-Reductase 3 (SRD5A3); (iii) Interferon Induced Transmembrane Protein 1 (IFITM1) and IFITM3. We have verified that the detected interactions between specific pairs of genes not only make it possible to predict the ethnicity, but also co-participate in biological processes that are known to have various intensity levels in individual ethnicities (see supplement for detailed analysis).

6 Conclusions

In this work we proposed a novel testing procedure which use chi-squared test or permutation test to detect conditional associations, depending on whether the dependence between the variables is weak or not. We showed that the commonly used chi-squared test detects much more false positives than allowed by its nominal significance level. We demonstrated that our method is superior to the standard tests in terms of type I error rate, power and computational complexity. Finally note that standard test IIPERM is computationally expensive and it would be difficult to apply it in the case of really large number of variables. On the other hand, IICHI is fast but it controls type I error rate only for independent $X_1$ and $X_2$. In the proposed method HYBRID we use permutation test only when the dependence between independent variables is strong. The experiments on real data indicated that strong dependence occurs relatively rare. Thus the computational complexity of our method is acceptable and unlike IICHI it also controls type I error rate. Future work will include the application of the proposed method on more real datasets related to predicting interesting traits (occurrence of disease, survival times, etc.) using SNPs, gene expression levels and epigenetic regulatory elements. It would be also interesting to compare the proposed method with more model-based approaches. Finally, an interesting challenge is to determine the exact distribution of II under null hypothesis (3) which would allow to avoid using permutation scheme.