1 Introduction

A broad range of physical phenomena can be described by hyperbolic conservation laws of the form

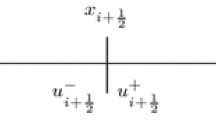
$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(1)

with the conserved variables \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and the flux function \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). The nonlinear behavior of f can lead to complex solutions, most notably shocks. It is well-known that high-order methods give good results for smooth data, but for discontinuous ones spurious oscillations are introduced. A popular class of methods to solve (1) is the finite volume method, which is based on a discretization in space … < x i−1∕2 < x i+1∕2 < … and the average values \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) of its cells C i = [x i−1∕2, x i+1∕2]. It is defined by the semi-discrete scheme

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(2)

where the numerical flux term F i+1∕2 depends on the values \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with 0 ≤ k ≤ p − 1. For more details we refer the reader to [15, 20, 22].

The class of essentially nonoscillatory (ENO) methods, introduced by Harten et al. [14], reduces spurious oscillations to a minimum. They are based on a monotone numerical flux function F(u, v) and high-order accurate reconstruction s i(x) for each cell i. The central idea is to choose the least oscillating interpolation function s i and define the numerical flux \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) being the evaluation of s i+1 and s i at the interface x i+1∕2. Based on the ENO method, Jiang and Shu [19] introduced the weighted ENO (WENO) method which considers different interpolation polynomials, based on different stencils, and combines them in a nonoscillatory manner to maximize the attainable accuracy. Further results on ENO and WENO methods can be found in [10, 11, 16].

2 CWENO

The CWENO method is based on the WENO method and was introduced by Levy et al. [23] as a third order method. Further analysis and generalization to higher orders on general grids can be found in [6, 7].

Let us consider the standard semi-discrete formulation (2) with a monotone flux function F(u, v). The goal is to construct a reconstruction P rec,i for each cell C i based on the stencil {C i−k, …, C i+k} for \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). In the smooth regions the algorithm should choose a polynomial of degree 2k which interpolates the central stencil \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) in the mean value sense. In case of a non-smooth solution it chooses a polynomial of degree k on one stencil {C i−k+l, …, C i+l} that avoids the discontinuity. Given the reconstruction, the high-order numerical flux is F i+1∕2 = F(P rec,i+1(x i+1∕2), P rec,i(x i+1∕2)).

Specifically, let us consider P opt as the polynomial of degree 2k that interpolates all data in the 2k + 1 stencil and the polynomials P l of degree k that interpolate the data on the stencil {C i−k+l−1, …, C i+l−1} for l = 1, …, k + 1. Furthermore, the reconstruction depends on the choice of the positive real coefficients d 0, …, d k+1 ∈ [0, 1] such that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), d 0 ≠ 0. Then, the reconstruction polynomial of degree 2k is

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(3)

with

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(4)

and the nonlinear coefficients ω l that are defined as

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(5)

where I[P l] indicates the smoothness of P l, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and t ≥ 2. A classical indicator of smoothness in the cell C for a polynomial is the Jiang–Shu indicator [19]

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(6)

The choice of \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is of importance: if it is too small, it might affect the order of convergence. On the other hand if it is too big, spurious oscillations may occur. Cravero et al. [7] show that the choice \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for p = 1, 2 leads to the maximal order of convergence. As proposed in [7] we define the coefficients d j over the temporary weights

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(7)

and we choose d 0 ∈ (0, 1) for the high-order polynomial. This gives us a possible choice for the coefficients

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(8)

The main difference with respect to the classical WENO method is that for the smooth case we are not constructing P opt out of the polynomials P l, but we build it independently by resolving an additional system of equations. This method has the advantage that it is easier to generalize on general grids in high dimensions, while maintaining high-order accuracy.

3 Radial Basis Functions

An alternative to the classical polynomial interpolation is the interpolation with radial basis functions (RBF). RBFs were proposed in the seminal work by Hardy [13]. They have been successfully applied in scattered data interpolation [4, 9, 17, 24, 27] and as a basis for a generalized finite difference method (RBF-FD) [5, 12]. The advantage is its flexibility in high dimensions and the possibility to reduce the risk of ill-conditioned point constellations. Its disadvantage is the ill-conditioning of the interpolation matrix for small grid sizes [8, 21, 26].

The RBF interpolation is based on a basis \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), obtained from a univariate continuous function \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), composed with the Euclidean norm centered at the data points

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(9)

with the shape parameter ε. Some common RBFs can be found in Table 1. Thus, for given scattered data points X = (x 1, …, x n)T with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and corresponding values \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) we look for

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(10)

with a polynomial \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), the interpolation condition s(x j) = f j and the additional constraints

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(11)

with the coefficients \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for all j = 1, …, n.

Table 1 Commonly used RBFs with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and ε > 0
Full size table

The same concept can be applied in the case of cell-averages. We seek functions

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(12)

such that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(13a)
$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(13b)

with the averaging operator \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). A well-known problem with RBFs is the high condition number of the interpolation matrix for small grid sizes or small shape parameters [8, 21, 26]. This problem can be resolved by using the vector-valued rational approximation method [28].

4 RBF-CWENO

Methods combining RBFs and essentially nonoscillatory methods have been proposed, e.g. RBFs with ENO [18, 25], RBFs with WENO [1,2,3]. The advantage of the CWENO method over the WENO method is its flexibility on general grids and its independence of the construction of a high-order interpolation function out of lower order ones. This facilitates the use of the whole grid in smooth regions and is important for non-polynomial interpolation functions which cannot be combined to an higher order function.

We propose the RBF-CWENO method which works as the classical CWENO method with the reconstruction function (3) and the weights (5), but as interpolation function we use RBFs instead of polynomials. Since the problem of the ill-conditioning can be solved by using the vector-valued rational approximation method [28], the main challenge for RBF methods is the choice of the smoothness indicator. For polyharmonic splines, Aboyar et al. [1] use the semi-norm of the Beppo-Levi space and Bigoni et al. [3] use a modified version of the Jiang-Shu indicator (6).

4.1 Smoothness Indicator

The smoothness indicator is the heart of the essentially nonoscillatory methods. We consider one based on the one introduced by Bigoni and Hesthaven [3]

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(14)

where the first part is the sum of the derivatives of the polynomial part and the second term expresses the highest derivative of the RBF-part. The original Jiang-Shu indicator applied to (12) would include the lower derivatives of the RBF-part plus all mixed terms, but we find this to be less efficient. For simplicity the integrals can be approximated with a simple mid-point rule.

We face again the problem of ill-conditioning when recovering the coefficients a i. Numerical examples indicate that small shape parameter improve the accuracy, but they do not affect the choice of the stencil using this smoothness indicator. Thus, we use a bigger shape parameter ε R, that is smaller than the smallest distance to a singularity

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(15)

which ensures the solvability of the system of equations [28].

5 Numerical Results

We now discuss the numerical results of the RBF-CWENO method and compare it with the RBF-WENO method [3] and the classical ENO method [14]. All methods are using the Lax-Friedrichs numerical flux and integration in time is done using the SSPRK-5 method [15] with time step dt = CFL ⋅ Δx∕λ max and the maximal eigenvalue λ max of ∇u F. Furthermore, we use the vector-valued rational approximation approach [28] to circumvent ill-conditioning of the interpolation matrix and a shape parameter ε = 0.1. For the nonlinear weights (5) we choose \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).

5.1 Linear Advection Equation

Let us consider the linear advection equation

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(16)

with wave speed a = 1, initial condition u 0(x) = sin(2πx) and periodic boundary conditions [22]. Note that for k = 3 we expect the order of convergence to be 7, therefore we use the reduced time step dt = CFL ⋅ Δx 7∕5∕λ max to recover the right order of convergence. The correct order of convergence of the RBF-CWENO method is shown in Table 2 and it seems to be more accurate than the RBF-WENO method.

Table 2 Convergence rates of RBF-CWENO using multiquadratics for the linear advection equation at time t = 0.05
Full size table

5.2 Burger’s Equation

Considering the Burger’s equation

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(17)

we analyze its robustness with respect to discontinuities. In Fig. 1 we report the results performed with CFL = 0.5 at t = 0.3. We observe no oscillations around the discontinuity at x = 0.5 and as expected an increasing accuracy for increasing number of elements.

Fig. 1
figure 1

Burger’s equation at t = 0.3 with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) solved by using RBF-CWENO method with MQ interpolants of order k = 3

Full size image
Fig. 2
figure 2

Results for the Sod shock tube problem at t = 0.2 solved by using RBF-CWENO with MQ interpolants of order k = 2, 3 on characteristic variables (left: k = 2, right: k = 3)

Full size image

5.3 Euler Equations

The one-dimensional Euler equations express conservation of mass, momentum and the total energy. They can be described by the density ρ, the mass flow m, the energy per unit volume E and the pressure p through

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(18)

with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for an ideal gas with the ratio of specific heat γ = 1.4 [15]. For k = 3 we need to change the nonlinear weights (5) by using \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to avoid oscillations.

5.3.1 Sod’s Shock Tube Problem

The Sod’s shock tube problem describes two colliding gases in [0, 1] with different densities given by the initial conditions

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(19)

This results in a rarefaction wave followed by a contact and a shock discontinuity which separates the domain into four domains with constant variables. The RBF-CWENO method resolves it well, see Fig. 2. For k = 3, we observe minor oscillations, but their amplitude decreases for increasing number of elements. Furthermore, we observe the increasing accuracy for k = 3 compared to k = 2.

5.3.2 Shu–Osher Shock-Entropy Wave Interaction Problem

The Shu–Osher problem describes the interaction of a discontinuity with a low frequency wave which introduces some high frequent waves. Its initial conditions are

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(20)

In Fig. 3, we observe on the left side the increasing accuracy for increasing number of elements for k = 2. On the right side we see its good approximative behaviour compared to the existing methods ENO2, ENO5 and the corresponding WENO. In particular we observe that the performance of the RBF-CWENO (k = 2) is comparable to ENO5 and superior to WENO (k = 2).

Fig. 3
figure 3

Results for the Euler shock entropy problem at t = 1.8 solved by using RBF-CWENO with MQ interpolants of order k = 2 on characteristic variables (Left) and a comparison with WENO, ENO2 and ENO5 for N = 256 cells (Right)

Full size image

6 Conclusion

In this work, we introduce the RBF-CWENO method that relies on the CWENO method [23] and the use of radial basis functions for the interpolation. We develop a smoothness indicator that is based on RBFs but works similarly to the one for polynomials. Furthermore, we tackle the problem about the choice of the weight \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). For \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) we get the right order of convergence, but for the 7th order method (k = 3) we choose \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to reduce spurious oscillations for the Euler equations.

Moreover, we should point out that the choice of the linear weight d 0 can influence the result; indeed if it is too close to 1 then the reconstruction almost coincides with P opt, which can lead to spurious oscillations in case of discontinuous solutions. We present multiple numerical examples to show the robustness of the method.

We can conclude that the RBF-CWENO method works comparable to the existing RBF-WENO and ENO methods in one dimension. The advantage of RBFs is clearer when considering unstructured grids in higher dimensions where polynomial reconstruction is complex.