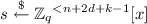Abstract
Middle-product learning with errors (MP-LWE) was recently introduced by Rosca, Sakzad, Steinfeld and Stehlé (CRYPTO 2017) as a way to combine the efficiency of Ring-LWE with the more robust security guarantees of plain LWE. While Ring-LWE is at the heart of efficient lattice-based cryptosystems, it involves the choice of an underlying ring which is essentially arbitrary. In other words, the effect of this choice on the security of Ring-LWE is poorly understood. On the other hand, Rosca et al. showed that a new LWE variant, called MP-LWE, is as secure as Polynomial-LWE (another variant of Ring-LWE) over any of a broad class of number fields. They also demonstrated the usefulness of MP-LWE by constructing an MP-LWE based public-key encryption scheme whose efficiency is comparable to Ring-LWE based public-key encryption. In this work, we take this line of research further by showing how to construct Identity-Based Encryption (IBE) schemes that are secure under a variant of the MP-LWE assumption. Our IBE schemes match the efficiency of Ring-LWE based IBE, including a scheme in the random oracle model with keys and ciphertexts of size \(\tilde{O}(n)\) (for n-bit identities).
We construct our IBE scheme following the lattice trapdoors paradigm of [Gentry, Peikert, and Vaikuntanathan, STOC’08]; our main technical contributions are introducing a new leftover hash lemma and instantiating a new variant of lattice trapdoors compatible with MP-LWE.
This work demonstrates that the efficiency/security tradeoff gains of MP-LWE can be extended beyond public-key encryption to more complex lattice-based primitives.
Work done while at MIT.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Cryptographic schemes based on the polynomial learning with errors problem (PLWE) [23] and the ring learning with errors problem (RLWE) [13] have the advantage of having key size and algorithm runtime that are quasi-linear in the security parameter. However, their security guarantees are not as strong as that of the original learning with errors problem (LWE) [20].
One of the main differences between these two settings is that the PLWE problem parametrized by some (say, irreducible) polynomial f, denoted \(\text {PLWE}^{(f)}\), is only known to be as hard as a worst-case problem on some class of lattices that depends on the polynomial f, which could possibly be easier to solve for some choices of f as compared to others. In particular, we do not have a clear understanding of the relative hardness of \(\text {PLWE}^{(f)}\) for different f, making it hard for a cryptosystem designer to pick the right f. In contrast, with the LWE problem, there is no such ambiguity. For essentially any choice of possible modulus q, LWE is as hard as worst-case problems on arbitrary lattices [17, 20]. In summary, the concrete efficiency gains of RLWE and PLWE have only been obtained through a trade-off involving making both quantitatively and qualitatively more questionable security assumptions.
Recently, following on an earlier work of Lyubashevsky [11] who initiated the study of ring-independent assumptions, Rosca et al. [21] introduced the “middle-product learning with errors” assumption (MP-LWE), a new variant of LWE that uses the “middle product” of polynomials modulo q. For any f in a broad class of polynomials, they show a reduction from \(\text {PLWE}^{(f)}\) to the MP-LWE problem, which is defined independently of any such f, freeing the cryptosystem designer from making an essentially arbitrary choice of f. They also describe a public key encryption (PKE) scheme that has quasi-linear (optimal) key size and algorithm runtime, while being IND-CPA secure under the MP-LWE assumption. Thus, they obtain a public-key encryption scheme with the same efficiency gains over LWE-based PKE as enjoyed by PLWE-based schemes, but prove security under a worst-case assumption on a comparatively broader class of lattices.
While the idea of using MP-LWE as an alternative to Ring-LWE, as proposed by [21], is intriguing, it is only currently known how to construct plain public-key encryption from MP-LWE. In this work, we consider and make progress on the following question.
Can we instantiate more complex lattice-based primitives using middle-product LWE while maintaining the improved efficiency/security tradeoff?
Indeed, it is explicitly left open by [21] to instantiate more complex lattice-based primitives, such as lattice trapdoors [8] and their applications, using MP-LWE.
1.1 Our Results
We construct an Identity-Based Encryption (IBE) scheme based on MP-LWE. This scheme is IND-CPA secure in the random oracle model under the MP-LWE assumption and has quasi-linear key size and algorithm runtime.
Our construction follows the “lattice trapdoors” paradigm of [8]. Specifically, we construct a “dual” of the public key encryption scheme in [21], then combine the dual scheme with Micciancio-Peikert style lattice trapdoors [15] to obtain the IBE scheme. In addition to our IBE scheme in the random oracle model, we sketch how techniques for constructing IBE schemes in the standard model [2, 3, 7] can also be adapted to the MP-LWE setting using our lattice trapdoors.
Our main IBE construction from MP-LWE can be stated informally as follows.
Theorem 1
(Informal). For any \(\epsilon \ge 2^{-\mathsf {poly}(\log n)}\), there is a \((T, \epsilon )\)-secure IBE scheme (in the random oracle model) under the \((T', \epsilon ')\) MP-LWE assumption with \(T' \approx T\), \(\epsilon ' \approx \epsilon \). This scheme has quasi-linear \(\tilde{O}(n)\) key size and encryption runtime.
By \((T, \epsilon )\)-security, we mean that any T-time adversary fails to break the primitive/assumption with advantage greater than \(\epsilon \). In particular, assuming that MP-LWE is hard for \(T(n) = 2^{\alpha n}\)-time adversaries, we show that our IBE scheme is hard to break in time roughly T with better than some inverse quasi-polynomial advantage.
Our IBE scheme demonstrates that the better efficiency/security trade-off obtained by [21] for public key encryption can be extended to more expressive cryptographic primitives such as IBE. Tables 1 and 2 compare the efficiency of our PKE and IBE schemes to prior works.
1.2 Technical Overview
As mentioned before, we follow the “lattice trapdoors” paradigm of [8]. We first recall the approach of [8] for constructing IBE from LWE. The high-level idea is as follows: using a random oracle H, design a key pair (distribution) \((\mathsf {mpk}, \mathsf {msk})\) such that for any identity \(\mathsf {id}\), \(\mathsf {pk}_{\mathsf {id}} := (\mathsf {mpk}, H(\mathsf {id}))\) is a valid public key for some public key encryption scheme \(\mathsf {PKE}\). In order for this to yield an IBE scheme, it must be possible to derive a corresponding secret key \(\mathsf {sk}_{\mathsf {id}}\), using \(\mathsf {msk}\), from the public value \(H(\mathsf {id})\). This is achieved in the following way.
-
Step 1: Dual Regev Encryption. First, [8] constructs a “dual” variant of Regev encryption [20] in which public keys are (statistically close to) uniformly random. In slightly more detail, public keys have the form \((A, u = Ar)\) for
 and
and  for some distribution \(\chi \) of “small numbers.” This step is done so that in an associated IBE scheme, \(u = H(\mathsf {id})\) can be interpreted as (part of) a dual Regev public key.
for some distribution \(\chi \) of “small numbers.” This step is done so that in an associated IBE scheme, \(u = H(\mathsf {id})\) can be interpreted as (part of) a dual Regev public key. -
Step 2: Lattice Trapdoors. The most technically complicated step in [8] is designing an alternative procedure \(\mathsf {TrapGen}\) that outputs a (statistically close to) uniformly random matrix A along with a trapdoor \(T_A\) that allows for sampling, given an input \(u\in \mathbb {Z}_q^n\), a random preimage \(r \leftarrow \chi ^m \mid Ar = u\). This step allows for efficient secret key extraction from a public key (A, u).
-
Step 3: Constructing IBE. As has been implicitly described already, [8] then write down an IBE scheme with a master key pair \((A, T_A)\) sampled using \(\mathsf {TrapGen}\), so that encryption for an identity \(\mathsf {id}\) uses dual Regev encryption with public key \((A, u = H(\mathsf {id}))\), and secret keys \(\mathsf {sk}_{\mathsf {id}} = r\) can be extracted from \((A, u = H(\mathsf {id}))\) using \(\mathsf {msk}= T_A\).
We now describe how we instantiate this framework using middle-product LWE.
Step 1: MP-LWE Based Dual Regev. Our first step is to develop an analogue of dual Regev encryption based on middle-product LWE. We first recall from [21] that the middle-product learning with errors assumption over \(\mathbb {Z}_q\) with degrees (n, d) is that the distribution
is computationally pseudorandom, where s is a uniformly random degree n polynomial,Footnote 1 each \(a_i\) is a uniformly random degree \(n-d\) polynomial, each \(e_i\) is a random “small” degree d polynomial, and \(a_i \, \odot _{d} \, s\) is the “middle product” consisting of the d “middle terms” of the polynomial product \(a \cdot s\). [21] show that this assumption suffices to construct a “primal Regev” public key encryption scheme, and show that this assumption follows from the hardness of \(\mathsf {PLWE}^{(f)}\) for various polynomials f.
We would like to develop a “dual Regev” public-key encryption scheme similar to the \(\mathsf {PKE}\) of [21], and a natural approach suggests itself (based on [21]): Let \(a_1, \ldots , a_t\) be t i.i.d. degree n polynomials, let \(r_1, \ldots , r_t\) be t i.i.d. degree k polynomials (for some additional parameter k), and set
Encrypting a message \(\mu \) then consists of sampling a random MP-LWE secret s and outputting middle productsFootnote 2 \((a_i \, \odot _{} \, s, + 2 e_i)_{i\le t}\) along with \(u \, \odot _{} \, s + 2 e' + \mu \). We would then like to argue, as in [21], that the security of this scheme follows from MP-LWE (with secret s).
Technical Challenges. However, there are two main issues that arise from this approach to Step 1 (which both arise again when implementing Step 2):
-
We need a new variant of the leftover hash lemma to argue that the polynomial \(u = \sum a_i r_i\) is (statistically close to) uniformly random. The reason that previous leftover hash lemma variants seem insufficient is related to the fact that the map \(r \mapsto \sum _i a_i r_i\) has a larger range (degree \(n+k\) polynomials) than its domain (degree k polynomials); this stands in contrast to the PLWE setting, where \(r\mapsto \sum a_i r_i \) (mod f) is reduced modulo a degree n polynomial f. Indeed, the hash function \(h_{a_1, \ldots , a_t}(r_1, \ldots , r_t) = \sum a_i r_i\) is not 2-universal, unlike the hash function considered in [21], so we have to argue the desired statistical indistinguishability directly. We state and prove our new variant of the LHL in Sect. 4. We use techniques from [14] designed to prove a variant of the LHL in the Ring-LWE setting; however, these techniques must be substantially modified to handle the distinction between multiplication of bounded-degree polynomials in \(\mathbb {Z}_q[x]\) (as in our setting) and multiplication over rings of the form \(R_q = \mathbb {Z}_q[x]/f(x)\) (as in the RLWE/PLWE setting).
-
Middle-product LWE as defined in [21] does not seem directly applicable to (the security of) our dual-Regev encryption scheme; the reason is that the “coefficient polynomials” \((a_1, \ldots , a_t, u)\) do not all have the same degree.Footnote 3 In order to prove security, we have to consider a new variant of MP-LWE in which “coefficient polynomials” \(\{a_i\}\) can have different degrees; we consider a variant in which the adversary can specify a new degree \(d_i\) for each sample in advance. In Sect. 3, we show that (a simple modification of) the [21] reduction from PLWE to MP-LWE carries over to our variant of MP-LWE, which we call “degree-parametrized MP-LWE.”
After addressing these two difficulties, the approach outlined in Step 1 can be made to work, yielding a dual-Regev encryption scheme based on MP-LWE.
Step 2: Lattice Trapdoors for MP-LWE. Having developed a variant of dual Regev encryption, we next turn to constructing lattice trapdoors [8] that are compatible with this new encryption scheme. To do so, we make use of the work [15], which gives a highly general roadmap for constructing lattice trapdoors.
Following the basic idea of [15], our procedure \(\mathsf {TrapGen}\) will produce polynomials \(a_1, \ldots , a_t, a_{t+1}, \ldots , a_{t'}\) such that for \(t < i \le t'\),
for random, small “trapdoor” polynomials \(\{w_{ij}\}\) and specific polynomials \(\{c_j = 2^u x^{dv}\}\) which are our analogue to the “G matrix” in plain LWE-based constructions. Similarly to the Ring-LWE setting, we can think of these polynomials as “structured matrices” by associating a polynomial g(x) with the “multiplication by g(x)” matrix acting on a vector space of bounded-degree polynomials. We show that with this choice of polynomials \(\{c_j\}\), the matrix A corresponding to \((a_1, \ldots , a_{t'})\) has a “G-trapdoor” (as defined in [15]) that can be efficiently described using our trapdoor \(\{w_{ij}\}\). The preimage sampling algorithm of [15] can then be adapted to yield a corresponding preimage sampling algorithm for polynomial sum-products; moreover, we show that our preimage sampling algorithm has the same \(\tilde{O}(n)\) efficiency gain over plain LWE that is enjoyed by Ring-LWE based constructions. See Sect. 5 for more details.
Finally, we note that we are implicitly relying on resolutions to both “technical challenges” mentioned above in this step; our leftover hash lemma is what guarantees that \(\mathsf {TrapGen}\) outputs a distribution \(\{(a_1, \ldots , a_{t'})\}\) that is statistically close to uniform, while our “degree-parametrized MP-LWE” allows us to redesign our dual Regev scheme to have public key \((a_1, \ldots , a_{t'}, u)\) such that \(\{a_1, \ldots , a_t\}\) and \(\{a_{t+1}, \ldots , a_{t'}\}\) have different degrees.
Step 3: Constructing IBE Schemes. Given our variant of dual Regev encryption from MP-LWE (Step 1) and our variant of lattice trapdoors compatible with this new encryption scheme (Step 2), constructing IBE is fairly straightforward given prior work. We describe constructions analogous to those of [8] (in the random oracle model) and [3] (in the standard model) using our new tools.
Remark On Concrete Efficiency/Security. As usual, some care is required when comparing the efficiency of various LWE-based cryptosystems to take into account their expected levels of security. We give an overview of the comparison of LWE/RLWE/MPLWE-based IBE schemes using concrete security [5].
The concrete security of all relevant lattice-based cryptosystems is based on assumptions of the following form.
Definition 1
(\((T, \epsilon )\)-secure X-LWE, Informal). Any time T adversary breaks the X-LWE assumption with advantage at most \(\epsilon \).
Our main IBE construction from MP-LWE (as stated in Theorem 1) constructs \((T, \epsilon )\)-secure IBE from roughly \((T, \epsilon )\)-secure LWE, as long as \(\epsilon \ge 2^{-\mathsf {poly}\log n}\). This technical limitation is due to the achievable parameters of our leftover hash lemma (which was already implicitly noted in [21]) when used in a standard hybrid argument to prove security of the IBE scheme. This barrier also appears in the Ring-LWE context (see, e.g., the signature scheme of [15]) when quasi-linear efficiency is desired. However, these works (and ours) still attain a meaningful form of concrete security because security is proved against adversaries that run in exponential time (assuming that the LWE variants are exponentially secure).
In addition, with some more work, it is possible to improve Theorem 1 to hold for smaller values of \(\epsilon \) (without sacrificing efficiency). This improved security proof is based on the use of Renyi divergence (as opposed to statistical distance), as demonstrated in [4], and will appear in the full version of this paper.
1.3 Organization
The rest of the paper is organized as follows. In Sect. 2, we review basic definitions and other preliminaries. In Sect. 3, we introduce and prove the hardness of our “degree-parametrized MP-LWE,” a slight variant on the original definition. In Sect. 4, we prove our new leftover hash lemma for bounded degree polynomials. In Sect. 5, we use our new LHL in combination with [15] to develop lattice trapdoors for middle-product LWE. Finally, in Sect. 6, we combine our new tools to construct MP-LWE based dual Regev public-key encryption and IBE.
2 Preliminaries
Negligible Functions. We use n to denote the security parameter. We use standard big-O notation to classify the growth of functions, and say that \(f(n) = \tilde{O}(g(n))\) if \(f(n) = O(g(n) \cdot \log ^c n)\) for some fixed constant c. We let \(\text {poly}(n)\) denote an unspecified function \(f(n) = O(n^c)\) for some constant c. We say that a function f(n) is negligible (denoted \(f(n) = \mathsf {negl}(n)\)) if \(f(n) = o(n^{-c})\) for every fixed constant c. We say that a probability (or fraction) is overwhelming if it is \(1 -\mathsf {negl}(n).\)
Statistical and Computational Indistinguishability. The statistical distance between two distributions X and Y over a countable domain \(\varOmega \) is defined to be \(\varDelta (X, Y):=\frac{1}{2} \cdot \sum _{d\in \varOmega } |X(d) - Y (d) |.\) We say that two distributions X, Y (formally, two ensembles of distributions indexed by n) are statistically indistinguishable if \(\varDelta (X, Y) =\mathsf {negl}(n),\) and write \(X \approx _s Y.\)
Two ensembles of distributions \(\{X_n\}\) and \(\{Y_n\}\) are computationally indistinguishable if for every probabilistic poly-time machine A, \(|\Pr [A(1^n, X_n) = 1] - \Pr [A(1^n , Y_n) = 1]|=\mathsf {negl}(n);\) we denote this relationship by \(X\approx _c Y.\)
Polynomials. Let R be a ring. For any integer \(d > 0\) and any set \(S \subseteq R,\) we let \(S^{<d}[x]\) denote the set of polynomials in R[x] of degree \(< d\) whose coefficients are in S. For any distribution \(\chi \) defined over R, let \(\chi ^d[x]\) denote the distribution on polynomials in \({R}^{<d}[x]\) where each coefficient is sampled independently according to \(\chi \).
Given a polynomial \(a =\sum _{i=0}^{d-1} a_i x^i \in R^{< d}[x],\) define the coefficient vector of a as \(\mathbf a :=(a_0,\cdots , a_{d-1})^T \in R^d.\) In particular, for any \(0\le i \le d-1\), \(\mathbf a _i\) denotes the coefficient of \(x^i\) in a.
Probability. For any distribution X defined on a countable domain \(\varOmega \), we define the collision probability

as well as the Renyi entropy of X,

and the min-entropy of X,
We remark that \(H_2(X)\ge H_\infty (X)\) for all distributions X. For a finite set \(\varOmega ,\) we let \(U(\varOmega )\) denote the uniform distribution over \(\varOmega \), and we use the notation  to denote that X is sampled uniformly at random from \(\varOmega \). For a distribution \(\chi \) over \(\mathbb {R},\) let \(\chi ^k\) denote the distribution over \(\mathbb {R}^k\) where each coordinate is independently sampled from \(\chi .\) For a distribution D over \(\mathbb {R}^k,\) let D[x] be the distribution over \({\mathbb {R}}^{<k}[x]\) where the coefficient vector of polynomials is sampled from D.
to denote that X is sampled uniformly at random from \(\varOmega \). For a distribution \(\chi \) over \(\mathbb {R},\) let \(\chi ^k\) denote the distribution over \(\mathbb {R}^k\) where each coordinate is independently sampled from \(\chi .\) For a distribution D over \(\mathbb {R}^k,\) let D[x] be the distribution over \({\mathbb {R}}^{<k}[x]\) where the coefficient vector of polynomials is sampled from D.
2.1 Identity-Based Encryption
We recall the standard syntax and definition of security under chosen-plaintext and chosen-identity attack [1, 6] for IBE. An IBE scheme consists of four algorithms.
-
A setup algorithm \(\mathsf {IBESetup}\) (on input \(1^n\)) outputs a master public key \(\mathsf {mpk}\) and master secret key \(\mathsf {msk}\).
-
A secret key extraction algorithm \(\mathsf {IBEExtract}\), given \(\mathsf {msk}\) and an identity \(\mathsf {id}\), outputs a secret key \(\mathsf {sk}_{\mathsf {id}}\).
-
An encryption algorithm \(\mathsf {Enc}\), given the master public key \(\mathsf {mpk}\), an identity \(\mathsf {id}\), and a message m, outputs a ciphertext c.
-
A decryption algorithm \(\mathsf {Dec}\), given the secret key \(\mathsf {sk}\) and a ciphertext c, outputs a message m.
We require that an IBE scheme \(\mathsf {IBE} = (\mathsf {IBESetup}, \mathsf {IBEExtract}, \mathsf {Enc}, \mathsf {Dec})\) satisfies two properties.
-
Correctness: For all identities \(\mathsf {id}\) and messages m, we have
$$\Pr [\mathsf {Dec}(\mathsf {sk}_{\mathsf {id}}, \mathsf {Enc}(\mathsf {mpk}, \mathsf {id}, m)) = m] = 1-\mathsf {negl}(n), $$where the probability is taken with respect to the randomness of \(\mathsf {IBESetup}, \mathsf {IBEExtract}, \mathsf {Enc}\), and \(\mathsf {Dec}\).
-
Security: Security is defined by the following game (defined for a given PPT adversary \(\mathcal A\)).
-
\((\mathsf {mpk}, \mathsf {msk}) \leftarrow \mathsf {IBESetup}(1^n)\) is sampled. Define a (randomized) oracle \(\mathcal O(\cdot )\) that on input \(\mathsf {id}\) outputs \(\mathsf {IBEExtract}(\mathsf {msk}, \mathsf {id})\).
-
\(\mathcal A^{\mathcal O(\cdot )}(\mathsf {mpk})\) outputs a challenge \((\mathsf {id}^*, m_0, m_1)\).
-
\(b\leftarrow U(\{0, 1\})\) is sampled uniformly at random.
-
\(\mathsf {ct}^* \leftarrow \mathsf {Enc}(\mathsf {mpk}, \mathsf {id}^*, m_b)\) is sampled.
-
\(\mathcal A^{\mathcal O(\cdot )}(\mathsf {ct}^*)\) outputs a bit \(b'\) and wins if (1) \(\mathcal O(\mathsf {id}^*)\) was not queried and (2) \(b' = b\).
We say that the scheme is secure if every PPT adversary \(\mathcal A\) wins the above game with probability at most \(\frac{1}{2} + \mathsf {negl}(n)\)
-
2.2 Middle Product of Polynomials [21]
Definition 2
([21], Definition 3.1). Let \(d_a, d_b, d, k\) be integers such that \(d_a + d_b -1 = d+2k.\) The middle product \(\odot _d: {R}^{<d_a}[x] \times {R}^{<d_b}[x] \rightarrow {R}^{<d}[x] \) is defined to be the map
where \(\mathbf a \) and \(\mathbf b \) are the coefficient vectors of a and b, respectively. In other words, \(a \, \odot _{d} \, b\) is obtained by deleting the k highest and k lowest degree terms of the polynomial product \(a\cdot b,\) then dividing the remaining d terms by \(x^k.\)
Immediately from Definition 2, the middle product is commutative, i.e., \(a \, \odot _{d} \, b = b\, \odot _{d} \, a\) for all polynomials a, b. The middle product also satisfies a “quasi-associative” property.
Lemma 1
([21]). Let \(d, k, n > 0.\) For all \(r \in {R}^{<k+1}[x], a \in {R}^{<n}[x], s \in {R}^{<n+d+k-1}[x],\) we have
2.3 Lattices
An n-dimensional lattice \(\varLambda \) is a discrete additive subgroup of \(\mathbb R^n.\) A lattice has rank \(k\le m\) if it is generated as the set of all \(\mathbb {Z}\)-linear combinations of some k linearly independent basis vectors \(\mathbf B = (\mathbf b _1, \cdots , \mathbf b _k);\) we say \(\varLambda \) is full-rank if \(k=m.\) The dual lattice \(\varLambda ^*\) is the set of all \(v \in \text {Span}_{\mathbb R}(\varLambda )\) such that \(\langle v, x \rangle \in \mathbb {Z}\) for every \(x\in \varLambda .\) If B is a basis of \(\varLambda ,\) then \(\mathbf B ^*=B(B^t B)^{-1}\) is a basis of \(\varLambda ^*.\) Note that when \(\varLambda \) is full-rank, B is invertible and hence \(\mathbf B ^*=\mathbf B ^{-1}.\)
For any set \(\mathbf S =(s_1, \cdots , s_k)\) of linearly independent vectors, let \(\tilde{\mathbf{S }}\) denote its Gram-Schmidt orthogonalization, defined iteratively in the following way: \(\tilde{s}_1 = s_1,\) and for each \(i=2, \cdots , n,\) \(\tilde{s}_i\) is the component of \(s_i\) orthogonal to \(\text {span }(s_1,\cdots , s_{i-1}).\)
For positive integers n, q and any matrix \(A \in \mathbb {Z}_q^{n\times m},\) let \(\varLambda ^{\perp }(A): = \{z \in \mathbb {Z}^m: Az = 0\mod q\}.\) For \(u\in \mathbb {Z}_q^n\) such that \(\exists t \in \mathbb {Z}_q^m\) satisfying \(A t = u,\) let \(\varLambda ^{\perp }_u(A) : = \{z\in \mathbb {Z}^m: Az = u \mod q\} = \varLambda ^{\perp }(A) +t. \)
Gaussian Distributions
Definition 3
(Continuous Gaussian distribution). For a positive semidefinite matrix \(\varSigma \in \mathbb {R}^{n\times n},\) the continuous Gaussian distribution \(D_{\varSigma }\) is the probability distribution over \(\mathbb {R}^n\) whose density is proportional to \(\rho _{\varSigma } (x) = \exp (-\pi x^T \varSigma ^{-1} x).\)
Definition 4
(Discrete Gaussian distribution). Given countable set \(S \subset \mathbb {R}^n\) and \(s>0\), the discrete Gaussian distribution \(D_{S,\sigma , \mathbf c }\) is the probability distribution over S whose density is proportional to \(\rho _{\sigma ,\mathbf c }(x):=\exp (-\pi \cdot ||\mathbf x - \mathbf c ||^2/\sigma ^2).\) That is, for \(x \in S: D_{S,\sigma , \mathbf c } = \frac{\rho _{\sigma ,\mathbf c }(x)}{\rho _{\sigma ,\mathbf c }(S)}.\) If \(\mathbf c = 0\), we can omit \(\mathbf c \) and write \(D_{S, \sigma }\) instead.
As usual, we will make use of various statistical properties of the discrete Gaussian \(D_{\varLambda , \sigma }\) when \(\sigma \) is large compared to the smoothing parameter of the lattice \(\varLambda \), defined below.
Definition 5
([16]). For any n-dimensional lattice \(\varLambda \) and real \(\epsilon > 0,\) the smoothing parameter \(\eta _{\epsilon }(\varLambda )\) is defined to be the smallest real \(s> 0\) such that \(\rho _{1/s} (\varLambda ^*\setminus \{\mathbf{0 }\}) \le \epsilon .\)
The following lemma gives an upper bound on the smoothing parameter of \(\varLambda \) in terms of its Gram-Schmidt basis \(\tilde{B}\).
Lemma 2
([8], Theorem 3.1). Let \(\varLambda \subset \mathbb {R}^n\) be a lattice with basis \(\mathbf {B}\) and real \(\epsilon > 0\). Then,
where \(\tilde{\mathbf {B}} = (\tilde{b}_1, \cdots , \tilde{b}_k)\) is the Gram-Schmidt orthogonalization of \(\mathbf {B}\) as defined in Sect. 2.3, and \(||\tilde{\mathbf {B}} || = \max _{i\in [k]} ||\tilde{b}_i ||.\)
We will make use of tail bounds on \(D_{\varLambda , \sigma }\) (for \(\sigma \) larger than the smoothing parameter).
Lemma 3
([8], Lemma 2.9). For any \(\epsilon \) > 0, any \(\sigma \ge \eta _{\epsilon }(\mathbb {Z})\), and any \(t > 0\), we have
In particular, for \(\epsilon \in (0,1/2)\) and \(t \ge \omega (\sqrt{\log n})\), the probability that \(|x - c | \ge t \cdot \sigma \) is negligible in n.
In addition, we will make use of entropy bounds on \(D_{\varLambda ,\sigma }\) (again for \(\sigma \) sufficiently large). In order to prove these bounds, we first recall the following approximation.
Lemma 4
([18], Lemma 2.10). Let \(\varLambda \subset \mathbb {R}^d\) be a full-rank lattice. For any \(s \ge \eta _{\epsilon } (\varLambda )\), we have
Using Lemma 4, we can bound \(H_\infty (D_{\varLambda , \sigma })\) and \(H_2(D_{\varLambda , \sigma })\).
Lemma 5
For a full-rank lattice \(\varLambda \subset \mathbb R^d\) and discrete Gaussian distribution \(\chi = D_{\varLambda , \sigma }\) with parameters \( \epsilon \in (0,1), \delta \in (0,1),\) and \(\sigma \ge \max (\sqrt{2}, \delta ^{-1})\cdot \eta _{\epsilon }(\varLambda )\), we have
and

Proof
Using Lemma 4, we obtain the bound
for all \(\mathbf x \in \varLambda \). Moreover, we assumed that \(\sigma \delta \ge \eta _\epsilon (\varLambda )\), so by Lemma 4 we also have
Combining this with the first inequality, we see that
yielding the desired bound on \(2^{-H_\infty (\chi )}\). In order to bound  , we write
, we write

where the last equality uses the identity \(\rho _{\sigma }(x)^2 = \rho _{\sigma /\sqrt{2}} (x)\). Since we assumed that \(\sigma > \delta \sigma \ge \eta _{\epsilon }(\varLambda ),\) Lemma 4 (applied three times, to parameters \(\sigma \), \(\frac{\sigma }{\sqrt{2}}\) and \(\sigma \delta \)) tells us that
completing the proof. \(\square \)
2.4 Polynomials and Matrices
For a vector \(\mathbf v \in \mathbb {R}^n\), let \(||v ||, ||v ||_{\infty }\) denote the Euclidean and sup norm respectively. We define the largest singular value of a matrix \(A\in \mathbb {R}^{m\times n}\) as \(\sigma _1(A) : = \max _{||u || = 1} ||A u ||.\)
Lemma 6
For any matrix \(A \in \mathbb {R}^{m\times n},\) we have \(\sigma _1(A) \le \sqrt{mn} \max _{i,j} |A_{ij} |.\)
We will make use of the following matrix representation of polynomial multiplication.
Definition 6
Let R be a ring and \(d, k, > 0\) be positive integers. For any polynomial \(a \in {R}^{<k}[x]\) of degree less than k, let \(T^{k,d}(a)\) denote the matrix in \(R^{(k+d-1) \times d}\) whose i-th column, for \(i = 1, \cdots , d,\) is given by the coefficients of \(x^{i-1}\cdot a,\) listed from lowest to highest degree. In particular, \(T^{k,1}(a)\) is the coefficient vector \(\mathbf a \) of the polynomial a (possibly with zeros appended).
Lemma 7
For \(\ell ,k,d > 0, a \in {R}^{<k}[x], b \in {R}^{<\ell }[x],\) \(T^{k,\ell +d-1}(a) \cdot T^{\ell ,d}(b) = T^{\ell +k-1, d}(a\cdot b). \)
Definition 7
([21], from[12]). Let \(f\in \mathbb {Z}[x]\) have degree m. The expansion factor of f is defined as

For our purposes, we are interested in polynomials with \(\text {poly}(n)\)-bounded expansion factors. One such class [12] is the family of all \(f = x^m + h\) where \(\deg (h) \le m/2\) and \(||h ||_{\infty } \le \text {poly}(n).\)
Definition 8
Let f be a monic polynomial over a ring R of degree m. Define the (Hankel) matrix \(\mathbf M _f\in R^{m\times m} \) such that for \(1\le i,j \le m,\) \((\mathbf M _f)_{i,j} \) is the constant coefficient of \(x^{i+j-2} \mod f.\)
Under suitable conditions on f, the matrix \(\mathbf M _f\) is guaranteed to be invertible.
Lemma 8
If \(f\in R[x]\) has constant coefficient \(f_0\) which is invertible in R, then \(\mathbf M _f\) is an invertible matrix.
Proof
Rearranging the columns of \(\mathbf M _f\) gives a triangular matrix whose diagonal is the constant coefficient of f. \(\square \)
Moreover, when \(f\in \mathbb {Z}[x]\), we will make use of singular value bounds on \(\mathbf M_f\) and related matrices in terms of the expansion factor of f. For a matrix \(A\in \mathbb {R}^{m\times n}\) let \(A^{(d)}\) denote the matrix whose rows are the first d rows of A.
Lemma 9
For any \(f\in \mathbb {Z}[x]\), 
Remark 1
This inequality generalizes and improves on [21, Theorem 2.8] by a factor of \(\sqrt{d}.\)
Proof
We want to show that for all nonzero vectors \(u\in \mathbb {R}^m\), the following inequality holds:

We first note that because \(\mathbb Q\) is dense in \(\mathbb {R}\), it suffices to show the same inequality for all nonzero \(u\in \mathbb Q^n\). Moreover, since the inequality is scale-invariant, we may further reduce to the case where \(u\in \mathbb {Z}^m\).
Given any nonzero vector \(u\in \mathbb {Z}^m\), we define \(v := \mathbf M _f u\). Then, letting \(g\in {\mathbb {R}}^{<m}[x]\) denote the degree \(<m\) polynomial with coefficient vector u, we know by [21, Lemma 2.4] that \(v_i\) is the constant coefficient of \(x^{i-1}\cdot g \mod f\). Thus,

We conclude that

where the last inequality holds because \(||u ||_{\infty }\le ||u ||.\) \(\square \)
3 Degree-Parametrized MP-LWE
In this section, we define and consider a variant of MP-LWE in which samples generated from a fixed secret s (which are polynomials with coefficients in \(\mathbb {Z}_q\)) can have varying (pre-specified) degrees. This is in contrast to the variant considered in [21], in which all samples have the same degree. We then prove a hardness reduction relating polynomial LWE (PLWE) to our variant of MP-LWE, which we call degree-parametrized MP-LWE.
For the rest of the paper, we will let \(\mathbb {R}_q\) denote \(\mathbb {R}/q\mathbb {Z}.\)
Definition 9
(Degree-Parametrized MP-LWE). Let \(n> 0, q \ge 2, m >0, \mathbf {d} \in [\frac{n}{2}]^t\), and let \(\chi \) be a distribution over \(\mathbb {R}_q\). For \(s \in {\mathbb {Z}_q}^{<n-1}[x],\) we define the distribution \(\mathrm {MP}_{q,n,\mathbf d ,\chi }(s)\) over \(\prod _{i=1}^t ({\mathbb {Z}_q}^{<n - \mathbf d _i}[x] \times {\mathbb {R}_q}^{<\mathbf d _i}[x])\) as follows.
-
For each \(i\in [t],\) sample
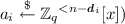 and sample \(e_i \leftarrow \chi ^\mathbf{d _i}\) (interpreted as a degree \(<\varvec{d}_i\) polynomial).
and sample \(e_i \leftarrow \chi ^\mathbf{d _i}\) (interpreted as a degree \(<\varvec{d}_i\) polynomial). -
Output \(\left( a_i, b_i := a_i \, \odot _{\varvec{d}_i} \, s + e_i \right) _{i\in [t]}. \)
The (degree-parametrized) MP-LWE problem consists of distinguishing between arbitrarily many samples from \(\mathrm {MP}_{q,n,\varvec{d},\chi }(s)\) and the same number of samples from \(\prod _{i=1}^t U({\mathbb {Z}_q}^{<n - \varvec{d}_i}[x] \times {\mathbb {R}_q}^{<\varvec{d}_i}[x])\) with non-negligible probability over the choice of  .
.
Following [21], we show that degree-parametrized MP-LWE is as hard as the polynomial-LWE problem \(\mathsf {PLWE}_f\) for a wide class of polynomials f. The reduction is effectively the same as that of [21], although we obtain better parameters due to an improved singular value bound on the matrix \(\mathbf {M}_f\) (Lemma 6). We recall the definition of \(\mathsf {PLWE}_f\), taken from [21].
Definition 10
(PLWE). Let \(q \ge 2, m > 0\), f a polynomial of degree m, \(\chi \) a distribution over \(\mathbb {R}[x]/f.\) The decision problem \(\mathsf {PLWE}^{(f)}_{q, \chi }\) consists in distinguishing between arbitrarily many samples

and the same number of samples from \(U(\mathbb {Z}_q[x]/f \times \mathbb {R}_q[x]/f)\) with non-negligible probability over choice of 
Theorem 2
(Hardness of MP-LWE). Let \(n> 0, q \ge 2, t >0, \varvec{d} \in [\frac{n}{2}]^t,\) and \(\alpha \in (0,1)\). For \(S >0,\) let \(\mathcal {F}(S, \varvec{d}, n)\) be the set of polynomials in \(\mathbb {Z}[x]\) that are monic, have constant coefficient coprime with q, have degree m in \(\bigcap _{i=1}^t [\varvec{d}_i, n - \varvec{d}_i]\) and satisfy  Then, there exists a ppt reduction from \(\mathsf {PLWE}_{D_{\alpha \cdot q}}^{(f)}\) for any \(f \in \mathcal {F}(S, \varvec{d}, n)\) to \(\mathsf {MPLWE}_{q, n, \varvec{d}, D_{\alpha '\cdot q}}\) with \(\alpha ' = \alpha \cdot \sqrt{\frac{n}{2}} \cdot S.\)
Then, there exists a ppt reduction from \(\mathsf {PLWE}_{D_{\alpha \cdot q}}^{(f)}\) for any \(f \in \mathcal {F}(S, \varvec{d}, n)\) to \(\mathsf {MPLWE}_{q, n, \varvec{d}, D_{\alpha '\cdot q}}\) with \(\alpha ' = \alpha \cdot \sqrt{\frac{n}{2}} \cdot S.\)
Proof
For \(d \in [n/2]\) and any polynomial f of degree \(m\in [d, n-d]\), we describe a ppt mapping
We will then show that \(\phi \) maps \(U(\mathbb {Z}_q[x]/f \times \mathbb {Z}_q[x]/f)\) to \(U({\mathbb {Z}_q}^{<n-d}[x] \times {\mathbb {Z}_q}^{<d}[x])\) and maps a random PLWE sample (with secret s) to a random MP-LWE sample with secret \(s'\) depending on s. This mapping (with slightly different parameters) was previously defined in [21].
Let \((a, b) \in \mathbb {Z}_q[x]/f \times \mathbb {R}_q[x]/f\) be an input pair. Then, the pair \((a', b') \leftarrow \phi _{n, d}(a, b)\) is sampled by the following process.
-
Define the matrix \(\varSigma = (\alpha ' q)^2 \mathbf {I}_d - (\alpha q)^2 \mathbf {J}_d \cdot \mathbf {M}^{(d)}_f \), where \(\mathbf {I}_d\) denotes the \(d\times d\) identity matrix and \(\mathbf {J}_{d}\) denotes the \(d\times d\) anti-diagonal matrix.
-
Sample
 and \(\epsilon \leftarrow D_{\varSigma } \).
and \(\epsilon \leftarrow D_{\varSigma } \). -
Set \(a' = a + h \cdot f\) and set \(b'\) to be the polynomial with coefficient vector \(\mathbf b ' =\mathbf J _d \cdot \mathbf M ^{(d)}_f \cdot \mathbf b + \epsilon \).
We note that the matrix \(\varSigma \) above is positive definite (and hence the distribution \(D_{\varSigma }\) is well-defined) by the following calculation: using Lemma 9,

We first show that if  , then \((a', b')\) is distributed uniformly on the set \({\mathbb {Z}_q}^{<n-d}[x] \times {\mathbb {R}_q}^{<d}[x]\). Since a and h are uniformly random distributed in \({\mathbb {Z}_q}^{<m}[x]\) and \({\mathbb {Z}_q}^{<n-d-m}[x]\) respectively, we see that \(a'\) is uniformly distributed over \({\mathbb {Z}_q}^{<n-d}[x].\) Moreover, if b is uniformly distributed in \(\mathbb {R}_q[x]/f,\) then its coefficient vector \(\mathbf {b}\) is uniformly distributed in \(\mathbb {R}_q^m.\) Since \(\mathbf {J}\) and \(\mathbf {M}_f\) are invertible (see Lemma 8), \(\mathbf {J}_d \cdot \mathbf {M}^{(d)}_f \cdot \mathbf {b} \) is therefore uniformly distributed (over \(\mathbb {R}_q^d\)), thus so is \( \mathbf {b}'\) and its polynomial representation \(b'\).
, then \((a', b')\) is distributed uniformly on the set \({\mathbb {Z}_q}^{<n-d}[x] \times {\mathbb {R}_q}^{<d}[x]\). Since a and h are uniformly random distributed in \({\mathbb {Z}_q}^{<m}[x]\) and \({\mathbb {Z}_q}^{<n-d-m}[x]\) respectively, we see that \(a'\) is uniformly distributed over \({\mathbb {Z}_q}^{<n-d}[x].\) Moreover, if b is uniformly distributed in \(\mathbb {R}_q[x]/f,\) then its coefficient vector \(\mathbf {b}\) is uniformly distributed in \(\mathbb {R}_q^m.\) Since \(\mathbf {J}\) and \(\mathbf {M}_f\) are invertible (see Lemma 8), \(\mathbf {J}_d \cdot \mathbf {M}^{(d)}_f \cdot \mathbf {b} \) is therefore uniformly distributed (over \(\mathbb {R}_q^d\)), thus so is \( \mathbf {b}'\) and its polynomial representation \(b'\).
We next show that if (a, b) is a PLWE-sample, then \((a', b')\) is a MP-LWE sample. Suppose that \(b = a \cdot s + e\) for \(s\in \mathbb {Z}_q[x]/f\) and error polynomial e with coefficient vector \(\mathbf e \leftarrow \chi ^d\). Let \(s'\in {\mathbb {Z}_q}^{<n-1}[x]\) be defined so that it has coefficient vector
where \(\mathbf B _{n-1,f} \in \mathbb {Z}_q^{n-1 \times m}\) is defined so that the ith row of \(\mathbf B _{n-1, f}\) is the coefficient vector of \(x^{i-1} \mod f\). Moreover, define \(e'\in {\mathbb {R}_q}^{<d}[x]\) to have coefficient vector
We refer to [21] for a proof that \(b' = a'\, \odot _{d} \,s' + e'.\) Since \(\epsilon \) is sampled independent of \(\mathbf e \), the distribution of \(\mathbf e '\) is \(D_{\alpha '\cdot q}\) by standard (continuous) Gaussian distribution identities.
As in [21], the collection of maps \(\phi _{n, d_i}\) (ranging over all \(i\in [t]\)) can be used to implement a MP-LWE oracle using a PLWE oracle, and hence immediately give a reduction from \(\mathsf {PLWE}_{D_{\alpha \cdot q}}^{(f)}\) for any \(f \in \mathcal {F}(S, \mathbf d , n)\) to \(\mathsf {MPLWE}_{q, n, \mathbf d , D_{\alpha '\cdot q}}\). \(\square \)
4 A Leftover Hash Lemma for Polynomials
In this section, we state and prove Theorem 3, a Leftover Hash Lemma for polynomials with bounded degree. The closest previous work is [14], in which the author proves a Leftover Hash Lemma for elements of the ring \(R:=\mathbb {Z}_q[\alpha ]/[\alpha ^n -1];\) the proof technique in [14] inspires our proof of Theorem 3. However, we encounter some subtleties as a result of working with bounded-degree polynomials; specifically, difficulties arise due to the fact that the set of bounded-degree polynomials is not closed under multiplication.
Let \(q = \mathsf {poly}(n)\) be a sequence of prime numbers, so that \(\mathbb {Z}_q\) is a field for every \(q = q(n)\). For polynomials \(z_1, \cdots , z_t \in \mathbb {Z}_q[x]\), we adopt the convention that \(\gcd (z_1, \cdots , z_t)\) is always monic.
Our goal is to prove that the hash function
with hash key \(\vec a = (a_1, \ldots , a_t)\) consisting of t polynomials drawn i.i.d. from \(U({\mathbb {Z}_q}^{<n}[x])\), extracts uniform randomness from high entropy sources of bounded-degree polynomials, in the special case of sources that are product distributions.
Following the approach of [14], we want to analyze, for any fixed input \(\vec z = (z_1, \ldots , z_t)\), the distribution of outputs \(H(\vec z) := h_{a_1, \ldots , a_t}(z_1, \ldots , z_t)\) over the choice of uniformly random hash key. In [14], the \(a_i\) and \(z_i\) are all elements of a ring R, so the set \(\left\{ h_{a_1,\cdots , a_t} (z_1, \cdots , z_t) |(a_1, \cdots , a_t) \in R^t \right\} \) is simply the ideal generated by \(z_1, \cdots , z_t\). Moreover, a simple argument shows that \(H(\vec z)\) is uniform over this set. Here, however, we are working with bounded degree polynomials, so the characterization of \(H(\vec z)\) is not as immediate. Lemma 10 characterizes \(H(\vec z).\)
Lemma 10
(Range of hash output). Consider \(z_1, \cdots , z_t \in {\mathbb {Z}_q}^{<n}[x]\) that are not all zero polynomials. Let I denote the set of degree-bounded linear combinations of \(\{z_i\}\), that is,
Moreover, let \(d = \max _i \deg (z_i)\), and let \(g = \gcd (z_1, \ldots , z_t)\). Then,
Moreover, for polynomials \((a_1, \ldots , a_t)\) sampled i.i.d. from \(U({\mathbb {Z}_q}^{<n}[x])\), the distribution \(\left\{ \sum _{i=1}^t a_i \cdot z_i\right\} \) is uniform on the set I.
Proof
Recall that \(g = \gcd (z_1, \cdots , z_t)\) is some monic polynomial in \(\mathbb {Z}_q[x]\) dividing each \(z_i\). Therefore, the inclusion
is immediate. For the rest of the proof, we aim to show the opposite inclusion. We assume without loss of generality that all \(z_i\) are nonzero and prove the claim by induction on t.
We begin with a base case of \(t =2 \) and further assume (at first) that \(g = 1\). Fix polynomials \((z_1, z_2)\) with \(\gcd (z_1, z_2) = 1\), and assume WLOG that \(d = \deg (z_1)\). We want to show that for every \(\alpha \in {\mathbb {Z}_q}^{<n+d}[x]\), there exists a key \((a_1, a_2)\) such that \(h_{a_1, a_2}(z_1, z_2) = \alpha \). To do this, we write
for polynomials (Q, R) satisfying \(\deg (Q) < n + d - \deg (z_1z_2) = n - \deg (z_2)\), \(\deg (R) < \deg (z_1z_2)\). By the Chinese remainder theorem, we know that there exist polynomials \(s_1, s_2\) satisfying \(\deg (s_1) < \deg (z_2)\), \(\deg (s_2) < \deg (z_1)\), and
Then, choosing \(a_1 = Q z_2 + s_1\) and \(a_2 = s_2\), we see that \(\deg (a_1) < n\), \(\deg (a_2) < n\), and
as desired.
In the case that \(\gcd (z_1, z_2) = g\ne 1\), for any \(\alpha \in g \mathbb {Z}_q[x] \cap {\mathbb {Z}_q}^{<n+d}[x]\) write \(\alpha = g \alpha '\) with \(\deg (\alpha ') < n + d - \deg (g)\). Since \(\gcd (\frac{z_1}{g}, \frac{z_2}{g}) = 1\), we just showed that there exist \(a_1, a_2\) with \(\deg (a_i) < n \) and \(a_1 \frac{z_1}{g} + a_2 \frac{z_2}{g} = \alpha '\), which implies that \(a_1 z_1 + a_2 z_2 = g \alpha ' = \alpha \). This completes the base case.
For the inductive step, consider any \(t\ge 3\) and any polynomials \((z_1, \ldots z_t)\) with \(d = \max _i \deg (z_i)\) and \(g = \gcd (z_1, \ldots , z_t)\). We want to show that for any \(\alpha \in g \mathbb {Z}_q[x] \cap {\mathbb {Z}_q}^{<n+d}[x]\), there exist polynomials \((a_1, \ldots , a_t)\) with \(\deg (a_i) < n\) and \(\sum _i a_i z_i = \alpha \).
We suppose without loss of generality that \(\deg (z_1) = d\). Then, let \(g' = \gcd (z_2, \ldots ,z_t)\), and note that by the base case, there exist polynomials \((a_1, a^*)\) such that \(\deg (a_1) < n\), \(\deg (a^*) < n\), and
The base case applies because \(\max (\deg (z_1), \deg (g')) = d\) and \(\gcd (z_1, g') = g\). Now, further note that \(\deg (a^* g') < n + \deg (g') \le n + \max _{2\le i\le t} \deg (z_i)\). Therefore, by the inductive hypothesis (applied to \((z_2, \ldots , z_t)\)), there exist polynomials \((a_2, \ldots , a_t)\) such that \(\deg (a_i) < n\) for all i, and
This completes the inductive step.
Finally, we prove the distributional claim. Our reasoning follows the proof of ([14], Lemma 4.4). For every \(\alpha \in I\), define the set
By construction, the sets \(S_\alpha \) for \(\alpha \in I\) partition \(({\mathbb {Z}_q}^{<n}[x])^t.\) In order to prove the distributional claim, we only need to show that \(|S_0 | = |S_\alpha |\) for all \(\alpha \in I.\) To see this, note that for a given \(\alpha \in I\), we have already shown that \(S_\alpha \ne \emptyset \), so there exist \(a'_1,\cdots , a'_t\) such that \(\deg (a'_i) < n\) and \(\sum _{i=1}^t a'_i z_i = b\). Then, the function \((a_i)_{i\le t} \mapsto (a_i-a'_i)_{i \le t}\) is a bijection from \(S_\alpha \) to \(S_0\), proving that \(|S_\alpha | = |S_0|\), as desired. \(\square \)
Having proved Lemma 10, we are ready to state and prove our variant of the leftover hash lemma.
Theorem 3
Let \(\chi \) be a distribution over \(\mathbb {Z}_q\) and \(\delta \in (0,1)\) be such that \(H_\infty (\chi ) \ge \log (\frac{1}{\delta })\). Define the distribution \(V:= (\vec a, h_{\vec a}(\vec r))\) over \(S = ({\mathbb {Z}_q}^{<n}[x])^t \times {\mathbb {Z}_q}^{<n+n'-1}[x],\) where \(\vec a = (a_1, \ldots a_t)\) consists of i.i.d. samples from \(U({\mathbb {Z}_q}^{<n}[x])\), and \(\vec r = (r_1, \ldots , r_t)\) consists of i.i.d. samples from \(\chi ^{n'}[x]\).
Then, for \(n' \le n\), if \(\delta ^t q = o(1)\),
In particular, for any \(q = \mathsf {poly}(n)\), if \(\delta ^{-1} = \omega (1)\) and \(n't/n = \varOmega (\log n),\) we have \(V\approx _s U(S)\).
Proof
By ([10], Claim 2) (i.e., by applying a generalized mean inequality), in order to prove that \(\varDelta (V, U(S)) \le \epsilon \), it suffices to show that  ; note that in our case, \(|S |= q^{nt} \times q^{n+n'-1}.\)
; note that in our case, \(|S |= q^{nt} \times q^{n+n'-1}.\)
More precisely, let \(\vec a = (a_i)_{i\in [t]}, \vec a' = (a'_i)_{i\in [t]}, \vec r = (r_i)_{i\in [t]}, \vec r' = (r'_i)_{i\in [t]}\) consist of i.i.d. samples from \(U({\mathbb {Z}_q}^{<n}[x])\) and \(\chi ^{n'}[x]\) respectively. We want to show that

We first partially evaluate the left-hand side of this inequality:
Defining the random variable \(\vec v = \vec r - \vec r'\), we then have

where \(I(z) := \left\{ \sum _{i=1}^t a_i z_i\, |\, a_i\in {\mathbb {Z}_q}^{<n}[x] \right\} = \gcd (z_1, \ldots , z_t) \mathbb {Z}_q[x] \cap {\mathbb {Z}_q}^{<n+\max _i \deg (z_i)}[x]\) as in Lemma 10. The last inequality follows from the distributional claim in Lemma 10.
To further simplify, we know by assumption that  . In addition, we group terms of the summation by the associated sets I(z). That is, for every monic polynomial \(g\in {\mathbb {Z}_q}^{<n'}[x]\) and degree \(d< n'\), we define \(I_{g, d} = g \mathbb {Z}_q[x] \cap {\mathbb {Z}_q}^{<n+d}[x]\) and obtain
. In addition, we group terms of the summation by the associated sets I(z). That is, for every monic polynomial \(g\in {\mathbb {Z}_q}^{<n'}[x]\) and degree \(d< n'\), we define \(I_{g, d} = g \mathbb {Z}_q[x] \cap {\mathbb {Z}_q}^{<n+d}[x]\) and obtain

We next bound the probability that \(I(\vec v)\subset I_{g, d}\) for any fixed g, d. To do this, we note by inspection that \(I(\vec v) \subset I_{g, d}\) if and only if \(v_i \in g \mathbb {Z}_q[x] \cap {\mathbb {Z}_q}^{<d+1}[x]\) for all i. For a fixed i, this occurs with probability

In order to bound this probability, we define random variables \(w_i, w'_i\) to be drawn i.i.d. from \(\chi ^{d+1}[x]\) and compute
Fix an arbitrary \(\bar{w}\). For a vector \(v \in \mathbb {Z}_q^{d+1-\deg (g)}\) let \(T_v\) be set of polynomials \(w_i \in {\mathbb {Z}_q}^{<d+1}[x]\) whose \((d+1-\deg (g))\) highest order coefficients are fixed to match v. Then, the “reduction mod g” map is a bijection from \(T_v\) to \({\mathbb {Z}_q}^{<\deg (g)}[x]\). Letting \(\bar{w}^v\) denote the unique inverse of \(\bar{w}\) in \(T_v\) and making use of the fact that \(H_\infty (\chi ) \ge \log (\frac{1}{\delta })\), we compute
Combining our calculations (Eqs. (1)–(6)), we conclude that

where the final inequality follows from the assumption that \(\delta ^t q^2 = o(1)\). This completes the proof of Theorem 3. \(\square \)
For our application to IBE, we are interested in applying Theorem 3 in the case of a discrete Gaussian input distribution \(D_{\mathbb {Z}, \sigma }\). We now show that the hypothesis of Theorem 3 holds for sufficiently large \(\sigma \).
Lemma 11
Let \(\chi := D_{\mathbb {Z}, \sigma }\) and \(\chi _q := \chi \!\mod q \). For \(\sigma = \mathsf {poly}(n), q = \omega (\sigma \log ^{1/2} n), \sigma = \omega (1),\) we have \(H_\infty (\chi _q) \ge \log (\frac{\sigma }{c})\) for some constant c.
Proof
Since \(q = \omega (\sigma \log ^{1/2} n)\), only a negligible fraction of \(\chi \)’s probability mass “wraps around,” i.e., is not contained in the interval \([-\frac{q}{2}, \frac{q}{2})\), so the min-entropy bound we proved about \(\chi \) directly gives a min-entropy bound on \(\chi _q\).
In more detail, fix \(\epsilon \in (0,1/2)\) to be a small constant. By Lemma 2, \(n_{\epsilon }(\mathbb {Z}) \le c' \log (1+ \epsilon ^{-1})\) for some constant \(c'.\) By Lemma 3 and our hypothesis, we see that
Given this, we can compute
The bound \(2^{-H_\infty }(\chi _q) \le \frac{c}{\sigma }\) then follows from Lemma 5 applied to parameter \(\delta = \sigma ^{-1} c' \log (1+\epsilon ^{-1}) < 1/\sqrt{2}\); this parameter setting is possible since \(\sigma = \omega (1)\). \(\square \)
5 Lattice Trapdoors for MP-LWE
In this section, we implement the “lattice trapdoors” paradigm of [8] for middle-product LWE. In particular, we show that the Micciancio-Peikert variant of lattice trapdoors [15] can be instantiated for MP-LWE.
In our setting, we want an algorithm \(\mathsf {TrapGen}\) for generating random polynomials \((a_1, \ldots , a_{t'})\) along with a trapdoor \(\mathsf {td}\) that allows for sampling polynomials \((r_i)\) satisfying
given any polynomial u (of the correct degree).
We briefly describe the method for generating \((a_i).\) Let \(t\le t', d, n\) and distribution \(\chi \) over \(\mathbb {Z}_q\) be parameters to be defined later. For \((i, j) \in [t] \times [t'-t]\), we sample  and \(w_{i,j} \leftarrow \chi ^{d}[x],\) and construct \(a_{t+j} = c_j - \sum _{i\le t} a_i \cdot w_{i,j},\) where \((c_j)_{j \in [t'-t]}\) is an analogue of matrix G in Definition 11. Note that \((a_i)_{i\le t'} \in ({\mathbb {Z}_q}^{<n}[x])^t \times ({\mathbb {Z}_q}^{<n+d-1}[x])^{t'-t}.\) We will choose d according to Theorem 3 to ensure that the distribution of each \(a_{t+j}\) is close to random. Finally, we will show that the trapdoor \(\{w_{ij}\}\) can be used to implement the preimage sampling algorithm of [15] by considering the polynomials \((a_i)\) as structured matrices, similarly to the Ring-LWE setting.
and \(w_{i,j} \leftarrow \chi ^{d}[x],\) and construct \(a_{t+j} = c_j - \sum _{i\le t} a_i \cdot w_{i,j},\) where \((c_j)_{j \in [t'-t]}\) is an analogue of matrix G in Definition 11. Note that \((a_i)_{i\le t'} \in ({\mathbb {Z}_q}^{<n}[x])^t \times ({\mathbb {Z}_q}^{<n+d-1}[x])^{t'-t}.\) We will choose d according to Theorem 3 to ensure that the distribution of each \(a_{t+j}\) is close to random. Finally, we will show that the trapdoor \(\{w_{ij}\}\) can be used to implement the preimage sampling algorithm of [15] by considering the polynomials \((a_i)\) as structured matrices, similarly to the Ring-LWE setting.
For the rest of this section, let \(\tau : = \lceil \log _2 q \rceil .\) We first recall the notion of a “G-trapdoor” from [15].
Definition 11
([15], Definition 5.2). Let \(G:=I_k \otimes \begin{bmatrix} 1&2&\cdots&2^{\tau -1} \end{bmatrix} \in \mathbb {Z}_q^{k \times k \tau }\). Then, given a matrix \(A \in \mathbb {Z}^{k \times (m+k\tau )}\), we say that a matrix \(R \in \mathbb {Z}^{m\times k\tau }\) is a \(\mathbf G \)-trapdoor for A if
We make use of the following result in [15], Section 5.4, which states that G-trapdoors allow for efficient Gaussian preimage sampling in the style of [8].
Theorem 4
([15], Theorem 5.5). Let \(G:=I_k \otimes \begin{bmatrix} 1&2&\cdots&2^{\tau -1} \end{bmatrix} \in \mathbb {Z}_q^{k \times k \tau }\) and matrices \(A \in \mathbb {Z}^{k \times (m+k\tau )}, R \in \mathbb {Z}^{m\times k\tau }\) be such that
There exists an efficient algorithm \(\mathcal {C} = (\mathcal C_1, \mathcal C_2)\) that operates as follows:
-
In the offline phase, \(\mathcal C_1(A, R, \sigma )\) does some polynomial-time preprocessing on input \((A, R, \sigma )\) and outputs a state \(\mathsf {st}\).
-
In the online phase, \(\mathcal C_2(\mathsf {st}, u)\), additionally given a vector u, samples from \(D_{\varLambda ^{\perp }_u (A), \sigma }\), as long as \(\sigma \ge \omega (\sqrt{\log k})\sqrt{7(\sigma _1(R)^2 +1)}.\)
Moreover, the runtime of \(\mathcal C_2\) is the time to compute Rz for \(z \in \mathbb {Z}^{k \tau }\) plus \(\tilde{O} (m + k\tau ).\)
We note that the proof of Theorem 4 given in [15] has a minor error that we correct in the Appendix. We now use Theorem 4 to instantiate lattice trapdoors for MP-LWE.
Theorem 5
Suppose that \(q= \mathsf {poly}(n), d\le n, dt/n = \varOmega (\log n),\sigma = \omega (\log ^2 n) \sqrt{n dt}\) and \(\gamma = \frac{n+2d-2}{d}\) is an integer. Then, there exist ppt algorithms \((\mathsf {TrapGen}, \mathsf {SamplePre})\) with the following properties.
-
\(\mathsf {TrapGen}(1^n)\) generates polynomials
$$ (a_1, \cdots , a_t, a_{t+1},\cdots , a_{t + \gamma \tau }) \approx _s U(({\mathbb {Z}_q}^{<n}[x])^t \times ({\mathbb {Z}_q}^{<n+d-1}[x])^{\gamma \tau }) $$together with a trapdoor \(\mathsf {td}\) that can be stored in \(O(n \tau t)\) space.
-
\(\mathsf {SamplePre}(\mathsf {td}, u)\) that operates as follow:
-
In the offline phase, does some polynomial-time preprocessing with trapdoor \(\mathsf {td}\) and parameter \(\sigma ,\) and output a state \(\mathsf {st}\).
-
In the online phase, given state \(\mathsf {st}\) and a syndrome \(u\in {\mathbb {Z}_q}^{<n+2d-2}[x],\) outputs \((r_i)_{i=1}^{t+\gamma \tau }\) satisfying
$$\sum _{i=1}^{t+\gamma \tau } a_i \cdot r_i = u $$in \(\tilde{O}(nt)\) time. Moreover, the output distribution of \((r_i)\) is exactly the conditional distribution
$$(D_{\mathbb {Z}^{2d-1}, \sigma } [x])^t \times (D_{\mathbb {Z}^d, \sigma }[x])^{\gamma \tau } \mid \sum _{i=1}^{t+\gamma \tau } a_i \cdot r_i = u, $$ -
Proof
Let \(\beta : = \left\lceil \frac{\log _2 n}{2}\right\rceil .\)
\(\mathsf {TrapGen}\)Algorithm: We first describe \(\mathsf {TrapGen}\) and prove that it outputs the right distribution of polynomials \((a_i)\).
-
For \( (i,j) \in [t] \times [\gamma \tau ]\), sample
 and \(w_{i,j} \leftarrow \chi ^{d}[x]\) where \(\chi =U(\{-\beta , \cdots , \beta \}).\) Since \(\beta \ll q/2,\) we can interpret samples from \(\chi \) as elements of \(\mathbb {Z}_q.\)
and \(w_{i,j} \leftarrow \chi ^{d}[x]\) where \(\chi =U(\{-\beta , \cdots , \beta \}).\) Since \(\beta \ll q/2,\) we can interpret samples from \(\chi \) as elements of \(\mathbb {Z}_q.\) -
For all \(j\in [\gamma \tau ]\), define polynomials
$$ u_j = \sum _{i=1}^t a_i \cdot w_{i,j} $$$$a_{t+j} =c_j - u_j $$for \(c_j \in {\mathbb {Z}_q}^{<n+d-2}[x]\) dependent only on j. Specifically, \(c_j = 2^{u} x^{dv}\) for \(j = v \tau + u + 1\) where \(u \in \{0,\cdots , \tau -1\}, v \in \{0, \cdots , \gamma -1\}.\)
-
Output \((a_1, \ldots , a_{t+\gamma \tau })\) with associated trapdoor \(\mathsf {td}= (w_{i,j})\).
We first note that the amount of space required to store \(\mathsf {td}= (w_{i,j})\) is \(O(d (\gamma \tau ) t) = O(n \tau t)\), since \(\gamma d = n+2d-2 \le 3n.\)
To see that the sampled polynomials \((a_1, \ldots , a_{t+\gamma \tau })\) are statistically close to uniform, we apply our Leftover Hash Lemma (Theorem 3). In particular, \(H_\infty (\chi )= \log (\frac{1}{\beta }) \ge \log \log n - 1.\) Therefore, by Theorem 3,
and so
\(\mathsf {SamplePre}\) Algorithm: We next describe \(\mathsf {SamplePre}\) using the algorithm from Theorem 4.
-
Implicitly define matrices A, L by the following equations.
$$\begin{aligned} \begin{aligned} \tilde{A}&=\begin{bmatrix} T^{n,2d-1}(a_1) | \cdots | T^{n,2d-1} (a_t)\end{bmatrix}\\ \tilde{L}&= \begin{bmatrix} T^{d, d}(w_{1,1}) &{} \cdots &{} T^{d, d}(w_{1,\gamma \tau }) \\ \vdots &{} &{} \vdots \\ T^{d, d}(w_{t,1}) &{} \cdots &{} T^{d, d}(w_{t,\gamma \tau })\end{bmatrix}\\ \varGamma (h)&= \begin{bmatrix}T^{n+d-1,d}(h) | \cdots | T^{n+d-1,d}(h2^{\tau -1}) \end{bmatrix}\\ G&=\begin{bmatrix}\varGamma (1) | \varGamma (x^d) | \cdots | \varGamma (x^{(\gamma -1) d}) \end{bmatrix} \\ I&= I_{\gamma d \tau } = \begin{bmatrix} T^{1,d}(1) &{} \cdots &{} \\ \cdots &{} &{} \cdots \\ &{} &{} T^{1,d}(1) \end{bmatrix}\\ A&= [\tilde{A} | G - \tilde{A} \tilde{L}]\\ L&= \begin{bmatrix} \tilde{L} \\ I \end{bmatrix} \end{aligned} \end{aligned}$$(7)so that \(A L = G =I_{\gamma d}\otimes [1 \cdots 2^{\tau -1}]\), i.e., L is a G-trapdoor for A.
-
Let \(\mathbf u = T^{n+2d-2}(u) \in \mathbb {Z}_q^{n+2d-2}\) be the coefficient vector of u.
-
Apply the algorithm from Theorem 4 (for \(k = \gamma d = n+2d-2\)) to sample \(\mathbf y \) from \(D_{\varLambda ^{\perp }_{\mathbf u} (A), \sigma }\) where
$$\sigma = \omega (\sqrt{\log (\gamma d)}) \beta \sqrt{7((\gamma d\tau )\cdot d \cdot t + 1)} = c\, \omega (\log ^2 n) \sqrt{n \cdot (dt)}, $$for some constant c.
-
Write \(\mathbf y \) as \(\begin{bmatrix} T^{2d-1,1}(r_1) \\ \vdots \\ T^{2d-1,1}(r_t) \\ T^{d,1}(r_{t+1}) \\ \vdots \\ T^{d,1}(r_{t+\gamma \tau }) \end{bmatrix},\) where \(\deg (r_i) {\left\{ \begin{array}{ll}<2d-1 \text { for }i\in [t] \\ < d \text { for }i\in \{t+1, \cdots , t+\gamma \tau \} \end{array}\right. }\)
-
Output \((r_1, \ldots , r_{t+\gamma \tau })\).
In order to analyze the correctness of \(\mathsf {SamplePre}\), we first note that by construction, \(\max _{i,j} |\tilde{L}_{ij} | \le \beta \), and so \(\sigma _1(\tilde{L}) \le \beta \sqrt{(\gamma d \tau ) \cdot (2d-1) t}\) by Lemma 6. Combined with Theorem 4 (for \(k = \gamma d = n+2d-2\)), this tells us that \(\mathbf y \) is sampled from from \(D_{\varLambda ^{\perp }_{\mathbf u}(A), \sigma }\) where
for some constant c. Theorem 4 applies because of our parameter settings of \(\gamma d = n+2 d-2 \le 3n\) and \(\tau = \theta (\log q) = \theta (\log n)\) for \(q = \mathsf {poly}(n).\)
Moreover, by Lemma 7 and Eq. (7),
Thus, \(\mathbf y \in \varLambda ^{\perp }_{\mathbf u}(A)\) if and only if \(\sum _{i=1}^{t+\gamma \tau } a_i \cdot r_i = u.\)
To prove the claim about distribution of \(\mathbf r = (r_i),\) we note that the columns of A generate \(\mathbb {Z}^{n+2d-2}\) since (1) the columns of G generate \(\mathbb {Z}^{n+2d-2}\) and (2) \(A L = G.\) Hence, there exists \(\mathbf {y}^*\) such that \(A\mathbf {y}^* = \mathbf u.\) Then, Lemma 5.2 in [8] applies, allowing us to conclude that the distribution of \(\mathbf {y}\) sampled by our algorithm is exactly
To see that the first equality of distributions holds, note that the two distributions have the same support (i.e., \(t + \varLambda ^{\perp }(A) = \varLambda ^{\perp }_{\mathbf u}(A)\)), and for all \(x \in \varLambda ^{\perp }_{\mathbf u}(A),\)
Thus, the conditional distribution of \(\mathbf r\) is as claimed. Finally, we analyze the runtime of \(\mathsf {SamplePre}\)’s online phase, which is precisely the runtime of \(\mathcal {C}_2.\) Computing \(\tilde{L} z\) for \(z \in \mathbb {Z}_q^{\gamma d \tau }\) can be performed, using polynomial multiplication, in \(O((d\log d) t \gamma \tau )= \tilde{O}(nt)\) time; this bound uses the fact that \(\gamma d \le 3n\), \(\log d \le \log n\) and \(\tau = \varTheta (\log n).\) \(\square \)
6 New Encryption Schemes from Middle-Product LWE
In this section, we describe how to build a “Dual Regev”-style public-key encryption scheme, as well as an identity-based encryption scheme, whose security is based on the hardness of MP-LWE. As in [8], our IBE scheme is constructed by combining the Dual Regev scheme with lattice trapdoors as constructed in Sect. 5.
6.1 Middle Product Dual Regev Encryption
Unless otherwise stated, the following parameters are positive integers.
Let \(q = q(n)\) be a prime, \(\tau : = \lceil \log _2 q \rceil , n, d, k\) be such that \(\gamma = \frac{n+2d-2}{d} \in \mathbb {N}\) and \(2d +k \le n.\) Let \(t>0, t'= t+\gamma \tau .\) Let \(\chi : =\lfloor D_{\alpha \cdot q} \rceil \) be the distribution over \(\mathbb {Z}\) in which \(\epsilon \leftarrow D_{\alpha \cdot q}\) is sampled and then rounded to the nearest integer.
Finally, let \(\sigma \in \mathbb {R}_{> 0}\) be a parameter to be specified later. We then define a public-key encryption scheme with message space \(\mathcal {M} = {\{0,1\}}^{<k+1}[x].\)
-
Key Generation: \(\mathsf {KeyGen}(1^n)\) operates as follows.
-
For \(1\le i \le t\), sample
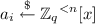 , \(r_i \leftarrow D_{\mathbb {Z}^{2d-1}, \sigma }[x]\);
, \(r_i \leftarrow D_{\mathbb {Z}^{2d-1}, \sigma }[x]\); -
For \(t+1 \le i \le t'\), sample
 , \(r_i \leftarrow D_{\mathbb {Z}^{d}, \sigma }[x]\).
, \(r_i \leftarrow D_{\mathbb {Z}^{d}, \sigma }[x]\). -
Compute \(u = \sum _{i=1}^{t'} a_i r_i\) and output \(\mathsf {pk}:= (a_1,\ldots , a_{t'}, u);\, \mathsf {sk}:=(r_1, \ldots , r_{t'})\)
-
-
Encryption: \(\mathsf {Enc}(\mathsf {pk}=((a_i)_{i\le t'}, u),\mu )\) operates as follows.
-
Sample
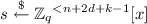
-
For \(1\le i\le t\), sample \(e_i \leftarrow \chi ^{2d+k}[x]\), and compute \(b_i = a_i \odot _{2d+k} s + 2 e_i\)
-
For \(t+1 \le i\le t'\), sample \(e_i \leftarrow \chi ^{d+k+1}[x]\), and compute \(b_i = a_i \odot _{d+k+1} s+2e_i\)
-
Sample \(e' \leftarrow \chi ^{k+1}[x]\), and compute \(c_1 = \mu + u\odot _{k+1} s + 2e' \)
-
Output \(c= (c_1, (b_i)_{i \le t'})\).
-
-
Decryption: \(\mathsf {Dec}(\mathsf {sk}= (r_i)_{i\le t}, c = (c_1, (b_i)_{i\le t'})\) outputs \((c_1 - \sum _{i=1}^{t'} b_i \odot _{k+1} r_i \mod q) \mod 2\).
Lemma 12
For \(\alpha ^{-1} > (4 \omega (\log n) \sigma K+1) \) where \(K:= t(2d-1) + \gamma \tau d,\) the scheme satisfies \((1-\mathsf {negl}(n))\)-correctness.
Proof
We want to show that \(\mathsf {Dec}(\mathsf {sk}, \mathsf {Enc}(\mathsf {pk}, \mu )) = 1\) with probability \(1-\mathsf {negl}(n)\) over the randomness of \(\mathsf {KeyGen}\) and \(\mathsf {Enc}\). Consider a random key pair \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {KeyGen}(1^n)\) and ciphertext \(c= (c_1, (b_i)_{i \le t'}) \leftarrow \mathsf {Enc}(\mathsf {pk}, \mu )\). By Lemma 1 (the quasi-associative law for middle products),
Therefore, we see that
We conclude that if \(\left| \left| \mu +2(e'- \sum _{i=1}^{t'} r_i \, \odot _{k+1} \, e_i)\right| \right| _{\infty } < q/2\), then \(\mathsf {Dec}(\mathsf {sk}, c)\) will indeed output the message \(\mu .\)
To complete the proof of correctness, we want to bound the coefficients of \(\sum _{i=1}^{t'} r_i \, \odot _{k+1} \, e_i.\) The coefficient of \(x^\ell \) in \(r_i \, \odot _{k+1} \, e_i\) is
Using our discrete Gaussian tail inequality (see Lemma 3) and a union bound, we obtain the following bounds on \(||\mathbf r_i ||_{\infty }\) and \(||\mathbf e_i ||_{\infty }\):
Thus, again by union bound, except with \(\mathsf {negl}(n)\) probability
for \(K : = t(2d-1) + \gamma \tau d \ge \sum _{i=1}^{t'} (\deg (r_i)+1)\). Picking \(\alpha < (4 \omega (\log n) \sigma K+1)^{-1} \), the above is less than q/4 and so the scheme is \((1-\mathsf {negl}(n))\)-correct. \(\square \)
Theorem 6
Assume that \(\sigma = \omega (1), dt/n= \varOmega (\log n),\) q is a prime polynomial in n, \(q =\varOmega (\alpha ^{-1}n^{1/2+1/2+c})\) and \(q = \omega (\log ^{1/2} n) \sigma . \) The scheme is semantically secure assuming \(\mathsf {PLWE}_{q,D_{\alpha '\cdot q}}^{(f)}\) is hard for some polynomial f such that the constant coefficient of f is coprime with  and error \(\alpha ' = \varOmega (\sqrt{\deg (f)}/q).\)
and error \(\alpha ' = \varOmega (\sqrt{\deg (f)}/q).\)
Proof
By Theorem 3, Lemma 11 and hypothesis on \(\sigma \) and dt, we have:

Since an honestly generated public key has the form \(\mathsf {pk}= (a_1\ldots , a_{t'}, u)\) for \(u = \sum _{i=1}^t a_i \cdot r_i +\sum _{i=t+1}^{t'} a_i \cdot r_i\), we see that \(\mathsf {pk}\) is computationally indistinguishable from a public key \(\widetilde{\mathsf {pk}}\) of the form

Thus, we see that for any message \(\mu \), we have
Moreover, we have
assuming the hardness of (degree-parametrized) \(\mathsf {MPLWE}_{q, {n+2d+k}, \mathbf d ,\lfloor D_{\alpha \cdot q}\rceil }\) with degree vector
The hardness of \(\mathsf {MPLWE}_{q, {n+2d+k}, \mathbf d ,\lfloor D_{\alpha \cdot q}\rceil }\) follows from the hardness of \(\mathsf {MPLWE}_{q, {n+2d+k}, \mathbf d , D_{\alpha \cdot q}}\) via a standard reduction that maps \((a,b)\in \mathbb {Z}_q[x] \times \mathbb {R}_q[x]\) to \((a, \lceil b\rfloor ),\) where \(\lceil b\rfloor \) is the polynomial obtained by rounding every coefficient of b to the nearest integer. Finally, Theorem 2 tells us that \(\mathsf {MPLWE}_{q, {n+2d+k}, \mathbf d , D_{\alpha \cdot q}}\) is hard assuming the hardness of \(\mathsf {PLWE}_{q,D_{\alpha '\cdot q}}^{(f)}\), for \(\alpha \cdot q =\varOmega (n^{1/2+1/2+c})\ge \alpha ' \cdot q \sqrt{\frac{n+2d+k}{2}} n^c\). This completes the proof of semantic security. \(\square \)
6.2 IBE in the Random Oracle Model
We construct an IBE scheme in the random oracle model by combining our “Dual Regev” scheme (Sect. 6.1) with our MP-LWE lattice trapdoors (Sect. 5). The IBE construction is essentially identical to that of [8]; we give an explicit description for completeness. Let the set of identity be \(\mathcal {I} = \mathbb {Z}_q^{n+2d-2}.\) We assume the parameters are chosen such that Theorem 5 holds. Use algorithm \(\mathsf {TrapGen}\) to generate mpk:= \((a_i)_{i=1}^{t'}\) and msk:= \(\tilde{L}.\) Given an identity id, interpret it as an element \(u \in {\mathbb {Z}_q}^{<n+2d-2}[x]\) and use algorithm \(\mathsf {SamplePre}\) to generate \(\mathsf {sk}_{id}:=(r_i)_{i=1}^{t'}\) such that \(\sum _{i=1}^{t'} a_i \cdot r_i = u.\) Then use the Dual Regev scheme with public key \(\mathsf {pk}:=((a_i)_{i=1}^{t'}, u)\) and secret key \(\mathsf {sk}: = (r_i)_{i=1}^{t'}\) for encryption/decryption of message.
-
Setup: The setup algorithm \(\mathsf {IBESetup}\) (on input \(1^n\)) calls \(\mathsf {TrapGen}(1^n)\), obtaining polynomials \((a_1, \ldots , a_{t'})\) along with a trapdoor \(\mathsf {td}\). It outputs master public key \(\mathsf {mpk}= (a_1, \ldots , a_{t'})\) and master secret key \(\mathsf {msk}= \mathsf {td}\).
-
Key Extraction: The secret key extraction algorithm \(\mathsf {IBEExtract}\), given \(\mathsf {msk}\) and an identity \(\mathsf {id}\), calls \(\mathsf {SamplePre}(\mathsf {td}, H(\mathsf {id}))\), where \(H(\cdot )\) is modelled as a random oracle. It outputs \(\mathsf {sk}_{\mathsf {id}} = (r_1, \ldots , r_{t'})\), the output of \(\mathsf {SamplePre}\).
-
Encryption: The encryption algorithm \(\mathsf {Enc}\), given the master public key \(\mathsf {mpk}= (a_1, \ldots , a_{t'})\), an identity \(\mathsf {id}\), and a message \(\mu \), computes \(u = H(\mathsf {id})\) and outputs a ciphertext \(c \leftarrow \mathsf {DualRegev}.\mathsf {Enc}(\mathsf {pk}_{\mathsf {id}}, \mu )\) (using the Dual Regev encryption algorithm) for \(\mathsf {pk}_{\mathsf {id}} = (a_1, \ldots , a_{t'}, u)\).
-
Decryption: The decryption algorithm \(\mathsf {Dec}\), given the secret key \(\mathsf {sk}_{\mathsf {id}} = (r_1, \ldots , r_{t'})\) and a ciphertext c, outputs \(\mathsf {DualRegev}.\mathsf {Dec}(\mathsf {sk}_{\mathsf {id}}, c)\).
Theorem 7
Assume the parameters are picked as in Theorems 5 and 6 (so that the Dual Regev Scheme is correct and semantically secure). Then the above IBE scheme is correct and CPA-secure in the random oracle model.
Proof
See ([8], Theorem 7.2). \(\square \)
Remark 2
(Efficiency). Pick \(d, k = \varTheta (n), t = \log n\) and \(\sigma , \alpha ^{-1}, q\) satisfying bounds in Theorems 5 and 6. By construction, the schemes in Subsects. 6.1 and 6.2 have key size and ciphertext size \(\tilde{O}(n)\). We show that encryption and decryption algorithms in these schemes take \(\tilde{O}(n)\) time. As in [21], products and middle products of polynomials can be computed in \(\tilde{O}(n)\) time using FFT-based techniques [9, 22]. By doing some preprocessing, sampling from \(\chi = \lfloor D_{\alpha \cdot q} \rceil \) can be done in quasi-constant time via table look-up as in [15]. Thus, encryption and decryption in our Dual-Regev like public key scheme and IBE scheme take \(\tilde{O}(n)\) time; since the message is of size \(k = \varTheta (n),\) runtime per encrypted bit is \(\tilde{O}(1)\).
6.3 IBE in the Standard Model
[2, 7] present IBE schemes secure in the standard model from the same framework of lattice trapdoors and dual-Regev encryption. A simplified version of one construction is presented in [3], Sect. 3. We give a brief summary of [3]’s IBE construction, and sketch how to adapt it to the MP-LWE setting.
Suppose we have an identity space \(\{0,1\}^{\ell }.\) Set \(m = O(n \log n).\) In \(\mathsf {IBESetup}\), the [3] scheme samples a random matrix \(A \in \mathbb {Z}_q^{n\times m}\) together with trapdoor \(T_A\), as well as random matrices \(H_{i,b} \in \mathbb {Z}_q^{n\times m}\) for \(i\in [\ell ]\) and \(b \in \{0,1\}.\) The public key is \((A, (H_{i,b})_{(i,b)\in [\ell ] \times \{0,1\}}, u_0)\) where \(u_0\) is a random vector in \(\mathbb {Z}_q^n.\) The master secret key is \(T_A.\) The key extraction algorithm \(\mathsf {IBEExtract}\), given an identity \(\mathsf {id}= \mathsf {id}_1 \cdots \mathsf {id}_{\ell },\) assembles \(H_{\mathsf {id}} = H_{1,\mathsf {id}_{1}} | \cdots | H_{\ell ,\mathsf {id}_{\ell }} \in \mathbb {Z}_q^{n \times \ell m}\) as the concatenation of \(\ell \) matrices. It then samples random vectors \(r_i \in \mathbb {Z}_q^{m}\), and constructs a vector \(r = (r_i)_{i\in \ell } \in \mathbb {Z}_q^{\ell m}\). Finally, the trapdoor \(T_A\) is used to sample preimages \(e \in \mathbb {Z}_q^m\) satisfying \(A\, e = u_0 + H_{\mathsf {id}}\, r \), i.e. \(\begin{bmatrix} A&| -H_{\mathsf {id}} \end{bmatrix} \begin{bmatrix}e \\ r \end{bmatrix} = u_0\), yielding a secret key \(\mathsf {sk}_{\mathsf {id}} = (e,r)\). Encryption and Decryption then proceed as in Dual Regev encryption.
[3] proves that their scheme is selective-ID secure in the standard model. Selective-ID security is defined by a game similar to that in Sect. 2.1, except that the adversary generates the challenge identity \(\mathsf {id}^*\) before seeing the public parameters of the scheme. [2]’s proof of selective-ID security relies on replacing each random matrix \(H_{i,b}\) with an indistinguishable matrix \(H'_{i,b}\) equipped with trapdoor \(T_{i,b}.\) Then, given an extraction query \(\mathsf {id}\) that differs from the challenge \(\mathsf {id}^*\), letting i denote an index on which \(\mathsf {id}_i \ne \mathsf {id}^*_i\), the trapdoor \(T_{i,\mathsf {id}_i}\) can be used to sample \(r_i\) such that \(H'_{i,\mathsf {id}_i}\, r_i = A\, e - \sum _{j\ne i} H'_{j,\mathsf {id}_j}\, r_j - u_0,\) where e and \(r_j\) are sampled randomly from \(\mathbb {Z}_q^{m},\) to produce a secret key \(\mathsf {sk}_\mathsf {id}= (e, r)\). Crucially, sampling (e, r) using trapdoor \(T_{i, \mathsf {id}_i}\) is (statistically) indistinguishable from the honest key extraction procedure (that uses \(T_A\)).
Our MP-LWE Dual Regev encryption scheme, combined with the lattice trapdoors of Theorem 5, can be used to create a standard model IBE scheme analogous to the one just described. Specifically, we replace the matrix A and its trapdoor \(T_A\) with tuple \((a_j)_{j \le t}\) of \(t = \tilde{O}(1)\) polynomials and its trapdoor as generated by Theorem 5. We replace each matrix \(H_{i,b}\) with tuple \(\bar{h}^{(i,b)} = (h_j)_{j\le t}^{(i,b)}\) of random polynomials, and replace random vector \(u_0\) with a random polynomial. Theorem 5 allows us to replace any particular \(\bar{h}^{(i,b)}\) with \(\tilde{h}^{(i,b)}\) that is equipped with a trapdoor \(T_{i, b}\), and our \(\mathsf {SamplePre}\) algorithm guarantees the same \((T_A, T_{i,b})\) indistinguishability that was leveraged by [3].
To summarize, this allows for an IBE scheme in the standard model based on MP-LWE with efficiency gains of \(\tilde{O}(n)\) over the [3] scheme.
Notes
- 1.
The parameters are slightly simplified for exposition.
- 2.
We omit some details regarding degrees; it turns out that the middle products \(a_i\odot s\) will have a different degree from the middle product \(u\odot s\) in order to get decryption correctness.
- 3.
In fact, after introducing lattice trapdoors, our scheme will be modified so that three different degrees will be used rather than two (as it is currently written).
- 4.
Our assumptions on \(\varSigma _y\) and \(\varSigma _p\) are slightly different from those of [15]; these minor modifications are without loss of generality with respect to the application to Gaussian sampling but necessary for the proof to go through.
References
Abdalla, M., et al.: Searchable encryption revisited: consistency properties, relation to anonymous IBE, and extensions. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 205–222. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_13
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Agrawal, S., Boyen, X.: Identity-based encryption from lattices in the standard model (2009)
Bai, S., Langlois, A., Lepoint, T., Stehlé, D., Steinfeld, R.: Improved security proofs in lattice-based cryptography: using the Rényi divergence rather than the statistical distance. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 3–24. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_1
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: Proceedings 38th Annual Symposium on Foundations of Computer Science, pp. 394–403. IEEE (1997)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13. http://dl.acm.org/citation.cfm?id=646766.704155
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_27
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, pp. 197–206. ACM (2008)
Hanrot, G., Quercia, M., Zimmermann, P.: The middle product algorithm I. Appl. Algebra Eng. Commun. Comput. 14(6), 415–438 (2004)
Impagliazzo, R., Zuckerman, D.: How to recycle random bits. In: 30th Annual Symposium on Foundations of Computer Science, pp. 248–253. IEEE (1989)
Lyubashevsky, V.: Digital signatures based on the hardness of ideal lattice problems in all rings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 196–214. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_7
Lyubashevsky, V., Micciancio, D.: Generalized compact knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_13
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Micciancio, D.: Generalized compact knapsacks, cyclic lattices, and efficient one-way functions from worst-case complexity assumptions. In: Proceedings of the 43rd Symposium on Foundations of Computer Science, FOCS 2002, pp. 356–365. IEEE Computer Society, Washington, DC, USA (2002). http://dl.acm.org/citation.cfm?id=645413.652130
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on Gaussian measures. SIAM J. Comput. 37(1), 267–302 (2007)
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of ring-LWE for any ring and modulus. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, pp. 461–473. ACM (2017)
Peikert, C., Rosen, A.: Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 145–166. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_8
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, pp. 84–93. ACM (2005)
Roşca, M., Sakzad, A., Stehlé, D., Steinfeld, R.: Middle-product learning with errors. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 283–297. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_10
Shoup, V.: Efficient computation of minimal polynomials in algebraic extensions of finite fields. In: Proceedings of the 1999 International Symposium on Symbolic and Algebraic Computation, Vancouver, BC (1999). Citeseer
Stehlé, D., Steinfeld, R., Tanaka, K., Xagawa, K.: Efficient public key encryption based on ideal lattices. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 617–635. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_36
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
We describe a minor correction to the proof of ([15], Theorem 5.5).
In [15], it is mistakenly claimed (see Sect. 2.1) that for positive semi-definite \(B\ge A \ge 0\), the inequality \(A^{+} \ge B^{+}\) holds. This is not true in general. For example, when B is positive definite (that is, \(B> 0\)), we have \(B^{+} = B^{-1} > 0;\) if \(A^{+} \ge B^{+} \) then \(A^{+} > 0\) so \(A> 0\) (a contradiction if A is not invertible).
However, the proof of ([15], Theorem 5.5) can be modified to avoid using the mistaken claim. The relevant setting is as follows: consider a matrix of the form
such that \(\varSigma _y = 2\begin{bmatrix} R \\ I\end{bmatrix} \begin{bmatrix} R^T&I\end{bmatrix}\) and \(\varSigma _p > 2\begin{bmatrix} R \\ I\end{bmatrix} \begin{bmatrix} R^T&I\end{bmatrix} \).Footnote 4 We want to prove that \(\varSigma _3 \ge \begin{bmatrix} R \\ I\end{bmatrix} \begin{bmatrix} R^T&I\end{bmatrix} \) (see p. 29)
To prove this, we write \(2 \begin{bmatrix} R \\ I\end{bmatrix} \begin{bmatrix} R^T&I\end{bmatrix} = Q \begin{bmatrix} D &{} 0 \\ 0 &{} 0\end{bmatrix} Q^T \) where Q is orthogonal and D is diagonal matrix of positive entries. Then, there exists some small \(\epsilon > 0\) s.t. \(\varSigma _p \ge Q \begin{bmatrix} D &{} 0 \\ 0 &{} \epsilon I\end{bmatrix} Q^T > 0.\) Thus,
and so
We conclude that
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Lombardi, A., Vaikuntanathan, V., Vuong, T.D. (2019). Lattice Trapdoors and IBE from Middle-Product LWE. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11891. Springer, Cham. https://doi.org/10.1007/978-3-030-36030-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-36030-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36029-0
Online ISBN: 978-3-030-36030-6
eBook Packages: Computer ScienceComputer Science (R0)


 and
and  for some distribution
for some distribution 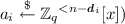 and sample
and sample  and
and  and
and 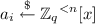 ,
,  ,
,