Abstract
Encryption is an indispensable tool for securing digital infra-structures as it reduces the problem of protecting the data to just protecting decryption keys. Unfortunately, this also makes it easier for users to share protected data by simply sharing decryption keys.
Kiayias and Tang (ACM CCS 2013) were the first to address this important issue pre-emptively rather than a posteriori like traitor tracing schemes do. They proposed leakage-deterring encryption schemes that work as follows. For each user, a piece of secret information valuable to her is embedded into her public key. As long as she does not share her ability to decrypt with someone else, her secret is safe. As soon as she does, her secret is revealed to her beneficiaries. However, their solution suffers from serious drawbacks: (1) their model requires a fully-trusted registration authority that is privy to user secrets; (2) it only captures a CPA-type of privacy for user secrets, which is a very weak guarantee; (3) in their construction which turns any public-key encryption scheme into a leakage-deterring one, the new public keys consist of linearly (in the bit-size of the secrets) many public keys of the original scheme, and the ciphertexts are large.
In this paper, we redefine leakage-deterring schemes. We remove the trust in the authority and guarantee full protection of user secrets under CCA attacks. Furthermore, in our construction, all keys and ciphertexts are short and constant in the size of the secrets. We achieve this by taking a different approach: we require users to periodically refresh their secret keys by running a protocol with a third party. Users do so anonymously, which ensures that they cannot be linked, and that the third party cannot perform selective failure attacks. We then leverage this refresh protocol to allow for the retrieval of user secrets in case they share their decryption capabilities. This refresh protocol also allows for the revocation of user keys and for the protection of user secrets in case of loss or theft of a decryption device. We provide security definitions for our new model as well as efficient instantiations that we prove secure.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Of course, if adversaries were to know the randomness used by security-game oracles, the outputs of those would be deterministic in the view of the adversaries, and even simple properties like IND-CPA would not be satisfiable.
- 2.
If time periods are short, then any useful device should be able to do so.
- 3.
\(\oplus \) here denotes the traditional XOR operation.
References
Au, M.H., Susilo, W., Mu, Y.: Constant-size dynamic \(k\)-TAA. Cryptology ePrint Archive, Report 2008/136 (2008). http://eprint.iacr.org/2008/136
Backes, M., Müller-Quade, J., Unruh, D.: On the necessity of rewinding in secure multiparty computation. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 157–173. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_9
Baldimtsi, F., et al.: Accumulators with applications to anonymity-preserving revocation. In: EuroS&P (2017)
Barak, B.: How to go beyond the black-box simulation barrier. In: 42nd FOCS, pp. 106–115. IEEE Computer Society Press, October 2001
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptol. 21(2), 149–177 (2008)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Boneh, D., Franklin, M.: An efficient public key traitor tracing scheme. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 338–353. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_22
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_34
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_27
Camenisch, J., Drijvers, M., Lehmann, A.: Anonymous attestation using the strong Diffie Hellman assumption revisited. Cryptology ePrint Archive, Report 2016/663 (2016). http://eprint.iacr.org/2016/663
Camenisch, J., Krenn, S., Lehmann, A., Mikkelsen, G.L., Neven, G., Pedersen, M.Ø.: Formal treatment of privacy-enhancing credential systems. In: Dunkelman, O., Keliher, L. (eds.) SAC 2015. LNCS, vol. 9566, pp. 3–24. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31301-6_1
Camenisch, J., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_8
Chor, B., Fiat, A., Naor, M.: Tracing traitors. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 257–270. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_25
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055717
Dwork, C., Lotspiech, J.B., Naor, M.: Digital signets: self-enforcing protection of digital information (preliminary version). In: 28th ACM STOC, pp. 489–498. ACM Press, May 1996
Guruswami, V., Indyk, P.: Expander-based constructions of efficiently decodable codes. In: 42nd FOCS, pp. 658–667. IEEE Computer Society Press, October 2001
Kiayias, A., Tang, Q.: How to keep a secret: leakage deterring public-key cryptosystems. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 943–954. ACM Press, New York (2013)
Kiayias, A., Tang, Q.: Traitor deterring schemes: using bitcoin as collateral for digital content. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, pp. 231–242. ACM Press, New York (2015)
Kiayias, A., Yung, M.: Traitor tracing with constant transmission rate. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 450–465. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_30
Kurosawa, K., Desmedt, Y.: Optimum traitor tracing and asymmetric schemes. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 145–157. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054123
Lewko, A.: Tools for simulating features of composite order bilinear groups in the prime order setting. Cryptology ePrint Archive, Report 2011/490 (2011). http://eprint.iacr.org/2011/490
Nakanishi, T., Fujii, H., Hira, Y., Funabiki, N.: Revocable group signature schemes with constant costs for signing and verifying. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 463–480. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_26
Nishimaki, R., Wichs, D., Zhandry, M.: Anonymous traitor tracing: how to embed arbitrary information in a key. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 388–419. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_14
Okamoto, T., Takashima, K.: Homomorphic encryption and signatures from vector decomposition. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 57–74. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85538-5_4
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Acknowledgements
This work supported by the ERC Grant PERCY #321310, and was done while the first two authors were at IBM Research – Zurich.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Preliminaries
A Preliminaries
We here give the hardness assumptions and instantiations of the building blocks on which our constructions rely.
1.1 A.1 Pairing Groups and Hardness Assumptions
This section introduces pairing groups and classical hardness assumptions underlying our constructions.
Asymmetric Bilinear Pairing Groups. An asymmetric bilinear pairing group (or simply pairing group) consists of a tuple  such that p is a prime number, \(\mathbb {G}_1, \mathbb {G}_2\) and \(\mathbb {G}_T\) are (cyclic) p-order groups, and \(e :\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficiently-computable non-degenerate bilinear map (also called pairing), i.e., \(e(P_1, P_2) \ne 1_{\mathbb {G}_T}\), and \(\forall a, b \in \mathbb {Z}_p, e(P_1^a, P_2^b) = e(P_1, P_2)^{ab}\). Let
such that p is a prime number, \(\mathbb {G}_1, \mathbb {G}_2\) and \(\mathbb {G}_T\) are (cyclic) p-order groups, and \(e :\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficiently-computable non-degenerate bilinear map (also called pairing), i.e., \(e(P_1, P_2) \ne 1_{\mathbb {G}_T}\), and \(\forall a, b \in \mathbb {Z}_p, e(P_1^a, P_2^b) = e(P_1, P_2)^{ab}\). Let  denote an algorithm that takes as an input a security parameter \( 1^{ \lambda }\), and outputs the description
denote an algorithm that takes as an input a security parameter \( 1^{ \lambda }\), and outputs the description  of a pairing group.
of a pairing group.
\({\varvec{q}}\)-Strong Diffie–Hellman Assumption. Let  and
and  be two p-order groups. The q-Strong Diffie–Hellman (qSDH) problem [5] in \((\mathbb {G}_1, \mathbb {G}_2)\) consists in computing a pair \(\left( y, P_1^{1/(u + y)} \right) \in \mathbb {Z}_p\backslash {\{-u\}} \times \mathbb {G}_1\) given a \((p+3)\)-tuple \((P_1, P_1^u, P_1^{u^2}, \ldots , P_1^{u^q}, P_2, P_2^u) \in \mathbb {G}_1^{p+1} \times \mathbb {G}_2^2.\) The qSDH assumption over \((\mathbb {G}_1, \mathbb {G}_2)\) is that no efficient algorithm has a non-negligible probability to solve the qSDH problem in \((\mathbb {G}_1,\mathbb {G}_2)\).
be two p-order groups. The q-Strong Diffie–Hellman (qSDH) problem [5] in \((\mathbb {G}_1, \mathbb {G}_2)\) consists in computing a pair \(\left( y, P_1^{1/(u + y)} \right) \in \mathbb {Z}_p\backslash {\{-u\}} \times \mathbb {G}_1\) given a \((p+3)\)-tuple \((P_1, P_1^u, P_1^{u^2}, \ldots , P_1^{u^q}, P_2, P_2^u) \in \mathbb {G}_1^{p+1} \times \mathbb {G}_2^2.\) The qSDH assumption over \((\mathbb {G}_1, \mathbb {G}_2)\) is that no efficient algorithm has a non-negligible probability to solve the qSDH problem in \((\mathbb {G}_1,\mathbb {G}_2)\).
Decisional Linear Assumption. The (2-)Decisional Linear (DLIN) assumption [6] over a p-order group  is that, for \(a, b, x, y, z \in _R \mathbb {Z}_p\), the distributions of \((P, P^a, P^b, P^{ax}, P^{by}, P^{x+y})\) and \((P, P^a, P^b, P^{ax}, P^{by}, P^z)\) are computationally indistinguishable.
is that, for \(a, b, x, y, z \in _R \mathbb {Z}_p\), the distributions of \((P, P^a, P^b, P^{ax}, P^{by}, P^{x+y})\) and \((P, P^a, P^b, P^{ax}, P^{by}, P^z)\) are computationally indistinguishable.
1.2 A.2 BBS+ Signature Scheme
The BBS+ signature scheme (as described by Au et al. [1] and inspired by a group signature [6] introduced by Boneh et al.) is a tuple of algorithms \((\mathsf {SignSetup}, \mathsf {SignKeyGen}, \mathsf {Sign}, \mathsf {Verify})\) with
-
 output
output  the description of a pairing group
the description of a pairing group  calling on
calling on 
-
 generate \(H_0, \ldots , H_n \in _R \mathbb {G}_1, u \in _R \mathbb {Z}_p\), computes \(U = P_2^u\), and output \({ sk}= u, vk = (U, H_0, \ldots , H_n)\)
generate \(H_0, \ldots , H_n \in _R \mathbb {G}_1, u \in _R \mathbb {Z}_p\), computes \(U = P_2^u\), and output \({ sk}= u, vk = (U, H_0, \ldots , H_n)\) -
\(\mathsf {Sign}({ sk}, \mathbf {m} \in \mathbb {Z}_p^n) \rightarrow \sigma :\) generate \(y, z \in _R \mathbb {Z}_p\), compute \(V = P_1 H_0^z \prod _{i \ge 1} H_i^{m_i}\) and \(W = V^{1/(u + y)}\), and outputs \(\sigma = (W, y, z)\)
-
\(\mathsf {Verify}( vk , \mathbf {m}, \sigma ) \rightarrow b \in \{0, 1\}:\) output 1 if \(\mathbf {m} \in \mathbb {Z}_p^n\), \(\sigma \) can be parsed as (W, y, z) and \(e(W, U P_2^y) = e\left( P_1 H_0^z \prod _{i \ge 1} H_i^{m_i}, P_2\right) \), and otherwise 0.
Camenisch et al. [10, Lemma 1] proved that the BBS+ signature scheme is existentially unforgeable against chosen-message attacks under the qSDH assumption over \((\mathbb {G}_1, \mathbb {G}_2)\). They showed [10, Section 4.5] how to prove knowledge of a BBS+ signature. We recall it in the full version.
1.3 A.3 Dual Pairing Vector Spaces
Dual Pairing Vector Spaces (DPVSs) were introduced by Okamoto and Takashima [24]. They provide a mechanism for parameter hiding [21] in prime-order pairing groups. The latter feature allows to proves the full security of functional encryption schemes in prime-order settings.
Definition 6 (Dual Pairing Vector Space)
Let \(N \ge 1\) be an integer. A dual pairing vector space by direct product of a pairing group  is a tuple \((p, \mathbb {V}, \mathbb {V}^*, \mathbb {G}_T, \mathbb {A}, \mathbb {A}^*, e)\) such that \(\mathbb {V}= \mathbb {G}_1^N\) and \(\mathbb {V}^* = \mathbb {G}_2^N\) are two N-dimensional \(\mathbb {Z}_p\) vector spaces, \(\mathbb {A}= (\mathbf {a}_1, \ldots , \mathbf {a}_N)\) is the canonical basis of \(\mathbb {V}\) (i.e., \(\mathbf {a}_i = (\mathbf {1}_{\mathbb {G}_1^{i-1}}, P_1, \mathbf {1}_{\mathbb {G}_1^{N-i}})\)), \(\mathbb {A}^* = (\mathbf {a}_1^*, \ldots , \mathbf {a}_N^*)\) is the canonical basis of \(\mathbb {V}^*\) (i.e., \(\mathbf {a}_i^* = (\mathbf {1}_{\mathbb {G}_2^{i-1}}, P_2, \mathbf {1}_{\mathbb {G}_2^{N-i}})\)) and
is a tuple \((p, \mathbb {V}, \mathbb {V}^*, \mathbb {G}_T, \mathbb {A}, \mathbb {A}^*, e)\) such that \(\mathbb {V}= \mathbb {G}_1^N\) and \(\mathbb {V}^* = \mathbb {G}_2^N\) are two N-dimensional \(\mathbb {Z}_p\) vector spaces, \(\mathbb {A}= (\mathbf {a}_1, \ldots , \mathbf {a}_N)\) is the canonical basis of \(\mathbb {V}\) (i.e., \(\mathbf {a}_i = (\mathbf {1}_{\mathbb {G}_1^{i-1}}, P_1, \mathbf {1}_{\mathbb {G}_1^{N-i}})\)), \(\mathbb {A}^* = (\mathbf {a}_1^*, \ldots , \mathbf {a}_N^*)\) is the canonical basis of \(\mathbb {V}^*\) (i.e., \(\mathbf {a}_i^* = (\mathbf {1}_{\mathbb {G}_2^{i-1}}, P_2, \mathbf {1}_{\mathbb {G}_2^{N-i}})\)) and
(note the abuse of notation) is a pairing, i.e., \(\mathbf {x} = \mathbf {1 }_{\mathbb {G}_1^N}\) if \(e(\mathbf {x},\cdot )\) is the \(1_{\mathbb {G}_T}\) map, and \(\forall a, b \in \mathbb {Z}_p, \mathbf {x} \in \mathbb {V}, \mathbf {y} \in \mathbb {V}^*, e(\mathbf {x}^a, \mathbf {y}^b) = e(\mathbf {x}, \mathbf {y})^{ab}\).
Note that for all \(1 \le i, j \le N, e(\mathbf {a}_i, \mathbf {a}_j^*) = e(P_1, P_2)^{\delta _{ij}}\), with \(\delta _{ij}\) being the Kronecker delta, i.e., \(\delta _{ij} = 1\) if \(i = j\), and otherwise 0.
Let  denote an algorithm that takes as an input a security parameter \( 1^{ \lambda }\), the description
denote an algorithm that takes as an input a security parameter \( 1^{ \lambda }\), the description  of a pairing group
of a pairing group  and an integer N, and outputs the description
and an integer N, and outputs the description  of a DPVS \((p, \mathbb {V}, \mathbb {V}^*, \mathbb {G}_T, \mathbb {A}, \mathbb {A}^*, e)\).
of a DPVS \((p, \mathbb {V}, \mathbb {V}^*, \mathbb {G}_T, \mathbb {A}, \mathbb {A}^*, e)\).
1.4 A.4 Okamoto–Takashima Adaptively-Secure CP-ABE Scheme
Let  be a dual-orthonormal-basis generator which proceeds as follows:
be a dual-orthonormal-basis generator which proceeds as follows:
-
1.
it generates a pairing group
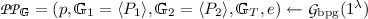 , a value \(\psi \in _R \mathbb {Z}_p^*\), and sets \(N_0 = 5\) and \(N_k = 3 n_k + 1\) for \(1 \le k \le d\)
, a value \(\psi \in _R \mathbb {Z}_p^*\), and sets \(N_0 = 5\) and \(N_k = 3 n_k + 1\) for \(1 \le k \le d\) -
2.
for \(0 \le k \le d\), it generates a Dual Pairing Vector Space (DPVS) (see Appendix A.3)
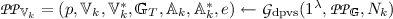 , generates a matrix \(\mathbf {X}_k \in _R \mathrm {GL}_{N_k}(\mathbb {Z}_p)\), and computes \(\mathbf {V}_k = \psi \left( \mathbf {X}_k^\mathrm {T} \right) ^{-1}\). Let \(\mathbf {M}_{\mathbb {A}_k}\) and \(\mathbf {M}_{\mathbb {A}_k^*}\) respectively denote the diagonal matrices \( {{\text {diag}}(P_1)} \in \mathbb {G}_1^{N_k \times N_k}\) and \( {{\text {diag}}(P_2)} \in \mathbb {G}_2^{N_k \times N_k}\). Generator
, generates a matrix \(\mathbf {X}_k \in _R \mathrm {GL}_{N_k}(\mathbb {Z}_p)\), and computes \(\mathbf {V}_k = \psi \left( \mathbf {X}_k^\mathrm {T} \right) ^{-1}\). Let \(\mathbf {M}_{\mathbb {A}_k}\) and \(\mathbf {M}_{\mathbb {A}_k^*}\) respectively denote the diagonal matrices \( {{\text {diag}}(P_1)} \in \mathbb {G}_1^{N_k \times N_k}\) and \( {{\text {diag}}(P_2)} \in \mathbb {G}_2^{N_k \times N_k}\). Generator  computes \(\mathbf {B}_k = \begin{bmatrix} \mathbf {b}_{k,1} \\ \vdots \\ \mathbf {b}_{k,n} \end{bmatrix} = \mathbf {X}_k \mathbf {M}_{\mathbb {A}_k} \in \mathbb {G}_1^{N_k \times N_k}\) and \(\mathbf {B}_k^* = \begin{bmatrix} \mathbf {b}_{k,1}^*\\ \vdots \\ \mathbf {b}_{k,n}^* \end{bmatrix} = \mathbf {V}_k \mathbf {M}_{\mathbb {A}_k^*} \in \mathbb {G}_2^{N_k \times N_k}\) with \(\mathbf {b}_{k,i} = \left( \mathbf {e}_i \cdot \mathbf {X}_k\right) \mathbf {M}_{\mathbb {A}_k} = \begin{bmatrix} P_1^{\mathbf {X}_{k,i,1}}&\cdots&P_1^{\mathbf {X}_{k,i,N_k}} \end{bmatrix}\) and \(\mathbf {b}_{k,i}^* = \left( \mathbf {e}_i \cdot \mathbf {V}_k\right) \mathbf {M}_{\mathbb {A}_k^*} = \begin{bmatrix} P_2^{\mathbf {V}_{k,i,1}}&\cdots&P_2^{\mathbf {V}_{k,i,N_k}} \end{bmatrix}\)
computes \(\mathbf {B}_k = \begin{bmatrix} \mathbf {b}_{k,1} \\ \vdots \\ \mathbf {b}_{k,n} \end{bmatrix} = \mathbf {X}_k \mathbf {M}_{\mathbb {A}_k} \in \mathbb {G}_1^{N_k \times N_k}\) and \(\mathbf {B}_k^* = \begin{bmatrix} \mathbf {b}_{k,1}^*\\ \vdots \\ \mathbf {b}_{k,n}^* \end{bmatrix} = \mathbf {V}_k \mathbf {M}_{\mathbb {A}_k^*} \in \mathbb {G}_2^{N_k \times N_k}\) with \(\mathbf {b}_{k,i} = \left( \mathbf {e}_i \cdot \mathbf {X}_k\right) \mathbf {M}_{\mathbb {A}_k} = \begin{bmatrix} P_1^{\mathbf {X}_{k,i,1}}&\cdots&P_1^{\mathbf {X}_{k,i,N_k}} \end{bmatrix}\) and \(\mathbf {b}_{k,i}^* = \left( \mathbf {e}_i \cdot \mathbf {V}_k\right) \mathbf {M}_{\mathbb {A}_k^*} = \begin{bmatrix} P_2^{\mathbf {V}_{k,i,1}}&\cdots&P_2^{\mathbf {V}_{k,i,N_k}} \end{bmatrix}\) -
3.
it computes \(G_T = e(P_1, P_2)^{\psi }\), sets
 , and eventually outputs
, and eventually outputs 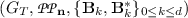 .
.
Notice that for all \(i, k, G_T = e(\mathbf {b}_{k,i}, \mathbf {b}_{k, i}^*)\). Indeed,
Consider now the (monotone-span-program) Okamato–Takashima CP-ABE scheme [25, Section 7.1] in the case \(d = 2\). The access structure associated to a ciphertext is determined by two 2-dimensional vectors \(\mathbf {v}_1\) and \(\mathbf {v}_2\). A pair of attributes (a pair of \(\mathbb {Z}_p\)-lines) represented by a pair of vectors \((\mathbf {x}_1, \mathbf {x}_2)\) is “accepted” by the structure if and only if \(\mathbf {x}_k \cdot \mathbf {v}_k^\mathrm {T} = 0\): that is, the structure specifies two accepted \(\mathbb {Z}_p\)-lines. Their CP-ABE scheme is defined as follows:
-
\(\mathsf {Setup}( 1^{ \lambda }, \mathbf {n} = (2; n_1 = 2, n_2 = 2)) \rightarrow ({ pk}, msk ):\) generate an orthonormal basis
 , set \(\hat{\mathbf {B}}_0 = \begin{bmatrix} \mathbf {b}_{0, 1}\\ \mathbf {b}_{0, 3}\\ \mathbf {b}_{0, 5} \end{bmatrix}, \hat{\mathbf {B}}_0^* = \begin{bmatrix} \mathbf {b}_{0, 1}^*\\ \mathbf {b}_{0, 3}^*\\ \mathbf {b}_{0, 4}^* \end{bmatrix}\), \(\hat{\mathbf {B}}_k = \begin{bmatrix} \mathbf {b}_{k, 1}\\ \mathbf {b}_{k, 2}\\ \mathbf {b}_{k, 7} \end{bmatrix}, \hat{\mathbf {B}}_k^* = \begin{bmatrix} \mathbf {b}_{k, 1}^*\\ \mathbf {b}_{k, 2}^*\\ \mathbf {b}_{k, 5}^*\\ \mathbf {b}_{k, 6}^* \end{bmatrix}\) for \(k = 1, 2\), and then output
, set \(\hat{\mathbf {B}}_0 = \begin{bmatrix} \mathbf {b}_{0, 1}\\ \mathbf {b}_{0, 3}\\ \mathbf {b}_{0, 5} \end{bmatrix}, \hat{\mathbf {B}}_0^* = \begin{bmatrix} \mathbf {b}_{0, 1}^*\\ \mathbf {b}_{0, 3}^*\\ \mathbf {b}_{0, 4}^* \end{bmatrix}\), \(\hat{\mathbf {B}}_k = \begin{bmatrix} \mathbf {b}_{k, 1}\\ \mathbf {b}_{k, 2}\\ \mathbf {b}_{k, 7} \end{bmatrix}, \hat{\mathbf {B}}_k^* = \begin{bmatrix} \mathbf {b}_{k, 1}^*\\ \mathbf {b}_{k, 2}^*\\ \mathbf {b}_{k, 5}^*\\ \mathbf {b}_{k, 6}^* \end{bmatrix}\) for \(k = 1, 2\), and then output 
-
\( \mathsf {KeyDer}( msk , \mathcal {A}= \{\mathbf {x}_{k = 1, 2} \in \mathbb {Z}_p^2 :\mathbf {x}_{k, 1} = 1\}) \rightarrow { sk}_{\mathcal {A}}:\) generate \(\alpha , y_0 \in _R \mathbb {Z}_p,\) \(\mathbf {y}_k \in _R \mathbb {Z}_p^2\) for \(k = 1, 2\), compute vectors \(\mathbf {k}_0^* = \begin{bmatrix} \alpha&0&1&y_0&0 \end{bmatrix} \mathbf {B}_0^* = \begin{bmatrix} \alpha&1&y_0 \end{bmatrix} \hat{\mathbf {B}}_0^* \), \(\mathbf {k}_k^* = \begin{bmatrix} \alpha \mathbf {x}_k&\mathbf {0}_{\mathbb {Z}_p^2}&\mathbf {y}_k&0 \end{bmatrix} \mathbf {B}_k^* = \begin{bmatrix} \alpha \mathbf {x}_k&\mathbf {y}_k \end{bmatrix} \hat{\mathbf {B}}_k^* \), and output secret key \({ sk}_{\mathcal {A}}= ({ pk}, \mathcal {A},\{\mathbf {k}_k^*\}_{k = 0, \ldots , 2})\)
-
\(\mathsf {Enc}({ pk}, M \in \mathbb {G}_T, \mathbb {S}= (\mathbf {v}_1, \mathbf {v}_2)) \rightarrow { ct}:\) generate uniformly random values \(a_1, a_2, \zeta ,\eta _0, \eta _k, \theta _k\) for \(k = 1, 2\) from \(\mathbb {Z}_p\), computes \(a = a_1 + a_2\),
$$\begin{aligned} \mathbf {c}_0&= \begin{bmatrix} -a&0&\zeta&0&\eta _0 \end{bmatrix} \mathbf {B}_0 = \begin{bmatrix} -a&\zeta&\eta _0 \end{bmatrix} \hat{\mathbf {B}}_0,\\ \mathbf {c}_k&= \begin{bmatrix} a_k \mathbf {e}_{k, 1} + \theta _k \mathbf {v}_k&\mathbf {0}_{\mathbb {Z}_p^4}&\eta _1 \end{bmatrix} \mathbf {B}_k = \begin{bmatrix} a_k \mathbf {e}_{k, 1} + \theta _k \mathbf {v}_k&\eta _1 \end{bmatrix} \hat{\mathbf {B}}_k \quad \text {for } k = 1, 2,\\ c_3&= G_T^{\zeta } M, \end{aligned}$$and output \({ ct}= (\mathbb {S}, \mathbf {c}_0, \mathbf {c}_1, \mathbf {c}_2, c_3) \in \mathbb {Z}_p^4 \times \mathbb {G}_1^{19} \times \mathbb {G}_T\) and
-
\(\mathsf {Dec}({ sk}_{\mathcal {A}}, { ct}) \rightarrow M:\) output \(M = c_3/e(\mathbf {c}_0, \mathbf {k}_0^*) e(\mathbf {c}_1, \mathbf {k}_1^*) e(\mathbf {c}_2, \mathbf {k}_2^*)\) if the key and the ciphertext can be properly parsed and \(\mathbf {x}_k \cdot \mathbf {v}_k^\mathrm {T} = 0 \mod p\) for \(k = 1,2\), and otherwise output \(\bot \).
Since attribute vectors have their first coordinates set to 1, (the second coordinates specify the slopes of the \(\mathbb {Z}_p\)-lines accepted by the access structure), the attribute set may be identified with \(\mathbb {Z}_p^2\). Okamoto and Takashima proved that this CP-ABE scheme is correct and adaptively payload-hiding against chosen-message attacks under the DLIN assumption over \(\mathbb {G}_1\) and \(\mathbb {G}_2\) [25, Theorem 2].
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Camenisch, J., Dubovitskaya, M., Towa, P. (2019). Efficient Fully Secure Leakage-Deterring Encryption. In: Albrecht, M. (eds) Cryptography and Coding. IMACC 2019. Lecture Notes in Computer Science(), vol 11929. Springer, Cham. https://doi.org/10.1007/978-3-030-35199-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-35199-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-35198-4
Online ISBN: 978-3-030-35199-1
eBook Packages: Computer ScienceComputer Science (R0)


 output
output  the description of a pairing group
the description of a pairing group  calling on
calling on 
 generate
generate 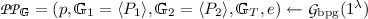 , a value
, a value 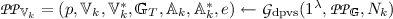 , generates a matrix
, generates a matrix  computes
computes  , and eventually outputs
, and eventually outputs 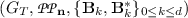 .
. , set
, set 