Abstract
We propose a Forward-Backward Truncated-Newton method (FBTN) for minimizing the sum of two convex functions, one of which smooth. Unlike other proximal Newton methods, our approach does not involve the employment of variable metrics, but is rather based on a reformulation of the original problem as the unconstrained minimization of a continuously differentiable function, the forward-backward envelope (FBE). We introduce a generalized Hessian for the FBE that symmetrizes the generalized Jacobian of the nonlinear system of equations representing the optimality conditions for the problem. This enables the employment of conjugate gradient method (CG) for efficiently solving the resulting (regularized) linear systems, which can be done inexactly. The employment of CG prevents the computation of full (generalized) Jacobians, as it requires only (generalized) directional derivatives. The resulting algorithm is globally (subsequentially) convergent, Q-linearly under an error bound condition, and up to Q-superlinearly and Q-quadratically under regularity assumptions at the possibly non-isolated limit point.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Due to apparent similarities with gradient descent iterations, having
 in FBS,
in FBS,  is also referred to as (generalized) gradient mapping, see, e.g., [17]. In particular, if g = 0, then
is also referred to as (generalized) gradient mapping, see, e.g., [17]. In particular, if g = 0, then  whereas if f = 0 then
whereas if f = 0 then  . The analogy will be supported by further evidence in the next section where we will see that, up to a change of metric, indeed
. The analogy will be supported by further evidence in the next section where we will see that, up to a change of metric, indeed  is the gradient of the forward-backward envelope function.
is the gradient of the forward-backward envelope function. - 2.
As detailed in the proof, under the assumptions the limit point indeed exists.
- 3.
From the chain rule of differentiation it follows that
 is strictly differentiable at x
⋆ if \(\operatorname {prox}_{\gamma g}\) is strictly differentiable at
is strictly differentiable at x
⋆ if \(\operatorname {prox}_{\gamma g}\) is strictly differentiable at 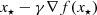 (strict differentiability is closed under composition).
(strict differentiability is closed under composition). - 4.
In case of complex-valued matrices, functions of this form are known as unitarily invariant [34].
- 5.
Consistently with the definition in [66], the polyhedron P can equivalently be expressed by means of only inequalities as
 , resulting indeed in
, resulting indeed in  .
.
References
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Mathematical Programming 137(1), 91–129 (2013). DOI 10.1007/s10107-011-0484-9
Bauschke, H.H., Combettes, P.L.: Convex analysis and monotone operator theory in Hilbert spaces. CMS Books in Mathematics. Springer (2017). DOI 10.1007/978-3-319-48311-5
Bauschke, H.H., Noll, D., Phan, H.M.: Linear and strong convergence of algorithms involving averaged nonexpansive operators. Journal of Mathematical Analysis and Applications 421(1), 1–20 (2015)
Beck, A.: First-Order Methods in Optimization. Society for Industrial and Applied Mathematics, Philadelphia, PA (2017). DOI 10.1137/1.9781611974997
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences 2(1), 183–202 (2009). DOI 10.1137/080716542
Becker, S., Fadili, J.: A quasi-Newton proximal splitting method. In: Advances in Neural Information Processing Systems, pp. 2618–2626 (2012)
Bertsekas, D.P.: Constrained optimization and lagrange multiplier methods. Computer Science and Applied Mathematics, Boston: Academic Press, 1982 (1982)
Bertsekas, D.P.: Convex Optimization Algorithms. Athena Scientific (2015)
Bhatia, R.: Matrix Analysis. Graduate Texts in Mathematics. Springer New York (1997)
Bochnak, J., Coste, M., Roy, M.F.: Real Algebraic Geometry. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics. Springer Berlin Heidelberg (2013)
Bolte, J., Daniilidis, A., Lewis, A.: Tame functions are semismooth. Mathematical Programming 117(1), 5–19 (2009). DOI 10.1007/s10107-007-0166-9
Chen, G., Teboulle, M.: Convergence analysis of a proximal-like minimization algorithm using Bregman functions. SIAM Journal on Optimization 3(3), 538–543 (1993). DOI 10.1137/0803026
Chen, X., Fukushima, M.: Proximal quasi-Newton methods for nondifferentiable convex optimization. Mathematical Programming 85(2), 313–334 (1999). DOI 10.1007/s101070050059
Chen, X., Qi, H., Tseng, P.: Analysis of nonsmooth symmetric-matrix-valued functions with applications to semidefinite complementarity problems. SIAM Journal on Optimization 13(4), 960–985 (2003). DOI 10.1137/S1052623400380584
Clarke, F.H.: Optimization and Nonsmooth Analysis. Society for Industrial and Applied Mathematics (1990). DOI 10.1137/1.9781611971309
Combettes, P.L., Pesquet, J.C.: Proximal Splitting Methods in Signal Processing, pp. 185–212. Springer New York, New York, NY (2011). DOI 10.1007/978-1-4419-9569-8_10
Drusvyatskiy, D., Lewis, A.S.: Error bounds, quadratic growth, and linear convergence of proximal methods. Mathematics of Operations Research (2018)
Eldén, L.: Matrix Methods in Data Mining and Pattern Recognition. Society for Industrial and Applied Mathematics (2007). DOI 10.1137/1.9780898718867
Facchinei, F., Pang, J.S.: Finite-dimensional variational inequalities and complementarity problems, vol. II. Springer (2003)
Fazel, M.: Matrix rank minimization with applications. Ph.D. thesis, Stanford University (2002)
Fazel, M., Hindi, H., Boyd, S.P.: A rank minimization heuristic with application to minimum order system approximation. In: Proceedings of the 2001 American Control Conference, vol. 6, pp. 4734–4739 (2001). DOI 10.1109/ACC.2001.945730
Fazel, M., Hindi, H., Boyd, S.P.: Rank minimization and applications in system theory. In: Proceedings of the 2004 American Control Conference, vol. 4, pp. 3273–3278 vol.4 (2004). DOI 10.23919/ACC.2004.1384521
Fukushima, M.: Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems. Mathematical Programming 53(1), 99–110 (1992). DOI 10.1007/BF01585696
Giselsson, P., Fält, M.: Envelope functions: Unifications and further properties. Journal of Optimization Theory and Applications (2018). DOI 10.1007/s10957-018-1328-z
Gowda, M.S.: Inverse and implicit function theorems for H-differentiable and semismooth functions. Optimization Methods and Software 19(5), 443–461 (2004). DOI 10.1080/10556780410001697668
Güler, O.: New proximal point algorithms for convex minimization. SIAM Journal on Optimization 2(4), 649–664 (1992). DOI 10.1137/0802032
Han, J., Sun, D.: Newton and quasi-Newton methods for normal maps with polyhedral sets. Journal of Optimization Theory and Applications 94(3), 659–676 (1997). DOI 10.1023/A:1022653001160
Hiriart-Urruty, J.B., Lemaréchal, C.: Fundamentals of Convex Analysis. Grundlehren Text Editions. Springer Berlin Heidelberg (2004)
Horn, R.A., Horn, R.A., Johnson, C.R.: Topics in Matrix Analysis. Cambridge University Press (1994)
Kanzow, C., Ferenczi, I., Fukushima, M.: On the local convergence of semismooth Newton methods for linear and nonlinear second-order cone programs without strict complementarity. SIAM Journal on Optimization 20(1), 297–320 (2009). DOI 10.1137/060657662
Lan, G., Lu, Z., Monteiro, R.D.C.: Primal-dual first-order methods with O(1∕ε) iteration-complexity for cone programming. Mathematical Programming 126(1), 1–29 (2011). DOI 10.1007/s10107-008-0261-6
Lee, J.D., Sun, Y., Saunders, M.: Proximal Newton-type methods for minimizing composite functions. SIAM Journal on Optimization 24(3), 1420–1443 (2014). DOI 10.1137/130921428
Lemaréchal, C., Sagastizábal, C.: Practical aspects of the Moreau-Yosida regularization: Theoretical preliminaries. SIAM Journal on Optimization 7(2), 367–385 (1997). DOI 10.1137/S1052623494267127
Lewis, A.S.: The convex analysis of unitarily invariant matrix functions. Journal of Convex Analysis 2(1), 173–183 (1995)
Lewis, A.S.: Convex analysis on the Hermitian matrices. SIAM Journal on Optimization 6(1), 164–177 (1996). DOI 10.1137/0806009
Lewis, A.S.: Derivatives of spectral functions. Mathematics of Operations Research 21(3), 576–588 (1996)
Lewis, A.S., Sendov, H.S.: Twice differentiable spectral functions. SIAM Journal on Matrix Analysis and Applications 23(2), 368–386 (2001). DOI 10.1137/S089547980036838X
Li, W., Peng, J.: Exact penalty functions for constrained minimization problems via regularized gap function for variational inequalities. Journal of Global Optimization 37(1), 85–94 (2007). DOI 10.1007/s10898-006-9038-8
Li, X., Sun, D., Toh, K.C.: On the efficient computation of a generalized Jacobian of the projector over the Birkhoff polytope. ArXiv e-prints (2017)
Lions Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM Journal on Numerical Analysis 16(6), 964–979 (1979). DOI 10.1137/0716071
Liu, Z., Vandenberghe, L.: Interior-point method for nuclear norm approximation with application to system identification. SIAM Journal on Matrix Analysis and Applications 31(3), 1235–1256 (2010). DOI 10.1137/090755436
Lu, Z.: Randomized block proximal damped Newton method for composite self-concordant minimization. SIAM Journal on Optimization 27(3), 1910–1942 (2017). DOI 10.1137/16M1082767
Luo, Z.Q., Tseng, P.: Error bounds and convergence analysis of feasible descent methods: a general approach. Annals of Operations Research 46(1), 157–178 (1993). DOI 10.1007/BF02096261
Maratos, N.: Exact penalty function algorithms for finite dimensional and control optimization problems (1978)
Martinet, B.: Brève communication. Régularisation d’inéquations variationnelles par approximations successives. Revue française d’informatique et de recherche opérationnelle. Série rouge 4(R3), 154–158 (1970)
Meng, F.: Moreau-Yosida regularization of Lagrangian-dual functions for a class of convex optimization problems. Journal of Global Optimization 44(3), 375 (2008). DOI 10.1007/s10898-008-9333-7
Meng, F., Sun, D., Zhao, G.: Semismoothness of solutions to generalized equations and the Moreau-Yosida regularization. Mathematical Programming 104(2), 561–581 (2005). DOI 10.1007/s10107-005-0629-9
Meng, F., Zhao, G., Goh, M., De Souza, R.: Lagrangian-dual functions and Moreau-Yosida regularization. SIAM Journal on Optimization 19(1), 39–61 (2008). DOI 10.1137/060673746
Mifflin, R.: Semismooth and semiconvex functions in constrained optimization. SIAM Journal on Control and Optimization 15(6), 959–972 (1977). DOI 10.1137/0315061
Mifflin, R., Qi, L., Sun, D.: Properties of the Moreau-Yosida regularization of a piecewise C 2 convex function. Mathematical Programming 84(2), 269–281 (1999). DOI 10.1007/s10107980029a
Moreau, J.J.: Proximité et dualité dans un espace hilbertien. Bulletin de la Société Mathématique de France 93, 273–299 (1965)
Morita, T., Kanade, T.: A sequential factorization method for recovering shape and motion from image streams. IEEE Transactions on Pattern Analysis and Machine Intelligence 19(8), 858–867 (1997). DOI 10.1109/34.608289
Nesterov, Y.: Introductory lectures on convex optimization: A basic course, vol. 87. Springer (2003)
Nesterov, Y.: Gradient methods for minimizing composite functions. Mathematical Programming 140(1), 125–161 (2013). DOI 10.1007/s10107-012-0629-5
Pang, J.S.: Error bounds in mathematical programming. Mathematical Programming 79(1), 299–332 (1997). DOI 10.1007/BF02614322
Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1(3), 127–239 (2014). DOI 10.1561/2400000003
Patrinos, P., Bemporad, A.: Proximal Newton methods for convex composite optimization. In: IEEE Conference on Decision and Control, pp. 2358–2363 (2013)
Patrinos, P., Sopasakis, P., Sarimveis, H.: A global piecewise smooth Newton method for fast large-scale model predictive control. Automatica 47(9), 2016–2022 (2011)
Patrinos, P., Stella, L., Bemporad, A.: Forward-backward truncated Newton methods for convex composite optimization. ArXiv e-prints (2014)
Qi, L., Sun, J.: A nonsmooth version of Newton’s method. Mathematical Programming 58(1), 353–367 (1993). DOI 10.1007/BF01581275
Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Review 52(3), 471–501 (2010). DOI 10.1137/070697835
Rennie, J.D.M., Srebro, N.: Fast maximum margin matrix factorization for collaborative prediction. In: Proceedings of the 22Nd International Conference on Machine Learning, ICML ’05, pp. 713–719. ACM, New York, NY, USA (2005). DOI 10.1145/1102351.1102441
Rockafellar, R.: Convex analysis (1970)
Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization 14(5), 877–898 (1976). DOI 10.1137/0314056
Rockafellar, R.T., Wets, R.J.B.: Variational analysis, vol. 317. Springer Science & Business Media (2011)
Scholtes, S.: Piecewise Differentiable Functions, pp. 91–111. Springer New York, New York, NY (2012). DOI 10.1007/978-1-4614-4340-7_4
Sopasakis, P., Freris, N., Patrinos, P.: Accelerated reconstruction of a compressively sampled data stream. In: 2016 24th European Signal Processing Conference (EUSIPCO), pp. 1078–1082 (2016). DOI 10.1109/EUSIPCO.2016.7760414
Srebro, N.: Learning with matrix factorizations. Ph.D. thesis, Cambridge, MA, USA (2004)
Stella, L., Themelis, A., Patrinos, P.: Forward-backward quasi-Newton methods for nonsmooth optimization problems. Computational Optimization and Applications 67(3), 443–487 (2017). DOI 10.1007/s10589-017-9912-y
Stella, L., Themelis, A., Patrinos, P.: Newton-type alternating minimization algorithm for convex optimization. IEEE Transactions on Automatic Control (2018). DOI 10.1109/TAC.2018.2872203
Stella, L., Themelis, A., Sopasakis, P., Patrinos, P.: A simple and efficient algorithm for nonlinear model predictive control. In: 2017 IEEE 56th Annual Conference on Decision and Control (CDC), pp. 1939–1944 (2017). DOI 10.1109/CDC.2017.8263933
Sun, D., Fukushima, M., Qi, L.: A computable generalized Hessian of the D-gap function and Newton-type methods for variational inequality problems. Complementarity and Variational Problems: State of the Art, MC Ferris and JS Pang (eds.), SIAM, Philadelphia, PA pp. 452–472 (1997)
Sun, D., Sun, J.: Semismooth matrix-valued functions. Mathematics of Operations Research 27(1), 150–169 (2002). DOI 10.1287/moor.27.1.150.342
Themelis, A., Patrinos, P.: Douglas-Rachford splitting and ADMM for nonconvex optimization: tight convergence results. ArXiv e-prints (2017)
Themelis, A., Stella, L., Patrinos, P.: Forward-backward envelope for the sum of two nonconvex functions: Further properties and nonmonotone linesearch algorithms. SIAM Journal on Optimization 28(3), 2274–2303 (2018). DOI 10.1137/16M1080240
Tomasi, C., Kanade, T.: Shape and motion from image streams under orthography: a factorization method. International Journal of Computer Vision 9(2), 137–154 (1992). DOI 10.1007/BF00129684
Tseng, P.: On accelerated proximal gradient methods for convex-concave optimization. Tech. rep. (2008)
Ulbrich, M.: Optimization Methods in Banach Spaces, pp. 97–156. Springer Netherlands, Dordrecht (2009). DOI 10.1007/978-1-4020-8839-1_2
Yamashita, N., Taji, K., Fukushima, M.: Unconstrained optimization reformulations of variational inequality problems. Journal of Optimization Theory and Applications 92(3), 439–456 (1997). DOI 10.1023/A:1022660704427
Yang, Z.: A study on nonsymmetric matrix-valued functions. Master’s thesis, National University of Singapore (2009)
Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 68(1), 49–67 (2006)
Zhou, G., Qi, L.: On the convergence of an inexact Newton-type method. Oper. Res. Lett. 34(6), 647–652 (2006). DOI 10.1016/j.orl.2005.11.001
Zhou, G., Toh, K.C.: Superlinear convergence of a Newton-type algorithm for monotone equations. Journal of Optimization Theory and Applications 125(1), 205–221 (2005). DOI 10.1007/s10957-004-1721-7
Acknowledgements
This work was supported by the Research Foundation Flanders (FWO) research projects G086518N and G086318N; KU Leuven internal funding StG/15/043; Fonds de la Recherche Scientifique—FNRS and the Fonds Wetenschappelijk Onderzoek—Vlaanderen under EOS Project no 30468160 (SeLMA).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Auxiliary Results
Appendix: Auxiliary Results
Lemma 1
Any proper lsc convex function with nonempty and bounded set of minimizers is level bounded.
Proof
Let h be such function; to avoid trivialities we assume that \( \operatorname {{\mathrm {dom}}} h\) is unbounded. Fix \(x_\star \in \operatorname *{\mathrm {argmin}} h\) and let R > 0 be such that  . Since \( \operatorname {{\mathrm {dom}}} h\) is closed, convex, and unbounded, it holds that h attains a minimum on the compact set \(\operatorname {bdry} B\), be it m, which is strictly larger than h(x
⋆) (since \(\operatorname {dist}( \operatorname *{\mathrm {argmin}} h,\operatorname {bdry} B)>0\) due to compactness of \( \operatorname *{\mathrm {argmin}} h\) and openness of B). For x∉B, let \(s_x=x_\star +R\tfrac {x-x_\star }{\|x-x_\star \|}\) denote its projection onto \(\operatorname {bdry} B\), and let \(t_x\mathrel{\mathop:}= \tfrac {\|x-x_\star \|}{R}\geq 1\). Then,
. Since \( \operatorname {{\mathrm {dom}}} h\) is closed, convex, and unbounded, it holds that h attains a minimum on the compact set \(\operatorname {bdry} B\), be it m, which is strictly larger than h(x
⋆) (since \(\operatorname {dist}( \operatorname *{\mathrm {argmin}} h,\operatorname {bdry} B)>0\) due to compactness of \( \operatorname *{\mathrm {argmin}} h\) and openness of B). For x∉B, let \(s_x=x_\star +R\tfrac {x-x_\star }{\|x-x_\star \|}\) denote its projection onto \(\operatorname {bdry} B\), and let \(t_x\mathrel{\mathop:}= \tfrac {\|x-x_\star \|}{R}\geq 1\). Then,
where in the first inequality we used the fact that t x ≥ 1. Since m − h(x ⋆) > 0 and t x →∞ as ∥x∥→∞, we conclude that h is coercive, and thus level bounded. □
Lemma 2
Let \(H\in \operatorname {S}_+(\mathbb {R}^n)\) with λ max(H) ≤ 1. Then \(H-H^2\in \operatorname {S}_+(\mathbb {R}^n)\) with

Proof
Consider the spectral decomposition  for some orthogonal matrix S and diagonal D. Then,
for some orthogonal matrix S and diagonal D. Then,  where \(\tilde D=D-D^2\). Apparently, \(\tilde D\) is diagonal, hence the eigenvalues of H − H
2 are exactly
where \(\tilde D=D-D^2\). Apparently, \(\tilde D\) is diagonal, hence the eigenvalues of H − H
2 are exactly  . The function λ↦λ − λ
2 is concave, hence the minimum in \(\operatorname {eigs}(\tilde H)\) is attained at one extremum, that is, either at λ = λ
min(H) or λ = λ
max(H), which proves the claim. □
. The function λ↦λ − λ
2 is concave, hence the minimum in \(\operatorname {eigs}(\tilde H)\) is attained at one extremum, that is, either at λ = λ
min(H) or λ = λ
max(H), which proves the claim. □
Lemma 3
For any γ ∈ (0, 2∕L
f) the forward-backward operator  (15.22) is nonexpansive (in fact, \(\frac {2}{4-\gamma L_f}\)
-averaged), and the residual
(15.22) is nonexpansive (in fact, \(\frac {2}{4-\gamma L_f}\)
-averaged), and the residual  is Lipschitz continuous with modulus \(\frac {4}{\gamma (4-\gamma L_f)}\).
is Lipschitz continuous with modulus \(\frac {4}{\gamma (4-\gamma L_f)}\).
Proof
By combining [2, Prop. 4.39 and Cor. 18.17] it follows that the gradient descent operator  is γL
f∕2-averaged. Moreover, since the proximal mapping is 1∕2-averaged [2, Prop. 12.28] we conclude from [2, Prop. 4.44] that the forward-backward operator T
γ is α-averaged with \(\alpha =\frac {2}{4-\gamma L_f}\), thus nonexpansive [2, Rem. 4.34(i)]. Therefore, by definition of α-averagedness there exists a 1-Lipschitz continuous operator S such that \(T_\gamma =(1-\alpha )\operatorname {id}+\alpha S\) and consequently the residual
is γL
f∕2-averaged. Moreover, since the proximal mapping is 1∕2-averaged [2, Prop. 12.28] we conclude from [2, Prop. 4.44] that the forward-backward operator T
γ is α-averaged with \(\alpha =\frac {2}{4-\gamma L_f}\), thus nonexpansive [2, Rem. 4.34(i)]. Therefore, by definition of α-averagedness there exists a 1-Lipschitz continuous operator S such that \(T_\gamma =(1-\alpha )\operatorname {id}+\alpha S\) and consequently the residual  is (2α∕γ)-Lipschitz continuous. □
is (2α∕γ)-Lipschitz continuous. □
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Themelis, A., Ahookhosh, M., Patrinos, P. (2019). On the Acceleration of Forward-Backward Splitting via an Inexact Newton Method. In: Bauschke, H., Burachik, R., Luke, D. (eds) Splitting Algorithms, Modern Operator Theory, and Applications. Springer, Cham. https://doi.org/10.1007/978-3-030-25939-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-25939-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25938-9
Online ISBN: 978-3-030-25939-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 in FBS,
in FBS,  is also referred to as (generalized) gradient mapping, see, e.g., [
is also referred to as (generalized) gradient mapping, see, e.g., [ whereas if f = 0 then
whereas if f = 0 then  . The analogy will be supported by further evidence in the next section where we will see that, up to a change of metric, indeed
. The analogy will be supported by further evidence in the next section where we will see that, up to a change of metric, indeed  is the gradient of the forward-backward envelope function.
is the gradient of the forward-backward envelope function. is strictly differentiable at x
⋆ if
is strictly differentiable at x
⋆ if 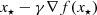 (strict differentiability is closed under composition).
(strict differentiability is closed under composition). , resulting indeed in
, resulting indeed in  .
.