Mesoscopic Approach to Nematic Fluids

Abstract

This chapter on mesoscopic approach to nematic fluids gives a brief introduction to the selected topics of the science of complex nematic fluids, which are fluids with internal orientational order of the building blocks, specifically focusing at the mesoscopic scale. We introduce basic approaches used to characterise and understand nematic fluids at mesoscopic scale, both in equilibrium and dynamics. Using relevant order parameters, we outline Landau–de Gennes free energy approach which is today the strong tool for determining equilibrium material behaviour, and the Ericksen–Leslie–Parodi and Beris–Edwards models which are strong tools for describing dynamics of nematic fluids. Second half of this chapter reviews some selected highlights of current research in the field of nematic fluids, focusing on nematic microfluidics and nematic colloids.

3.1 Introduction to Nematic Fluids

Nematic liquid crystalline fluids are complex anisotropic fluids characterised by internal orientational order of its constituent building blocks [1, 2], which ranges in scales from molecules, macromolecules like DNA, to colloidal rods or platelets. Typically, the orientational order emerges at some temperature or concentration range of building blocks as a result of the geometrical shapes of prolate or oblate building blocks. More recently, nematic order emerged also as an important characteristic of various active fluids, i.e. fluids that can self-propel. Nematic fluids are inherently soft materials, with the orientational order responding as an effective elastic medium to external perturbations, like surfaces or electromagnetic fields. And it is this soft and—optically or structure wise—strong response to external fields which makes nematic fluids potent materials in various applications, including in the fields of optics, photonics, and sensors. The broadest range of applications and experiments with nematic fluids is as at the scales of multiple building elements (which, for example, for molecular nematics, is in the micrometre regime), where mesoscopic approaches prove to be the strongest to describe the systems, as compared to molecular and effective molecular approaches [3, 4], which are used at smaller scales. In view of this, this chapter will present mesoscopic approach to nematic fluids, based on continuum description of the nematic mechanisms and phenomena.

Nematic orientational order is characterised at the mesoscopic scale primarily with the average orientation of the building blocks (also called nematogens), called the director n with apolar n → −n symmetry. This symmetry can be seen from the basic model system of nematic fluids, i.e. fluid of rods, where opposite orientations of a rod are equivalent. The fluctuations and possible asymmetry in the fluctuations of the individual building blocks open additional degrees of freedom given by the nematic degree of order S and biaxiality which then are embedded in the nematic tensor order parameter Q, which further will be defined and explained in this chapter. Overall, the full anisotropic configuration of nematic ordering can vary in three spatial dimensions and can be also time dependent [1]. Equilibrium nematic configurations correspond to a minimum of the free energy. Uniform nematic ordering can be broken by electromagnetic fields or interaction with the boundaries, such as cell or particle surfaces. To satisfy these constraints, often regions of a frustrated orientational order—topological defects—emerge. In a defect, the singularity in the director field is accompanied by a reduction of S, thus effectively melting the nematic into the isotropic state. The shape of topological defects ranges from point defects to line defects and defect walls [2]. Although the topology of a local nematic field is given by the constraints at the boundary, the shape and the metastability of the nematic structures are dictated by the free energy.

Out of the equilibrium nematic alignment is strongly coupled to the velocity field. There are three main effects of the nematic ordering to the velocity field: (1) the rotation of nematic molecules induces material flow, which is known as backflow, (2) even at a fixed nematic configuration (i.e. fixed Q) the fluid viscosity is anisotropic, (3) in active nematics active force dipoles drive the fluid flow. The nematic ordering is affected by the fluid flow through the advection process and the tumbling/aligning dynamics. The coupling between fluid flow and orientational order shows remarkable complexity and provides another aspect to the low Reynolds number fluid mechanics. Out of the equilibrium dynamics can be understood as a competition between effective nematic elasticity, which drives the system towards the equilibrium, and the velocity field and other time modulating fields that promote further deformations of the orientational order. The solutions of such competition range from low Reynolds number turbulence to complex mutually interacting structures in both velocity and Q-tensor fields. Several approaches to the coupled behaviour between fluid flow and nematic ordering were developed, among the most commonly used are Beris–Edwards [5] and Qian–Sheng [6] model of nematodynamics. Velocity effects on the Q-tensor are introduced through the generalised advection terms that compete with the molecular forces that promote the relaxation to the minimum of the free energy. The effect of the orientational order on the fluid flow is given by the stress tensor that is included in the Navier–Stokes equation. The above-mentioned models are based on full Q-tensor, but rather extensively also models based on only director dynamics are used, such as Ericksen–Leslie–Parodi model [1].

Orientational order and material flow of nematic fluids can be shaped into complex microfluidic structures, as a result of combined soft response to the external electromagnetic fields, confinement, and pressure boundary conditions, coupled with the internal effective elasticity and possibly even intrinsic activity [1, 2]. Fascinating field structures in nematic fluids are revealed by theory and experiments, for example, in the context of assisted assembly of colloidal crystals [7], study of complex topological states [8, 9], and sensing applications [10]. Studied systems out of the equilibrium include quench transitions [11], back flow effects [12, 13], and nematic flow in various Poiseuille geometries [14, 15]. Dependence of the nematic viscosity on the director orientation can be used in microfluidic circuits to control the direction of flow and transport of material with selected recent works including defect line assisted transport of colloidal cargo [16] and nematic fluid resistance tunable by electric field [17]. Optical sensors are developed in Ref. [18]. A lot of attention has been also given to the subject of active nematics, both from the experimental and theoretical point of view [19]. The rich variety of structures in mutually coupled fields, each with its own intrinsic symmetry, calls for a deeper understanding of their interactions and potential applications.

Defects in liquid crystals can form regular or irregular structures, depending on the type of confinement, inserted colloidal particles, external fields, and flow [20,21,22,23]. Confinement and the surface anchoring can impose and affect defects in liquid crystal. If the confinement has a regular structure, the transition from regular to irregular structures is controllable [20] and the created system can even have a memory effect. Colloidal particles inserted in the liquid crystal introduce the topological defects on their surface. These defects attract each other, so if the colloids have an appropriate design—such as geometry and surface imposed anchoring—this can cause self-assembly of colloidal crystals [7]. Even the passive or active flow itself can cause the reorientation of the director via backflow mechanism, at certain circumstances this gives birth to the structures in the director field [24]. A recently developed system for studying topological defects in passive materials uses confined nematics and nematic colloids [11, 20, 25, 26] where defects of high complexity can be realised ranging from topological defect knots [27], handlebody topological colloids [28], chiral nematic solitons of torons [22] and hopfions [29], quasicrystalline colloidal tilings [30], and droplets with holes [31]. The joint feature of these passive complex defect structures is that defects in 3D generally become delocalised and emerge in the form of topological loops or even networks, called nematic braids. In parallel to their observation, there was also a major development of experimental and theoretical, especially topological, methods for characterisation and control of these advanced defects [26, 32,33,34].

Complex materials based on nematic fluids are recently attracting a lot of attention, including because of novel ways to control birefringence and the possibility to form complex topological structures. Notably, these specific systems include chiral nematics [22, 27, 35,36,37,38] and lyotropic liquid crystals [39,40,41,42] which will not be explained in this chapter due to space limitations. Additionally, active matter is a major growing field of science, where nematicity is emerging as an important characteristic of multiple systems. Finally, the goal of this chapter is to give basic introduction to mesoscopic approach to nematic fluids and show some selected exciting fields of development in nematic fluids, such as nematic colloids, topology, and microfluidics.

3.2 Nematic Order Parameters

Nematic liquid crystal fluids consist typically of rod-like or disk-like molecules (building blocks) with no long-range positional order. Due to their anisotropic shape, molecules exhibit orientational order and tend to align along some common direction, usually referred as director n with both directions n and −n being equivalent. The director is a vectorial-like order parameter, which corresponds to the time or ensemble average of molecular orientations u (see Fig. 3.1).

Fig. 3.1

Nematic ordering of rod-like molecules along the director n. θ is the tilt angle of individual molecules with respect to director

The director n bears no information about the degree of orientational order, i.e. the degree of fluctuations of molecular orientations u; therefore, nematic degree of order (scalar order parameter) S is introduced. Nematic molecules in thermodynamic equilibrium assume some direction according to some probability distribution ρ(u). We want to characterise the alignment by one parameter, not the full distribution function ρ(u), which can be quite general. Without loss of generality one can choose z axis along n and characterise spatial directions of u by azimuthal angles ϕ and polar angles θ. The first idea would be to use the average $\left \langle {\mathbf {a}\cdot \mathbf {n}}\right \rangle =\left \langle {\cos \theta }\right \rangle$, but this vanishes because the molecules have no distinction between head and tail. The first non-trivial moment is the quadrupole, which is then used to determine the nematic degree of order S as:

$$\displaystyle \begin{aligned} S=\left\langle{P_2(\cos\theta)}\right\rangle=2\pi\int_0^{\pi}P_2(\cos\theta)\rho(\theta)\sin{}(\theta)\text{d}\theta, \end{aligned} $$

(3.1)

where P ₂ is the associated Legendre polynomial of the second order and $\left \langle {\cdot }\right \rangle$ average over all molecular orientations. The values of S lie on the interval $\left [ -\frac {1}{2}, 1 \right ]$. When all the molecules are perfectly aligned with the director, the nematic degree of order is S = 1, whereas S = 0 corresponds to the isotropic phase, in which the molecules are oriented randomly, and $S=-\frac {1}{2}$ represents the state where all the molecules are aligned perpendicular to the director.

The full orientational order in liquid crystals is described by the tensor order parameter Q _ij that contains both degree of order S and director n and also possible biaxiality P. Q _ij reads

$$\displaystyle \begin{aligned} Q_{ij}=\frac{S}{2}\left(3n_in_j-\delta_{ij} \right) + \frac{P}{2}\left( e_i^{(1)}e_j^{(1)} - e_i^{(2)}e_j^{(2)} \right), \end{aligned} $$

(3.2)

where e ⁽¹⁾ is the secondary director (perpendicular to n) that characterises the biaxial ordering, and e ⁽²⁾ = n ×e ⁽¹⁾. Values of P are in the interval $\left [-\frac {3}{2}, \frac {3}{2} \right ]$, where P = 0 characterises uniaxial ordering and $|P|=\frac {3}{2}$ corresponds to the perfect ordering along the secondary director e ⁽¹⁾. Order parameter tensor Q _ij is a real, symmetric, and traceless tensor. It has five degrees of freedom: nematic degree of order S, biaxiality P, orientation of the director n (two angles), and orientation of the secondary director e ⁽¹⁾ relative to the director (one angle). Order parameter tensor has three eigenvalues, namely S, $-\frac {1}{2}(S+P)$ and $-\frac {1}{2}(S-P)$, with the corresponding eigenvectors n, e ⁽¹⁾, and e ⁽²⁾.

3.3 Landau–de Gennes Free Energy Approach

A strong approach at the mesoscopic level to characterise the equilibrium properties of nematic fluids is to use the Landau–de Gennes free energy volume density f, which can be written as:

$$\displaystyle \begin{aligned} f=f_{\text{NI}}+f_{\text{E}}. {} \end{aligned} $$

(3.3)

The model consists of two main bulk free energy density contributions: first contribution f _NI describes the phase transition from nematic to isotropic mesophase and second contribution f _E accounts for the spatial elastic deformations of tensor order parameter Q _ij.

3.3.1 Landau Theory of Nematic Phase Transition

The stability of nematic mesophases in most nematic fluids depends either on temperature or concentration of the building blocks. In thermotropic nematic liquid crystals, temperature drives the phase transition between the nematic phase with orientational order and isotropic phase with no long-range orientational order, with consequently the order parameter Q _ij abruptly dropping to zero. Phenomenological Landau theory is a mean field theory and a well-established approach to model phase transitions. The Gibbs free energy is expanded in vicinity of the transition with respect to the scalar invariants of the order parameter tensor Q _ij up to the fourth order [1]. Expansion reads

$$\displaystyle \begin{aligned} f_{\text{NI}}=\frac{1}{2}A(T)Q_{ij}Q_{ji}+\frac{1}{3}BQ_{ij}Q_{jk}Q_{ki}+\frac{1}{4}C(Q_{ij}Q_{ji})^2,\end{aligned} $$

(3.4)

where A, B, and C are material parameters and summation over repeated indices is assumed. Parameter A = a(T − T ^∗) contains temperature dependence which governs the nematic to isotropic transition [2]. In nematic phase, below the temperature T ^∗, both A and B are negative, but C must be positive to ensure that the free energy density functional is bounded from below. Typical values for molecular nematic liquid crystal are ≈ 10⁶ J∕m³. Free energy functional can be rewritten only with S, assuming homogeneous n and no biaxiality, as:

$$\displaystyle \begin{aligned} f_{\text{NI}}^{SI}=\frac{3}{4}a(T-T^*)S^2+\frac{1}{4}BS^3+\frac{9}{16}CS^4,\end{aligned} $$

(3.5)

where now the free energy functional exhibits dependence shown in Fig. 3.2. First term drives the transition, second breaks the symmetry of S, and the third bounds the f _NI from below. The minimisation of the free energy gives the equilibrium nematic degree of order S _eq

$$\displaystyle \begin{aligned} S_{\text{eq}}=\frac{1}{2}\left( -\frac{B}{3C} + \sqrt{\left( \frac{B}{3C} \right)^2 -\frac{8A(T)}{3C} } \right)\end{aligned} $$

(3.6)

that holds for T < T _c and homogeneous nematic under no external field.

Fig. 3.2

Free energy density $f_{\text{NI}}^{SI}$ as a function of the nematic degree of order S for some typical temperatures. Minimum of the free energy density changes with variation of temperature. For T > T _c free energy has stable minimum at S = 0 (isotropic phase), but for T < T _c, the minimum corresponds to S ≠ 0 (nematic phase). At temperature T _c, we have coexistence of both phases and transition is of first order. Below the super-cooling temperature T ^∗ the isotropic phase is unstable. T ^∗∗ represents super-heating temperature of nematic phase

3.3.2 Elastic Free Energy

Organisation of nematic into a uniform and homogeneous pattern is energetically preferred. However, such organisation is usually not compatible with boundary conditions and external fields. While subjected to spatial variations of orientational ordering, nematic material effectively acts as an elastic medium, where the elastic deformation can be decomposed into three basic deformation modes, splay, twist, and bend, presented in Fig. 3.3. The elastic free energy is an expansion in small gradients of the order parameter tensor Q that penalise nematic distortions from the uniform configuration. The terms are second order in derivatives because first-order terms are disallowed by the symmetry of an achiral nematic [2]. Free energy density reads

$$\displaystyle \begin{aligned} f_{\text{E}}=\frac{1}{2}L_1\frac{\partial Q_{ij}}{\partial x_k}\frac{\partial Q_{ij}}{\partial x_k} + \frac{1}{2}L_2\frac{\partial Q_{ij}}{\partial x_j}\frac{\partial Q_{ik}}{\partial x_k} + \frac{1}{2}L_3 Q_{ij}\frac{\partial Q_{kl}}{\partial x_i}\frac{\partial Q_{kl}}{\partial x_j}, {} \end{aligned} $$

(3.7)

where L ₁, L ₂, and L ₃ are tensorial elastic constants, x _i are Cartesian coordinates, and summation over repeated indices is assumed. Three elastic constants are introduced to quantify all three basic elastic modes. More third-order terms in Q are possible in Eq. (3.7), but the choice of three terms is sufficient for matching into three Frank elastic constants. If one assumes uniaxial approximation of the order parameter tensor Q (S = const. and P = 0), the free energy can be rewritten into the Frank–Oseen free energy density, which is expressed in terms of director n and its derivatives [43, 44]:

$$\displaystyle \begin{aligned} f_{\text{E}}^{\text{FO}}=\frac{1}{2}K_{1}(\nabla\cdot\mathbf{n})^2 + \frac{1}{2}K_{2}(\mathbf{n}\cdot(\nabla\times\mathbf{n}))^2 + \frac{1}{2}K_{3}(\mathbf{n}\times(\nabla\times \mathbf{n}))^2, {} \end{aligned} $$

(3.8)

where the terms directly account for splay, twist, and bend deformation modes of the nematic. By comparing both expansions [Eqs. (3.7) and (3.8)] one can get the mapping between tensorial constants L _i and Frank elastic constants K _i, which are usually measured in experiments [45]:

$$\displaystyle \begin{aligned} K_1&=\frac{9S^2}{4}(2L_1+L_2-L_3S), \end{aligned} $$

(3.9)

$$\displaystyle \begin{aligned} K_2&=\frac{9S^2}{4}(2L_1-L_3S), \end{aligned} $$

(3.10)

$$\displaystyle \begin{aligned} K_3&=\frac{9S^2}{4}(2L_1+L_2+2L_3S). \end{aligned} $$

(3.11)

Fig. 3.3

Basic nematic elastic deformation modes: (a) splay, (b) twist, and (c) bend

Usually, a single elastic constant approximation is used, which sets L ₁ = L, L ₂ = L ₃ = 0, and K ₁ = K ₂ = K ₃ = K. The elastic free energy densities than reduce to

$$\displaystyle \begin{aligned} f_{\text{E}}=&\frac{1}{2}L\frac{\partial Q_{ij}}{\partial x_k}\frac{\partial Q_{ij}}{\partial x_k}, \end{aligned} $$

(3.12)

$$\displaystyle \begin{aligned} f_{\text{E}}^{\text{FO}}=&\frac{1}{2}K\left[ (\nabla\cdot \mathbf{n})^2 + (\nabla \times \mathbf{n})^2 \right]. {} \end{aligned} $$

(3.13)

The eligibility of one-constant approximation strongly depends on the choice of the material. For a nematic liquid crystal such as 5CB, the values of elastic constants are in the range 10⁻¹²–10⁻¹¹ N and differ for around 40% [46]. Elastic constants K _i can also be strongly temperature dependent, but usually not with the same rate; therefore, ratios K ₃∕K ₁ and K ₂∕K ₁ typically also vary [47].

The effective ratio between the ordering free energy f _NI and elastic f _E contribution to the Landau–de Gennes free energy determines a characteristic length scale of nematics—the nematic correlation length ξ _N. Within single elastic constant approximation and uniaxial order parameter tensor, ξ _N equals [48]

$$\displaystyle \begin{aligned} \xi_{\text{N}}=\sqrt{\frac{L}{A+BS_{\text{eq}}+\frac{9}{2}CS_{\text{eq}}^2}}. \end{aligned} $$

(3.14)

Nematic correlation length determines spatial length scale for the variation of nematic degree of order; therefore, it roughly sets the defects size. For example, in molecular nematics, ξ _N is of the order of few nm.

3.3.3 Surface Anchoring

The Landau–de Gennes free energy density (Eq. (3.3)) determines the distortion energies in the bulk of the nematic fluids, and needs to be extended in the presence of surfaces with also surface free energy terms. Surfaces surrounding the nematic can affect the nematic ordering by imposing both preferred orientation and the degree of order. Surfaces can in principle impose arbitrary direction in space, with planar (tangential) anchoring and homeotropic (normal) anchoring being most common [49].

Uniform surface anchoring (homeotropic or other fixed direction) can be well described by using Rapini–Papoular like surface free energy density functional [50]:

$$\displaystyle \begin{aligned} f_{\text{H}}=\frac{1}{2}W_{\text{H}}(Q_{ij}-Q_{ij}^0)^2, {} \end{aligned} $$

(3.15)

which quadratically penalises all deviations from the surface-preferred order parameter tensor $Q_{ij}^0$ with the strength W _H. Besides the preferred direction at the surface, tensor $Q_{ij}^0$ imposes also surface degree of order and biaxiality. In case of homeotropic anchoring, the preferred tensor is constructed using the surface normal ν, so that $Q_{ij}^0=\frac {S_{\text{eq}}}{2}(3\nu _i\nu _j -\delta _{ij})$. Typically values of the anchoring strength W _H range from 10⁻³ J∕m² (strong anchoring) to 10⁻⁷ J∕m² (weak anchoring) [51].

Some surfaces favour planar degenerate anchoring, where molecules have tendency to align along any direction within a plane, so all azimuthal angles are equally possible. Such anchoring can be described by introducing surface free energy potential [52]:

$$\displaystyle \begin{aligned} f_{\text{PD}}=W_{\text{PD}}\left( \tilde{Q}_{ij} - \tilde{Q}_{ij}^{\perp} \right)^2, {} \end{aligned} $$

(3.16)

where W _PD is a constant measuring surface anchoring strength. Model penalises any deviations of $\tilde {Q}_{ij}=Q_{ij}+\frac {S_{\text{eq}}}{2}\delta _{ij}$ from its projection to the surface $\tilde {Q}_{ij}^{\perp } = P_{ik}\tilde {Q}_{kl}P_{lj}$. The projection matrix is defined using the surface normal ν _i as P _ij = δ _ij − ν _i ν _j. The term quadratically penalises deviations of $\tilde {Q}_{ij}$ from its projection. Anchoring strength is frequently characterised with the Kleman–de Gennes extrapolation length ξ _S, which is defined as follows [1]:

$$\displaystyle \begin{aligned} \xi_{\text{S}}=K/W. \end{aligned} $$

(3.17)

It effectively measures relative strength between nematic elasticity and surface anchoring. Typically, extrapolation length is of the order of 10 nm for surfaces with strong anchoring and ranges to ξ _S ∼ 10 μm for surfaces with weak anchoring.

3.3.4 Electric Field Effects

Due to their polarisability, nematics are highly responsive to external electric fields. In the Landau–de Gennes framework, the dielectric coupling between nematic and external electric field can be introduced as an additional free energy contribution f _D as

$$\displaystyle \begin{aligned} f_{\text{D}}=-\frac{1}{2}\epsilon_0 \left( \bar{\epsilon}\delta_{ij} + \frac{2}{3}\epsilon_a^{\text{mol}}Q_{ij} \right)E_iE_j, {} \end{aligned} $$

(3.18)

where E _i is the external electric field, 𝜖 ₀ the dielectric vacuum permittivity constant, $\bar {\epsilon }=(2\epsilon _{\perp } + \epsilon _{\parallel })/3$ the average liquid crystal permittivity, and $\epsilon _{\text{a}}^{\text{mol}}=\epsilon _{\parallel }^{\text{mol}}-\epsilon _{\perp }^{\text{mol}}$ the molecular dielectric anisotropy, which is connected to macroscopic dielectric anisotropy $\epsilon _{\text{a}}=S\epsilon _{\text{a}}^{\text{mol}}$. $\epsilon _{\perp }^{\text{mol}}$ and $\epsilon _{\parallel }^{\text{mol}}$ are eigenvalues of dielectric permittivity tensor and correspond to eigenvectors perpendicular and parallel to the director. Typical values for 5CB at room temperature are 𝜖 _a = 11 and S = 0.525, giving $\epsilon _{\text{a}}^{\text{mol}}=21$ [53].

The strength of the electric field can be characterised by introducing another length scale—the electric coherence length ξ _E. The comparison between free energy due to the electric field [Eq. (3.18)] and elasticity (Eq. (3.7)) gives [1]

$$\displaystyle \begin{aligned} \xi_{\text{E}}=\frac{1}{E}\sqrt{\frac{L_1}{\epsilon_a \epsilon_0}}, \end{aligned} $$

(3.19)

where E is a typical electric field in the sample. The effects of electric field are perceptible when the ξ _E is small compared to the system size. In a typical nematic (L ₁ ≈ 10⁻¹¹ N, 𝜖 _a ≈ 10) and electric field E = 1 V∕μm the electric coherence length is ξ _E ≈ 0.3 μm.

The competition between elasticity and electric field can be more comprehensively studied in the Fréedericksz cell [54]. It consists of nematic liquid crystal being oriented between two solid plates with strong anchoring. The preferential direction imposed by the surfaces may be parallel or perpendicular to the plates, whereas the electric field is always applied perpendicular to the orientational axis imposed by the surface anchoring. There are three different cell setups and each exactly refers to one of the three basic elastic deformation modes (Fig. 3.3), namely splay, twist, and bend [55]. If the electric field exceeds the threshold E _c, the director field deforms. Critical electric field E _c is given as:

$$\displaystyle \begin{aligned} E_{\text{c}}=\frac{\pi}{d}\sqrt{\frac{K_i}{\epsilon_0 |\epsilon_{\text{a}}|}}, {} \end{aligned} $$

(3.20)

where 𝜖 ₀ is the vacuum permittivity, 𝜖 _a the dielectric anisotropy, d the thickness of the cell, and K _i the elastic constant for splay, twist, and bend, respectively. In typical liquid crystals (K _i ≈ 10⁻¹¹ N and 𝜖 _a ≈ 10) in a Freedericksz cell with separation d = 20 μm the critical electric field is E _c ≈ 0.05 V∕μm.

3.3.5 Magnetic Field Effects

Many nematic fluids are diamagnetic. For example, the diamagnetism is especially enhanced when the molecule is aromatic, because the benzene ring effectively acts as a coil. Free energy contribution describing the diamagnetic coupling f _H can be introduced in analogous way as for the electric field, namely

$$\displaystyle \begin{aligned} f_{\text{H}}=-\frac{1}{2}\mu_0 \left( {\bar\chi \delta_{ij} + \frac{2}{3}\chi_{\text{a}}^{\text{mol}}Q_{ij}} \right)H_i H_j, {} \end{aligned} $$

(3.21)

where H _i is the external magnetic field, μ ₀ the vacuum permeability constant, ${\bar \chi }=(2\chi _{\perp }+\chi _{\parallel })/3$ the average liquid crystal magnetic susceptibility, and $\chi _{\text{a}}^{\text{mol}}= \chi _{\parallel }^{\text{mol}}-\chi _{\perp }^{\text{mol}}$ the molecular dielectric anisotropy, which is connected to macroscopic magnetic susceptibility $\chi _{\text{a}}=S \chi _{\text{a}}^{\text{mol}}$. $\chi _{\perp }^{\text{mol}}$ and $\chi _{\parallel }^{\text{mol}}$ are eigenvalues of magnetic susceptibility tensor and correspond to eigenvectors perpendicular and parallel to the director. Values for a typical representative of thermotropic molecular nematic fluids MBBA at room temperature are χ _a = 1.23 × 10⁻⁷ and S = 0.525, giving $\chi _{\text{a}}^{\text{mol}}=2.34\times 10^{-7}$ [1].

The strength of the magnetic field can be characterised by introducing the magnetic coherence length ξ _B which determines the relative comparison between the free energy contributions due to the magnetic field [Eq. (3.21)] and the nematic elasticity (Eq. (3.7)) gives [1]

$$\displaystyle \begin{aligned} \xi_{\text{B}}=\frac{1}{B}\sqrt{\frac{L_1}{\chi_{\text{a}}\mu_0}}, \end{aligned} $$

(3.22)

where B is typical magnetic field in the sample.

3.4 Topological Defects

Frustration of nematic ordering by opposing surfaces or external fields leads to formation of defect regions, where molecular orientation is frustrated and has no preferential orientation. Defect regions are characterised by severe drop of nematic degree of order S (to S = 0) and strong spatial distortions of the nematic director n. Defects in nematic liquid crystal can be either points or lines [56] and are usually characterised by topological charges and winding numbers [2, 57,58,59].

Singular point defects form either in the bulk or on the surfaces. Frequently, point defects in the bulk are named “hedgehogs”, whereas those on the surfaces are called “boojums”. The topological charge q of point defects can be introduced as an integral over a closed defect-free surface Ω surrounding the defect [2]

$$\displaystyle \begin{aligned} q=\frac{1}{8\pi}\oint limits_{\Omega}\epsilon_{ijk}\mathbf{n}\cdot\left( \frac{\partial \mathbf{n}}{\partial x_j} \times \frac{\partial \mathbf{n}}{\partial x_k} \right) \text{d}S_i, {} \end{aligned} $$

(3.23)

where 𝜖 _ijk is the Levi-Civita totally antisymmetric tensor and x _i are Cartesian coordinates. Notice that q is odd in n, which causes that topological charge in nematics is not uniquely defined due to the n →−n symmetry. Three typically observed configurations of point defects with charge magnitude |q| = 1 are: radial $\mathbf {n}=(x, y, z)/\sqrt {x^2+y^2+z^2}$, circular $\mathbf {n}=(y, -x, z)/\sqrt {x^2+y^2+z^2}$, and hyperbolic $\mathbf {n}=(-x,-y,z)/\sqrt {x^2+y^2+z^2}$ hedgehog.

The ± sign differentiates two vector fields with opposite topological charge (±), but represents the same physical director field. This sign ambiguity is always present in the nematic systems. Frequently, a convention of assigning + 1 to the radial charge and − 1 to the hyperbolic is used, but in general, the vectors in the entire sample must be oriented consistently and the topological charges assigned accordingly [33]. The elastic free energy of isolated singular point defects scales as KR, where R is the size of liquid crystal volume and K some value of Frank elastic constants.

Line defects, named also disclinations, are locally quantified with winding number (strength) m which characterises the symmetry of surrounding director field at some cross-section. For simplification let the disclination line be aligned parallel with the z-axis and the director field is observed in plane perpendicular to it. The in-plane director field can be parameterised with the director azimuthal angle α and the integral over closed loop Γ gives local winding number

$$\displaystyle \begin{aligned} m=\frac{1}{2\pi}\oint limits_{\Gamma}\text{d}\alpha. \end{aligned} $$

(3.24)

Winding number m can be integer and also half-integer, since the states n and −n are physically indistinguishable (Fig. 3.4). Note that the definition of winding number assumes that the director is confined to the 2D plane, perpendicular to the disclination. The in-plane director field of a disclination at the coordinate origin can be written as:

$$\displaystyle \begin{aligned} \mathbf{n}=(\cos\alpha, \sin\alpha, 0)=(\cos{}(m\phi+c), \sin{}(m\phi+c), 0), \end{aligned} $$

(3.25)

with c being typically a constant, which sets the shape and relative orientation of the director field regarding the coordinate frame.

Fig. 3.4

Schematic representation of director field surrounding disclination lines with various winding numbers m. c = 0 was used

By surface integrating the Frank–Oseen free energy density (Eq. (3.13)) over the in-plane director field (using single elastic approximation), one can calculate free energy per unit length of the disclination line [2]

$$\displaystyle \begin{aligned} W_{\text{def}}(m)=\pi K m^2 \ln\left( \frac{R}{r_{\text{core}}} \right) + W_{\text{core}}, \end{aligned} $$

(3.26)

where r _core is the core radius with energy per unit length W _core ∼ πm ² K, K is some function of Frank elastic constants, and R is the system size. Frank–Oseen approach does not apply for large gradients of the director; hence, the core is introduced to avoid the discontinuity of the director field in the centre of disclination. The proportionality W ∝ m ² implies that one disclination of strength m = ±1 bears two times more energy than two disclinations of strength m = ±1∕2. As a result in 2D systems only ± 1∕2 disclinations are stable. Note that total energy of the disclination line is linearly proportional with its length. Line defects can be also closed to loops.

3.4.1 Umbilic Defects

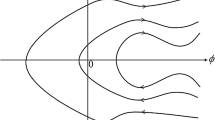
In contrast to the standard defects in liquid crystals, with a discontinuity of the director field at the centre, umbilic defects are continuous everywhere and have no melted (isotropic) core. However, the discontinuity emerges only in the projection of the director field to a distinct plane (xy) perpendicular to the far-field orientation (z-axis) [60]. Therefore, it is necessary to bear in mind that umbilics are not fundamentally topological, as they can be continuously transformed into a homogeneous field. Umbilic defects are most commonly created by using electric fields in Hele-Shaw cells [61] with strong homeotropic anchoring, containing a nematic monocrystal with a negative dielectric anisotropy. The external field (above the critical value E _c (Eq. (3.20))), applied perpendicular to the cell surfaces, induces bend distortions to the homogeneous alignment of the director field [55]. The situation is reminiscent to the Fréedericksz transition, the molecules tend to lie parallel to the surface in order to minimise free energy, but importantly no particular direction is preferred in this plane. This degeneration of the tilt direction leads to formation of umbilic defects (Fig. 3.5).

Fig. 3.5

Schematic representation of umbilic defects with ϕ ₀ = 0. (a) Hele-Shaw cell with the side view of the umbilic defect m = +1. The discontinuity emerges only in the projection of the director field to the plane parallel with the plates (purple). (b) Umbilic defects of various umbilic charge (top view)

The distorted director field of umbilic defects can be written as [60,61,62]:

$$\displaystyle \begin{aligned} \mathbf{n}=(\cos{}(m\phi+\phi_0)\sin\theta, \sin{}(m\phi+\phi_0)\sin\theta, \cos\theta),\end{aligned} $$

(3.27)

where ϕ is the azimuthal angle in xy plane, ϕ ₀ some arbitrary constant, and θ the tilt angle. In Hele-Shaw cell of thickness d (plates being at − d∕2 and d∕2) the tilt angle θ depends on the intensity of the electric field E and can be written as:

$$\displaystyle \begin{aligned} \theta(z)=\theta_0 \cos\left( \frac{\pi z}{d} \right), \end{aligned} $$

(3.28)

where

$$\displaystyle \begin{aligned} \theta_0\approx 2\sqrt{\frac{E-E_{\text{c}}}{E_{\text{c}}}}. \end{aligned} $$

(3.29)

Direction of the tilt may be described with the two-dimensional unit vector c, which resides in the xy plane, and gives the projected structure of the defect. The tilt directions c and −c are not equivalent, because c is an oriented vector, as a result umbilic charge m must be an integer. The core of umbilics is continuous, which allows for a full calculation of the elastic free energy. For example, for umbilics of strength m = +1, the free energy per unit length is proportional to $W \propto K_1\cos ^2\phi _0 + K_2\sin ^2\phi _0$, whereas for the umbilics of strength m = −1 it is $W\propto \frac {K_1+K_2}{2}$ [60, 63].

3.4.2 Basics of Topological Theory of Defects

A comprehensive topological description of defects in liquid crystals requires involvement of the theory of homotopy [64]. The order parameter, namely the director, is a map from a real space, excluding the singularities, to the ground state manifold, which is the topological space of all possible states the director can occupy. The ground state manifold of nematic is real projective plane $\mathbb {R}P^2$, the top half of a unit sphere with opposite points on the equator identified [58]. The main consideration are mappings of i-dimensional spheres enclosing the defects in real space. A line defect can be enclosed by a linear contour (i = 1), whereas the point defect by a sphere (i = 2); therefore, they are mapped to $\mathbb {R}P^2$ with different homotopy groups $\mathcal {H}_i$. Each element of homotopy group corresponds to a class of topologically stable defects, which can be continuously deformed one to the other [2]. They are topological invariants, previously referred to as the topological charges of the defects [59]. A defect-free state, where director field n is equivalent to a constant, corresponds to an identity element of the homotopy group and zero topological charge.

Defect loops and point defects can both be enclosed in a sphere S ² and thus have a topological index in the second homotopy group. We say they are equivalent in sense of topology as they can be continuously deformed one into another. The winding number m defines the local symmetry of the director field surrounding the defect loop. However, it is the topological charge of a loop q (Eq. (3.23)), as in the case of point defects, that defines its global topological properties.

Topological charge needs to be preserved, also in the process of annihilation or creation of defects. As a result defects in form of points or lines can be created and annihilated in pairs of opposite sign. However, if the confining surfaces impose some preferential direction, this may, in addition with the genus of the surface, determine a non-zero net total topological charge. For example, in the case of droplet with homeotropic anchoring at the surface, the total net topological charge of the nematic within the droplet is q = 1. Similarly, the colloidal particles with certain surface anchoring effectively behave as point defects of certain topological charge q. This is compensated by the surrounding nematic with introduction of the defect with the opposite sign − q in order to preserve the total topological charge.

3.5 Nematodynamics

In this section we shall discuss hydrodynamics of nematic liquid crystals, considering the coupling between the nematic orientational ordering and the material flow. The flow field of nematic is given by the generalised Navier–Stokes equation

$$\displaystyle \begin{aligned} \rho\left[\frac{\partial v_i}{\partial t}+\left(v_j\partial_j\right)v_i\right]=\partial_j\sigma_{ij}, {} \end{aligned} $$

(3.30)

where ρ is the density, v the velocity, and σ the stress tensor which includes beside the standard pressure also the dependence on the anisotropic nematic order in the system. The stress tensor can be written as a sum of the Ericksen stress tensor σ ^Er which includes the elasticity effects, and viscous stress tensor σ ^viscous. The incompressibility condition

$$\displaystyle \begin{aligned} \partial_jv_j=0 {} \end{aligned} $$

(3.31)

is assumed. Equations (3.30) and (3.31) have to be complemented by the equation for the evolution of the nematic order parameter, written either in the director or in the Q-tensor form. In the presented formulation, we use typical assumptions from the literature when considering dynamics of liquid crystals (in comparison to statics): two elastic constants and negligible moment of inertia of nematic molecules. Also, we omit the contributions of the electric and magnetic fields to the nematodynamics, which are sufficiently discussed elsewhere [1, 6].

3.5.1 Ericksen Stress Tensor

Elasticity of the nematic internal structure can transmit stresses through the bulk. Consider, for instance, a pair of colloidal particles in a nematic held by an external force at distance d apart. The distortion of the director field and the nematic free energy depend on d. The force between colloidal particles is mediated by the director field and can be calculated through the Ericksen stress tensor. Ericksen stress tensor is derived by considering changes in the free energy due to displacement of nematic molecules [1]. In the director formulation, Ericksen stress is given by

$$\displaystyle \begin{aligned} \sigma_{ij}^{\text{Er}}=-\frac{\delta \mathcal{F}}{\delta\partial_jn_k}\partial_in_k -\left(p_0-f\right)\delta_{ij}. {} \end{aligned} $$

(3.32)

In the tensorial formulation, a similar expression holds:

$$\displaystyle \begin{aligned} \sigma_{ij}^{\text{Er}}=-\frac{\delta \mathcal{F}}{\delta\partial_jQ_{kl}}\partial_iQ_{kl}-\left(p_0-f\right)\delta_{ij}, {} \end{aligned} $$

(3.33)

where p ₀ is the external pressure, $\mathcal {F}$ the total free energy of the nematic, and f the bulk free energy density (Eq. (3.3)). In equilibrium, nematic may exert stress on the confining boundaries; however, equilibrium bulk forces, calculated from the divergence of the stress tensor, are exactly zero.

3.5.2 Ericksen–Leslie–Parodi Approach

Ericksen–Leslie–Parodi (ELP) approach formulates the description of nematic hydrodynamics, which determines the coupling between the nematic director field and the velocity field. The model is written in terms of stress tensor σ _ij, molecular field $h_i=-\frac {\delta \mathcal {F}}{\delta n_i}$, rotation rate of the director with respect to the background fluid $N_i=\dot {n}_i-\left (\left (\nabla \times \mathbf {v}\right )\times \mathbf {n}\right )_i/2$, and symmetric velocity gradient tensor $A_{ij}=\left (\partial _iv_j+\partial _jv_i\right )/2$. ELP approach relies on considering the processes that contribute to the entropy production as expressions of thermodynamic forces (σ _ij and h _i) and thermodynamics fluxes (A _ij and N _i). Phenomenological relations between forces and fluxes must reflect the nematic symmetry n →−n and obey the Onsager reciprocal relations. The resulting expression for the molecular field is [1]

$$\displaystyle \begin{aligned} h_i=\gamma_1N_i+\gamma_2A_{ij}n_j, {} \end{aligned} $$

(3.34)

where γ ₁ and γ ₂ are the viscosity coefficients discussed below. The equation for the time derivative of n, derived from Eq. (3.34) has to include a Lagrange multiplier Λ to preserve the unit length of the director:

$$\displaystyle \begin{aligned} \dot{n}_i=\frac{1}{2}\left(\left(\nabla\times\mathbf{v}\right)\times\mathbf{n}\right)_i+\frac{1}{\gamma_1}h_i-\frac{\gamma_2}{\gamma_1}A_{ij}n_j-\Lambda n_i. {} \end{aligned} $$

(3.35)

Stress tensor is written within the ELP theory as:

$$\displaystyle \begin{aligned} \sigma_{ij}^{\text{viscous}}=\alpha_1 n_in_jn_kn_lA_{kl} +\alpha_2n_jN_i+\alpha_3n_iN_j +\alpha_4A_{ij} +\alpha_5n_jn_kA_{ik} +\alpha_6n_in_kA_{jk}. {} \end{aligned} $$

(3.36)

The viscosity coefficients γ ₁ and γ ₂ are functions of the Leslie viscosities α _i:

$$\displaystyle \begin{aligned} \gamma_1=\alpha_3-\alpha_2, \end{aligned} $$

(3.37)

$$\displaystyle \begin{aligned} \gamma_2=\alpha_6-\alpha_5=\alpha_2+\alpha_3. {} \end{aligned} $$

(3.38)

Six Leslie viscosities α _i are constrained by Eq. (3.38), meaning that there are five independent parameters within the ELP approach. For typical thermotropic liquid crystals, such as 5CB or MBBA, they are of the order of magnitude 0.001–0.1 Pa s [1] and can be measured by a variety of experimental techniques, such as observing liquid crystals under laminar flow, sound attenuation, time-dependent variation of orienting external fields, or scattering of light [1].

In order to better quantify nematic flow, one can construct and use relevant dimensionless numbers, as is also extensively used in general fluid dynamics. In experiments and simulation involving nematic flow, Reynolds number is typically smaller than 1. Also, Reynolds number does not include effects of orientational order. Better insight into nematic nature of flow is given by comparing elastic forces to the viscous forces in Eq. (3.34), which gives the Ericksen number

$$\displaystyle \begin{aligned} \text{Er}=\frac{\gamma_1 v/l}{K/l^2}=\frac{\gamma_1 vl}{K}, \end{aligned} $$

(3.39)

where v is a typical velocity of the problem and l a typical length scale. At small Ericksen numbers, the director dynamics is governed by the elastic terms. At large Ericksen numbers the dynamics is dictated by the velocity profile. Typical values for Ericksen number are Er ∼ 1 when considering annihilation of defect pairs [12, 13] or moderately slow flow in microchannels [14] and Er ∼ 20 for strong flow in microchannels [14].

Looking at the governing equations of the ELP approach, one can identify the basic mechanisms of nematic hydrodynamics. Below we show few selected basic examples of nematic flows. In Sect. 3.3 we have discussed how the nematic equilibrium orientation profile is defined by a minimum of the free energy. However, out of the equilibrium, nematic orientation field is deformed also by the velocity effects, as described, for example, by Eq. (3.35). Within ELP approach, the director field is distorted by velocity gradients that impose a hydrodynamic torque Γ = n ×h upon nematic molecules. At strong flows (i.e. strong Ericksen numbers) the director tends to align in the direction where the hydrodynamic torque Γ vanishes. Director tilt angle, at which this condition is satisfied, is in simple geometries given by the Leslie angle $\theta _{\text{L}}=\frac {1}{2}\arccos \frac {1}{\lambda }$, where λ is the alignment parameter, calculated from Leslie viscosities $\lambda =-\frac {\gamma _2}{\gamma _1}$. Figure 3.6 shows director structure for (a) Couette and (b) Poiseuille flow of a nematic fluid at Er ∼ 80 and λ = 1.1. The cell surface imposes strong homeotropic anchoring and the director deforms in the bulk due to hydrodynamic torques. For a Couette flow the director tilt angle in the middle of the sample is close to Leslie angle; however, next to the surfaces, it is continuously deformed to satisfy the boundary condition. Similar situation takes place in the Poiseuille geometry, only that the director tilts in the opposite direction when the shear is reversed. Alignment parameter λ typically reflects the shape of nematic molecules. For |λ| < 1, hydrodynamic torque does not vanish and the director field continuously deforms in time. An example of such tumbling motion is discussed in Sect. 3.6. λ can also have negative values, in which case it is associated with discotic molecules [65].

Fig. 3.6

Director distortion in (a) Couette and (b) Poiseuille flow at Er ∼ 80. Hydrodynamic torque due to velocity gradient tends to align the director tilt angle θ towards Leslie angle θ _L

Viscous stress tensor (Eq. (3.36)) includes six terms that couple local viscous losses to the director and its time derivative. The meaning of the anisotropy in the stress tensor is clearly seen in a simple geometry, as first considered by Miesowicz. In Miesowicz geometry a nematic is confined between parallel plates and subjected to shear flow. Nematic director is fixed by a strong magnetic or electric field in the direction (Fig. 3.7a) perpendicular to the flow and to the shear, (Fig. 3.7b) along the flow, or (Fig. 3.7c) along the shear. In each of the three cases, stress tensor is substantially simplified and an effective viscosity can be determined. For MBBA, values for the Miesowicz viscosities are η _a ≈ 0.042 Pa s, η _b ≈ 0.024 Pa s, and η _c ≈ 0.104 Pa s [1]. Measurement of Miesowicz viscosities is an important contribution when determining a full set of Leslie viscosities α _i in nematic fluids [1]. For MBBA, the lowest effective viscosity is in the case of the director pointing along the velocity field. For example, this characteristic can be used in flow-guiding through microfluidic junctions, as discussed in Sect. 3.6.

Fig. 3.7

Miesowicz geometry of shear flow in nematic microfluidics. Homogeneous director field is fixed by a strong external field (a) perpendicular to the flow and the shear, (b) along the flow, or (c) along the shear. An effective viscosity η _a, η _b, or η _c can be determined from the viscous stress tensor

Viscous stress tensor (Eq. (3.36)) is dependent not only on the direction of the director, but also on its time derivative, which means that time-variation of the director field may induce flows in a nematic, as, for example, in the process of relaxation to a free energy minimum or adaptation to time-varying external fields. Such example is the annihilation of a defect pair, which induces a flow field due to the relaxation of the orientational structure. Interestingly, the speed of the defects is substantially altered by the presence of flow. In annihilation of a $\pm \frac {1}{2}$ defect pair, in particular $+\frac {1}{2}$ defect is advected by the flow, increasing the rate at which the defects are approaching each other [12, 13]. Figure 3.8 shows an example of the annihilation of two opposite-charged umbilic defects, which also approach each other and annihilate [61].

Fig. 3.8

Director and flow field during the annihilation process of two opposite-charged umbilic defects. Director field is shown with white rods and flow field with green arrows. The position of approaching − 1 and + 1 umbilic is indicated by red dots. Reprinted figure with permission from [I. Dierking, M. Ravnik, E. Lark, J. Healey, G.P. Alexander, J.M. Yeomans, Phys. Rev. E 85, 21703 (2012)]. Copyright (2012) by the American Physical Society

ELP approach gives the nematic contribution to the material flow and velocity contribution to the orientational dynamics in a formulation, where individual mechanisms are easily recognisable. It is particularly useful when considering analytical solutions to the problems of nematic hydrodynamics. However, it suffers from the drawbacks of a director formulation, in particular the defect cores have to be always exempt from the calculation, which can make modelling or theoretical analysis difficult. In the next two sections, we present Beris–Edwards and Qian–Sheng models that not only recover the ELP equations at uniform degree of order S, but also include the coupling between the flow field and the degree of order. These two models are among most commonly used among many different formulations of nematodynamics within the tensorial nematic order parameter [66,67,68,69]. Since formulation of nematodynamic equations in terms of the tensor order parameter eliminates the need for the special treatment of defects, it allows to explore problems of further complexity.

3.5.3 Beris–Edwards Model

Beris and Edwards formulate their equations for nematic hydrodynamics through tensorial description of nematic order, where they utilise a generalisation of the Poisson bracket description of thermodynamics [5]. In a typical formulation, their equations are written as [70]:

$$\displaystyle \begin{aligned} \dot{Q}_{ij}=S_{ij}+\Gamma H_{ij}, \end{aligned} $$

(3.40)

(3.41)

(3.42)

where $\Omega _{ij}=\left (\partial _iv_j-\partial _jv_i\right )/2$ and H is the molecular field defined as:

$$\displaystyle \begin{aligned} H_{ij}=-\frac{1}{2}\left(\frac{\delta \mathcal{F}}{\delta Q_{ij}}+\frac{\delta \mathcal{F}}{\delta Q_{ji}}\right)+\frac{1}{3}Tr \left(\frac{\delta \mathcal{F}}{\delta Q_{kl}}\right)\delta_{ij}. \end{aligned} $$

(3.43)

Beris–Edwards model as formulated above has three independent viscosity parameters Γ, ζ, and η, from which Leslie viscosities can be determined [70]:

$$\displaystyle \begin{aligned} \begin{aligned}[c] \alpha_1&=\frac{\zeta^2}{\Gamma}\frac{9S^2}{2}\left(3S^2-2S-1\right),\\ \alpha_2&=-\frac{\zeta}{\Gamma}\frac{S}{4}\left(3S+4\right)-\frac{1}{\Gamma}\frac{9S^2}{4},\\ \alpha_3&=-\frac{\zeta}{\Gamma}\frac{S}{4}\left(3S+4\right)+\frac{1}{\Gamma}\frac{9S^2}{4},\\ \end{aligned} \begin{aligned}[c] \alpha_4&=\frac{\zeta^2}{\Gamma}\left(S-\frac{2}{3}\right)^2+2\eta,\\ \alpha_5&=-\frac{\zeta^2}{\Gamma}\frac{S}{4}\left( 3S-8\right)+\frac{\zeta}{\Gamma}\frac{S}{4}\left( 3S+4\right),\\ \alpha_6&=-\frac{\zeta^2}{\Gamma}\frac{S}{4}\left( 3S-8\right)-\frac{\zeta}{\Gamma}\frac{S}{4}\left( 3S+4\right). \end{aligned} \end{aligned} $$

(3.44)

The parameters in the Beris–Edwards model have a clear physical meaning. Rotational diffusion constant Γ sets up the typical time scale of the dynamical processes in the nematic at a given length scale. Parameter ζ is directly related to the alignment parameter in the ELP representation $\lambda =\frac {3S+4}{9S}\zeta$, thus prescribing the Leslie angle in the shear flow or tumbling nature of the nematic. Parameter η affects the isotropic viscosity in the system.

3.5.4 Qian–Sheng Model

A different nematodynamic model based on Q-tensor was formulated by Qian and Sheng [6]. Similar to ELP approach, in their derivation they follow the formalism of thermodynamic fluxes and forces, only within the description of the tensorial nematic order. Viscous stress tensor is written in Qian–Sheng formulation as:

(3.45)

where N _ij is the corotational derivative of the Q-tensor

$$\displaystyle \begin{aligned} N_{ij}=\dot{Q}_{ij}+\Omega_{ik}Q_{kj}-Q_{ik}\Omega_{kj}. {} \end{aligned} $$

(3.46)

Time evolution of the Q-tensor is given by

$$\displaystyle \begin{aligned} \dot{Q}_{ij}=\frac{H_{ij}}{\mu_1}-\frac{\mu_2A_{ij}}{2\mu_1}+Q_{ik}\Omega_{kj}-\Omega_{ik}Q_{kj}. {} \end{aligned} $$

(3.47)

Note that from Eqs. (3.46) and (3.47) the corotational derivative N _ij in the equation for the stress tensor can be expressed in terms of the molecular field H _ij, which is a form more similar to Beris-Edwards expression (Eq. (3.42)).

Qian–Sheng model is formulated with six viscosity coefficients β ₁, β ₄, β ₅, β ₆, μ ₁, and μ ₂, linked by relation β ₆ − β ₅ = μ ₂ The number of coefficients is exactly the same as in the Ericksen–Leslie theory. At a constant degree of order, coefficients can be exactly mapped between the two theories, thus allowing for the use of all of the experimentally measured viscosity coefficients given within the ELP formalism.

3.5.5 Towards Active Nematics

Materials that exhibit inherent activity are chemically or biologically different than standard nematic liquid crystalline fluids. However, selected active materials show nematic order, as, for example, kinesin driven microtubule, bacterial colonies, or flocks of animals [19]. A possible approach to describe in particular dense suspensions of such active constituents is to adapt equations of nematic hydrodynamics, as discussed in previous sections, for example, by including an active stress tensor. Active stress arises due to the force profiles that active particles apply on the surrounding, and can be written in the form of [71]

$$\displaystyle \begin{aligned} \sigma_{ij}^{\text{active}}=-\alpha Q_{ij}. {} \end{aligned} $$

(3.48)

The active stress is proportional to nematic tensor order parameter, with the proportionality constant α being the activity. For active particles that exert contractile stress α < 0, and for extensile α > 0. In such model, if nematic alignment is homogeneous, divergence of the active stress tensor is zero and there are no effective active forces present. However, even in homogeneous alignment, active nematics and polar gels are prone to instabilities [72]. Active forces are particularly high close to defects, where gradients of Q are high. As shown in Fig. 3.9, active forces give rise to the self-propulsion of + 1∕2 defects, which is an important mechanism in chaotic flows in active layers [73], or—at the interface with the passive nematic—active defects can even drive the distortion of the passive medium [74]. Note that in the addition to the presented there are other approaches for describing active nematic systems, such as Vicsek-like models [75], multiscale approaches [76], and minimal hydrodynamic models in terms of solely the velocity field [77].

Fig. 3.9

Active flow, developed around + 1∕2 topological defect for active extensile nematic in cylindrical confinement. The director field (solid red lines) and the velocity field (blue arrows) show the mechanism of self-propulsion of a + 1∕2 defect, which competes with the elastic forces on the defect, leading to a fixed nematic structure in time. For contractile active nematics, the direction of self-propulsion of + 1∕2 defects is exactly opposite. Reprinted figure with permission from [M. Ravnik, J. Yeomans, Phys. Rev. Lett. 110, 26001 (2013)]. Copyright (2013) by the American Physical Society

3.6 Nematic Microfluidics

In this section we show selected examples of nematic flow in typically confined environment. Fluidity of nematics can have important consequences in many applications, such as in liquid crystal displays [78, 79], or it can lead to complex pattern formation, as, for example, in the process of electroconvection [80, 81]. Rheological properties have been studied for variety of liquid crystalline materials, ranging from thermotropic liquid crystals [14] to cholesterics [82] and suspensions of viruses [83].

3.6.1 Nematic Flows in Channels

In Fig. 3.6 we showed nematic orientation in Couette and Poiseuille geometry at large Ericksen number and with strong homeotropic anchoring at the walls. Similar setup where the preferred alignment of the director at the walls is planar and perpendicular to the flow was investigated by Pieranski and Guyon [84]. An undistorted configuration in such Poiseuille geometry is shown in Fig. 3.10a. In particular at moderate Ericksen numbers, where nematic orientation is at a competition between elastic and hydrodynamic effects, there are two possible director orientations in such geometries of the shear flow, as shown in Fig. 3.10b. These two conformations occur in nematics with Leslie viscosities α ₂ and α ₃ of the same sign due to hydrodynamic torques that act on the director as soon as it slightly fluctuates from the undistorted alignment in Fig. 3.10a [2]. Since these director distortions compete with the planar anchoring at the surfaces, the transition to the distorted state occurs after a certain finite shear threshold is exceeded [84]. Above the threshold the director configuration varies in the z direction, leading to an additional force in the x direction F _A = ∂ _z σ _xz that is shown in Fig. 3.10c. The force leads to the creation of rolls in the velocity profile (Fig. 3.10c), which have a well-defined wavelength. The rolls coincide with the two solutions for the director reorientation. In fact, depending on the driving pressure difference and frequency, a range of mechanisms can be found, which lead to hydrodynamic instability and creation of rolls [84, 85]. Figure 3.10d shows a photograph, revealing rolls with different wavelengths due to different hydrodynamic instabilities in nematics. This example shows the creation of instabilities in the velocity field and in the nematic orientation, once the coupling terms are introduced into the stress tensor and the equation for the director orientation.

Fig. 3.10

Instabilities in the Poiseuille flow in nematic channels with anchoring perpendicular to the flow and flow gradient. (a) Geometry of the problem with the director field undistorted by the flow. (b) Two possible configurations of the director in the weak shear gradient. Left cylinder shows the alignment preferred by the nematic elasticity and surface anchoring. (c) Creation of the rolls in the velocity field due to the force F _A, two solutions shown in (b) alternate along the channel. (d) Experimental photograph of flow instabilities in Poiseuille geometry. Reused and adapted with permission from publisher [E. Guyon, P. Pieranski, Poiseuille flow instabilities in nematics. J. Phys. Colloq. 36, C1 (1975)]

As discussed in Sect. 3.5.2, in nematics with alignment parameter |λ| > 1, hydrodynamic torque disappears for certain angles of the director with respect to shear flow. For |λ| < 1 this is no longer the case and the hydrodynamic torque prefers to continuously rotate the director. In Ref. [86] two-dimensional nematic channels were explored in aligning and in tumbling regime. In the aligning regime, the director profile reaches a stationary orientation, which is not the case for tumbling motion. For straight channels, tumbling regime shows a series of π turns of the director across the channel. This turns are continuously generated and annihilated in time. In channels with variable width, director structure with π turns becomes unstable and pairs of opposite-charged defects are generated.

Dependence of the nematic viscosity on the director orientation can be used in microfluidic circuits to control the direction of flow and transport of material. One such example is given in Ref. [17], where electric field is used to switch nematic orientation in a channel. In Ref. [17] the preferred alignment of the director is along the channel, providing an effective Miesowicz viscosity η _b to the flow. Local electric field was used to impose director alignment along the shear, effectively increasing the viscosity for a factor of ∼4 to the Miesowicz value of η _c. When flow reached a Y-junction, most of the nematic fluid flows to the branch with the lower effective viscosity. It was shown that this mechanism could be used for particle sorting by turning the electric field on and off in individual branches of a Y-junction and by doing so controlling the flow through the junction. The colloidal particles go into the channel which has a stronger flow rate. Note that switching nematic orientation in the channel is not the only mechanism to transport and guide the cargo in nematic microfluidic circuits. Sengupta and co-workers demonstrated that in channels with hybrid anchoring conditions (anchoring along the normal at three sides of the rectangular channel, and anchoring along the channel at on side), a defect line can be guided through crossings of different channels. Colloidal cargo is then pinned to the defect line and advected along it by the flow [16].

3.6.2 Nematic Microfluidic Junctions

Complex flow field profiles, as induced, for example, in junctions of nematic microchannels, can be used to create and study topological nematic defects in a controlled environment. In Ref. [87] junctions of 4, 6, and 8 microchannels are used to create nematic defects with effective charge − 1, − 2, and − 3, respectively (Fig. 3.11a–c). The main mechanism for the creation of such defects is the fact that in the centre of a nematic microchannel at sufficiently large Ericksen numbers, the director turns along the channel, with the mechanism shown in Fig. 3.6b. Total net topological charge of − 2 and − 3 imposed in the junctions is realised by multiple defects with 3D topological charge of − 1 as this is indeed energetically more favourable state that cannot be further divided in smaller individual charges. In observed microjunctions two topological structures are present—a defect in the orientational field of the nematic and a stagnation point in the velocity field. Figure 3.11d–g shows how the cross-talk between this two topological singularities is probed by applying a pressure pulse in one of the channels. A fast shift of the stagnation point is always followed by a slow response of the nematic defect. In a stable configuration the position of both structures coincides. If the pressure was reduced in one of the outflowing channels (Fig. 3.11e, g) nematic defect first moves downstream and then gradually approaches the stagnation point, moving against the velocity direction. During the shift of the nematic defect, the stagnation point is more or less stationary. This is an example of a cross-talk between topological structures of different fields.

Fig. 3.11

Creation of topological defects within nematic microfluidic junctions [87]. One, two, and three defects of charge − 1 are created in junctions of 4, 6, and 8 microchannels, respectively. (a) Polarisation micrograph of the nematic structure. (b) Hydrodynamic stagnation point in the centre of a junction shown by epifluorescent imaging of fluorescent tracers. Panels (a and b) are courtesy of A. Sengupta. (c) Details of the nematic structure revealed by numerical simulations. The effective interaction between the stagnation point and the defect in the topological nematic orientation is probed by inducing a pressure pulse in (d) West or (e) South channel. The pressure pulse quickly shifts the stagnation point, marked by a white spot in the colourmap of the velocity magnitude. In (d) the relocation of the stagnation point is followed by a gradual shift of the nematic defect, as shown in (f). In (e and g) after the stagnation point is shifted, nematic defect first moves away from the stagnation point and only then gradually moves towards it. In both cases the stagnation point and the nematic defect return to original position after the pressure is restored

Nematic liquid crystals confined to porous networks are of particular interest due to their memory effects and switching possibilities, providing a route towards new optic and photonic materials [20, 88, 89]. The nematic alignment inside porous confinement can be controlled by flow [90, 91]. In Fig. 3.12 we show flow-induced dynamics of a defect structure inside a junction of six cylindrical capillaries. In a cylindrical confinement with homeotropic anchoring and without flow, nematic director prefers the escaped alignment, in which case the director in the middle of the channel points along the channel direction. This leads to a variety of equilibrium structures, depending on the direction of the director escape in individual channels [89]. One of such structures is shown in the first snapshot of Fig. 3.12, where a − 1 topological defect resides in the centre of the junction. Preferred nematic alignment in a capillary when flow is switched on is with the direction of the director escape along the flow. This leads to the flow-induced reconfiguration of the defect structure in a microjunction (Fig. 3.12). Upon the director escape reversal in left and right channel two + 1 defects are created. They merge with the − 1 defect in the junction centre, forming a defect structure with topological charge of + 1. Similar process is repeated as a − 1 defect is created in the up and in the down channel which merge with the preexisting + 1 defect, leading to the formation of a − 1 defect in the junction. The position of the defect is slightly off-centre since it is advected by the flow. Fig. 3.12 shows a transformational dynamics of a − 1 nematic defect, induced by the flow through the channels. Depending on the geometry of the initial equilibrium structure and the arrangement of the flow towards and away from the junction, a variety of switching processes and flow-stabilised structures is possible [92]. This example shows how porous networks with microfluidic functionality can be turned into advanced platform for generation of various topological field states.

Fig. 3.12

Flow-induced nematic structures in porous microfluidic channel networks [92]. Transformational dynamics of a − 1 nematic defect in a junction of six cylindrical micropores is observed with the direction of the director escape in the initial equilibrium configuration away from the junction in left and right channel, and towards the junction in up, down, front, and back channel. Transformational dynamics is characterised by flow-induced director escape reversal in individual channels and merging of multiple defects into one. Time is measured in units of nematic characteristic time scale $\tau _{\text{N}}= \frac {\xi _{\text{N}}^2}{\Gamma L}$

3.6.3 Colloidal Particles in Nematic Microfluidic Environment

In nematic colloidal dispersions, the drag force exerted upon the spherical particles is dependent on the particle velocity with respect to the director far field and the nematic structure around the particle [93]. Similar to the viscosity in the Miesowicz geometry, the effective viscosity for spherical particles is higher if they are dragged perpendicular to the director, compared to the movement along the director. The problem of drag force on spherical particles even gains in complexity, if colloids are introduced in chiral nematic liquid crystals, as, for example, in Ref. [94], where spherical particles with planar degenerate anchoring were dragged through cholesteric by a constant force at small Ericksen numbers. It was observed that for Er ≪ 1 the drag force on the particle scales linearly with the velocity. However, there is a distinct dependence on the particle radius R: for the motion along the cholesteric pitch, effective viscosity scales as η(R) ∼ R ^0.7, while for the particle motion perpendicular to the cholesteric pitch no definite scaling of η with particle radius is observed [94]. In the next section we shall discuss further implications of colloidal nematic systems, in particular in the view of self-assembly and nematic configurations due to complex-shaped microparticles.

3.7 Nematic Colloids

Nematic colloids are a soft material composed of particles, droplets, or bubbles embedded in a nematic fluid [21]. Nematic colloids attract great interest as they show effective elastic interaction between the particles, which originates from the nematic elasticity, shown in Sect. 3.7, in addition to conventional colloidal interactions such as steric, Coulomb, and van der Waals interactions. The exact profile, strength, and range of such elastic interactions are strongly affected by the surface properties of the particles, their shape, size, and topology, as well as external confinement, geometry, and possible external field. Nematic colloids are notably explored as novel materials with complex topological properties and as novel birefringent photonic materials, including for use as photonic crystals and metamaterials.

In this chapter we give review of selected nematic colloidal systems. First possible nematic director field configurations around a single spherical particle immersed in a liquid crystal are shown. Then elastic interparticle interactions are explained, which allow to organise colloids into larger structures. In the last part we introduce complex-shaped particles and particles with different topologies and their features.

3.7.1 Single Spherical Particle

A colloidal particle immersed in a nematic deforms the director field where the deformation depends strongly on the boundary conditions at the surface of the particle. The resulting nematic configuration is typically governed by an interplay between the bulk elastic and surface free energy.

In case of weak homeotropic anchoring (Fig. 3.13c), the surface terms in the total free energy are smaller than the bulk terms and the director field remains almost undistorted. No topological defects occur in the bulk. However, if the anchoring is strong, the director around the particle typically imposes frustration on the surrounding bulk orientation. Therefore, the nematic director cannot adapt to this frustration without creating orientational singularities. A point like hyperbolic − 1 defect (hedgehog) or a ring defect is formed around the particle with hometropic surface anchoring to achieve net zero topological charge characteristic of uniform field (Fig. 3.13a) [95]. The nematic configuration of particle accompanied with the hyperbolic − 1 defect has the symmetry and profile of an elastic dipole. Namely, the defect causes the deformations of the nematic far-field director that mimic the dipolar electric field caused by electric charge distributions and have the same positional dependence in terms of multipolar expansion.

Fig. 3.13

Director field profiles around a spherical particle with homeotropic anchoring immersed in nematic fluid: (a) elastic dipole with hyperbolic − 1 defect, (b) elastic quadrupole with singular Saturn ring defect, and (c) elastic quadrupole with no singular defect

In addition to the elastic dipoles, an elastic quadrupole can form and is characterised by a − 1∕2 disclination loop encircling the particle (Fig. 3.13b) [96]. Saturn ring emerges in regimes of generally smaller anchoring strength, smaller particle size, or stronger confinement with geometry or external fields. Effectively, it can be pushed to the surface of the particle (or virtually even within the particle) if anchoring is weak enough. By opening the point defect into a ring, the head–tail symmetry is established when the ring reaches the equatorial plane and the defect structure together with the sphere represents an elastic quadrupole. Note also, that hedgehog − 1 point defect is topologically equivalent to a − 1∕2 disclination loop (Saturn ring). In case of degenerate planar anchoring, two surface—boojum—defects are formed at the opposite poles of the particle, which also result in the quadrupolar nature of the structure. The nematic elasticity of the liquid crystals causes highly anisotropic interparticle interactions—i.e. with repulsive and attractive directions—and can lead to self-assembly of particles into larger structures.

3.7.2 Interparticle Interactions

Elastic deformations of the nematic director field, caused by colloidal particles are energetically unfavourable which leads to inter-interactions between the particles that minimise regions of such distortions. The long-range orientational order of liquid crystal is reflected also in long-range nematic interparticle interactions.

The type of long-range interactions depends on the symmetries of the distortions in the director field, induced by particles. The force between two colloidal particles in a nematic host medium can be measured experimentally and it has been shown that the interaction potential between particles with strong surface anchoring, which generates hedgehog defect, is anisotropic and proportional to the third power of inverse distance between the particles, similar as dipole electrostatic interaction [25]. The interaction potential between particles with weak anchoring or with Saturn ring defect was shown to have quadrupolar symmetry and is proportional to the fifth power of the inverse distance between the particles [97]. The binding energy of approximately micron sized colloids can reach the order of 1000 k _B T for dipolar type interactions and of the order of 100 k _B T for quadrupolar interactions. Landau–de Gennes free energy approach—presented above—has been used to calculate interparticle interaction, giving excellent agreement with the experiments [48, 98].

Two equally oriented elastic dipoles in a uniform nematic cell attract if they are collinear (Fig. 3.14a). However, if oriented in the opposite directions they repel in the direction along the far-field director, but attract sideways (Fig. 3.14b). Because there are only two attractive sites available around the sphere for dipoles oriented in the same directions, they form linear chains along the direction of the director (Fig. 3.15) [99, 100]. One should also note that the particles do not come in full contact with each other—they are separated by a small margin, which indicates the presence of short range repulsion. Typically, those short range repulsive interactions are again of elastic origin resulting from significant short-particle distance director field deformations.

Fig. 3.14

Micrographs, director field configurations, and polarisation micrographs for stable particle pair configurations of (a) parallel elastic dipoles, (b) anti-parallel elastic dipoles, and (c) elastic quadrupoles. From [S. Žumer, I. Muševic, M. Ravnik, M. Škarabot, I. Poberaj, D. Babič, U. Tkalec, Nematic colloidal assemblies: towards photonic crystals and metamaterials, SPIE Proc. 6911, 69110C (2008)]. Reprinted with permission from SPIE Publications

Fig. 3.15

Aggregation of dipolar nematic colloids. (a) Optical micrograph of a single colloidal particle with the defect structure of dipolar symmetry. (b) Schematic presentation of the nematic director field, where A denotes the actual hyperbolic point defect and B the virtual radial point defect inside the particle. Together they form a topological dipole. (c) Elastic dipoles form linear chains. (d) Chains bond together into 2D crystalline colloidal cluster. Letters denote different types of bonds. Reprinted figure with permission from [M. Škarabot, M. Ravnik, S. Žumer, U. Tkalec, I. Poberaj, D. Babič, N. Osterman, I. Muševič, Phys. Rev. E 76, 51406 (2007) ] Copyright (2007) by the American Physical Society

Elastic quadrupoles bind in different directions as elastic dipoles. Analogous to the electric case, quadrupoles repel if they are perfectly aligned (θ = 0^∘) or perpendicular (θ = 90^∘) to each other and attract for some finite angle θ (Figs. 3.14c, 3.16a, b), which depends on multiple parameters and is generally in the range of θ ∼20–30^∘. Elastic quadrupoles form zig-zag chains, generally perpendicular to the director field (Fig. 3.16c). The particles pairs can form via four different attractive sites, as shown also in 2D colloidal crystals (Figs. 3.15d, 3.16d). Typically, interactions of elastic quadrupoles are of one order of magnitude weaker than the interactions of elastic dipoles [101].

Fig. 3.16

Particles assemble along different directions and form (a) kinked chains, (b) linear chains, (c) longer self-assembled chain structures and (d) 2D quadrupolar crystal-like structures. Reprinted figure with permission from [M. Škarabot, M. Ravnik, S. Žumer, U. Tkalec, I. Poberaj, D. Babič, N. Osterman, I. Muševič, Phys. Rev. E 77(3), 31705 (2008)]. Copyright (2008) by the American Physical Society

Interparticle interactions strongly depend on the configuration of the director field. In examples presented so far, colloidal particles were immersed in a nematic cell with a uniform field. However, additional types of structures can be observed in more complex field configurations. As a strong example, multiple emulsions of nematic liquid crystal and water droplets were used to study colloidal interactions in a radial director field [101]. Conservation of topological charge was observed experimentally and the effects of different types of anchoring were studied.

In addition to dipole and quadrupole interactions, colloidal particles can be also bound by escaped defect lines, where the director escapes in the third dimension. Two particles with homeotropic anchoring can share an escaped—i.e. non-singular—line with an effective topological charge of − 2 in a so-called bubble-gum configuration [102] with the binding force being almost independent of the separation between the particles. In a nematic cell such configuration is rarely observed as the state is metastable; however, in twisted (chiral) cells such pairs form spontaneously and can also connect into larger 2D colloidal crystals [103].

Differently, two particles with Saturn ring defect can be entangled by a single escaped loop, acting as an elastic string [26]. Three different nematic configurations can be achieved by applying laser tweezers and thermally quenching (Fig. 3.17) the nematic around the particles: figure-of-eight (Fig. 3.17a), figure-of-omega (Fig. 3.17c, g), and figure-of-theta (Fig. 3.17d, h). The states are again metastable in a uniform nematic cell, but enable binding multiple particles into linear structures. Spontaneous entanglement can be realised in a twisted nematic cell, which allowed for the investigation of the knot theory on the defect lines [104].

Fig. 3.17

Assembling entangled nematic colloidal pairs by thermal quench using light. (a) Figure-of-eight. (b) Numerical simulation of the time evolution of entanglement measured in the number of iteration steps. (c) Evolution of figure-of-omega state. (d) Figure-of-omega state transformed into figure-of-theta. (e and f) Numerically calculated structures. Reprinted figure with permission from [M. Ravnik, M. Škarabot, S. Žumer, U. Tkalec, I. Poberaj, D. Babič, N. Osterman, I. Muševič, Phys. Rev. Lett. 99, 247801 (2007)]. Copyright (2007) by the American Physical Society

3.7.3 Assembly and Self-assembly of Colloidal Structures

Colloidal systems attract major interest also because of their ability to interact with light [105]. Periodic structures of dielectric media with a cell size, comparable to wavelength of light, also known as photonic crystals, enable guiding and control of the light at the microscale level. Nematic colloids present an interesting platform for development of soft matter photonics due to their self- and directed-assembly, responsiveness to external stimuli, and strong binding interactions. They also show interesting potential in the development and research of topological photonic materials and metamaterials, including at nanoscale [106, 107].

A method to assemble larger colloidal structures is by directed assembly using laser tweezers, which can capture and guide a single colloidal particle [99]. Particles are manipulated into vicinity of each other, close enough that structural forces can bind them into stable and ordered clusters. To create 2D crystal structures, thin nematic cells with properly processed surfaces are used, so that only one layer of colloids is formed in the middle of the cell. For example, clusters and 2D colloidal crystals are assembled from elastically dipolar particles by joining two oppositely oriented linear chains, which attract due to sideways dipolar attraction, or from quadrupolar particles by joining several kinked chains, which attract due to quadrupolar interactions [108].

In addition to homogeneous crystals, a range of binary structures were realised by using combinations of elastic dipoles and quadrupoles [109] or by using different sized particles, creating hierarchical superstructures (Fig. 3.18) [110]. 3D colloidal crystal with tetragonal symmetry and interesting material properties, such as strong electrostriction and electro-rotation, has also been assembled by joining anti-parallel chains of elastic dipoles [7].

Fig. 3.18

Hierarchical multi-particle nematic colloidal structure. (a) Smaller colloidal particles are trapped into the topological defect loop, twisting around a larger colloidal pair. Images are taken at different height of focus. (b) Polarising microscope image shows the distortions of the director field around the colloids. Reprinted figure with permission from [M. Škarabot, M. Ravnik, S. Žumer, U. Tkalec, I. Poberaj, D. Babič, I. Muševič, Phys. Rev. E 77, 61706 (2008)]. Copyright (2008) by the American Physical Society

Approaches in which particles are controlled to occupy predesigned sites are developed by creating spatially variable nematic profiles. Since minimal energy configurations are different for particles with homeotropic or planar anchoring, they tend to localise in different regions, such as particles with homeotropic anchoring in regions of splay and particles with planar anchoring in regions of bend deformations [111]. Also sculpting a flat surface with a cavity that is similar to the particle in size and shape can change the sign of the interaction between the particle and the surface and lead to key-lock mechanisms for trapping the particles [112]. Topographic modulation of the surfaces can be used to select and localise particles by using convex and concave deformations [113].

The director field can also be altered by changing the geometry of the cell, containing the nematic host medium, which can lead to emergence of variety of defects, depending on the shape of the surface. For example, if a nematic medium is introduced into the cell with an array of cylindrical microposts, defects occur around them in the bulk and attract colloidal particles (Fig. 3.19a–g). Colloids assemble to mimic the defect structure in the bulk even if they are remote, i.e. on the surface of the liquid crystal layer in which microposts are submerged. In the case of high packing fraction, a triangular colloidal lattice is formed (Fig. 3.19h) [114]. In a different study, colloidal chains of elastic dipoles were found to follow the disclination lines and curved director field in the geometry of groovy cells [115].

Fig. 3.19

If the geometry of the cell is altered by using microposts, the emergence of ring defects, which guide the assembly of remote colloidal particles, is enforced. (a) The director field in the corners of the cell with homeotropic anchoring can assume two different configurations with the opposite 2D topological charges. (b–d) The bulk director field corresponds to the minimum of free energy and has to satisfy the topological charge conservation. If the field in the corners has the same topological charge, the ring defect occurs to neutralise it. (e) By curving the edge, the configuration with positive winding number is favoured. (f) SEM image of experimentally realised curved microposts. (g) At moderate surface coverage, ordered rings assemble around the micropost due to attraction by the bulk defect and repel one another via long-range interparticle repulsion. (h) At higher particle density elastic interactions force them into higher order structures. Reused and adapted with permission from publishers [M. Cavallaro, M.A. Gharbi, D.A. Beller, S. Copar, Z. Shi, T. Baumgart, S. Yang, R.D. Kamien, K.J. Stebe, Exploiting imperfections in the bulk to direct assembly of surface colloids. Proc. Natl. Acad. Sci. 110, 18804 (2013)]

Nematic interparticle interactions depend strongly also on the shape of the particles. For example, polygonal particle platelets with odd number of sides exhibit dipolar symmetry and therefore dipolar interactions, while the ones with even number of sides act as elastic quadrupoles [116]. Since nonspherical particles may interact as dipoles/quadrupoles at long range, but their short range interactions depend on the geometry, they are suitable for realising 2D and 3D crystalline, quasicrystalline, and various locally ordered low-symmetry structures, which cannot be assembled from colloidal spheres [30]. Similar results were observed when using colloidal pyramidal cones and octahedrons made from thin nanofoil, which are physical analogues of mathematical surfaces with boundaries and induce no defects when flat [117]. Also switching between repulsion and attraction through re-pinning the disclinations at different edges of polygonal prism using laser tweezers has been demonstrated [118].

Among other ways of control, chemical treatment can be used to switch between different types of cell surface anchoring even at the nanoscale and control colloids by inducing defects [119] or to switch between anchoring types on colloids and therefore manipulate the type of interaction [120]. If ferromagnetic particles are used, also magnetic field can be used to control the orientation of the particles and their mutual interactions [121].

3.7.4 Complex-Shaped and Topological Colloids

The emergence of advanced chemical, physical, and biosynthetic methods in recent years enabled creation of complex-shaped anisotropic colloidal particles and even particles with different topologies. Combining such particles with liquid crystal medium lead to a wide variety of topological field states and configurations. In comparison to low temperature and magnetic systems at atomic scale, where topological phases also emerge, experiments with topology in liquid crystals can be observed at much larger optical scales. Additionally, complex structure of topological particles can lead to interesting assembly properties and interactions with light, which makes them suitable for photonic applications based on topological materials.

Topological colloidal particles with non-zero genus g (i.e. effectively, the number of holes in the particle) were demonstrated [28], which stabilise a wide variety of complex nematic profiles when immersed in nematic liquid crystal. The topology of the director field is governed by the topological charge conservation and by the Gauss–Bonnet and Poincare–Hopf theorems, which must be obeyed. By integrating the local Gaussian curvature K over the entire surface of the particle, its Euler characteristic, which is directly connected to the genus g, can be calculated as [28]:

$$\displaystyle \begin{aligned} 2(1-g)=\chi=\dfrac{1}{2\pi}\oint K\mathrm{d}S. \end{aligned} $$

(3.49)

The Euler characteristic acts as a topological invariant, which means that is preserved during the continuous transformations of the particle surface and also equals the topological charge of the surface. Net topological charge of the defects that emerge in the liquid crystal after the non-trivial particle is immersed in it is exactly determined by topological charge conservation, but the exact number of defects and their types depend on the shape and orientation of the particle with respect to the bulk field, which is determined by the minimum of the total free energy. Various possible configurations of defects in the vicinity of toroidal colloids with different genus numbers have been demonstrated [28].

Knot-shaped colloidal particles present another interesting platform to study interplay of the topologies of the particles, the nematic field, and the induced defects, which lead to knotted, linked, and other topologically non-trivial field configurations. Particle links in nematics were realised also as an example of topologically conditioned nematic colloidal material [8]. An example of configuration of linked rings, also known as Hopf link, with planar surface anchoring is shown in Fig. 3.20. Topological transitions by changing the shape and genus of the knot particles have been also studied numerically [122].

Fig. 3.20

Hopf link colloidal particle with tangential anchoring in nematic. (a, b) Polarising optical micrographs of a Hopf link in a nematic cell without and with a lambda plate, respectively, with far-field nematic director n ₀ marked on the image. (c, d) Experimental and theoretical in-plane cross-section with a director field around it. (e) Elastic free energy dependence on the deviation from equilibrium angle and centre-to-centre distance of the two link components—rings. (f–h) Three perspective views from mutually orthogonal directions of a numerically calculated director field around the link. (i) Landau–de Gennes free energy vs. angle θ _1,2 between bulk director orientation and the plane bisecting the angle θ _1,2 = 20^∘ between the rings at fixed radius R and d = 0.22, with the energy minimum corresponding to the configuration f. Inset in (i, j) Metastable configurations. Reused and adapted with permission from publishers [A. Martinez, L. Hermosillo, M. Tasinkevych, I.I. Smalyukh, Linked topological colloids in a nematic host. Proc. Natl. Acad. Sci. 112, 4546 (2015)]

Current research in the field of nematic colloids is more and more directed towards finding new possible interactions between particles, which are governed by their topologically non-trivial or fractal shape [123] that induces tangled director fields and defects in the liquid crystal medium. Such particles can nowadays be fabricated and used in experiments and show a lot of promise in photonic applications. A strong recent direction is also in exploring motile “active” colloids in anisotropic nematic background, which can be driven by external fields or internally via self-propelled particles such as motile bacteria or molecular motors [74, 124, 125].

3.8 Conclusions

Nematic fluids cover a span of materials, from molecular fluids, colloidal dispersion to viruses, with their main material characteristic being orientational order of the building blocks. This orientational order is soft and as an effective elastic medium responsive to external stimuli, including mechanical fields, pressure, light, electric and magnetic fields. The strong susceptibility to external stimuli makes nematic fluids potent materials in systems that require controllability and tunability, which is today extensively used in display and optical applications, with strong development also towards photonics and metamaterial applications.

A major emergent direction in nematic fluids are also active nematic materials, which are inherently out-of-equilibrium systems based on motile building blocks that can show nematic ordering. Active nematic systems include systems of kinesin driven microtubules, bacterial colonies, or flocks of animals. Topological defects in active fluids are emerging as major elements that determine the active material properties. And there exists an interesting route for transfer of knowledge from passive nematic fluids to active nematic fluids. For example, in terms of structure, nematic braids realised by temperature quench in passive nematics are probably the closest passive analogues to three-dimensional active turbulence, as one of the top-level challenges in understanding of active nematics.

Finally, nematic fluids is a topic that is naturally in an interdisciplinary way reaching towards other field of science and technology, notably including complex flows and active fluids.