Abstract
Term graphs are the concept at the core of important implementation techniques for functional programming languages, and are also used as internal data structures in many other symbolic computation setting, including in code generation back-ends for example in compilers. To our knowledge, there are no formally verified term graph manipulation systems so far; we present an approach to formalising term graphs, as a relatively complex example of graph structures, in the dependently-typed programming language and proof system Agda in a way that both the mathematical theory and useful executable implementations can be obtained as instances of the same abstract definition.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Terms (or expressions) are the conceptual data structure at the heart of almost all symbol manipulation for mathematical reasoning and programming language implementation. Terms as a data structure are a kind of trees, and in many applications, intermediate or result terms arise that contain multiple copies of equal subterms. To save space in software implementations of such applications, all these copies are frequently represented by references to a single copy: Conceptually, the tree is replaced by a (directed, and for the purposes of the current paper always acyclic) graph, a term graph. Nowadays, term graphs are typically considered as jungles, a kind of directed hypergraphs introduced for this purpose by Hoffmann and Plump (1991) and Corradini and Rossi (1993).
For the purpose of creating a toolset for term graph manipulation supported by machine-checked correctness proofs, we develop a flexible formalisation of term graphs in a categorial setting, with the following goals:
-
We want to use the formalisation to develop mathematical theories of term graph transformation and how it can be used in particular for correct-by-construction compiler optimisation passes.
-
We want to use that same formalisation as basis for executable implementations of these compiler optimisation passes.
As our formalisation setting, we use the dependently-typed programming language and proof assistant Agda (Norell 2007). Agda permits us to write definitions essentially in the way they are written for mathematical purposes, and prove properties about them, but all function definitions are also executable, making this a good environment for correct-by-construction tool development.
The body of this paper will start from a sequence of mathematical definitions (expressed in Agda) of datatypes for somewhat simplified term graphs, then consider also an implementation-oriented definition, and proceed to abstract both to a common generalisation. The full complexity of term graphs is the recovered in a few more refinements.
The result is a simple language for defining not only term graphs, but any of a large class of different kind of graph datastructures, when recognising these as coalgebras possibly including dependently-typed operations, as far as dependencies are used with a certain discipline.
2 Jungle Representation of Term Graphs
We think of term graphs as a kind of data-flow graphs, and we draw the flow from inputs (labelled by their positions in triangles) at the top to output positions at the bottom. We use the jungle approach of Hoffmann and Plump (1991); Corradini and Rossi (1993): We define term graphs as hypergraphs, where each (hyper-)edge is labelled with an operation name, and connected via “input tentacles” (drawn as arrows to the box representing the hyperedge) to the edge’s input nodes, and via a single “output tentacle” (pointing away from the edge) to its output node. Term graph inputs correspond to variables in terms; so if we map each input position i to the variable \(x_i\), then the term graph in the following drawing to the left represents the term \((x_1 + x_2) * x_2\):

The term graph drawn above to the right has two output positions, and therefore should be interpreted as a pair of terms; in this case the two output positions are “fed” from the same node, so this is just the pair \(\langle (x_1 + x_2) * x_2, \; (x_1 + x_2) * x_2\rangle \). (We could easily switch to considering multi-output edges, but for the purposes of the current paper this would only result in some duplication, without introducing any additional interesting aspects, so we stick with single-output edges.)
The pure “directed hypergraph” aspect of term graph structure, without considering inputs and outputs, and without restricting the edge output assignment to be bijective onto non-input nodes, can be captured via the following signature:

This is a coalgebraic signature in the sense used in (Kahl 2014, 2015): the argument type of each operation symbol is a single sort, and the result type is a term in a language of functor symbols (here including the constant symbol L and the unary \(\mathord {\textsf {List}}\) functor symbol) over the sorts (as variables).
3 Directed Hypergraphs—Simplified
To proceed towards capturing the full term graph structure and reduce ad-hoc notations, we now switch to using Agda Norell (2007) as our mathematical notation. The following Agda record type definition defines the type \(\mathsf {DHG}_{00}\) to be the type of tuples containing the four setsFootnote 1 \(\mathord {\textsf {Input}}\), \(\mathord {\textsf {Output}}\), \(\mathord {\textsf {Inner}}\), and \(\mathord {\textsf {Edge}}\), together with the five functions \(\mathord {\textsf {gOut}}\), \(\mathord {\textsf {eOut}}\), \(\mathord {\textsf {eArity}}\), \(\mathord {\textsf {eLabel}}\), and \(\mathord {\textsf {eIn}}\). The choice to have separate functions for assigning each edge its arity (number of edge input positions), its label, and its actual input node sequence has been made to introduce the right kind of problems for discussion in the current paper.
Different input positions need to be associated with different nodes — for simplicity, we identify input positions and input nodes, and introduce a separate carrier set for “inner” nodes, that is, nodes that are not input nodes. Both input nodes and inner nodes can be used as edge inputs, so we introduce the abbreviationFootnote 2 “\(\mathord {\textsf {Node}}\)” for the set of all nodes, constructed as the disjoint sum of the input node set and the inner node set:

This models directed hypergraphs with input and output interfaces, but not yet term graphs where \(\mathord {\textsf {eOut}}\) needs to be bijective—we will come back to that only in Sect. 11. Dealing with directed hypergraphs is motivated by the fact that we use them as setting for double-pushout (DPO) rewriting of term graphs—directed hypergraphs include the “term graphs with holes” that occur as gluing and host graphs in DPO rewriting steps.
The \(\mathsf {DHG}_{00}\) record type declaration corresponds again to a coalgebraic signature in the sense explained above, after expanding the \(\mathord {\textsf {Node}}\) abbreviation, as can be seen in the following reformulation:

Since the presence of the local definition for \(\mathord {\textsf {Node}}\) may perhaps be confusing for readers unfamiliar with Agda, we will stick with continue our development from this expanded version.
4 Interface-Parameterised Directed Hypergraphs
We will need to implement several operations on our directed hypergraphs, in particular sequential composition: If the set of output positions of \(G_1\) coincides with the set of input positions of \(G_2\), then their sequential composition  results from “gluing them together” along this common interface.
results from “gluing them together” along this common interface.
Since we want type-checking to guarantee well-definedness of any applications of  we use in programs manipulating term graphs, the input and output interfaces need to be part of the type of \(G_1\) and \(G_2\). In Agda, this is achieved by making the record type parameterised:
we use in programs manipulating term graphs, the input and output interfaces need to be part of the type of \(G_1\) and \(G_2\). In Agda, this is achieved by making the record type parameterised:

(Mathematically, this corresponds to defining a functor from trivial two-sort coalgebras to coalgebras of shape \(\mathsf {DHG}_{01}\).)
5 Implemented Directed Hypergraphs
So far, the record types we defined are mathematical datatypes, with sets as components, exactly in the way used for mathematical studies of term graphs. Since we used Agda as our mathematical language, and Agda can be used as a proof checker, we can build a mathematical theory of directed hypergraphs and term graphs on top of these definitions.
However, since Agda is also a programming language, we would like to also use our definitions for data structures used in programs that manipulate term graphs. However, records containing \(\mathord {\textsf {Set}}\) fields are hard to use—how do you save one of those to a file? The field \(\mathord {\textsf {Edge}}\) could be a set of functions...
To come from the opposite perspective, consider now what a plausible implementation datatype for directed hypergraphs might look like. We present a “proof-of-concept” implementation based on arrays, using the \(\mathord {\textsf {Vec}}\) datatype constructor for dependently-typed vectors from the Agda standard library (Danielsson et al. 2018)—the type “\(\mathord {\textsf {Vec}}\;\mathord {\textsf {A}}\;\mathord {\textsf {n}}\)” is the type of \(\mathord {\textsf {n}}\)-element vectors with elements of type \(\mathord {\textsf {A}}\). (A “production” implementation might for example use some kind of binary trees, or a type of arrays with constant-time access.)
A plausible design is then to use as carrier sets only sets constructed by \(\mathord {\textsf {Fin}}\); for a natural number \(\mathord {\textsf {n}}\), the type “\(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}}\)” is the type of natural numbers less than \(\mathord {\textsf {n}}\). The elements of “\(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}}\)” are precisely the indices that can be used with vectors of type “\(\mathord {\textsf {Vec}}\;\mathord {\textsf {A}}\;\mathord {\textsf {n}}\)”.
However, where the mathematical data structure contains \(\mathord {\textsf {Set}}\)s of size \(\mathord {\textsf {n}}\), the implementation data structure will contain only the index \(\mathord {\textsf {n}}\):

It is straight-forward to write a function that maps each element of “\(\mathsf {VecDHG}_{1}\,\,\mathsf {m}\,\mathsf {n}\)” to the mathematical representation of that graph in the type “\(\mathsf {DHG}_{02}\,\,\textsf {(Fin}\,\textsf {m)}\,\,\textsf {(Fin}\,\textsf {n)}\)”, and this would populate also the \(\mathord {\textsf {Inner}}\) and \(\mathord {\textsf {Edge}}\) fields with \(\mathord {\textsf {Fin}}\) types. However, it is quite cumbersome to attempt to define even a partial inverse to that, which makes it essentially infeasible to use operations defined on the “mathematical implementation” \(\mathsf {DHG}_{02}\) to induce operations on the “executable implementation” \(\mathsf {VecDHG}_{1}\).
Perhaps more importantly, there is no good way to “obtain” the definition of \(\mathsf {VecDHG}_{1}\) “from” that of \(\mathsf {DHG}_{02}\), or even more generally, to adapt \(\mathsf {DHG}_{02}\) to finite node and edge sets—one could do this via an extension that adds finiteness proofs. But using this approach to restrict \(\mathsf {DHG}_{02}\text {s}\) to those having node and edge sets of shape “\(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}}\)” would involve a type-level propositional equality that would be extremely awkward to use.
The solution to this problem is to obtain both as instances of a generalised, abstract definition, with essentially the goal of being able to
-
instantiate with \(\mathord {\textsf {Set}}\) and
 to obtain the mathematical theory, and
to obtain the mathematical theory, and -
instantiate with \({{\mathbb {N}}}\) and \(\mathord {\textsf {flip}}\;\mathord {\textsf {Vec}}\) to obtain the desired implementation.
After putting it this way, the natural option is to use a category as parameter.
6 Abstract Directed Hypergraphs—First Attempt
We now assume that we are in a setting where \({\mathcal {C}}\) is an arbitrary but fixed category with coproducts—the Agda way of expressing this is to locate the development in a parameterised module (with additional parameters for \(\mathord {\textsf {ListF}}\) etc.):

Then occurrences of \(\mathord {\textsf {Set}}\) in \(\mathsf {DHG}_{02}\) are replaced with the type of objects of category \({\mathcal {C}}\), and operations become morphisms instead of functions:

We shall use the name \(\mathord {\textsf {vecCategory}}\) for the category with natural numbers as objects, and where the type of morphisms from \(\mathord {\textsf {m}}\) to \(\mathord {\textsf {n}}\) is “\(\mathord {\textsf {Vec}}\;(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}})\;\mathord {\textsf {m}}\)”; the coproduct there is just addition.
Trying to instantiate \({\mathcal {C}}\) with \(\mathord {\textsf {vecCategory}}\) presents the problem that that even if \(\mathord {\textsf {obj}}{\mathbb {N}}\) and \(\mathord {\textsf {ListF}}\) are supplied as module parameters in  , we will not find any \(\mathord {\textsf {n}}\) such that \(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}}\) represents \({{\mathbb {N}}}\) respectively
, we will not find any \(\mathord {\textsf {n}}\) such that \(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}}\) represents \({{\mathbb {N}}}\) respectively  . (For the sake of the argument, we will ignore the option to restrict to some maximal arity that might be sufficient for some particular application.)
. (For the sake of the argument, we will ignore the option to restrict to some maximal arity that might be sufficient for some particular application.)
7 Abstract Directed Hypergraphs—Second Attempt
The solution to this problem is to make use of the type discipline of a coalgebra: Only sorts occur as argument types; infinite types like \({{\mathbb {N}}}\) and  only occur in the result types. We translate this into a setting where we do not need morphisms starting from all types—we embed the parameter \({\mathcal {C}}\) (that we plan to instantiate with \(\mathord {\textsf {vecCategory}}\)), used for the morphisms between all relevant finite sets, including the carrier sets, in a semigroupoidFootnote 3 \(\mathcal {S}\) that provides objects also for \({{\mathbb {N}}}\) and
only occur in the result types. We translate this into a setting where we do not need morphisms starting from all types—we embed the parameter \({\mathcal {C}}\) (that we plan to instantiate with \(\mathord {\textsf {vecCategory}}\)), used for the morphisms between all relevant finite sets, including the carrier sets, in a semigroupoidFootnote 3 \(\mathcal {S}\) that provides objects also for \({{\mathbb {N}}}\) and  .
.
The semigroupoid \(\mathcal {S}\) will need to have morphisms from objects of \({\mathcal {C}}\) to the object \(\mathord {\textsf {obj}}{\mathbb {N}}\) implementing \({{\mathbb {N}}}\), and in the context of our implementation, these can all be implemented as vectors of the types “\(\mathord {\textsf {Vec}}\;{{\mathbb {N}}}\;\mathord {\textsf {k}}\)” for natural numbers \(\mathord {\textsf {k}}\). However, \(\mathcal {S}\) does not need any morphisms starting at \(\mathord {\textsf {obj}}{\mathbb {N}}\), so we can characterise \(\mathcal {S}\) in a way that precisely fits this vector-based implementation: Vectors can contain elements of infinite types, but vectors cannot be infinite.
The (full and faithful, coproduct-preserving, ...) semigroupoid functor \(\mathcal {F}\) embedding \({\mathcal {C}}\) in \(\mathcal {S}\) becomes another important part of the setting we now adopt:

Functions “between sorts”, here \(\mathord {\textsf {gOut}}\) and \(\mathord {\textsf {eOut}}\), are now morphisms in the parameter category \({\mathcal {C}}\), while functions from a sort to an “arbitrary” (potentially infinite) type are morphisms in the parameter semigroupoid \(\mathcal {S}\), starting from the \(\mathcal {F}\)-image of the sort.

Instantiating \({\mathcal {C}}\) with the category \({Set }\) and \(\mathcal {S}\) with the underlying semigroupoid makes the resulting \(\mathsf {ADHG}_{1}\) directly equivalent with \(\mathsf {DHG}_{02}\).
Instantiating \({\mathcal {C}}\) with \(\mathord {\textsf {vecCategory}}\) and \(\mathcal {S}\) with a carefully constructed semigroupoid (\({\mathcal S}^{\mathcal F}\) in Appendix B) with arbitrary vectors as morphisms resulting \(\mathsf {ADHG}_{1}\) directly equivalent with \(\mathsf {VecDHG}_{1}\).
Other easy instantiations are useful, too: For example, instantiating \({\mathcal {C}}\) with the category of all finite sets and \(\mathcal {S}\) with the semigroupoid of all sets gives us the variant of \(\mathsf {DHG}_{02}\) restricted to finite carrier sets.
8 Directed Hypergraphs—Dependently Typed
A different issue with \(\mathsf {DHG}_{02}\) is the fact that the types do not enforce that the length of an edge’s input node list corresponds to its arity: In terms of \(\mathsf {DHG}_{02}\), we want to add the following restriction:

It would be possible to add this in the spirit of datatype invariants as the type of an additional  to the record, which then induces a proof obligation at every record construction site. Therefore it is far more attractive to move this invariant into the type system, which is possible in Agda due to its support for dependent types: A dependent function type “
to the record, which then induces a proof obligation at every record construction site. Therefore it is far more attractive to move this invariant into the type system, which is possible in Agda due to its support for dependent types: A dependent function type “ ” contains functions mapping each \(\mathord {\textsf {e}}\;\mathbin {:}\;\mathord {\textsf {Edge}}\) to an element of type “\(\mathord {\textsf {R}}\;\mathord {\textsf {e}}\)”, where
” contains functions mapping each \(\mathord {\textsf {e}}\;\mathbin {:}\;\mathord {\textsf {Edge}}\) to an element of type “\(\mathord {\textsf {R}}\;\mathord {\textsf {e}}\)”, where  is assumed to be some “result” type constructor depending on an \(\mathord {\textsf {Edge}}\) argument.
is assumed to be some “result” type constructor depending on an \(\mathord {\textsf {Edge}}\) argument.
We use the additional expressivity provided by dependent types to move from \(\mathord {\textsf {List}}\) to \(\mathord {\textsf {Vec}}\) in the result type of \(\mathord {\textsf {eIn}}\), and for each result vector we supply the arity of the edge in question as length:

At the same time, we also switched the type of edge labels to come from an arity-indexed label set  .
.
Although this is not anymore of the shape of a coalgebra signature as described in Sect. 2, this is still a type of coalgebras mathematically, due to the fact that the dependent arguments are used only as arguments to other operations.
9 Implementation of Dependently-Typed Fields
The implementation type \(\mathsf {VecDHG}_{1}\) is easily adapted to such dependent fields, exploiting the presence of dependent pair types (\(\varSigma \)-types): The type “ ” is inhabited by pairs “\(\mathord {\textsf {a}}\;\mathord {\textsf {,}}\;\mathord {\textsf {b}}\)” where \(\mathord {\textsf {a}}\;\mathbin {:}\;\mathord {\textsf {A}}\) and \(\mathord {\textsf {b}}\;\mathbin {:}\;\mathord {\textsf {B}}\;\mathord {\textsf {a}}\) (where
” is inhabited by pairs “\(\mathord {\textsf {a}}\;\mathord {\textsf {,}}\;\mathord {\textsf {b}}\)” where \(\mathord {\textsf {a}}\;\mathbin {:}\;\mathord {\textsf {A}}\) and \(\mathord {\textsf {b}}\;\mathbin {:}\;\mathord {\textsf {B}}\;\mathord {\textsf {a}}\) (where  is a type constructor taking an argument of type \(\mathord {\textsf {A}}\)).
is a type constructor taking an argument of type \(\mathord {\textsf {A}}\)).
Straight-forwardly embedding the type constructors for labels and input vectors in \(\varSigma \)-types yields the following refined implementation type:

Such structures will then be subject to the following datatype invariants:

A more rational implementation (which can easily be obtained by a systematic transformation from \(\mathsf {VecDHG}_{2}\)) would store these three equal values only once, and at the same time also be closer to directly representing the functor underlying the coalgebra type here:

10 Dependently-Typed Abstract Directed Hypergraphs
For abstracting dependently-typed operations into the category-semigroupoid setting of Sect. 7, we introduce an minimal interface to dependent objects that can be seen as individual building blocks of a type-category as described by Pitts (2001), adapted so that it “does not demand existence of too many morphisms” for our semigroupoid:
Definition 10.1
For an object I of \(\mathcal {S}\), an object \(\mathord {\textsf {D}}\) of \(\mathcal {S}\) is a dependent object indexed over I iff for every object \(\mathord {\textsf {Y}}\;\mathbin {:}\;{\mathcal {C}.Obj}\) and every morphism \(\mathord {\textsf {f}}\) from \(\mathcal {F}\,\mathord {\textsf {Y}}\) to \(\mathord {\textsf {D}}\) in \(\mathcal {S}\) there is a morphism \(\mathord {\textsf {ind}}_{D}\ \mathord {\textsf {f}}\) from \(\mathcal {F}\,\mathord {\textsf {Y}}\) to I in \(\mathcal {S}\) such that the operation \(\mathord {\textsf {ind}}_{D}\) commutes with \({\mathcal {C}}\)-pre-composition, that is, for every object X of \({\mathcal {C}}\) and every morphism \(\mathord {\textsf {g}}\) from \(\mathord {\textsf {X}}\) to \(\mathord {\textsf {Y}}\) in \({\mathcal {C}}\), the following holds:

\(\square \)
The \(\varSigma \)-types of Sect. 9 are an instance of dependent objects by virtue of implementing \(\mathord {\textsf {ind}}_{D}\ \mathord {\textsf {f}}\) as \(\textsf {(Vec.map}\,\mathsf {proj}_{1}\,{\textsf {f)}}\), extracting the index from dependent pairs. The “trick” of dependent objects is that the dependent-pair-projection \(\mathsf {proj}_{1}\) used here does not need to be a morphism of the semigroupoid \(\mathcal {S}\), making it possible to define \(\mathcal {S}\) in a way that all its morphisms can be implemented based on vectors.
For the abstract variant, we assume a dependent objects \(\mathord {\textsf {Label}}\) and a “dependent functor” \(\mathord {\textsf {VecF}}\); the latter needs to map any object \(\mathord {\textsf {A}}\) of \(\mathcal {S}\) to a dependent object with the common index \(\mathord {\textsf {obj}}{\mathbb {N}}\). (The dependent functor image of a morphism \(\mathord {\textsf {f}}\) can be implemented as \(\mathord {\textsf {f}}\) itself tagged with a name of the functor, see Appendix B.)
We introduce two new abbreviations, so that operation types now can be of the following three kinds (due to the coalgebra nature, all have to “conceptually start” at sorts, which are objects of \({\mathcal {C}}\)):

That is,  contains pairs of shape \((\mathord {\textsf {g}}\;\mathord {\textsf {,}}\;\mathord {\textsf {p}})\) where
contains pairs of shape \((\mathord {\textsf {g}}\;\mathord {\textsf {,}}\;\mathord {\textsf {p}})\) where  and \(\mathord {\textsf {p}}\) is a proof for the morphism equality of \(\mathord {\textsf {ind}}_{D}\ \mathord {\textsf {g}}\) with f.
and \(\mathord {\textsf {p}}\) is a proof for the morphism equality of \(\mathord {\textsf {ind}}_{D}\ \mathord {\textsf {g}}\) with f.
For the instance \(\mathsf {VecDHG}_{2}\), these proofs are exactly proofs for the datatype invariants mentioned there. The final abstract version of our directed hypergraph type therefore also starts closer to \(\mathsf {VecDHG}_{2}\) than to \(\mathsf {VecDHG}_{3}\):

While  is essentially just a kind of “casting” that emphasises the “starting at a sort” intention, the type constructor
is essentially just a kind of “casting” that emphasises the “starting at a sort” intention, the type constructor  is the real innovation here; thanks to
is the real innovation here; thanks to  , the presentation of \(\mathsf {ADHG}_{2}\) does not require local variable binders;
, the presentation of \(\mathsf {ADHG}_{2}\) does not require local variable binders;  therefore introduces the possibility of result type dependencies on the result of other operations into coalgebraic signatures while preserving the overall character of traditional signatures. (Technically,
therefore introduces the possibility of result type dependencies on the result of other operations into coalgebraic signatures while preserving the overall character of traditional signatures. (Technically,  and
and  can be considered as parts of a shallowly-embedded DSL for a novel kind of coalgebra signatures.)
can be considered as parts of a shallowly-embedded DSL for a novel kind of coalgebra signatures.)
Expanding definitions, we see that  from above is a dependent pair of type
from above is a dependent pair of type  ; for convenience, we give individual names to the two constituents of this pair, which then have the following types, the second of which corresponds to the first datatype invariant in Sect. 9 (where \(\mathord {\textsf {fst}}\) implements \(\mathord {\textsf {ind}}_{\mathord {\textsf {Label}}}\)).
; for convenience, we give individual names to the two constituents of this pair, which then have the following types, the second of which corresponds to the first datatype invariant in Sect. 9 (where \(\mathord {\textsf {fst}}\) implements \(\mathord {\textsf {ind}}_{\mathord {\textsf {Label}}}\)).

11 GS-Monoidal Categories of Abstract Term Graphs
The definition of abstract directed hypergraphs we actually use also has the \(\mathord {\textsf {Node}}\) definition again, and therefore is even more readable:

As mentioned in Sect. 2, we are really interested in jungles, which are directed hypergraphs with a one-to-one correspondence between edges and inner nodes established by \(\mathord {\textsf {eOut}}\). Since we need directed hypergraphs as common substrate for an adapted kind of double-pushout term graph rewriting, we define jungles separately as “\(\mathsf {ADHG}_{3}\text {s}\) where \(\mathord {\textsf {eOut}}\) is an isomorphism in \({\mathcal {C}}\)”, in Agda:

The full setting used as context for this includes a few properties not yet mentioned in Sect. 7; it consists of the following items:
-
A category \({\mathcal {C}}\) intended to have (representations of) all possible carrier sets as objects, and (representations of) functions between these as morphisms.
\({\mathcal {C}}\) needs to have coproducts, a terminal object, and a strict initial object.
-
A semigroupoid \(\mathcal {S}\) intended to have (representations of) all possible value sets (including label sets,
 , vector sets) as objects.
, vector sets) as objects.\(\mathcal {S}\) is only required to contain the morphisms associated with the additional structure below; it can be quite “sparse”.
-
A full and faithful semigroupoid functor \(\mathcal {F}\) from the semigroupoid underlying \({\mathcal {C}}\) to \(\mathcal {S}\) that preserves identity morphisms, coproducts, and initial objects.
This functor is understood as embedding \(\mathcal {C}\) into \(\mathcal {S}\).
-
Specifically as setting for the \(\mathord {\textsf {ADHG}}\) definitions, a natural number object \(\mathord {\textsf {obj}}{\mathbb {N}}\), an \(\mathord {\textsf {obj}}{\mathbb {N}}\)-indexed dependent object \(\mathord {\textsf {Label}}\), and an \(\mathord {\textsf {obj}}{\mathbb {N}}\)-indexed dependent functor \(\mathord {\textsf {VecF}}\) for vectors satisfying an appropriate vector specification.
In this setting, we have implemented large parts of the theory of gs-monoidal categories introduced by Corradini and Gadducci (1999): For term graphs, monoidal composition \(\otimes \) is “parallel composition” that “concatenates” (via coproduct) the input and output interfaces; gs-monoidal categories are monoidal categories with additional transformations ! and \(\nabla \):
-
 is the terminator and introduces garbage, and
is the terminator and introduces garbage, and -
 is the duplicator and introduces sharing.
is the duplicator and introduces sharing.
These are present also in cartesian categories such as Lawvere theories, and there they are natural transformations. In gs-monoidal categories they do not need to be natural, which is important for term graphs, where garbage and sharing make a difference.
We have implemented (Zhao 2018a, b) Agda-verified gs-monoidal categories with \(\mathord {\textsf {ADHG}}\)s respectively \(\mathord {\textsf {Jungle}}\)s as morphisms fully at the abstract level in the category-semigroupoid setting described above. We also implemented \(\mathord {\textsf {Jungle}}\) decomposition and proved it correct, which is the core of the result of Corradini and Gadducci (1999) that term graphs (i.e., jungles) form a free gs-monoidal category. For this part, we followed Corradini and Gadducci’s set-up, which specialises \(\mathcal {C}.\mathord {\textsf {obj}}\) to \({{\mathbb {N}}}\), interpreting \(\mathord {\textsf {n}}\;\mathbin {:}\;{{\mathbb {N}}}\) as the type \(\mathord {\textsf {Fin}}\;\mathord {\textsf {n}}\)—this is justified by the fact that there will be a forgetful functor from every practically useful gs-monoidal category mapping the object monoid to \({{\mathbb {N}}}\), and this functor will reflect decomposition. We used this specialisation for decomposition of wiring graphs (which have no edges); apart from that, we elaborated the proofs at the abstract category-semigroupoid level as far as we found feasible. An improved library of dependent functors will make fully abstract proofs possible in the future. We also started to develop a rewriting mechanism for these \(\mathord {\textsf {Jungle}}\)s via constrained DPO rewriting steps in the category of \(\mathord {\textsf {ADHG}}\) matchings, see (Kahl and Zhao 2019).
12 Conclusion
An important observation arising from the development of our \(\mathord {\textsf {ADHG}}\) formalisations is that categorial abstraction is frequently enhanced by embedding a “nice” category in a “big” semigroupoid. Careful choices then allow us to develop theory and implementations at the abstract level, and obtain the conventional \({Set }\)-based mathematical theory as one instantiation, while correct-by-construction executables can be generated via instantiations with concrete datatypes. In this way, we achieve re-usability of theoretical developments as implementations that are tunable for efficiency.
Notes
- 1.
We gloss over the fact that in any real Agda development of these mathematical definitions, \(\mathord {\textsf {Setoid}}\) types will normally be used instead of \(\mathord {\textsf {Set}}\). A variant using setoids of the definitions of the current section can be found in (Kahl 2011, Sect. 3).
- 2.
Agda
 declarations simultaneously define modules, and as such can contain other definitions besides field declarations.
declarations simultaneously define modules, and as such can contain other definitions besides field declarations. - 3.
A semigroupoid is a “category without identity morphisms”, analogous to how a semigroup is a “monoid without identity element”.
References
Corradini, A., Gadducci, F.: An algebraic presentation of term graphs, via GS-monoidal categories. Appl. Categ. Struct. 7(4), 299–331 (1999). https://doi.org/10.1023/A:1008647417502. ISSN 1572–9095
Corradini, A., Rossi, F.: Hyperedge replacement jungle rewriting for term-rewriting systems and logic programming. Theor. Comput. Sci. 109(1–2), 7–48 (1993). https://doi.org/10.1016/0304-3975(93)90063-Y
Danielsson, N.A., Daggit, M., et al.: Agda standard library, version 0.17 (2018). http://tinyurl.com/AgdaStdlib
Hoffmann, B., Plump, D.: Implementing term rewriting by jungle evaluation. Informatique théorique et applications/Theor. Inform. Appl. 25(5), 445–472 (1991). https://doi.org/10.1051/ita/1991250504451
Kahl, W.: Dependently-typed formalisation of typed term graphs. In: Echahed, R. (ed.) Proceedings of 6th International Workshop on Computing with Terms and Graphs, TERMGRAPH 2011. EPTCS, vol. 48, pp. 38–53 (2011). https://doi.org/10.4204/EPTCS.48.6
Kahl, W.: Categories of coalgebras with monadic homomorphisms. In: Bonsangue, M.M. (ed.) CMCS 2014 2014. LNCS, vol. 8446, pp. 151–167. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44124-4_9. Agda theories at http://RelMiCS.McMaster.ca/RATH-Agda/
Kahl, W.: Graph transformation with symbolic attributes via monadic coalgebra homomorphisms. ECEASST 71, 5.1–5.17 (2015). https://doi.org/10.14279/tuj.eceasst.71.999
Kahl, W., Zhao, Y.: Dependently-typed formalisation of typed term graphs. In: Fernández, M., Mackie, I. (eds.) Proceedings of Tenth International Workshop on Computing with Terms and Graphs, TERMGRAPH 2018. EPTCS, vol. 288, pp. 26–37 (2019). https://doi.org/10.4204/EPTCS.288.3
Norell, U.: Towards a practical programming language based on dependent type theory. Ph.D. thesis, Department of Computer Science and Engineering, Chalmers University of Technology (2007). See also http://wiki.portal.chalmers.se/agda/pmwiki.php
Pitts, A.M.: Categorical logic. In: Abramsky, S., Gabbay, D.M., Maibaum, T.S.E. (eds.) Handbook of Logic in Computer Science, vol. 5, pp. 39–128. Oxford University Press, Oxford (2001)
Zhao, Y.: A machine-checked categorial formalisation of term graph rewriting with semantics preservation. Ph.D. thesis, McMaster University (2018a)
Zhao, Y.: A formalisation of term graph rewriting in Agda – TGR1. Mechanically checked Agda development, with 283 pages literate document output (2018b). http://relmics.mcmaster.ca/RATH-Agda/TGR1/
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Representation Contexts
We now provide a more fine-grained abstraction for the category-semigroupoid setting of Sections Sects. 7 and 11. Recall that the key idea is to provide a separate interface, the category \({\mathcal C}\), for objects that can be used as carriers of coalgebra sorts, and “extend” this category to an encompassing semigroupoid \({\mathcal S}\) that can contain also other objects that may be used to interpret the result type expressions of coalgebra function symbols. For example, the (conceptually) infinite datatype \(\mathord {\textsf {String}}\) will never be used as node set of a graph, but it may well be used for node labels. In addition, a type of “representations” for \({\mathcal S}\)-morphisms that “start at \({\mathcal C}\)-objects” is assumed—these are the morphisms that may serve as interpretations of coalgebra function symbols. The “upwards arrows” are motivated by visualising the semigroupoid \({\mathcal S}\) above the category \({\mathcal C}\), which is “embedded” into \({\mathcal S}\) via \({\mathcal R}\).
Definition A.1
A representation context  consists of
consists of
-
a category \({\mathcal C}\)
-
a semigroupoid \({\mathcal S}\)
-
a full and faithful semigroupoid functor
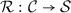 that preserves identities
that preserves identities -
for each object k of \({\mathcal C}\) and each object A of \({\mathcal S}\), a collection
 of representations, together with a bijection \({\mathbb {S}}_{k,A}\) between
of representations, together with a bijection \({\mathbb {S}}_{k,A}\) between  and the \({\mathcal S}\)-homset
and the \({\mathcal S}\)-homset  ,
, -
for any two objects k and m of \({\mathcal C}\), a bijection \({\mathbb {R}}_{k,m}\) between the \({\mathcal C}\)-homset
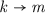 and
and  , and
, and -
for each representation
 and each \({\mathcal S}\)-morphism
and each \({\mathcal S}\)-morphism  a composition
a composition  in
in 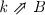
such that the following are satisfied:

The implementation setting described in Sect. 7 for obtaining \(\mathsf {VecDHG}_{1}\) from \(\mathsf {ADHG}_{1}\) can be explained as a representation context where
-
\({\mathcal C}\) has
 as object collection, and
as object collection, and  as homset from m to n;
as homset from m to n; -
\({\mathcal S}\) is the semigroupoid underlying \({Set }\);
-
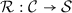 maps
maps 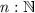 to the set \(\mathord {\textsf {Fin}}\ n\), and is the identity on morphisms;
to the set \(\mathord {\textsf {Fin}}\ n\), and is the identity on morphisms; -
for each
 and each set A, the type of representations is
and each set A, the type of representations is 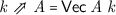 , and \({\mathbb {S}}_{k,A}\) is the canonical isomorphism between \(\mathord {\textsf {Vec}}\ A\ k\) and
, and \({\mathbb {S}}_{k,A}\) is the canonical isomorphism between \(\mathord {\textsf {Vec}}\ A\ k\) and  ;
; -
for each
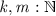 , the canonical isomorphism between
, the canonical isomorphism between  and \(\mathord {\textsf {Vec}}\ (\mathord {\textsf {Fin}}\ m)\ k\) is used as \({\mathbb {R}}_{k,m}\);
and \(\mathord {\textsf {Vec}}\ (\mathord {\textsf {Fin}}\ m)\ k\) is used as \({\mathbb {R}}_{k,m}\); -
for each vector \(U : \mathord {\textsf {Vec}}\ A\ k\) and each \({Set }\)-morphism
 , the composition is
, the composition is  .
.
Note that there are “more” vectors than there are morphisms in \({\mathcal C}\), and yet more set functions in \({\mathcal S}\) than there are vectors.
Theoretically, one could choose to identify  with the \({\mathcal S}\)-homset
with the \({\mathcal S}\)-homset  , but we consider it useful to keep the two separate: The point of having
, but we consider it useful to keep the two separate: The point of having  as a separate component of representation contexts is that it can be instantiated with morphism implementations for which \({\mathbb {S}}\) provides the semantics in terms of the semigroupoid \({\mathcal S}\), which in turn is intended to provide the connection to \({Set }\).
as a separate component of representation contexts is that it can be instantiated with morphism implementations for which \({\mathbb {S}}\) provides the semantics in terms of the semigroupoid \({\mathcal S}\), which in turn is intended to provide the connection to \({Set }\).
For interpretation of coalgebra signatures (as shown in Sect. 2), we assume a fixed interpretation function \({\mathcal F}\) that maps n-ary functor symbols to semigroupoid functors from \({\mathcal S}^n\) to \({\mathcal S}\) that preserve identities (and correspond to meet-preserving relators). If a structure A provides an interpretation of sort symbols as objects in \({\mathcal C}\), then let  be the resulting interpretation of the type expression t, where each sort s is interpreted as
be the resulting interpretation of the type expression t, where each sort s is interpreted as  , and functor symbol applications are interpreted as the corresponding functor applications:
, and functor symbol applications are interpreted as the corresponding functor applications:

For each type expression T, this gives rise to an identity-preserving semigroupoid functor, written  , from the sort-indexed product category \({\mathcal C}^{Sort_{\varSigma }}\) to \({\mathcal S}\).
, from the sort-indexed product category \({\mathcal C}^{Sort_{\varSigma }}\) to \({\mathcal S}\).
Definition A.2
Let a coalgebraic signature \(\varSigma \) and a representation context  be given. A \(\varSigma \)-\({\mathcal X}\)-coalgebra A consists of
be given. A \(\varSigma \)-\({\mathcal X}\)-coalgebra A consists of
-
for each sort s an object \(s_A\) of \({\mathcal C}\)
-
for each function symbol
 a representation
a representation 
Given two such coalgebras A and B, a \(\varSigma \)-\({\mathcal X}\)-coalgebra homomorphism \(\phi \) from A to B consists of
-
for each sort s a representation
 of the \({\mathcal C}\) morphism
of the \({\mathcal C}\) morphism 
 ,
, -
such that for each function symbol
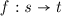 , the following homomorphism property holds:
, the following homomorphism property holds: 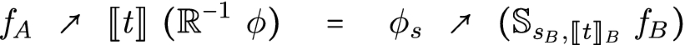
This homomorphism property is an equality of representations; in concrete applications this will be a decidable equivalence.
It is easy to see that the \(\varSigma \)-\({\mathcal X}\)-coalgebra homomorphisms of Definition A.2 form a category; this is a “good implementation” of \(\varSigma \)-coalgebras in the following sense:
Theorem A.3
Let a coalgebraic signature \(\varSigma \), and a representation context  using the full category \({Set }\) for \({\mathcal S}\) be given. For each \(\varSigma \)-\({\mathcal X}\)-coalgebra A, applying \({\mathcal R}\) to each carrier object \(s_A\), and applying \({\mathbb {S}}\) to each function symbol interpretation \(f_A\) maps the \(\varSigma \)-\({\mathcal X}\)-coalgebra A to a conventional \({Set }\)-based coalgebra in a way that gives rise to a full and faithful functor. \(\square \)
using the full category \({Set }\) for \({\mathcal S}\) be given. For each \(\varSigma \)-\({\mathcal X}\)-coalgebra A, applying \({\mathcal R}\) to each carrier object \(s_A\), and applying \({\mathbb {S}}\) to each function symbol interpretation \(f_A\) maps the \(\varSigma \)-\({\mathcal X}\)-coalgebra A to a conventional \({Set }\)-based coalgebra in a way that gives rise to a full and faithful functor. \(\square \)
In the setting of Sect. 7, the category of \(\varSigma \)-\({\mathcal X}\)-coalgebras is therefore equivalent to the subcategory of \(\varSigma \)-coalgebras over \({Set }\) which results from restriction to finite carrier sets.
B Concretised Representation Context
For an implementation based on, for example, the vectors of Sect. 5, the question arises how to represent not only the components of coalgebras and of morphisms, both of which are representations, but also the results of functor application to morphisms, which are used in the context of the dependent functors mentioned in Sect. 10.
We now assume a language \({\mathcal F}\) of functor symbols (with arity). Our goal is to move from an abstract semigroupoid \({\mathcal S}\), such as \({Set }\), to one that has a concrete representation amenable to implementation using finite datastructures. (Objects of \({Set }\), as far as relevant in this context, are considered to be implemented as datatype identifiers or type expressions.)
Given a representation context  and a functor symbol semantics that maps each functor symbol \(F : {\mathcal F}\) to a semigroupoid endofunctor
and a functor symbol semantics that maps each functor symbol \(F : {\mathcal F}\) to a semigroupoid endofunctor  (of corresponding arity) on \({\mathcal S}\), we construct a new concretised representation context
(of corresponding arity) on \({\mathcal S}\), we construct a new concretised representation context  over the same base category \({\mathcal C}\), where:
over the same base category \({\mathcal C}\), where:
-
A \({\mathcal S}^{\mathcal F}\) object is
-
either \(\mathord {\textsf {LIFT}}\ k\) for a \({\mathcal C}\) object k,
-
or \(\mathord {\textsf {EMBED}}\ A\) for an \({\mathcal S}\) object A,
-
or \(\mathord {\textsf {WRAP}}\ F\ (Q_1, \ldots , Q_n)\) for an n-ary functor symbol F and \({\mathcal S}^{\mathcal F}\) objects \(Q_1, \ldots , Q_n\).
\({\mathcal S}^{\mathcal F}\) objects are assigned a straightforward “semantics” as \({\mathcal S}\) objects:
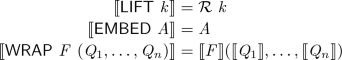
-
-
\({\mathcal S}^{\mathcal F}\) morphisms are
-
either
 for a representation
for a representation 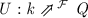 , which is a representation in
, which is a representation in  ,
, -
or
 for an n-ary functor symbol F and morphisms
for an n-ary functor symbol F and morphisms 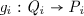 .
.
-
(There are no morphisms starting from \(\mathord {\textsf {EMBED}}\) objects.)
-
Morphisms are also given a straightforward semantics in \({\mathcal S}\).
-
-
\({\mathbb {R}}^{\mathcal F}\), the composition
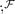 in \({\mathcal S}^{\mathcal F}\), and the composition
in \({\mathcal S}^{\mathcal F}\), and the composition  are determined by the semantics; \({\mathcal R}^{\mathcal F}\) is induced by \(\mathord {\textsf {LIFT}}\).
are determined by the semantics; \({\mathcal R}^{\mathcal F}\) is induced by \(\mathord {\textsf {LIFT}}\).
\({\mathcal X}^{\mathcal F}\) is a well-defined representation context, and if \({\mathcal R}\) preserves finite colimits, so does \({\mathcal R}^{\mathcal F}\). Note that \({\mathcal S}^{\mathcal F}\) is only a semigroupoid, and cannot be a category, since there are no morphisms starting at \(\mathord {\textsf {EMBED}}\) objects, not even identity morphisms. This fact is the motivation for asking only for a semigroupoid in this place in a representation context.
For signatures \(\varSigma \) over the functors in \({\mathcal F}\), the concretised representation context \({\mathcal X}^{\mathcal F}\) generates the same \(\varSigma \)-coalgebras as the (possibly abstract) context \({\mathcal X}\), but extends the concretely implementable morphisms to “exactly all morphisms ever required while reasoning about \(\varSigma \)-coalgebra transformation”.
Theorem B.1
The category of \(\varSigma \)-\({\mathcal X}^{\mathcal F}\)-coalgebras is equivalent to the subcategory of the corresponding category of \(\varSigma \)-coalgebras in \({\mathcal S}\) restricted to carriers in \({\mathcal C}\). \(\square \)
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Kahl, W., Zhao, Y. (2019). A Flexible Categorial Formalisation of Term Graphs as Directed Hypergraphs. In: Fiadeiro, J., Țuțu, I. (eds) Recent Trends in Algebraic Development Techniques. WADT 2018. Lecture Notes in Computer Science(), vol 11563. Springer, Cham. https://doi.org/10.1007/978-3-030-23220-7_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-23220-7_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23219-1
Online ISBN: 978-3-030-23220-7
eBook Packages: Computer ScienceComputer Science (R0)





 to obtain the mathematical theory, and
to obtain the mathematical theory, and , vector sets) as objects.
, vector sets) as objects. is the terminator and introduces garbage, and
is the terminator and introduces garbage, and is the duplicator and introduces sharing.
is the duplicator and introduces sharing. declarations simultaneously define modules, and as such can contain other definitions besides field declarations.
declarations simultaneously define modules, and as such can contain other definitions besides field declarations.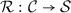 that preserves identities
that preserves identities of representations, together with a bijection
of representations, together with a bijection  and the
and the  ,
,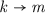 and
and  , and
, and and each
and each  a composition
a composition  in
in 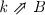
 as object collection, and
as object collection, and  as homset from m to n;
as homset from m to n;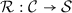 maps
maps 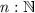 to the set
to the set  and each set A, the type of representations is
and each set A, the type of representations is 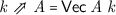 , and
, and  ;
;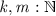 , the canonical isomorphism between
, the canonical isomorphism between  and
and  , the composition is
, the composition is  .
. a representation
a representation 
 of the
of the 
 ,
,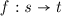 , the following homomorphism property holds:
, the following homomorphism property holds: 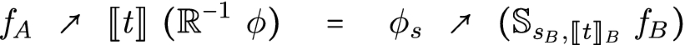
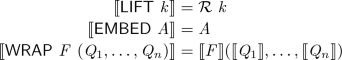
 for a representation
for a representation 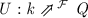 , which is a representation in
, which is a representation in  ,
, for an n-ary functor symbol F and morphisms
for an n-ary functor symbol F and morphisms 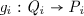 .
.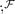 in
in  are determined by the semantics;
are determined by the semantics; 