Keywords

1 Introduction

Neural Networks (NNs) for Multi-Input- Multi-Output (MIMO) problems have gained wide attention in many scientific fields [3, 6], especially regarding complex non-linear systems without a closed-form solution. In these applications, a NN, able to learn non-linear relationship between quantities by means of a dataset, represents a reasonable alternative to the use of mathematical models [17, 19]. The main drawback of any neural model is, however, the necessity of a large amount of data/measurements for its set up; in fact, a NN with m inputs and n outputs can be directly implemented to approximate a non-linear function, provided the amount of data to manage is not too large; moreover the high computational cost, needed for the wide size of training patterns and for complex NN architecture, makes the direct approach inefficient.

Therefore, several authors make the problem easier by dividing MIMO NN into a collection of n Multi-Input-Single-Output (MISO) NNs [8, 9], further, split into several Single-Input-Single-Output (SISO) NNs; in this way, their structure appears to be considerably simplified and the time required by the whole learning process results to be lower. Singular Value Decomposition (SVD) turns out to be a powerful instrument for switching between MISO NNs and a group of SISO NNs, since it is defined for any array of data and it provides a low-rank matrix, which is a good approximation to the original one [1, 7]; the efficiency of this approach has already demonstrated in different works [12, 16]. The presented paper concerns the implementation of parallel algorithm on a PC-cluster that is able to address the SISO NN training process to a cluster node, separately, decreasing strongly the computational cost. Moreover, the parallel architecture obtained from SVD-based approximation is applied to magnetic hysteresis data and the study of its ability to model the magnetic hysteresis constitutes the main issue of this work. Indeed, although the magnetic hysteresis problem has been already solved by the authors through a suitably trained NN [2, 10, 11, 13], it is still a difficult task [4, 5, 14], especially when dealing with materials having large variance in characteristics and NN must be trained with a dataset describing these conditions. Obtaining such data involves a whole set of measurements that can be very difficult to perform; thus, to solve this problem in a feasible way, the parallel SVD-based algorithm is applied to a 2D-array, which represents the magnetic permeability, \(\mu \), obtained starting from experimental values of magnetic field, H, and flux density, B [15].

This paper is organized as follows: Sect. 2 summarizes some of the main properties of the SVD technique, emphasizing the decomposition of bidimensional functions. Section 3 focuses on the parallel algorithm implemented for training each SISO NN: firstly, MISO-SISO decomposition is introduced, pointing out the training of each SISO NN, then, PC-cluster characteristics are introduced. In Sect. 4 the performances of parallel algorithm are evaluated by using magnetic hysteresis data and, finally, in Sect. 5, the conclusions follow.

2 The Approximation Method: SVD

Among the methods used to simplify a MISO problem into a collection of SISO, the SVD represents a valid tool, that allows to approximate a multivariate functions without losing accuracy.

The SVD of a rectangular matrix A \(\in R^{m \times n}\) is the factorization of A into the product of three matrices: \(\mathbf {A = U \Sigma V^{T}}\) where U = \((u_{1} \dots u_{m}) \in R^{m \times m}\), V = \((v_{1} \dots v_{n}) \in R^{n \times n}\) and \(\mathbf {\Sigma }\) \(\in R^{m \times n}\) is a diagonal one having its non-zero diagonal entries equal to the singular values \(\sigma _{k,k}\) with \(k=\,1,...,p\) and p = min(m,n), written in descending order \(\sigma _{1,1}>\sigma _{2,2}>...>\sigma _{p,p}>0\). Thus:

(1)

where and are orthonormal vectors coincident with the column vectors of matrices U and V\(^T\), respectively. Usually, the smallest singular values are neglected and an approximated version of (1) is considered:

(2)

with \(\sigma _{1,1}>\sigma _{2,2}>...>\sigma _{\hat{p},\hat{p}}>0\) and \(\hat{p}<min(m,n)\), whereas \(\sigma _{j,j}\) is forced to be 0, for \(\hat{p}<j<p\).

Let us assume that the A entries are coming from the sampling of a bivariate function \(f(x_{1}, x_{2})\), so \(A_{i,j}=f(x_{1,i}, x_{2,j})\) with \(i=1 \dots m\) and \(j=1 \dots n\). Correspondingly, the columns of the matrices U and \({V}^{{T}}\) are arising from the sampling of unknown univariate functions, \(u_{k,i}=\psi _{k}(x_{1,i})\) and \(v_{k,j}^T=\eta _{k}(x_{2,j})\). Once obtained \(\hat{p}\) with a fixed accuracy \(\varepsilon \), the approximation can be written as follows:

$$\begin{aligned} \hat{A}_{i,j}=\hat{f}(x_{1,i}, x_{2,j})= \sum _{s=1}^{\hat{p}} \sigma _{s} \hat{\psi }_{s}(x_{1,i}) \hat{\eta }_{s}(x_{2,j}) \end{aligned}$$
(3)

The different unknown univariate functions in (3) can be evaluated by appropriate curve fitting techniques, such as NNs.

3 Parallel Algorithm for SISO NNs Training

3.1 MISO NN Decomposition

The SVD-based approximation of bivariate functions described in the previous section can be exploited for optimizing the feed-forward MISO NNs learning process. Thus, the idea is to split the MISO NN into several SISO NN by applying the SVD-based approximation of multivariate functions, to reduce the time of learning process and to simplify the NN architecture.

Let us consider an array of data A, obtained by sampling a 2D-function \(f(x_{1},x_{2})\), and define a decomposition operator, D, which indicates the SVD of function \(f(x_{1},x_{2})\), \(D\{f(x_{1},x_{2})\}=\sum _{i=1}^{\hat{p}}\sigma _{i}\psi _{i}(x_{1})\eta _i(x_{2})\).

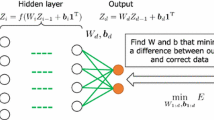
When the operator is applied, it generates \(2 \times \hat{p} \) univariate functions and each of them can be approximated by a SISO NN, as shown in Fig. 3.

Every SISO NN presents a simple feed-forward architecture, composed by an input neuron, one hidden layer and an output neuron. The main advantage is that each NN is independent from the other, so its training can be implemented as a stand-alone process being part of a larger parallel architecture.

3.2 Parallel Computing in a PC-Cluster System

The principal aim of using a PC-cluster is to improve the performance for large computational task, such as MISO NN training, that can be divided into smaller tasks distributed around the nodes. The SISO NN training is implemented on a high performance computing, HPC, cluster, that consists of 4 compute nodes, each one composed of 24 CPUs. A Single Program Multiple Data, SPMD, parallel model is performed; thus, the master node sends the program, involving training set and algorithm, to the others computational nodes and it commands every one to execute the learning process of a SISO NN. The communication is realized through the Message Passing Interface standard, MPI, which allows the programmer to easily pass the message from one of computers to the others by calling the function offered from the libraries. Generally, a parallel process requires a communicator, containing a group of processes, whose number defines its size, r; each process has a rank inside the communicator, namely a number that permits to recognize it. So, the implementation of parallel NNs training involves a communicator having \(n \times \hat{p}\) size, where n indicates the dimension of the initial array of data; especially, \(r=2 \times \hat{p}\) for 2-D array, n = 2. As shown in Fig. 2, each process returns a SISO NN, able to approximate the one-dimensional function, representing the U matrix columns or \(\mathbf {V^T}\) matrix rows. Once, the U and V matrices have been reconstructed, the approximation of original array can be obtained, by using Eq. 2.

Fig. 1.
figure 1

Scheme of parallel algorithm implemented for SISO NNs training.

Full size image

4 Validation of SVD-Based Parallel Algorithm: Magnetic Hysteresis Data

With the aim to validate the presented approach, the parallel algorithm is used to train a neural network implemented for modelling magnetic hysteresis. A collection of asymmetric loops has been generated for building the data set for NN training by employing Preisach model in Matlab environment [18]. Each loop has been sampled in n points and for every couple of coordinates \([H_{k},B_{k}]\) the corresponding differential magnetic permeability, \(\mu _{k}\) has been computed. As a result, an array of data \(\mu (B_{n},H_{n})\) function of H and B variables is obtained to test the SVD-based algorithm.

Thus, assuming \(x_{1}=B_{1},...,B_{m}\), \(x_{2}=H_{1},..., H_{n}\) and \(f(x_{1}, x_{2})=\mu (H,B)\), the SVD applied to bivariate function returns

$$\begin{aligned} \mu _{i,j}=\mu (B_{i}, H_{j})=\sum _{s=1}^p \sigma _{s}\psi _{s}(B_{i})\eta _{s}(H_{j}) \end{aligned}$$
(4)

To reduce the total number of NNs required for reconstructing the original function, a threshold value is fixed to \(\epsilon =0.001\) in order to obtain a reduced SVD form with \(\hat{p}=3\).

$$\begin{aligned} \hat{\mu }_{i,j}=\sum _{s=1}^3 \sigma _{s}\hat{\psi }_{s}(B_{i})\hat{\eta }_{s}(H_{j}) \end{aligned}$$
(5)
Fig. 2.
figure 2

Parallelization of training process. From left to right: transformation of MISO NN into several SISO NNs. Each NN training represents a process of rank k, with \(k=1...\hat{p}\), executed by a cluster node.

Full size image
Fig. 3.
figure 3

Results on validation test of NNs: left \(\psi _{s}(B)\); right \(\eta _{s}(H)\).

Full size image

After decomposition, the total number of SISO NNs results to be 6:3 univariate functions of B, \(\psi _{1}(B), \psi _{2}(B), \psi _{3}(B)\); 3 univariate functions of H, \(\eta _{1}(H), \eta _{2}(H), \eta _{3}(H)\). Each SISO NN has a feed-forward architecture and it was trained by using Levenberg Marquardt algorithm. The NN architecture consists of a input neuron, representing the B or H variable sampled in n points, the hidden layer is composed by 8 neurons and the output neuron returns the one dimensional function \(\psi (B)\) or \(\eta (H)\), respectively. The training set for each NN is made by 70 of 100 sampled points belonging to the univariate function, which is intended to approximate. So, for computing the parallel learning process, the master node has to send a program, including the training set and Levenberg Marquardt algorithm, to the others one. Hence, a communicator, involving 6 processes distributed between the 4 available compute nodes, is set up as shown in Fig. 1, with the purpose to minimize the computational effort of a single node. The performance of NN is compared with the points excluding the ones in the training, especially, test set is composed by 30 samples. The NN shows a good accuracy in modelling, Fig. 3 shows that each NN is able to reproduce the univariate function trend, with a \(MSE\simeq 10^{-8}\). Finally, the NN outputs are exploited to reconstruct the \(\mu \) array, following the Eq. 5. Table 1 shows a comparison between the time required by whole learning process with and without parallel architecture implementation; a strong reduction of computational time is achieved.

Table 1. Computational time results achieved for the bivariate function, \(\mu (B,H)\).
Full size table

5 Conclusions

An optimization algorithm able to perform parallel learning process of SISO NNs, by exploiting the SVD properties has been presented. A well-known challenging topic is constituted by the modelling of magnetic hysteresis, a typical MISO problem. Thus, a procedure for magnetic hysteresis loops identification has been proposed. The method is based on the parallelization of NNs training processes, that allows to accurately model the hysteresis problem achieving a reduction of computational cost. The implemented SISO-based approach allows to provide a solution, even when the conventional use of a MISO strategy fails. Results show that the proposed method is a suitable tool for modelling the magnetic hysteresis, it is capable of reducing the processing time strongly and, at the same time, preserving the accuracy of solution. The presented technique constitutes an effective solution based on which the more complex problem of 3D magnetic hysteresis can be solved, hence, should be considered a valid starting point for future developments. In particular, it is worth noticing that the method can, in general, suit any multidimensional problem.