Abstract
We define a new UC functionality (DL-extractable commitment scheme) that allows committer to open a commitment to a group element \(g^x\); however, the simulator will be able to extract its discrete logarithm x. Such functionality is useful in situations where the secrecy of x is important since the knowledge of x enables to break privacy while the simulator needs to know x to be able to simulate the corrupted committer. Based on Fujisaki’s UC-secure commitment scheme and the Damgård-Fujisaki integer commitment scheme, we propose an efficient commitment scheme that realizes the new functionality. As another novelty, we construct the new scheme in the weaker RPK (registered public key) model instead of the CRS model used by Fujisaki.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A commitment scheme is one of the most basic primitives in cryptography. Essentially, it implements a digital safe: in the commitment phase, the committer puts her message to the safe, locks it, and hands it to the receiver. In the open phase, the committer uses her key to open the safe. Thus, a commitment scheme satisfies at least the following two properties: it is binding (the committer cannot change the committed message) and hiding (before the opening, the receiver does not know which message was committed to).
In many applications, commitment schemes must satisfy stronger properties. In the case of UC-security [8], one first defines an ideal functionality (e.g., the functionality of the commitment scheme) and then constructs a protocol that UC-realizes this functionality. Such protocol is said to be UC-secure. Due to Canetti’s composition theorem [8], a UC-secure protocol enjoys secure composability with arbitrary protocols, without the need to reprove its security. Importantly, UC-secure protocols do not have to be modified to be secure in a specific software environment and thus can be used as a black-box by practitioners. As such, UC is the recommended best practice in cryptographic engineering.
The first UC-commitment scheme was proposed by Canetti and Fischlin [9]. A UC-commitment scheme was shown to be complete for the construction of UC-secure zero knowledge protocols [9, 14] and two-party and multi-party computations [10]. UC-commitment schemes have to satisfy the properties of extractability (the simulator can unambiguously extract the committed message) and equivocability (the simulator can open a commitment to an arbitrary value) at the same time, and thus they cannot be constructed without an additional setup assumption [9]. The most widely known setup assumption is the common reference string (CRS, [6]) model that allows for a universally trusted entity that generates the CRS from the correct distribution without revealing its trapdoor.
Many different CRS-model UC-commitment schemes are known, starting with [7, 9, 10, 14]. Lindell [21] proposed the first efficient scheme based on an ordinary prime-order group. Blazy et al. [5] corrected a bug in Lindell’s scheme and proposed a new scheme with additional optimizations. Fujisaki [16] further optimized the scheme of Blazy et al., obtaining the most efficient currently known UC-commitment scheme \(\mathsf {Fuj}\) in an ordinary prime-order group.
The main idea of the UC-commitment schemes of [5, 16, 21] is that the committer \(\mathsf {C}\) encrypts a message m. During the open phase, \(\mathsf {C}\) outputs m together with an interactive proof (a \(\varSigma \)-protocol) that she encrypted m. She also erases the used randomizer (hence, these commitments schemes assume secure erasure). The UC simulator simulates the \(\varSigma \)-protocol using the CRS trapdoor; to achieve UC-security, the \(\varSigma \)-protocol has to be straight-line extractable. Due to the use of a \(\varSigma \)-protocol, [5, 16, 21] have either an interactive commit phase (resulting in adaptive security) or an interactive open phase (resulting in static security). Within this paper, we will concentrate on adaptively secure variants. Fischlin, Libert, and Manulis [15] used a Groth-Sahai proof [19] instead of a \(\varSigma \)-protocol to construct a non-interactive adaptive UC-commitment scheme; however, their scheme is computationally less efficient and uses bilinear pairings.
An important question, often asked by practitioners, is how to implement the CRS model. More precisely, how can one guarantee the existence of a single party  that can be trusted by everybody to choose the CRS from the correct distribution without leaking its trapdoors? Fortunately, weaker setup models are known. Barak, Canetti, Nielsen, and Pass [2] introduced the weaker registered public key (RPK) model where it is essentially required that each party
that can be trusted by everybody to choose the CRS from the correct distribution without leaking its trapdoors? Fortunately, weaker setup models are known. Barak, Canetti, Nielsen, and Pass [2] introduced the weaker registered public key (RPK) model where it is essentially required that each party  must trust some key registration authority
must trust some key registration authority  who registers his key. The authorities
who registers his key. The authorities  can coincide or be different, depending on the application. They do not need to trust each other. In particular, the CRS model is a very strong case of the RPK model where there is only one authority
can coincide or be different, depending on the application. They do not need to trust each other. In particular, the CRS model is a very strong case of the RPK model where there is only one authority  whom all parties have to trust. Barak et al. [2] proposed a UC-commitment scheme that is secure in the RPK model: in fact, they used the property of a known UC-commitment scheme in the CRS model that its CRS can be divided into two parts: a binding part (trusted by the receiver \(\mathsf {R}\)) and a hiding part (trusted by the committer \(\mathsf {C}\)). Thus, the binding part can be registered by the authority of \(\mathsf {R}\) and the hiding part can be registered by the authority of \(\mathsf {C}\). Unfortunately, their scheme is quite inefficient.
whom all parties have to trust. Barak et al. [2] proposed a UC-commitment scheme that is secure in the RPK model: in fact, they used the property of a known UC-commitment scheme in the CRS model that its CRS can be divided into two parts: a binding part (trusted by the receiver \(\mathsf {R}\)) and a hiding part (trusted by the committer \(\mathsf {C}\)). Thus, the binding part can be registered by the authority of \(\mathsf {R}\) and the hiding part can be registered by the authority of \(\mathsf {C}\). Unfortunately, their scheme is quite inefficient.
Moreover, the functionality of UC-commitments is not always sufficient. E.g., consider the following generic class of (UC-secure) pairing-based multiplicative public key generation protocols. (This protocol is motivated by a non-UC-secure CRS-generation protocol for SNARKs [17, 18, 22] from [4] that can be used also to generate the CRS of UC-secure SNARKs like [20].) Let  be an (asymmetric) prime-order bilinear group where \(g_i\) is a generator of \(\mathbb {G}_i\). Different parties
be an (asymmetric) prime-order bilinear group where \(g_i\) is a generator of \(\mathbb {G}_i\). Different parties  , \(i \in [1 \, .. \, \nu ]\), sample their one-time public keys \((g_{1}^{\sigma _i}, g_{2}^{\sigma _i})\), for secret key \(\sigma _i\), and UC-commit to them. After all parties have committed, everybody opens commitments to their public keys. Next, they enact a sequential protocol where the ith party computes \(g_{1}^{\sigma ^*_i} := g_{1}^{\prod _{j = 1}^i \sigma _j}\) as \(g_{1}^{\sigma ^*_i} \leftarrow \left( g_{1}^{\sigma ^*_{i - 1}}\right) ^{\sigma _i}\), by using a public group element \(g_{1}^{\sigma ^*_{i - 1}}\) and a secret integer \(\sigma _i\). Under the minimal assumption that at least one
, \(i \in [1 \, .. \, \nu ]\), sample their one-time public keys \((g_{1}^{\sigma _i}, g_{2}^{\sigma _i})\), for secret key \(\sigma _i\), and UC-commit to them. After all parties have committed, everybody opens commitments to their public keys. Next, they enact a sequential protocol where the ith party computes \(g_{1}^{\sigma ^*_i} := g_{1}^{\prod _{j = 1}^i \sigma _j}\) as \(g_{1}^{\sigma ^*_i} \leftarrow \left( g_{1}^{\sigma ^*_{i - 1}}\right) ^{\sigma _i}\), by using a public group element \(g_{1}^{\sigma ^*_{i - 1}}\) and a secret integer \(\sigma _i\). Under the minimal assumption that at least one  is honest, it is required that the joint public key \(g_{1}^{\sigma ^*_{\nu }}\) is uniformly random and that no coalition of less than \(\nu \) knows the corresponding secret key \(\sigma ^*_{\nu }\). Due to this, \(\sigma _i\) should not be leaked while opening to \(g_{2}^{\sigma _i}\) is needed for public verification of the correctness of the operation of
is honest, it is required that the joint public key \(g_{1}^{\sigma ^*_{\nu }}\) is uniformly random and that no coalition of less than \(\nu \) knows the corresponding secret key \(\sigma ^*_{\nu }\). Due to this, \(\sigma _i\) should not be leaked while opening to \(g_{2}^{\sigma _i}\) is needed for public verification of the correctness of the operation of  . Namely, for this, one needs to check that \(\hat{e}(g_{1}^{\sigma ^*_i}, g_{2}) = \hat{e}(g_{1}^{\sigma ^*_{i - 1}}, g_{2}^{\sigma _i})\); thus, avoiding the use of costly zero-knowledge protocols.
. Namely, for this, one needs to check that \(\hat{e}(g_{1}^{\sigma ^*_i}, g_{2}) = \hat{e}(g_{1}^{\sigma ^*_{i - 1}}, g_{2}^{\sigma _i})\); thus, avoiding the use of costly zero-knowledge protocols.
On the other hand, in the security proof, the UC simulator  needs to recover \(\sigma _i\) (and not only \((g_{1}^{\sigma _i}, g_{2}^{\sigma _i})\)) to be able to simulate the operation of a corrupted party. Hence, we have arrived to the requirement that after the committer commits to a message m, it should be opened to \((g_{1}^{m}, g_{2}^{m})\) while the simulator must be able to extract m from the functionality.
needs to recover \(\sigma _i\) (and not only \((g_{1}^{\sigma _i}, g_{2}^{\sigma _i})\)) to be able to simulate the operation of a corrupted party. Hence, we have arrived to the requirement that after the committer commits to a message m, it should be opened to \((g_{1}^{m}, g_{2}^{m})\) while the simulator must be able to extract m from the functionality.
Similar functionality is needed to achieve security in other UC protocols, especially in the setting where one uses a DL-based cryptosystem (or a commitment scheme) to encrypt the witness yet needs to extract the witness for simulation purposes. It can be implemented by encrypting the witness (that has to be extractable) bitwise, and then giving a NIZK argument that each ciphertext encrypts a Boolean value  . Protocols using such a technique have obviously huge communication.
. Protocols using such a technique have obviously huge communication.
Finally, non-falsifiable assumptions (e.g., knowledge assumptions [12, 23]) are usually used to (i) extract a unique long message from a succinct commitment, one can avoid such use of non-falsifiable assumptions by having a linearly-long commitment (as done, say, in [20]), and (ii) extract the exponent from a group element, for example, in the case one uses the Groth-Sahai commitment scheme for scalars [19]. To avoid using non-falsifiable assumptions in this case, one can use a DL-extractable commitment scheme that we define in the current paper.
Our Contributions. Let \(\mathbb {G}\) be a prime-order group with generator g. We will define the new ideal functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) of a DL-extractable commitment scheme. Intuitively, the main difference between \(\mathcal {F}_{\mathsf {mcomdl}}\) and the standard functionality \(\mathcal {F}_{\mathsf {mcom}}\) of UC-commitment schemes [9] is that in \(\mathcal {F}_{\mathsf {mcomdl}}\), the committer sends m to the functionality who stores m. When opening the commitment, the functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) only sends \(g^m \in \mathbb {G}\) (while \(\mathcal {F}_{\mathsf {mcom}}\) sends m itself) to the receiver. Since the functionality stores m, it means that after the committer is corrupted, the UC simulator will get to know m.
We seem to be the first to formalize \(\mathcal {F}_{\mathsf {mcomdl}}\) as a separate functionality (see Remark 1 in Sect. 3 for a comparison to the notion of P-extractability of Belenkiy et al. [3]); such a formalization creates a common language and enables other researchers to use our implementation of \(\mathcal {F}_{\mathsf {mcomdl}}\) as a black-box. At this moment it is even difficult to search for papers that implicitly use this functionality due to lack of agreed-upon language and notation. We expect there to be more applications after the current work establishes the common language.
After that, we construct a commitment scheme \(\mathsf {\Gamma }_{\mathsf {dl}}\) that UC-realizes \(\mathcal {F}_{\mathsf {mcomdl}}\) in the \(\mathcal {F}_{\mathsf {rpk}}\)-hybrid model, i.e., assuming availability of a UC-secure realization of the RPK model. Essentially, \(\mathsf {\Gamma }_{\mathsf {dl}}\) is based on Fujisaki’s CRS-model UC-commitment scheme \(\mathsf {Fuj}\) [16] with the following important modifications. First, [5, 16, 21] all work in the CRS model. We crucially observe that the commitment key of \(\mathsf {Fuj}\) consists of two independent parts, one guaranteeing hiding and another one guaranteeing binding. Relying on this separation, we will lift \(\mathsf {Fuj}\) (and also its DL-extractable version) to the weaker RPK model. Since the RPK model seems to be relatively unknown in the community, reintroducing it and constructing an efficient commitment scheme in this model can be seen as another major contribution of the current work.
Second, to guarantee DL-extractability, we proceed as follows. One of the optimizations of Fujisaki compared to [5, 21] is the use of the efficient IND-PCA secure Short Cramer-Shoup (SCS, [1]) public-key cryptosystem. We couple an SCS encryption of \(g^m\) with an additively homomorphic Paillier encryption [24] of m, an integer commitment [13] to m, and a straight-line extractable \(\varSigma \)-protocol showing that these three encryptions/commitments of m are mutually consistent. The UC simulator uses the Paillier encryption (importantly, the simulator does not rewind the \(\varSigma \)-protocol) to extract m from a corrupted committer. Thus, the Paillier encryption is needed for extraction while the integer commitment is needed to prove that the SCS plaintext \(g^{m_1}\) and the Paillier plaintext \(m_2\) satisfy \(m_1 \equiv m_2 \pmod {p}\) where p is the order of \(\mathbb {G}\).
The construction of \(\mathsf {\Gamma }_{\mathsf {dl}}\) and its security proof are somewhat subtle due to the use of three different algebraic/number-theoretic settings (prime-order bilinear groups, Paillier encryption modulo \(N = P Q\), and an integer commitment scheme). However, most of this subtlety is needed to construct the \(\varSigma \)-protocol and to prove its security.
Finally, the functionality of a DL-extractable commitment scheme can be straightforwardly generalized to that of a preimage-extractable commitment scheme where the map \(m \mapsto g^m\) is replaced by \(m \mapsto F (m)\) for any one-way permutation F. We leave study of such a generalization to the future work.
2 Preliminaries
Let PPT denote probabilistic polynomial-time. Let  be the information-theoretic security parameter, in practice, e.g.,
be the information-theoretic security parameter, in practice, e.g.,  . All adversaries will be stateful. For an algorithm
. All adversaries will be stateful. For an algorithm  , let
, let  denote the random tape of
denote the random tape of  , and let
, and let  denote sampling of a randomizer r of sufficient length for
denote sampling of a randomizer r of sufficient length for  ’s needs. By
’s needs. By  we denote that
we denote that  , given an input x and a randomizer r, outputs y. We denote by
, given an input x and a randomizer r, outputs y. We denote by  an arbitrary negligible function, and by
an arbitrary negligible function, and by  an arbitrary polynomial function. \(\mathcal {D}_1 \approx _c \mathcal {D}_2\) means that the distributions \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are computationally indistinguishable.
an arbitrary polynomial function. \(\mathcal {D}_1 \approx _c \mathcal {D}_2\) means that the distributions \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are computationally indistinguishable.
UC Security. We work in the standard universal composability framework of Canetti [8] with static corruptions of parties. For consistency, we use the definition of computational indistinguishability, denoted by \(\approx _c\), from that work. The UC framework defines a PPT environment machine \(\mathcal {Z}\) that oversees the execution of a protocol in one of two worlds. The “ideal world” execution involves “dummy parties” (some of whom may be corrupted by an ideal adversary/simulator  ) interacting with a functionality \(\mathcal {F}\). The “real world” execution involves PPT parties (some of whom may be corrupted by a PPT real world adversary
) interacting with a functionality \(\mathcal {F}\). The “real world” execution involves PPT parties (some of whom may be corrupted by a PPT real world adversary  ) interacting only with each other in some protocol \(\pi \). We refer to [8] for a detailed description of the executions, and a definition of the real world ensemble
) interacting only with each other in some protocol \(\pi \). We refer to [8] for a detailed description of the executions, and a definition of the real world ensemble  and the ideal world ensemble
and the ideal world ensemble  .
.
A protocol \(\pi \) UC-securely computes \(\mathcal {F}\) if there exists a PPT  such that for every non-uniform PPT \(\mathcal {Z}\) and PPT
such that for every non-uniform PPT \(\mathcal {Z}\) and PPT  ,
,  .
.
The importance of this definition is a composition theorem that states that any protocol that is universally composable is secure when run concurrently with many other arbitrary protocols; see [8, 10] for discussions and definitions.
In the registered public key (RPK, [2]) model, it is assumed that each party  trusts some key-registration authority
trusts some key-registration authority  and has registered her key with
and has registered her key with  . (The same
. (The same  can be used by several parties, or each party can choose to trust a separate authority.) If
can be used by several parties, or each party can choose to trust a separate authority.) If  is honest, then the secret key exists and the public key comes from correct distribution (in this case, the public key is said to be “safe”). If
is honest, then the secret key exists and the public key comes from correct distribution (in this case, the public key is said to be “safe”). If  is dishonest, the secret key still exists (and the public key has been computed from it honestly) but there is no guarantee about its distribution (in this case, the public key is said to be “well-formed”). See Fig. 1 for the description of the functionality of the key registration from [2].
is dishonest, the secret key still exists (and the public key has been computed from it honestly) but there is no guarantee about its distribution (in this case, the public key is said to be “well-formed”). See Fig. 1 for the description of the functionality of the key registration from [2].
Several different variants (most importantly, the “traditional proof-of-knowledge” version where the secret key and the public key are generated by  who then sends the public key to
who then sends the public key to  and proves the knowledge of the secret key to
and proves the knowledge of the secret key to  by using a stand-alone zero-knowledge proof) of the RPK model are known. The new commitment can be implemented in any of such variants of the RPK model; in particular the definition of the \(\mathcal {F}_{\mathsf {rpk}}\)-hybrid model does not depend on the variant. We assume that each party knows the identities of all other parties and their key-registration authorities, see [2] for discussion.
by using a stand-alone zero-knowledge proof) of the RPK model are known. The new commitment can be implemented in any of such variants of the RPK model; in particular the definition of the \(\mathcal {F}_{\mathsf {rpk}}\)-hybrid model does not depend on the variant. We assume that each party knows the identities of all other parties and their key-registration authorities, see [2] for discussion.
In the CRS model [6], there is a single, universally trusted, third party (TTP) that picks a common reference string \(\mathsf {crs}\) from a well-defined probability distribution and makes it available to all parties. An ideal functionality realizing the CRS model is presented on Fig. 1. In a usual implementation, \(\mathsf {crs}\) comes with a secret trapdoor \(\mathsf {td}\), such that \(\mathsf {td}\) is sampled from a well-defined distribution \(\mathcal {D}_{\mathsf {td}}\), and for some public function f, we have \(\mathsf {crs}\leftarrow f (\mathsf {td})\). In the case of a NIZK argument system, the knowledge of \(\mathsf {td}\) allows the simulator to prove statements outside of the language. Here, it is assumed that TTP only provides \(\mathsf {td}\) to the simulator but not to the adversary. The CRS model can be seen as a very strong version of the RPK model where all parties  trust the same TTP
trust the same TTP  .
.
We denote an execution of \(\pi \) in the RPK-hybrid (the CRS-hybrid case is similar) model by  . A protocol \(\pi \) UC-securely computes \(\mathcal {F}\) in the \(\mathcal {F}^f_{\mathsf {rpk}}\)-hybrid model if there exists a PPT
. A protocol \(\pi \) UC-securely computes \(\mathcal {F}\) in the \(\mathcal {F}^f_{\mathsf {rpk}}\)-hybrid model if there exists a PPT  such that every non-uniform PPT \(\mathcal {Z}\) and PPT
such that every non-uniform PPT \(\mathcal {Z}\) and PPT  ,
,  .
.
Root Assumption. An integer is  -smooth if all its prime factors are at most
-smooth if all its prime factors are at most  , and
, and  -rough [13] if all its prime factors are larger than
-rough [13] if all its prime factors are larger than  .
.
Let \(\tilde{\mathbb {G}}= \mathbb {U}\times \mathbb {H}\) be a multiplicative abelian group such that \(\mathbb {H}\) has order divisible only by large primes. That is, let  and
and  be two functions from
be two functions from  to
to  , such that
, such that  is superpolynomial and
is superpolynomial and  is polynomial. Let \(2^B\) be an efficiently computable upperbound on \(|\tilde{\mathbb {G}}|\), \(2^B \ge {\text {ord}}(\tilde{\mathbb {G}})\). Denote \(l_{\tilde{\mathbb {G}}} := {\text {ord}}(\mathbb {U})\). We assume
is polynomial. Let \(2^B\) be an efficiently computable upperbound on \(|\tilde{\mathbb {G}}|\), \(2^B \ge {\text {ord}}(\tilde{\mathbb {G}})\). Denote \(l_{\tilde{\mathbb {G}}} := {\text {ord}}(\mathbb {U})\). We assume  , the description \({\text {descr}}(\tilde{\mathbb {G}})\) of \(\tilde{\mathbb {G}}\) includes \(l_{\tilde{\mathbb {G}}}\), and that it is easy to verify whether some bitstring represents an element of \(\tilde{\mathbb {G}}\). Let
, the description \({\text {descr}}(\tilde{\mathbb {G}})\) of \(\tilde{\mathbb {G}}\) includes \(l_{\tilde{\mathbb {G}}}\), and that it is easy to verify whether some bitstring represents an element of \(\tilde{\mathbb {G}}\). Let  generate \({\text {descr}}(\tilde{\mathbb {G}})\) that has the mentioned properties. In the following instantiation, the root assumption is the same as the well-known Strong RSA assumption. (Another known instantiation [13] is based on class groups.)
generate \({\text {descr}}(\tilde{\mathbb {G}})\) that has the mentioned properties. In the following instantiation, the root assumption is the same as the well-known Strong RSA assumption. (Another known instantiation [13] is based on class groups.)
Note that if \(\tilde{\mathbb {G}}= \mathbb {U}\times \mathbb {H}\) is the multiplicative group modulo \(N = P Q\) where \(P = 2 P' + 1\) and \(Q = 2 Q' + 1\) are safe primes, then \({\text {ord}}(\tilde{\mathbb {G}}) = \varphi (N) = 4 P' Q'\). (This setting is often recommended if one uses the RSA or the Paillier cryptosystem [24].) In this case,  is a group of order \(l_{\tilde{\mathbb {G}}} = 4\) and \(\mathbb {H}\) is a group of order \(P' Q'\). Here, \({\text {descr}}(\tilde{\mathbb {G}}) = \{N, l_{\tilde{\mathbb {G}}}\}\).
is a group of order \(l_{\tilde{\mathbb {G}}} = 4\) and \(\mathbb {H}\) is a group of order \(P' Q'\). Here, \({\text {descr}}(\tilde{\mathbb {G}}) = \{N, l_{\tilde{\mathbb {G}}}\}\).
Consider the following experiment:

The root assumption [13] holds relative to \(\mathcal {G}\), if for all  and PPT
and PPT  ,
,  .
.
Commitment Schemes. A commitment scheme  is defined by three PPT algorithms: (i)
is defined by three PPT algorithms: (i)  generates a public key (CRS) \(\mathsf {\Gamma }.\mathsf {ck}\) and a secret key (trapdoor) \(\mathsf {\Gamma }.\mathsf {td}\); (ii) \(\mathsf {\Gamma }.\mathsf {Com}(\mathsf {\Gamma }.\mathsf {ck}; m; r)\) commits to \(m\) under the CRS \(\mathsf {ck}\), using the random coins r. It outputs commitment \(\mathsf {c}\) and opening information \(\mathsf {op}\); (iii)
generates a public key (CRS) \(\mathsf {\Gamma }.\mathsf {ck}\) and a secret key (trapdoor) \(\mathsf {\Gamma }.\mathsf {td}\); (ii) \(\mathsf {\Gamma }.\mathsf {Com}(\mathsf {\Gamma }.\mathsf {ck}; m; r)\) commits to \(m\) under the CRS \(\mathsf {ck}\), using the random coins r. It outputs commitment \(\mathsf {c}\) and opening information \(\mathsf {op}\); (iii)  verifies that \(\mathsf {c}\) is a commitment to \(m\).
verifies that \(\mathsf {c}\) is a commitment to \(m\).
It is required that for any  (where \(\mathsf {\Gamma }.\mathsf {td}\) is unused unless \(\mathsf {\Gamma }\) has a trapdoor property), message \(m\), randomizer r, and \((\mathsf {c}, \mathsf {op}) \leftarrow \mathsf {\Gamma }.\mathsf {Com}(\mathsf {\Gamma }.\mathsf {ck}; m; r)\), it holds that
(where \(\mathsf {\Gamma }.\mathsf {td}\) is unused unless \(\mathsf {\Gamma }\) has a trapdoor property), message \(m\), randomizer r, and \((\mathsf {c}, \mathsf {op}) \leftarrow \mathsf {\Gamma }.\mathsf {Com}(\mathsf {\Gamma }.\mathsf {ck}; m; r)\), it holds that  . \(\mathsf {\Gamma }\) is statistically hiding, if the distributions of commitment \(\mathsf {c}\), corresponding to any two values of \(m\), are statistically indistinguishable. \(\mathsf {\Gamma }\) is computationally binding, if given \(\mathsf {ck}\) and \(\mathsf {c}\), no PPT adversary
. \(\mathsf {\Gamma }\) is statistically hiding, if the distributions of commitment \(\mathsf {c}\), corresponding to any two values of \(m\), are statistically indistinguishable. \(\mathsf {\Gamma }\) is computationally binding, if given \(\mathsf {ck}\) and \(\mathsf {c}\), no PPT adversary  can create two different messages \(m_i\) with corresponding openings \(\mathsf {op}_i\), such that
can create two different messages \(m_i\) with corresponding openings \(\mathsf {op}_i\), such that  with a non-negligible probability.
with a non-negligible probability.
A commitment scheme \(\mathsf {\Gamma }\) is trapdoor if there exists a PPT algorithm \(\mathsf {\Gamma }.\mathsf {tdOpen}\), such that given the trapdoor \(\mathsf {\Gamma }.\mathsf {td}\) (corresponding to commitment key \(\mathsf {\Gamma }.\mathsf {ck}\)), two messages \(m_1\) (with opening \(\mathsf {op}_1\)) and \(m_2\), and any commitment \(\mathsf {c}\): if  then \(\mathsf {\Gamma }.\mathsf {tdOpen}(\mathsf {\Gamma }.\mathsf {td}; m_1, \mathsf {op}_1, m_2) = \mathsf {op}_2\), such that
then \(\mathsf {\Gamma }.\mathsf {tdOpen}(\mathsf {\Gamma }.\mathsf {td}; m_1, \mathsf {op}_1, m_2) = \mathsf {op}_2\), such that  . The Pedersen trapdoor commitment scheme
. The Pedersen trapdoor commitment scheme  [25] in cyclic group \(\mathbb {G}\), with generator \(g\), is defined as follows:
[25] in cyclic group \(\mathbb {G}\), with generator \(g\), is defined as follows:
-
 : sample
: sample  , set \(h \leftarrow g^{\mathsf {td}}\), and output \((\mathsf {Ped}.\mathsf {ck}= (g, h), \mathsf {Ped}.\mathsf {td}\leftarrow \mathsf {td})\).
, set \(h \leftarrow g^{\mathsf {td}}\), and output \((\mathsf {Ped}.\mathsf {ck}= (g, h), \mathsf {Ped}.\mathsf {td}\leftarrow \mathsf {td})\). -
\(\mathsf {Ped}.\mathsf {Com}(\mathsf {Ped}.\mathsf {ck}; m; r)\) for
 ,
,  : output \((\mathsf {c}, \mathsf {op}) = (g^mh^r, r)\).
: output \((\mathsf {c}, \mathsf {op}) = (g^mh^r, r)\). -
 : output 1 if \(\mathsf {c}= g^mh^r\) and 0 otherwise.
: output 1 if \(\mathsf {c}= g^mh^r\) and 0 otherwise. -
\(\mathsf {Ped}.\mathsf {tdOpen}(\mathsf {Ped}.\mathsf {td}; m_1, \mathsf {op}_1 = r_1, m_2)\): output \(\mathsf {op}_2 = r_2 \leftarrow (m_1 - m_2)/\mathsf {td} + r_1\).
It is well-known that \(\mathsf {Ped}\) is perfectly hiding, computationally binding under the discrete logarithm assumption, and trapdoor.
A commitment scheme is an ICS if the messages come from domain  . Thus, statistical hiding means that it is intractable to compute two different integers
. Thus, statistical hiding means that it is intractable to compute two different integers  and corresponding openings \(\mathsf {op}_1\) and \(\mathsf {op}_2\), such that
and corresponding openings \(\mathsf {op}_1\) and \(\mathsf {op}_2\), such that  . In the case of Pedersen, \(m\) and \(m+ p\) have the same commitments and thus \(\mathsf {Ped}\) is not an ICS. Let \(\tilde{\mathbb {G}}\) be a group where the root assumption holds. The Damgård-Fujisaki ICS [13] over \(\tilde{\mathbb {G}}\) works as follows:
. In the case of Pedersen, \(m\) and \(m+ p\) have the same commitments and thus \(\mathsf {Ped}\) is not an ICS. Let \(\tilde{\mathbb {G}}\) be a group where the root assumption holds. The Damgård-Fujisaki ICS [13] over \(\tilde{\mathbb {G}}\) works as follows:
-
 :
:  chooses an \(\tilde{h}\in \tilde{\mathbb {G}}\) s.t. \({\text {ord}}(\tilde{h})\) is
chooses an \(\tilde{h}\in \tilde{\mathbb {G}}\) s.t. \({\text {ord}}(\tilde{h})\) is  -rough, and sets \(\tilde{g}\leftarrow \tilde{h}^\alpha \) where
-rough, and sets \(\tilde{g}\leftarrow \tilde{h}^\alpha \) where  .
.  sends
sends  to
to  and proves that \(\tilde{g}\in \langle \tilde{h}\rangle \).
and proves that \(\tilde{g}\in \langle \tilde{h}\rangle \). -
 for
for  ,
,  : output
: output  , \(\mathsf {op}= (1, r)\).
, \(\mathsf {op}= (1, r)\). -
 : check that
: check that  and \(\mu ^{l_{\tilde{\mathbb {G}}}} = 1\).
and \(\mu ^{l_{\tilde{\mathbb {G}}}} = 1\).
See [13] for a discussion on \(\mu \) and other details. As proven in [13], \(\mathsf {DF}\) is statistically hiding and computationally binding under the root assumption.
A (multi-use) UC-commitment scheme [9] implements the functionality \(\mathcal {F}_{\mathsf {mcom}}\) (see Fig. 2). The \(\mathcal {F}_{\mathsf {mcom}}\) functionality takes as an additional input another unique “commitment identifier” \(\mathsf {cid}\), which is used if a sender commits to the same receiver multiple times within a session. We assume that the combination of \((\mathsf {sid}, \mathsf {cid})\) is globally unique, [9]. UC-commitment schemes have to satisfy the properties of extractability (the simulator can unambiguously extract the committed message) and equivocability (the simulator can open a commitment to an arbitrary value) at the same time, and thus they cannot be constructed without an additional setup assumption [9].
Cryptosystems. A labelled public-key cryptosystem \(\varPi \) is defined by three PPT algorithms: (i)  generates a public key
generates a public key  and a secret key
and a secret key  ; (ii)
; (ii)  encrypts the message \(m\) under the key
encrypts the message \(m\) under the key  with label \(\mathsf {lbl}\), using the random coins r; (iii)
with label \(\mathsf {lbl}\), using the random coins r; (iii)  decrypts the ciphertext \(\mathsf {c}\), using the secret key
decrypts the ciphertext \(\mathsf {c}\), using the secret key  with label \(\mathsf {lbl}\). It is required that for all
with label \(\mathsf {lbl}\). It is required that for all  , all labels \(\mathsf {lbl}\), all random coins r and all messages \(m\),
, all labels \(\mathsf {lbl}\), all random coins r and all messages \(m\),  .
.
IND-CPA (indistinguishability under the chosen plaintext attack) and IND-PCA (indistinguishability under the plaintext checking attacks, [1]) are defined by using the following experiments:

The experiment-dependent oracle is defined as follows: (i) in  , \(\mathcal {O} (\cdot , \cdot , \cdot )\) returns always 0. (ii) in
, \(\mathcal {O} (\cdot , \cdot , \cdot )\) returns always 0. (ii) in  , \(\mathcal {O} (\mathsf {lbl}, \mathsf {c}, m)\) adds \((\mathsf {lbl}, \mathsf {c})\) to \(\mathcal {Q}\). It returns 1 if the decryption of \(\mathsf {c}\) under the label \(\mathsf {lbl}\) is \(m\). Otherwise, it returns 0.
, \(\mathcal {O} (\mathsf {lbl}, \mathsf {c}, m)\) adds \((\mathsf {lbl}, \mathsf {c})\) to \(\mathcal {Q}\). It returns 1 if the decryption of \(\mathsf {c}\) under the label \(\mathsf {lbl}\) is \(m\). Otherwise, it returns 0.
\(\varPi \) is IND-CPA secure if for any PPT adversary  ,
,  . \(\varPi \) is IND-PCA secure if for any PPT adversary
. \(\varPi \) is IND-PCA secure if for any PPT adversary  ,
,  .
.
The IND-PCA-secure Short Cramer-Shoup (SCS) labelled cryptosystem  [1] works as follows:
[1] works as follows:
-
 :
:  ;
;  ; \(h \leftarrow g^z\), \(c \leftarrow g^{x_1} h^{x_2}\), \(d \leftarrow g^{y_1} h^{y_2}\). Choose \(\mathsf {H}\) from a collision-resistant hash function family \(\mathcal {H}\). Return
; \(h \leftarrow g^z\), \(c \leftarrow g^{x_1} h^{x_2}\), \(d \leftarrow g^{y_1} h^{y_2}\). Choose \(\mathsf {H}\) from a collision-resistant hash function family \(\mathcal {H}\). Return  and
and  .
. -
 : sample
: sample  ; set \((u, e, v) \leftarrow (g^r, g^{m} h^r, (c d^\tau )^r)\), where
; set \((u, e, v) \leftarrow (g^r, g^{m} h^r, (c d^\tau )^r)\), where  . Return the ciphertext \((u, e, v)^\top \).
. Return the ciphertext \((u, e, v)^\top \). -
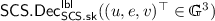 : set \(\tau \leftarrow \mathsf {H}(\mathsf {lbl}, u, e)\), \(g^m \leftarrow e/u^z\); if \(u^{x_1 + y_1 \tau } (e/g^{m})^{x_2 + y_2 \tau } \ne v\) then abort. Otherwise, output \(g^m\).
: set \(\tau \leftarrow \mathsf {H}(\mathsf {lbl}, u, e)\), \(g^m \leftarrow e/u^z\); if \(u^{x_1 + y_1 \tau } (e/g^{m})^{x_2 + y_2 \tau } \ne v\) then abort. Otherwise, output \(g^m\).
Abdalla et al. [1] proved that SCS is IND-PCA secure given \(\mathcal {H}\) is a collision-resistant hash function family and DDH is hard in \(\mathbb {G}\).
An additively homomorphic public-key cryptosystem has plaintext space equal to  for integer N, s.t. the product of two ciphertexts decrypts to the sum of the two corresponding plaintexts. We will use the Paillier cryptosystem \(\mathsf {Pai}\) [24]. It encrypts plaintexts from
for integer N, s.t. the product of two ciphertexts decrypts to the sum of the two corresponding plaintexts. We will use the Paillier cryptosystem \(\mathsf {Pai}\) [24]. It encrypts plaintexts from  , where N is a well-chosen RSA modulus, and outputs ciphertexts from
, where N is a well-chosen RSA modulus, and outputs ciphertexts from  :
:  . See [24] for more details, including the decryption algorithm. \(\mathsf {Pai}\) is IND-CPA secure under the DCRA assumption [24].
. See [24] for more details, including the decryption algorithm. \(\mathsf {Pai}\) is IND-CPA secure under the DCRA assumption [24].
\(\varSigma \)-Protocols [11] in the RPK Model. Let \(\mathbf {R}= \{\mathsf {x}, \mathsf {w}\}\) be an NP-relation. A \(\varSigma \)-protocol  is a three-round protocol between the prover
is a three-round protocol between the prover  and the verifier
and the verifier  , such that the first and the third messages are by the prover, and the second message is by the verifier. Let
, such that the first and the third messages are by the prover, and the second message is by the verifier. Let  be the public key of the verifier.
be the public key of the verifier.  has input
has input  and
and  has input
has input  . The first message is denoted as
. The first message is denoted as  , where
, where  is sampled from the randomizer space of the protocol. The second message e is chosen uniformly at random from
is sampled from the randomizer space of the protocol. The second message e is chosen uniformly at random from  ,
,  . The third message is denoted as
. The third message is denoted as  . The verifier accepts iff
. The verifier accepts iff  .
.
A \(\varSigma \)-protocol is complete for \(\mathbf {R}\) if an honest verifier always accepts an honest prover. A \(\varSigma \)-protocol is specially sound for \(\mathbf {R}\) if given an input \(\mathsf {x}\) and two acceptable views \((a, e_1, z_1)\) and \((a, e_2, z_2)\), \(e_1 \ne e_2\), one can efficiently extract a witness \(\mathsf {w}\), such that \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\). A \(\varSigma \)-protocol is statistically special honest-verifier zero-knowledge (SSHVZK) for \(\mathbf {R}\) if for any  , \(\mathsf {x}\) and e,
, \(\mathsf {x}\) and e,  can first choose a z and then a, such that the simulated view (a, e, z) and the real view, given the same e, have negligible statistical distance.
can first choose a z and then a, such that the simulated view (a, e, z) and the real view, given the same e, have negligible statistical distance.
3 New Functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) and Instantiation
In a DL-extractable UC-commitment scheme, one commits to an integer m from  but the opening is to a group element \(g^m \in \mathbb {G}\). (In particular, m should stay secret from other participants even after the opening.) Nevertheless, we require that there exists an efficient extraction algorithm that can retrieve the discrete logarithm (i.e., the committed integer)
but the opening is to a group element \(g^m \in \mathbb {G}\). (In particular, m should stay secret from other participants even after the opening.) Nevertheless, we require that there exists an efficient extraction algorithm that can retrieve the discrete logarithm (i.e., the committed integer)  of \(g^m\). That is, while opening returns \(g^m\), the extraction returns m. See Fig. 3 for the corresponding functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) that is parametrized by
of \(g^m\). That is, while opening returns \(g^m\), the extraction returns m. See Fig. 3 for the corresponding functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) that is parametrized by  and \(\mathbb {G}\) (this means that
and \(\mathbb {G}\) (this means that  and \(\mathbb {G}\) are “hard-coded” into the functionality). We formalize our goal by letting parties to commit to an integer m (which will be stored by the functionality and thus can be extracted) but opening the commitment to \(g^m\). Hence, any commitment scheme that implements \(\mathcal {F}_{\mathsf {mcomdl}}\) must necessarily be DL-extractable.
and \(\mathbb {G}\) are “hard-coded” into the functionality). We formalize our goal by letting parties to commit to an integer m (which will be stored by the functionality and thus can be extracted) but opening the commitment to \(g^m\). Hence, any commitment scheme that implements \(\mathcal {F}_{\mathsf {mcomdl}}\) must necessarily be DL-extractable.
Remark 1
Belenkiy et al. [3] defined P-extractable commitment scheme, for an efficient function P, as a commitment scheme where one commits to m and opens to m but where the extractor is able to extract P(m). DL-extractable commitment is a variant of P-extractable commitment for \(P = \text {DL}\) being an intractable function. If \(P (m) = g^m =: \exp _g(m)\) then one obtains a functionality, dual to \(\mathcal {F}_{\mathsf {mcomdl}}\). (However, [3] did not consider UC-security and thus did not use the language of functionalities.) Compared to DL-extractability, \(\exp _g\)-extractability is trivial to implement: indeed, the notion of \(\exp _g\)-extractability was motivated by the fact that well-known commitment schemes like the Groth-Sahai commitment scheme for scalars [19] had this property. (The extractor of this commitment scheme obtains \(g^m\) by Elgamal-decrypting the commitment. Since computing DL is intractable, one arrives to the notion of a \(\exp _g\)-extractable commitment.) Obtaining DL-extractability is non-trivial since DL is a hard function and thus one has to take special care about making the DL of a message extractable. \(\square \)
The functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) can be straightforwardly generalized to the functionality \(\mathcal {F}_{\mathsf {mcom}\text {-}F^{-1}}\) for an arbitrary one-way permutation F, where the opening message includes \(y \leftarrow F (m)\) instead of \(y \leftarrow g^m\). Since we are interested in the applications of \(\mathcal {F}_{\mathsf {mcomdl}}\), we will omit further discussion.
We implement \(\mathcal {F}_{\mathsf {mcomdl}}\) as follows: for  , we encrypt the group element \(g^m\) by using the Short Cramer-Shoup encryption [1], encrypt the integer m by using the Paillier [24] additively homomorphic public-key cryptosystem, and finally commit to the integer m by using the Damgård-Fujisaki [13] ICS. We add a \(\varSigma \)-protocol
, we encrypt the group element \(g^m\) by using the Short Cramer-Shoup encryption [1], encrypt the integer m by using the Paillier [24] additively homomorphic public-key cryptosystem, and finally commit to the integer m by using the Damgård-Fujisaki [13] ICS. We add a \(\varSigma \)-protocol  proving the knowledge of m that was used in all cases; importantly, only \(g^m\) can be extracted from
proving the knowledge of m that was used in all cases; importantly, only \(g^m\) can be extracted from  and in particular, m will remain secret. Since UC-security does not permit to use rewinding to retrieve m, we use straight-line extraction techniques from [16]. The \(\varSigma \)-protocol is started during the commit phase, and after that the committer \(\mathsf {C}\) erases the used random coins. In the open phase, \(\mathsf {C}\) opens the commitment to \(g^m\) by finishing
and in particular, m will remain secret. Since UC-security does not permit to use rewinding to retrieve m, we use straight-line extraction techniques from [16]. The \(\varSigma \)-protocol is started during the commit phase, and after that the committer \(\mathsf {C}\) erases the used random coins. In the open phase, \(\mathsf {C}\) opens the commitment to \(g^m\) by finishing  . When simulating an honest committer, the UC simulator
. When simulating an honest committer, the UC simulator  first commits to 0;
first commits to 0;  uses the properties of a trapdoor commitment scheme and the SSHVZK property to simulate
uses the properties of a trapdoor commitment scheme and the SSHVZK property to simulate  . (This guarantees equivocability.) If \(\mathsf {C}\) is corrupted then
. (This guarantees equivocability.) If \(\mathsf {C}\) is corrupted then  uses the knowledge of the Paillier secret key to decrypt the Paillier encryption of m and thus obtains m. (This guarantees extractability.) Thus, we obtain a DL-extractable commitment scheme.
uses the knowledge of the Paillier secret key to decrypt the Paillier encryption of m and thus obtains m. (This guarantees extractability.) Thus, we obtain a DL-extractable commitment scheme.
3.1 \(\varSigma \)-Protocol 
Let \(\mathsf {SCS}\) be the SCS cryptosystem and \(\mathsf {Pai}\) be the Paillier cryptosystem. Recall that the plaintext space of \(\mathsf {SCS}\) is \(\mathbb {G}\) (of order \(p\)) and the plaintext space of \(\mathsf {Pai}\) is  for an \(N > p\). (The case \(N = p\) is straightforward to handle.) Let
for an \(N > p\). (The case \(N = p\) is straightforward to handle.) Let

where  . Let \(\mathsf {\mathbf {L}_{eq}}= \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in \mathsf {\mathbf {R}_{eq}}\}\) be the corresponding language. Thus, \(\mathsf {x}\in \mathsf {\mathbf {L}_{eq}}\) iff the two ciphertexts encrypt \(g^m\) and \(m'\) respectively, such that \(m \equiv m' \pmod {p}\). Note that \(g^m\) is public while m is not; this corresponds to the use of \(g^m\) in the new DL-extractable UC-commitment scheme.
. Let \(\mathsf {\mathbf {L}_{eq}}= \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in \mathsf {\mathbf {R}_{eq}}\}\) be the corresponding language. Thus, \(\mathsf {x}\in \mathsf {\mathbf {L}_{eq}}\) iff the two ciphertexts encrypt \(g^m\) and \(m'\) respectively, such that \(m \equiv m' \pmod {p}\). Note that \(g^m\) is public while m is not; this corresponds to the use of \(g^m\) in the new DL-extractable UC-commitment scheme.
The proof of the following theorem uses ideas from the proof given in Sect. 5.1 of [13]. Note that in the next theorem, we actually do not need the public key to be registered. We will assume it here for the sake of convenience since registration is needed in the new DL-extractable UC-commitment scheme.
Theorem 1
(Security of  ). Let \(\mathsf {H}\) be sampled from a collision-resistant hash function family, \(\mathsf {SCS}\) be the SCS cryptosystem, \(\mathsf {Pai}\) be the Paillier cryptosystem, and \(\mathsf {DF}\) be the Damgård-Fujisaki ICS. Assume
). Let \(\mathsf {H}\) be sampled from a collision-resistant hash function family, \(\mathsf {SCS}\) be the SCS cryptosystem, \(\mathsf {Pai}\) be the Paillier cryptosystem, and \(\mathsf {DF}\) be the Damgård-Fujisaki ICS. Assume  has registered her public key
has registered her public key  . Let T be a public constant such that \(m < T\), e.g. \(T = p\); let
. Let T be a public constant such that \(m < T\), e.g. \(T = p\); let  and let \(2^B\) be a close upperbound on \({\text {ord}}(\tilde{\mathbb {G}})\). Assume
and let \(2^B\) be a close upperbound on \({\text {ord}}(\tilde{\mathbb {G}})\). Assume  . The \(\varSigma \)-protocol
. The \(\varSigma \)-protocol  in Fig. 4 (where
in Fig. 4 (where  will be defined in the SSHVZK proof) is complete and SSHVZK for \(\mathsf {\mathbf {R}_{eq}}\). The protocol
will be defined in the SSHVZK proof) is complete and SSHVZK for \(\mathsf {\mathbf {R}_{eq}}\). The protocol  is computationally specially sound under the root assumption in \(\tilde{\mathbb {G}}\).
is computationally specially sound under the root assumption in \(\tilde{\mathbb {G}}\).
Proof
 consider two accepting views \((a, e, \mathbf {z})\) and \((a, e', \mathbf {z}')\) with \(e \ne e'\). Let \(m^* \leftarrow (z_2' - z_2)/(e' - e) \mod p\) and \(r^* \leftarrow (z_1' - z_1)/(e' - e) \mod p\). We get from the first four verification equations respectively that
consider two accepting views \((a, e, \mathbf {z})\) and \((a, e', \mathbf {z}')\) with \(e \ne e'\). Let \(m^* \leftarrow (z_2' - z_2)/(e' - e) \mod p\) and \(r^* \leftarrow (z_1' - z_1)/(e' - e) \mod p\). We get from the first four verification equations respectively that


For example, from (b) we get \(g^{e m} \cdot a_3 = g^{z_2}\) and \(g^{e m'} \cdot a_3 = g^{z_2'}\). It follows that \(g^{(e' - e) m} = g^{z_2 - z_2'}\) and thus \(g^{m} = g^{(z_2 - z_2') / (e' - e)} = g^{m^*}\).
 (2). Since \(\tilde{g}= \tilde{h}^\alpha \), \(\tilde{a}_1^{e' - e} = \tilde{h}^\delta \) for \(\delta := \alpha (z_2' - z_2) + (z_4' - z_4)\). We will next consider three possible cases. Let
(2). Since \(\tilde{g}= \tilde{h}^\alpha \), \(\tilde{a}_1^{e' - e} = \tilde{h}^\delta \) for \(\delta := \alpha (z_2' - z_2) + (z_4' - z_4)\). We will next consider three possible cases. Let  be the event that we either have the case (i) or the case (ii).
be the event that we either have the case (i) or the case (ii).
(i) \((e' - e) \not \mid \delta \) as an integer.
Write \(\gamma = \gcd (\delta , e' - e)\). By the Extended Euclidean algorithm, there exist i and j (where  ), such that \(j \delta + i (e' - e) = \gamma \). Thus, \(\tilde{h}^\gamma = \tilde{h}^{j \delta + i (e' - e)} = \tilde{a}_1^{j (e' - e)} \tilde{h}^{i (e' - e)} = (\tilde{a}_1^j \tilde{h}^i)^{e' - e} \). Set now \(\mu \leftarrow (\tilde{a}_1^j \tilde{h}^i)^{(e' - e)/\gamma }/\tilde{h}\). Thus, \(\mu ^\gamma = 1\). Since
), such that \(j \delta + i (e' - e) = \gamma \). Thus, \(\tilde{h}^\gamma = \tilde{h}^{j \delta + i (e' - e)} = \tilde{a}_1^{j (e' - e)} \tilde{h}^{i (e' - e)} = (\tilde{a}_1^j \tilde{h}^i)^{e' - e} \). Set now \(\mu \leftarrow (\tilde{a}_1^j \tilde{h}^i)^{(e' - e)/\gamma }/\tilde{h}\). Thus, \(\mu ^\gamma = 1\). Since  , \({\text {ord}}(\mu )\) is
, \({\text {ord}}(\mu )\) is  -smooth and thus \(\mu ^{l_{\tilde{\mathbb {G}}}} = 1\). Since \(\tilde{h}= \mu ^{-1} (\tilde{a}_1^j \tilde{h}^i)^{(e' - e)/\gamma }\), \(((e' - e)/\gamma , \tilde{a}_1^j \tilde{h}^i, \mu ^{-1})\) is a solution to the root problem.
-smooth and thus \(\mu ^{l_{\tilde{\mathbb {G}}}} = 1\). Since \(\tilde{h}= \mu ^{-1} (\tilde{a}_1^j \tilde{h}^i)^{(e' - e)/\gamma }\), \(((e' - e)/\gamma , \tilde{a}_1^j \tilde{h}^i, \mu ^{-1})\) is a solution to the root problem.
(ii) \((e' - e) \mid \delta \) as an integer, but either \((e' - e) \not \mid (z_2' - z_2)\) or \((e' - e) \not \mid (z_4' - z_4)\).
Let q be a prime factor of \(e' - e\), such that \(q^j\) is the highest power of q dividing \(e' - e\) and at least one of \(z_2' - z_2\) or \(z_4' - z_4\) is non-zero modulo \(q^j\) (such q exists due to the assumption of non-divisibility). If \(q^j \mid (z_2' - z_2)\) then (due to the definition of \(\delta \) and \(q^j\)) also \(q^j \mid (z_4' - z_4)\), a contradiction. Thus, \(z_2' - z_2 \not \equiv 0 \pmod {q^j}\).
Write \(\alpha = a + b \cdot {\text {ord}}(\tilde{h})\) for some \(a < {\text {ord}}(\tilde{h})\) and b. The adversary only has information about \(\alpha \) via the value \(\tilde{g}\); moreover, \(\tilde{g}\) completely determines a while it contains no information about b. Since \(q^j \mid \delta \),
Because q is a prime factor of \(e' - e\) and  ,
,  and thus \({\text {ord}}(\tilde{h}) \not \equiv 0 \pmod {q}\). From the adversary’s viewpoint, b is chosen uniformly at random from a set of at least
and thus \({\text {ord}}(\tilde{h}) \not \equiv 0 \pmod {q}\). From the adversary’s viewpoint, b is chosen uniformly at random from a set of at least  values, and it must satisfy Eq. (3) for
values, and it must satisfy Eq. (3) for  to be true. Equation (3) has at most \(\eta := \gcd ((z_2' - z_2) \cdot {\text {ord}}(\tilde{h}), q^j)\) solutions. Clearly, \(\eta \) is a power of q but it is at most \(q^{j - 1}\). Since
to be true. Equation (3) has at most \(\eta := \gcd ((z_2' - z_2) \cdot {\text {ord}}(\tilde{h}), q^j)\) solutions. Clearly, \(\eta \) is a power of q but it is at most \(q^{j - 1}\). Since  , the distribution of \(b \mod q^j\) is statistically close to uniform in
, the distribution of \(b \mod q^j\) is statistically close to uniform in  , with the probability that b satisfies Eq. (3) being at most
, with the probability that b satisfies Eq. (3) being at most  . Thus, given the event
. Thus, given the event  , the case (i), where we can solve the root problem, happens with high probability.
, the case (i), where we can solve the root problem, happens with high probability.
(iii) \((e' - e) \mid (z_2' - z_2)\) and \((e' - e) \mid (z_4' - z_4)\) as an integer.
Let  and
and  . Let \(\mu \leftarrow \tilde{g}^{m^\dagger } \tilde{h}^{r^\dagger }/\tilde{a}_1\). W.l.o.g., assume \(e' > e\). By Eq. (2), \(\mu ^{e' - e} = (\tilde{g}^{m^\dagger } \tilde{h}^{r^\dagger }/\tilde{a}_1)^{e' - e} = \tilde{g}^{z_2' - z_2} \tilde{h}^{z_4' - z_4}/\tilde{a}_1^{e' - e} = 1\). Since
. Let \(\mu \leftarrow \tilde{g}^{m^\dagger } \tilde{h}^{r^\dagger }/\tilde{a}_1\). W.l.o.g., assume \(e' > e\). By Eq. (2), \(\mu ^{e' - e} = (\tilde{g}^{m^\dagger } \tilde{h}^{r^\dagger }/\tilde{a}_1)^{e' - e} = \tilde{g}^{z_2' - z_2} \tilde{h}^{z_4' - z_4}/\tilde{a}_1^{e' - e} = 1\). Since  then \({\text {ord}}(\mu )\) is
then \({\text {ord}}(\mu )\) is  -smooth and hence \(\mu ^{l_{\tilde{\mathbb {G}}}} = 1\). Thus, we can open \(\tilde{a}_1\) to \((m^\dagger , r^\dagger , \mu )\).
-smooth and hence \(\mu ^{l_{\tilde{\mathbb {G}}}} = 1\). Thus, we can open \(\tilde{a}_1\) to \((m^\dagger , r^\dagger , \mu )\).
Since  by the last verification equation (Item 4e), we get that
by the last verification equation (Item 4e), we get that  .
.
 (1). Since N and
(1). Since N and  are coprime, there exist integers \(\alpha \) and \(\beta \), such that \(\alpha N + \beta (e' - e) = 1\). Let \(r_2 \leftarrow \mathsf {c}_2^\alpha (z_3'/z_3)^\beta \mod N^2\). Thus, due to Eq. (1), \( \mathsf {c}_2^{1 - \alpha N} = \mathsf {c}_2^{\beta (e' - e)} \equiv (1 + N)^{\beta (z_2' - z_2)} (z_3'/z_3)^{\beta N} \pmod {N^2} \), and thus \( \mathsf {c}_2 \equiv (1 + N)^{\beta (z_2' - z_2)} r_2^N \pmod {N^2} \). Clearly, \(\beta (z_2' - z_2) = \beta (e' - e) m^\dagger \) as an integer. Thus, due to the definition of \(\beta \), \( \beta (z_2' - z_2) = \beta (e' - e) m^\dagger = (1 - \alpha N) m^\dagger \equiv m^\dagger \pmod {N} \) and thus \(\mathsf {c}_2 \equiv (1 + N)^{m^\dagger } r_2^N \pmod {N^2}\). Since directly by the definition of \(m^*\) and \(m^\dagger \), \(m^* \equiv m^\dagger \pmod {p}\), we get that \(\mathbf {\mathsf {c}}_1\) and \(\mathsf {c}_2\) encrypt the same element \(m^*\) modulo \(p\).
are coprime, there exist integers \(\alpha \) and \(\beta \), such that \(\alpha N + \beta (e' - e) = 1\). Let \(r_2 \leftarrow \mathsf {c}_2^\alpha (z_3'/z_3)^\beta \mod N^2\). Thus, due to Eq. (1), \( \mathsf {c}_2^{1 - \alpha N} = \mathsf {c}_2^{\beta (e' - e)} \equiv (1 + N)^{\beta (z_2' - z_2)} (z_3'/z_3)^{\beta N} \pmod {N^2} \), and thus \( \mathsf {c}_2 \equiv (1 + N)^{\beta (z_2' - z_2)} r_2^N \pmod {N^2} \). Clearly, \(\beta (z_2' - z_2) = \beta (e' - e) m^\dagger \) as an integer. Thus, due to the definition of \(\beta \), \( \beta (z_2' - z_2) = \beta (e' - e) m^\dagger = (1 - \alpha N) m^\dagger \equiv m^\dagger \pmod {N} \) and thus \(\mathsf {c}_2 \equiv (1 + N)^{m^\dagger } r_2^N \pmod {N^2}\). Since directly by the definition of \(m^*\) and \(m^\dagger \), \(m^* \equiv m^\dagger \pmod {p}\), we get that \(\mathbf {\mathsf {c}}_1\) and \(\mathsf {c}_2\) encrypt the same element \(m^*\) modulo \(p\).

 sets
sets  ,
,  ,
,  ,
,  (thus,
(thus,  is statistically but not perfectly zero knowledge),
is statistically but not perfectly zero knowledge),  , \(z_4 \leftarrow s_1 e + s_5\),
, \(z_4 \leftarrow s_1 e + s_5\),  (this is indistinguishable from a commitment to m since \(\mathsf {DF}\) is statistical hiding), \(\mathbf {a}_2 \leftarrow ((g^{z_1}, g^{e m} h^{z_1}, (c d^\tau )^{z_1}) / \mathbf {\mathsf {c}}_1)^\top \), \(a_3 \leftarrow g^{z_2 - e m}\), \(a_4 \leftarrow (1 + z_2 N) z_3^N \mathsf {c}_2^{-e} \mod N^2\), \(\tilde{a}_5 \leftarrow \tilde{g}^{z_2} \tilde{h}^{z_4} \tilde{a}_1^{-e}\). The simulator outputs \((a, \mathbf {z})\). The claim follows. \(\square \)
(this is indistinguishable from a commitment to m since \(\mathsf {DF}\) is statistical hiding), \(\mathbf {a}_2 \leftarrow ((g^{z_1}, g^{e m} h^{z_1}, (c d^\tau )^{z_1}) / \mathbf {\mathsf {c}}_1)^\top \), \(a_3 \leftarrow g^{z_2 - e m}\), \(a_4 \leftarrow (1 + z_2 N) z_3^N \mathsf {c}_2^{-e} \mod N^2\), \(\tilde{a}_5 \leftarrow \tilde{g}^{z_2} \tilde{h}^{z_4} \tilde{a}_1^{-e}\). The simulator outputs \((a, \mathbf {z})\). The claim follows. \(\square \)
3.2 New DL-Extractable UC-Commitment Scheme
The following DL-extractable UC-commitment scheme \(\mathsf {\Gamma }_{\mathsf {dl}}\) (see Fig. 5) is similar to Fujisaki’s UC-commitment scheme \(\mathsf {Fuj}\) [16], with the following two key differences. (i) Based on our observation that the CRS of \(\mathsf {Fuj}\) can be divided into two parts, one guaranteeing binding and the second one guaranteeing hiding, we redefine it in the (weaker) RPK model instead of the CRS model. Importantly, the RPK model can also be used after the modification in the next step. (ii) We replace the \(\varSigma \)-protocol (a proof of the knowledge of the \(\mathsf {SCS}\)-encrypted message \(g^m\)) from [16] with  , interpreted as the proof of knowledge of the discrete logarithm m of the \(\mathsf {SCS}\) -encrypted message. As explained above,
, interpreted as the proof of knowledge of the discrete logarithm m of the \(\mathsf {SCS}\) -encrypted message. As explained above,  achieves this by additionally encrypting m by using \(\mathsf {Pai}\); hence, the UC simulator, knowing the secret key
achieves this by additionally encrypting m by using \(\mathsf {Pai}\); hence, the UC simulator, knowing the secret key  , decrypts \(\mathsf {c}_2\) to get m, and returns \(m \bmod p\). (See the beginning of Sect. 3 for a longer intuition behind the construction of \(\mathsf {\Gamma }_{\mathsf {dl}}\).)
, decrypts \(\mathsf {c}_2\) to get m, and returns \(m \bmod p\). (See the beginning of Sect. 3 for a longer intuition behind the construction of \(\mathsf {\Gamma }_{\mathsf {dl}}\).)
Due to this, if one assumes the security of  then the security proof of \(\mathsf {\Gamma }_{\mathsf {dl}}\) is similar to that given in [16]. Hence, we refer the reader to [16] for any additional intuition about Fujisaki’s commitment scheme. While the description of \(\mathsf {\Gamma }_{\mathsf {dl}}\) in Fig. 5 looks long, it is mainly so because of the use of three different encryptions/commitments which means that certain steps in the Fujisaki’s commitment scheme are tripled.
then the security proof of \(\mathsf {\Gamma }_{\mathsf {dl}}\) is similar to that given in [16]. Hence, we refer the reader to [16] for any additional intuition about Fujisaki’s commitment scheme. While the description of \(\mathsf {\Gamma }_{\mathsf {dl}}\) in Fig. 5 looks long, it is mainly so because of the use of three different encryptions/commitments which means that certain steps in the Fujisaki’s commitment scheme are tripled.
We divide the public key \(\mathsf {rpk}_{i}\) of  in \(\mathsf {\Gamma }_{\mathsf {dl}}\) into the binding part (used when
in \(\mathsf {\Gamma }_{\mathsf {dl}}\) into the binding part (used when  acts as the receiver \(\mathsf {R}\)) and the hiding part (used when
acts as the receiver \(\mathsf {R}\)) and the hiding part (used when  acts as the committer \(\mathsf {C}\)). \(\mathsf {C}\) and \(\mathsf {R}\) use
acts as the committer \(\mathsf {C}\)). \(\mathsf {C}\) and \(\mathsf {R}\) use  from \(\mathsf {C}\)’s public key \(\mathsf {rpk}_\mathsf {C}\) and \(\mathsf {rpk}^{\mathsf {b}}_\mathsf {R}= (\mathsf {Ped}.\mathsf {ck}_\mathsf {R}, \mathsf {DF}.\mathsf {ck}_\mathsf {R}, \mathsf {H}^{\mathsf {b}}_\mathsf {R})\) from \(\mathsf {R}\)’s public key \(\mathsf {rpk}_\mathsf {R}\). Obviously, \(\mathsf {C}\) knows \(\mathsf {rpk}_\mathsf {C}\) while she has to retrieve \(\mathsf {rpk}_\mathsf {R}\) from
from \(\mathsf {C}\)’s public key \(\mathsf {rpk}_\mathsf {C}\) and \(\mathsf {rpk}^{\mathsf {b}}_\mathsf {R}= (\mathsf {Ped}.\mathsf {ck}_\mathsf {R}, \mathsf {DF}.\mathsf {ck}_\mathsf {R}, \mathsf {H}^{\mathsf {b}}_\mathsf {R})\) from \(\mathsf {R}\)’s public key \(\mathsf {rpk}_\mathsf {R}\). Obviously, \(\mathsf {C}\) knows \(\mathsf {rpk}_\mathsf {C}\) while she has to retrieve \(\mathsf {rpk}_\mathsf {R}\) from  .
.
See Fig. 5 for the full description of \(\mathsf {\Gamma }_{\mathsf {dl}}\). Here, \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {Gen}\) for party  is executed by the key registration authority
is executed by the key registration authority  as usual in the RPK model, \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {Com}\) and \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {Open}\) are executed by \(\mathsf {C}\), and
as usual in the RPK model, \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {Com}\) and \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {Open}\) are executed by \(\mathsf {C}\), and  is executed by \(\mathsf {R}\). The algorithms \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {tdOpen}\) and
is executed by \(\mathsf {R}\). The algorithms \(\mathsf {\Gamma }_{\mathsf {dl}}.\mathsf {tdOpen}\) and  are only executed within the security proof. To get straight-line simulation, we use the same method as [16]. Finally, note we have included \((\mathsf {lbl}, \mathsf {c}_3, e)\) to \(\mathsf {op}\) mainly to simplify the notation.
are only executed within the security proof. To get straight-line simulation, we use the same method as [16]. Finally, note we have included \((\mathsf {lbl}, \mathsf {c}_3, e)\) to \(\mathsf {op}\) mainly to simplify the notation.
Theorem 2
Assume that \(\mathsf {SCS}\) is an IND-PCA secure and \(\mathsf {Pai}\) is an IND-CPA secure additively homomorphic cryptosystem, \(\mathsf {Ped}\) is a computationally binding and perfectly hiding trapdoor commitment scheme and \(\mathsf {DF}\) is a computationally binding and statistically hiding ICS. Assume secure erasure. Then \(\mathsf {\Gamma }_{\mathsf {dl}}\) from Fig. 5 UC-realizes \(\mathcal {F}_{\mathsf {mcomdl}}\) in the \(\mathcal {F}_{\mathsf {rpk}}\)-hybrid model against adaptive attackers, i.e., it is a secure DL-extractable UC-commitment scheme in the RPK model.
The proof of Theorem 2 follows closely the security proof of Fujisaki’s UC-commitment scheme [16], with a few notable differences (the use of the RPK model instead of the CRS model, and the use of a different \(\varSigma \)-protocol, which causes us to use one more game to handle Paillier encryption).
Proof
As usual, we consider a sequence of hybrid games in which we change the rules of games step by step. We denote the changes by using  .
.
 This is the real world game in the RPK model (\(\textsc {Hybrid}^{\mathcal {F}_{\mathsf {rpk}}}\)). In \(\mathsf {Game}_{0}\), the real protocol is executed between the committer \(\mathsf {C}\) and the receiver \(\mathsf {R}\). The environment \(\mathcal {Z}\) adaptively chooses the input for honest committer \(\mathsf {C}\) and receives the output of honest parties. Adversary
This is the real world game in the RPK model (\(\textsc {Hybrid}^{\mathcal {F}_{\mathsf {rpk}}}\)). In \(\mathsf {Game}_{0}\), the real protocol is executed between the committer \(\mathsf {C}\) and the receiver \(\mathsf {R}\). The environment \(\mathcal {Z}\) adaptively chooses the input for honest committer \(\mathsf {C}\) and receives the output of honest parties. Adversary  attacks the real protocol in the real world, i.e., she can see the interactions between the honest parties or interact with the honest parties as playing the role of some parties after they are corrupted. When a party is corrupted,
attacks the real protocol in the real world, i.e., she can see the interactions between the honest parties or interact with the honest parties as playing the role of some parties after they are corrupted. When a party is corrupted,  can read her current inner state and
can read her current inner state and  also fully controls her. \(\mathcal {Z}\) can control
also fully controls her. \(\mathcal {Z}\) can control  and see the inside of the execution of the protocol (the interactions between the honest parties or between the honest parties and the adversary) via the view of
and see the inside of the execution of the protocol (the interactions between the honest parties or between the honest parties and the adversary) via the view of  .
.
 In \(\mathsf {Game}_{1}\),
In \(\mathsf {Game}_{1}\),  simulates the authorities
simulates the authorities  generating the registered public keys \(\mathsf {rpk}_\mathsf {C}\) and \(\mathsf {rpk}_\mathsf {R}\) used by \(\mathsf {C}\) and \(\mathsf {R}\).
generating the registered public keys \(\mathsf {rpk}_\mathsf {C}\) and \(\mathsf {rpk}_\mathsf {R}\) used by \(\mathsf {C}\) and \(\mathsf {R}\).  stores \(\mathsf {td}_{\mathsf {C}\mathsf {R}} = (\mathsf {td}^{\mathsf {h}}_\mathsf {C}, \mathsf {td}^{\mathsf {b}}_\mathsf {R})\).
stores \(\mathsf {td}_{\mathsf {C}\mathsf {R}} = (\mathsf {td}^{\mathsf {h}}_\mathsf {C}, \mathsf {td}^{\mathsf {b}}_\mathsf {R})\).  simulates honest parties as in \(\mathsf {Game}_{0}\), except for the case where \(\mathsf {R}\) is honest but \(\mathsf {C}\) is corrupted. After obtaining \((\mathsf {lbl}, \mathsf {c}_3; e; \mathsf {c})\) from the view of the protocol between \(\mathsf {C}\) and \(\mathsf {R}\) in the commit phase, where \(\mathsf {lbl}= (\mathsf {sid}, \mathsf {cid}, \mathsf {C}, \mathsf {R})\),
simulates honest parties as in \(\mathsf {Game}_{0}\), except for the case where \(\mathsf {R}\) is honest but \(\mathsf {C}\) is corrupted. After obtaining \((\mathsf {lbl}, \mathsf {c}_3; e; \mathsf {c})\) from the view of the protocol between \(\mathsf {C}\) and \(\mathsf {R}\) in the commit phase, where \(\mathsf {lbl}= (\mathsf {sid}, \mathsf {cid}, \mathsf {C}, \mathsf {R})\),  stores
stores  as a part of the state. In the open phase, when \(\mathsf {C}\) successfully opens to \(g^m\),
as a part of the state. In the open phase, when \(\mathsf {C}\) successfully opens to \(g^m\),  sends
sends  to \(\mathcal {Z}\).
to \(\mathcal {Z}\).
In the case of adaptive corruption of \(\mathsf {R}\) before the open phase,  simply reveals
simply reveals  to
to  . Honest \(\mathsf {R}\) has no secret.
. Honest \(\mathsf {R}\) has no secret.
Lemma 1
If  is specially sound, \(\mathsf {Ped}\) is computationally binding, and \(\mathsf {H}^{\mathsf {b}}_{\mathsf {R}}\) is collision-resistant then \(\mathcal {Z}\) distinguishes \(\mathsf {Game}_{0}\) and \(\mathsf {Game}_{1}\) with a negligible probability.
is specially sound, \(\mathsf {Ped}\) is computationally binding, and \(\mathsf {H}^{\mathsf {b}}_{\mathsf {R}}\) is collision-resistant then \(\mathcal {Z}\) distinguishes \(\mathsf {Game}_{0}\) and \(\mathsf {Game}_{1}\) with a negligible probability.
Proof
(Proof of Lemma 1). The only difference from \(\mathsf {Game}_{0}\) is that in \(\mathsf {Game}_{1}\),  (playing as honest \(\mathsf {R}\)) outputs \(g^{m^*}\) instead of \(g^m\) at the open phase.
(playing as honest \(\mathsf {R}\)) outputs \(g^{m^*}\) instead of \(g^m\) at the open phase.  opens \(g^{m^*}\) after \(\mathsf {C}\) decommits to \(g^m\) in a verifiable way. If not,
opens \(g^{m^*}\) after \(\mathsf {C}\) decommits to \(g^m\) in a verifiable way. If not,  outputs nothing. Denote by
outputs nothing. Denote by  the event that \(m^* \not \equiv m \pmod {p}\) where \(g^m\) is the value successfully opened by \(\mathsf {C}\). We claim that
the event that \(m^* \not \equiv m \pmod {p}\) where \(g^m\) is the value successfully opened by \(\mathsf {C}\). We claim that  occurs only with a negligible probability; otherwise, either the soundness of
occurs only with a negligible probability; otherwise, either the soundness of  , the binding of \(\mathsf {Ped}\), or the collision resistance of \(\mathsf {H}^{\mathsf {b}}_\mathsf {R}\) is broken.
, the binding of \(\mathsf {Ped}\), or the collision resistance of \(\mathsf {H}^{\mathsf {b}}_\mathsf {R}\) is broken.
Assume that \(m^* \not \equiv m \pmod {p}\) at least in one of such executions. In the first such execution, we rewind the adversary at the step (*) in the commit phase and send a new random challenge \(e'\). Assume, by contradiction, that \(\mathsf {C}\) returns \(\mathsf {c}' = (\mathbf {\mathsf {c}}_1', \mathsf {c}_2')\) such that \(\mathsf {c}' \ne \mathsf {c}\) but still successfully decommits to some value \(m'\) with \(a'\). Then it implies breaking of the binding of \(\mathsf {Ped}\) or the collision-resistancy of \(\mathsf {H}^{\mathsf {b}}_\mathsf {R}\), because we can simulate it without knowing the trapdoor key. For the same reason, \(\mathsf {x}' = \mathsf {x}\) (and thus \(m' = m\)) holds except with a negligible probability. Thus, rewinding the commit phase, \(\mathsf {C}\) outputs the same \(\mathsf {st}_\mathsf {C}= (\mathsf {c}, g^m, \mathsf {op})\) except with a negligible probability when it can successfully decommit. Note that \(m^* \not \equiv m \pmod {p}\) implies that \(\mathsf {x}\not \in \mathsf {\mathbf {L}_{eq}}\). Since \(\mathsf {x}\) (and thus m) is now fixed with an overwhelming probability, \(\mathsf {C}\) can convince \(\mathsf {R}\) on false instance \(\mathsf {x}\) only with probability  (this follows from the special soundness of
(this follows from the special soundness of  ), which is negligible in
), which is negligible in  . Hence,
. Hence,  occurs only with a negligible probability and the views of \(\mathcal {Z}\) in the two games are computationally indistinguishable. We stress that we rewind just in the proof of binding, but not in the simulation. \(\square \)
occurs only with a negligible probability and the views of \(\mathcal {Z}\) in the two games are computationally indistinguishable. We stress that we rewind just in the proof of binding, but not in the simulation. \(\square \)
 identical to \(\mathsf {Game}_{1}\) except following cases.
identical to \(\mathsf {Game}_{1}\) except following cases.
Honest \(\mathsf {C}\): In the open phase, upon receiving \((\mathtt {open}, \mathsf {sid}, \mathsf {cid})\) from \(\mathcal {Z}\),  sets
sets  and sends
and sends  to \(\mathsf {R}\); Importantly, in the simulation of honest \(\mathsf {C}\)in the open phase,
to \(\mathsf {R}\); Importantly, in the simulation of honest \(\mathsf {C}\)in the open phase,  does not have to know \(\mathsf {w}\).
does not have to know \(\mathsf {w}\).
\(\mathsf {C}\) was adaptively corrupted before receiving e: in the commit phase,  sets
sets  and then reveals the current secret state
and then reveals the current secret state  to \(\mathcal {Z}\).
to \(\mathcal {Z}\).
\(\mathsf {C}\) was adaptively corrupted after receiving e but before the open phase:  simulates \(\mathsf {C}\) honestly. Note that \((\mathsf {w}, \mathbf {s})\) is supposed to be erased by honest \(\mathsf {C}\) before sending \(\mathsf {c}\), and thus,
simulates \(\mathsf {C}\) honestly. Note that \((\mathsf {w}, \mathbf {s})\) is supposed to be erased by honest \(\mathsf {C}\) before sending \(\mathsf {c}\), and thus,  does not need to reveal it. The proof of the following lemma is straightforward.
does not need to reveal it. The proof of the following lemma is straightforward.
Lemma 2
If  is SHVZK and \(\mathsf {Ped}\) is trapdoor, then \(\mathcal {Z}\) distinguishes \(\mathsf {Game}_{1}\) and \(\mathsf {Game}_{2}\) with negligible probability.
is SHVZK and \(\mathsf {Ped}\) is trapdoor, then \(\mathcal {Z}\) distinguishes \(\mathsf {Game}_{1}\) and \(\mathsf {Game}_{2}\) with negligible probability.
 In this game, we do the following changes.
In this game, we do the following changes.
Honest \(\mathsf {C}\): In the commit phase, after receiving \((\mathtt {commit}, \mathsf {lbl}, m)\) from \(\mathcal {Z}\), when it receives e,  computes
computes  and sends
and sends  to \(\mathsf {R}\). In the open phase, upon receiving input \((\mathtt {open}, \mathsf {sid}, \mathsf {cid})\) from \(\mathcal {Z}\),
to \(\mathsf {R}\). In the open phase, upon receiving input \((\mathtt {open}, \mathsf {sid}, \mathsf {cid})\) from \(\mathcal {Z}\),  first sets
first sets  where
where  because
because  .
.
In the case of adaptive corruption of \(\mathsf {C}\):  simulates \(\mathsf {C}\) as in \(\mathsf {Game}_{2}\).
simulates \(\mathsf {C}\) as in \(\mathsf {Game}_{2}\).
Security analysis. The only difference from the previous game is that in \(\mathsf {Game}_{3}\), the simulator  (playing as honest \(\mathsf {C}\)) computes
(playing as honest \(\mathsf {C}\)) computes  encrypting \(1\) instead of \(g^m\). As in [16], we run the (multi-message) IND-PCA game to show this game is indistinguishable from the previous game. Denote by
encrypting \(1\) instead of \(g^m\). As in [16], we run the (multi-message) IND-PCA game to show this game is indistinguishable from the previous game. Denote by  the event in \(\mathsf {Game}_{i}\) that \(m^* \not \equiv m \pmod {p}\) where m is the value successfully opened by \(\mathsf {C}\). As analysed above,
the event in \(\mathsf {Game}_{i}\) that \(m^* \not \equiv m \pmod {p}\) where m is the value successfully opened by \(\mathsf {C}\). As analysed above,  . In addition, \(\mathsf {Game}_{1}\) is statistically close to \(\mathsf {Game}_{2}\) and so,
. In addition, \(\mathsf {Game}_{1}\) is statistically close to \(\mathsf {Game}_{2}\) and so,  . We use this fact to prove the following lemma.
. We use this fact to prove the following lemma.
Lemma 3
If \(\mathsf {SCS}\) is IND-PCA secure then \(\mathcal {Z}\) distinguishes \(\mathsf {Game}_{2}\) and \(\mathsf {Game}_{3}\) with only a negligible probability.
Proof
(Proof of Lemma 3). The proof is a variant of the proof in [16], App. A. We define the multi-message IND-PCA security for a public-key cryptosystem \(\varPi \). Let  be the following experiment:
be the following experiment:

Here, the oracles are defined as follows:
-
 rejects it if
rejects it if  . Otherwise, it adds \(\mathsf {lbl}^*\) to
. Otherwise, it adds \(\mathsf {lbl}^*\) to  and returns
and returns  .
. -
 rejects it if
rejects it if  . Otherwise, it adds \(\mathsf {lbl}\) to
. Otherwise, it adds \(\mathsf {lbl}\) to  , and returns 1 iff \(\mathbf {\mathsf {c}}\) is a proper ciphertext of \(g^m\) on label \(\mathsf {lbl}\).
, and returns 1 iff \(\mathbf {\mathsf {c}}\) is a proper ciphertext of \(g^m\) on label \(\mathsf {lbl}\).
\(\varPi \) is multi-message indistinguishable against the plaintext checkable attacks (mIND-PCA secure) if  for all non-uniform PPT
for all non-uniform PPT  .
.
By using the standard hybrid argument, for any mIND-PCA adversary  against \(\varPi \) with at most
against \(\varPi \) with at most  queries to the encryption oracle, there exists an IND-PCA adversary
queries to the encryption oracle, there exists an IND-PCA adversary  against \(\varPi \), s.t.
against \(\varPi \), s.t.  , where the running time of
, where the running time of  is roughly bounded by the running time of
is roughly bounded by the running time of  plus \(q-1\) encryption operations. We construct mIND-PCA adversary
plus \(q-1\) encryption operations. We construct mIND-PCA adversary  using \(\mathcal {Z}\) and the adversary
using \(\mathcal {Z}\) and the adversary  as follows. W.l.o.g., assume that
as follows. W.l.o.g., assume that  , where
, where  is the random variable assigning the output bit of the environment \(\mathcal {Z}\) in \(\mathsf {Game}_{i}\).
is the random variable assigning the output bit of the environment \(\mathcal {Z}\) in \(\mathsf {Game}_{i}\).  is given
is given  as an instance in the mIND-CPA game.
as an instance in the mIND-CPA game.  sets up \(\mathsf {rpk}_\mathsf {C}\) and \(\mathsf {rpk}_\mathsf {R}\) by picking the remaining parameters. Here, she knows \(\mathsf {Ped}.\mathsf {td}_\mathsf {R}\) but does not know
sets up \(\mathsf {rpk}_\mathsf {C}\) and \(\mathsf {rpk}_\mathsf {R}\) by picking the remaining parameters. Here, she knows \(\mathsf {Ped}.\mathsf {td}_\mathsf {R}\) but does not know  .
.  runs \(\mathcal {Z}\) and
runs \(\mathcal {Z}\) and  and plays the role of simulator
and plays the role of simulator  as in \(\mathsf {Game}_{2}\) (or \(\mathsf {Game}_{3}\)), except for the following two cases:
as in \(\mathsf {Game}_{2}\) (or \(\mathsf {Game}_{3}\)), except for the following two cases:
-
(i)
If \(\mathsf {C}\) is honest and
 receives \((\mathsf {lbl}, \mathsf {c}_3)\) from \(\mathcal {Z}\),
receives \((\mathsf {lbl}, \mathsf {c}_3)\) from \(\mathcal {Z}\),  submits \((\mathsf {lbl}, g^m, 1)\) to the oracle
submits \((\mathsf {lbl}, g^m, 1)\) to the oracle  and receives \(\mathbf {\mathsf {c}}\). Then,
and receives \(\mathbf {\mathsf {c}}\). Then,  plays the role of the simulator in \(\mathsf {Game}_{2}\) (or equivalently, in \(\mathsf {Game}_{3})\).
plays the role of the simulator in \(\mathsf {Game}_{2}\) (or equivalently, in \(\mathsf {Game}_{3})\). -
(ii)
If \(\mathsf {R}\) is honest but \(\mathsf {C}\) is corrupted, after receiving all three messages in the commit phase with \(\mathsf {C}\),
 simply stores it. In the open phase, when \(\mathsf {C}\) successfully decommits to \(g^m\),
simply stores it. In the open phase, when \(\mathsf {C}\) successfully decommits to \(g^m\),  submits \((\mathsf {lbl}, g^m, \mathbf {\mathsf {c}}_1)\) to the oracle
submits \((\mathsf {lbl}, g^m, \mathbf {\mathsf {c}}_1)\) to the oracle  and receives the answer bit. If the answer bit is 1, then
and receives the answer bit. If the answer bit is 1, then  outputs \((\mathtt {open}, \mathsf {lbl}, g^m)\) to the environment. Otherwise, she halts and outputs 1 (break point).
outputs \((\mathtt {open}, \mathsf {lbl}, g^m)\) to the environment. Otherwise, she halts and outputs 1 (break point).
If such an event does not occur,  proceeds the game with \(\mathcal {Z}\) and
proceeds the game with \(\mathcal {Z}\) and  as playing the role of
as playing the role of  . When \(\mathcal {Z}\) outputs a bit \(b'\),
. When \(\mathcal {Z}\) outputs a bit \(b'\),  outputs \(b'\) in the mIND-PCA game.
outputs \(b'\) in the mIND-PCA game.
Security Analysis. Above,  perfectly simulates \(\mathsf {Game}_{2}\) when \(b = 0\) just before the break point. Recall that
perfectly simulates \(\mathsf {Game}_{2}\) when \(b = 0\) just before the break point. Recall that  denotes the event in \(\mathsf {Game}_{i}\) that \(m^* \not \equiv m \pmod {p}\) where \(g^m\) is the value successfully decommitted to by corrupted \(\mathsf {C}\). The probability that the break occurs is equal to the probability that
denotes the event in \(\mathsf {Game}_{i}\) that \(m^* \not \equiv m \pmod {p}\) where \(g^m\) is the value successfully decommitted to by corrupted \(\mathsf {C}\). The probability that the break occurs is equal to the probability that  occurs, which is negligible. Similarly,
occurs, which is negligible. Similarly,  perfectly simulates \(\mathsf {Game}_{3}\) when \(b = 1\) just before the break point. We do not know
perfectly simulates \(\mathsf {Game}_{3}\) when \(b = 1\) just before the break point. We do not know  . However, since
. However, since  , we can conclude \(b = 1\) if the break happens. If the break never happens,
, we can conclude \(b = 1\) if the break happens. If the break never happens,  perfectly simulates either \(\mathsf {Game}_{2}\) or \(\mathsf {Game}_{3}\) according to b. Thus, the difference of the output of \(\mathcal {Z}\) is bounded by the advantage of
perfectly simulates either \(\mathsf {Game}_{2}\) or \(\mathsf {Game}_{3}\) according to b. Thus, the difference of the output of \(\mathcal {Z}\) is bounded by the advantage of  :
:  . Thus,
. Thus,  . \(\square \)
. \(\square \)
 In this game,
In this game,  enacts the following changes compared to \(\mathsf {Game}_{3}\).
enacts the following changes compared to \(\mathsf {Game}_{3}\).
If \(\mathsf {C}\) is honest: upon receiving input \((\mathtt {commit}, \mathsf {lbl}, m)\) from \(\mathcal {Z}\), after receiving e,  computes
computes  and returns
and returns  to \(\mathsf {R}\).
to \(\mathsf {R}\).
In the open phase, upon receiving input \((\mathtt {open}, \mathsf {sid}, \mathsf {cid})\) from \(\mathcal {Z}\),  first sets
first sets  where \(\mathsf {x}\not \in \mathsf {\mathbf {L}_{eq}}\) because
where \(\mathsf {x}\not \in \mathsf {\mathbf {L}_{eq}}\) because  and
and  .
.
If \(\mathsf {C}\) is adaptively corrupted:  simulates \(\mathsf {C}\) identically as in \(\mathsf {Game}_{3}\).
simulates \(\mathsf {C}\) identically as in \(\mathsf {Game}_{3}\).
Security Analysis. The only difference from \(\mathsf {Game}_{3}\) is that in \(\mathsf {Game}_{4}\), the simulator  (playing as honest
(playing as honest  ) computes
) computes  instead of
instead of  . We run the (multi-message) IND-CPA game to show \(\mathsf {Game}_{4}\) is indistinguishable from \(\mathsf {Game}_{3}\).
. We run the (multi-message) IND-CPA game to show \(\mathsf {Game}_{4}\) is indistinguishable from \(\mathsf {Game}_{3}\).
Lemma 4
If \(\mathsf {Pai}\) is IND-CPA secure then \(\mathcal {Z}\) distinguishes \(\mathsf {Game}_{3}\) and \(\mathsf {Game}_{4}\) with only a negligible probability.
Proof
The proof is a variation of the proof of Lemma 3. We now analyse \(\mathsf {Pai}\), and define CPA-related security games (like mIND-CPA) instead of PCA-related security games. \(\square \)
 In the ideal world, there additionally exists an ideal functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) and the task of the honest parties in the ideal world is simply to convey inputs from \(\mathcal {Z}\) to the ideal functionalities and vice versa (the ideal honest parties communicate only with \(\mathcal {Z}\) and the ideal functionalities).
In the ideal world, there additionally exists an ideal functionality \(\mathcal {F}_{\mathsf {mcomdl}}\) and the task of the honest parties in the ideal world is simply to convey inputs from \(\mathcal {Z}\) to the ideal functionalities and vice versa (the ideal honest parties communicate only with \(\mathcal {Z}\) and the ideal functionalities).

By construction, this game is identical to the previous game. \(\square \)
References
Abdalla, M., Benhamouda, F., Pointcheval, D.: Public-key encryption indistinguishable under plaintext-checkable attacks. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 332–352. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_15
Barak, B., Canetti, R., Nielsen, J.B., Pass, R.: Universally composable protocols with relaxed set-up assumptions. In: 45th FOCS, pp. 186–195 (2004)
Belenkiy, M., Chase, M., Kohlweiss, M., Lysyanskaya, A.: P-signatures and noninteractive anonymous credentials. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 356–374. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_20
Ben-Sasson, E., Chiesa, A., Green, M., Tromer, E., Virza, M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: 2015 IEEE Symposium on Security and Privacy, pp. 287–304 (2015)
Blazy, O., Chevalier, C., Pointcheval, D., Vergnaud, D.: Analysis and improvement of Lindell’s UC-secure commitment schemes. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 534–551. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38980-1_34
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112 (1988)
Camenisch, J., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_8
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145 (2001)
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_2
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: 34th ACM STOC, pp. 494–503 (2002)
Cramer, R., Damgård, I., Schoenmakers, B.: Proofs of partial knowledge and simplified design of witness hiding protocols. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 174–187. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_19
Damgård, I.: Towards practical public key systems secure against chosen ciphertext attacks. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 445–456. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_36
Damgård, I., Fujisaki, E.: A statistically-hiding integer commitment scheme based on groups with hidden order. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 125–142. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_8
Damgård, I., Nielsen, J.B.: Perfect hiding and perfect binding universally composable commitment schemes with constant expansion factor. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 581–596. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_37
Fischlin, M., Libert, B., Manulis, M.: Non-interactive and re-usable universally composable string commitments with adaptive security. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 468–485. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_25
Fujisaki, E.: Improving practical UC-secure commitments based on the DDH assumption. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 257–272. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_14
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Kosba, A.E., et al.: C\(\emptyset \)C\(\emptyset \): a framework for building composable zero-knowledge proofs. Technical report 2015/1093, IACR (2015). http://eprint.iacr.org/2015/1093. Accessed 9 Apr 2017
Lindell, Y.: Highly-efficient universally-composable commitments based on the DDH assumption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 446–466. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_25
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Pedersen, T.P.: Non-interactive and information-theoretic secure verifiable secret sharing. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 129–140. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_9
Acknowledgement
The authors were supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 780477 (project PRIViLEDGE), and by the Estonian Research Council grant PRG49. The work was done while Zając was working at the University of Tartu.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Abdolmaleki, B., Baghery, K., Lipmaa, H., Siim, J., Zając, M. (2019). DL-Extractable UC-Commitment Schemes. In: Deng, R., Gauthier-Umaña, V., Ochoa, M., Yung, M. (eds) Applied Cryptography and Network Security. ACNS 2019. Lecture Notes in Computer Science(), vol 11464. Springer, Cham. https://doi.org/10.1007/978-3-030-21568-2_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-21568-2_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21567-5
Online ISBN: 978-3-030-21568-2
eBook Packages: Computer ScienceComputer Science (R0)







 : sample
: sample  , set
, set  ,
,  : output
: output  : output 1 if
: output 1 if  :
:  chooses an
chooses an  -rough, and sets
-rough, and sets  .
.  sends
sends  to
to  and proves that
and proves that  for
for  ,
,  : output
: output  ,
,  : check that
: check that  and
and 
 :
:  ;
;  ;
;  and
and  .
. : sample
: sample  ; set
; set  . Return the ciphertext
. Return the ciphertext 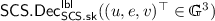 : set
: set 


 for
for  and
and  . Here,
. Here,  ,
,  .
.
 rejects it if
rejects it if  . Otherwise, it adds
. Otherwise, it adds  and returns
and returns  .
. rejects it if
rejects it if  . Otherwise, it adds
. Otherwise, it adds  , and returns 1 iff
, and returns 1 iff  receives
receives  submits
submits  and receives
and receives  plays the role of the simulator in
plays the role of the simulator in  simply stores it. In the open phase, when
simply stores it. In the open phase, when  submits
submits  and receives the answer bit. If the answer bit is 1, then
and receives the answer bit. If the answer bit is 1, then  outputs
outputs