Parameter Selection for Regularized Electron Tomography Without a Reference Image

Abstract

Regularization has been introduced to electron tomography for enhancing the reconstruction quality. Since over-regularization smears out sharp edges and under-regularization leaves the image too noisy, finding the optimal regularization strength is crucial. To this end, one can either manually tune regularization parameters by trial and error, or compute reconstructions for a large set of candidate values and compare them to a reference image. Both are cumbersome in practice. In this paper, we propose an image quality metric Q to quantify the reconstruction quality for automatically determining the optimal regularization parameter $\lambda$ without a reference image. Specifically, we use the oriented structure strength described by the highest two responses in orientation space to simultaneously measure the sharpness and noisiness of reconstruction images. We demonstrate the usefulness of Q on a recently introduced total nuclear variation regularized reconstruction technique using simulated and experimental datasets of core-shell nanoparticles. Results show that it can replace the full-reference correlation coefficient to find the optimal $\lambda$. Moreover, observing that the curve of Q versus $\lambda$ has a distinct maximum attained for the best quality, we adopt the golden section search for the optimum to effectively reduce the computational time by 85%.

This work is partially supported by the Dutch Technology Foundation STW, which is part of the Netherlands Organization for Scientific Research, and partially by the Ministry of Economic Affairs, Agriculture and Innovation under project number 13314.

1 Introduction

Electron tomography enables materials scientists to characterize nanoparticles in three dimensions (3D) [12]. Scanning transmission electron microscopy (STEM) has many imaging modes such as high-angle annular dark-field (HAADF) [12], in which the sample under study is exposed to a focused electron beam and tilted to obtain two-dimensional (2D) projections at different angles. In tomography, the collection of projections is called a tilt-series, from which we can reconstruct a 3D image that represents the sample. Although HAADF tomography can clearly reveal the inner structure of the sample, it cannot explicitly provide its compositional information. To better understand samples with more complex chemical compositions, spectral imaging techniques like energy dispersive X-ray spectroscopy (EDS) [19] must be pursued. EDS tomography, however, is currently hampered by slow data acquisition, resulting in a limited number of elemental maps with low signal-to-noise ratio (SNR) [19].

Electron tomography is an ill-posed inverse problem whose solution is not stable and unique. Therefore, $l_1$ regularizations (e.g., total variation (TV) [8] and higher order total variation (HOTV) [16, 17]) have been introduced to enhance the reconstruction quality. However, regularizations, especially the common TV, inevitably aggravate jaggy edges and staircase artifacts when being applied to the (noisy) EDS datasets. To alleviate such artifacts yet still benefiting from regularization, Zhong et al. incorporated the HAADF-STEM projections with high SNR into EDS maps using total nuclear variation (TNV) to enforce anti-/parallel gradients and common edges in joint reconstructions [21]. Like other regularization-based approaches, TNV also requires a fine-tuning parameter $\lambda$ to determine the strength of regularization. The “best” $\lambda$ is now chosen by computing reconstructions for a large set of candidate values and comparing them to a reference image with the correlation coefficient [21]. Since this is infeasible if the reference is unavailable, we need to automatically measure the reconstruction quality for determining the optimal $\lambda$.

So far, many no-reference quality assessment algorithms have been proposed to set appropriate parameters for inverse problems. For instance, Zhu and Milanfar developed a structure tensor based image content index to optimize denoising algorithms [22]. Since this index is easy to compute, it has also been adopted to determine the optimal regularization parameter for the TV reconstruction technique [11]. Applications dedicated to electron tomography also exist [9, 13]. For example, Okariz et al. derived the optimal number of iterations for simultaneous iterative reconstruction technique (SIRT) by statistically analyzing the edge profile of reconstructions [13]. Furthermore, we recently proposed a non-distortion-specific image quality metric to quantify the cross-atomic contamination and noise so as to select the optimal weighting factor for bimodal tomography [9]. However, automatically selecting parameters for regularized electron tomography has still not been widely investigated to the best of our knowledge.

In this paper, we aim to automatically find the optimal regularization parameter $\lambda$ for TNV in the absence of a reference image. Specifically, we extend the concept of image content index [22] to orientation space (OS) [5], in which we develop a metric Q to assess the reconstruction quality regarding the sharpness and noisiness. We demonstrate our Q on simulated and experimental datasets of core-shell nanoparticles containing gold and silver. Results show that this OS-based Q is more robust to noise than the original tensor-based version. Moreover, it can replace the full-reference correlation coefficient used in [21] to determine the optimal $\lambda$. In Sect. 2, we introduce the TNV-regularized reconstruction technique and its relations to TV. Section 3 elaborates the orientation space as prior work, followed by our quality assessment framework for parameter determination. We present the experiments and results in Sect. 4, and summarize our work in Sect. 5.

2 TNV Regularized Electron Tomography

Originally proposed for color images [10], total nuclear variation (TNV) has later been applied to multi-channel spectral CT data for encouraging common edge locations and a shared gradient direction among the different channels [15]. Let us assume that an arbitrary 3D image $\mathbf {A}$ has a number of L channels, in which $\mathbf {A}_n=[A_n^{(1)},\cdots ,A_n^{(L)}]^T\in \mathbb {R}^{L\times 1}$ is the intensity value tuple of its n-th voxel. Denote the Jacobian matrix of $\mathbf {A}$ as $\mathbf {J}_n{\mathbf {A}}$ [21], then TNV of $\mathbf {A}$ is

$$\begin{aligned} \text {TNV}(\mathbf {A})=\sum _n\left\| {\mathbf {J}_n{\mathbf {A}}}\right\| _\star \end{aligned}$$

(1)

where $\left\| {\mathbf {J}_n{\mathbf {A}}}\right\| _\star$, the nuclear norm of $\mathbf {J}_n{\mathbf {A}}$, is the sum of its singular values [15]. When $L=1$, TNV reduces to the isotropic ($l_2$-norm) TV [21].

We consider a specimen with a number of E different chemical elements. Each element $e=1,\cdots ,E$ has its EDS map $\mathbf {p}^{(e)}\in \mathbb {R}^{M^e\times 1}$, and is associated with one unknown reconstruction volume $\mathbf {x}^{(e)}\in \mathbb {R}^{N\times 1}$. $M^e$ is the number of pixels in the map and N the number of discretized voxels to be reconstructed. Similarly, let $\mathbf {p}^h\in \mathbb {R}^{M^h\times 1}$ and $\mathbf {x}^{h}\in \mathbb {R}^{N\times 1}$ be the projection and volumetric reconstruction of HAADF, respectively. Note that $M^h$, the number of pixels in the HAADF projection, is not equal to $M^e$ if the HAADF tilt-series has more acquisition angles than the EDS.

Given $\mathbf {A}_n$ as a two-channel image $\mathbf {A}_n=[x_n^{(e)},x_n^h]^T$, i.e., one element of interest plus HAADF, the TNV-regularized EDS and HAADF joint tomography is [21]

$$\begin{aligned} \mathbf {x}^{(e)*},\mathbf {x}^{h*}=\mathop {\text {arg min}}\limits _{\mathbf {x}^{(e)},\mathbf {x}^{h}}\left\| {\mathbf {p}^{(e)}-\mathbf {W}^{(e)}\mathbf {x}^{(e)}}\right\| _2^2+\left\| {\mathbf {p}^{h}-\mathbf {W}^h\mathbf {x}^h}\right\| _2^2+\lambda \text {TNV}(\mathbf {x}^{(e)},\mathbf {x}^h). \end{aligned}$$

(2)

Extending $\mathbf {A}_n$ to multiple channels with more than one element is also possible, as long as they share common edges [21]. In Eq. (2), $\mathbf {W}^{(e)}\in \mathbb {R}^{M^e\times N}$ and $\mathbf {W}^{h}\in \mathbb {R}^{M^h\times N}$ are the projection matrices of the EDS and HAADF, respectively, whose entries $w^{(e)}_{mn}$ and $w^{h}_{mn}$ are determined by the intersected area between the m-th ray integral and n-th voxel. When the HAADF term is removed and $A_n=x_n^{(e)}$, Eq. (2) reduces to the TV-regularized EDS tomography [8].

The parameter $\lambda$ in Eq. (2) determines the strength of TNV regularization. A large $\lambda$ may blur sharp edges and produce an over-smoothed reconstruction, whereas a small one may make the regularization ineffective. To choose this crucial parameter, Zhong et al. computed the reconstructions $\mathbf {x}^{(e)*}$ for a large set of $\lambda$ (e.g., 100 values uniformly sampled from $10^{-3}$ to $10^1$ on the logarithmic scale) and compared them to a noise-free image using the correlation coefficient [21]. Since this is infeasible in industry, we need a no-reference quality metric to quantify the reconstruction quality so as to (blindly) determine the optimal $\lambda$.

3 No-Reference Regularization Parameter Determination

Considering that the effect of regularization varies spatially, we propose to use the local oriented structure strength (OSS) to measure the image quality; it has large values for well structured patches containing lines and edges and small values for blurry/noisy ones. In this section, we first introduce the concept of orientation space [5], from which we then present our OSS-based quality assessment framework.

3.1 Orientation Space

The linear orientation space of a 3D input image $I(\mathbf {x})$ can be constructed as

$$\begin{aligned} I_h(\mathbf {x},\phi ,\theta )=I(\mathbf {x})*h(\mathbf {x};\phi ,\theta ) \end{aligned}$$

(3)

where $\mathbf {x}$ is the Cartesian coordinate tuple containing x, y and z. Operator $*$ denotes convolution. $h(\mathbf {x};\phi ,\theta )$ is obtained by rotating an elongated template filter $h(\mathbf {x})$ over angles $\phi$ and $\theta$ in a unit sphere. $\phi \in [0,2\pi )$ is the counter-clockwise angle measured from the positive x-axis in the xy-plane; $\theta \in [0,\pi )$ is the angular distance from the positive z-axis [5]. One promising candidate for $h(\mathbf {x})$ is a Gabor filter [4]; however, it cannot produce a zero response to a constant signal. Therefore, we use a similar filter which is zero for a constant signal [5].

According to van Ginkel et al., the choice of the template filter $h(\cdot )$ is largely free, as long as the scale and orientation can be dealt with separately [7]. To this end, Faas and van Vliet constrained the Fourier transform of $h(\mathbf {x})$ to have separable radial and angular parts, that is, $\mathcal {F}\{h(\mathbf {x})\}=H(\mathbf {f})=H_\mathtt {rad}(f)H_\mathtt {ang}(\phi ,\theta )$ where $\mathbf {f}$ is the polar coordinate tuple containing f, $\phi$ and $\theta$ in the Fourier domain [5]. The radial component $H_\mathtt {rad}(f;f_c,b_f)$ is a Gaussian-like bandpass filter where $f_c$ and $b_f$ are the central frequency and bandwidth of the Gaussian profile, respectively. It reaches its maximum for $f=f_c$ and goes to zero for $f=0$. The angular component $H_\mathtt {ang}(\phi ,\theta ;N)$ relies on a parameter N to control the orientation selectivity, which is the number of orientations in the upper half of the unit sphere formed by $\phi$ and $\theta$. For details of mathematical expressions see [5]. When $\theta$ is removed, $H(\mathbf {f})$ becomes the 2D filterbank presented in [7].

$I_h(\mathbf {x},\phi ,\theta )$ has a number of peaks: the amplitude of the strongest peak $A_1(\mathbf {x})=\max _{\phi ,\theta }|I_h(\mathbf {x},\phi ,\theta )|$ captures highly regular regions with one single orientation; the amplitude of the second strongest peak $A_2(\mathbf {x})$ highlights special patterns such as deformation and bifurcation; the remaining peaks and noise are described by a residue term $R(\mathbf {x},\phi ,\theta )$ which reflects chaotic regions [7]. Intuitively, a large $A_1$ and a small $A_2$ indicate a prominent elongated structure.

3.2 Reconstruction Quality Assessment Using Orientation Space

Our patch-based quality assessment algorithm consists of three steps: (i) construct an orientation space; (ii) compute the local and (iii) global quality metrics, see Fig. 1. Note that this method is currently implemented and discussed here in 2D in a first result.

Fig. 1.

Framework for reconstruction quality assessment. Details in Sect. 3.2.

Construct Orientation Space. For each reconstruction slice I(x, y), we first construct its orientation space $I_h(x,y,\phi )$ using Eq. (3). Then, we extract the amplitudes of the two strongest peaks $A_1(x,y)$ and $A_2(x,y)$. Throughout this paper, $I_h(x,y,\phi )$, $A_1(x,y)$ and $A_2(x,y)$ are computed with the open source DIPimage toolbox [1]. Moreover, we set $f_c=0.25$, $b_f=0.8f_c$ and $N=8$, so that the template filter $h(x,y;f_c,b_f,N)$ behaves as a line/edge detector [7].

Compute Local Metric. Divide I(x, y) into a number of K non-overlapped rectangular patches $P_k$, $k=1,\cdots ,K$; each goes through two modules: structure detector and strength estimator. The structure detector determines whether $P_k$ contains any prominent structure (e.g., edges) by measuring its contrast. To eliminate outliers such as noise, we define the contrast of $P_k$ as the interquartile range (75 percentile minus 25 percentile) rather than the full range (maximum minus minimum) of its pixel intensities. We set $\text {is\_stru}_k=1$ if the contrast of $P_k$ is larger than the average intensity of I(x, y), and $\text {is\_stru}_k=0$ otherwise. The strength estimator quantifies the saliency of patch $P_k$, for which the gradient structure tensor has been considered earlier. For instance, Zhu and Milanfar proposed the image content index [22]

$$\begin{aligned} q=s_1\frac{s_1-s_2}{s_1+s_2} \end{aligned}$$

(4)

where $s_1$ and $s_2$ are the singular values of the $2\times 2$ tensor matrix. In this paper, we replace $s_1$ and $s_2$ by the amplitudes $A_1$ and $A_2$, because the latter two are more sensitive to fine structures under noise [6]. Consequently, the oriented structure strength of $P_k$ is given by

$$\begin{aligned} \text {OSS}_k=1-\frac{\text {geomean}\{q_i\}}{\text {mean}\{q_i\}},\quad q_i=A_{1,i}\frac{A_{1,i}-A_{2,i}}{A_{1,i}+A_{2,i}},\quad i\in P_k, \end{aligned}$$

(5)

in which $\text {geomean}\{\cdot \}$ and $\text {mean}\{\cdot \}$ represent the geometric- and arithmetic mean, respectively. The underlying rationale is that the more “spiky" q is, the stronger the oriented structure in $P_k$. Moreover, if $P_k$ is constant or exactly at the boundary between two orientation fields (i.e., $A_{1,i}=A_{2,i}=0$, or $A_{1,i}=A_{2,i}$, $\forall i\in P_k$ [7]), we set $\text {OSS}_k=0$. Finally, we compute the local quality metric by multiplying the outputs of the two independent modules: $Q_k=\text {is\_stru}_k\times \text {OSS}_k$.

Compute Global Metric. We define the global quality metric Q as the geometric mean of all nonzero $Q_k$, that is, $Q=\text {geomean}\{Q_k\}$, $Q_k\ne 0$, $k=1,\cdots ,K$. We do not consider the arithmetic mean because it (unwanted) gives higher weight to $Q_k$ with larger numeric range.

4 Experiments and Results

In this section, we demonstrate that our quality metric Q can select a close-to-optimal $\lambda$ for the TNV-regularized reconstruction technique. Hereinafter, we consider simulated and experimental datasets of core-shell nanoparticles containing gold (Au) in the core and silver (Ag) in the shell. These two chemical elements have distinct atomic numbers ($Z_\mathtt {Au}=79$, $Z_\mathtt {Ag}=47$), and hence can produce high Z-contrast HAADF-STEM projections for the TNV to augment EDS maps. Moreover, the TNV-regularized tomography was realized by Douglas-Rachford primal-dual splitting algorithm with the operator discretization library [2]. We set 400 iterations to guarantee convergence, and sampled 100 points for $\lambda$ which were uniformly distributed between 0.001 and 1.0 on the logarithmic scale.

4.1 Simulated Dataset

To begin with, we simulated a noise-free multislice dataset using a AuAg nanoparticle in a box with a size of $40~\text {nm}\times 40~\text {nm}\times 40~\text {nm}$, see Fig. 2(a). For details of simulation see [3]. HAADF-STEM projections and EDS maps with a size of $128~\text {pixel}\times 128~\text {pixel}$ ($\approx$4Å/pixel) were simulated in every $2.5^\circ$ over $[0^\circ ,180^\circ )$. We used a focused electron beam normalized to an intensity of 1, a convergence angle of 10 mrad, and a detector with an inner angle of 90 mrad and outer 230 mrad. Since we did not include any (spherical) aberration, we set the accelerating voltage to 120 kV rather than 200 kV [19] for a broader beam.

Fig. 2.

(a) Atomic design of a core-shell nanoparticle consisting of gold (Au, yellow) and silver (Ag, white). (b) Simulated HAADF-STEM projection and (c) superposed EDS map at $7.5^\circ$. (Color figure online)

Fig. 3.

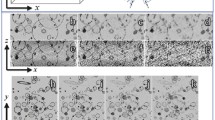
Au (upper) and Ag (lower) xy-slices for the simulated dataset at $z=24$. (a) Ground truth, hand-segmented from SIRT reconstructions with 100 iterations using 72 elemental maps between $[0,180^\circ )$; (b)–(d) TNV reconstructions with regularization parameter $\lambda \in \{0.001,0.1233,0.1748\}$. The size of the reconstruction volume is $128\times 128\times 128$ pixels. (Color figure online)

Then, we introduced several post-processing steps to make this noiseless dataset more realistic. HAADF-STEM projections were blurred by Gaussian smoothing ($\sigma =1.0$ pixel), and corrupted by Poisson noise with a mean of the number of electron counts (up to $10^5$ per pixel) and Gaussian noise with a standard deviation of 0.2. Projections suffering from the channelling effect were removed [18]. For EDS maps, we set the maximum X-ray count per pixel to 4 for Au and 3 for Ag, so that the total number of X-ray counts per angle were comparable to real experimental data [19]. Since EDS maps were much noisier, we employed a Gaussian filter ($\sigma =1.0$ pixel) for denoising. Finally, we subsampled the EDS tilt-series by a factor of 2, as in practice the number of EDS maps is typically smaller than HAADF projections due to acquisition time. The resulting HAADF-STEM and EDS data are shown in Fig. 2.

Figure 3 illustrates the xy-slices of Au and Ag at $z=24$, which are reconstructed with TNV using different $\lambda$. Two binary images in Fig. 3(a) are the ground truth segmented from SIRT reconstructions with 100 iterations given the full-view noiseless EDS maps. Figure 3(b) shows 16 patches with four different types of structures: foreground ($P_{11}$), background ($P_4$, $P_{16}$), background with streak artifacts ($P_1$, $P_{13}$), and edge ($P_6$, $P_8$, $P_{10}$, $P_{12}$). For $\lambda =0.001$, a weak regularization leads to an overall noisy reconstruction. However, when $\lambda$ is increased up to a certain level (e.g., $\lambda =0.1748$), strong regularization starts to nonuniformly degrade the sharp edges, see yellow circles in Fig. 3(d).

Fig. 4.

Oriented structure strength $\text {OSS}_k$ and local quality metric $Q_k$ versus $\lambda$ for four patches $P_k$ in Fig. 3. $P_1$: background with streak artifacts; $P_4$: background; $P_6$: edge; $P_{11}$: foreground. Results are averaged over ten noise realizations.

Figure 4(a) plots the oriented structure strength (OSS) as a function of $\lambda$ for four patches selected from Fig. 3. OSS curves of the background patches $P_1$ and $P_4$ (w/ and w/o perceptible streak artifacts) are decreasing when $\lambda$ is increasing, because stronger regularization can more effectively suppress the noise. In addition, OSS curves of the edge ($P_6$) and foreground ($P_{11}$) patches are similar, whereas the former has a clearer unique maximum. Figure 4(b) shows the corresponding local quality metrics, in which only $Q_6$ with $\text {is\_stru}_6=1$ is nonzero.

Fig. 5.

Global quality metric Q and correlation coefficient versus $\lambda$ for the simulated dataset at $z=24$. Q is derived either from the orientation space (OS) or structure tensor (ST); CC is obtained by comparing reconstructions to the ground truth in Fig. 3(a). Results are averaged over ten noise realizations.

Figure 5 depicts our main result, in which we plot the global quality metric Q and correlation coefficient (CC) as a function of $\lambda$. Q is derived either from our orientation space (OS) or from the structure tensor (ST) [22]; CC is calculated by comparing reconstructions to the binary segmentation of the noiseless SIRT reconstruction. It can be observed that our OS-based Q has a very good agreement with CC for the optimal $\lambda$, i.e., $\lambda$ values around the maxima of OS-based Q and CC are almost the same. Moreover, our OS-based Q has a higher dynamic range than the ST-based version especially for Ag, see Fig. 5(b). As a result, it would be more robust to small fluctuations such as noise in practice.

Note that TNV is an iterative technique that takes significant amount of time for reconstruction. For example, it took 10 h to compute reconstructions for 100 different $\lambda$. Many efficient one-dimensional search algorithms are available for time reduction, and we choose the golden section search [14]. This algorithm assumes that the objective function is unimodal within a certain range, and evaluates it at triples of points whose values form the golden ratio [14]. Since the golden section search can narrow the original 100 values of $\lambda$ down to no more than 15, it would effectively reduce the total computational time by approximately 85%.

4.2 Experimental Dataset

Our experimental AuAg core-shell nanoparticle was scanned in a FEI Tecnai Osiris microscope which was operated with an accelerating voltage of 120 kV and equipped with four Super-X energy dispersive silicon drift detectors [20]. HAADF-STEM projections with a size of $300~\text {pixels}\times 300~\text {pixels}$ were acquired at 31 tilt angles, ranging from $-75^\circ$ to $+75^\circ$ with an increment of $5^\circ$. In addition, one X-ray spectral image has also been recorded at each angle for 300 seconds. The raw dataset was then processed before reconstruction. The HAADF-STEM tilt-series was aligned using cross-correlation; X-ray spectral images were denoised by principal component analysis and deconvolved into two equi-sized elemental maps, one for Au and the other for Ag [20]. Figure 6 gives an example of the post-processed experimental dataset, for which we hand-segmented the HAADF reconstruction to obtain the ground truth of EDS.

Fig. 6.

Experimental (a) HAADF-STEM projections and (b) superposed EDS maps of a Au-Ag core-shell nanoparticle at $-45^\circ$ and $+45^\circ$.

Figure 7 shows the variation of the optimal $\lambda$ w.r.t. different slices. $\lambda$ values found by our no-reference metric Q and the full-reference metric CC are comparable, considering that the search space spans over 3 orders of magnitude. Moreover, golden section search and exhaustive search lead to the same $\lambda$ most of the time, though the former may terminate at the local maximum before reaching the global one (e.g., slice number 81 in Fig. 7(a)). Note that Fig. 7(b) has two “outliers”, and we show the details of slice number 91 in Fig. 8. It is obvious that the Ag reconstruction computed from Q maintains finer structure than the one from CC, especially at the edges of the outer ring. From Fig. 8(d) we can see that the curve of CC strangely “jumps” after a certain $\lambda$, even though the underlying structures have already been smeared out. This shows that even using CC as a metric to choose the optimal $\lambda$ for the TNV-regularized electron tomography is not always reliable.

Fig. 7.

Optimal regularization parameter $\lambda$ versus slice index for the experimental dataset. The size of the reconstruction volume is $300\times 300\times 300$ pixels.

Fig. 8.

(a) Ag TNV reconstructions at $z=91$ with $\lambda$ found by quality metric Q and correlation coefficient (CC), compared to the hand-segmented ground truth (GT). The corresponding curves of Q and CC versus $\lambda$ are shown in (b).

5 Discussion and Conclusion

In this paper, we developed a no-reference quality metric Q to score the oriented structure strength of reconstruction images for detecting over- and under-regularization. Based on simulated and experimental datasets of AuAg core-shell nanoparticles, we demonstrated that our Q can replace the full-reference correlation coefficient to automatically determine the optimal regularization parameter $\lambda$ for the recently proposed TNV reconstruction technique. Since the original experimental dataset was noisy, we further binned the tilt-series by a factor of 3 to increase the SNR. Consequently, the size of the reconstruction volume was reduced from $300\times 300\times 300$ pixels to $100\times 100\times 100$ pixels, for which Q still achieved a relatively high accuracy in terms of parameter determination. More interestingly, the optimal $\lambda$ found in this case became larger, probably because the dataset with less noise did not produce severe paintbrush/staircase artifacts under a stronger regularization.

Compared to the iterative TNV reconstruction, time spent for the quality assessment is minor, e.g., 10 h versus 5 min for 100 different $\lambda$ on a desktop equipped with eight Intel Xeon X5550 CPU cores (24 GB memory) and one NVIDIA GeForce GTX670 GPU (4 GB memory). Considering that the curve of reconstruction quality versus $\lambda$ is unimodal with a distinct maximum, we adopted the golden section search to “predict” the optimal $\lambda$, which effectively reduced the total computational time (reconstruction plus assessment) by 85%.

As for future work, we consider testing the applicability of our quality metric to other iterative reconstruction techniques with (e.g., TV and HOTV) and/or without (e.g., SIRT) regularizations. Moreover, we will also extend the current framework to 3D.