Good Line Cutting: Towards Accurate Pose Tracking of Line-Assisted VO/VSLAM

Abstract

This paper tackles a problem in line-assisted VO/VSLAM: accurately solving the least squares pose optimization with unreliable 3D line input. The solution we present is good line cutting, which extracts the most-informative sub-segment from each 3D line for use within the pose optimization formulation. By studying the impact of line cutting towards the information gain of pose estimation in line-based least squares problem, we demonstrate the applicability of improving pose estimation accuracy with good line cutting. To that end, we describe an efficient algorithm that approximately approaches the joint optimization problem of good line cutting. The proposed algorithm is integrated into a state-of-the-art line-assisted VSLAM system. When evaluated in two target scenarios of line-assisted VO/VSLAM, low-texture and motion blur, the accuracy of pose tracking is improved, while the robustness is preserved.

This work was supported, in part, by the National Science Foundation under Grant No. 1400256 and 1544857.

1 Introduction

Visual Odometry (VO) and Visual SLAM (VSLAM) methods typically exploit point features as they are the simplest to describe and manage. A sensible alternative or addition is to consider lines given that edges are also fairly abundant in images; especially within man-made environments where sometimes the quantity of points may be lacking to the detriment of VO/VSLAM. The canonical examples being corridors and hallways, whose low-texture degrades the performance of point features methods. Under these circumstances, lines become more reliable constraints versus points.

Compared to points, additional benefits of lines is that their detection is less sensitive to the noise associated to video capturing, and that lines are trivially stable under a wide range of viewing angles [1, 2]. Additionally, lines are more robust to motion blur [3]. Even with heavily blurred input image, one would expect some lines that are parallel to the local direction of blur to remain trackable. That said, lines don’t provide as strong a motion constraint as points, so incorporating whatever points exist within the scene is usually a good idea.

Rather than explicitly tracking points and lines, direct VO/VSLAM methods implicitly associate these strong features over time [4, 5]. Direct SLAM optimizes the photometric error of sequential image registration over the space of possible pose changes between captured images. Since feature extraction is no longer needed, direct methods typically require less computational power. However, compared to feature-based methods, direct methods are more sensitive to several factors: image noise, geometric distortion, large displacement, lighting change, etc. Therefore, feature-based methods are more viable as SLAM solutions for robust and accurate pose tracking.

Adding line features to VO/VSLAM is not a trivial task. Significant progress has been made in line detection [6] and matching [7]. Yet triangulation of 3D lines still remains problematic. Triangulating a 3D line from 2D measurements requires more measurements and is more sensitive to measurement noise, compared to points. Lines are generally weak in constraining the correspondence along its direction of expansion. It is hard to establish reliable point-to-point correspondence between two lines (as segments), which degrades triangulation accuracy. In addition, lines are usually partially-occluded, which brings the challenge of deciding the endpoint correspondence. Accurately solving line-based pose estimation requires resolving the low-reliability of triangulated 3D lines.

Fig. 1.

A toy case illustrating the proposed good line cutting approach. Left: Giving 3 line matchings with confidence ellipsoids (dashed line), the least squares pose estimation has high uncertainty. Right: Line-cutting applied to the line-based least squares problem. The cut line segments and their corresponding confidence ellipsoids are in red. The confidence ellipsoid of the new pose estimation improves. (Color figure online)

To reduce the impact of unreliable 3D lines, a common practice is to model the uncertainty of the 3D line, and weight the contribution of each line accordingly in pose optimization. The information matrix of the line residual [8,9,10,11] is one of such weighting terms. The residuals of uncertain lines get less weight so that the optimized pose is biased in favor of the certain lines. However, uncertainty of line residual does not immediately imply incorrect pose estimation (though there is some correlation): a certain line residual term might barely contribute to pose estimation, whereby it would make no sense to weight it highly. We posit that, in lieu of the uncertainty of line residual, the uncertainty of pose estimation should be assessed and exploited.

Another way to reduce uncertainty is to simply drop highly-uncertain lines when numerically constructing the pose optimization problem. However, line features are typically low in quantity (e.g. tens of lines). Too much information could be lost by dropping line features. Furthermore, there is a high risk of forming ill-conditioned optimization problem.

As opposed to line weighting and dropping, this paper aims to improve pose optimization through the concept of good line cutting. The goal of good line cutting is simple: for each 3D line, find the line segment that contributes the largest amount of information to pose estimation (a.k.a. a good line), and select only those informative segments to solve pose optimization. With line cutting, the conditioning of the optimization problem improves, leading to more accurate pose estimation than the original problem. An illustration of good line cutting can be found at Fig. 1. To the best of the authors’ knowledge, this is the first paper discussing the role of line cutting in line-based pose optimization. The contributions of this paper are:

• (1) Demonstration that good line cutting improves the overall conditioning of line-based pose optimization;

• (2) An efficient algorithm for real-time applications that approaches the computationally more involved joint optimization solution to good line cutting; and

• (3) Integration of proposed algorithm into a state-of-the-art line-assisted VSLAM system. When evaluated in two target scenarios (low-texture and motion blur), the proposed line cutting leads to accuracy improvements over line-weighting, while preserving the robustness of line-assisted pose tracking.

2 Related Work

This section first reviews related work on line-assisted VO/VSLAM, then examines the literature of feature selection(targeted for point features mostly), and discusses the connection between (point) feature selection and the proposed good line cutting method.

2.1 Line-Assisted VO/VSLAM

There has been continuous effort investigating line features in the SLAM community. In the early days of visual SLAM, lines are used to cope with large view change of monocular camera tracking [1, 2]. In [1], the authors integrate lines into a point-based monocular Extended Kalman Filter SLAM (EKF-SLAM). Real-time pose tracking with lines only are demonstrated in [2] by using a Unscented Kalman Filter (UKF). Both methods model 3D lines as endpoint-pairs, project lines to image, then measure the residual. Alternatively, edges are extracted and utilized [3]. For the convenience of projection, a 12-DOF over-parameterization is used to model 3D edge. Again, the edge residual is measured after 3D-to-2D projection.

More recently, line-assisted VO/VSLAM are extended to 3D visual sensors, such as RGB-D sensor and stereo camera. In [8], a line-assisted RGB-D odometry system is proposed. It involves parameterizing the 3D lines as 3D endpoint-pairs and minimizing the endpoint residual in SE(3). However, directly working in SE(3) has the disadvantage of being sensitive to inaccurate depth measurements. With the progress in line detectors (e.g. LSD [6]) and descriptors (e.g. LBD [7]), growing attention has been paid towards stereo-base line VO/VSLAM, e.g. [11,12,13]. Though alternative parameterizations have been explored (e.g. Plücker coordinate [14], orthonormal representation [15]), most line-assisted VO/VSLAM continued to use the 3D endpoint-pair parametrization because it conveniently combines with the well-established point-based optimization. Pose estimation typically jointly minimizes the reprojection errors of both point and line matches. For line features, the endpoint-to-line distance is commonly used as the reprojection error term, i.e., the line residual. To cope with the 3D line uncertainty, a covariance matrix is maintained for each 3D line. Each line residual term is weighted by the inverse of the covariance matrix obtained by propagating the covariance from the 3D line to the endpoint-to-line distance.

Line features within monocular VO/VSLAM also gained attention recently [10, 16, 17]. The pipeline of [16] is similar to that of stereo pipelines. A more robust variant for the endpoint-to-line distance is defined in [9]. Line-assisted methods building from direct VO/VSLAM have also been developed [10, 17]. Interestingly, neither of them use direct measurements (e.g. photometric error) for line terms in the joint optimization objective. Instead, the line residual is the least squares of endpoint-to-line distance, which is identical to other feature-based approaches.

Research into line-assisted VO/VSLAM is still ongoing. Among the systems described above, modules commonly employed are: (1) 3D lines parameterized as 3D endpoint-pairs; (2) endpoint-to-line distance and variants serve as the line residual; (3) in the optimization objective (pose only and joint), line residuals are weighted by some weighting matrix. The proposed good line cutting approach in this paper expands on these three modules.

2.2 Feature Selection

Feature selection has been part of VO/VSLAM for a long time. The goal of feature selection is to find subset of features with best value for pose estimation, so as to improve the efficiency and accuracy of VO/VSLAM. Two sources of information are typically used to guide the selection: image appearance and structural & motion information. Our work is a variant of the second one.

It is well-understood that covariance/information matrix captures the structural & motion information: it approximately represents the uncertainty/confident ellipsoid of pose estimation. Feature selection is effectively modeled as an optimization problem: the goal is to select a subset of features that minimize the covariance matrix (i.e. maximize the information matrix) under some metrics, e.g. information gain [18, 19], entropy [20], covariance ratio [21], trace [22], minimum eigenvalue [23, 24], and log-determinant [25].

The basic assumption of (point) feature selection is the availability of a large number of features (e.g. hundreds of points). In such case, the pose optimization problem will remain well-determined with only a subset of features. Since line features occur in low quantities, there is a high risk of forming an ill-conditioned optimization problem when a subset of lines are selected and utilized. Instead, identify the (sub-)segment of each line that contributes the largest amount of information so that all line segments get used for pose optimization. Doing so avoids the risk of ill-conditioning.

3 Least Squares Pose Optimization with Lines

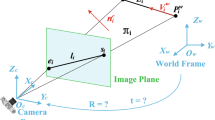
In line-assisted VO/VSLAM, the goal of pose optimization is to estimate the pose x of calibrated camera(s) given a set of 3D features, i.e. points $\{P_i\}$ and lines $\{L_i\}$, and their corresponding 2D projections, i.e. points $\{p_i\}$ and lines $\{l_i\}$, in the image. As aligned with the current practice, endpoint-pairs are used to represent 3D lines $\{L_i\}$. Without loss of generality, the least squares objective of pose optimization with both point and lines can be written as,

$$\begin{aligned} \hat{x} = \arg \min \{ \left\| p - h(x, P) \right\| ^2 + \left\| l^T h(x, L) \right\| ^2 \} \end{aligned}$$

(1)

where p and l are stacked matrices of 2D point measurements $\{p_i\}$ and 2D line coefficients $\{l_i\}$, respectively. P is the stacked matrix of 3D points $\{P_i\}$, while L is the stacked matrix of all endpoints from the 3D line set $\{L_i\}$. h(x, P) consists of the pose transformation (decided by x) and pin-hole projection. Some researchers [16] suggest using the dual form of the line residual term in (1), which minimizes the distance between projection of 3D line and measured endpoint. Though we follow the definition of line residual as in (1) in this paper, the proposed good line cutting can be updated to the dual form easily. For simplicity, the least squares (1) is referred to as line-LSQ problem.

Solving the line-LSQ (1) often involves the first-order approximation of the non-linear measurement function. For instance, the endpoint-to-line distance h(x, L) on image plane can be approximated as,

$$\begin{aligned} h(x, L) = h(x_0, L) + H_x (x - x_0) \end{aligned}$$

(2)

so that the least squares of line residual term can be minimized with Gauss-Newton method, which iteratively updates the pose estimate:

$$\begin{aligned} \hat{x} = x_0 - (l^T H_x)^+ l^T (h(x_0, L)) \end{aligned}$$

(3)

Accuracy of $\hat{x}$ is affected by two types of error in line features: 2D line measurement error and 3D line triangulation error. As mentioned earlier, 3D line triangulation is sensitive to noise and less-reliable than 3D point triangulation. Therefore, here we only consider the error of 3D line endpoint L while assuming the 2D measurement l is accurate. Again, with the first-order approximation of $h(x_0, L)$ at the initial pose $x_0$ and triangulated 3D endpoint $L_0$, we may connect the pose optimization error $\epsilon _x$ and 3D line endpoint error $\epsilon _L$,

$$\begin{aligned} \epsilon _x = (l^T H_x)^+ l^T H_L \epsilon _L = H^T \epsilon _L \end{aligned}$$

(4)

where $H^T=(l^T H_x)^+ (l^T H_L)$. Here we intentionally ignore the error in point residual term. The reason is, when available, point features are known to be more accurate. Therefore, the main source of error in line-LSQ problem is from 3D line triangulation $\epsilon _L$, which is propagated by factor H.

3.1 Information Matrix in Line-LSQ Problem

Common practice models the 3D endpoint-pair error $\epsilon _L$ as i.i.d. Gaussian under the proper parametrization, e.g. inverse-depth. With first-order approximation (4), we may write the pose information matrix $\varOmega _x$ as,

$$\begin{aligned} \varOmega _x = H^T \varOmega _L H = \sum H_i^T \varOmega _{L_i} H_i \end{aligned}$$

(5)

where $H_i$ is the corresponding row block in H for line $L_i$, and $\varOmega _{L_i}$ is the information matrix of 3D endpoint-pair used to parametrize $L_i$. Notice that $\varOmega _{L_i}$ is a block diagonal matrix under the i.i.d. assumption on 3D endpoint error. Set $\varOmega _{L_i(0)}$, $\varOmega _{L_i(1)}$ as the two diagonal blocks of $\varOmega _{L_i}$, and $H_i(0)$, $H_i(1)$ the corresponding row block in $H_i$, then (5) can be further broken down into:

$$\begin{aligned} \begin{aligned} \varOmega _x&= \sum [ H_i^T(0) \varOmega _{L_i(0)} H_i(0) + H_i^T(1) \varOmega _{L_i(1)} H_i(1) ] \\&= \sum H_i^T(\alpha _i) \varOmega _{L_i(\alpha _i)} H_i(\alpha _i) \end{aligned} \end{aligned}$$

(6)

where we extend the range of i from n lines to 2n endpoints, and set $[\alpha _i]$ as a $2n \times 1$ chessboard vector filled with 0 and 1.

As pointed out in the literature of point-feature selection [22,23,24,25], the spectral property of the pose information matrix has strong connection with the error of least squares pose optimization. For example, the worst-case error variance is quantified by the inverse of minimum eigenvalue of $\varOmega _x$ [23, 24]. Large min-eigenvalue of $\varOmega _x$ is preferred to avoid fatal error in line-LSQ solving. Also, the volume of the confidence ellipsoid in pose estimation can be effectively measured with the log-determinant of $\varOmega _x$ [25]. For accurately solving the line-LSQ problem, large log-determinant of $\varOmega _x$ is pursued. In what follows, we quantify the spectral property of $\varOmega _x$ with log-determinant, i.e. $\log \det (\varOmega _x)$.

As mentioned early, line selection/dropping has a high risk of forming ill-conditioned line-LSQ problem. In what follows, we will describe an alternative method to improve $\log \det (\varOmega _x)$, which is a better fit for line-LSQ problem.

4 Good Line Cutting in Line-LSQ Problem

4.1 Intuition of Good Line Cutting

Compared with points that are typically modeled as sizeless entity, lines are modeled to be able to extend along one certain dimension. For a 3D line $L_i$ defined by endpoint-pair $L_i(0)$ and $L_i(1)$ in Euclidean space, the following equations hold for any intermediate 3D point $L_i(\alpha )$ that lies on $L_i$:

$$\begin{aligned} \begin{aligned} L_i(\alpha )&= (1-\alpha ) L_i(0) + \alpha L_i(1) \\ \varOmega _{L_i(\alpha )}&= \varSigma _{L_i(\alpha )}^{-1} = \{(1-\alpha )^2 \varSigma _{L_i(0)} + \alpha ^2 \varSigma _{L_i(1)}\}^{-1}, \end{aligned} \end{aligned}$$

where $\alpha$ is the interpolation ratio, and $\varSigma _{L_i(*)}$ is the covariance matrix of 3D point $L_i(*)$.

The covariance matrix of the intermediate 3D point, $\varSigma _{L_i(\alpha )}$, is convex to the interpolation ratio $\alpha$, as both $\varSigma _{L_i(0)}$ and $\varSigma _{L_i(1)}$ are positive semi-definite. At some specific $\alpha _m \in [0,1]$, $\varSigma _{L_i(\alpha _m)}$ reaches a global minimum (and $\varOmega _{L_i(\alpha _m)}$ a global maximum). In other word, at some intermediate 3D position $L_i(\alpha _m)$ (both endpoints included) the corresponding 3D uncertainty is minimized. The same conclusion holds when extending from a single 3D point to the 3D point-pair $\left\langle L_i(\alpha _1), L_i(\alpha _2) \right\rangle$ lying on the 3D line $L_i$: both 3D points share the least-uncertain position $L_i(\alpha _m)$. To minimize the amount of uncertainty introduced with 3D line endpoints, the 3D line $L_i$ will shrink to a single 3D point!

However, the pose information $\varOmega _x$ is not only dependent on endpoint information matrix $\varOmega _{L_i(\alpha )}$, but also the Jacobian term $H_i(\alpha )=(l_i^T H_x(\alpha ))^+ (l_i^T H_L(\alpha ))$. Cutting 3D line into smaller segments will affect the corresponding Jacobian term as well. Intuitively, line cutting could hurt the spectral property of measurement Jacobian block $H_x(\alpha )$: if a 3D line gets cut to a single point, the corresponding measurement Jacobian will degenerate from rank-2 to rank-1, thereby losing one of the two constraints provided by the original 3D line matching.

Therefore, the objective of good line cutting can be written as follow,

$$\begin{aligned}{}[\alpha _i]&= \arg \max \log \det (\varOmega _x) \\ \nonumber&= \arg \max \log \det [\sum H_i^T(\alpha _i) \varOmega _{L_i(\alpha _i)} H_i(\alpha _i) + \varOmega _x^{pt}] \end{aligned}$$

(7)

where we include a constant term $\varOmega _x^{pt}$ to capture the information from point features, if applicable. Naturally, this objective can be solved with nonlinear optimization techniques.

4.2 Validation of Good Line Cutting

Before describing the optimization of (7), we would like to validate the idea of line cutting. One natural question towards line cutting with (7) being, is it possible that the Jacobian term $H_i^T(\alpha _i)$ has much stronger impact towards (7) than 3D uncertainty reduction, so that one should always use the full-length of 3D line? To address this question, we study the minimal case, single line cutting: only one pair of cutting ratio $\left\langle \alpha _1, \alpha _2 \right\rangle$ can be changed, while the remaining $n-1$ lines are not cut.

It is cumbersome to derive the function from line cut ratio $\alpha$ to Jacobian term $H_i(\alpha )$: it is highly non-linear, and the Jacobian term vary under different SE(3) parameterizations of camera and 3D lines. Instead, a set of line-LSQ simulation are conducted to validate line cutting.

The testbed is developed based on the simulation framework of [26]. A set of 3D lines that form a cuboid are simulated, under homogeneous-points line (HPL) parameterization. To simulate the error in 3D line triangulation, the endpoints of 3D lines are perturbed with zero-mean Gaussians in inverse-depth space, as illustrated with blue lines in Fig. 2 left. For the 3D line in red, the optimal line cutting ratio, found through brute-force search, is plotted versus camera pose in Fig. 2 right. The boxplots indicate that cutting happens when the 3D line is orthogonal or parallel to the camera frame. In these cases, the measurement Jacobian of the red 3D line scales poorly with line length. Taking a smaller segment/point is preferred so as to introduce less noise into the least squares problem. According to Fig. 2, line cutting adapts to the information and uncertainty of the tracked lines based on the relative geometry.

Fig. 2.

Line cutting behavior under different camera poses. A pair $\left\langle 0, 100 \right\rangle$ indicates full line selection. Identical ratio pair, e.g. $\left\langle 45, 45 \right\rangle$ indicates cutting to a point. (Color figure online)

To visualize the outcomes of different line cutting ratios, we used brute-force sweep to generate the surface of $\log \det (\varOmega _x)$ as a function of the line cutting ratio parameters. Three example surfaces are illustrated in Fig. 3. In the 1st example, global maximum of $\log \det (\varOmega _x)$ is at $\left\langle \alpha _1 = 0, \alpha _2 = 1.0 \right\rangle$, which indicates the full-length of 3D line should be used. The 2nd one has global maximum at $\left\langle \alpha _1 = 0, \alpha _2 = 0.76 \right\rangle$, which encourages cutting out part of the line. In column 3, $\log \det (\varOmega _x)$ is maximized at $\left\langle \alpha _1 = 0.52, \alpha _2 = 0.52 \right\rangle$, which means the original 3D line should be aggressively cut to a 3D point. To maximize pose information, line cutting is definitely preferred in some cases (e.g. Fig. 3 columns 2 and 3).

Fig. 3.

Example surfaces of $\log \det (\varOmega _x)$ in single line cutting set-up and HPL parameterization. The global maximum of $\log \det (\varOmega _x)$ is marked with red cross. (Color figure online)

5 Efficient Line Cutting Algorithm

5.1 Single Line Cutting

To begin with, consider the single line cutting problem as simulated previously. Based on Fig. 3, we notice the mapping from $\left\langle \alpha _1, \alpha _2 \right\rangle$ to $\log \det (\varOmega _x)$ is continuous, and concave within a certain neighborhood. Therefore, by doing gradient ascent in each of the concave regions, the global maximum of $\log \det (\varOmega _x)$ is expected to be found. One possible triplet of initial pairs are: full-length $\left\langle \alpha _1 = 0, \alpha _2 = 1.0 \right\rangle$, 1st endpoint only $\left\langle \alpha _1 = 0, \alpha _2 = 0 \right\rangle$, and 2nd endpoint only $\left\langle \alpha _1 = 1.0, \alpha _2 = 1.0 \right\rangle$.

The effectiveness of the multi-start gradient ascent is demonstrated with 100-run repeated test. Two commonly used endpoint-pair parameterizations of 3D lines [26] are tested here: homogeneous-points line (HPL) and inverse-depth-points line (IDL). The error of endpoint estimation is simulated with i.i.d. Gaussian in inverse-depth space (standard deviation of 0.005 and 0.015 unit are used), and propagated to SE(3) space. Five different sizes (6, 10, 15, 20 and 30) of 3D line set are tested. Under both HPL and IDL parametrization, we compare the best pair from the 3 gradient ascends with the brute-force result. The differences of line cutting ratios are smaller than 0.01 for over 99% of the cases. Therefore, single line cutting problem can be solved effectively using the outcomes from a combination of three gradient ascents.

5.2 Joint Line Cutting

Now extend the single line cutting to the complete problem of joint line cutting: how to find the line cutting ratios for all n 3D lines, so that the $\log \det$ of pose information matrix generated from n line matchings is maximized?

Naturally, the joint line cutting objective (7) can be approached with nonlinear optimizers, e.g. interior-point [27], active-set [28]. Meanwhile, an alternative approach would be simple greedy heuristic: instead of optimizing the joint problem (or a smaller subproblem), simply searching for the local maximum for each 3D line as single line cutting problem, and iterating though all n lines. As demonstrated previously, single line cutting can be effectively solved with a combination of 3 gradient ascends. Besides, the 3 independent gradients ascends can execute in parallel. Compared with nonlinear joint optimization that typically requires $\mathcal {O}(\epsilon ^{-c})$ iterations of the full problem (c some constant), greedy approach has a much well-bounded computation complexity. It takes n iterations to complete, while at each iteration the single line cutting is solved in $\mathcal {O}(m)$ (m the maximum number of steps in gradient ascend). The efficiency of joint line cutting is crucial, since only minimum overhead (e.g. milliseconds) shall be introduced to the real time pose tracking of targeted line-assisted VO/VSLAM applications.

The greedy algorithm for efficient joint line cutting is described in Algorithm 1. The component of pose information matrix from a full-length line $L_i$ is denoted by $\varOmega _x^i(0, 1)$, while a line cut from $\left\langle \alpha _1, \alpha _2 \right\rangle$ is denoted by $\varOmega _x^i(\alpha _1, \alpha _2)$. With the line-LSQ simulation platform, the effectiveness of greedy joint line cutting is demonstrated with 100-run repeated test. The Matlab implementations of interior-point [27], as well as three variants of active-set [28], are chosen to compare against the greedy algorithm. The results are presented as boxplots in Fig. 4. Under both 3D line parameterizations (HPL and IDL), greedy algorithm provides the largest increase of $\log \det (\varOmega _x)$ (on average and in the worst case).

Fig. 4.

Boxplots of joint line cutting with different approaches. Left: with HPL parametrization. Right: with IDL parametrization. Boxplots are presented in order: (1) original $\log \det (\varOmega _x)$, (2) after line cutting with greedy approach, (3)–(6) after line cutting with nonlinear joint optimizers.

6 Experiments on Line-Assisted VSLAM

This section evaluates the performance of the proposed line cutting approach. Two target scenarios of line-assisted VSLAM are set up for experiments: low-texture and motion blur.

We base the line cutting experiment on a state-of-the-art line-assisted VSLAM system, PL-SLAM [11]. As a stereo vision based system, it tracks both ORB [29] point features and LSD [6] line features between frames, and perform an on-manifold pose optimization with weighted residual terms of both feature types. One weakness of the original PL-SLAM¹ is that the point feature front-end is not as well tuned as other point-only VSLAM system, e.g. ORB-SLAM2 [30]. Two modifications were made by us in response: (1) replacing the OpenCV ORB extractor with the ORB-SLAM2 implementation, which provides a larger number of (and well-distributed) point matchings than the original version; (2) changing the point feature matching strategy from global brute force search to local search (similar to ORB-SLAM2 implementation), which handles the increasing amount of point features efficiently.

The proposed good line cutting algorithm is integrated into the modified PL-SLAM in place of the original line-weighting scheme. It takes all feature matchings as input: lines are to be refined with line cutting, while points serve as constant terms in the line cutting objective. After line cutting, all features (points and cut lines) are sent to pose optimization. The loop closing module of PL-SLAM is turned off since the focus of this paper is real-time pose tracking.

For comprehensively evaluating the value of line cutting, five variants of the modified PL-SLAM are assessed: (1) point-only SLAM (P), (2) line-only SLAM (L), (3) line-only SLAM with line cutting ($L+Cut$), (4) point & line SLAM (PL), and (5) point & line SLAM with line cutting ($PL+Cut$). To better benchmarking the performance of point features, we also report the results of ORB-SLAM2² [30] (referred as ORB2) and SVO2³ [4]. SVO2 is a state-of-the-art direct VO system that supports stereo input. It tracks both image patches and edgelets. All systems above were running on an Intel i7 quadcore 4.20 GHz CPU (passmark score of 2583 per thread).

Accuracy of real-time pose tracking is evaluated with two relative metrics between ground truth track and SLAM estimated track: (1) Relative Position Error(RPE) [31], which captures the average drift of pose tracking in a short period of time; (2) Relative Orientation Error(ROE), which captures the average orientation error of pose tracking with the same estimation pipeline as RPE. Both RPE and ROE are estimated with a fixed time window of 3 s. Compared with the absolute metrics (e.g. RMSE of whole track), relative metrics are more suited for measuring the drift in real-time pose tracking [31].

Due to the fact that most SLAM systems have some level of randomness (e.g. feature extractor, multi-thread), all experiments in the following are repeated with 10 times. For those failed more than 2 times in 10 trials, we ignore the results due to the lack of consistency. For the rest, the average of relative metrics (RPE and ROE) are reported.

Fig. 5.

Example frames of line cutting PL-SLAM running in challenging scenarios: (1) low-texture, (2) motion blur, (3) lighting change. Detected features are in green, while projected are in red. Notice the length of projected line being much shorter than the measurement, after line cutting. (Color figure online)

6.1 Low-Texture

To the authors’ knowledge, no publicly available, low-texture stereo benchmark exists. To evaluate the proposed approach, we synthesized a low-texture stereo sequence with Gazebo. An example frame of the low-texture sequence is provided as the 1st plot in Fig. 5.

Relative errors are summarized in Table 1. After applying line cutting to line-assisted baseline (L and PL), the average relative errors are cut down by almost 40%, as highlighted in bold. The lowest tracking error (i.e. best accuracy) is achieved when combining point and line features, and cutting the lines with the proposed method ($PL+Cut$). Meanwhile, systems that only utilize point features perform poorly: point-only SLAM (P) has high ROE; ORB-SLAM2 (ORB2) failed to track. The direct approach SVO2 succeeded in tracking the whole low- texture sequence, but has the highest relative errors.

The evaluation results suggest that, line features are valuable for pose tracking in low-texture scenarios. However, simply using the full-length of lines for pose optimization may cause large tracking error. With the proposed line cutting, the accuracy of line-assisted pose tacking improves.

Table 1. Relative error on synthetic low-texture sequence

6.2 Motion Blur

Motion blur happens when the camera is moving too fast (e.g. on a flying vehicle) or when the scenario contains rapidly moving objects. Though the second case is also challenging for VO/VSLAM, it is beyond the scope of this work (as it violates the common assumption of static world). Here we focus on tracking the pose of a fast-moving camera, under different levels of motion blur.

The dataset chosen is the EuRoC MAV dataset [32]. It contains 11 sequences of stereo images recorded from a micro aerial vehicle. For each sequence, a precise ground-truth track is provided with external motion capture systems (Vicon & Leica MS50). Instead of running on all 11 sequences, only 6 fast-motion sequences recorded in a Vicon-equipped room (with high potential to exhibit motion blur) are used for motion blur evaluation. The RPEs are summarized in the upper half of Table 2. For each sequence, we compare the line-assisted baseline with the line cutting version, and highlight the better one in bold. Among all 7 methods evaluated here, the one that leads to the lowest error is marked with a star sign.

Compared with the line-assisted baselines (L and PL), the line cutting versions ($L\,+\,Cut$ and $PL\,+\,Cut$) clearly have lower level of RPEs on most sequences. The improvement is less significant on V1-01-easy, mostly due to the relative accurate line triangulation (the RPE of L is close to the lowest). Meanwhile, the performance of ORB2 is not as consistent: when tracking succeed, ORB2 has the lowest RPE among all 7 methods. However it failed to function reliably on the last 2 sequences. This is not surprising: when available, point features are known to be more accurate for pose tracking; they are just not as robust as lines under motion blur. Lastly, the direct SVO2 failed to track on 4 out of 6 sequences, similar to the results reported in [4] (failed on 3 out of 6). It is expected since direct approach are more sensitive to fast motion and lighting changes (e.g. the 3rd plot in Fig. 5) than feature-based ones.

The level of motion blur for the original EuRoC sequence is not severe: the shot of each camera is strictly controlled, and the vehicle is only doing fast motion at several moments during the entire sequence. To assess the performance under severe motion blur, we smooth the 6 Vicon sequences with a $5\times 5$ box filter, and rerun all 7 VO/VSLAM methods on the blurred ones. Corresponding results are reported in the bottom half of Tables 2 and 3.

Table 2. Relative position(m/s) error on EuRoC sequences with fast motion

Table 3. Relative orientation(deg/s) error on EuRoC sequences with fast motion

Under the severe motion blur, point-based approaches (P and ORB2) become much less accurate than before, while also easy to loss track. Meanwhile, the line-assisted approaches are more robust to the blur. More importantly, the accuracy of line-assisted approaches are clearly improved with line cutting: $PL\,+\,Cut$ reaches the lowest RPE on 3 sequences, while $L+Cut$ wins on another one. One exception is on V2-01-easy blurred, where PL is already accurate and line cutting leads to slight degeneracy. Last, SVO2 does slightly better than $PL+Cut$ on sequence V2-03-dif blurred, while has the highest RPE on other 5 sequences. One potential reason that SVO2 tracks on all 6 blurred sequences while failing on 4 original ones is that the blurring acts to pre-condition the direct objective (original highly non-smooth). The convergence rate of optimizing the direct objective improves and positively impacts the tracking rate.

Similarly, we also report the ROE in Table 3. The outcomes are consistent with the RPE outcomes and analysis. Compared to point features, line features are robust to motion blur while preserving accurate position information. The proposed line cutting further improves the tracking accuracy of line-assisted VO/VSLAM.

Lastly, we briefly discuss the computation cost of line cutting. Since the baseline PL-SLAM does not maintain covariance matrix for each 3D line, we do so with a simple error model: (1) assume a constant i.i.d. Gaussian at the inverse-depth space of each 3D line endpoint; (2) propagate the endpoint covariance matrix from inverse-depth space of the previous frame to the Euclidean space of current frame. Then we run the greedy line cutting algorithm (Algorithm 1) with these covariance/information matrices. Most of compute time is spent on the iterative greedy algorithm. When averaged over the EuRoC sequences, the line cutting module takes 3 ms to process 60 lines per frame.

7 Conclusion and Future Work

This paper presents good line cutting, which deals with the uncertain 3D line measurements to be used in line-assisted VO/VSLAM. The goal of good line cutting is to find the (sub-)segment within each uncertain 3D line that contributes the most information towards pose estimation. By only utilizing those informative (sub-)segments, line-based least squares is solved more accurately. We also describe an efficient, greedy algorithm for the joint line cutting problem. With the efficient approximation, line cutting is integrated into a state-of-the-art line-assisted VSLAM system. When evaluated on two target scenarios of line-assisted VO/VSLAM(low-texture; motion blur), accuracy improvements are demonstrated, while robustness is preserved. In the future, we plan to extend line cutting to other 3D line parametrization, e.g. Plücker coordinates. The joint feature tuning problem, namely point selection & line cutting, is also worth exploring further.