Geometric Flow Equations

Abstract

In this minicourse, we study hypersurfaces that solve geometric evolution equations. More precisely, we investigate hypersurfaces that evolve with a normal velocity depending on a curvature function like the mean curvature or Gauß curvature. In three lectures, we address

• hypersurfaces, principal curvatures and evolution equations for geometric quantities like the metric and the second fundamental form.

• the convergence of convex hypersurfaces to round points. Here, we will also show some computer algebra calculations.

• the evolution of graphical hypersurfaces under mean curvature flow.

Appendices

Appendix 1: Parabolic Maximum Principles

The following maximum principle is fairly standard. For non-compact, strict or other maximum principles, we refer to [11] or [24], respectively.

We will use C ^2;1 for the space of functions that are two times continuously differentiable with respect to the space variables and once continuously differentiable with respect to the time variable.

Theorem 18 (Weak Parabolic Maximum Principle)

Let $\varOmega \subset {\mathbb {R}}^n$ be open and bounded and T > 0. Let a ^ij , b ⁱ ∈ L ^∞(Ω × [0, T]). Let a ^ij be strictly elliptic, i.e. a ^ij(x, t) > 0 in the sense of matrices. Let $u\in C^{2;1}(\varOmega \times [0,T))\times C^0\left (\overline \varOmega \times [0,T]\right )$ fulfill

$$\displaystyle \begin{aligned}\dot u\le a^{ij}u_{ij}+b^iu_i\quad \mathit{\text{in }}\varOmega\times(0,T).\end{aligned}$$

Then we get for (x, t) ∈ Ω × (0, T)

$$\displaystyle \begin{aligned}u(x,t)\le\sup\limits_{\mathscr P\left(\varOmega\times(0,T)\right)} u,\end{aligned}$$

where $\mathscr P\left (\varOmega \times (0,T)\right ):=(\varOmega \times \{0\}) \cup (\partial \varOmega \times (0,T))$.

Proof

• (i) Let us assume first that $\dot u<a^{ij}u_{ij}+b^iu_i$ in Ω × (0, T). If there exists a point (x ₀, t ₀) ∈ Ω × (0, T) such that $u(x_0,t_0)>\sup \limits _{\mathscr P\left (\varOmega \times (0,T)\right )} u$, we find (x ₁, t ₁) ∈ Ω × (0, T) and t ₁ minimal such that u(x ₁, t ₁) = u(x ₀, t ₀). At (x ₁, t ₁), we have $\dot u\ge 0$, u _i = 0 for all 1 ≤ i ≤ n, and u _ij ≤ 0 (in the sense of matrices). This, however, is impossible in view of the evolution equation.

• (ii) Define for 0 < ε the function v := u − εt. It fulfills the differential inequality

  $$\displaystyle \begin{aligned}\dot{\mathrm{v}} =\dot u-{\varepsilon}<\dot u\le a^{ij}u_{ij}+b^iu_i =a^{ij}\mathrm{v}_{ij}+b^i\mathrm{v}_i.\end{aligned}$$

  Hence, by the previous considerations,

  $$\displaystyle \begin{aligned}u(x,t)-{\varepsilon} t=\mathrm{v}(x,t)\le\sup\limits_{\mathscr P(\varOmega\times(0,T))} \mathrm{v} =\sup\limits_{\mathscr P(\varOmega\times(0,T))} u-{\varepsilon} t\end{aligned}$$

  and the result follows as .

□

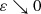There is also a parabolic maximum principle for tensors, see [19, Theorem 9.1]. (See the AMS-Review for a small correction of the proof.)

A tensor N _ij depending smoothly on M _ij and g _ij, involving contractions with the metric, is said to fulfill the null-eigenvector condition, if N _ijvⁱv^j ≥ 0 for all null-eigenvectors v of M _ij.

Theorem 19

Let (M _ij)_i,j be a tensor, defined on a closed Riemannian manifold (M, g(t)), fulfilling

$$\displaystyle \begin{aligned}{\frac{\partial}{\partial t}} M_{ij}=\varDelta M_{ij}+b^k\nabla_kM_{ij}+N_{ij}\end{aligned}$$

on a time interval [0, T), where b is a smooth vector field and N _ij fulfills the null-eigenvector condition. If M _ij ≥ 0 at t = 0, then M _ij ≥ 0 for 0 ≤ t < T.

Appendix 2: Some Linear Algebra

Lemma 14

We have

$$\displaystyle \begin{aligned}\frac\partial{\partial a_{ij}}\det(a_{rs}) =\det(a_{rs})a^{ji},\end{aligned}$$

if a _ij is invertible with inverse a ^ij , i.e. if $a^{ij}a_{jk}=\delta ^i_k$.

Proof

It suffices to prove that the claimed equality holds when we multiply it with a _ik and sum over i. Hence, we have to show that

$$\displaystyle \begin{aligned}\frac\partial{\partial a_{ij}} \det(a_{rs})a_{ik}=\det(a_{rs})\delta^j_k.\end{aligned}$$

We get

$$\displaystyle \begin{aligned}\frac\partial{\partial a_{ij}}\det(a_{rs})= \det\begin{pmatrix} a_{1\,1} & \hdots & a_{1\,j-1} & 0 & a_{1\,j+1} & \hdots & a_{1\,n}\\ \vdots & & \vdots & \vdots & \vdots & & \vdots\\ a_{i-1\,1} & \hdots & a_{i-1\,j-1} & 0 & a_{i-1\,j+1} & \hdots & a_{i-1\,n}\\ 0 & \hdots & 0 & 1 & 0 & \hdots & 0\\ a_{i+1\,1} & \hdots & a_{i+1\,j-1} & 0 & a_{i+1\,j+1} & \hdots & a_{i+1\,n}\\ \vdots & & \vdots & \vdots & \vdots & & \vdots\\ a_{n\,1} & \hdots & a_{n\,j-1} & 0 & a_{n\,j+1} & \hdots & a_{n\,n}\\ \end{pmatrix}.\end{aligned}$$

and thus

$$\displaystyle \begin{aligned} \frac\partial{\partial a_{ij}}\det(a_{rs})\cdot a_{ik}=& \det\begin{pmatrix} 0&\hdots&0&a_{1\,k}&0&\hdots&0\\ a_{2\,1}&\hdots&a_{2\,j-1}&0&a_{2\,j+1}&\hdots&a_{2\,n}\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n\,1}&\hdots&a_{n\,j-1}&0&a_{n\,j+1}&\hdots&a_{n\,n} \end{pmatrix}\\ &+\det\begin{pmatrix} a_{1\,1}&\hdots&a_{1\,j-1}&0&a_{1\,j+1}&\hdots&a_{1\,n}\\ 0&\hdots&0&a_{2\,k}&0&\hdots&0\\ a_{3\,1}&\hdots&a_{3\,j-1}&0&a_{3\,j+1}&\hdots&a_{3\,n}\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n\,1}&\hdots&a_{n\,j-1}&0&a_{n\,j+1}&\hdots&a_{n\,n} \end{pmatrix}\\ &+\hdots\\ =&\det\begin{pmatrix} a_{1\,1}&\hdots&a_{1\,j-1}&a_{1\,k}&a_{1\,j+1}&\hdots&a_{1\,n}\\ a_{2\,1}&\hdots&a_{2\,j-1}&0&a_{2\,j+1}&\hdots&a_{2\,n}\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n\,1}&\hdots&a_{n\,j-1}&0&a_{n\,j+1}&\hdots&a_{n\,n} \end{pmatrix}\\ &+\det\begin{pmatrix} a_{1\,1}&\hdots&a_{1\,j-1}&0&a_{1\,j+1}&\hdots&a_{1\,n}\\ a_{2\,1}&\hdots&a_{2\,j-1}&a_{2\,k}&a_{2\,j+1}&\hdots&a_{2\,n}\\ a_{3\,1}&\hdots&a_{3\,j-1}&0&a_{3\,j+1}&\hdots&a_{3\,n}\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n\,1}&\hdots&a_{n\,j-1}&0&a_{n\,j+1}&\hdots&a_{n\,n} \end{pmatrix}\\ &+\hdots\\ =&\det\begin{pmatrix} a_{1\,1}&\hdots&a_{1\,j-1}&a_{1\,k}&a_{1\,j+1}&\hdots&a_{1\,n}\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n\,1}&\hdots&a_{n\,j-1}&a_{n\,k}&a_{n\,j+1}&\hdots&a_{n\,n} \end{pmatrix}\\ =&\delta^j_k\det(a_{rs}). \end{aligned} $$

□

Lemma 15

Let a _ij(t) be differentiable in t with inverse a ^ij(t). Then

$$\displaystyle \begin{aligned}{\frac{d}{dt}} a^{ij}=-a^{ik}a^{lj}{\frac{d}{dt}} a_{kl}.\end{aligned}$$

Proof

We have

$$\displaystyle \begin{aligned}a^{ik}a_{kj}=\delta^i_j.\end{aligned}$$

There exists $\tilde a^{ij}$ such that

$$\displaystyle \begin{aligned}a_{ik}\tilde a^{kj}=\delta^j_i.\end{aligned}$$

Then $a^{ij}=\tilde a^{ij}$, as

$$\displaystyle \begin{aligned}a^{ij}=a^{ik}\delta^j_k=a^{ik}\left(a_{kl}\tilde a^{lj}\right) =\left(a^{ik}a_{kl}\right)\tilde a^{lj}=\tilde a^{ij}.\end{aligned}$$

We differentiate and obtain

$$\displaystyle \begin{aligned}0={\frac{d}{dt}}\delta^i_j={\frac{d}{dt}}\left(a^{ik}a_{kj}\right) ={\frac{d}{dt}} a^{ik}a_{kj}+a^{ik}{\frac{d}{dt}} a_{kj}.\end{aligned}$$

Hence

$$\displaystyle \begin{aligned}{\frac{d}{dt}} a^{il}={\frac{d}{dt}} a^{ik}\delta^l_k ={\frac{d}{dt}} a^{ik}a_{kj}a^{jl} =-a^{ik}{\frac{d}{dt}} a_{kj}a^{jl}.\end{aligned}$$

□