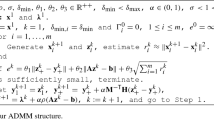Abstract
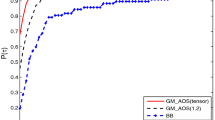
New conjugate directions algorithms are proposed, which are based on an orthogonalization procedure and do not perform line searches. The orthogonalization procedure prevents the conjugate vectors set from the degeneracy, eliminates high sensitivity to computation errors pertinent to methods of conjugate directions, and thus enable us to solve large-scale minimization problems without preconditioning. Numerical experiments have confirmed high efficiency of the algorithms for minimizing large-scale quadratic functions.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Broyden C.G. The Convergence of a Class of Double-rank Minimization Algorithms. J. Inst. Maths. Applies. 1970; 6: 76–90.
Goldfarb D. A Family of Variable Metric Updates Derived by Variational Means. Mathematics of Computing 1970; 24: 23–26.
Shanno D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Mathematics of Computing 1970; 24: 647–656.
Dixon L.C.W. Conjugate Directions without Linear Searches. J. Inst. Maths. Applic. 1973; 11: 317–328.
Nazareth L. A Conjugate Direction Algorithm without Line Searches. Journal of Optimization Theory and Applications 1977; 23: 373–387.
Fletcher R. Practical Methods of Optimization. Vol. 1. J. Wiley: 1980.
Byrd R.H., Schnabel R.B. and Shultz G.A. Approximate Solution of the Trust Region Problem By Minimization over Two-Dimensional Subspaces. Mathematical Programming 1988; 40: 247–263.
Manevich A.I. and Polyanchikov P.I. Single-step method of conjugate directions. Izvestija of USSR Academy of Sciences, Technical Cybernetics 1984; 6: 41–47 (in Russian).
Gilbert J.C. and Nocedal J. Global Convergence Properties of Conjugate Gradient Methods for Optimization. SIAM Journal on Optimization 1992; 2: 21–42.
Branch M.A., Coleman T.F. and Li Y. A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained minimization Problems. SIAM Journal on Scientific Computing 1999; 21(1): 1–23.
Manevich A.I. and Boudinov E. An efficient conjugate directions method without linear minimization. Nuclear Instruments and Methods in Physics Research 2000; A 455: 698–705.
Optimization Toolbox for Use with MATLAB. User’s Guide. Version 2. The MathWorks Inc., 2000.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Boudinov, E., Manevich, A.I. (2005). An Efficient Conjugate Directions Method Without Linear Searches. In: Fleuren, H., den Hertog, D., Kort, P. (eds) Operations Research Proceedings 2004. Operations Research Proceedings, vol 2004. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-27679-3_41
Download citation
DOI: https://doi.org/10.1007/3-540-27679-3_41
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-24274-1
Online ISBN: 978-3-540-27679-1
eBook Packages: Business and EconomicsBusiness and Management (R0)