Abstract
Let G be an almost simple simply connected group over ℂ, and let Bun a G (ℙ2, ℙ1) be the moduli scheme of principalG-bundles on the projective plane ℙ2, of second Chern class a, trivialized along a line ℙ1 ⊂ ℙ2.
We define the Uhlenbeck compactification \( \mathfrak{U}_G^a \) of Bun a G (ℙ2, ℙ1), which classifies, roughly, pairs (ℱG, D), where D is a 0-cycle on \( \mathbb{A}^2 = \mathbb{P}^2 - \mathbb{P}^1 \) of degree b, and ℱG is a point of Bun a−b G (ℙ2, ℙ1), for varying b.
In addition, we calculate the stalks of the Intersection Cohomology sheaf of \( \mathfrak{U}_G^a \). To do that we give a geometric realization of Kashiwara’s crystals for affine Kac-Moody algebras.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
R. Bezrukavnikov, Perverse Coherent Sheaves (after Deligne), preprint, 2000; math.AG/0005152.
A. Beilinson, J. Bernstein, and P. Deligne, Faisceaux pervers, in Analyse et topologie sur les espaces singulières I (Luminy, 1981), Astérisque 100, Société Mathématique de France, Paris, 1982, 5–171.
V. Baranovsky and V. Ginzburg, Algebraic Construction of the Uhlenbeck Moduli Space, manuscript, 1998.
A. Braverman, M. Finkelberg, D. Gaitsgory, and I. Mirković, Intersection Cohomology of Drinfeld’s compactifications, Selecta Math. (N.S.), 8 (2002), 381–418.
A. Braverman and D. Gaitsgory, Crystals via the affine Grassmannian, Duke Math. J., 107 (2001), 561–575.
A. Braverman and D. Gaitsgory, Geometric Eisenstein series, Invent. Math., 150 (2002), 287–384.
W. Crawley-Boevey, Normality of Marsden-Weinstein reductions for representations of quivers, Math. Ann., 325-1 (2003), 55–79.
S. K. Donaldson, Connections, cohomology and the intersection forms of four-manifolds, J. Differential Geom., 24 (1986), 275–341.
S. K. Donaldson and P. Kronheimer, The Geometry of Four-Manifolds, Oxford Mathematical Monographs, Oxford University Press, London, 1990.
G. Faltings, Algebraic loop groups and moduli spaces of bundles, J. European Math. Soc., 5 (2003), 41–68.
B. Feigin, M. Finkelberg, A. Kuznetsov, and I. Mirković, Semi-infinite flags, AMS Transl., 194 (1999), 81–148.
M. Finkelberg, D. Gaitsgory, and A. Kuznetsov, Uhlenbeck spaces for \( \mathbb{A}^2 \) and affine Lie algebra \( \widehat{\mathfrak{s}\mathfrak{l}}_n \), Publ. RIMS Kyoto Univ., (4), 39 721–766.
M. Finkelberg, A. Kuznetsov, N. Markarian, and I. Mirković, Anote on a symplectic structure on the space of G-monopoles, Comm. Math. Phys., 201 (1999), 411–421.
D. Gaitsgory, Construction of central elements in the affine Hecke algebra via nearby cycles, Invent. Math., 144 (2001), 253–280.
D. Gieseker, On the moduli of vector bundles on an algebraic surface, Ann. Math. (2), 106 (1977), 45–60.
J. Greenstein and A. Joseph, A Chevalley-Kostant presentation of basic modules for \( \widehat{sl(2)} \) and the associated affine KPRV determinants at q = 1, Bull. Sci. Math., 125 (2001), 85–108.
A. Joseph, On an affine quantum KPRV determinant at q = 1, Bull. Sci. Math., 125 (2001), 23–48.
M. Kashiwara, The flag manifold of Kac-Moody Lie algebra, in Algebraic Analysis, Geometry, and Number Theory: Proceedings of the JAMI Inaugural Conference, Johns Hopkins University Press, Baltimore, 1989, 161–190.
M. Kashiwara, private communication.
M. Kashiwara, Kazhdan-Lusztig conjecture for a symmetrizable Kac-Moody Lie algebra, Progr. Math., 87 (1990), 407–433.
M. Kashiwara, Crystallizing the q-analogue of universal enveloping algebras, Duke Math. J. 63 (1991), 465–516.
M. Kashiwara, Crystal base and Littelmann’s refined Demazure character formula, Duke Math. J., 71 (1993), 839–858.
M. Kashiwara, On crystal bases, CMS Conf. Proc., 16 (1995), 155–197.
M. Kashiwara and Y. Saito, Geometric construction of crystal bases, Duke Math. J., 89 (1997), 9–36.
B. Kim and R. Pandharipande, The Connectedness of the Moduli Space of Maps to Homogeneous Spaces, preprint, 2000; math.AG/0003168.
J. Li, Algebraic geometric interpretation of Donaldson’s polynomial invariants, J. Differential Geom., 37 (1993), 417–466.
J. W. Morgan, Comparison of the Donaldson polynomial invariants with their algebro-geometric analogues, Topology, 32 (1993), 449–488.
H. Nakajima, Lectures on Hilbert Schemes of Points on Surfaces, AMS University Lecture Series 18, American Mathematical Society, Providence, 1999.
N. Perrin, Courbes rationelles sur les variétés homogènes, Ann. Inst. Fourier, 52 (2002), 105–132.
J. F. Thomsen, Irreducibility of
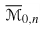 , Internat. J. Math., 9 (1998), 367–376
, Internat. J. Math., 9 (1998), 367–376K. K. Uhlenbeck, Connections with L p bounds on curvature, Comm. Math. Phys., 83 (1982), 31–42.
G. Valli, Interpolation theory, loop groups and instantons, J. Reine Angew. Math., 446 (1994), 137–163.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Birkhäuser Boston
About this chapter
Cite this chapter
Braverman, A., Finkelberg, M., Gaitsgory, D. (2006). Uhlenbeck Spaces via Affine Lie Algebras. In: Etingof, P., Retakh, V., Singer, I.M. (eds) The Unity of Mathematics. Progress in Mathematics, vol 244. Birkhäuser Boston. https://doi.org/10.1007/0-8176-4467-9_2
Download citation
DOI: https://doi.org/10.1007/0-8176-4467-9_2
Publisher Name: Birkhäuser Boston
Print ISBN: 978-0-8176-4076-7
Online ISBN: 978-0-8176-4467-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



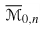 , Internat. J. Math., 9 (1998), 367–376
, Internat. J. Math., 9 (1998), 367–376