Introduction

Quasiparticles that can propagate at the interface between conductor and dielectric due to collective charge oscillations are known as surface plasmon polaritons (SPP). Various forms of them have been recognized ranging from freely propagating electron density waves along metal surfaces to localized electron oscillations on metal nanoparticles. Unique properties of surface plasmons, i.e., their sensitivity to a changing environment at a nanoscale, enable a wide range of practical applications, including light guiding [1], manipulation at nanoscale [2], biodetection [3, 4], high-resolution optical imaging [5], optical switching [6, 7], and many others [8].

We limit ourselves to plasmon excitation on metallic surface in contact with photochromic polymer. There are many ways to excite the SPP on a metal surface [9]: using prism coupling in Otto or Kretschmann configurations, near-optical field excitation, highly focused optical beam technique, excitation on discontinuities, and imperfections in metallic layers like holes, ridges, or their arrays. In this work, we focused our attention to light coupling into SPP occurring on a periodic array of corrugated polymer surface and rectangular metallic ridges that could be fabricated on a metal surface [10]. Light diffracted on periodic structures can fulfill necessary conditions of momentum matching with SPP and increase the plasmon excitation efficiency. Grating excitation method limits the dispersion distribution of excited SPP to a very narrow frequency range being precisely defined by the grating parameters and metal dielectric permittivity. Generally, grating structures offer a possibility of tuning frequency of the excited SPP by changing grating geometrical parameters, like grating period, ridge height or grating duty factor [11], and properties of dielectric medium. Recent studies [12] have shown that an efficiency of SPP excitation by grating method can reach ∼22%, what usually is sufficient for experimental observations of plasmons as well as for fabrication of plasmonic sensors [13] and light switching devices [8]. In this work, we investigate the possibility of SPP excitation on finite metal and polymeric gratings and plasmon frequency shift caused by an external stimulus in the form of light which changes the polymer refractive index.

Excitation of SPP and FDTD Method Description

Light coupling on the grating and subsequent excitation of the SPP requires energy and momentum conservation of the photon and surface plasmon polariton:

$$ \hbar \omega_{\text{light}} = \hbar \omega_{\text{SPP}}, $$
(1)
$$ k \cdot \sin \left( \theta \right) + mK = \pm \beta, $$
(2)

where k = 2π/λ is a propagation vector of light, β is an SPP propagation vector, \( K = 2\pi /\Lambda \) is a wavevector of an infinite grating and m is an integer number. The same conditions must be fulfilled when the SPP is excited in a flat metallic layer due to light diffraction on a surface relief grating (SRG) formed in a thin polymeric layer deposited over the metal surface. The surface relief grating on polymer layer can be made by a holographic method, and in that case, its shape could be described by a cosine function.

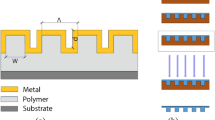
In fact, we performed calculations for a few different shapes of ridges and found that differences are not significant, therefore in this article we limit our study only to sinusoidal shapes of the grating that can be easily prepared by holographic laser illumination. In Fig. 1, we schematically show the rectangular metallic grating over bulk metal together with the chosen coordinate system and grating (K), light (k), and SPP (β SPP) wavevectors. The surface relief grating formed in a polymeric layer covering the flat metal surface is also shown in Fig. 1. It is well-known [8] that for a flat metal–dielectric interface, an SPP wave vector β fulfills a dispersion equation:

Fig. 1
figure 1

Schematic view of metal grating and surface relief grating in polymer over a flat metal. Momentum conservation conditions of light coupling into SPP on metal grating with left (β LSPP) and right (β RSPP) SPP propagation constants are given as well

Full size image
$$ \beta \left( \omega \right) = \sqrt {{\frac{{\varepsilon_{\text{d}} \cdot \varepsilon_{\text{m}}\left( \omega \right)}}{{\varepsilon_{\text{d}} + \varepsilon_{\text{m}}\left( \omega \right)}}}}, $$
(3)

where ε d is a dielectric permittivity of a polymer or air assumed as nondispersive ones in the respective frequency range and ε m(ω) is a complex permittivity of a metal which can be described within the Drude–Lorentz oscillator approximation [8] as:

$$ {\varepsilon_{\text{m}}}\left( \omega \right) = \varepsilon_{\infty } - \frac{{\omega_p^2}}{{\omega^2 + i\gamma \omega }} + \sum\limits_j {\frac{{f_j\omega_j^2}}{{\omega_j^2 - \omega_j^2 - i\gamma_j\omega }}}, $$
(4)

where \( \omega_{\text{p}} = \sqrt {{\frac{{{\text{Ne}}^2}}{{\varepsilon_0m_{\text{e}}}}}} \) is the plasma frequency and γ is the dumping constant of a free electron gas, f j , ω j , γ j are strength, frequency, and dumping constants of the jth Lorentz’s oscillator. We use the two-dimensional (2D) finite-difference time-domain (FDTD) method with auxiliary differential equation for Lorentz-like media having permittivity in the form given by an equation (Eq. 4). The FDTD method relies on the numerical solving of the Maxwell equations for electromagnetic wave propagation on the so-called Yee grid based on the second-order central differences [14]. The FDTD method is successfully used in simulation of plasmonic and optical switching structures [15–17].

In order to model the dielectric permittivity for pure gold (Au) layer we used a dielectric permittivity at infinite frequencies, plasma frequency, and damping coefficient as given in Ref. [18, 19], i.e., ε ∞ = 6.2136, ω p = 1.3323 × 1016 Hz, and γ = 1.3235 × 1014 Hz. For the sake of simplicity (to shorten calculation time) we limited metal permittivity just to the Drude model, i.e., neglecting all Lorentz’s terms in Eq. (4). We also assumed that the polymer layer is dispersionless and lossless, so its dielectric permittivity is constant and real, therefore for optical frequencies we took: \( \varepsilon_{\text{d}} = n_{\text{d}}^2 \) where n d is a refractive index of the polymer.

The 2D structure is covered with the uniform Yee grid. The period of the Yee grid is dx = dy = 5 nm and the time period, dt = 10−17 s. The light source is taken as a sum of linear monochromatic sources with wavelengths ranging from 300 to 1,000 nm every 10 nm which are what defines a discrete polychromatic light source. Incoming light polarization is TM with a magnetic field component parallel to the z-axis. The electromagnetic wave was calculated either using Bloch boundary conditions for grating infinitely in the x direction or without it for finite gratings having several ridges along the x-axis. The structure is surrounded by the properly chosen boundary conditions represented here by Berenger’s perfect matching layers for uniaxial mediums with refraction factor R = 10−4 [14]. A light beam has been assumed to have a Gaussian intensity profile in calculations of finite grating structures and a flat profile in calculations of infinite gratings.

An example of SPP excitation in a finite grating structure with EM field components calculated by the FDTD method is shown in Fig. 2. The FDTD method gives a time dependence of the electric and magnetic field components within the structure. In order to obtain results in the function of wavelength, the Fourier transformation of the electric or magnetic fields were calculated: \( \left\langle {H\left( \lambda \right)} \right\rangle = F\left\{ {H(t)} \right\} \) for the magnetic field or \( \left\langle {E_{ \bot }\left( \lambda \right)} \right\rangle = F\left\{ {E_{ \bot }(t)} \right\} \) for the electric field perpendicular to the metal surface, where λ = 2πc/ω is the light wavelength in the vacuum.

Fig. 2
figure 2

Plot of calculated electromagnetic field intensity of normally incident light with wavelength in vacuum λ = 600 nm coupled into the SPP on the dielectric layer (n = 1.5) with surface relief grating and a flat metal surface underneath. Parameters of SRG are H = 100 nm, h = 100 nm, and Λ = 500 nm (cf. Fig. 1)

Full size image

Results of Simulation of the SPP Excitation on Different Gratings

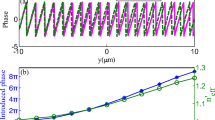
The SPP resonance peak spectrum for a purely metallic (Au) grating formed by rectangular protrusion ridges of Λ = 700 nm period is shown in Fig. 3. We calculated a magnetic field strength in a small distance from the metal surface and light source position which illuminated the sample at an incidence angle θ = 15°. The three main peaks correspond to momentum conservation laws as shown in Fig. 3. The central peak corresponds to the forward SPP propagation with respect to the position of the light source while the remaining two to the back SPP propagation. The absorption of incident photon energy in metal makes the amplitudes of the respective plasmons differ significantly depending on their wavelengths λ SPP. Plasmons could be excited in a flat metal layer also due to light diffraction on a surface relief grating made on the top of the photochromic polymer film. It was interesting to compare, for the same light source, the efficiency of SPP excitation on metal surface due to metal ridges and due to surface relief of the same period inscribed in the top of the polymer layer. The dielectric SRG has been assumed to have a sinusoidal shape because such a shape can easily be obtained in azo-substituted polymers by laser holographic method [20]. In all simulations, the refractive index of the photochromic polymer is assumed to be n = 1.5. Calculating the SPP excitation efficiency on metal grating with a rectangular shape, we kept the same height of the ridges h as was the amplitude of a relief grating. Preliminary calculations of the electric field distribution in metal–polymer–air (MPA) structure resulted in the observation of several resonances (cf. Fig. 4). Their appearance is connected with light wave guiding properties of the polymer layer itself. Therefore, it was necessary to distinguish between purely electromagnetic wave-guided p-polarized modes (dielectric modes) in polymer and true SPP modes characteristic for the metal–dielectric interface. To do this, we precisely calculated the light energy distribution in the bulk of metal, polymer, and air after the illumination of the structure with polychromatic light. The structures were made of infinite thickness metal with a polymer layer over it (having a mean thickness H from 100 to 1,000 nm and refractive index n d = 1.5). Additionally, the polymer layer had an infinite surface relief grating of period Λ = 500 nm with a relief amplitude of h = 100 nm. For comparative purposes, we calculated similar wave guiding structures with air instead of a metal, i.e., classic air–polymer layer–air (APA) planar waveguide. For structures with relatively thick polymer layers H we have found a series of well-defined modes (c.f. Fig. 4c) propagating at various frequencies or wavelengths. Four among the modes appeared both in the MPA and APA structures, what is demonstrated in Fig. 4a, b. The profiles of field distribution are characteristic for the lowest and subsequent higher planar waveguide modes. We concluded that these modes are not the SPP modes, but dielectric ones [21] and labeled them from m0 to m3. Their characteristic wavelengths evolved together with polymer thickness H (cf. Fig. 4c). Exclusively for MPA structures, two additional modes appear, which we consider as SPP ones: for λ = 330 nm and for λ = 690–790 nm (cf. Fig. 4d inset). The former SPP 330 nm mode is highly confined in metal with very short characteristic propagation distance L = (2 Im(β))−1 equal to 0.58 μm. The latter SPP mode is much less confined in the metal, and its propagation distance is considerably larger, L = 11.66 μm. Both plasmonic modes have maximum of electric field at the metal–dielectric interface and both decay exponentially in the direction y perpendicular to the metal and polymer interface. An electric field amplitude for the SPP at 790 nm in the vicinity of the metal–polymer interface in the function of distance y from the interface is shown in Fig. 4d; the field penetration depths are d Au = 50 nm and d polym = 200 nm, respectively. In the forthcoming calculations presented in this paper, we will investigate the properties of the SPP mode characterized by a larger propagation length, L.

Fig. 3
figure 3

Plot calculated by FDTD method. SPP resonance bands for metal grating with a period of Λ = 700 nm and at light incidence angle θ = 15°. For each band, a corresponding momentum conservation relation is indicated

Full size image
Fig. 4
figure 4

Calculated by FDTD method. Profiles of electric field distribution in air–polymer–air (a) and metal–polymer–air (b) structures with H = 950 nm. Modes labeled m0, m1, m2, and m3 are the light-guided modes in the polymer layer. Dependence of the mode frequency on the polymer layer thickness, H (c). The electric field distribution close to the gold–polymer interface for SPP at 790 nm; inset: electric field distribution profiles for two SPP modes (d)

Full size image

In order to investigate the properties of SPP excited via SRG grating inscribed on a polymer surface and directly on a metal grating, we performed numerical investigations for the case of finite gratings having only N = 8 ridges and infinite gratings to which the Bloch boundary conditions were applied. Calculations were performed for two exemplary grating periods Λ = 400 nm and Λ = 550 nm. For these calculations, the constant grating parameters were kept: ridge height, h = 50 nm; polymer layer thickness, H = 100 nm; polymer refractive index, n d = 1.5. The respective results are gathered in Figs. 5 and 6. Upon analyzing them, we have found that the same period of dielectric and metal grating results in obtaining different wavelengths of SPP excitation (cf. Fig. 5). For example, the SRG grating on the dielectric with a period of Λ = 400 nm couples the SPP at a wavelength of λ = 675 nm, and a metallic ridge grating of the same period couples SPP at a much longer wavelength of λ = 745 nm. For a finite number of ridges, N = 8, the plasmon wavelength almost does not change, and efficiencies of its coupling for dielectric and metal gratings are comparable (cf. Fig. 6). Obviously, an increase of plasmonic band width with respect to that observed for the infinite grating case is observed.

Fig. 5
figure 5

Plot of electric field amplitude perpendicular to the metal surface F{E ⊥} inside the infinite grating. Comparison of electric field amplitudes for two exemplary grating periods Λ = 400 nm and Λ = 550 nm (a) and dependence of excited SPP wavelength on period of the grating Λ (b) for metallic and dielectric gratings

Full size image
Fig. 6
figure 6

Plot of electric field amplitude perpendicular to the metal surface F{E ⊥} for the finite grating at a constant distance from the grating end. Comparison of electric field amplitudes for two exemplary grating periods Λ = 400 nm and Λ = 550 nm (a) and dependence of maximal field amplitude perpendicular to the metal surface F{E ⊥} of excited SPP on period of the grating Λ (b) for metallic and dielectric gratings

Full size image

Results are distinctively different when infinite gratings are involved. The coupled SPP wavelengths agree with the trend observed for the finite grating case, but large differences can be observed in their electric field amplitudes (cf. Fig. 5). Dielectric infinite grating couples light into SPPs with ten times lower efficiency than does metal grating (cf. Fig. 5a). However, the electric field measured inside the grating (for the infinite grating this is the only possibility) is composed of the SPP and light propagating and scattered in all possible directions. Also, the infinitely expanded light source can affect the results. Therefore, we conclude that the observation of SPP at some distance after the grating end should give more reliable results. In this case, the SPP excitation efficiency is similar for metal and polymer gratings—what is shown in Fig. 6a, b.

Furthermore, using the FDTD method, we investigated how the number of ridges influences the coupled SPP peak shape, e.g., its intensity and spectral width. The exemplary SPP bands calculated for the different number of ridges are shown in Fig. 7. One can notice that for N = 6, an SPP peak is already well characterized. In Fig. 7b, we plotted the SPP peak intensity and the full width at half maximum (FWHM) of the band in function of a number of ridges for excitation with two different Gaussian light beams with diameters, D = 3 μm and D = 6 μm, respectively. It can be seen that the SPP peak intensity reaches the maximum value for a certain number of ridges, N, which are related to the diameter D of the light beam. Let us define this number of ridges as the efficient number (EN) of ridges and the cumulative length corresponding to it as the efficient length (EL) of the grating. We suppose that for the EN ridges, the efficiency of SPP coupling and reflection plus decoupling are equal. Any supplementary ridge makes that reflection or/and decoupling of SPP start to dominate. The FWHM decreases with the number of ridges and reaches a minimal value that depends on the excitation beam radius or more precisely on the EN. For the most effective coupling, the EL of grating is larger than the used Gaussian beam diameter. For D = 3 μm, the beam diameter EN = 12 and EL = 6 μm; for D = 6 μm, EN = 24 and EL = 12 μm. It can be seen that the EN and EL scale linearly with the Gaussian beam diameter D, and EL is about two times larger than D.

Fig. 7
figure 7

a Plot of electric field amplitude perpendicular to the metal surface F{E⊥} peak at a constant distance from the grating. SPP was coupled via dielectric grating, Gaussian beam diameter, D = 3 μm. b Plot of maximal perpendicular component of electric field F{E⊥} and FWHM of excited SPP band for two Gaussian beam diameters, D = 3 μm (solid line) and D = 6 μm (dashed line)

Full size image

By the FDTD method, we have shown that the wavelength of the coupled SPP is nearly a linear function of the n d refractive index of the polymer layer. In the range of 1.45–1.6, the SPP wavelength shifts from 680 nm to 770 nm for Λ = 500 nm.

In conclusion, we have presented a numerical investigation of the excitation of surface plasmon polaritons using infinite and finite grating inscribed in a polymer layer deposited over a flat gold surface. The geometrical parameters of the gratings have been optimized for the enhanced excitation of SPP showing that a grating amplitude of less than 100 nm is sufficient for an effective light coupling into plasmon excitation even for a small number of ridges not exceeding ten. The excitation efficiency of SPP for finite dielectric grating is comparable with similar gratings made in metal. Studies of SPP excitation on a different number of ridges show that light beam diameter and number of ridges should carefully be adjusted to achieve efficient SPP excitation.