Introduction

The relationship between eye movements predicted by Listing's law and the compensatory eye movements of the vestibuloocular reflex (VOR) is a problem of considerable contemporary scientific interest. Previous studies have examined this relationship in two ways. First, eye position was varied while the head was rotated about an Earth-vertical axis (Fetter et al. 1992; Misslisch et al. 1994; Palla et al. 1999; Thurtell et al. 1999; Tian et al. 2005; Crane et al. 2005). Second, using a change in vergence, Listing's plane could be varied while the head was rotated about an Earth-horizontal axis (Migliaccio et al. 2003). These studies concluded that a “compromise” strategy between Listing's law and a perfectly compensatory VOR determined the axis of eye rotation. In the present study, we altered the axis of head rotation by pitching the head at various angles relative to Earth-vertical, but always rotating the head about an Earth-vertical axis so that eye position in the orbit and the orientation of Listing's plane were unchanged. This experimental paradigm enabled us to examine the contribution of central neural mechanisms to the VOR/Listing's law compromise.

The relationship between torsional eye position and the location of the line of sight, i.e., the horizontal and vertical coordinates of eye position, is defined by Donders's and Listing's laws. Donders's law states that there is only one torsional eye position for each combination of horizontal and vertical eye positions (gaze directions). Listing's law is a special case of Donders's law and quantitatively specifies the torsional angle about the line of sight for each gaze direction. It states that when the head is upright and not moving, the three-dimensional positions (horizontal, vertical, and torsional) that the eye can adopt are constrained such that when they are expressed as a rotation around a single axis from a fixed reference position, the resulting axes all lie in a single head-fixed plane known as the “displacement” plane (Helmholtz 1867; Haustein 1989). The orientation of the displacement plane changes when the reference eye position is changed. The reference eye position can be represented by a reference-gaze vector that lies parallel to the line-of-sight when the eye is at the reference position. When the reference-gaze vector is perpendicular to the resulting displacement plane, it represents a unique reference eye position called “primary position,” and the associated unique displacement plane is “Listing's plane.” This relationship between reference eye position and the displacement plane is very precise during steady fixation, during saccadic and smooth-pursuit eye movements, and during the translational vestibuloocular reflex, i.e., the rotation vectors representing instantaneous eye position during these eye movements all lie in a single plane (Ferman et al. 1987; Tweed and Vilis 1990; Tweed et al. 1992; Haslwanter et al. 199l; Straumann et al. 1991, 1995; Angelaki et al. 2003; Walker et al. 2004). The eye movements that follow this relationship are described as obeying “Listings law.”

The geometric requirement necessary for eye movements to obey Listing's law is that the eye-velocity vector is confined to a plane with a normal that is the angle bisector between the initial direction of gaze and the primary position (reference) gaze vector. This relationship is often known as the 1/2 angle rule because a singular change in the initial direction of gaze by α° results in a α/2° change in tilt of the eye-velocity vector (Tweed and Vilis 1990; Tweed et al. 1990) (Fig. 1A). During far viewing, Listing's plane is close to parallel to the coronal plane or only slightly rotated temporally (Bergamin et al. 2004). During near viewing, Listing's plane rotates in the temporal direction by an amount proportional to the vergence angle (the angle between the two lines of sight) (e.g., Mok et al. 1992; Somani et al. 1998; Porrill et al. 1999; Steffen et al. 2000; Migliaccio et al. 2003). Although there is a slight tilt of Listing's plane in humans with a change in the pitch orientation of the head, it is exceedingly small even over a large range, e.g., <3.4° change when the head is pitched between ±90° from upright (Bockisch and Haslwanter 2001; also see Furman and Schor 2003).

Fig. 1
figure 1

Panel (A) shows how the plane in which the axes of eye rotations are confined when Listing's law is obeyed, can be calculated for a given initial gaze position and Listing's plane. The axis of eye rotations are confined to a plane with a normal that is the angle bisector between the initial direction of gaze and the Listing's primary position vector. Note that if the direction of gaze were parallel to Listing's primary position, then the eye rotations would all lie in Listing's plane. Panel (B) shows where the axis of eye rotation during the VOR would lie if a 50–50 VOR/Listing's compromise were obeyed.

Full size image

A perfectly compensatory VOR should not obey Listing's law because, in order to maintain the orientation of the eye in space during head rotations, the axes of eye and head rotation should be parallel. Therefore, unlike eye movements that obey Listing's law, the axis of eye rotation during the angular VOR should not be affected by the initial direction of gaze and/or Listing's plane. It has been shown, however, that the axis of eye rotation during the VOR does not meet the needs for perfect 3D gaze stabilization during head rotation.

Two paradigms provide evidence of a compromise between Listing's law and a perfectly compensatory VOR. First, when a subject changes gaze between an up to a down far target during a passive head rotation about Earth-vertical with the head upright in neutral position, the axis of eye rotation pitches backwards or forwards depending on the vertical position of the eye in the orbit, even though Listing's plane has not changed its orientation (Fetter et al. 1992; Misslisch et al. 1994; Palla et al. 1999; Thurtell et al. 1999). Second, when a subject changes fixation between a far and a near target placed directly in front of one eye, the orientation of Listing's plane rotates temporally but the position of the fixing eye does not change (Kapoula et al. 1999; Steffen et al. 2000). During a passive pitch head rotation about Earth-horizontal (with the head initially upright in neutral position), the axis of eye rotation rotates temporally toward the direction of Listing's plane during near viewing (Migliaccio et al. 2003). In both of these paradigms, the axis of eye rotation during the VOR lies approximately halfway between the axis that would be specified by Listing's law and the axis that would be necessary for a perfectly compensatory VOR (this is often known as the 1/4 angle rule) (Fetter et al. 1992; Misslisch et al. 1994; Migliaccio et al. 2003) (Fig. 1B).

However, previous studies have not determined whether the axis of eye rotation during the VOR also depends on the orientation of the head relative to the axis of head rotation, because the axis of head rotation in these prior studies was fixed, whereas the initial gaze position or the orientation of Listing's plane was varied. Also, because it has been shown that the extraocular muscle tendons pass through innervated muscle pulley sheaths that change position for different eye positions and/or vergence states (Demer et al. 1995; Clark et al. 2000), it is not possible to discern from these experiments whether the axis of eye rotation during the VOR tilts as a result of passive mechanical changes in the ocular periphery (the “plant”).

In two previous studies, the axis of eye rotation was measured during low-velocity, low-frequency, sinusoidal, whole-body rotations about pure Earth-vertical with the head fixed at different pitch orientations (Fetter et al. 1992; Solomon et al. 1997). Subjects in these studies were instructed to look at the location of an imaginary far target along the nasooccipital axis so that eye position and Listing's primary position would be fixed. In their experiments, however, eye positions were not carefully controlled because their subjects were tested in the dark. Furthermore, the orientations of Listing's plane in their subjects were not reported. Although these studies showed that the axis of eye rotation during the VOR tilted in pitch for the different head pitch orientations, the amount of axis tilt was less than that predicted from Listing's law. This difference was attributed to a difference in gain between the torsional and horizontal components of the VOR.

Here we reexamined these issues using a similar paradigm but with high-velocity, high-acceleration, transient head rotations. In addition, we used a fixation target to carefully control the initial position of the eye, and focused our analysis on the initial VOR eye movement before any visual feedback or predictive mechanisms could influence the response. Initial gaze position and Listing's primary position in our paradigm remain approximately parallel even though the head is pitched up or down. In this case, the rotation vectors representing eye movements, if they obeyed Listing's law, should lie approximately in the coronal plane. In contrast, if the rotation vectors representing eye movements are generated by a perfectly compensatory VOR, they should align close to the Earth-vertical axis. Therefore, if in our paradigm the brain still opts for an axis of eye rotation between what is called for by Listing's law and what is required for perfect geometrical compensation, the axis of eye rotation during the VOR should tilt between the Earth-vertical axis and the coronal plane. If there were no tilt, this would suggest that the axis tilt observed in previous experiments (in which eye position or Listing's plane was varied) was attributable to passive mechanical changes in the ocular plant.

Material and methods

Subjects

We studied eight normal subjects (mean age 38; range 24–49 years). No subject had a history or clinical signs of vestibular disease. Participation in this study was voluntary, and informed consent was obtained as approved by the Johns Hopkins School of Medicine Institutional Review Board.

Recording system

The movements of both eyes were recorded in three dimensions by using dual-axis scleral search coils embedded in a silastic annulus. The instrumentation and technique using the identical system and setup have been described in detail elsewhere (Straumann et al. 1995; Migliaccio et al. 2004). A search coil embedded in a bite block was used to measure head rotation. Chair, eye, and head angular position signals were filtered with a single-pole, low-pass analog filter that had a 3-dB bandwidth of 100 Hz. They were then sampled at 500 Hz at 16-bit resolution, and digitally filtered with a 50-tap, zero-phase, low-pass FIR filter with a bandwidth of 50 Hz.

Each subject was tested while seated upright with the head centered within a uniform magnetic field with the interpupillary line in the Earth-horizontal plane. The magnetic frame was a 102-cm cube. There is a 10-cm3 region of linearity at the center of this cube within which there is no effect of translation of the search coil on its orientation within the magnetic field. The chair and magnetic field system are coupled and can rotate together about an Earth-vertical axis. The head of the subject was positioned so that Frankfurt's line (from the top of the external acoustic meatus to the cephalic aspect of the lowest point of the infraorbital rim) is oriented in one of five positions with respect to the Earth-horizontal plane: 0°, 15° nose down, 30° nose down, 15° nose up, and 30° nose up. It was not mechanically possible for the chair to tilt so the subject's torso was upright for every trial. During each trial, the room was completely dark except for a target light-emitting diode (LED), upon which subjects were instructed to fix. The LED was positioned directly in front of the nose of the subject at 124–143 cm (vergence angle 1.5–1.3°) along the nasooccipital axis. During the first 5 s of each data file, eye and head angular position were calibrated by positioning the head in neutral position (Frankfurt's line at 0° re: space) and instructing the subject to fix upon a far target (124 cm) at 0° (re: space). After 5 s, and before the onset of the head impulse, Frankfurt's line and the fixation target were oriented at one of the five angles described above. Head impulse rotations about an Earth-vertical axis were delivered head-on-trunk (with chair locked in neutral) and whole body (head-and-trunk with chair unlocked).

Horizontal head-and-trunk “impulses” were passive manual body rotations, unpredictable in time and direction (leftward, rightward), with peak-amplitude ∼20°, velocity ∼80°/s, and acceleration ∼1000°/s2. During whole-body rotations, the subject's head was held fixed in position by using a padded box-like head restraint device with adjustable width fixed to the chair and coils system and a custom-molded bite block attached to a bar rigidly fixed to the chair and coils system. Horizontal head-on-trunk “impulses” consisted of passive, unpredictable in time and direction, manual head rotations with peak amplitude ∼20°, velocity ∼150°/s, and acceleration ∼3000°/s2 (Halmagyi and Curthoys 1988). The investigator delivering these impulses tried to rotate the head about an axis as close to Earth-vertical as possible. In four subjects, we also measured the torsional VOR gain by delivering roll head-on-trunk impulses (peak-amplitude ∼20°, peak-velocity ∼150°/s, and peak-acceleration ∼3000°/s2). Before the start of each roll head-on-trunk impulse, the head was positioned upright with Frankfurt's line and eye position at 0° (re: space).

Data analysis

Eye and head angular positions were represented by rotation vectors with roll, pitch, and yaw coordinates (Haslwanter 1995; Migliaccio and Todd 1999). The orientation of each eye relative to the head was also quantified using rotation vectors. The velocity vectors of head-in-chair, eye-in-chair, and eye-in-head were calculated from the corresponding rotation vectors (Hepp 1990). Eye-in-space and head-in-space velocity vectors during whole-body chair rotations were calculated using the chair-in-space velocity vectors. Head velocity was calculated with reference to a head-fixed coordinate frame using the methods described by Aw et al. (1996); thus eye and head velocities were both expressed in a head coordinate frame.

The onset of each head impulse was calculated from the magnitude of the head-in-space velocity vector by fitting a 15-order polynomial curve to the head-in-space velocity vs. time. The point when the magnitude of the fitted curve was greater than 2% of the curve's peak magnitude (typically this threshold was 4°/s) was defined as the time of onset. As the time between the onset of the impulse and the maximum velocity of the impulse was <150 ms, the analysis of the impulse data was restricted to a period of 150 ms from the onset. This meant that the effects of nonvestibular systems such as visual following (smooth pursuit, optokinetic) were minimal because these generally have longer latencies than the VOR (Halmagyi et al. 1990; Carl and Gellman 1987; Tychsen and Lisberger 1986). The cervicoocular reflex has a latency of ∼50 ms and may contribute to the VOR response during head-on-trunk head impulses in our 150-ms analysis window (Bronstein and Hood 1986). The contribution of the cervicoocular reflex, however, is small (gain <0.02 during sinusoidal rotations <1.5 Hz; gain decreases at higher frequencies) in normal subjects (Schubert et al. 2004). Trials of head impulse data that included blinks or other artifacts were not included for analysis. Head impulses with an atypical velocity profile [peak-velocity ∼20% different from the mean, duration (from onset to peak-velocity) ∼20% different from the mean] were likewise excluded. The eye and head axes of rotation in space were calculated from eye and head velocity prior to peak head velocity and before the first saccade.

We averaged data from the two eyes because there were no significant differences between the eye rotation axes (point-by-point paired t test: p = 0.79). The horizontal and torsional VOR gains were calculated by dividing the negative of the horizontal, or torsional, eye velocity vector component by the respective head velocity vector component during the 30-ms period prior to peak head velocity. Eye and head axis tilts in pitch on the midsagittal plane were calculated by determining the slope of a linear regression fit of the torsional and horizontal components of the respective velocity vectors (described in space coordinates). Results were described as means ± SD.

Listing's plane

Each subject was seated upright and centered within a uniform magnetic field, with the interpupillary line in the Earth-horizontal plane and the subject's head held fixed by biting down on a custom molded bite block attached to a bar rigidly fixed to the chair. The subject was instructed to repeatedly fix on nine fixation targets (separated horizontally and vertically by 45 cm) positioned on a screen directly in front of the subject at a 124-cm distance during a 60-s period. A best fit for Listing's plane was determined using a singular value decomposition algorithm (Press et al. 1988).

$$ r_{x} = f + f_{\nu } r_{y} + f_{h} r_{z} $$

where r x , r y , and r z are the components of the rotation vector representing the torsional, vertical, and horizontal components of the rotation, respectively, and f, f ν , and f h are coefficients. The x-axis is nasooccipital (forward, positive), the y-axis is interaural (left, positive), and the z-axis is rostrocaudal (up, positive). Primary position was calculated to show the orientation of Listing's plane (Tweed 1997).

Results

Listing's plane

For all subjects (n = 8), Listing's plane was tilted by a slight amount with respect to the yz (coronal) plane, by <±1.3° vertically and <±2.2° horizontally. The thickness of Listing's plane was small; the standard deviation averaged 0.5° across all subjects and ranged 0.3–0.8°.

Head-and-trunk (whole-body) rotations

During head-and-trunk rotations, the head-velocity axis of rotation (re: space) was within 0.2 ± 1.1° of Earth-vertical. The eye-velocity axis of rotation (re: space) pitched away from the head velocity axis, i.e., Earth-vertical, by an amount proportional to the angle between the head-velocity axis and the initial pitch head position (30° up, 15° up, 0°, 15° down, 30° down). The raw data for subject no. 5 when the head was pitched up 30°, which is representative for all subjects, is shown in Figure 2A (rightward and leftward whole-body rotations are shown). Figure 2A shows that the torsional eye velocity is negative for rightward head rotations and positive for leftward rotations; thus the axis of eye rotation is tilted in the same direction from Earth-vertical and by about the same amount during both leftward and rightward rotations. Figure 2B shows the torsional vs. horizontal components of eye and head velocity rotation axes for repeated trials of whole-body impulses in this subject. The eye-velocity axes for this subject lie about halfway between the head-rotation axis and the initial pitch head position. The mean (± SD) proportionality constant relating the tilt of the eye velocity axis to pitch head orientation for all eight subjects was 0.51 ± 0.09 (P < 0.05, R 2 = 0.97) (Table 1).

Fig. 2
figure 2

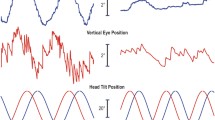
Eye and head velocity rotation data for subject no. 5. (A) Raw data obtained during leftward and rightward head-and-trunk (whole-body) impulses about Earth-vertical while gaze and head position are oriented 30° up. (B) During head-and-trunk impulses, the eye velocity axes for this subject lie about halfway between the head rotation axis and the initial head pitch position (30° nose-up, 0°, 30° nose-down). (C) Similarly, when the head is initially pitched up 30° during head-on-trunk impulses, the eye velocity axes for this subject lie about halfway between the head rotation axes and the initial head pitch position. When the head is pitched down 30° during head-on-trunk impulses, however, the axis of head rotation also pitched forward so the effect of head orientation during earth vertical head rotation on the eye-velocity axis could not be determined.

Full size image
Table 1 Eye rotation axis tilt with respect to Earth-vertical (forward tilt is positive, backward tilt is negative) during head-and-trunk (whole-body) impulses about Earth-vertical
Full size table

Head-on-trunk (head-only) rotations

Figure 2C shows the torsional vs. horizontal components of head and eye velocity rotation axes for repeated trials of head-only impulses in subject no. 5. When the head position is tilted nose up 30°, it is still rotating around an Earth-vertical axis (0°, left panel). The VOR eye velocity axes for this subject lie about halfway between the ideal VOR axis (coincident with the axis of head rotation) and the ideal Listing's law axis (coincident with the pitch of the initial orientation of the head). The ideal Listing's law behavior would have the eyes rotate about an axis also tilted back vertically (nose up) 30°, but the perfectly compensatory VOR axis would be the same as the rotation axis of the head. The tilt of the measured VOR axis from the ideal VOR axis is 15.4°. The ratio of this tilt to the angle between the ideal VOR axis and the Listing's law axis (30°) is 0.51.When head position is tilted nose down 30°, the head rotation axis (ideal VOR axis) rotates around a similarly tilted axis (28.4°, right panel), despite the investigator attempting to rotate the head about a purely Earth-vertical axis.

Across all subjects (n = 8), the mean proportionality constant relating eye velocity axis tilt away from the head velocity axis and toward the axis predicted by Listing's law was 0.39 ± 0.08 (0°, 15° up, and 30° up) (P < 0.05, R 2 = 0.91). For all subjects, during all the head-on-trunk rotations the investigator attempted to rotate the head about a purely Earth-vertical axis. There were deviations from Earth-vertical, however, most marked when the head was pitched forward, most likely due to the mechanical properties of the neck and the angle at which the hands of the examiner were placed on the head relative to the desired axis of head rotation. When the head was pitched up from Earth-vertical by a given static tilt (15°, 30° up), the axis of head rotation (re: space) was tilted up from Earth-vertical by an angle ranging between 2 and 36% of the static head tilt (Table 2). This deviation in the axis of head rotation from Earth-vertical was more pronounced when the head was pitched down (15° down, and 30° down) from Earth-vertical; the axis of head rotation was tilted down by ∼88% of the static head tilt. Thus, we could not use data with the head pitched down to compare with our head pitched down head-and-trunk rotations. Instead, we relied upon the head pitched up stimuli to make the comparison.

Table 2 Eye and head rotation axis tilts with respect to Earth-vertical during head-on-trunk (head-only) rotations about Earth-vertical
Full size table

The horizontal and torsional VOR gains for head-only impulses were tested for subjects 2, 4, 6, and 7. The horizontal VOR gains were 0.91 ± 0.04, 1.01 ± 0.03, 0.99 ± 0.07, and 1.03 ± 0.03 (mean = 0.99 ± 0.05), and the torsional VOR gains were 0.75 ± 0.08, 0.68 ± 0.05, 0.69 ± 0.07, and 0.90 ± 0.07 (mean = 0.76 ± 0.10), respectively.

Discussion

The axis of eye rotation changes with initial pitch head position

Our data show that during head-and-trunk (whole-body) impulses, the axis of eye rotation tilts in the same direction, and by an amount proportional (0.51 ± 0.09), to the initial pitch orientation of the head. This result is consistent with a compromise strategy in which the contributions of the VOR and of Listing's law are weighted equally (50–50 VOR/Listing's compromise), and confirms the results from other studies that the axis of eye rotation during the VOR lies approximately halfway between the axis of eye rotation required for a perfectly compensatory VOR and an axis of eye rotation that obeys Listing's law (Fetter et al. 1992; Misslisch et al. 1994; Palla et al. 1999; Thurtell et al. 1999; Migliaccio et al. 2003; Crane et al. 2005; Tian et al. 2005). In these previous studies, however, either gaze position or vergence angle (which produces a rotation of Listing's plane) was varied, thus likely altering the position of the muscle pulleys through which the oculomotor muscle tendons pass (Demer et al. 1995; Clark et al. 2000). Changes in the positions of the ocular pulleys in these paradigms could account for changes in the axis of eye rotation during head rotation (Clark et al. 2000; Demer et al. 2000; Demer 2004). But in our experiments, gaze position and vergence angle were fixed and a VOR/Listing's compromise was still observed, showing that passive changes in the positions of ocular muscle pulleys are unlikely to explain the VOR/Listing's law compromise.

Vectorial summation of the gains obtained for rotations about the major head axes

In several previous studies, during whole-body sinusoidal rotations in the dark about Earth-vertical, the axis of eye rotation changed with vertical head position. Fetter et al. (1994) (stimulus: 0.3 Hz, peak velocity 37.5°/s) showed that the average tilt from Earth-vertical when the head was pitched down 30° was 11.9 ± 4.2°. Solomon et al. (1997) (stimulus: 0.4 Hz, peak velocity 50°/s) showed that for the head pitched up or down 35°, the average tilt was 14.7°. The values from both studies are close to our mean value of 14.5° when the head was pitched down 30°, and 16.1° when the head was pitched up 30°. In these previous studies, the tilt in the axis of eye rotation for different initial pitch head positions was attributed to the difference between the pure torsional and the pure horizontal VOR gains. As the head is increasingly pitched from neutral, the contribution from the torsional VOR increasingly dominates during head rotations about pure Earth-vertical. Because the torsional VOR gain is typically ∼30% less than the horizontal VOR gain, the axis of eye rotation during head rotations about Earth-vertical tilts away from Earth-vertical as the pitch head position increases. This explanation assumes that vectorial summation of the pure torsional and horizontal VOR gains can be used to calculate the axis of eye rotation given the axis of head rotation. Under this assumption, given the horizontal and torsional VOR gains and pitch head position, one can estimate the tilt in the axis of eye rotation as a result of this difference in gains using the following formula:

$${\text{Axis tilt}} {\text{ = }} Q_{{{\text{head}}\,{\text{pitch}}\,{\text{angle}}}} * a{\text{ tan}}{\left[ {{\text{tan}}{\left( {Q_{{{\text{head}}\,{\text{pitch}}\,{\text{angle}}}} } \right)} * {\left( {{{\text{VOR}}_{{{\text{gain}}\,{\text{tor}}}} } \mathord{\left/ {\vphantom {{{\text{VOR}}_{{{\text{gain}}\,{\text{tor}}}} } {{\text{VOR}}_{{{\text{gain}}\,{\text{hor}}}} }}} \right. \kern-\nulldelimiterspace} {{\text{VOR}}_{{{\text{gain}}\,{\text{hor}}}} }} \right)}} \right]}$$
(1)

Because of mechanical limitations in our chair system, we could not obtain the pure torsional VOR for whole-body axis rotation. In four subjects, however, we measured the response to head-only rotations around the pure roll head-axis. The mean torsional VOR gain was 0.76, and the mean horizontal VOR gain was 0.99. The VOR gain ratio was, therefore, 0.78. From Eq. (1), a head pitch angle of 30° up should produce an axis tilt of 5.8°, which is ∼50% of the average axis tilt of 11.1° in these four subjects during head-only impulses when the head was pitched up 30° (11.1° = 0.37 × 30°, 0.37 ± 0.04 is the mean ± SD “axis tilt” divided by “initial pitch head position” in these four subjects; P < 0.05, R 2 = 0.88). Thus, the difference between horizontal and torsional VOR gains can only explain ∼50% of the axis tilt during head-only impulses. A VOR/Listing's law compromise, however, could explain the entire axis tilt.

VOR/Listing's compromise ratio and the magnitude of the stimulus

It has been shown that the axis of eye rotation during the VOR also depends on the magnitude of the stimulus. For example, an angular head rotation with peak-acceleration of ∼10,000°/s2 results in an axis of eye rotation that is closer to the ideal perfectly compensatory VOR response compared to a lower-acceleration stimulus (Palla et al. 1999). Thus, we investigated in our paradigm the possibility that a higher-acceleration rotational stimulus would result in a different axis of eye rotation. Because of mechanical limitations in our chair system, we could not deliver higher-acceleration whole-body impulses. Instead, we delivered manual head-only impulses about an Earth-vertical axis. We found that tilts in the axis of eye rotation were in the same direction as, and by an amount proportional (0.39 ± 0.08) to, the initial pitch head position. This proportionality constant differed, however, from that during the lower peak-acceleration head-and-trunk impulses (0.51 ± 0.09, P < 0.05), and also differed from the axis of eye rotation predicted by a 50–50 VOR/Listing's compromise (P < 0.05). It is unlikely that this difference was attributable to a smaller contribution of the torsional VOR during head-only vs. whole-body rotations. With the head pitched up (we did not use head-only head pitched down data for comparison), it was not always possible to manually rotate the head (-only) about a pure Earth-vertical axis, i.e., in some subjects the axis of head rotation tilted with the head. If the torsional VOR contributed to the axis tilt, then closer alignment between the axis of head rotation and superior–inferior axis of the head during head-only rotations would reduce the axis tilt proportionality constant by only ∼3% (When the axis of head rotation is tilted up from Earth-vertical by an angle equal to 20% of the static head tilt, then the axis of eye rotation tilt due to lesser contribution from the torsional VOR would be ∼3% less.), which is considerably lower than our difference of 24% ((0.51 − 0.39)/0.51 × 100). What might cause this difference in tilt between head-only rotations and whole-body rotations? There could be changes in the signals to the global layer of ocular muscles that actually rotate the globe, or to the orbital layer of ocular muscles that are attached to the orbital pulleys, which can alter the position of the pulleys and in turn the axis of eye rotation. As it has been shown that higher head accelerations alone can alter the axis of eye rotation (Palla et al. 1999), it is likely that the above-mentioned signals change with head-acceleration. Our results are consistent with those of Palla et al. (1999), who reported a decrease in the axis of eye rotation tilt at higher head accelerations. It is unlikely that neck afferents stimulated during head-only (but not whole-body) rotation are providing a signal used by the VOR to alter the tilt angle, because neck afference has been shown to have little influence on the VOR during head-only impulses in normal subjects (Schubert et al. 2004). Another possible explanation for this difference is that the passive properties of the ocular plant are different at different head accelerations such that the axis of eye rotation tilt is less during higher accelerations. This explanation, however, can only explain the difference between head-only and whole-body axis of eye rotation tilt, i.e., the passive properties of the ocular plant alone cannot explain the amount of axis tilt observed during this paradigm.

Implementation of VOR/Listing's compromise

Here we have shown that a VOR/Listing's compromise exists in the initial response of the VOR to high-acceleration head rotations about Earth-vertical with the head in different pitch orientations, even when vertical eye position in the orbit and the orientation of Listing's plane are unchanged. Furthermore, this response cannot be explained by a simple vectorial addition of the different VOR gains during pure yaw and pure roll head rotations, but implies that the central nervous system specifically alters the axis of eye rotation when the head is rotated under these stimulus parameters.

How might the central nervous system alter the VOR axis? Recordings of cyclovertical extra ocular motoneurons in monkeys suggest that these neurons do not carry the appropriate motor drive to generate an axis of eye rotation consistent with a VOR/Listing's compromise (Ghasia and Angelaki 2005); however, the head rotation stimuli used in that study were not high-frequency, high-acceleration impulses. It is also possible that central vestibular mechanisms are activating the orbital muscles attached to the pulleys (Radtke et al. 2003). For example, a signal to the inframedial orbital muscle, a smooth muscle band extending from the inferior rectus to the medial rectus pulleys (Miller et al. 2003), would displace the inferior rectus pulley. If this motion is elastically coupled to the other rectus pulleys through the known connective tissue bands (Kono et al. 2002), then this would alter the position of those rectus pulleys as well (Demer and Clark 2005). Demer and Clark (2005) showed during static ocular counterroll a counterrotational repositioning of the rectus pulley arrays (observed in the coronal plane) of both orbits. The source of the signal affecting the pulley positions is most likely from the otoliths because these detect static head tilt. In our experiment, the static head pitch position is also sensed by the otoliths, which could alter the muscle pulley positions. Thus we can speculate that for rotations around a single Earth-vertical axis, the different axis of eye rotation for each head pitch position (with eye position in the orbit being fixed) is related to a dynamic change in pulley position, and that this forms the basis for the VOR/Listing's law compromise strategy.