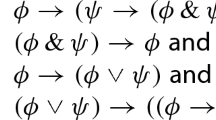1 Introduction

Research in Automated Deduction, also known as Automated Theorem Proving (ATP), has resulted in systems with a remarkable performance. Yet, deep mathematical theorems or otherwise complex statements still withstand any of the systems’ attempts to find a proof. The present paper is motivated by the thesis that the reason for the failure in more complex problems lies in the local orientedness of all our current methods for proof search like resolution or connection calculi in use.

In order to find out more global features for directing proof search we start out here to study the structures of proofs for complex formulas in some detail and compare human proofs with those generated by systems. Complex formulas of this kind have been considered by Łukasiewicz in [19]. They are complex in the sense that current systems require tens of thousands or even millions of search steps for finding a proof if any, although the length of the formulas is very short indeed. How come that Łukasiewicz found proofs for those formulas although he could never carry out more than, say, a few hundred search steps by hand? Which global strategies guided him in finding those proofs? Could we discover such strategies from the formulas’ global features?

By studying the proofs in detail we hope to come closer to answers to those questions. Thus it is proofs, rather than just formulas or clauses as usually in ATP, which is in the focus of our study. In a sense we are aiming at an ATP-oriented part of Proof Theory, a discipline usually pursued in Logic yet under quite different aspects. This meta-level perspective has rarely been taken in ATP for which reason we cannot rely on the existing conceptual basis of ATP but have to build an extensive conceptual basis for such a study more or less from scratch.

This investigation thus analyzes structures of, and operations on, proofs for formulas of the form “axiom(s) and rule(s) imply goal(s)”. It renders condensed detachment, a logical rule historically introduced in the course of studying these complex proofs, as a restricted form of the Connection Method (CM) in ATP. All this is pursued with the goal of enhancing proof search in ATP in mind. As noted, our investigations are guided by a close inspection into proofs by Łukasiewicz and Meredith. In fact, the work presented here amounts at the same time to a very detailed reconstruction of those historical proofs.

The rest of the paper is organized as follows: In Sect. 2 we introduce the problem and a formal human proof that guides our investigations and compare different views on proof structures. We then reconstruct in Sect. 3 the historical method of condensed detachment in a novel way as a restricted variation of the CM where proof structures are represented as terms. This is followed in Sect. 4 by results on reducing the size of such proof terms for application in proof shortening and restricting the proof search space. Section 5 presents a detailed feature table for the investigated human proof, and Sect. 6 shows first experiments where the features and new techniques are used to supplement the inputs of ATP systems with lemmas. Section 7 concludes the paper. Supplementary technical material including proofs is provided in the report [37]. Data and tools to reproduce the experiments are available at http://cs.christophwernhard.com/cd.

2 Relating Formal Human Proofs with ATP Proofs

In 1948 Jan Łukasiewicz published a formal proof of the completeness of his shortest single axiom for the implicational fragment (IF), that is, classical propositional logic with implication as the only logic operator [19]. In his notation the implication \(p \rightarrow q\) is written as \( Cpq \). Following Frank Pfenning [27] we formalize IF on the meta-level in the first-order setting of modern ATP with a single unary predicate \(\mathsf {P}\) to be interpreted as something like “provable” and represent the propositional formulas by terms using the binary function symbol \(\mathsf {i}\) for implication. We will be concerned with the following formulas.

figure a

IF can be axiomatized by the set of the three axioms Simp, Peirce and Syll, known as Tarski-Bernays Axioms. Alfred Tarski in 1925 raised the problem to characterize IF by a single axiom and solved it with very long axioms, which led to a search for the shortest single axiom, which was found with the axiom nicknamed after him in 1936 by Łukasiewicz [19]. In 1948 he published his derivation that Łukasiewicz entails the three Tarski-Bernays Axioms, expressed formally by the method of substitution and detachment. Detachment is also familiar as modus ponens. Łukasiewicz ’s proof involves 34 applications of detachment. Among the Tarski-Bernays axioms Syll is by far the most challenging to prove, hence his proof centers around the proof of Syll, with Peirce and Simp spinning off as side results. Carew A. Meredith presented in [24] a “very slight abridgement” of Łukasiewicz ’s proof, expressed in his framework of condensed detachment [28], where the performed substitutions are no longer explicitly presented but implicitly assumed through unification. Meredith’s proof involves only 33 applications of detachment. In our first-order setting, detachment can be modeled with the following meta-level axiom.

In Det the atom \(\mathsf {P}x\) is called the minor premise, \(\mathsf {P}\mathsf {i}xy\) the major premise, and \(\mathsf {P}y\) the conclusion. Let us now focus on the following particular formula.

“Problem ŁDS ” is then the problem of determining the validity of the first order formula ŁDS. In view of the CM [1,2,3], a formula is valid if there is a spanning and complementary set of connections in it. In Fig. 1 ŁDS is presented again, nicknames dereferenced and quantifiers omitted as usual in ATP, with the five unifiable connections in it. Observe that p, q, r, s on the left side of the main implication are variables, while \(\mathsf {p},\mathsf {q},\mathsf {r}\) on the right side are Skolem constants. Any CM proof of ŁDS consists of a number of instances of the five shown connections. Meredith’s proof, for example, corresponds to 491 instances of Det, each linked with three instances of its five incident connections.

Fig. 1.
figure 1

ŁDS along with its five unifiable connections.

Full size image
Fig. 2.
figure 2

A proof in different representations.

Full size image

Figure 2 compares different representations of a short formal proof with the Det meta axiom. There is a single axiom, Syll Simp, and the theorem is \(\forall pqrstu\, \mathsf {P}\mathsf {i}(p,\mathsf {i}(q,\mathsf {i}(r,\mathsf {i}(s,\mathsf {i}(t,\mathsf {i}us)))))\). Figure 2a shows the structure of a CM proof. It involves seven instances of Det, shown in columns \(D_1, \ldots , D_7\). The major premise \(\mathsf {P}\mathsf {i}x_i y_i\) is displayed there on top of the minor premise \(\mathsf {P}x_i\), and the (negated) conclusion \(\lnot \mathsf {P}y_i\), where \(x_i, y_i\) are variables. Instances of the axiom appear as literals \(\lnot \mathsf {P}a_i\), with \(a_i\) a shorthand for the term \(\mathsf {i}(\mathsf {i}(\mathsf {i}p_i q_i,r_i),\mathsf {i}q_i r_i)\). The rightmost literal \(\mathsf {P}g\) is a shorthand for the Skolemized theorem. The clause instances are linked through edges representing connection instances. The edge labels identify the respective connections as in Fig. 1. An actual connection proof is obtained by supplementing this structure with a substitution under which all pairs of literals related through a connection instance become complementary.

Figure 2b represents the tree implicit in the CM proof. Its inner nodes correspond to the instances of Det, and its leaf nodes to the instances of the axiom. Edges appear ordered to the effect that those originating in a major premise of Det are directed to the left and those from a minor premise to the right. The goal clause \(\mathsf {P}g\) is dropped. The resulting tree is a full binary tree, i.e., a binary tree where each node has 0 or 2 children. We observe that the ordering of the children makes the connection labeling redundant as it directly corresponds to the tree structure.

Figure 2c presents the proof in Meredith’s notation. Each line shows a formula, line 1 the axiom and lines 2–4 derived formulas, with proofs annotated in the last column. Proofs are written as terms in Polish notation with the binary function symbol \(\mathsf {D}\) for detachment where the subproofs of the major and minor premise are supplied as first and second, resp., argument. Formula 4, for example, is obtained as conclusion of Det applied to formula 2 as major premise and as minor premise another formula that is not made explicit in the presentation, namely the conclusion of Det applied to formula 3 as both, major and minor, premises. An asterisk marks the goal theorem.

Fig. 3.
figure 3

Proof MER, Meredith’s refinement [24] of Łukasiewicz ’s proof [19].

Full size image

Figure 2d is like Fig. 2b, but with a different labeling: Node labels now refer to the line in Fig. 2c that corresponds to the subproof rooted at the node. The blank node represents the mentioned subproof of the formula that is not made explicit in Fig. 2b. An inner node represents a condensed detachment step applied to the subproof of the major premise (left child) and minor premise (right child).

Figure 2e shows a DAG (directed acyclic graph) representation of Figure 2d. It is the unique maximally factored DAG representation of the tree, i.e., it has no multiple occurrences of the same subtree. Each of the four proof line labels of Fig. 2c appears exactly once in the DAG.

We conclude this introductory section with reproducing Meredith’s refinement of Łukasiewicz ’s completeness proof in Fig. 3, taken from [24]. Since we will often refer to this proof, we call it MER. There is a single axiom (1), which is Łukasiewicz. The proven theorems are Syll (17), Peirce (18) and Simp (19). In addition to line numbers also the symbol \(\mathrm {n}\) appears in some of the proof terms. Its meaning will be explained later on in the context of Def. 19. For now, we can read \(\mathrm {n}\) just as “1”. Dots are used in the Polish notation to disambiguate numeric identifiers with more than a single digit.

3 Condensed Detachment and a Formal Basis

Following [4], the idea of condensed detachment can be described as follows: Given premises \(F \rightarrow G\) and H, we can conclude \(G'\), where \(G'\) is the most general result that can be obtained by using a substitution instance \(H'\) as minor premise with the substitution instance \(F' \rightarrow G'\) as major premise in modus ponens. Condensed detachment was introduced by Meredith in the mid-1950s as an evolution of the earlier method of substitution and detachment, where the involved substitutions were explicitly given. The original presentations of condensed detachment are informal by means of examples [17, 25, 28, 29], formal specifications have been given later [4, 13, 16]. In ATP, the rendering of condensed detachment by hyperresolution with the clausal form of axiom Det is so far the prevalent view. As overviewed in [23, 31], many of the early successes of ATP were based on condensed detachment. Starting from the hyperresolution view, structural aspects of condensed detachment have been considered by Robert Veroff [34] with the use of term representations of proofs and linked resolution. Results of ATP systems on deriving the Tarski-Bernays axioms from Łukasiewicz are reported in [11, 22, 23, 27, 39]. Our goal in this section is to provide a formal framework that makes the achievements of condensed detachment accessible from a modern ATP view. In particular, the incorporation of unification, the interplay of nested structures with explicitly and implicitly associated formulas, sharing of structures through lemmas, and the availability of proof structures as terms.

Our notation follows common practice [6] (e.g., expresses that t subsumes s, and \(s \mathrel {\unrhd }t\) that t is a subterm of s) with some additions [37]. For formulas F we write the universal closure as \(\forall F\), and for terms s, t, u we use \(s{[}t \mapsto u{]}\) to denote s after simultaneously replacing all occurrences of t with u.

3.1 Proof Structures: D-Terms, Tree Size and Compacted Size

In this section we consider only the purely structural aspects of condensed detachment proofs. Emphasis is on a twofold view on the proof structure, as a tree and as a DAG (directed acyclic graph), which factorizes multiple occurrences of the same subtree. Both representation forms are useful: the compacted DAG form captures that lemmas can be repeatedly used in a proof, whereas the tree form facilitates to specify properties in an inductive manner. We call the tree representation of proofs by terms with the binary function symbol \(\mathsf {D}\) D-terms.

Definition 1

(i) We assume a distinguished set of symbols called primitive D-terms. (ii) A D-term is inductively specified as follows: (1.) Any primitive D-term is a D-term. (2.) If \(d_1\) and \(d_2\) are D-terms, then \(\mathsf {D}(d_1,d_2)\) is a D-term. (iii) The set of primitive D-terms occurring in a D-term  d is denoted by \( \mathcal {P}rim (d)\). (iv) The set of all D-terms that are not primitive is denoted by \(\mathcal {D}\).

A D-term is a full binary tree (i.e, a binary tree in which every node has either 0 or 2 children), where the leaves are labeled with symbols, i.e., primitive D-terms. An example D-term is

(i)

which represents the structure of the proof shown in Fig. 2 and can be visualized by the full binary tree of Fig. 2d after removing all labels with exception of the leaf labels. The proof annotations in Fig. 2c and Fig. 3 are D-terms written in Polish notation. The expression \(\mathsf {D}2\mathsf {D}33\) in line 4 of Fig. 2, for example, stands for the D-term \(\mathsf {D}(2,\mathsf {D}(3,3))\). \( \mathcal {P}rim (\mathsf {D}(2,\mathsf {D}(3,3))) = \{2,3\}\).

A finite tree and, more generally, a finite set of finite trees can be represented as DAG, where each node in the DAG corresponds to a subtree of a tree in the given set. It is well known that there is a unique minimal such DAG, which is maximally factored (it has no multiple occurrences of the same subtree) or, equivalently, is minimal with respect to the number of nodes, and, moreover, can be computed in linear time [7]. The number of nodes of the minimal DAG is the number of distinct subtrees of the members of the set of trees. There are two useful notions of measuring the size of a D-term, based directly on its tree representation and based on its minimal DAG, respectively.

Definition 2

(i) The tree size of a D-term d, in symbols \(\mathsf {t-size}(d)\), is the number of occurrences of the function symbol \(\mathsf {D}\) in d. (ii) The compacted size of a D-term d is defined as (iii) The compacted size of a finite set D of D-terms is defined as

The tree size of a D-term can equivalently be characterized as the number of its inner nodes. The compacted size of a D-term is the number of its distinct compound subterms. It can equivalently be characterized as the number of the inner nodes of its minimal DAG. As an example consider the D-term d defined in formula (i), whose minimal DAG is shown in Fig. 2e. The tree size of d is \(\mathsf {t-size}(d) = 7\) and the compacted size of d is \(\mathsf {c-size}(d) = 4\), corresponding to the cardinality of the set \(\{e \in \mathcal {D}\mid d \mathrel {\unrhd }e \}\) of compound subterms of d, i.e., \(\{\mathsf {D}(1,1),\; \mathsf {D}(1,\mathsf {D}(1,1)),\; \mathsf {D}(\mathsf {D}(1,\mathsf {D}(1,1)),\mathsf {D}(1,\mathsf {D}(1,1))),\; d\}.\)

As will be explicated in more detail below, each occurrence of the function symbol \(\mathsf {D}\) in a D-term corresponds to an instance of the meta-level axiom \(\text {\textit{Det}} \) in the represented proof. Hence the tree size measures the number of instances of \(\text {\textit{Det}} \) in the proof. Another view is that each occurrence of \(\mathsf {D}\) in a D-term corresponds to a condensed detachment step, without re-using already proven lemmas. The compacted size of a D-term is the number of its distinct compound subterms, corresponding to the view that the size of the proof of a lemma is only counted once, even if it is used multiply. Tree size and compacted size of D-terms appear in [34] as CDcount and length, respectively.

3.2 Proof Structures, Formula Substitutions and Semantics

We use a notion of unifier that applies to a set of pairs of terms, as convenient in discussions based on the CM [1, 8, 9].

Definition 3

Let M be a set of pairs of terms and let \(\sigma \) be a substitution. (i) \(\sigma \) is said to be a unifier of M if for all \(\{s,t\} \in M\) it holds that \(s\sigma = t\sigma \). (ii) \(\sigma \) is called a most general unifier of M if \(\sigma \) is a unifier of M and for all unifiers \(\sigma '\) of M it holds that . (iii) \(\sigma \) is called a clean most general unifier of M if it is a most general unifier of M and, in addition, is idempotent and satisfies \( \mathcal {D}om (\sigma ) \cup \mathcal {VR}ng (\sigma ) \subseteq \mathcal {V}ar (M)\).

The additional properties required for clean most general unifiers do not hold for all most general unifiers.Footnote 1 However, the unification algorithms known from the literature produce clean most general unifiers [9, Remark 4.2]. If a set of pairs of terms has a unifier, then it has a most general unifier and, moreover, also a clean most general unifier.

Definition 4

(i) If M is a set of pairs of terms that has a unifier, then \(\mathsf {mgu}(M)\) denotes some clean most general unifier of M. M is called unifiable and \(\mathsf {mgu}(M)\) is called defined in this case, otherwise it is called undefined. (ii) We make the convention that proposition, lemma and theorem statements implicitly assert their claims only for the case where occurrences of \(\mathsf {mgu}\) in them are defined.

Since we define \(\mathsf {mgu}(M)\) as a clean most general unifier, we are permitted to make use of the assumption that it is idempotent and that all variables occurring in its domain and range occur in M. Convention 4.ii has the purpose to reduce clutter in proposition, lemma and theorem statements.

The structural aspects of condensed detachment proofs represented by D-terms, i.e., full binary trees, will now be supplemented with associated formulas. Condensed detachment proofs, similar to CM proofs, involve different instances of the input formulas (viewed as quantifier-free, e.g., clauses), which may be considered as obtained in two steps: first, “copies”, that is, variants with fresh variables, of the input formulas are created; second a substitution is applied to these copies. Let us consider now the first step. The framework of D-terms permits to give the variables in the copies canonical designators with an index subscript that identifies the position in the structure, i.e., in the D-term, or tree.

Definition 5

For all positions p and positive integers i let \(x^{i}_{p}\) and \(y_p\) denote pairwise different variables.

Recall that positions are path specifiers. For a given D-term  d and leaf position p of d the variables \(x^{i}_{p}\) are for use in a formula associated with p which is the copy of an axiom. Different variables in the copy are distinguished by the upper index i. If p is a non-leaf position of d, then \(y_p\) denotes the variable in the conclusion of the copy of \({\textit{Det}} \) that is represented by p. In addition, \(y_p\) for leaf positions p may occur in the antecedents of the copies of \({\textit{Det}} \). The following substitution \(\mathsf {shift}_{p}\) is a tool to systematically rename position-associated variables while preserving the internal relationships between the index-referenced positions.

Definition 6

For all positions p define the substitution \(\mathsf {shift}_{p}\) as follows: .

The application of \(\mathsf {shift}_{p}\) to a term s effects that p is prepended to the position indexes of all the position-associated variables occurring in s. The association of axioms with primitive D-terms is represented by mappings which we call axiom assignments, defined as follows.

Definition 7

An axiom assignment \(\alpha \) is a mapping whose domain is a set of primitive D-terms and whose range is a set of terms whose variables are in \(\{x^{i}_{\epsilon } \mid i \ge 1\}\). We say that \(\alpha \) is for a D-term  d if \( \mathcal {D}om (\alpha ) \supseteq \mathcal {P}rim (d)\).

We define a shorthand for a form of Łukasiewicz that is suitable for use as a range element of axiom assignments. It is parameterized with a position p.

(ii)

The mapping is an axiom assignment for all D-terms  d with \( \mathcal {P}rim (d) = \{1\}\). The second step of obtaining the instances involved in a proof can be performed by applying the most general unifier of a pair of terms that constrain it. The tree structure of D-terms permits to associate exactly one such pair with each term position. Inner positions represent detachment steps and leaf positions instances of an axiom according to a given axiom assignment. The following definition specifies these constraining pairs.

Definition 8

Let d be a D-term and let \(\alpha \) be an axiom assignment for d. For all positions \(p \in \mathcal {P}\!os (d)\) define the pair of terms and \(\{y_{p.1},\, \mathsf {i}(y_{p.2}, y_p)\} \text { if } p \in \mathcal {I}nner\mathcal {P}\!os (d)\).

A unifier of the set of pairings of all positions of a D-term  d equates for a leaf position p the variable \(y_p\) with the value of the axiom assignment \(\alpha \) for the primitive D-term at p, after “shifting” variables by p. This “shifting” means that the position subscript \(\epsilon \) of the variables in the axiom argument term \(\alpha (d|_p)\) is replaced by p, yielding a dedicated copy of the axiom argument term for the leaf position p. For inner positions p the unifier equates \(y_{p.1}\) and \(\mathsf {i}(y_{p.2}, y_p)\), reflecting that the major premise of Det is proven by the left child of p.

The substitution induced by the pairings associated with the positions of a D-term allow to associate a specific formula with each position of the D-term, called the in-place theorem (IPT). The case where the position is the top position \(\epsilon \) is distinguished as most general theorem (MGT).

Definition 9

For D-terms  d, positions \(p \in \mathcal {P}\!os (d)\) and axiom assignments \(\alpha \) for d define the in-place theorem (IPT) of d at p for \(\alpha \), \( Ipt _{\alpha }(d,p)\), and the most general theorem (MGT) of d for \(\alpha \), \( Mgt _{\alpha }(d)\), as (i)  \(\mathsf {P}(y_{p}\mathsf {mgu}(\{\mathsf {pairing}_{\alpha }(d, q) \mid q \in \mathcal {P}\!os (d)\})).\) (ii) .

Since \( Ipt \) and \( Mgt \) are defined on the basis of \(\mathsf {mgu}\), they are undefined if the set of pairs of terms underlying the respective application of \(\mathsf {mgu}\) is not unifiable. Hence, we apply the convention of Def. 4.ii for \(\mathsf {mgu}\) also to occurrences of \( Ipt \) and \( Mgt \). If \( Ipt \) and \( Mgt \) are defined, they both denote an atom whose variables are constrained by the clean property of the underlying application of \(\mathsf {mgu}\). The following proposition relates IPT and MGT with respect to subsumption.

Proposition 10

For all D-terms  d, positions \(p \in \mathcal {P}\!os (d)\) and axiom assignments \(\alpha \) for d it holds that

By Prop. 10, the IPT at some position p of a D-term  d is subsumed by the MGT of the subterm \(d|_p\) of d rooted at position p. An intuitive argument is that the only constraints that determine the most general unifier underlying the MGT are induced by positions of \(d|_p\), that is, below p (including p itself). In contrast, the most general unifier underlying the IPT is determined by all positions of d.

The following lemma expresses the core relationships between a proof structure (a D-term), a proof substitution (accessed via the IPT) and semantic entailment of associated formulas.

Lemma 11

Let d be a D-term and let \(\alpha \) be an axiom assignment for d. Then for all \(p \in \mathcal {P}\!os (d)\) it holds that: (i) If \(p \in \mathcal {L}eaf\mathcal {P}\!os (d)\), then (ii) If \(p \in \mathcal {I}nner\mathcal {P}\!os (d)\), then

Based on this lemma, the following theorem shows how Detachment together with the axioms in an axiom assignment entail the MGT of a given D-term.

Theorem 12

Let d be a D-term and let \(\alpha \) be an axiom assignment for d. Then

Theorem 12 states that Det together with the axioms referenced in the proof, that is, the values of \(\alpha \) for the leaf nodes of d considered as universally closed atoms, entail the universal closure of the MGT of d for \(\alpha \). The universal closure of the MGT is the formula exhibited in Meredith’s proof notation in the lines with a trailing D-term, such as lines 2–19 in Fig. 3.

4 Reducing the Proof Size by Replacing Subproofs

The term view on proof trees suggests to shorten proofs by rewriting subterms, that is, replacing occurrences of subproofs by other ones, with three main aims: (1) To shorten given proofs, with respect to the tree size or the compacted size. (2) To investigate given proofs whether they can be shortened by certain rewritings or are closed under these. (3) To develop notions of redundancy for use in proof search. A proof fragment constructed during search may be rejected if it can be rewritten to a shorter one.

It is obvious that if a D-term  \(d'\) is obtained from a D-term  d by replacing an occurrence of a subterm e with a D-term \(e'\) such that \(\mathsf {t-size}(e) \ge \mathsf {t-size}(e')\), then also \(\mathsf {t-size}(d) \ge \mathsf {t-size}(d')\). Based on the following ordering relations on D-terms, which we call compaction orderings, an analogy for reducing the compacted size instead of the tree size can be stated.

Definition 13

For D-terms d, e define (i)  (ii) 

The relations \(d \mathrel {\ge _{\mathrm {c}}}e\) and \(d \mathrel {>_{\mathrm {c}}}e\) compare D-terms  d and e with respect to the superset relationship of their sets of those strict subterms that are compound terms. For example, \(\mathsf {D}(\mathsf {D}(\mathsf {D}(1,1),1),1) \mathrel {>_{\mathrm {c}}}\mathsf {D}(1,\mathsf {D}(1,1))\) because \(\{\mathsf {D}(1,1),\, \mathsf {D}(\mathsf {D}(1,1),1)\} \supseteq \{\mathsf {D}(1,1)\}\).

Theorem 14

Let \(d,d',e,e'\) be D-terms such that e occurs in d, and \(d' = d{[}e \mapsto e'{]}\). It holds that (i) If \(e \in \mathcal {D}\) and \(e \mathrel {\ge _{\mathrm {c}}}e'\), then \(\mathsf {c-size}(d) \ge \mathsf {c-size}(d')\). (ii) If \(e \mathrel {>_{\mathrm {c}}}e'\), then \(\mathsf {sc-size}(d) > \mathsf {sc-size}(d')\), where, for all D-terms  d .

Theorem 14.i states that if \(d'\) is the D-term obtained from d by simultaneously replacing all occurrences of a compound D-term  e with a “c-smaller” D-term  \(e'\), i.e., \(e \mathrel {\ge _{\mathrm {c}}}e'\), then the compacted size of \(d'\) is less or equal to that of d. As stated with the supplementary Theorem 14.ii, the \(\mathsf {sc-size}\) is a measure that strictly decreases under the strict precondition \(e \mathrel {>_{\mathrm {c}}}e'\), which is useful to ensure termination of rewriting. The following proposition characterizes the number of D-terms that are smaller than a given D-term w.r.t the compaction ordering \(\mathrel {\ge _{\mathrm {c}}}\).

Proposition 15

For all D-terms d it holds that \(|\{e \mid d \mathrel {\ge _{\mathrm {c}}}e \text { and } \mathcal {P}rim (e) \subseteq \mathcal {P}rim (d)\}| = (\mathsf {c-size}(d) - 1 + | \mathcal {P}rim (d)|)^2 + | \mathcal {P}rim (d)|.\)

By Prop. 15, for a given D-term  d, the number of D-terms  e that are smaller than d with respect to \(\mathrel {\ge _{\mathrm {c}}}\) is only quadratically larger than the compacted size of d and thus also than the tree size of d. Hence techniques that inspect all these smaller D-terms for a given D-term can efficiently be used in practice.

According to Theorem 12, a condensed detachment proof, i.e., a D-term  d and an axiom assignment \(\alpha \), proves the MGT of d for \(\alpha \) along with instances of the MGT. In general, replacing subterms of d should yield a proof of at least these theorems. That is, a proof whose MGT subsumes the original one. The following theorem expresses conditions which ensure that subterm replacements yield a proof with a MGT that subsumes original one.

Theorem 16

Let d, e be D-terms, let \(\alpha \) be an axiom assignment for d and for e, and let \(p_1, \ldots , p_n\), where \(n \ge 0\), be positions in \( \mathcal {P}\!os (d)\) such that for all \(i,j \in \{1,\ldots ,n\}\) with \(i \ne j\) it holds that \(p_i \not \le p_j\). If for all \(i \in \{1, \ldots , n\}\) it holds that , then .

Theorem 16 states that simultaneously replacing a number of occurrences of possibly different subterms in a D-term by the same subterm with the property that its MGT subsumes each of the IPTs of the original occurrences results in an overall D-term whose MGT subsumes that of the original overall D-term. The following theorem is similar, but restricted to a single replaced occurrence and with a stronger precondition. It follows from Theorem 16 and Prop. 10.

Theorem 17

Let d, e be D-terms and let \(\alpha \) be an axiom assignment for d and for e. For all positions \(p \in \mathcal {P}\!os (d)\) it then holds that if , then .

Simultaneous replacements of subterm occurrences are essential for reducing the compacted size of proofs according to Theorem 14. For replacements according to Theorem 17 they can be achieved by successive replacements of individual occurrences. In Theorem 16 simultaneous replacements are explicitly considered because the replacement of one occurrence according to this theorem can invalidate the preconditions for another occurrence. Theorem 17 can be useful in practice because the precondition can be evaluated on the basis of \(\alpha \), e and just the subterm \(d|_p\) of d, whereas determining \( Ipt _{\alpha }(d,p)\) for Theorem 16 requires also consideration of the context of p in d. Based on Theorems 16 and 14 we define the following notions of reduction and regularity.

Definition 18

Let d be a D-term, let e be a subterm of d and let \(\alpha \) be an axiom assignment for d. For D-terms \(e'\) the D-term \(d{[}e \mapsto e'{]}\) is then obtained by C-reduction from d for \(\alpha \) if \(e \mathrel {>_{\mathrm {c}}}e'\), \( Mgt _{\alpha }(e')\) is defined, and for all positions \(p \in \mathcal {P}\!os (d)\) such that \(d|_p = e\) it holds that . The D-term  d is called C-reducible for \(\alpha \) if and only if there exists a D-term  \(e'\) such that \(d{[}e \mapsto e'{]}\) is obtained by C-reduction from d for \(\alpha \). Otherwise, d is called C-regular.

If \(d'\) is obtained from d by C-reduction, then by Theorem 16 and 14 it follows that , \(\mathsf {c-size}(d) \ge \mathsf {c-size}(d')\) and \(\mathsf {sc-size}(d) > \mathsf {sc-size}(d')\). C-regularity differs from well known concepts of regularity in clausal tableaux (see, e.g., [14]) in two respects: (1) In the comparison of two nodes on a branch (which is done by subsumption as in tableaux with universal variables) for the upper node the stronger instantiated IPT is taken and for the lower node the more weakly instantiated MGT. (2) C-regularity is not based on relating two nested subproofs, but on comparison of all occurrences of a subproof with respect to all proofs that are smaller with respect to the compaction ordering.

Proofs may involve applications of Det where the conclusion \(\mathsf {P}y\) is actually independent from the minor premise \(\mathsf {P}x\). Any axiom can then serve as a trivial minor premise. Meredith expresses this with the symbol \(\mathrm {n}\) as second argument of the respective D-term. Our function \(\mathsf {simp-n}\) simplifies D-terms by replacing subterms with \(\mathrm {n}\) accordingly on the basis of the preservation of the MGT.

Definition 19

If d is a D-term and \(\alpha \) is an axiom assignment for d, then the n-simplification of d with respect to \(\alpha \) is the D-term \(\mathsf {simp-n}_{\alpha }(d)\), where \(\mathsf {simp-n}\) is the following function: ; if \( Mgt _{\alpha '}\mathsf {D}(d_1,\mathrm {n}) = Mgt _{\alpha }\mathsf {D}(d_1,d_2)\), where \(\alpha ' = {\alpha \cup \{\mathrm {n}\mapsto \mathsf {k}\}}\) for a fresh constant \(\mathsf {k}\); \(\mathsf {D}(\mathsf {simp-n}_{\alpha }(d_1),\mathsf {simp-n}_{\alpha }(d_2))\), else.

5 Properties of Meredith’s Refined Proof

Our framework renders condensed detachment as a restricted form of the CM. This view permits to consider the expanded proof structures as binary trees or D-terms. On this basis we obtain a natural characterization of proof properties in various categories, which seem to be the key towards reducing the search space in ATP. Table 1 shows such properties for each of the 34 structurally different subproofs of proof MER (Fig. 3). Column M gives the number of the subproof in Fig. 3. We use the following short identifiers for the

Table 1. Properties of all subproofs of the proof MER [24] shown in Fig. 3.
Full size table

Structural Properties of the D-terms. These properties refer to the respective subproof as D-term or full binary tree. DT, DC, DH: Tree size, compacted size, height. DK\(_L\), DK\(_R\): “Successive height”, that is, the maximal number of successive edges going to the left (right, resp.) on any path from the root to a leaf. DP: Is “prime”, that is, DT and DC are equal. DS: Relationship between the subproofs of major and minor premise. Identity is expressed with \(=\), the subterm and superterm relationships with \(\lhd \) and \(\rhd \), resp., and the compaction ordering relationship (if none of the other relationships holds) with and . In addition it is indicated if a subproof is an axiom or \(\mathrm {n}\). DD: “Direct sharings”, that is, the number of incoming edges in the DAG representation of the overall proof of all theorems. DR: “Repeats”, that is, the total number of occurrences in the set of expanded trees of all roots of the DAG.

Properties of the MGT. These properties refer to the argument term of the MGT of the respective subproof. TT, TH: Tree size (defined as for D-terms) and height. TV: Number of different variables occurring in the term. TO: Is “organic” [21], that is, the argument term has no strict subterm s such that \(\mathsf {P}(s)\) itself is a theorem. We call an atom weakly organic (indicated by a gray bullet) if it is not organic and the argument term is of the form \(\mathsf {i}(p,t)\) where p is a variable that does not occur in the term t and \(\mathsf {P}(t)\) is organic. For axiomatizations of fragments of propositional logic, organic can be checked by a SAT solver.

Regularity. RC: The respective subproof as D-term is C-regular (see Def. 18).

Comparisons with all Proofs of the MGT. These properties relate to the set of all proofs (as D-terms) of the MGT of the respective subproof. MT, MC: Minimal tree size and minimal compacted size of a proof. These values can be hard to determine such that in Table 1 they are often only narrowed down by an integer interval. To determine them, we used the proof MER, proofs obtained with techniques described in Sect. 6, and enumerations of all D-terms with defined MGT up to a given tree size or compacted size.

Properties of Occurrences of the IPTs. The respective subproof has DR occurrences in the set of expanded trees of the roots of the DAG, where each occurrence has an IPT. The following properties refer to the multiset of argument terms of the IPTs of these occurrences. IT\(_U\), IT\(_M\): Maximal tree size and rounded median of the tree size. IH\(_U\), IH\(_M\): Maximal height and rounded median of the height. In Table 1 these values are much larger than those of the corresponding columns for the MGT, i.e, TT and TH, illustrating Prop. 10.

6 First Experiments

First experiments based on the framework developed in the previous sections are centered around the generation of lemmas where not just formulas but, in the form of D-terms, also proofs are taken into account. This leads in general to preference of small proofs and to narrowing down the search space by restricted structuring principles to build proofs. The experiments indicate novel potential calculi which combine aspects from lemma-based generative, bottom-up, methods such as hyperresolution and hypertableaux with structure-based approaches that are typically used in an analytic, goal-directed, way such as the CM. In addition, ways to generate lemmas as preprocessing for theorem proving are suggested, in particular to obtain short proofs. This resulted in a refinement of Łukasiewicz ’s proof [19], whose compacted size is by one smaller than that of Meredith’s refinement [24] and by two than Łukasiewicz ’s original proof.

Table 2. Proof dimensions of various proofs of problem ŁDS.
Full size table

Table 2 shows compacted size DC, tree size DT and height DH of various proofs of ŁDS. Asterisks indicate that n-simplification was applied with reducing effect on the system’s proof. Proof (1.) is the one by Łukasiewicz [19], translated into condensed detachment, proof (2.) is proof MER (Fig. 3) [24]. Rows (3.)–(5.) show results from Prover9, where in (5.) the value of max_depth was limited to 7, motivated by column TH of Table 1. Proof (4.) illustrates the effect of n-simplification.Footnote 2 For proofs (6.)–(9.) additional axioms were supplied to Prover9 and CMProver [5, 35, 36], a goal-directed system that can be described by the CM. Columns indicate the lemma computation method, the number of lemmas supplied to the prover and the time used for lemma computation. Method PrimeCore adds the MGTs of subproof 18 from Table 1 and all its subproofs as lemmas. Subproof 18 is the largest subproof of proof MER that is prime and can be characterized on the basis of the axiom – almost uniquely – as a proof that is prime, whose MGT has no smaller prime proof and has the same number of different variables as the axiom, i.e., 4, and whose size, given as parameter, is 17. Method ProofSubproof is based on detachment steps with a D-term and a subterm of it as proofs of the premises, which, as column DS of Table 1 shows, suffices to justify all except of two proof steps in MER. It proceeds in some analogy to the given clause algorithm on lists of D-terms: If d is the given D-term, then the inferred D-terms are all D-terms that have a defined MGT and are of the form \(\mathsf {D}(d,e)\) or \(\mathsf {D}(e,d)\), where e is a subterm of d. To determine which of the inferred D-terms are kept, values from Table 1 were taken as guide, including RC and TO. The first parameter of ProofSubproof is the number of iterations of the “given D-term loop”. Proof (9.) can be combined with Peirce and Syll to the overall proof with compacted size 32, one less than MER. The maximal value of DK\(_L\) is shown as second parameter, because, when limited to 7, proof (9.) cannot be found. Proof (10.), which has a small tree size, was obtained from (8.) by rewriting subproofs with a variation of C-reduction that rewrites single term occurrences, considering also D-terms from a precomputed table of small proofs.

7 Conclusion

Starting out from investigating Łukasiewicz ’s classic formal proof [19], via its refinement by Meredith [24] we arrived at a formal reconstruction of Meredith’s condensed detachment as a special case of the CM. The resulting formalism yields proofs as objects of a very simple and common structure: full binary trees which, in the tradition of term rewriting, appear as terms, D-terms, as we call them. To form a full proof, formulas are associated with the nodes of D-terms: axioms with the leaves and lemmas with the remaining nodes, implicitly determined from the axioms through the node position and unification. The root lemma is the most general proven theorem. Lemmas also relate to compressed representations of the binary trees, for example as DAGs, where the re-use of a lemma directly corresponds to sharing the structure of its subproof. For future work we intend to position our approach also in the context of earlier works on proofs, proof compression and lemma introduction, e.g., [12, 38], and think of compressing D-Terms in forms that are stronger than DAGs, e.g., by tree grammars [18].

The combination of formulas and explicitly available proof structures naturally leads to theorem proving methods that take structural aspects into account, in various ways, as demonstrated by our first experiments. This goes beyond the common clausal tableau realizations of the CM, which in essence operate by enumerating uncompressed proof structures. The discussed notions of regularity and lemma generation methods seem immediately suited for further investigations in the context of first-order theorem proving in general. For other aspects of the work we plan a stepwise generalization by considering further single axioms for the implicational fragment IF [19, 21, 32], single axioms and axiom pairs for further logics [32], the about 200 condensed detachment problems in the LCL domain of the TPTP, problems which involve multiple non-unit clauses, and adapting D-terms to a variation of binary resolution instead of detachment. In the longer run, our approach aims at providing a basis for approaches to theorem proving with machine learning (e.g. [10, 15]). With the reification of proof structures more information is available as starting point. As indicated with our exemplary feature table for Meredith’s proof, structural properties are considered thereby from a global point of view, as a source for narrowing down the search space in many different ways in contrast to just the common local view “from within a structure”, where the narrowing down is achieved for example by focusing on a “current branch” during the construction of a tableau. A general lead question opened up by our setting is that for exploring relationships between properties of proof structures and the associated formulas in proofs of meaningful theorems. One may expect that characterizations of these relationships can substantially restrict the search space for finding proofs.