Abstract
We report on the implementation of ultracold atoms as a source in a state of the art atom gravimeter. We perform gravity measurements with 10 nm s−2 statistical uncertainties in a so-far largely unexplored temperature range for such a high accuracy sensor, down to 50 nK. This allows for an improved characterization of the most limiting systematic effect, related to wavefront aberrations of light beamsplitters. A thorough model of the impact of this effect onto the measurement is developed and a method is proposed to correct for this bias based on the extrapolation of the measurements down to zero temperature. Finally, an uncertainty of 13 nm s−2 is obtained in the evaluation of this systematic effect, which can be improved further by performing measurements at even lower temperatures. Our results clearly demonstrate the benefit brought by ultracold atoms to the metrological study of free falling atom interferometers. By tackling their main limitation, the method presented here allows reaching record-breaking accuracies for inertial sensors based on atom interferometry.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Atom gravimeters constitute today the most mature application of cold atom inertial sensors based on atom interferometry. They reach performances better than their classical counterparts, the free fall corner cube gravimeters, both in terms of short term sensitivity [1, 2] and long term stability [3]. They offer the possibility to perform high repetition rate continuous measurements over extended periods of time [3, 4], which represents an operation mode inaccessible to other absolute gravimeters that suffer from mechanical wear. These features have motivated the development of commercial cold atom gravimeters [5], addressing in particular applications in the fields of geophysics. Nevertheless, the accuracy of these sensors, though comparable, is today slightly worse. Best accuracies in the 30–40 nm s−2 range have been reported [3, 4] and validated through the participation of these instruments to international comparisons of absolute gravimeters since 2009 [6, 7], to be compared with the claimed accuracy of the best commercial state of the art corner cube gravimeters, of order of 20 nm s−2 [8].
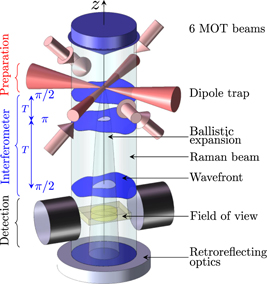
The dominant limit in the accuracy of cold atom gravimeters is due to the wavefront distortions of the lasers beamsplitters. This effect is related to the ballistic expansion of the atomic source through its motion in the beamsplitter laser beams, as illustrated in figure 1, and cancels out at zero atomic temperature. In practice, it has been tuned by increasing the atomic temperature [4] and/or by using truncation methods, such as varying the size of the detection area [9] or of the Raman laser beam [10]. Comparing these measurements with measured or modelled wavefronts allows to gain insight on the amplitude of the effect, and estimate the uncertainty on its evaluation. This effect can be reduced by improving the optical quality of the optical elements of the interferometer lasers, or by operating the interferometer in a cavity [11], in order to filter the spatial mode of the lasers, and/or by compensating the wavefront distortions, using for instance a deformable mirror [12].
Figure 1. Scheme of the experimental setup, illustrating the effect of wavefront aberrations. Due to their ballistic expansion across the Raman beam, the atoms sample different parasitic phase shifts at the three π/2 − π − π/2 Raman pulses due to wavefront distortions (displayed in blue as a distorted surface). This leads to a bias in the gravity measurement, resulting from the average of the effect over all atomic trajectories, filtered by finite size effects, such as related to the waist and clear aperture of the Raman beam and to the finite field of view at the detection.
Download figure:
Standard image High-resolution imageSuch wavefront distortions may also lead to significant intensity inhomogeneities, which in principle evolve along the laser propagation. These lead to coupling and light shift inhomogeneities, which are source of interferometer contrast reduction and systematics. In the case of beamsplitters based on Bragg transitions, intensity inhomogeneities lead to even larger parasitic interferometer phase shifts. The impact of these diffraction phases and strategies for their mitigation have been studied in detail, for example in [13–15]. More, for noisy wavefronts with short scale phase fluctuations, such as due to the use of poor quality optics, local correlations building up in the laser beam during its propagation between intensity and phase fluctuations may lead to a bias in the phase of atom interferometers, as shown recently in [16]. Nevertheless, the effect calculated in [16] is negligible for our interferometer parameters, especially considering our use of high quality optics.
In this paper, we consider the opposite case of long-scale phase fluctuations, assuming an ideal Gaussian intensity profile, free from intensity noise, a situation which is more relevant to our instrument. The strategy we pursue here to evaluate the impact of these wavefront aberrations consists in reducing the atomic temperature below the limits imposed by laser cooling in optical molasses or, even lower, in Raman sideband cooling [17], in order to study the temperature dependence of the wavefront aberration bias over a wider temperature range, and down to the lowest possible temperature. For that, we use ultracold atoms produced by evaporative cooling as the atomic source in our interferometer.
Such sources, eventually Bose–Einstein condensed, show high brightness and reduced spatial and velocity spread. These features allow for the improvement of the contrast of the interferometer [18], a drastic increase in the interaction time, on the ground [19] or in space [20], for the efficient implementation of large momentum transfer beamsplitters [21–23], and for the development of new detection methods [24]. The potential gain in sensitivity has been largely demonstrated (for instance, by up to two orders of magnitude in [19] for acceleration measurements). But it is only recently that a gain was demonstrated in the measurement sensitivity of an actual inertial quantity, in a differential interferometer configuration [25], when compared to state of the art sensors based on the more traditional approach exploiting two-photon Raman transitions and laser cooled atoms.
Here, implementing such a source in a state of the art absolute gravimeter, we demonstrate that ultracold atom sources also improve the accuracy of atom interferometers, by providing an ideal tool for the precise study of their most limiting systematic effect, related to the transverse motion of the atoms across the interferometer laser wavefronts.
2. Gravity measurements
2.1. The experimental setup
We briefly detail here the main features of our cold atom gravimeter. A more detailed description can be found in [4]. It is based on an atom interferometer [26] based on two-photon Raman transitions, performed on free-falling 87Rb atoms. A measurement sequence is as follows. We start by collecting in an ultra high vacuum chamber a sample of cold or ultracold atoms, which is then released in free fall for about 200 ms. After a preparation phase, which combines microwave and Raman pulses for selecting the atoms, in their  magnetic state and in a narrow (vertical) velocity distribution, a sequence of three Raman pulses drives a Mach Zehnder type interferometer. These three pulses, separated by free evolution times of duration T = 80 ms, respectively split, redirect and recombine the matter waves, creating a two-wave interferometer. The total duration of the interferometer is thus 2T = 160 ms. The populations in the two interferometer output ports N1 and N2 are finally measured at the bottom of the chamber by a state selective fluorescence detection method, and the transition probability P is calculated out of these populations (P = N1/(N1 + N2)). This transition probability depends on the phase difference accumulated by the matter waves along the two arms of the interferometer that is, in our geometry, given by
magnetic state and in a narrow (vertical) velocity distribution, a sequence of three Raman pulses drives a Mach Zehnder type interferometer. These three pulses, separated by free evolution times of duration T = 80 ms, respectively split, redirect and recombine the matter waves, creating a two-wave interferometer. The total duration of the interferometer is thus 2T = 160 ms. The populations in the two interferometer output ports N1 and N2 are finally measured at the bottom of the chamber by a state selective fluorescence detection method, and the transition probability P is calculated out of these populations (P = N1/(N1 + N2)). This transition probability depends on the phase difference accumulated by the matter waves along the two arms of the interferometer that is, in our geometry, given by  , where
, where  is the effective wavevector of the Raman transition and
is the effective wavevector of the Raman transition and  the gravity acceleration. Gravity measurements are then repeated in a cyclic manner, at a repetition rate that depends on the method used to prepare the atomic source. Using laser cooled atoms, repetition rates of about 3 Hz are achieved which allows for a fast averaging of the interferometer phase noise, dominated by parasitic vibrations. With a combination of passive isolation and vibration correction techniques [27], we have demonstrated a best short term sensitivity of 56 nm s−2 at 1 s measurement time [1], which can average down to below 1 nm s−2. These performances are comparable to the ones of the two other best atom gravimeters developed so far [2, 3].The use of ultracold atoms reduces the cycling rate due to the increased duration of the preparation of the source. Indeed, to increase the initial number of atoms, we first load the magneto-optical trap for 1 s (to be compared with 80 ms only when using the laser cooled source) and then transfer the atoms in a far detuned dipole trap. This trap is realized using a 30 W fibre laser at 1550 nm, which is first focused onto the atoms with a 170 μm waist (radius at 1/e2), before being recycled and sent back at a 90° angle and tightly focused with a 27 μm waist. The two beams form a crossed dipole trap aligned in the horizontal plane, with an initial depth of about 700 μK. The transfer in the trap is optimized by increasing the detuning of the cooling laser by −185 MHz, in order to compensate for the large light shift that the dipole trap induces on the 2P excited state [28], and reducing the intensity in the repumping beam. The cooling and repumping lasers are then switched off, and we end up with about 3 × 108 atoms trapped at a temperature of 26 μK. Evaporative cooling is then implemented by decreasing the laser powers from 14.5 W and 8 W to 2.9 W and 100 mW typically in the two arms over a duration of 3 s. We finally end up with atomic samples in the low 100 nK range containing 104 atoms, detected at the top of the chamber using fluorescence imaging on a CCD camera. Changing the intensities in the trap at the end of the evaporation sequence allows to vary the temperature over a large temperature range, from 50 nK to 7 μK. The total preparation time is then 4.22 s, and the cycle time 4.49 s, which reduces the repetition rate down to 0.22 Hz. Furthermore, at the lowest temperatures, the number of atoms is reduced down to the level (below 104 atoms) where the detection noise becomes comparable to the vibration noise. The short term sensitivity when using ultracold atoms is thus significantly degraded with respect to when using laser cooled atoms. It varies in our experiment in the 1200–3000 nm s−2 range at 1 s measurement time, depending on the final temperature of the sample.
the gravity acceleration. Gravity measurements are then repeated in a cyclic manner, at a repetition rate that depends on the method used to prepare the atomic source. Using laser cooled atoms, repetition rates of about 3 Hz are achieved which allows for a fast averaging of the interferometer phase noise, dominated by parasitic vibrations. With a combination of passive isolation and vibration correction techniques [27], we have demonstrated a best short term sensitivity of 56 nm s−2 at 1 s measurement time [1], which can average down to below 1 nm s−2. These performances are comparable to the ones of the two other best atom gravimeters developed so far [2, 3].The use of ultracold atoms reduces the cycling rate due to the increased duration of the preparation of the source. Indeed, to increase the initial number of atoms, we first load the magneto-optical trap for 1 s (to be compared with 80 ms only when using the laser cooled source) and then transfer the atoms in a far detuned dipole trap. This trap is realized using a 30 W fibre laser at 1550 nm, which is first focused onto the atoms with a 170 μm waist (radius at 1/e2), before being recycled and sent back at a 90° angle and tightly focused with a 27 μm waist. The two beams form a crossed dipole trap aligned in the horizontal plane, with an initial depth of about 700 μK. The transfer in the trap is optimized by increasing the detuning of the cooling laser by −185 MHz, in order to compensate for the large light shift that the dipole trap induces on the 2P excited state [28], and reducing the intensity in the repumping beam. The cooling and repumping lasers are then switched off, and we end up with about 3 × 108 atoms trapped at a temperature of 26 μK. Evaporative cooling is then implemented by decreasing the laser powers from 14.5 W and 8 W to 2.9 W and 100 mW typically in the two arms over a duration of 3 s. We finally end up with atomic samples in the low 100 nK range containing 104 atoms, detected at the top of the chamber using fluorescence imaging on a CCD camera. Changing the intensities in the trap at the end of the evaporation sequence allows to vary the temperature over a large temperature range, from 50 nK to 7 μK. The total preparation time is then 4.22 s, and the cycle time 4.49 s, which reduces the repetition rate down to 0.22 Hz. Furthermore, at the lowest temperatures, the number of atoms is reduced down to the level (below 104 atoms) where the detection noise becomes comparable to the vibration noise. The short term sensitivity when using ultracold atoms is thus significantly degraded with respect to when using laser cooled atoms. It varies in our experiment in the 1200–3000 nm s−2 range at 1 s measurement time, depending on the final temperature of the sample.
2.2. Gravity measurements versus atom temperature
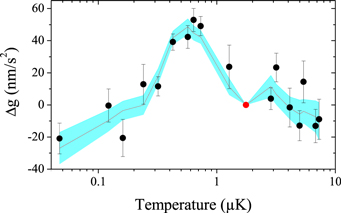
We use the possibility to easily adjust the temperature of the atoms to perform differential measurements of the gravity value derived from the phase of the interferometer as a function of the temperature of the source, which we vary over more than two orders of magnitude. The results are displayed as black circles in figure 2, which reveals a non-trivial behaviour, with a fairly flat behaviour in the 2–7 μK range, consistent with previous measurements obtained with optical molasses [4], and a rapid variation of the measurements below 2 μK. This shows that a naive linear extrapolation to zero temperature based on high temperature data taken with laser cooled atoms can lead to a significant error. These measurements have been performed for two opposite orientations of the experiment (with respect to the direction of the Earth rotation vector) and showed the same behaviour, indicating that these effects are not related to Coriolis acceleration [4], but rather related to aberrations. Moreover, the measurements are performed by averaging measurements with two different orientations of the Raman wavevector, which suppresses the effect of many systematic effects, including differential light shifts of the Raman lasers that could vary with the temperature, as it depends on the intensities seen by the atoms at the three pulses [4].
Figure 2. Gravity measurements as a function of the atom temperature. The measurements, displayed as black circles, are performed in a differential way, with respect to a reference temperature of 1.8 μK (displayed as a red circle). The red line is a fit to the data with a subset of five Zernike polynomials and the filled area the corresponding 68% confidence area.
Download figure:
Standard image High-resolution image3. Monte Carlo model of the experiment
3.1. Description of the model
To interpret these data, we have developed a full Monte Carlo model of the experiment, which averages the contributions to the interferometer signal of atoms randomly drawn in the initial position and velocity distributions. It takes into account the selection and interferometer processes, by including the finite size and finite coupling of the Raman lasers, and the detection process, whose finite field of view cuts the contribution of the hottest atoms to the measured atomic populations [29]. This model is used to calculate the effect of wavefront aberrations onto the gravity measurement as a function of the experimental parameters. For that, we calculate for each randomly drawn atom its trajectory and its positions at the three pulses in the Raman beams, and take into account the phase shifts which are imparted to the atomic wavepackets at the Raman pulses: δϕ = kδzi, where δzi is the flatness defect at the ith pulse. We sum the contributions of a packet of 104 atoms to the measured atomic populations to evaluate a mean transition probability. The mean phase shift is finally determined from consecutive such determinations of mean transition probabilities using a numerical integrator onto the central fringe of the interferometer, analogous to the measurement protocol used in the experiment [4]. With 104 such packets, we evaluate the interferometer phase shift with a relative uncertainty smaller than 10−3. We decompose the aberrations δz onto the basis of Zernike polynomials  , taking as a reference radius the finite size of the Raman beam (which is set by a 28 mm diameter aperture in the optical system). Assuming that the atoms are initially centred onto the Raman mirror, as well as into the detection zone, the effect of all polynomials with no rotation symmetry (
, taking as a reference radius the finite size of the Raman beam (which is set by a 28 mm diameter aperture in the optical system). Assuming that the atoms are initially centred onto the Raman mirror, as well as into the detection zone, the effect of all polynomials with no rotation symmetry ( ) averages to zero, due to the symmetry of the position and velocity distributions [12]. This assumption is discussed in section 3.4. We thus consider here only Zernike polynomials with no angular dependence that correspond to the curvature of the wavefront (or defocus) and to higher order spherical aberrations.
) averages to zero, due to the symmetry of the position and velocity distributions [12]. This assumption is discussed in section 3.4. We thus consider here only Zernike polynomials with no angular dependence that correspond to the curvature of the wavefront (or defocus) and to higher order spherical aberrations.
3.2. Impact of finite size effects
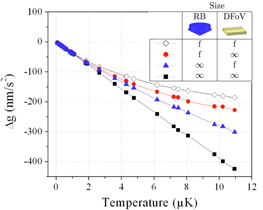
To illustrate the impact of finite size effects, we display in figure 3 calculated gravity shifts corresponding to different cases, for a defocus ( ) with a peak-to-peak amplitude of
) with a peak-to-peak amplitude of  across the size of the reference radius, which corresponds to
across the size of the reference radius, which corresponds to  , with r the normalized radial distance. The black squares corresponds to the ideal case of infinite Raman laser radius size and detection field of view. It gives a linear dependence versus temperature, which can easily be retrieved analytically by simply averaging over the velocity distribution. The circles (resp. triangles) correspond to the case of finite beam waist and infinite detection field of view (resp. infinite beam waist and finite detection field of view), and finally diamonds include both finite size effects. Deviations from the linear behaviour arise from the reduction or suppression of the contribution of the hottest atoms. The effect of the finite Raman beam waist is found to be more pronounced than the effect of the finite detection area. Finally, we calculate for this simple study case a bias of −63 nm s−2 at the temperature of 1.8 μK, for a peak-to-peak amplitude of 20 nm. This implies that, at the temperature of laser cooled samples and for a pure curvature, a peak-to-peak amplitude of less than 3 nm (λ/260 PV) over a reference diameter of 28 mm is required for the bias to be smaller than 10 nm s−2.
, with r the normalized radial distance. The black squares corresponds to the ideal case of infinite Raman laser radius size and detection field of view. It gives a linear dependence versus temperature, which can easily be retrieved analytically by simply averaging over the velocity distribution. The circles (resp. triangles) correspond to the case of finite beam waist and infinite detection field of view (resp. infinite beam waist and finite detection field of view), and finally diamonds include both finite size effects. Deviations from the linear behaviour arise from the reduction or suppression of the contribution of the hottest atoms. The effect of the finite Raman beam waist is found to be more pronounced than the effect of the finite detection area. Finally, we calculate for this simple study case a bias of −63 nm s−2 at the temperature of 1.8 μK, for a peak-to-peak amplitude of 20 nm. This implies that, at the temperature of laser cooled samples and for a pure curvature, a peak-to-peak amplitude of less than 3 nm (λ/260 PV) over a reference diameter of 28 mm is required for the bias to be smaller than 10 nm s−2.
Figure 3. Calculation of the impact of the size of the Raman beam waist (RB) and of the detection field of view (DFoV) on the gravity shift induced by a defocus as a function of the atomic temperature. The peak-to-peak amplitude of the defocus is 20 nm. The total interferometer time is  ms. The results displayed here correspond to four different cases, depending on whether the sizes of the Raman beam waist and detection field of view are taken as finite or infinite.
ms. The results displayed here correspond to four different cases, depending on whether the sizes of the Raman beam waist and detection field of view are taken as finite or infinite.
Download figure:
Standard image High-resolution image3.3. Impact of the first Zernike polynomials
We then calculate the effect of the 7 first  polynomials (for even n ranging from 2 to 14) for the same peak-to-peak amplitude of
polynomials (for even n ranging from 2 to 14) for the same peak-to-peak amplitude of  as a function of the atomic temperature. Figure 4 displays the results obtained, restricted for clarity to the first five polynomials. All orders exhibit as common features a linear behaviour at low temperatures and a tendency for saturation at high temperatures. Interestingly, we find non monotonic behaviours in the temperature range we explore and the presence of local extrema. The value of the temperatures corresponding to these extrema decreases when increasing the polynomial order.
as a function of the atomic temperature. Figure 4 displays the results obtained, restricted for clarity to the first five polynomials. All orders exhibit as common features a linear behaviour at low temperatures and a tendency for saturation at high temperatures. Interestingly, we find non monotonic behaviours in the temperature range we explore and the presence of local extrema. The value of the temperatures corresponding to these extrema decreases when increasing the polynomial order.
Figure 4. Gravity shifts calculated for the parameters of our experiment, for the five first Zernike polynomials with rotation symmetry  (n = 2, 4, 6, 8, 10) for peak-to-peak amplitudes of 20 nm.
(n = 2, 4, 6, 8, 10) for peak-to-peak amplitudes of 20 nm.
Download figure:
Standard image High-resolution image3.4. Discussion on the restriction to m = 0 polynomials
In the simulation, the cloud position corresponds to the centre of the Raman beam and the expansion is taken as symmetric, which allows to restrict the Zernike basis to m = 0 polynomials. In the presence of position errors, as well as residual drift velocities, other Zernike polynomials will enter into play. In principle, an ideal Gaussian beam being infinite, but not the reference radius of the Zernike polynomials, the wavefront decomposition could be performed around any arbitrary centre position (with a possible choice corresponding to the very centre of the atomic cloud, but not necessarily to the centre of the Gaussian Raman beam). Nevertheless, given that our beam has a finite aperture, and that the reference diameter we have chosen corresponds to the aperture size, the centre of the wavefront corresponds to the centre of this aperture (which do not necessarily correspond to the centre of the Gaussian profile). There is thus a finite sensitivity to other polynomials if the position of the cloud is not centred onto this aperture, or if there is a residual mean velocity. In addition, coupling inhomogeneities arising from the Gaussian Raman beam profile, and more important in our case, offset positions with respect to the centre of the detection [29], will play a role.
We have calculated the influence of position shifts and velocity drifts on non m = 0 orders. We found their effect for large position offsets of up to 1 mm and velocity drifts of up to 1 mm s−1 to be smaller than the order m = 0 by more than an order of magnitude. Using time of flights measurements of the expansion of the cloud in the transverse directions with absorption imaging, velocity drifts are measured to be compatible with zero (with an uncertainty of order of 100 μm s−1). These measurements also confirm that the expansion is symmetric, as expected for a thermalized atomic sample. As for the offset in position, we assume it here to be null, with a maximum error of about 0.5 mm. Its stability is ensured by the stability of the crossing of the dipole trap beams. It was measured to fluctuate by no more than 10 μm over the whole measurement campaign.
4. Analysis of the measurements
4.1. Reconstructing a model for the wavefront
Using the phase shifts calculated at the different temperatures at which the measurements were performed, the data of figure 2 can now be adjusted, using a weighted least square adjustment, by a combination of the contribution of the first Zernike polynomials, which then constitute a finite size basis for the decomposition of the wavefront. The adjustment was realized for increasing numbers of polynomials, so as to assess the impact of the truncation of the polynomial basis onto the results of the fit. We give in table 1 the values of the correlation coefficient R and the extrapolated value at zero temperature as a function of the number of polynomials. We obtain stable values for both R and the extrapolated value to zero temperature, of about −55 nm s−2, when the number of polynomials is larger than 5. This indicates that the first 5 polynomials are enough to faithfully reconstruct a model wavefront that well reproduces the data. When increasing the number of polynomials, we find that the reconstructed wavefront is dominated by the lowest polynomial orders: the fitted coefficients of the higher orders are an order of magnitude smaller than the ones of the lowest terms The results of the adjustment with 5 polynomials is displayed as a red line in figure 2 and the 68% confidence bounds as a filled area. The flatness of the reconstructed wavefront at the centre of the Raman laser beam is found to be as small as 22 nm PV (peak valley) over a diameter of 20 mm.
Table 1. Results of the linear adjustments for increasing number of Zernike polynomials. The error bars correspond to 1σ uncertainties (68% confidence).
| Number of | R | Extrapolated value |
|---|---|---|
| polynomials | to zero temperature (nm s−2) | |
| 2 | 0.587 | 37(17) |
| 3 | 0.764 | 09(18) |
| 4 | 0.871 | −19(18) |
| 5 | 0.963 | −56(13) |
| 6 | 0.964 | −54(13) |
| 7 | 0.964 | −55(15) |
4.2. Discussion
We can now compare this reconstructed wavefront with the measured flatness of the involved optics. In the standard configuration we use here, with Raman beams retroreflected on a common mirror, wavefront aberrations are mainly due to the imperfect flatness of the retroreflecting optics. Wavefront distortions due to the optics placed before this retroreflection, such as the input window of the vacuum system, are common mode to the two Raman lasers, and thus strongly suppressed, but not completely, due to the inherent path difference between the counterpropagating lasers. Our model also captures this effect, but only partially. Indeed, it does not make any assumption on the source of the wavefront aberrations, but do not take into account the deformation of this wavefront along the interferometer due to its propagation. In our system, retroreflecting optics comprise a mirror and a quarter wave plate, which we have put under vacuum in order to avoid any additional contribution from the exit viewport. These two optical elements had measured flatness of respectively 3 and 10 nm PV over a 20 mm diameter. We calculated out of their measured shape the expected bias and its dependence versus temperature and found biases in the few tens of nm s−2 range, but with a significantly different behaviour with temperature. At such level of flatness though, the mechanical stress from the mounting of these optics in their support and the subsequent baking of the whole experiment most probably impacted their planarity. An in situ characterization with a high performance wavefront sensor would be necessary to assess the validity of the reconstructed wavefront, but this would require to break the vacuum.
The bias due to the optical aberrations at the reference temperature of 1.8 μK, which corresponds to the temperature of the laser cooled atom source, is −56(13) nm s−2. Its uncertainty is three times better than its previous evaluation [4], which in principle will improve accordingly our accuracy budget.
4.3. Investigating the impact of atomic interactions
On the other hand, interatomic interactions in ultracold sources can induce significant phase shifts [30, 31] and phase diffusion [32], leading to bias and loss of contrast for the interferometer. Nevertheless, the rapid decrease of the atomic density when interrogating the atoms in free fall reduces drastically the impact of the interactions [33–35]. To investigate this, we have performed a differential measurement for two different atom numbers at the temperature of 650 nK. At this temperature, the density after expansion is actually maximum. Indeed, given the evolution in the number of atoms and temperature during the evaporation, we observe that this density exhibits a fairly broad extremum in the temperature range [250 nK–1.3 μK]. This maximal mean density is evaluated to be about 3 × 109 atoms cm−3 at the time of the first π/2 Raman pulse. The number of atoms was thus varied from 25 000 to 5000 by changing the efficiency of a microwave pulse in the preparation phase, which leaves the spatial distribution and temperature unchanged. We measured an unresolved difference of −7(12) nm s−2. This allows us to put an upper bound on the effect of interactions, which we find lower than 1 nm s−2 per thousand atoms.
5. Prospects
The uncertainty in the evaluation of the bias related to optical aberrations can be improved further by performing measurements at even lower temperatures, which will require in our set-up to improve the efficiency of the evaporative cooling stage. A larger number of atoms would allow to limit the degradation of the short term sensitivity and to perform measurements with low enough statistical uncertainties, of order of 10 nm s−2 or better, after about one hour-long averaging time. More, absorption imaging with a vertical probe beam would allow for spatially resolved phase measurements across the cloud [19], which would allow for improving the reconstruction of the wavefront.
The temperature can also be drastically reduced, down to the low nK range, using delta kick collimation techniques [36, 37]. In addition to a reduced ballistic expansion, the use of ultracold atoms also offers a better control of the initial position and mean velocity of the source with respect to laser cooled sources, which suffer from fluctuations induced by polarisation and intensity variations of the cooling laser beams. Such an improved control reduces the fluctuations of systematic effects related to the transverse motion of the atoms, such as the Coriolis acceleration and the bias due to aberrations, and thus will improve the long term stability [35].
With the above-mentioned improvements, and after a careful re-examination of the accuracy budget [7], accuracies better than 10 nm s−2 are within reach. This will make quantum sensors based on atom interferometry the best standards in gravimetry. Furthermore, the improved control of systematics and the resulting gain in stability will open new perspectives for applications, in particular in the field of geophysics. Resolving long term fluctuations of the Earth gravity field in the nm s−2 range will allow improving the knowledge of mass transport phenomena [38], with an important impact in hydrology, volcanology and reservoir monitoring for instance.
Finally, the method proposed here, which relies on the use of ultracold atoms as a source, can be applied to any atomic sensor based on light beamsplitters, which are inevitably affected by distortions of the lasers wavefronts. The improved control of systematics it provides will have significant impact in high precision measurements with atom interferometry, with important applications to geodesy [39, 40], fundamental physics tests [20, 41, 42] and to the development of highest grade inertial sensors [43].
Acknowledgments
We acknowledge the contributions from X Joffrin, J Velardo and C Guerlin in earlier stages of this project. We thank R Geiger and A Landragin for useful discussions and careful reading of the manuscript.