Skip to main content
SpringerLink
Log in

Discrete bright–dark soliton solutions and parameters controlling for the coupled Ablowitz–Ladik equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

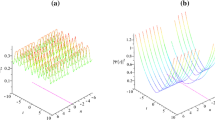
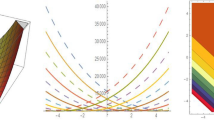
We consider the nonautonomous discrete vector bright–dark solutions and their controllable behaviors in the coupled Ablowitz–Ladik equation with variable coefficients, which possesses complicated wave propagation in time. Based on the differential–difference symmetry transformation and the Lamé polynomial solutions, we use the Jacobi elliptic functions \(\hbox {sn}(n, m), \hbox {cn}(n, m)\), \(\hbox {dn}(n, m)\) and present the nonautonomous discrete vector bright–dark solutions, which are localized in space and keep the localization longer in time. Moreover, we also exhibit the wave propagation of nonautonomous Lamé polynomial solutions of higher order and their dynamics for some chosen parameters and functions. And the managements and dynamic behaviors of these solutions are investigated analytically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Fermi, E., Pasta, J., Ulam, S.: Collected Papers of Enrico Ferm. Chicago Press, Chicago (1965)

    Google Scholar 

  2. Levi, D., Yamilov, R.I.: Conditions for the existence of higher symmetries of evolutionary equations on the lattice. J. Math. Phys. 38, 6648–6674 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  3. Sokolov, V.V., Shabat, A.B.: Classification of integrable evolution equations. Sov. Sci. Rev. C Math. Phys. Rev. 4, 221–280 (1984)

    MathSciNet  MATH  Google Scholar 

  4. Ablowitz, M.J., Segur, H.: Solitons and the Inverse Scattering Transform. SIAM, Philadelphia (1981)

    Book  MATH  Google Scholar 

  5. Ablowitz, M.J., Ladik, J.: Nonlinear differential–difference equations. J. Math. Phys. 16, 598–603 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  6. Aceves, A.B., Angelis, C.D., Peschel, T., et al.: Discrete self-trapping, soliton interactions, and beam steering in nonlinear waveguide arrays. Phys. Rev. E 53, 1172 (1996)

    Article  Google Scholar 

  7. Calini, A., Ercolani, N.M., McLaughlin, D.W., Schober, C.M.: Analysis of numerically induced chaos in the nonlinear Schrodinger equation. Phys. D 89, 227–260 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  8. Marquie, P., Bilbault, J.M., Remoissenet, M.: Observation of nonlinear localized modes in an electrical lattice. Phys. Rev. E 51, 6127 (1995)

    Article  Google Scholar 

  9. Hennig, D., Tsironis, G.P.: Wave transmission in nonlinear lattices. Phys. Rep. 307, 333–342 (1999)

    Article  MathSciNet  Google Scholar 

  10. Ablowitz, M.J., Ladik, J.: Nonlinear differential–difference equations and Fourier-analysis. J. Math. Phys. 17, 1011–1018 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  11. Ablowitz, M.J., Ladik, J.: A nonlinear difference scheme and inverse scattering. Stud. Appl. Math. 55, 213–229 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  12. Kako, F., Mugibayashi, N.: Complete integrability of general nonlinear differential–difference equations solvable by the inverse method. Prog. Theor. Phys. 61, 776–790 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chowdhury, A.R., Mahato, G.: A Darboux–Backlund transformation associated with a discrete nonlinear Schrodinger equation. Lett. Math. Phys. 7, 313–317 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  14. Amaral, L., Behar, M., Maciel, A., Saitovitch, H.: Anomalous temperature behaviour of the electric field gradients in an in semiconductor compound. Phys. Lett. A 102, 45–48 (1984)

    Article  Google Scholar 

  15. Bogolyubov, N.N., Prikarpatskii, A.K., Samoilenko, V.G.: Discrete periodic problem for the modified nonlinear Korteweg-de Vries equation. Sov. Phys. Dokl. 26, 490–492 (1981)

    Google Scholar 

  16. Bogolyubov, N.N., Prikarpatskii, A.K.: The inverse periodic problem for a discrete approximation of a nonlinear Schrrödinger equation. Sov. Phys. Dokl. 27, 113 (1982)

    Google Scholar 

  17. Ahmad, S., Chowdhury, A.R.: The quasiperiodic solutions to the discrete nonlinear Schrödinger equation. J. Math. Phys. 28, 134–137 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ahmad, S., Chowdhury, A.R.: On the quasiperiodic solutions to the discrete nonlinear Schrödinger equation. J. Phys. A 20, 293–303 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  19. Wang, D.S., Wei, X.Q.: Integrability and exact solutions of a two-component Korteweg-de Vries system. Appl. Math. Lett. 51, 60–67 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  20. Wang, D.S., Yin, Y.B.: Symmetry analysis and reductions of the two-dimensional generalized Benney system via geometric approach. Compu. Math. Appl. 71, 748–757 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Christodoulides, D.N., Joseph, R.J.: Discrete self-focusing in nonlinear arrays of coupled waveguides. Opt. Lett. 193, 794–796 (1988)

    Article  Google Scholar 

  22. Kevrekidis, P.G., Rasmussen, K.O., Bishop, A.R.: The discrete nonlinear Schrödinger equation: a survey of recent results. Int. J. Mod. Phys. B 15, 2833 (2001)

    Article  Google Scholar 

  23. Tian, S.F.: Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method. J. Diff. Equ. 262, 506–558 (2017)

    Article  MATH  Google Scholar 

  24. Wang, D.S., Zhang, D.J., Yang, J.K.: Integrable properties of the general coupled nonlinear Schrödinger equations. J. Math. Phys. 51, 023510 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Tian, S.F.: The mixed coupled nonlinear Schrödinger equation on the half-line via the Fokas method. Proc. R. Soc. Lond. A 472, 20160588 (2016)

    Article  Google Scholar 

  26. Dai, C.Q., Wang, Y.Y.: Controllable combined Peregrine soliton and Kuznetsov–Ma soliton in PT-symmetric nonlinear couplers with gain and loss. Nonlinear Dyn. 80, 715–721 (2015)

    Article  MathSciNet  Google Scholar 

  27. Dai, C.Q., Wang, Y.Y.: Spatiotemporal localizations in (3+1)-dimensional PT-symmetric and strongly nonlocal nonlinear media. Nonlinear Dyn. 83, 2453–2459 (2016)

    Article  MathSciNet  Google Scholar 

  28. Kong, L.Q., Dai, C.Q.: Some discussions about variable separation of nonlinear models using Riccati equation expansion method. Nonlinear Dyn. 81, 1553–1561 (2015)

    Article  MathSciNet  Google Scholar 

  29. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Nonautonomous solitons in external potentials. Phys. Rev. Lett. 98, 074102 (2007)

    Article  Google Scholar 

  30. Serkin, V.N., Hasegawa, A.: Novel soliton solutions of the nonlinear Schrödinger equation model. Phys. Rev. Lett. 85, 4502 (2000)

    Article  Google Scholar 

  31. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Solitary waves in nonautonomous nonlinear and dispersive systems: nonautonomous solitons. J. Mode Optic. 57, 1456–1472 (2010)

    Article  MATH  Google Scholar 

  32. Yan, Z.Y., Zhang, X.F., Liu, W.M.: Nonautonomous matter waves in a waveguide. Phys. Rev. A 84, 023627 (2011)

    Article  Google Scholar 

  33. Eilbeck, J.C., Lomdahl, P.S., Scott, A.C.: Soliton structure in crystalline acetanilide. Phys. D 16, 318–338 (1985)

    Article  MathSciNet  Google Scholar 

  34. Ablowitz, M.J., Ladik, J.F.: A nonlinear difference scheme and inverse scattering. Stud. Appl. Math. 55, 213–229 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  35. Ankiewicz, A., Akhmediev, N., Soto-Crespo, J.M.: Discrete rogue waves of the Ablowitz–Ladik and Hirota equations. Phys. Rev. E 82, 026602 (2010)

    Article  MathSciNet  Google Scholar 

  36. Yan, Z.Y., Jiang, J.D.: Nonautonomous discrete rogue wave solutions and interactions in an inhomogeneous lattice with varying coefficients. J. Math. Anal. Appl. 395, 542–549 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  37. Chen, Z., Yang, J., Bezryadina, A., Makasyuk, I.: Observation of two-dimensional lattice vector solitons. Opt. Lett. 29, 1656–1658 (2004)

    Article  MATH  Google Scholar 

  38. Hennig, D., Tsironis, G.P.: Wave transmission in nonlinear lattices. Phys. Rep. 307, 333 (1999)

    Article  MathSciNet  Google Scholar 

  39. Kartashov, Y.V., Malomed, B.A., Torner, L.: Solitons in nonlinear lattices. Rev. Mod. Phys. 83, 247–306 (2011)

    Article  Google Scholar 

  40. Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrodinger Systems. Cambridge University Press, Cambridge (2004)

    MATH  Google Scholar 

  41. Takeno, S., Hori, K.: A propagating self-localized mode in a one-dimensional lattice with quartic anharmonicity. J. Phys. Soc. Jpn. 59, 3037–3040 (1990)

    Article  Google Scholar 

  42. Akhmediev, N., Ankiewicz, A.: Modulation instability, Fermi–Pasta–Ulam recurrence, rogue waves, nonlinear phase shift, and exact solutions of the Ablowitz–Ladik equation. Phys. Rev. E 83, 046603 (2011)

    Article  Google Scholar 

  43. Doktorov, E.V., Matsuk, N.P., Rothos, V.M.: Dynamics of the Ablowitz–Ladik soliton train. Phys. Rev. E 69, 056607 (2004)

    Article  MathSciNet  Google Scholar 

  44. Maruno, K., Ohta, Y.: Casorati determinant form of dark soliton solutions of the discrete nonlinear Schrodinger equation. J. Phys. Soc. Jpn. 75, 054002 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  45. Boiti, M., Leon, J., Pempinelli, F.: Nonlinear spectral characterization of discrete data. Phys. Rev. E 54, 5739 (1996)

    Article  Google Scholar 

  46. Mohamadou, A., Fopa, F., Crepin Kofane, T., Mohamadou, A.: Modulational instability and spatial structures of the Ablowitz–Ladik equation. Optics. Commun. 266, 648–655 (2006)

    Article  Google Scholar 

  47. Cai, D., Bishop, A.R., Gronbech-Jensen, N.: Localized states in discrete nonlinear Schrodinger equations. Phys. Rev. Lett. 72, 591–595 (1994)

    Article  Google Scholar 

  48. Narita, K.: Soliton solution for discrete Hirota equation. J. Phys. Soc. Jpn. 59, 3528–3530 (1990)

    Article  MathSciNet  Google Scholar 

  49. Mieck, B., Graham, R.: Bose–Einstein condensate of kicked rotators with time-dependent interaction. J. Phys. A 38, L139–144 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  50. Ablowitz, M.J., Ladik, J.F.: On the solution of a class of nonlinear partial differential equations. Stud. Appl. Math. 57, 1–12 (1977)

    Article  MATH  Google Scholar 

  51. Khare, A., Saxena, A.: Solutions of several coupled discrete models in terms of Lam polynomials of order one and two. Pramana J. Phys. 78, 187–213 (2012)

    Article  Google Scholar 

  52. Vakhnenko, O.O., Vakhnenko, V.O.: Physically corrected Ablowitz–Ladik model and its application to the Peierls–Nabarro problem. Phys. Lett. A 196, 307–312 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  53. Yan, Z.Y.: Financial rogue waves appearing in the coupled nonlinear volatility and option pricing model. Phys. Lett. A 375, 4274 (2011)

    Article  MATH  Google Scholar 

  54. Dai, C.Q., Zhang, J.F.: Exact spatial similaritons and rogons in 2D graded-index waveguides. Opti. Lett. 35, 2651–2653 (2010)

    Article  Google Scholar 

  55. Yu, F.J.: Nonautonomous rogue waves and ‘catch’ dynamics for the combined Hirota-LPD equation with variable coefficients. Commun. Nonlinear Sci. Numer. Simulat. 34, 142–153 (2016)

    Article  MathSciNet  Google Scholar 

  56. Yu, F.J.: Multi-rogue waves for a higher-order nonlinear Schrodinger equation in optical fibers. Appl. Math. Comput. 220, 176–184 (2013)

    MathSciNet  MATH  Google Scholar 

  57. Kimura, T., Goto, T., Shintani, H., Ishizaka, K., Arima, T., Tokura, Y.: Magnetic control of ferroelectric polarization. Nature 426, 55–58 (2003)

    Article  Google Scholar 

  58. Fiebig, M., Lottermoser, T., Pisarev, R.V.: Spin-rotation phenomena and magnetic phase diagrams of hexagonal RMnO. J. Appl. Phys. 93, 8194–8196 (2003)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by Natural Science Foundations of Liaoning Province, China (Grant No. 201602678) and (Grant No. 2015020029).

Author information

Authors and Affiliations

  1. School of Mathematics and Systematic Sciences, Shenyang Normal University, Shenyang, 110034, China

    Li Li & Fajun Yu

Authors
  1. Li Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fajun Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fajun Yu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Yu, F. Discrete bright–dark soliton solutions and parameters controlling for the coupled Ablowitz–Ladik equation. Nonlinear Dyn 89, 2403–2414 (2017). https://doi.org/10.1007/s11071-017-3593-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3593-z

Keywords

Search

Navigation