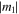Abstract
A set of the coherently-coupled nonlinear Schrödinger equations with the positive coherent coupling terms, which are related to the optical fiber communication, are studied through the binary Darboux transformation with the dimensional reduction. Formalisms of the solutions appear as the mixtures of the polynomial functions with exponential functions. When the spectral parameter is real, we obtain different kinds of the solutions, such as the soliton, degenerate-soliton, periodic, and soliton-like rational solutions. When the spectral parameter is complex with a non-zero imaginary part, we obtain the rogue waves and twisted rogue-wave pairs, and show that an eye-shaped rogue wave splits into a twisted rogue-wave pair.
Export citation and abstract BibTeX RIS
1. Introduction
Solitons, which are a kind of the localized waves, preserve their shapes during the propagation via the balance between the nonlinear and dispersive effects [1, 3–8]. Envelope solitons of the nonlinear Schrödinger (NLS)-type equations have been seen in nonlinear optics [1, 2], plasma physics [9] and Bose–Einstein condensation [10]. Besides, the Peregrine soliton has been used to describe the rogue wave (RW), a nonlinear wave of the NLS equation localized in both time and space [11]. The RWs have been observed experimentally in different physical systems [12], such as the optical fibers [13, 14], water-wave tank [15] and plasmas with negative ions [16]. Twist RW (TRW) pairs and soliton-like rational solutions have been found for the Sasa–Satsuma equation, which possess different properties from those for the NLS equation [17–19]. In the physical systems describing interacting wave components, such as the Bose–Einstein condensates and optical fibers, vector RWs have been introduced and studied [20–22]. Experimental demonstration of the optical dark RWs and second order RWs have also been provided [23, 24].
With the consideration of the simultaneous propagation of the optical pulses with different frequencies or polarizations in the birefringent fibers or multi-mode fibers, the coupled NLS equations have been investigated [25–34]. For example, the Manakov system has been claimed to the left- and right-polarized modes of the electromagnetic waves [34].
For the coupled NLS equations, there have been two categories of the coupling effects: incoherent coupling and coherent coupling [35–37]. It has been reported that the coherence happens when the nonlinear fiber is weakly birefringent [25, 35–38]. Simultaneous propagation of two optical pulses with different frequencies or polarizations in a weakly birefringent fiber has been governed by the following coherently-coupled NLS equations [33, 39, 40]:
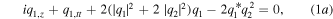
where q1 and q2 are the slowly varying envelopes of two interacting optical modes, the variables z and t, respectively, correspond to the normalized distance and retarded time, the asterisk denotes the complex conjugate, the terms  and
and  represent the self-phase modulation (SPM), the terms
represent the self-phase modulation (SPM), the terms 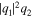 and
and  represent the XPM, and the terms
represent the XPM, and the terms 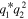 and
and 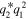 represent the coherent coupling terms governing the energy exchange between two axes of the fiber [39]. As the ratio between the coefficients of the XPM terms and the coherent coupling terms in equations (1) is −2, the coherent coupling has been called the negative coherent coupling [40]. Integrability properties and soliton solutions of equations (1) have been obtained [33].
represent the coherent coupling terms governing the energy exchange between two axes of the fiber [39]. As the ratio between the coefficients of the XPM terms and the coherent coupling terms in equations (1) is −2, the coherent coupling has been called the negative coherent coupling [40]. Integrability properties and soliton solutions of equations (1) have been obtained [33].
Furthermore, researchers have concentrated their attention on the following coherently-coupled NLS equations [38, 39, 41]:
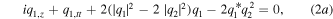
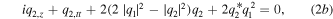
obtained by means of the Ablowitz–Kaup–Newell–Segur (AKNS) technology [41]. Compared with that in equations (1), the ratio between the coefficients of the XPM and the coherent coupling terms in equations (2) is positive. Conserved quantities, Lax pair and Darboux transformation of equations (2) have been derived [41]. Vector solitons possessing single- or double-hump profiles of equations (2) as well as their interactions have been discussed via the Hirota method [39]. Bound-soliton, breather and RW solutions of equations (2) with the complex spectral parameters have been derived via the Darboux transformation (DT) [38].
However, the case that the spectral parameter is real has not been considered for the DT in [38], with respect to equations (2). In this paper, we will construct the binary DT (BDT) of equations (2) with the real or complex spectral parameters, and present the vector TRW pairs, solitons, periodic and soliton-like rational solutions of equations (2), which have not been obtained, to our knowledge. In section 2, we will give the formation of the one-fold BDT of equations (2). In section 3, vector analytic solutions of equations (2) from the non-zero seed solutions will be presented. Section 4 will be the discussion. Section 5 will be the conclusion.
2. Lax pair and BDT of equations (2)
Lax pair of equations (2) is [38, 41]
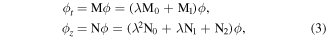
with
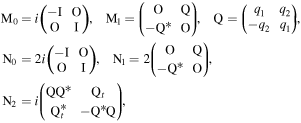
where 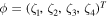 is a 4 × 1 vector, ζα's (α = 1, 2, 3, 4) are functions of z and
is a 4 × 1 vector, ζα's (α = 1, 2, 3, 4) are functions of z and 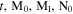 ,
, 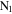 and
and 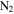 are the 4 × 4 matrices,
are the 4 × 4 matrices, 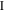 is the 2 × 2 unit matrix,
is the 2 × 2 unit matrix, 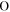 is the 2 × 2 zero matrix,
is the 2 × 2 zero matrix, 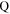 is a 2 × 2 matrix, λ is a complex spectral parameter, the superscript
is a 2 × 2 matrix, λ is a complex spectral parameter, the superscript 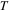 denotes the matrix transpose and '*' denotes the matrix complex conjugate. The compatibility condition
denotes the matrix transpose and '*' denotes the matrix complex conjugate. The compatibility condition 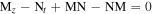 , which is known as the zero-curvature equation [42], reproduces equations (2).
, which is known as the zero-curvature equation [42], reproduces equations (2).
Suppose that 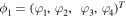 is a vector solution of Lax pair (3) corresponding to the complex spectral parameter λ1, and φα's are the functions of z and t. We can infer that
is a vector solution of Lax pair (3) corresponding to the complex spectral parameter λ1, and φα's are the functions of z and t. We can infer that 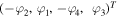 is a vector solution of Lax pair (3) corresponding to λ1, and
is a vector solution of Lax pair (3) corresponding to λ1, and 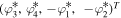 is a vector solution corresponding to
is a vector solution corresponding to 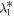 .
.
For simplicity, we use Φ1, Φ2, Φ3 and Φ4 to denote the 1 × 4 row vectors of the 4 × 4 martix Σ1 as
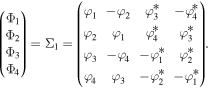
Via the dimensional reduction [43], we can build the one-fold BDT for equations (2) as
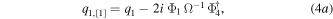

where the superscript '−1' denotes the matrix inverse, the superscript † denotes the conjugate transpose, q1,[1] and q2,[1] are the solutions of equations (2), the mark [1] represents the first iteration of q1 or q2, and Ω is the 4 × 4 matrix derived from the algebraic condition
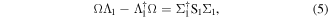
where  , and the details to determine Ω are described in the appendix.
, and the details to determine Ω are described in the appendix.
3. Vector analytic solutions of equations (2)
To obtain the vector analytic solutions on the non-zero background of equations (2) via BDT (4), we use the following non-zero seed solutions of equations (2):
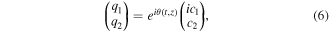
where 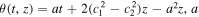 , c1 and c2 are the real constants. The vector solutions of Lax pair (3) corresponding to λ1 can be expressed as
, c1 and c2 are the real constants. The vector solutions of Lax pair (3) corresponding to λ1 can be expressed as
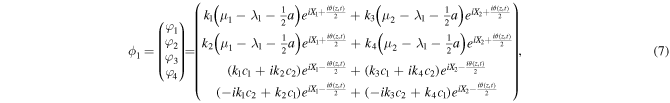
where
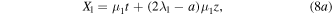
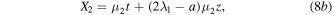
kα's (α = 1, 2, 3, 4) are the complex constants, and
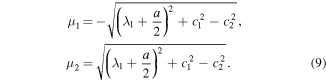
Based on the process in the appendix, Ω is expressed as
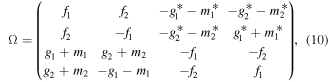
where m1 and m2 are the real constants, and f1, f2, g1 and g2 are expressed as follows. Two cases need to be considered:
3.1. λ1 is complex with a non-zero imaginary part
Substituting expression (7) into expression (A.7), we have


Via limitation (A.5), we have
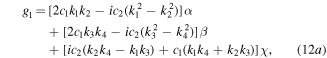
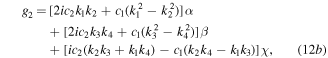
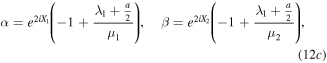
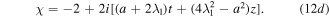
To obtain the RW and TWR pair solutions, we take  and
and 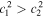 . From expressions (9), we know that μ2 tends to 0. In that case, g1 and g2 will be singular. To avoid that, we need kα's to satisfy the following conditions:
. From expressions (9), we know that μ2 tends to 0. In that case, g1 and g2 will be singular. To avoid that, we need kα's to satisfy the following conditions:
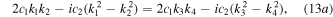

and have
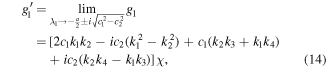
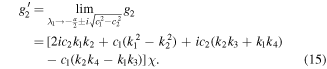
Substituting  ,
, 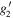 and χ into BDT (4), we obtain the rational solutions corresponding to the RWs and TRW pairs.
and χ into BDT (4), we obtain the rational solutions corresponding to the RWs and TRW pairs.
3.2. λ1 is real
We have either  (b = 1, 2) with
(b = 1, 2) with 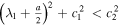 or
or 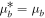 with
with 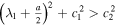 . Expressions (11) can be written as
. Expressions (11) can be written as
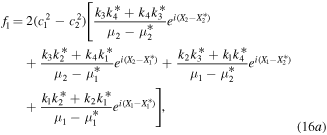
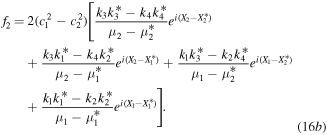
However, we should note that kα's also have some restrictions to ensure that f1 and f2 are non-singular. When 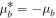 , i.e.,
, i.e., 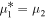 and
and 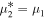 , we have
, we have  and kα's in expressions (16) must satisfy that
and kα's in expressions (16) must satisfy that 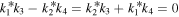 . When
. When  , we have
, we have  and kα's must satisfy that
and kα's must satisfy that 
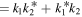
 .
.
Up to now, we have introduce the formalisms of the vector analytic solutions with some restrictions on kα's in different cases. The solutions of equations (2) are also characterized by five real parameters a, c1, c2, m1, m2 and a complex spectral parameter λ1. In the next section, we will discuss different types of the analytic solutions based on the formalisms.
4. Discussions
4.1. The RWs with complex spectral parameter
With k1 = k3 = 1 and k2 = k4 = 0 in conditions (13), we obtain the vector RW solutions
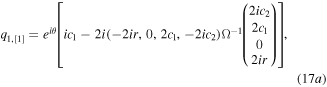
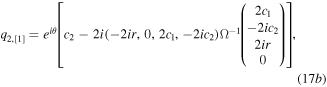
where
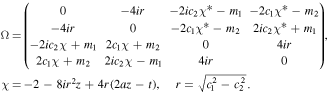
When m1 = m2 = 0, solutions (17) can be reduced to
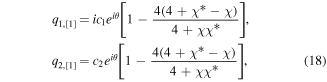
which are the vector generalization of the Peregrine soliton, as shown in figure 1. In that case, q1 is proportional to q2. The amplitudes  's (b = 1, 2) are peaked at
's (b = 1, 2) are peaked at 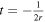 with the maximum values as
with the maximum values as 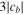 at z = 0.
at z = 0.
Figure 1. The vector RW via solutions (18) with a = 0, c1 = 1 and c2 = 0.8.
Download figure:
Standard image High-resolution imageFurther inspection of Ω shows that we should restrict m1 and m2 to satisfy 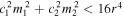 to guarantee
to guarantee 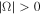 , and promise that the RW solutions have no singular point.
, and promise that the RW solutions have no singular point.
Under the restriction 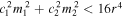 , we find that the centres of the RWs locate at
, we find that the centres of the RWs locate at  , and the amplitudes of the RWs can be expressed as
, and the amplitudes of the RWs can be expressed as
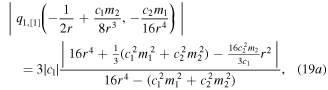
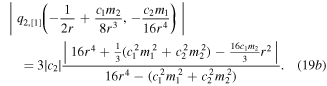
Hereby, with different m1 and m2, we obtain the eye-shaped RWs (analogous to the Peregrine soliton) in the q1 component while the TRW pairs in the q2 component.
Figures 2(a), (c) and (e) show the eye-shaped RWs, each of which has one hump and two valleys in the q1 component, and the amplitudes of the RWs become higher with m2 increasing. While in the q2 component, the structures of the RWs are more complicated, as shown in figures 2(b), (d) and (f). With m2 = 1, we illustrate a four-petaled RW which has two humps and two valleys in figure 2(b). With m2 = 1.4, we illustrate a RW which has four valleys in figure 2(d). With m2 = 1.6, we illustrate a RW which has one hump and four valleys in figure 2(f).
Figure 2. The same as figure 1 except that (a) and (b) m2 = 1; (c) and (d) m2 = 1.4; (e) and (f) m2 = 1.6.
Download figure:
Standard image High-resolution imageIn fact, figures 1(b), 2(b), (d) and (f) show that an eye-shaped RW splits into a pair of the RWs. Amplitudes of the RWs in the q2 component first decrease then increase with the increasing m2. While  , the RWs could not separate completely and be named as the TRW pairs [18].
, the RWs could not separate completely and be named as the TRW pairs [18].
With m1 = 0.1, we illustrate an eye-shaped RWs in the q1 component, while a TRW pair which have three valleys in the q2 component, as shown in figure 3. Comparing figures 3(a)–(b) with figures 3(c)–(d), we can observe that the RWs in both of the two components extend in the z axis when m1 = 0.4. When m1 = −0.4 in figures 3(e) and (f), the structures of the eye-shaped RW in the q1 component and TWR pair in the q2 component are the same as those in figures 3(c) and (d), while the inclinations of the central peaks or valleys of the RWs are opposite. Thus we can conclude that, as 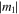 decreases, the RWs will be reduced in the z dimension, and the sign of m1 defines the inclination of the central peaks or valleys of the RWs.
decreases, the RWs will be reduced in the z dimension, and the sign of m1 defines the inclination of the central peaks or valleys of the RWs.
Figure 3. The same as figure 1 except that m2 = 1.2, (a) and (b) m1 = 0.1; (c) and (d) m1 = 0.4; (e) and (f) m1 = −0.4.
Download figure:
Standard image High-resolution imageTypes of the vector RWs presented in this section are shown in table 1.
Table 1. Types of the vector RWs.
| q1 component | q2 component |
|---|---|
| An eye-shaped RW | An eye-shaped RW |
| An eye-shaped RW | A four-petaled RW |
| An eye-shaped RW | A TRW with four valleys |
| An eye-shaped RW | A TRW with one hump and four valleys |
| An eye-shaped RW | A TRW with three valleys |
4.2. Solutions with real spectral parameter
If 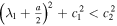 , we have known that kα's must satisfy that
, we have known that kα's must satisfy that 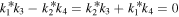 . We can set that k1 = 1, k2 = k3 = k4 = 0 or k2 = k4 = ik1 = ik3 = i for simplicity, and the solutions will correspond to the soliton solutions or the so-called 'degenerate soliton' solutions on the non-zero background, respectively. The degenerate soliton can be regarded as the nonlinear superposition of a soliton upon itself [44].
. We can set that k1 = 1, k2 = k3 = k4 = 0 or k2 = k4 = ik1 = ik3 = i for simplicity, and the solutions will correspond to the soliton solutions or the so-called 'degenerate soliton' solutions on the non-zero background, respectively. The degenerate soliton can be regarded as the nonlinear superposition of a soliton upon itself [44].
When k1 = 1, k2 = k3 = k4 = 0, we have
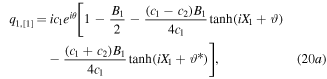
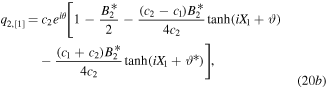
where
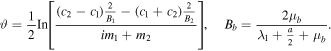
With ϑ = ϑ*,

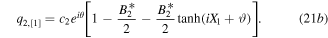
As 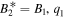 is proportional to q2. The vector soliton is grey typed [1], because the cavity depth of the soliton
is proportional to q2. The vector soliton is grey typed [1], because the cavity depth of the soliton  is
is 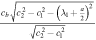 , related to λ1. Velocity of the grey soliton is v = −(2λ1 − a), and the centre of the soliton locates on the line iX1 + ϑ = 0.
, related to λ1. Velocity of the grey soliton is v = −(2λ1 − a), and the centre of the soliton locates on the line iX1 + ϑ = 0.
With 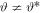 , q1 is not proportional to q2 and the solitons we obtain in here will possess different profiles. Figure 4(a) shows a W-shaped soliton (in the q1 component), while figure 4(b) shows a grey soliton (in the q2 component). Figure 4(c) shows an anti-dark soliton (in the q1 component) which has the form of a bright soliton on a non-zero background, while figure 4(d) shows an M-shaped soliton (in the q2 component).
, q1 is not proportional to q2 and the solitons we obtain in here will possess different profiles. Figure 4(a) shows a W-shaped soliton (in the q1 component), while figure 4(b) shows a grey soliton (in the q2 component). Figure 4(c) shows an anti-dark soliton (in the q1 component) which has the form of a bright soliton on a non-zero background, while figure 4(d) shows an M-shaped soliton (in the q2 component).
Figure 4. Solitons via solutions (20) with a = 0, c1 = 0.6, c2 = 1, λ1 = 0.76, (a) and (b)  and
and  (c) and (d)
(c) and (d) 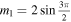 and
and 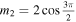 .
.
Download figure:
Standard image High-resolution imageWhen k2 = k4 = ik1 = ik3 = i, from expressions (12) we can see that q1 and q2 become the combination of the exponential and polynomial functions of z and t, and they form two coincident solitons with the same spectral parameter upon a first-order RW. In figure 5(a), the wave profile consists of two lines of the anti-dark soliton upon a RW which has one hump and two valleys, while in figure 5(b), the wave profile consists of two lines of the dark soliton upon one dark RW which has two valleys.
Figure 5. Degenerate solitons via expressions (16) with 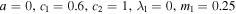 and m2 = 0.
and m2 = 0.
Download figure:
Standard image High-resolution imageIf 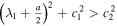 , we have known that X1 and X2 in expressions (12) and (16) are the real functions and kα's must satisfy that
, we have known that X1 and X2 in expressions (12) and (16) are the real functions and kα's must satisfy that 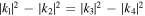
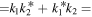
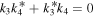 . When we choose k1 = 1, k2 = −i, k3 = k4 = 0, the solutions of equations (2) are the periodic solutions, as shown in figure 6. Compared with the elliptic periodic functions, we should notice that those periodic solutions obtained here are consist of the real trigonometric functions only, and 2μ2 is the frequency of the solutions.
. When we choose k1 = 1, k2 = −i, k3 = k4 = 0, the solutions of equations (2) are the periodic solutions, as shown in figure 6. Compared with the elliptic periodic functions, we should notice that those periodic solutions obtained here are consist of the real trigonometric functions only, and 2μ2 is the frequency of the solutions.
Figure 6. Periodic solutions via expressions (16) with a = 0.5, c1 = 1, c2 = 0.6, λ1 = 0, m1 = 2 and m2 = 0.
Download figure:
Standard image High-resolution imageWhen we choose 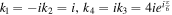 , the solutions is the so-called 'degenerate solutions', which can be regarded as the nonlinear superposition of a periodic solution upon itself [45], as shown in figure 7. The wave profiles consist of a line of periodic peaks upon a periodic background.
, the solutions is the so-called 'degenerate solutions', which can be regarded as the nonlinear superposition of a periodic solution upon itself [45], as shown in figure 7. The wave profiles consist of a line of periodic peaks upon a periodic background.
Figure 7. Degenerate solutions via expressions (16) with a = 0.5, c1 = 1, c2 = 0.6, λ1 = 0, m1 = 50 and m2 = 0.
Download figure:
Standard image High-resolution imageSimilar to the process of obtaining the RWs in section 3.1, we carry out the same limit 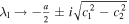 with
with 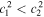 , i.e.,
, i.e.,  , and the periodic solutions become the rational solutions as long as kα's satisfy the conditions
, and the periodic solutions become the rational solutions as long as kα's satisfy the conditions
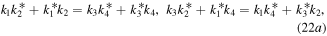
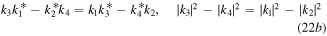
in expressions (16), and the longest period arises in that limit. For instance, we choose k1 = k3 = 1 and k2 = k4 = 0 to satisfy conditions (13) and (22), so that
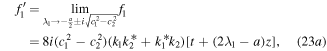
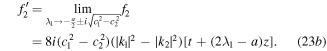
Substituting 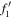 ,
,  and
and  ,
,  into BDT (4), we obtain the rational solutions, as shown in figure 8. It can be seen that the rational solutions preserve their profiles during the evolution. We should note that, although figures 4 and 8 have the similar wave profiles, analytic forms of the solutions are different (the first of which is exponential while the latter one is rational). Velocity of the rational soliton is v = −(2λ1 − a).
into BDT (4), we obtain the rational solutions, as shown in figure 8. It can be seen that the rational solutions preserve their profiles during the evolution. We should note that, although figures 4 and 8 have the similar wave profiles, analytic forms of the solutions are different (the first of which is exponential while the latter one is rational). Velocity of the rational soliton is v = −(2λ1 − a).
Figure 8. Soliton-like rational solutions via expressions (23) with a = −1.6, c1 = 0.6, c2 = 1, (a) and (b) m1 = 0 and m2 = 1; (c) and (d) m1 = 3 and m2 = 0.
Download figure:
Standard image High-resolution image5. Conclusion
In this paper, based on Lax pair (3), we have defined one-fold BDT (4) of equations (2) with condition (5), and constructed some vector analytic solutions of the coherently-coupled NLS equations with the positive coherent coupling terms, i.e., equations (3), which are related to the optical fiber communication.
Our main results from BDT (4) are proposed as follows:
- When the spectral parameter λ1 is complex with non-zero imaginary part, we have obtained the RWs via solutions (17) with the parameters m1 and m2. Figure 1 has displayed the vector generalization of the Peregrine soliton with m1 = m2 = 0. With m2 increasing, figures 2(a), (c) and (e) have displayed the eye-shaped RWs in the q1 component which have one hump and two valleys. In the q2 component, figure 2(b) has displayed a four-petaled RW which has two humps and two valleys, figure 2(d) has displayed a RW which has four valleys, and figure 2(f) has displayed a RW which has one hump and four valleys. In fact, figures 1(b), 2(b), (d) and (f) have shown that an eye-shaped RW splits in the q2 component with m2 increasing. Figure 3 has shown that the RWs in the two components are reduced in the z dimension with
 decreasing, and the inclinations of the RWs are dependent on the sign of m1. Summarisation of the vector RWs obtained in this paper have been given in table 1.
decreasing, and the inclinations of the RWs are dependent on the sign of m1. Summarisation of the vector RWs obtained in this paper have been given in table 1. - When λ1 is real, we have obtained the soliton and soliton-like rational solutions on the non-zero background. Figure 4 has shown the soliton solutions via Solutions (20). Besides, via expressions (16), figure 5–7 have shown the degenerate soliton solutions, periodic solutions, and degenerate solutions, respectively. Figure 8 has shown the soliton-like rational solutions via expressions (23).
Acknowledgments
This work has been supported by the National Natural Science Foundation of China under Grant Nos. 11772017, 11272023 and 11471050, by the Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications), China (IPOC: 2017ZZ05), and by the Fundamental Research Funds for the Central Universities of China under Grant No. 2011BUPTYB02.
Appendix
In this section, we will determine the matrix Ω in BDT (4) under condition (5). Two 4 × 2 matrixes ϒ and  are used to denote the first and last two columns of the 4 × 4 matrix Σ1, respectively, so that Σ1 can be written as
are used to denote the first and last two columns of the 4 × 4 matrix Σ1, respectively, so that Σ1 can be written as

where 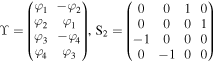 is a 4 × 4 matrix. Ω and Λ1 can be expressed as
is a 4 × 4 matrix. Ω and Λ1 can be expressed as
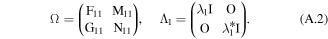
Substituting expressions (A.2) into condition (5), we have
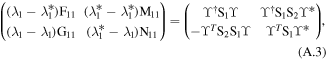
where F11, G11, M11, N11 are the 2 × 2 matrices, and section I is the 2 × 2 unit matrix, O is the 2 × 2 zero matrix, and S1S2 = S2S1.
However, as 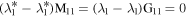 and
and  , we cannot calculate G11 and M11. The limit technique will help us to handle this problem [46]. We suppose that
, we cannot calculate G11 and M11. The limit technique will help us to handle this problem [46]. We suppose that
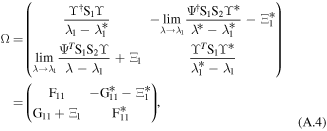
where 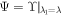 is a 4 × 2 matrix, and Ξ1 is a 2 × 2 complex constant matrix.
is a 4 × 2 matrix, and Ξ1 is a 2 × 2 complex constant matrix.
G11 can be expressed as
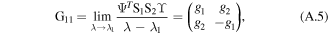
where g1 and g2 are the complex functions of z and t.
As Ξ1 is introduced via the limitation in expression (A.5), we set Ξ1 similar to G11 as

where m1 and m2 are the complex constants.
F11 can be expressed as
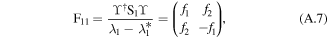
where 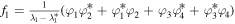 ,
, 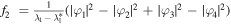 , and
, and 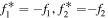 . Thus,
. Thus, 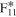 can be expressed as
can be expressed as
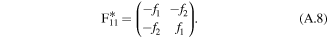
If the spectral parameter  , we have
, we have 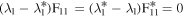 . To keep the non-singularity of Ω, we require ϒ to satisfy
. To keep the non-singularity of Ω, we require ϒ to satisfy  . In that case, we can suppose that
. In that case, we can suppose that
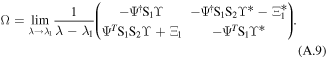
For simplicity, m1 and m2 are regarded as the real constants.