Acceleration control of Airy beams with optically induced photonic lattices

Airy beams are a well-known class of stationary freely accelerating wave forms [1]. The finite-energy Airy beam is characterized by the main intensity lobe that decays exponentially to zero on one side and decays with damped oscillations on the other. The interest in these beams lies in the fact that, if they have sufficiently wide apodization, the main intensity lobe of the Airy beam propagates free of diffraction bending in the direction transverse to propagation, or the main intensity lobe of the Airy pulse propagates free of dispersion accelerating along the propagation direction. The ballistic-like properties of the Airy beam [2] lend it to particular applications ranging from trapping of particles along curved paths [3] and self-bending plasma channels [4] to ultrafast self-accelerating pulses [5] and Airy light bullets accelerating in both transverse dimensions and in time [6].

Over the years, the propagation of Airy beams has been investigated in plasmonics, nonlinear photorefractive materials and photonic crystals [7–12]. It was shown that it is possible to generate self-accelerating nonlinearly self-trapped beams in various types of nonlinear media, ranging from Kerr and saturable Kerr-like media to quadratic nonlinearities. Also, it was shown that nonlinear Airy beams can invert the direction of acceleration by carefully adjusting the phase mismatch of the nonlinear processes involved [10].

Optical waves propagating in photonic periodic structures are known to exhibit fundamentally different behavior when compared with their homogeneous counterparts in bulk materials. These configurations provide an effective approach to control the propagation dynamics of light in a way that would have been otherwise impossible in bulk. Novel opportunities are offered when nonlinear material response to light intensity is taken into account. Studies of such nonlinear photonic lattices have shown that light propagation is governed by two competing processes: linear coupling among different lattice sites and energy localization due to nonlinearity. Self-localized states, called lattice solitons, can be obtained when these counteracting effects are in exact balance [13, 14].

To extend the ideas of these two concepts, here we analyze the effect of an optically induced photonic lattice on the acceleration dynamics of Airy beams. We demonstrate that it is possible to control the transverse acceleration of Airy beams when propagating in a photonic lattice. Modifying the lattice intensity as well as the strength of a medium's nonlinearity, the acceleration can be reduced to the point of creating a beam that propagates similar to discrete solitons, or simple solitary waves. We show that such propagating behavior is a result of two opposite effects, one due to the beam and the other to the photonic lattice. We also study the accelerating properties of such structures near the boundaries of the photonic lattice and demonstrate that the lattice surface produces a strong stabilizing effect and suppresses Airy beam acceleration for high enough lattice intensity. A novel type of Airy surface mode is observed in the lattice corner, for high lattice intensity or/and high nonlinearity of the medium.

The acceleration of Airy beams in optically induced photonic lattices is studied, and compared with corresponding Gaussian beam propagation. To examine the behavior of optical Airy wave packets in a photonic lattice, we consider the scaled nonlinear Schrödinger equation for the electric field amplitude E:

$$\begin{equation} \mathrm{i}\,\frac{\partial E}{\partial z}=-\Delta E-\gamma |E|^{2} E-VE, \end{equation} \tag{ 1 }$$

where Δ is the transverse Laplacian, γ is the dimensionless strength of the nonlinearity and V (x,y) is the periodic transverse lattice potential, with peak intensity V₀. A scaling x/x₀ → x, y/x₀ → y, z/L_D → z is utilized for the dimensionless equation, where x₀ is the typical full-width at half-maximum (FWHM) beam waist and L_D is the corresponding diffraction length. The propagation equation is solved numerically by employing a beam propagation method developed earlier [15].

Here we study the acceleration and the dynamics of finite-power Airy beams by considering their exponentially decaying version [16]:

$$\begin{equation} E(x,y,z=0)=\mathrm{Ai}(x)\mathrm{Ai}(y)\exp[(ax)+(ay)], \end{equation} \tag{ 2 }$$

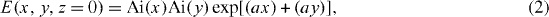
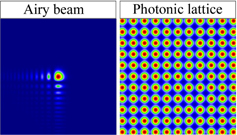
where a > 0 is a positive quantity to ensure containment of the infinite Airy tail. Input Airy beam distribution as well as intensity distribution of the photonic lattice is presented in figure 1. Corresponding Gaussian beam propagation is also investigated. We choose Gaussian beams having the same input FWHM as the appropriate main lobe of the Airy beam. We launch Airy as well as Gaussian beams positioned at the lattice site, perpendicular to the lattice, and investigate their propagation.

Zoom In Zoom Out Reset image size

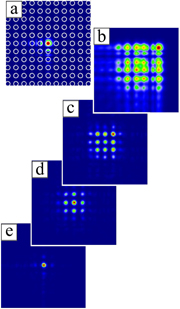
We start with investigation of the propagation effects of Airy beams in photonic lattices. First, we study a linear regime. This means that the nonlinearity is turned off (γ = 0). We choose a square photonic lattice, and launch Airy beams positioned at the lattice site: the lattice period is chosen such that the lattice sites fit the main and neighboring lobes of the Airy beam (figure 2(a)). Series of numerical measurements with different photonic lattices are performed to manipulate the acceleration of Airy beams. To study how photonic lattices influence Airy beam acceleration, we change the input lattice peak intensity. Typical results are summarized in figure 2. For lower lattice intensity, one can observe Airy beam acceleration (figure 2(b)), but with slight reshaping of the Airy beam: the presence and influence of the lattice are visible. On further increasing the lattice intensity, we discover discrete lattice solitons but first with more pronounced intensity of the main lobe of the Airy beam pinned to one lattice site (figure 2(c)). With very high lattice intensity one can observe typical solitary-like beams (figure 2(e)). This effect is a sign of competition between two joint effects: beam acceleration and influence of photonic lattices on beam propagation.

Zoom In Zoom Out Reset image size

We also study the accelerating properties of such structures in different nonlinear regimes (γ > 0). For higher nonlinearity of the medium, there are strong stabilizing effects. The suppression of Airy beam acceleration, in the nonlinear regime, is observed even for very low lattice intensities (not shown). We discovered that with various joint influences of lattice intensity and a medium's nonlinearity, it is possible to control and manipulate Airy beam acceleration in photonic lattices.

Next, we compare our result with the propagation of a single Gaussian beam in an optically induced photonic lattice. We choose a Gaussian beam such that its input FWHM is the same as the main lobe FWHM of the Airy beam. Figure 3 presents typical results of Gaussian beam propagation in a photonic lattice. As is well known, for lower lattice intensities there are discrete lattice solitons (figure 3(b)); however, one can observe a real soliton for high lattice intensity (figure 3(c)). But, while the Gaussian beam undergoes significant spreading, the Airy beam propagates almost undiffracted. Higher lattice intensities or/and higher nonlinearity of the medium are necessary to observe solitons if an input Airy beam is used when compared to the corresponding input Gaussian beam.

Zoom In Zoom Out Reset image size

Spatial surface solitons propagating in waveguide arrays and two-dimensional photonic lattices have attracted considerable attention for their potential in all-optical photonic applications [17, 18]. The edges joining planar interfaces have a strong impact on soliton formation. Since the truncation of the lattice represents a major distortion in the periodicity, one would expect that the presence of a boundary would enhance the beam stabilization.

Here, we study the propagation of Airy beams near the surface of a truncated photonic lattice optically induced in a photorefractive crystal, and describe novel types of Airy surface modes, localized in the lattice corners. We launch Airy beams positioned at the lattice corner (figure 4(a)). Figure 4 presents typical behavior of Airy beams propagating near the lattice boundaries. For lower lattice intensity, Airy beams still accelerate (figure 4(b)). However, by increasing the lattice intensity one can suppress beam acceleration (figures 4(c)–(e)). In such a case, it is possible to observe Airy surface modes (figure 4(e)). Similar behavior is observed on increasing the medium's nonlinearity, or considering the influence of both the medium's nonlinearity and lattice intensity.

Zoom In Zoom Out Reset image size

In conclusion, we analyzed numerically the effect of an optically induced photonic lattice on the acceleration of Airy beams. We demonstrated that it is possible to control the transverse acceleration of Airy beams by changing the strength of a medium's nonlinearity and lattice intensity. We have shown that acceleration can be reduced to the point of creating a beam similar to discrete solitons, or simple solitary waves. The accelerating properties of Airy beams near the lattice boundaries have also been studied. Airy surface modes have been observed in the lattice corner, with conclusions that the lattice surface produces a strong stabilizing effect and suppresses Airy beam acceleration for high lattice intensities or/and a medium's nonlinearity.

This work was supported by the Ministry of Education and Science of the Republic of Serbia (project OI 171036). DMJ expresses gratitude to the Alexander von Humboldt foundation for the Fellowship for Postdoctoral Researchers.