Introduction

Sedimentation is one of the critical issues in the geomorphological processes within a basin. Due to sediment transport dynamics, various geological, hydrological, and hydraulic sedimentation issues are caused due to sediment transport dynamics (Adib and Mahmoodi 2017; Gholami et al. 2018; Jian et al. 2014). In the construction of hydraulic systems on various watershed sections, sediment content is often impacted. Thus, sediment loads are decisively calculated (Choubin et al. 2018; Kuriqi et al. 2020; Moeeni and Bonakdari 2018). It is essential to correctly estimate the amount of river sediment to design dams, storage structures, and canals, evaluate environmental effects, and decide the effectiveness of watershed management and other catchment treatments. Regression-based sediment rating curves are often used to estimate a river’s sediment load. Generalization capability problems subject to multi-linear regression (MLR) and curve fitting techniques have proven insufficient (Kisi 2005). The high degree of scattering that can be reduced but not eliminated is an inherent problem in the rating curve technique (Jain 2001). Asselman (2000) used the sediment rating curve approach at four separate sites along the Rhino River and its major tributaries, showing that rating curves obtained from logarithmically transformed results are likely to underestimate sediment transport levels by 10 50%. Diverse studies contrast-suspended concentration, which has been carried out and predicted, shows that conventional rating curves can significantly underestimate existing sediment concentrations (Adib and Mahmoodi 2017; Asselman 2000; Hauser-Davis et al. 2010).

More advanced methods based on artificial neural networks (ANN) algorithms have been developed for sediment transport and accumulation estimation in different rivers and lakes (Banadkooki et al. 2020; Cigizoglu 2004; Cobaner et al. 2009; Jain 2012; Kumar et al. 2016; Partal and Cigizoglu 2008). ANN is an adaptive framework that can predict previously encountered datasets but with specific features connected to input datasets, learning input/output relationships (Gholami et al. 2018; Kisi 2005). ANN was used to model the stage–discharge that usually performs better than traditional ones (Ajmera and Goyal 2012; Hasanpour Kashani et al. 2015; Heggen 1999; Song et al. 2013; Sudheer and Jain 2003).

The support vector machine (SVM) algorithm is also successfully used in several hydraulic and hydrologic-related problems (Cherkassky and Ma 2004; Jain 2012). The SVM follows the principle of structural risk mitigation of upper binding to generalization mistake instead of minimizing a training error greater than the philosophy of methodological risk minimization (Jain 2012). This is an effective way to address nonlinear classifications, regression processes, and time series (Wang et al. 2008). The SVM stands for kernel-based learning utilizing a high-dimension linear theory space called feature space as a supervised machine learning environment that has become quite popular. The SVM works by mapping data to a higher-dimensional space using inferred kernel functions (Sivapragasam and Muttil 2005). SVMs are used effectively by many scientists in hydrological studies (Ghorbani et al. 2013; Jain 2012; Khan and Coulibaly 2006; Kisi and Cimen 2011; Malik and Kumar 2015; Rahgoshay et al. 2018; Wu et al. 2008).

In conjunction with ANN, many research types used wavelet techniques for water management and environmental engineering issues (Kişi 2010). Combined methods have recently gained growing popularity. Wavelet analysis (WA) is a standard analysis technique as spectral and temporal data can be seen simultaneously in a single signal (Nourani et al. 2009). Kim and Valdés (2003) predict droughts using wavelet-ANN in Mexico. Adib and Mahmoodi (2017) developed a hybrid wavelet-ANN model for the monthly rainfall–runoff research in Italy. Kişi (2008) investigated the precision in monthly streamflow prediction for wavelets-ANN and single ANN models and found that wavelets-ANN function much better than single ANNs. Nourani et al. (2009) examine the impact of data preprocessing on the outcomes of ANN models using continuous and discrete wavelet transformations. Partal and Cigizoglu (2008) suggested utilizing wavelets and neural networks in a study to estimate and forecast a load of rivers’ suspended sediment. These studies showed that the preprocessed data with wavelet analysis performs better than the undecomposed raw data. It can be shown that the different features of the suspended sediment load prediction time series can be expressed by the sub-time series obtained using wavelets (Kuo et al. 2010). Short- and long-term forecasts’ accuracy is enhanced (Nourani et al. 2018; Sharghi et al. 2018; Shiri and Kisi 2010).

However, while machine learning models have shown to be reliable in general, they are still not widely used for estimating the stage–discharge–sediment relationship in some situations. As a result, applying techniques to model, this dynamic relationship is motivated by previous use of effective learning strategies for various hydrological and hydraulic issues. Using specific actual datasets with ANN, SVM, WAAN, WSVM, and MLR, this work explores how current data-driven models are applied to explore the stage–discharge–sediment relationships Adityapur and Ghatshila sites of the Subernrekha river basin. According to the author’s understanding, there has been less work to use modeling to estimate suspended sediment using the stage as input parameters. No work has been done using the given model for the given study site. This research aims to apply modern data-driven models to water management to solve various complex problems in hydraulics and hydrology in the study area.

Materials and methods

Study area and data acquisition

This study was carried out in the Adityapur and Ghatshila sites in the Saraikela Kharsawan districts of Jharkhand, India. Adityapur site is at Kharkai River, a major tributary of the Subernrekha River, which lies at a latitude of 22° 47′29ʺ N and longitude 86° 10′06ʺ E. The Ghatshila site is situated on the main river course of Subernrekha, having a latitude of 22° 34′49ʺ N and a longitude of 86° 20′08ʺ E. Map for the studied area is shown in Fig. 1.

Fig. 1
figure 1

Location map of the Ghatshila watershed

Full size image

The area contributing runoff to the study site is 8335.25 km2. It is located at the height of 140 m above sea level. The study site’s estimated annual rainfall ranges from 1000 to 1400 mm. The southwest monsoon generally influences the study area, which has onset timing in June and extended up to October. The temperature variations during the summer season are from 35 to 40 °C, while during the winter season, it varies from 10 to 15 °C. The topography is generally flat with some undulations, small hillocks, and scattered ridges. The different rock types included in the study area are mica-schist, quartz-mica, quartzite, and schistose amphibolite of the Precambrian age. The vegetal cover is sparse, and the primary crop grown is wheat, rice, and maize, among others. The daily stage, discharge, and suspended sediment concentration (SSC) of the study area from June 1, 2004, to October 31, 2013, are considered in the analysis. Figure 2a–c presents the dataset of total data length of the period mentioned above as 1530 in which 70% (2004–2010) were used for training the dataset for model development, while the rest 30% (2011–2013) was used for the testing phase and validation purpose. The data are acquired from the government portal https://indiawris.gov.in.

Fig. 2
figure 2

Time-series representation: a stage, b discharge and c SSC for the Adityapur and Ghatshila site

Full size image

Statistical analysis

The statistical analysis of daily stage (m), discharge (m3/s), and suspended sediment concentration (SSC, g/l) for the Adityapur site and Ghatshila site (Jharkhand, India) is presented in Tables 1, 2. Statistical analysis for the datasets collected containing the training and the testing sets includes the meaning, median, minimum, maximum, standard deviation (Std. Dev.), coefficients of variations (C.V.), and skewness values. In general, Tables 1 and 2 showed statistical characteristics for all data, training sets, and testing sets that were more or less comparable in terms of mean, median, standard deviation, C.V., and skewness.

Table 1 Statistical investigation for all data, training data, and testing data of stage (m), discharge (m3/s), and SSC (g/l) for the Adityapur site
Full size table
Table 2 Statistical investigation for all data, training data, and testing data of stage (m), discharge (m3/s), and SSC (g/l) for the Ghatshila site
Full size table

The mean values of stage and discharge are greater for testing data than all data and training sets, but SSC’s value is lesser for the testing set than for the other two. The values of the stage range from 1.380 to 13.950 m and 1.60 to 12.59 m, respectively, for Adityapur and Ghatshila. The discharge values for Adityapur and Ghatshila range from 0.001 to 5.856 (× 103 m3/s), and 0.007 to 9.609 (× 103 m3/s), respectively, and the SSC ranges from 0.0 to 2.085 g/l and 0.0 to 1.76 g/l, respectively. The skewness values in Tables 1 and 2 show that the distribution is positively skewed (Ghorbani et al. 2013; Liu et al. 2013; Rajaee et al. 2011). The skewness coefficients for discharge values are more significant, followed by SSC and stage values.

Artificial neural network (ANN)

The ANN technique is used to simulate a similar process as the human brain’s problem-solving process. The ANN technique has received much attention in the last few decades to model and predict the nonlinear hydrologic and hydraulics processes’ nonlinear behavior. Among ANN, the feed-forward back-propagation techniques have drawn much attention due to their less complexity (Choubin et al. 2018; Solomatine and Ostfeld 2008). The ANN technique has three layers: (i) the input layer, I (ii) the hidden layer (j), and (iii) the output layer (j) (k) (Fig. 3).

Fig. 3
figure 3

adapted from Kişi (2010)

Structure for the three-layer artificial neural network,

Full size image

Between the layers of neurons (1, 2,…, L, M, N), entangled weight Wij and Wjk are used to link them. An input layer’s neurons coordinate in a forward direction. The output for the given input value is computed during a nonlinear function called the activation function. The weight value is adjusted during training using the trial-and-error process (Alp and Cigizoglu 2007; Kişi 2010). Overfitting is one of the biggest challenges during training processes. In this analysis, Levenberg–Marquardt was used to train the model. The hyperbolic tangent sigmoid transfer function was used to calculate the layer’s output from its net input.

Support vector machine (SVM)

The SVM approach depends on the theory of statistical learning (Vapnik 1999). The SVM is a community of artificial networks notable for its overall success in classifying patterns and nonlinear regression (Cao and Tay 2003). The SVM is used for evaluating variable time series regression to estimate and simulate the same variables. The SVM model’s relationship is as follows Kisi et al. (2017).

In the case of a training dataset, T, which is denoted by

$$T = \, \left\{ {\left( {x_{1} , \, y_{1} } \right), \, \left( {x_{2} , \, y_{2} } \right), \ldots ,\left( {x_{m} , \, y_{m} } \right)} \right\}$$
(1)

where x ϵ X and ℝn are the training inputs and y ϵ Y and ℝn are the training outputs. Assume that f(x) is a nonlinear equation and given by:

$$f \, \left( x \right) = {\varvec{w}}^{{\varvec{T}}} {{\varvec{\Phi}}}({\varvec{x}}_{{\varvec{i}}} ) + b$$
(2)

where w refers to the weight vector, b corresponds to the bias, and Φ(xi) denotes the high-dimensional feature space, linearly mapped from the input space x. SVM aims to reduce the gap between data from observations and simulations. Thus, SVM techniques reduce the objective function to minimize errors depending on the process of optimization. The error function ignores errors that are smaller than the threshold ε.

$$\begin{aligned} {\text{minimize}}: & \frac{1}{2}{\varvec{w}}^{{\varvec{T}}} {\varvec{w}} \\ {\text{subject}}\;{\text{to}}: & \left\{ {\begin{array}{*{20}c} {y_{i} {-} \left( {{\varvec{w}}^{{\varvec{T}}} {{\varvec{\Phi}}}\left( {{\varvec{x}}_{{\varvec{i}}} } \right) + b} \right) \le \varepsilon } \\ { y_{i} {-} \left( {{\varvec{w}}^{{\varvec{T}}} {{\varvec{\Phi}}}\left( {{\varvec{x}}_{{\varvec{i}}} } \right) + b} \right) \ge \varepsilon } \\ \end{array} } \right. \\ \end{aligned}$$
(3)

where ε (≥ 0) represents the maximum acceptable deviation.

For solving Eq. (3), the slack variables account for possible infeasible optimization problems. This may further lead to the following formulation as given by Vapnik (1995):

$$\begin{aligned} {\text{minimize}}: & \frac{1}{2}{\varvec{w}}^{{\varvec{T}}} {\varvec{w}} + {\varvec{C}}\,\mathop \sum \limits_{{{\varvec{i}} = 1}}^{{\varvec{m}}} \left( {\xi_{i}^{ + } + {\upxi }_{i}^{ - } } \right) \\ {\text{subject to}}: & \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {y_{i} {-}{\varvec{w}}^{{\varvec{T}}} {{\varvec{\Phi}}}\left( {{\varvec{x}}_{{\varvec{i}}} } \right) - b \le \varepsilon + \xi_{i}^{ + } } \\ {{\varvec{w}}^{{\varvec{T}}} {{\varvec{\Phi}}}\left( {{\varvec{x}}_{{\varvec{i}}} } \right) + b - y_{i} \le \varepsilon + \xi_{i}^{ - } } \\ {\xi_{i}^{ + } ,\xi_{i}^{ - } \ge 0} \\ \end{array} } \\ { } \\ \end{array} } \right. \\ \end{aligned}$$
(4)

where C is the penalty coefficient represents the weight loss function. The term wTw represented the regularization term and makes them as ‘flat’ as possible; second term C \(\mathop \sum \limits_{{{\varvec{i}} = 1}}^{{\varvec{m}}} \left( {\xi_{i}^{ + } + \xi_{i}^{ - } } \right)\) is called a practical term and measures ε-incentive loss function. The slack variables, i.e., \(\xi_{i}^{ + } ,\xi_{i}^{ - }\) represents upper and lower deviations, respectively. The highest deviation represents the ε-tube. Since all of the data points in this tube are equal to 0, they do not refer to the regression model (Fig. 4).

Fig. 4
figure 4

Schematic presentation of the support vector machine structure

Full size image

The values of the above parameters are then substituted in Eq. 2 to obtain f(x). Nonlinear time series can be predicted and analyzed using the SVM model. Thus, the final expansion of support vector regression is given by:

$$f\left( x \right) = \mathop \sum \limits_{i = 1}^{m} \left( {\alpha_{i}^{ + } - \alpha_{i}^{ - } } \right)K\left( {x_{i} , x_{j} } \right) + b$$
(5)

where \(\alpha_{i}^{ + }\),\(\alpha_{i}^{ - }\) are Lagrangian multipliers which are used to remove a few primary variables, and the term \(K\left( {x_{i} , x_{j} } \right)\) is the kernel function. It has the advantage of independent of both dimensionalities of the input space X and the sample size m. The kernel function of the SVM technique allows nonlinear approximations. Linear function was the kernel function that was used in this analysis (L.F.). The most basic kernel function is as follows Han et al. (2007):

$$K\left( {x_{i} , x_{j} } \right) = \left( {x_{i} , x_{j} } \right)$$
(6)

The efficiency of the SVM techniques depends on the environment for an ε-insensitive loss of the function of three parameters of the training process (kernel, C, \(\gamma\), and ε). For each kernel type, though, the values of C and ε affect the complexity of the final model. This value measures the number of support vectors (S.V.) used for projections. The greater value of ε intuitively results in fewer supporting vectors leading to less complex regression estimates. On the other hand, the value of C is a trade-off between model complexity and the variance allowed within the optimization formulation. As a result, a higher C value reduces model complexity (Cherkassky and Ma 2004). The optimal values for these training parameters (C and ε) ensure fewer complex models. This is an active research field.

Wavelet transform

Wavelet transform overcomes conventional solution issues by delivering the most potent way to dismantle signals into two-dimensional space: time or space (Sharghi et al. 2018). Like the Fourier transform, the wavelet transform allows for time conversion of the different frequency parts of a data set. However, with one crucial difference, the short-term Fourier transform produces a more accurate window width operation. Therefore, both the resolution of the time and the resulting transformations’ frequency must be provisionally established. Still, in wavelet transform, the study will adjust its time width to the frequency. Higher-frequency waves become very narrow, while lower-frequency waves become very broad (Khan and Coulibaly 2006). The wavelet transform’s ability to concentrate on brief intervals for high-frequency components and extended periods for low-frequency components improves signal processing of concentrated impulses and oscillation. As a result, wavelet decomposition is an excellent choice for evaluating transient signals and obtaining a more accurate comparison and discrimination process (Wang et al. 2008; Youssef 2003).

A continuous-time signal, x(t), is transformed by the wavelet time-scale as Addison et al. (2001):

$$T \, \left( {a, \, b} \right) = \frac{1}{\sqrt a }\mathop \smallint \limits_{ - \infty }^{ + \infty } g^{*} \left( {\frac{t - b}{a}} \right)x\left( t \right) \cdot dt$$
(7)

where ‘a’ and ‘b’ denote the function’s dilatation factor and temporal localization g(t), respectively, to enable the study of the signal around ‘b,’ * denotes equivalent to the complex conjugation, and g(t) denotes the wavelet or mother wavelet function (Youssef 2003).

Equation (7) discretization is perhaps the simplest discretization based on the trapezoidal law of a continuous wavelet transformation (CWT). From the given data set of length N, the above transformation method yields N2 coefficients; thus, obsolete information is plugged inside the coefficients, which might or might not be desirable (Kişi 2010; Rajaee et al. 2011). For overcoming this complexity, uniform logarithmic spacing can be used for a correspondingly coarser resolution of b positions, allowing a complete definition of a signal length N by N transforming coefficients. A discrete wavelet of this kind has the following shape:

$$g_{m,n} \left( t \right) = \frac{1}{{\sqrt {a_{0}^{m} } }}g\left( {\frac{{t - nb_{0} a_{0}^{m} }}{{a_{0}^{m} }}} \right)$$
(8)

WANN and WSVM model

The present study used a discrete wavelet transformation to hybridize the model. Hybridized approaches for model creation and validation were used for the wavelet-based artificial neural network (WANN) (Kumar et al. 2016; Liu et al. 2013) and wavelet-based support vector machine (WSVM). To begin, the time-series data for the measured stage (h), discharge (Q), and sediment (S) were decomposed into many frequencies. Figure 5 represents the decomposed time series by wavelet transform (Sudheer and Jain 2003).

Fig. 5
figure 5

Construction of proposed WANN and SVM model

Full size image

The decomposed components of time series by DWT like hDi(t), …, hDi(t − n), hAi(t),.., hAi(t − n), QDi(t),…, QDi(t − n), QAi(t),.., QAi(t − n), and SDi(t − 1),..,SDi(t − n), SAi(t − 1),..,SAi(t − n) were used for stage–discharge–sediment modeling, where, hDi(t), …, hDi(t − n) and hAi(t),.., hAi(t − n) are the details and approximate sub-signals of stage time series. QDi(t),…, QDi(t − n) and QAi(t),.., QAi(t − n) are the details and approximate sub-signals of discharge time series, respectively. SDi(t − 1), …, SDi(t − n) and SAi(t − 1), …, SAi(t − n) are the detail and approximation coefficients of SSC time series, respectively (Bajirao et al. 2021). The original h, Q, and SSC time series selected per the Gamma test were decomposed using Haar á trous mother wavelet at appropriate decomposition levels. Afterward, these decomposed time-series values act as input for ANN and SVM techniques to predict the output value.

Multiple linear regression (MLR)

MLR is a form of linear regression analysis that involves more than one independent variable. The advantage of MLR is that it is simple, which shows how dependent variables are with independent variables (Choubin et al. 2018). The overall model of the MLR is:

$$y = c_{0} + c_{1} x_{1} + c_{2} x_{2} + \ldots + c_{n} x_{n}$$
(9)

Y represents the dependent variable, and x1, x2,..,xn refer to independent variables, c1, c2, …,cn correspond to regression coefficients, and c0 is intercepted. The least-square rule or regression rule is used to measure these values, representing the local actions (Kisi and Cimen 2011).

Gamma test

The Gamma test is a versatile and impartial method for assessing each input parameter’s significant potential. Stefánsson et al. (1997) pioneered gamma testing in modeling, later adopted by other researchers (Kumar et al. 2016; Malik and Kumar 2015; Nourani et al. 2009). The Gamma test was used for any input–output dataset to estimate a minimum standard error for continuous nonlinear models. A linear regression line is built to measure gamma as:

$${\varvec{Y}} = {\varvec{A}}\Delta \, + \, \Gamma$$
(10)

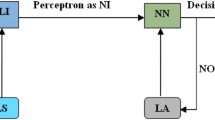
Y denotes the regression line’s output vector, A represents the gradient, and Γ corresponds to the intercept (Δ = 0). The value of Γ corresponds to the output at Δ = 0. The smaller value of Γ (close to zero) is acceptable. The gamma test was processed in ‘winGamma’ software (Hassangavyar et al. 2020). The flowchart of the adopted methodology in this study is shown in Fig. 6.

Fig. 6
figure 6

Flowchart of SSC estimation methodology in the study area

Full size image

Model development and performance evaluation

This research was undertaken to establish the relationship between stage–discharge–sediment for the Adityapur site of Jharkhand, India. The modeling included ANN, SVM, WAAN, WSVM, and MLR techniques to develop and validate the model. ANN and wavelet decomposed data were developed using MATLAB (R2015a) software. SVM models were developed in R-Studio and MLR models constructed in MS-Excel 2019 software. The model’s performance was assessed using quantitative metrics (RMSE, PCC, and WI) and qualitative metrics (time variance map, scatter plot, and Taylor diagram) between observed and expected SSC (g/l) values. The input variables for the ANN, SVM, WAAN, WSVM, and MLR models developed were selected by gamma test based on minimum gamma value.

Three performance standards were used in the present study to assess the model’s performance. These are Pearson correlation coefficient (PCC), root mean square error (RMSE), Nash–Sutcliffe efficiency, and Wilmot index (WI). The combined use of RMSE (Bajirao et al. 2021; Kumar et al. 2016; Malik and Kumar 2015) and WI (Willmott 1984) provides an adequate evaluation of the results. It compares the exactness of the various measurement and modeling techniques used in this study, further discussed by Ghorbani et al. (2013).

The PCC value ranges from − 1 to + 1, and the value close to + 1 represents the best fit. Its aim in hydrological studies is to determine the degree of collinearity between observed and predicted variables. It is oversensitive to extreme value (Liu et al. 2013), from 0 to infinity, the RMSE value ranges. The value close to zero represents the model’s better performance. The RMSE value has the same unit as the model output and reports the typical error size. The NSE was initially proposed by McCuen et al. (2006) and frequently used to assess the hydrologic model’s performance. It determines the relative magnitude of residual variance compared to measured data variance. NSE values vary from − ∞ to 1. The WI value ranges from 0 to 1. The values close to 1 represent the best fit, while 0 means disagreement between observed and predicted data. It is also known as the index of agreement.

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{{{\varvec{i}} = 1}}^{{\varvec{N}}} \left( {{\varvec{S}}_{{{\varvec{p}}_{{{\mathbf{obs}}\user2{,i}}} }} - {\varvec{S}}_{{{\varvec{p}}_{{{\mathbf{pre}}\user2{,i}}} }} } \right)^{2} }}{{\varvec{N}}}}$$
(11)
$${\text{PCC}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {S_{{p_{{{\text{obs}},i}} }} - \overline{S}_{{p_{{{\text{obs}},i}} }} } \right)\left( {S_{{p_{{{\text{pre}},i}} }} - \overline{S}_{{p_{{{\text{pre}},i}} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {S_{{p_{{{\text{obs}},i}} }} - \overline{S}_{{p_{{{\text{obs}},i}} }} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{N} \left( {S_{{p_{{{\text{pre}},i}} }} - \overline{S}_{{p_{{{\text{pre}},i}} }} } \right)^{2} } }}$$
(12)
$${\text{NSE}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {{\varvec{S}}_{{{\varvec{p}}_{{{\mathbf{obs}},{\varvec{i}}}} }} - {\varvec{S}}_{{{\varvec{p}}_{{{\mathbf{pre}},{\varvec{i}}}} }} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {S_{{p_{{{\mathbf{obs}},{\varvec{i}}}} }} - \overline{S}_{{p_{{{\mathbf{pre}},\user2{ i}}} }} } \right)^{2} }}} \right]$$
(13)
$${\text{WI}} = 1 - \frac{{\mathop \sum \nolimits_{{{\varvec{i}} = 1}}^{{\varvec{N}}} \left( {{\varvec{S}}_{{{\varvec{p}}_{{{\mathbf{obs}},{\varvec{i}}}} }} - {\varvec{S}}_{{{\varvec{p}}_{{{\mathbf{pre}},{\varvec{i}}}} }} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\left| {S_{{p_{{{\text{pre}},i}} }} - \overline{S}_{{p_{{{\text{obs}},i}} }} } \right| + \left| {\overline{S}_{{p_{{{\text{obs}},i}} }} - \overline{S}_{{p_{{{\text{obs}},i}} }} } \right|} \right)^{2} }}$$
(14)

Results and discussion

This section discusses the outcomes of dividing the stage–discharge–sediment model into two sections. The first section contains the results of the gamma test used to pick input variables, and the second section contains the results of model creation and output for both the Adityapur and Ghatshila sites.

Input selection: gamma test

The first step in every modeling process is to choose input variables. Many scientists have stated that the present-day suspended sediment concentration (SSC) can be estimated more accurately by the simultaneous current day stage (h), discharge (Q), along with previous day h, Q, and SSC values (Cigizoglu 2004; Jain 2012). Therefore, current day (t), one-day lag (t − 1), two-day lag (t − 2), and three-day lag (t − 3) time steps ht, ht−1, ht−2, ht−3, Qt, Qt−1, Qt−2, Qt−3, St−1, St−2, and St−3 which is represented by model 48 (mask-11111111111) and 0 represents the absence of that variables in other combinations (Table 2). A total of forty-eight combinations were created using different time steps of the stage, discharge, and SSC data, as seen in Tables 3 and 4 for the Adityapur and Ghatshila sites. The gamma value (Γ), variance ratio (Vratio), and mask for various combinations of input variables for model creation are shown in Tables 3 and 4.

Table 3 Findings of the gamma test obtained for different combinations of input variables for the Adityapur site
Full size table
Table 4 Findings of the gamma test obtained for different combinations of input variables for the Ghatshila site
Full size table

The selection process depends on the smallest value of Γ and Vratio (Jain 2012; Malik et al. 2019; Nourani et al. 2018). Vratio tests its predictability with the available inputs for the specified output. Vratio near 1 indicates that the fundamental model is not quite close to being smooth. However, Vratio near 0 demonstrates that the results are generated from the smooth model (Malik et al. 2019). As shown in Table 3, the integration of ht + ht−1 + Qt + Qt−1 + Qt−2 + St−1 (Model no.-19) showed the most negligible value of Γ and Vratio as 0.0813 and 0.3253, respectively.

Therefore, the combination (mask-11001110100) of ht + ht−1 + Qt + Qt−1 + Qt−2 + St−1 was selected as input variables for ANN, SVM, WAAN, WSVM, and MLR models for Adityapur site. Likewise, Table 4 showed the combination ht + Qt + St−1 + St−2 + St−3 (Model-3) observed the minimum values of Γ and Vratio as 0.0046 and 0.1853, respectively. As a result, for the Ghatshila location, the combination (mask-10001000111) of ht + Qt + St−1 + St−2 + St−3 variables was chosen as input variables for ANN, SVM, WAAN, WSVM, and MLR models. As shown in Fig. 7, the correlation between output St and other input variables was satisfactory for all datasets (a, b).

Fig. 7
figure 7

Correlation graph of input variables for all dataset with output St. at a Adityapur, b Ghatshila

Full size image

Trials of models

The ANN, WANN, SVM, WSVM, and MLR were analyzed in two phases to select the best model. The first phase involves developing the model during the training phase—the second phase checks to validate the model. The model’s performance was evaluated based on the lower value of RMSE (0: + ∞: good: poor), a higher value of PCC, NSE, and WI (close to + 1) for selections of the best model (Kumar et al. 2020). Several trials were conducted for single output on the best model for ANN, WANN, SVM, and WSVM (Tables 5 and 6). The number of neurons in hidden layers was varied in ANN trials. An input layer, a hidden layer, and an output layer make up the ANN architecture. Considering architecture 6-4-1, 6 represents the number of input parameters, and the number of neurons in the un-seen layer is 4. The output is 1.

Table 5 Performance indicators of ANN, WANN, SVM, WSVM, and MLR models during the training and testing at the Adityapur site
Full size table
Table 6 Performance indicators of ANN, WANN, SVM, WSVM, and MLR models during the training and testing at the Ghatshila site
Full size table

The 24 represents the input parameters in the WANN architecture, 9 represents the number of hidden layer neurons, and 1 represents the output. Simultaneously, SVM trails were run using a variety of SVM-γ, SVM-c, and SVM-ε parameter values. All sites’ cost parameters (SVM-c) were taken as 10 based on separate trials, whereas ε is an insensitive loss feature. Training effects were not taken into account in this analysis to prevent the biases and overfitting of data.

Results at Adityapur site

At the Adityapur location, Table 5 displayed the quantitative results of all produced models. For the training period, PCC values ranged from 0.783 to 0.801, RMSE values ranged from 0.106 to 0.111 g/l, and NSE values were found in the range of 0.613 to 0.644 WI values ranged from 0.866 to 0.894. During the testing process, PCC values ranged from 0.562 to 0.632, RMSE values ranged from 0.097 to 0.106 g/l, NSE values ranged from − 0.425 to − 0.216, and WI values ranged from 0.690 to 0.729 for ANN techniques. During the training phase, the performance of WANN models showed that the PCC values were obtained in the range of 0.835–0.863. RMSE values were obtained in the range 0.090–0.099, the values of NSE obtained in the range of 0.691–0.745 while for WI were 0.899–0.921. The PCC values for WANN models ranged from 0.634 to 0.718, the RMSE values ranged from 0.071 to 0.078 g/l, the NSE values ranged from 0.232 to 0.356, and the WI ranged values from 0.767 to 0.812 during the testing process. During the training period of SVM models, PCC values ranged from 0.760 to 0.768, RMSE values ranged from 0.114 to 0.117, NSE values ranged from 0.568 to 0.586, and WI values ranged from 0.857 to 0.859. During the SVM models’ performance testing phase, the values of PCC ranged from 0.572 to 0.610, the values of RMSE were obtained in the range of 0.086–0.094, the NSE values ranged from − 0.139 to 0.046, and WI values ranged from 0.724 to 0.760. The performance of the hybrid techniques of wavelet support vector machine (WSVM) during training phase, the values of PCC ranged from 0.844 to 0.847. RMSE was obtained around 0.095 to 0.096 g/l, the values of NSE ranged from 0.711 to 0.714, and WI values ranged from 0.906 to 0.907. During the testing period, PCC values ranged from 0.745 to 0.781, RMSE ranged from 0.057 to 0.062, NSE ranged from 0.516 to 0.591, and WI varied from 0.856 to 0.878.

Table 5 shows that the WSVM model found the most reliable models out of all the existing models. During the training and testing processes, PCC, RMSE, NSE, and WI values were 0.844 and 0.781, 0.096 g/l and 0.057 g/l, 0.711 and 0.591 0.907 and 0.878, respectively. In contrast to other models, the NSE values for the WSVM model during the testing process significantly increased. The MLR model did not do well.

Figures 8a–e and 9a–e show the line diagram and scatter plots for all created models. These figures qualitatively represent the results of all developed models. On nearly all simulations, the expected values were over-predicted for lower SSC values and under-predicted for higher SSC values. The determination coefficient was the highest for the WSVM model (0.6096), followed by WANN values (0.5159). The R2 value was poorly obtained for the MLR model (0.2890).

Fig. 8
figure 8

Line diagram of developed models a ANN, b WANN, c SVM, d WSVM and e MLR during the testing phase for Adityapur sites

Full size image
Fig. 9
figure 9

Scatter plots of developed models a ANN, b WANN, c SVM, d WSVM and e MLR during the testing phase for Adityapur sites

Full size image

The sequence of models results from best to poor in order WSVM > WANN > ANN > SVM > MLR for Adityapur site. Hence, the WSVM model can be used to estimate SSC for the Adityapur site.

Results at Ghatshila site

Table 6 shows the results of the various performance metrics that were used to choose the best model. Table 6 shows that during training and testing, the values of r, RMSE (g/l), NSE, and WI ranged from 0.906 to 0.919 and 0.548 to 0.580, 0.054 to 0.131 and 0.131 to 0.139, 0.819 to 0.843 and 0.030 to 0.125, and 0.946 to 0.956 and 0.722 to 0.746, respectively. A-3 model with architecture (5-9-1) was observed to be superior model as compared to other ANN models. Likewise, the values of r, RMSE (g/l), NSE, and WI for WANN model varied from 0.940 to 0.950 and 0.703 to 0.725, 0.099 to 0.107 and 0.099 to 0.115, 0.884 to 0.902 and 0.333 to 0.500, and 0.968 to 0.971 and 0.827 to 0.845, respectively, during training and testing phases. W-1 model with architecture (20-3-1) found best among all WANN models. From Table 5, it is clear that the values of r, RMSE, NSE, and WI for SVM ranged from 0.886 to 0.891 and 0.579 to 0.586, 0.144 to 0.148 g/l and 0.125 to 0.128 g/l, 0.779 to 0.791 and 0.177 to 0.206, and 0.940 to 0.942 and 0.748 to 0.753, respectively, during training and testing. S-1 with structure (C = 10, γ = 0.2, ε = 0.1) found superior among SVM. During the training and testing phases of the hybridized wavelet SVM model, the values for r, RMSE, NSE, and WI ranged from 0.928 to 0.929 and 0.749 to 0.751, 0.116 to 0.117 g/l and 0.095 to 0.096, 0.861 to 0.862 and 0.538 to 0.543, and 0.962 and 0.859, respectively. Of all WSVM models, WS-1 with structure (C = 10, = 0.05, ε = 0.1) was found to be superior.

Table 6 reveals that the WSVM model observed the most accurate models among all developed models at the Ghatshila site. PCC, RMSE, NSE, and WI values were obtained as 0.928 and 0.751, 0.117 g/l and 0.095 g/l, 0.861 and 0.541, and 0.962 and 0.859, respectively, during training and testing phases. The results also showed that the NSE values for the WSVM model during the testing phase significantly improved compared to other models.

The line diagram and scatter plots at the Ghatshila site for all created models are shown in Figs. 10a–e and 11a–e. The qualitative results from the figures showed that the predicted values were over-predicted and under-predicted for SSC values for almost all models. The R2 values obtained maximum for WSVM model (0.5639) followed by WANN values (0.5250) and then followed by MLR model (0.2890).

Fig. 10
figure 10

Line diagram of developed models a ANN, b WANN, c SVM, d WSVM and e MLR during the testing phase for Ghatshila sites

Full size image
Fig. 11
figure 11

Scatter plots of developed models a ANN, b WANN, c SVM, d WSVM and e MLR during testing for Adityapur sites

Full size image

Thus, based on the obtained results discussed above for the Ghatshila site, the wavelet hybridized model (WSVM and WANN) outperformed all other models by a large margin. The sequence of the best to poor performance of models given as WSVM > WANN > MLR > SVM > ANN.

The comparative results of each of the best-developed Adityapur and Ghatshila sites are shown in Table 7. This table shows that the wavelet hybridized model was found to be superior to all other models. It is because of the application of the wavelet transform that may find various sub-series of the primary time series data that have extra information obscured by the original time series data. Wavelet transform improves the model performance because it simultaneously considers both time and frequency information available within the signal (Nourani et al. 2009).

Table 7 Comparative results of models during testing for both sites
Full size table

Our results are similar to Nourani et al. (2018), who applied the SVM technique with different input combinations to predict monthly suspended sediment load and stated that the correlation coefficient values ranged from 0.49 to 0.91 RMSE varied from 0.015 to 0.9. Furthermore, for the SVM in sediment yield prediction, our findings agree with Kumar et al. (2016), who found that correlation coefficients ranged from 0.66 to 0.90 for training models and from 0.24 to 0.93 for the testing phase. For SVM, the findings of this model are close and in line with Choubin et al. (2018), who concluded that the SVM gave correlations varied from 0.43 to 0.67 under different combinations for forecasting the suspended sediment. Moreover, Sharafati et al. (2020) used WSVM and SVM models in sediment yield (SY) modeling. They observed that the WSVM model produced better results than other algorithms. Their outcomes are acceptable and agree with our results. They showed that the use of WSVM is a more reliable alternative to conventional SY models. Besides, the efficiency of a wavelet-based model in the prediction of suspended sediment load was investigated by Nourani et al. (2009). They used WSVM and WANN wavelet complementary versions, respectively. Their outputs pointed out that the WSVM integrated model generated more reliable results than WANN. Liu et al. (2013) developed a WANN complement model. When the findings from WANN and ANN were compared, it was discovered that the WANN model could better forecast the extremely nonlinear time series than ANN. Also, as reported by, Partal and Cigizoglu (2008), the wavelet-ANN model demonstrated higher levels of accuracy than both the conventional ANN and the SRC. The results show that wavelet-ANN is capable of capturing better approximations for peak values. Jain (2012) applied ANN, fuzzy logic, and evolutionary algorithms in river stage–discharge–sediment rating modeling. When the findings of SVR were compared to those of ANNs, it was discovered that SVR outperformed ANNs.

The results for both the sites are also verified from the Taylor diagram. The Taylor diagram consists of a line designated as a straight line and standard deviation and root-mean-square difference (RMSD) designated as curvilinear (Fig. 12). Because of the highest correlation values and lower standard deviation and RMSD values for both locations, the findings of the wavelet hybridized model were found to be superior. The Taylor diagram also shows that the WSVM model got closer to the observed SSC values for both locations. On both sites, the Taylor diagram yields the same series of models as previously mentioned.

Fig. 12
figure 12

Taylor diagram of ANN, SVM, WANN, WSVM, and MLR models during the testing period at a Adityapur site and b Ghatshila site

Full size image

Conclusions

Estimating river sediment volumes is vital for measuring river sediment flow, designing dams, storage structures, and canals, evaluating environmental effects, and deciding the effectiveness of watershed management and other catchment treatments. In the present analysis, daily SSC model estimation was studied at the Adityapur site and Ghatshila site in the Saraikela Kharsawan district of Jharkhand, India. Hydrological datasets containing the daily stage (h), discharge (Q), and SSC for 10 years (2004–2013) period from June to October were taken for analysis. Five data-driven approaches, namely artificial neural network (ANN), support vector machine (SVM), wavelet-based artificial neural network (WANN), wavelet-based support vector machine (WSVM), and multi-linear regression (MLR) techniques were employed for modeling SSC for the study area. The gamma test was used for selecting input variables for the model, as mentioned earlier. The combination showed the most negligible value of Γ and Vratio as 0.0813 and 0.3253, respectively, for input combinations based on the gamma test ht + ht−1 + Qt + Qt−1 + Qt−2 + St−1 (mask-11001110100). Likewise, the combination ht + Qt + St−1 + St−2 + St−3 (mask-10001000111) observed the minimum values of Γ, and Vratio as 0.0046 and 0.1853, respectively. Therefore, it was considered as input variables for modeling. The performance of the model was evaluated through quantitative indicators (RMSE, PCC, and WI) and qualitative indicators (time variance map, scatter plot, and Taylor diagram) between actual and expected SSC (g/l) values. According to our findings, the WSVM model was the most reliable model among all existing models. Throughout the training and testing operations at the Adityapur location, PCC, RMSE, NSE, and WI values were 0.844 and 0.781, 0.096 g/l and 0.057 g/l, 0.711 and 0.591, and 0.907 and 0.878, respectively. It was also the most precise model on the Ghatshila site. During the training and testing stages, the PCC, RMSE, NSE, and WI values were 0.928 and 0.751, 0.117 g/l and 0.095 g/l, 0.861 and 0.541, and 0.962 and 0.859, respectively. The WSVM model outperformed the ANN, WANN, SVM, and model MLR models. The wavelet hybridized model (WSVM and WANN) performed better at both locations than the non-wavelet hybridized model. Also, the WSVM and WANN models’ best performance can assist researchers’ in the future in using extremely variable SSC data for such modeling.