Abstract
Finite-temperature effects in the first-principles calculations of electronic transport up to now include almost exclusively only electronic temperatures by means of the Fermi-distribution function neglecting the influence of lattice vibrations. Here, employing the linear response Kubo formalism as implemented in a fully relativistic multiple-scattering Korringa–Kohn–Rostoker Green function method a systematic first-principles study of the anomalous Hall conductivity (AHC) of the 3d-transition metals Fe, Co and Ni is presented. It is shown that the inclusion of both correlations and thermal lattice vibrations is needed to give a material-specific description of the AHC in transition metals. The employed general framework will allow a first-principles description of other transverse transport phenomena treating correlations, finite temperatures and disorder on the same footing, giving valuable insights for experiments.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The simple experiment by Hall [1] driving a current through a ferromagnet and observing the anomalous Hall effect (AHE) as a transverse voltage has fruitfully spurred the development of experimental and theoretical methods dealing with transport in solids. It now stands as a paradigm for understanding related transverse transport phenomena, such as e.g. the spin Hall- (SHE), anomalous- and spin-Nernst effects that have received intense interest in recent years. They all share a common origin, namely they are obviously spin–orbit-driven relativistic effects.
The AHE has for decades eluded theoretical understanding—it took more than 50 years for Karplus and Luttinger [2] to put forward an insight that initiated modern theories of the AHE. They identified the anomalous velocity as an interband matrix element of the current operator that is today the foundation of semiclassical approaches that give a topological formulation of the AHE in terms of the Berry phase of Bloch bands in pure crystals [3, 4]. The latter is used to define the so-called intrinsic contribution to the AHE. Already early on Smit [5, 6] and Berger [7] discussed other extrinsic origins of the AHE, namely skew- and side-jump scattering. There are extrinsic contributions to the AHE that fall in neither category [4]; however, it is now commonly established that we separate the AHE into an intrinsic and a skew-scattering contribution and declare the difference to the total AHE as side-jump scattering [8]. Experiments then rely on a scaling mechanism to extract these contributions from the raw data.
Besides a wealth of model calculations (see the review [8] and references therein) that are tailored to identify general trends but miss the material specific aspect a number of first-principles calculations building on a density-functional theory (DFT) framework have been undertaken recently to compute the anomalous Hall conductivity (AHC) in the transition metals (TMs) [9–12]. Almost all of them rely on the Berry phase formulation for pure crystals and therefore are only able to deal with the intrinsic contribution. Boltzmann transport theory-based formulations have been used in the context of the SHE [13] to compute the skew-scattering contributions in the dilute limit for alloys. Covering the whole concentration range of alloys and including all contributions to the AHE has recently been done [14, 16] on the basis of a Kubo–Středa formulation [17, 18].
The role of correlations in the electronic structure of the 3d-TM has only very recently been addressed in the context of the AHE [10, 11]. Employing the local spin-density approximation (LSDA), or generalized gradient approximation (GGA), gives unfavorable agreement with experiment, and with the AHE being a property of the Fermi surface [9, 19] it became clear that the LSDA/GGA does not supply the proper band structure. This is demonstrated, in particular, for the case of Ni (see also table 1) where the LSDA/GGA strongly overestimates the magnitude of the AHC. Employing the LSDA/GGA + U remedies this problem, by moving down d-bands relative to the Fermi energy (EF), thereby making the X2 hole pocket present in LSDA/GGA disappear.
Table 1. Intrinsic AHC σxy in (Ω cm)−1 of the ferromagnetic TMs Fe, Co and Ni from first-principles theoretical (present work compared to others) as well as experimental (Exp.) studies. The magnetization has been assumed to be oriented along the [001] direction.
| bcc-Fe | hcp-Co | fcc-Co | fcc-Ni | |
|---|---|---|---|---|
| LSDA, present work | 685 | 325 | 213 | −2062 |
| LSDA+U, present work | 703 | 390 | 379 | −1092 |
| LSDA/GGA | 753a,767b | 477a | 249c | −2203a,−2200d |
| 650e | 481c | 360e | −2410e | |
| LSDA+U/GGA+U | 643f | −960d,−900b | ||
| Exp. | 1032g | 813h | −646(@RT)i | |
| −1100(5K)j |
aWang et al [9]. bWeischenberg et al [10]. cRoman et al [33]. dFuh and Guo [11]. eTurek et al [16]. fTung et al [12]. gDheer [34]. hVolkenshtein et al [36]. iLavine [35]. jYe et al [21].
A further important aspect of the AHE that is addressed in experimental studies but rarely in theoretical considerations is the temperature dependence of the AHE. For the pure 3d-systems, measurements of the AHE are typically done on commercially available specimens or thick layers grown on a substrate [20–22] and the temperature is changed in order to vary the resistivity. The latter makes the discussion of the temperature dependence very delicate when trying to disentangle different mechanisms and contributions to the AHE (inelastic scattering: scattering by phonons/magnons, etc). It is advocated, however, as an empirical fact [8, 23] that inelastic scattering processes suppress the skew scattering at higher temperatures with the intrinsic and side-jump (see however the remark above) contributions dominantly prevailing. This then again is used to experimentally analyze the AHE. Recently, model calculations [23] studied the role of inelastic scattering by phonons employing a Kubo formalism and introducing a phenomenological scattering rate γ as the imaginary part of the self-energy. To our knowledge, no first-principles approach has been used so far to deal with the temperature dependence of AHE in 3d-TMs.
In this work, we present a generally applicable formalism and results of a first-principles approach for calculating the AHC of TMs and their alloys. We show that the inclusion of both finite-temperature and correlation effects leads to a unified material-specific description of these systems.
2. Theoretical approach
As the AHE is inherently a relativistic phenomenon, we choose to work within a fully relativistic approach employing the Kohn–Sham–Dirac equation as formulated in spin-polarized DFT employing the Hamiltonian
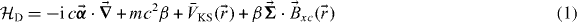
as implemented within the multiple-scattering Korringa–Kohn–Rostoker (KKR) Green function method [24]. Here 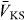 and
and 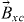 are the spin-averaged and spin-dependent part of the one-particle potential, respectively, m the electron mass, c the velocity of light and the relativistic matrices
are the spin-averaged and spin-dependent part of the one-particle potential, respectively, m the electron mass, c the velocity of light and the relativistic matrices 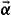 , β and
, β and 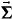 have the usual meaning [25–27]. Using the fully relativistic Dirac approach has the important advantage [18] that disorder (see below) can be treated elegantly without recourse to a Pauli approach, which poses difficulties in calculating the vertex corrections (vc). To determine longitudinal and transverse components of the conductivity tensor, a natural starting point is the linear response Kubo framework that can also be used to derive the Berry phase-related semiclassical approach [3, 4, 28]. The Kubo approach has important advantages as compared to the latter. It allows one to straightforwardly include disorder, and is therefore able to describe not only pure systems but also alloys in the full concentration range including intrinsic and extrinsic contributions to the AHE [14, 16]. Further making use of an alloy-analogy model (see below), finite temperatures can be accounted for. It also allows one to include correlations beyond LSDA in the framework of LSDA + U or LSDA + DMFT (dynamical mean field theory) [29, 30]. For cubic and hexagonal systems with the magnetization pointing along the
have the usual meaning [25–27]. Using the fully relativistic Dirac approach has the important advantage [18] that disorder (see below) can be treated elegantly without recourse to a Pauli approach, which poses difficulties in calculating the vertex corrections (vc). To determine longitudinal and transverse components of the conductivity tensor, a natural starting point is the linear response Kubo framework that can also be used to derive the Berry phase-related semiclassical approach [3, 4, 28]. The Kubo approach has important advantages as compared to the latter. It allows one to straightforwardly include disorder, and is therefore able to describe not only pure systems but also alloys in the full concentration range including intrinsic and extrinsic contributions to the AHE [14, 16]. Further making use of an alloy-analogy model (see below), finite temperatures can be accounted for. It also allows one to include correlations beyond LSDA in the framework of LSDA + U or LSDA + DMFT (dynamical mean field theory) [29, 30]. For cubic and hexagonal systems with the magnetization pointing along the 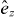 -direction, the AHE in the Kubo–Středa formalism is given [17, 18] by the off-diagonal tensor element σyx = −σxy of
-direction, the AHE in the Kubo–Středa formalism is given [17, 18] by the off-diagonal tensor element σyx = −σxy of
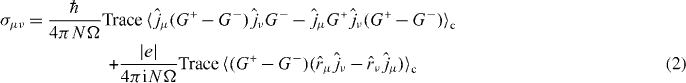
with the relativistic current operator 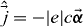 and the electronic retarded and advanced Green functions G± (calculated at EF) which in the framework of the presented KKR approach are given in a relativistic multiple scattering representation [24]. The angular brackets denote a configurational average that here is carried out using the coherent potential approximation (CPA), which allows one to include vc, which are of utter importance for the quantitative determination of both the longitudinal and transversal conductivity in alloys. As has been argued and also shown [8, 14, 16], calculations omitting the vc give the intrinsic AHC. Thereby, subtracting the latter from the AHC obtained from the value including the vc, the extrinsic part can be extracted.
and the electronic retarded and advanced Green functions G± (calculated at EF) which in the framework of the presented KKR approach are given in a relativistic multiple scattering representation [24]. The angular brackets denote a configurational average that here is carried out using the coherent potential approximation (CPA), which allows one to include vc, which are of utter importance for the quantitative determination of both the longitudinal and transversal conductivity in alloys. As has been argued and also shown [8, 14, 16], calculations omitting the vc give the intrinsic AHC. Thereby, subtracting the latter from the AHC obtained from the value including the vc, the extrinsic part can be extracted.
Several sources of electron scattering at finite temperatures will determine the
T-dependence of the AHE. We neglect the redistribution of states due to finite temperature in the electronic subsystem as well as electron–magnon interaction that can be treated as spin-disorder scattering in a pseudo-alloy as has been done recently for Pd–Fe alloys [15]. Here, we consider as a dominant effect only thermal lattice vibrations. To include the latter as a source of electron scattering, one could generalize equation (2) to finite temperatures by including the electron–phonon self-energy Σel–ph when calculating the Green function G±. This, however, is computationally very expensive. Therefore, the consideration is restricted to elastic scattering processes by using a quasi-static representation of the thermal displacements of the atoms from their equilibrium positions as has already been used successfully by the authors in the theory of Gilbert damping [31]. Treating each displaced atom as an alloy partner, we introduce an alloy-analogy model to average over a discrete set of displacements that is chosen to reproduce the thermal root mean square average displacement 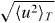 for a given temperature T. This was chosen according to
for a given temperature T. This was chosen according to ![${\langle u^2\rangle _T} = \frac {3\hbar ^2}{mk\Theta _{\mathrm {D}}}[\frac {\Phi (\Theta _{\mathrm {D}}/T)}{\Theta _{\mathrm {D}}/T} +\frac {1}{4}]$](https://content.cld.iop.org/journals/1367-2630/15/5/053009/revision1/nj461489ieqn8.gif) with Φ(ΘD/T) the Debye function, ℏ the reduced Planck constant, k the Boltzmann constant and ΘD the Debye temperature [32]. Ignoring the zero temperature term and assuming a frozen potential for the atoms, the situation can be dealt with in full analogy to the treatment of disordered alloys using the CPA.
with Φ(ΘD/T) the Debye function, ℏ the reduced Planck constant, k the Boltzmann constant and ΘD the Debye temperature [32]. Ignoring the zero temperature term and assuming a frozen potential for the atoms, the situation can be dealt with in full analogy to the treatment of disordered alloys using the CPA.
To study the impact of correlations (beyond LSDA), we employed an implementation of the LSDA + DMFT framework into the KKR [30] and obtained the LSDA + U by retaining the static part of the self-energy. Around mean field double counting corrections have been used. The chosen values for U and J are commonly used in the description of 3d-TMs.
3. Results and discussion
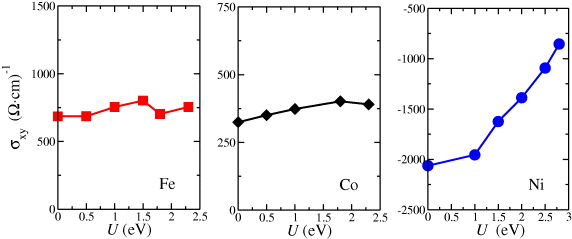
We performed LSDA as well as LSDA + U calculations of the AHC of 3d-TMs. The LSDA + U calculations were performed keeping J = 0.9 eV fixed and scanning the U-range up to typical values employed for the 3d-TMs. In figure 1 the dependence of the intrinsic AHE at T = 0 K for bcc-Fe, hcp-Co and fcc-Ni is shown. Whereas for Fe and Co only small variations of the AHC are observed, a pronounced U-dependence for Ni is seen with the experimentally extracted intrinsic value of −1100 S cm−1 recovered at a U-value of around 2.5 eV (this value is also used in calculation of the T-dependence below). Analysis shows that this is due to a downshift of minority 3d-bands w.r.t. EF and a vanishing hole pocket at the X2 point, as has already been recently discussed [11]. In table 1, we show the calculated values for Fe (U = 1.8 eV), Co (hcp and fcc, U = 2.3 eV ) and Ni (U = 2.5 eV) in comparison with other calculations as well as experiment. (Note that in our previous calculation [14], we obtained for Ni a value of −1635 S cm−1, which deviates by 20% from the value reported here. This was due to an inappropriate small setting for the muffin-tin radii rMT (i.e. no touching spheres) used in the calculations which employ the atomic-sphere approximation (ASA, rASA) for the potential construction. The muffin-tin zero in the KKR calculation is obtained by averaging over the area between rMT and rASA. For Ni it turns out that the AHC is very sensitive to such an inappropriate setting. We checked this issue for Fe and Co and found no such sensitivity, i.e. shrinking rMT by 5% only changed the AHC values by at most 2%.) In addition, we report the spin- and orbital-magnetic moments of the 3d-TMs calculated in LSDA and LSAD + U in table 2.
Figure 1. Dependence of the AHC (T = 0 K) for bcc-Fe (left), hcp-Co (middle) and fcc-Ni (right) as a function of the U-value in the LSDA + U calculation.
Download figure:
Standard image High-resolution imageTable 2. Spin- and orbital-magnetic moments in μB for the 3d-TMs at T = 0 K as calculated in LSDA and LSDA + U (using the U- and J-values mentioned in the text).
| bcc-Fe | hcp-Co | fcc-Co | fcc-Ni | |
|---|---|---|---|---|
| LSDA, spin | 2.26 | 1.60 | 1.64 | 0.64 |
| LSDA+U, spin | 2.21 | 1.61 | 1.66 | 0.65 |
| LSDA, orbital | 0.05 | 0.08 | 0.08 | 0.05 |
| LSDA+U, orbital | 0.13 | 0.12 | 0.22 | 0.08 |
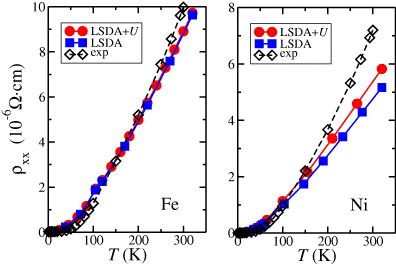
Another important aspect is the temperature dependence of the transverse AHC. To assess in a first step the validity of the presented approach to deal with thermal lattice displacements, the longitudinal resistivities were calculated for the 3d-TMs making use of the Kubo–Greenwood expression for the symmetric part of the conductivity tensor [37–39]. The results for ρxx are shown in figure 2 and compared with experimental data taken from the literature. As can be seen, the agreement is rather good. Therefore, we expect the aforementioned framework to be a reasonable approximation to properly describe electron–phonon scattering and the temperature dependence of the AHE (Note that deviation from the experimental data becomes larger in the high-temperature range. This could be attributed to the effect of spin disorder, which however has been neglected in the current study. In particular, Ni shows a larger deviation which might be due to the fact that it has a smaller Curie temperature resulting in a stronger effect of the spin disorder.)
Figure 2. Temperature dependence of the longitudinal resistivity ρxx of Fe (left) and Ni (right) as calculated in LSDA and LSDA + U compared to experiment [40].
Download figure:
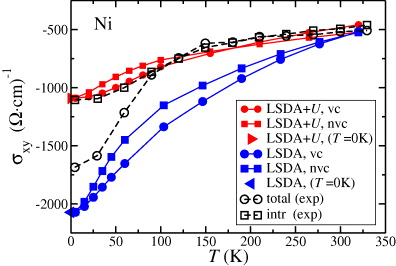
Standard image High-resolution imageEarly measurements of the AHE in Ni report a value of −646 S cm−1 at room temperature [35]. Recent experimental work [21] analyzed this in more detail claiming the AHE to consist of an intrinsic component of about −1100 S cm−1 and a sizable skew-scattering contribution at low temperatures, which both diminish at higher temperatures albeit with different rates. In figure 3 the calculated temperature dependence of the AHE in Ni using LSDA and LSDA + U (U = 2.5, J = 0.9 eV) as well as experimental results [21] are shown. As could be expected from the above, the LSDA result strongly overestimates the magnitude over the whole temperature range, whereas LSDA + U fairly well reproduces the experimental result. This demonstrates that both correlations beyond LSDA as well as temperature-induced thermal vibrations combined need to be taken into account. The vc due to the lattice vibrations have little impact in the low-T regime and are negligible at higher temperatures such that, as seen in experiment, the intrinsic contribution survives. We attribute the deviation from the total AHC in the low-T range to possible impurities that might be present in the sample. In contrast to Ni, the temperature dependence in Fe (see figure 4) is found to be small.
Figure 3. Temperature dependence of the AHC of Ni. Shown are theoretical results obtained by LSDA and LSDA + U both including (vc) and excluding (nvc) vertex corrections and experimental data [21]. Triangle symbols denote the zero temperature intrinsic AHE values for LSDA and LSDA + U, respectively.
Download figure:
Standard image High-resolution imageFigure 4. Temperature dependence of the AHC of Fe as calculated in LSDA and LSDA + U.
Download figure:
Standard image High-resolution imageIn the context of both the SHE and the AHE [13, 14, 41, 42], it has already been shown that in the dilute/super-clean limit large skew-scattering contributions can arise with the AHC scaling as σxy∝σxx. To demonstrate this and put it in the context of the recent experiment by Ye et al [21], we performed calculations for Mg impurities and Fe impurities in Ni, employing the CPA for both the impurities and the thermal lattice vibrations. As can be seen in figure 5, the calculated full AHC (including vc) approaches the experimental curve for higher temperatures. However in the low-temperature regime, larger deviations are visible. Taking the difference between the calculation with vc and that without vc (intrinsic values), one also observes that the impurity-induced extrinsic contribution for Mg shows the same sign as seen in experiment, i.e. it increases the absolute value, whereas for Fe impurities the opposite behavior is seen. This highlights again the fact that the skew-scattering component in an impurity-specific way determines the quantitative low-temperature behavior of the AHC in clean 3d-metals but also that the experimental determination of 'clean' systems is extremely challenging.
Figure 5. Temperature dependence of the AHC of Ni0.98Mg0.02 (left) and Ni0.98Fe0.02 (right) as calculated in LSDA + U compared to experiment [21].
Download figure:
Standard image High-resolution imageIn summary, we have used the linear response Kubo formalism as implemented in a fully relativistic multiple-scattering KKR Green function method to study systematically from first principles the AHC of the 3d-TMs Fe, Co and Ni. Going beyond the LSDA in DFT employing the LSDA + U and including finite temperatures by using a CPA-alloy analogy for the lattice displacements provided the necessary means to allow for a material-specific description of the AHC. Further, the impact of dilute impurities has been analyzed. The presented framework is now ready to be applied to the whole concentration range of correlated TM-alloys. Treating correlations beyond the static limit (LSDA + U) of the LSDA + DMFT combined with a linear response transport formalism is a major issue for future work. Further, the developed method is straightforwardly applicable to a number of related transverse transport phenomena, e.g. the spin Hall- and spincaloric effects such as the anomalous- and spin-Nernst effects [41, 43, 44].
Acknowledgments
The authors thank the DFG for financial support within the SFB 689, FOR 1346 and SPP 1538. Discussions with Sergiy Mankovsky are gratefully acknowledged.