A Formal Proof of the Expressiveness of Deep Learning

Abstract

Deep learning has had a profound impact on computer science in recent years, with applications to image recognition, language processing, bioinformatics, and more. Recently, Cohen et al. provided theoretical evidence for the superiority of deep learning over shallow learning. We formalized their mathematical proof using Isabelle/HOL. The Isabelle development simplifies and generalizes the original proof, while working around the limitations of the HOL type system. To support the formalization, we developed reusable libraries of formalized mathematics, including results about the matrix rank, the Borel measure, and multivariate polynomials as well as a library for tensor analysis.

1 Introduction

Deep learning algorithms enable computers to perform tasks that seem beyond what we can program them to do using traditional techniques. In recent years, we have seen the emergence of unbeatable computer go players, practical speech recognition systems, and self-driving cars. These algorithms also have applications to image recognition, bioinformatics, and many other domains. Yet, on the theoretical side, we are only starting to understand why deep learning works so well. Recently, Cohen et al. [16] used tensor theory to explain the superiority of deep learning over shallow learning for one specific learning architecture called convolutional arithmetic circuits (CACs).

Machine learning algorithms attempt to model abstractions of their input data. A typical application is image recognition—i.e., classifying a given image in one of several categories, depending on what the image depicts. The algorithms usually learn from a set of data points, each specifying an input (the image) and a desired output (the category). This learning process is called training. The algorithms generalize the sample data, allowing them to imitate the learned output on previously unseen input data.

CACs are based on sum–product networks, also called arithmetic circuits [37]. Such a network is a rooted directed acyclic graph with input variables as leaf nodes and two types of inner nodes: sums and products. The incoming edges of sum nodes are labeled with real-valued weights, which are learned by training.

CACs impose the structure of the popular convolutional neural networks (CNNs) onto sum–product networks, using alternating convolutional and pooling layers, which are realized as collections of sum nodes and product nodes, respectively. These networks can be shallower or deeper—i.e., consist of few or many layers—and each layer can be arbitrarily small or large, with low- or high-arity sum nodes. CACs are equivalent to similarity networks, which have been demonstrated to perform at least as well as CNNs [15].

Cohen et al. prove two main theorems about CACs: the “fundamental” and the generalized theorem of network capacity (Sect. 4). The generalized theorem states that CAC networks enjoy complete depth efficiency: in general, to express a function captured by a deeper network using a shallower network, the shallower network must be exponentially larger than the deeper network. By “in general”, we mean that the statement holds for all CACs except for a Lebesgue null set $S$ in the weight space of the deeper network. The fundamental theorem is a special case of the generalized theorem where the expressiveness of the deepest possible network is compared with the shallowest network. Cohen et al. present each theorem in a variant where weights are shared across the networks and a more flexible variant where they are not.

As an exercise in mechanizing modern research in machine learning, we developed a formal proof of the fundamental theorem with and without weight sharing using the Isabelle/HOL proof assistant [33, 34]. To simplify our work, we recast the original proof into a more modular version (Sect. 5), which generalizes the result as follows: $S$ is not only a Lebesgue null set, but also a subset of the zero set of a nonzero multivariate polynomial. This stronger theorem gives a clearer picture of the expressiveness of deep CACs.

The formal proof builds on general libraries that we either developed or enriched (Sect. 6). We created a library for tensors and their operations, including product, CP-rank, and matricization. We added the matrix rank and its properties to Thiemann and Yamada’s matrix library [41], generalized the definition of the Borel measure by Hölzl and Himmelmann [25], and extended Lochbihler and Haftmann’s polynomial library [22] with various lemmas, including the theorem stating that zero sets of nonzero multivariate polynomials are Lebesgue null sets. For matrices and the Lebesgue measure, an issue we faced was that the definitions in the standard Isabelle libraries have too restrictive types: the dimensionality of the matrices and of the measure space is parameterized by types that encode numbers, whereas we needed them to be terms.

Building on these libraries, we formalized both variants of the fundamental theorem (Sect. 7). CACs are represented using a datatype that is flexible enough to capture networks with and without concrete weights. We defined tensors and polynomials to describe these networks, and used the datatype’s induction principle to show their properties and deduce the fundamental theorem.

Our formalization is part of the Archive of Formal Proofs [2] and is described in more detail in Bentkamp’s M.Sc. thesis [3]. It comprises about 7000 lines of Isabelle proofs, mostly in the declarative Isar style [43], and relies only on the standard axioms of higher-order logic.

An earlier version of this work was presented at ITP 2017 [4]. This article extends the conference paper with a more in-depth explanation of CACs and the fundamental theorem of network capacity, more details on the generalization obtained as a result of restructuring the proof, and an outline of the original proof by Cohen et al. Moreover, we extended the formalization to cover the theorem variant with shared weights. To make the paper more accessible, we added an introduction to Isabelle/HOL (Sect. 2).

2 Isabelle/HOL

Isabelle [33, 34] is a generic proof assistant that supports many object logics. The metalogic is based on an intuitionistic fragment of Church’s simple type theory [14]. The types are built from type variables ${\alpha }$, ${\beta }$, ... and n-ary type constructors, normally written in postfix notation (e.g., ${\alpha \;{\textit{list}}}$). The infix type constructor ${\alpha \Rightarrow \beta }$ is interpreted as the (total) function space from ${\alpha }$ to ${\beta }$. Function applications are written in a curried style (e.g., $\mathsf {f}\; x \; y$). Anonymous functions $x \mapsto y_{ x }$ are written $\lambda x .\ y_{ x }$. The notation $t \,{:}{:}\, {\tau }$ indicates that term t has type ${\tau }$.

Isabelle/HOL is an instance of Isabelle. Its object logic is classical higher-order logic supplemented with rank-1 polymorphism and Haskell-style type classes. The distinction between the metalogic and the object logic is important operationally but not semantically.

Isabelle’s architecture follows the tradition of the theorem prover LCF [21] in implementing a small inference kernel that verifies the proofs. Trusting an Isabelle proof involves trusting this kernel, the formulation of the main theorems, the assumed axioms, the compiler and runtime system of Standard ML, the operating system, and the hardware. Specification mechanisms help us define important classes of types and functions, such as inductive datatypes and recursive functions, without introducing axioms. Since additional axioms can lead to inconsistencies, it is generally good style to use these mechanisms.

Our formalization is mostly written in Isar [43], a proof language designed to facilitate the development of structured, human-readable proofs. Isar proofs allow us to state intermediate proof steps and to nest proofs. This makes them more maintainable than unstructured tactic scripts, and hence more appropriate for substantial formalizations.

Isabelle locales are a convenient mechanism for structuring large proofs. A locale fixes types, constants, and assumptions within a specified scope. For example, an informal mathematical text stating “in this section, let A be a set of natural numbers and B a subset of A” could be formalized by introducing a locale $\textit{AB}\_\textit{subset}$ as follows:

Definitions made within the locale may depend on $\mathsf {A}$ and $\mathsf {B}$, and lemmas proved within the locale may use the assumption that $\mathsf {B}\subseteq \mathsf {A}$. A single locale can introduce arbitrarily many types, constants, and assumptions. Seen from the outside, the lemmas proved in a locale are polymorphic in the fixed type variables, universally quantified over the fixed constants, and conditional on the locale’s assumptions. It is good practice to provide at least one interpretation after defining a locale to show that the assumptions are consistent. For example, we can interpret the above locale using the empty set for both $\mathsf {A}$ and $\mathsf {B}$ by proving that $\emptyset \subseteq \emptyset$:

Types can be grouped in type classes. Similarly to locales, type classes fix constants and assumptions, but they must have exactly one type parameter. Type classes are used to formalize the hierarchy of algebraic structures, such as semigroups, monoids, and groups.

The Sledgehammer tool [35] is useful to discharge proof obligations. It heuristically selects a few hundred lemmas from the thousands available (using machine learning [9]); translates the proof obligation and the selected lemmas to first-order logic; invokes external automatic theorem provers on the translated problem; and translates any proofs found by the external provers to Isar proof texts that can be inserted in the formalization.

3 Mathematical Preliminaries

We provide a short introduction to tensors and the Lebesgue measure. We expect familiarity with basic matrix and polynomial theory.

3.1 Tensors

Tensors can be understood as multidimensional arrays, with vectors and matrices as the one- and two-dimensional cases. Each index corresponds to a mode of the tensor. For matrices, the modes are called “row” and “column”. The number of modes is the order of the tensor. The number of values an index can take in a particular mode is the dimension in that mode. Thus, a real-valued tensor $\mathscr {A} \in \mathbb {R}^{M_{1}\times \dots \times M_{N}}$ of order N and dimension $M_{i}$ in mode i contains values $\mathscr {A}_{d_{1},\dots ,d_{N}}\in \mathbb {R}$ for $d_{i}\in \{1,\dots ,M_i\}$.

Like for vectors and matrices, addition $+$ is defined as componentwise addition for tensors of identical dimensions. The product is a binary operation that generalizes the outer vector product. For real tensors, it is associative and distributes over addition. The canonical polyadic rank, or CP-rank, associates a natural number with a tensor, generalizing the matrix rank. The matricization $[\mathscr {A}]$ of a tensor $\mathscr {A}$ is a matrix obtained by rearranging $\mathscr {A}$’s entries using a bijection between the tensor and matrix entries. It has the following property:

Lemma 1

Given a tensor $\mathscr {A}$, we have ${{\mathrm{rank\,}}}[\mathscr {A}] \le {{\mathrm{CP-rank\,}}}\mathscr {A}\!$.

3.2 Lebesgue Measure

The Lebesgue measure is a mathematical description of the intuitive concept of length, surface, or volume. It extends this concept from simple geometrical shapes to a large amount of subsets of $\mathbb {R}^n$, including all closed and open sets, although it is impossible to design a measure that caters for all subsets of $\mathbb {R}^n$ while maintaining intuitive properties. The sets to which the Lebesgue measure can assign a volume are called measurable. The volume that is assigned to a measurable set can be a nonnegative real number or $\infty$. A set of Lebesgue measure 0 is called a null set. If a property holds for all points in $\mathbb {R}^n$ except for a null set, the property is said to hold almost everywhere.

The following lemma [13] about polynomials will be useful for the proof of the fundamental theorem of network capacity.

Lemma 2

If $p\not \equiv 0$ is a polynomial in d variables, the set of points $\mathbf {x}\in \mathbb {R}^{d}$ with $p(\mathbf {x})=0$ is a Lebesgue null set.

4 The Theorems of Network Capacity

A CAC is defined by the following parameters: the number of input vectors N, the depth d, and the dimensions of the weight matrices $r_{-1}, \dots , r_d$. The number N must be a power of 2 and d can be any number between 1 and $\log _2 N$. The size of the input vectors is $M = r_{-1}$ and the size of the output vector is $Y = r_d$.

The evaluation of a CAC—i.e., the calculation of its output vector given the input vectors—depends on learned weights. The results by Cohen et al. are concerned only with the expressiveness of these networks and are applicable regardless of the training algorithm. The weights are organized as entries of a collection of real matrices $W_{l,j}$ of dimension $r_l \times r_{l-1}$, where l is the index of the layer and j is the position in that layer where the matrix is used. A CAC has shared weights if the same weight matrix is applied within each layer l—i.e., $W_{l,1} = \dots = W_{l,\nicefrac {N}{2^l}}$. The weight space of a CAC is the space of all possible weight configurations.

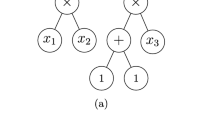
Figure 1 gives the formulas for evaluating a CAC and relates them to the network’s hierarchical structure. The inputs are denoted by $\mathbf {x}_1,\dots ,\mathbf {x}_N\in \mathbb {R}^M$ and the output is denoted by $\mathbf {y}\in \mathbb {R}^Y$. The vectors $\mathbf {u}_{l,j}$ and $\mathbf {v}_{l,j}$ are intermediate results of the calculation, where $\mathbf {u}_{0,j} = \mathbf {x}_j$ are the inputs and $\mathbf {v}_{d,1} = \mathbf {y}$ is the output. For a given weight configuration, the network expresses the function $(\mathbf {x}_1,\dots ,\mathbf {x}_N)\mapsto \mathbf {y}.$ The network consists of alternating convolutional and pooling layers. The convolutional layers yield $\mathbf {v}_{l,j}$ by multiplication of $W_{l,j}$ and $\mathbf {u}_{l,j}$. The pooling layers yield $\mathbf {u}_{l+1,j}$ by componentwise multiplication of two or more of the previous layer’s $\mathbf {v}_{l,i}$ vectors. The $*$ operator denotes componentwise multiplication. The first $d - 1$ pooling layers consist of binary nodes, which merge two vectors $\mathbf {v}_{l,i}$ into one vector $\mathbf {u}_{l+1,j}$. The last pooling layer consists of a single node with an arity of $\nicefrac {N}{2^{d-1}} \ge 2$, which merges all vectors $\mathbf {v}_{d-1,i}$ of the $(d-1)$th layer into one $\mathbf {u}_{d,1}$.

Fig. 1

Definition and hierarchical structure of a CAC with d layers

Fig. 2

A CAC with concrete weights evaluated on concrete input vectors

Figure 2 presents a CAC with parameters $N=4$, $d=2$, $r_{-1}=2$, $r_{0}=2$, $r_{1}=3$, and $r_{2}=2$. The weights are not shared, resulting in a total of 34 weights. Therefore, the network’s weight space is $\mathbb {R}^{34}$. The figure shows a concrete weight configuration from this space. Given this configuration, the network evaluates the inputs (1, 0), (0, 2), $(1, -1)$, (2, 1) to the output (2, 4).

Fig. 3

Evaluation formulas and hierarchical structure of a shallow CAC

Theorem 3

(Fundamental theorem of network capacity) We consider two CACs with identical N, M, and Y parameters: a deep network of depth $d=\log _2 N$ with weight matrix dimensions $r_{1,l}$ and a shallow network of depth $d = 1$ with weight matrix dimensions $r_{2,l}$. Let $r =\min (r_{1,0}{,}\; M)$ and assume $r_{2,0}<\smash {r^{\nicefrac {N}{2}}}$. Let $S$ be the set of configurations in the weight space of the deep network that express functions also expressible by the shallow network. Then $S$ is a Lebesgue null set. This result holds for networks with and without shared weights.

The fundamental theorem compares the extreme cases $d=1$ and $d=\log _2 N$. This is the theorem we formalized. Figure 3 shows the shallow network, which is the extreme case of a CAC with $d=1$. Intuitively, to express the same functions as the deep network, almost everywhere in the weight space of the deep network, $r_{2,0}$ must be at least $\smash {r^{\nicefrac {N}{2}}}$, which means the shallow network needs exponentially larger weight matrices than the deep network.

The generalized theorem compares CACs of any depths $1 \le d_2 < d_1 \le \log _2 N$. The fundamental theorem corresponds to the special case where $d_1=\log _2 N$ and $d_2=1$.

Theorem 4

(Generalized theorem of network capacity) Consider two CACs with identical N, M, and Y parameters: a deeper network of depth $d_1$ with weight matrix dimensions $r_{1,l}$ and a shallower network of depth $d_2 < d_1$ with weight matrix dimensions $r_{2,l}$. Let $r =\min \, \{M{,}\; r_{1,0}{,}\; \dots {,}\; r_{1,d_2-1}\}$ and assume

$$\begin{aligned} r_{2,d_2-1}<\smash {r^{\nicefrac {N}{2^{d_2}}}} \end{aligned}$$

Let $S$ be the set of configurations in the weight space of the deeper network that express functions also expressible by the shallower network. Then $S$ is a Lebesgue null set. This result holds for networks with and without shared weights.

Intuitively, to express the same functions as the deeper network, almost everywhere in the weight space of the deeper network, $r_{2,d_2-1}$ must be at least $\smash {r^{\nicefrac {N}{2^{d_2}}}}$, which means the shallower network needs exponentially larger weight matrices in its last two layers than the deeper network in its first $d_2 + 1$ layers. Cohen et al. further extended both theorems to CACs with an initial representational layer that applies a collection of nonlinearities to the inputs before the rest of the network is evaluated.

The proof of either theorem depends on a connection between CACs and measure theory, using tensors, matrices, and polynomials. Briefly, the CACs and the functions they express can be described using tensors. Via matricization, these tensors can be analyzed as matrices. Polynomials bridge the gap between matrices and measure theory, since the matrix determinant is a polynomial, and zero sets of polynomials are Lebesgue null sets (Lemma 2).

Cohen et al. proceed as follows to prove Theorem 4:

• i. They describe the function expressed by a CAC and its sub-CACs for a fixed weight configuration using tensors. Given a weight configuration w, let $\Phi ^{l,j,i}(w)$ be the tensor representing the function mapping inputs to the ith entry of $v_{l,j}$ in the deeper network.

• ii. They define a function $\varphi$ that reduces the order of a tensor. The CP-rank of $\varphi (\mathscr {A})$ indicates how large the shallower network must be to express a function represented by a tensor $\mathscr {A}$. More precisely, if the function expressed by the shallower network is represented by $\mathscr {A}\!,$ then $\smash {r_{2,d_2-1}\ge {{\mathrm{CP-rank\,}}}(\varphi (\mathscr {A}))}$.

• iii. They prove by induction that almost everywhere in the weight space of the deeper network, ${{\mathrm{rank\,}}}[\varphi (\Phi ^{l,j,i})] \ge r^{2^{l-d_2}}$ for all j, i and all $l=d_2, \dots , d_1-1$.

  • (a) Base case: They construct a polynomial mapping the weights of the deeper network to a real number. Whenever this polynomial is nonzero, ${{\mathrm{rank\,}}}[\varphi (\Phi ^{d_2,j,i})] \ge r$ for that weight configuration. They show that it is not the zero polynomial. By Lemma 2, it follows that ${{\mathrm{rank\,}}}[\varphi (\Phi ^{d_2,j,i})] \ge r$ almost everywhere.

  • (b) Induction step: They show that the tensors associated with a layer can be obtained via the tensor product from the tensors of the previous layer. By constructing another nonzero polynomial and using Lemma 2, they show that hence the rank of $\varphi (\Phi ^{l,j,i})$ increases quadratically almost everywhere.

• iv. Given step iii, they show that for all i, almost everywhere ${{\mathrm{rank\,}}}[\varphi (\Phi ^{d_1,1,i})] \ge \smash {r^{\nicefrac {N}{2^{d_2}}}}$. They employ a similar argument as in step iiib.

By step i, the tensors $\Phi ^{d_1,1,i}$ represent the function expressed by the deeper network. In conjunction with Lemma 1, step iv implies that the inequation ${{\mathrm{CP-rank\,}}}(\varphi (\Phi ^{d_1,1,i}))\ge \smash {r^{\nicefrac {N}{2^{d_2}}}}$ holds almost everywhere. By step ii, we need $\smash {r_{2,d_2-1}\ge r^{\nicefrac {N}{2^{d_2}}}}$ almost everywhere for the shallower network to express functions the deeper network expresses.

The core of this proof—steps iii and iv—is structured as a monolithic induction over the deeper network structure, which interleaves tensors, matrices, and polynomials. The induction is complicated because the chosen induction hypothesis is weak. It is easier to show that the set where ${{\mathrm{rank\,}}}[\varphi (\Phi ^{l,j,i})] < \smash {r^{2^{l-d_2}}}$ is not only a null set but contained in the zero set of a nonzero polynomial, which is a stronger statement by Lemma 2. As a result, measure theory can be kept isolated from the rest, and we can avoid the repetitions in steps iii and iv.

5 Restructured Proof of the Theorems

Before launching Isabelle, we restructured the proof into a more modular version that cleanly separates the mathematical theories involved, resulting in the following sketch:

• I. We describe the function expressed by a CAC for a fixed weight configuration using tensors. We focus on an arbitrary entry $y_i$ of the output vector $\mathbf {y}$. If the shallower network cannot express the output component $y_i$, it cannot represent the entire output either. Let $\mathscr {A}_i(w)$ be the tensor that represents the function $(\mathbf {x}_1,\dots ,\mathbf {x}_N)\mapsto y_i$ expressed by the deeper network with a weight configuration w.

• II. We define a function $\varphi$ that reduces the order of a tensor. The CP-rank of $\varphi (\mathscr {A})$ indicates how large the shallower network must be to express a function represented by a tensor $\mathscr {A}$: if the function expressed by the shallower network is represented by $\mathscr {A}\!,$ then $\smash {r_{2,d_2-1}\ge {{\mathrm{CP-rank\,}}}(\varphi (\mathscr {A}))}$.

• III. We construct a multivariate polynomial p that maps the weights configurations w of the deeper network to a real number p(w). It has the following properties:

  • (a) If $p(w)\not =0$, then ${{\mathrm{rank\,}}}[\varphi (\mathscr {A}_i(w))]\ge \smash {r^{\nicefrac {N}{2^{d_2}}}\!.}$ Hence ${{\mathrm{CP-rank\,}}}(\varphi (\mathscr {A}_i(w)))\ge \smash {r^{\nicefrac {N}{2^{d_{2}\!}}}}$ by Lemma 1.

  • (b) The polynomial p is not the zero polynomial. Hence its zero set is a Lebesgue null set by Lemma 2.

By properties IIIa and IIIb, the inequation ${{\mathrm{CP-rank\,}}}(\varphi (\mathscr {A}_i(w)))\ge \smash {r^{\nicefrac {N}{2^{d_2}}}}$ holds almost everywhere. By step ii, we need $\smash {r_{2,d_2-1}\ge r^{\nicefrac {N}{2^{d_2}}}}$ almost everywhere for the shallower network to express functions the deeper network expresses.

Step I corresponds to step i of the original proof. The tensor $\mathscr {A}_i(w)$ corresponds to $\Phi ^{d_1,1,i}$. The new proof still needs the tensors $\Phi ^{l,j,\gamma }(w)$ representing the functions expressed by the sub-CACs to complete step IIIb, but they no longer clutter the proof outline. Steps II and ii are identical. The main change is the restructuring of steps iii and iv into step III.

The monolithic induction over the deep network structure in steps iii and iv is replaced by two smaller inductions. The first one uses the evaluation formulas of CACs and some matrix and tensor theory to construct the polynomial p. The second induction employs the tensor representations of expressed functions and some matrix theory to prove IIIb. The measure theory in the restructured proof is restricted to the final application of Lemma 2, outside of the induction argument.

Fig. 4

Two-dimensional slice of the weight space of the deeper network. a The set $S$ in Euclidean space, b discrete counterpart of $S$ and c the $\varepsilon$-neighborhood of $S$

The restructuring helps keep the induction simple, and we can avoid formalizing some lemmas of the original proof. Moreover, the restructured proof allows us to state a stronger property, which Cohen et al. independently discovered later [18]: the set $S$ in Theorem 4 is not only a Lebesgue null set, but also a subset of the zero set of the polynomial p. This can be used to derive further properties of $S$. Zero sets of polynomials are well studied in algebraic geometry, where they are known as algebraic varieties.

This generalization partially addresses an issue that arises when applying the theorem to actual implementations of CACs. To help visualize this issue, Fig. 4a depicts a hypothetical two-dimensional slice of the weight space of the deeper network and its intersection with $S$, which will typically have a one-dimensional shape, since $S$ is the zero set of a polynomial. Cohen et al. assume that the weight space of the deeper network is a Euclidean space, but in practice it will always be discrete, as displayed in Fig. 4b, since a computer can only store finitely many different values. They also show that $S$ is a closed null set, but since these can be arbitrarily dense, this gives no information about the discrete counterpart of $S$.

We can estimate the size of this discrete counterpart of $S$ using our generalization in conjunction with a result from algebraic geometry [12, 31] that allows us to estimate the size of the $\varepsilon$-neighborhood of the zero set of a polynomial. The $\varepsilon$-neighborhood of $S$ is a good approximation of the discrete counterpart of $S$ if $\varepsilon$ corresponds to the precision of computer arithmetic, as displayed in Fig. 4c. Unfortunately, the estimate is trivial, unless we assume $\varepsilon$ to be unreasonably small. For instance, under the realistic assumption that $N = 65{,}536$ and $r_{1,i} = 100$ for $i\in \{-1,\dots ,d\}$, we can derive nontrivial estimates only for $\varepsilon <2^{-170{,}000}$, which greatly exceeds the precision of modern computers (of roughly $2^{-64}$). Thus, if we take into account that calculations are performed using floating-point arithmetic and therefore discretized, the gap in expressiveness between shallow and deep networks may not be as dramatic as suggested by Theorem 4. On the other hand, our analysis is built upon inequalities, which only provide an upper bound. A mathematical result estimating the size of $S$ with a lower bound would call for an entirely different approach.

6 Formal Libraries

Our proof requires basic results in matrix, tensor, polynomial, and measure theory. For matrices and polynomials, Isabelle offers several libraries, and we chose those that seemed the most suitable. We adapted the measure theory from Isabelle’s analysis library and developed a new tensor library.

6.1 Matrices

We had several options for the choice of a matrix library, of which the most relevant were Isabelle’s analysis library and Thiemann and Yamada’s matrix library [41]. The analysis library fixes the matrix dimensions using type parameters, a technique introduced by Harrison [24]. The advantage of this approach is that the dimensions are part of the type and need not be stated as conditions. Moreover, it makes it possible to instantiate type classes depending on the type arguments. However, this approach is not practical when the dimensions are specified by terms. Therefore, we chose Thiemann and Yamada’s library, which uses a single type for matrices of all dimensions and includes a rich collection of lemmas.

We extended the library in a few ways. We contributed a definition of the matrix rank, as the dimension of the space spanned by the matrix columns:

Moreover, we defined submatrices and proved that the rank of a matrix is at least the size of any submatrix with nonzero determinant, and that the rank is the maximum amount of linearly independent columns of the matrix.

6.2 Tensors

The Tensor entry [38] of the Archive of Formal Proofs might seem to be a good starting point for a formalization of tensors. However, despite its name, this library does not contain a type for tensors. It introduces the Kronecker product, which is equivalent to the tensor product but operates on the matricizations of tensors.

The Group-Ring-Module entry [29] of the Archive of Formal Proofs could have been another potential basis for our work. Unfortunately, it introduces the tensor product in a very abstract fashion and does not integrate well with other Isabelle libraries.

Instead, we introduced our own type for tensors, based on a list that specifies the dimension in each mode and a list containing all of its entries:

We formalized addition, multiplication by scalars, product, matricization, and the CP-rank. We instantiated addition as a semigroup ($semigroup\_ add$) and tensor product as a monoid ($monoid\_ mult$). Stronger type classes cannot be instantiated: their axioms do not hold collectively for tensors of all sizes, even though they hold for fixed tensor sizes. For example, it is impossible to define addition for tensors of different sizes while satisfying the cancellation property . We left addition of tensors of different sizes underspecified.

For proving properties of addition, scalar multiplication, and product, we devised a powerful induction principle on tensors, which relies on tensor slices. The induction step amounts to showing a property for a tensor $\mathscr {A}\in \mathbb {R}^{M_{1}\times \dots \times M_{N}}$ assuming it holds for all slices $\mathscr {A}_i\in \mathbb {R}^{M_{2}\times \dots \times M_{N}},$ which are obtained by fixing the first index $i\in \{1,\dots ,M_1\}$.

Matricization rearranges the entries of a tensor $\mathscr {A}\in \mathbb {R}^{M_1\times \cdots \times M_N}$ into a matrix $[\mathscr {A}]\in \mathbb {R}^{I\times J}$ for some suitable I and J. This rearrangement can be described as a bijection between $\{0,\dots ,M_1-1\}\times \cdots \times \{0,\dots ,M_N-1\}$ and $\{0,\dots ,I-1\}\times \{0,\dots , J-1\}$, assuming that indices start at 0. The operation is parameterized by a partition of the tensor modes into two sets $\{r_1<\dots<r_K\}\mathrel \uplus \{c_1<\dots <c_L\} = \{1, \dots , N\}$. The proof of Theorem 4 uses only standard matricization, which partitions the indices into odd and even numbers, but we formalized the more general formulation [1]. The matrix $[\mathscr {A}]$ has $I=\prod _{i=1}^K r_i$ rows and $J=\prod _{j=1}^L c_{\!j}$ columns. The rearrangement function is

$$\begin{aligned} (i_1,\dots ,i_N) \,\mapsto \, \left( \sum \limits _{k=1}^{K} \left( i_{r_k}\cdot \prod \limits _{k'=1}^{k-1}M_{r_{k'\!}}\right) \!{,}~ \sum \limits _{l=1}^{L} \left( i_{c_l}\cdot \prod \limits _{l'=1}^{l-1}M_{c_{l'\!}}\right) \right) \end{aligned}$$

The indices $i_{r_1}, \dots , i_{r_K}$ and $i_{c_1}, \dots , i_{c_L}$ serve as digits in a mixed-base numeral system to specify the row and the column in the matricization, respectively. This is perhaps more obvious if we expand the sum and product operators and factor out the bases $M_i$:

$$\begin{aligned} (i_1,\dots ,i_N) \,\mapsto \, \bigl (\begin{array}[t]{@{}l@{}l@{}l@{}l@{}l@{}l@{}l@{}l@{}} i_{r_{1\!}} &{} {} + M_{r_{1\!}} &{} {} \cdot (i_{r_2} &{} {} + M_{r_2} &{} {} \cdot \ldots \cdot (i_{r_{K-1}} &{} {} + M_{r_{K-1\!}} &{} {} \cdot i_{r_K}&{})\ldots )), \\ i_{c_{1\!}} &{} {} + M_{c_{1\!}} &{} {} \cdot (i_{c_2} &{} {} + M_{c_2} &{} {} \cdot \ldots \cdot (i_{c_{L-1}} &{} {} + M_{c_{L-1\!}} &{} {} \cdot i_{c_L}&{})\ldots ))\bigr )\end{array} \end{aligned}$$

To formalize the matricization operation, we defined a function that calculates the digits of a number $n$ in a given mixed-based numeral system:

where $\mathrel \#$ is the “cons” list-building operator, which adds an element $b$ to the front of an existing list $bs$. We then defined matricization as

The matrix constructor $\mathsf {mat}$ takes as arguments the matrix dimensions and a function that computes each matrix entry from the indices $r$ and $c$. Defining this function amounts to finding the corresponding indices of the tensor, which are essentially the mixed-base encoding of $r$ and $c$, but the digits of these two encoded numbers must be interleaved in an order specified by the set $R =\{r_1,\dots ,r_K\}.$

To merge two lists of digits in the correct way, we defined a function $\mathsf {weave}$. This function is the counterpart of $\mathsf {nths}$:

The function $\mathsf {nths}$ reduces a list to those entries whose indices belong to a set I (e.g., $\mathsf {nths}\;[a,b,c,d]\;\{0,2\}=[a,c]$). The function $\mathsf {weave}$ merges two lists $xs$ and $ys$ given a set I that indicates at what positions the entries of $xs$ should appear in the resulting list (e.g., $\mathsf {weave}\;[a,c]\;[b,d]\;\{0,2\}=[a,b,c,d]$). The main concern when defining $\mathsf {weave}$ is to determine how it should behave in corner cases—in our scenario, when $I = \{\}$ and $xs$ is nonempty. We settled on a definition such that the property $\mathsf {length}\;(\mathsf {weave}\; I \; xs \; ys ) = \mathsf {length}\; xs \mathrel + \mathsf {length}\; ys$ holds unconditionally:

where the $\mathrel !$ operator returns the list element at a given index. This definition allows us to prove lemmas about $\mathsf {weave}\> I \> xs \> ys \mathrel !a$ and $\mathsf {length}\;(\mathsf {weave}\; I \; xs \; ys )$ easily. Other properties, such as the $\textit{weave}\_\textit{nths}$ lemma above, are justified using an induction over the length of a list, with a case distinction in the induction step on whether the new list element is taken from $xs$ or $ys$.

Another difficulty arises with the rule ${{\mathrm{rank\,}}}[\mathscr {A} \otimes \mathscr {B}] = {{\mathrm{rank\,}}}[\mathscr {A}] \cdot {{\mathrm{rank\,}}}[\mathscr {B}]$ for standard matricization and tensors of even order, which seemed tedious to formalize. Restructuring the proof eliminated one of its two occurrences (Sect. 5). The remaining occurrence is used to show that ${{\mathrm{rank\,}}}[\mathbf {a}_1\otimes \cdots \otimes \mathbf {a}_N] = 1$, where $\mathbf {a}_1,\dots ,\mathbf {a}_N$ are vectors and N is even. A simpler proof relies on the observation that the entries of the matrix $[\mathbf {a}_1\otimes \cdots \otimes \mathbf {a}_N]$ can be written as $f(i) \cdot g(j)$, where f depends only on the row index i, and g depends only on the column index j. Using this argument, we can show ${{\mathrm{rank\,}}}[\mathbf {a}_1\otimes \cdots \otimes \mathbf {a}_N] = 1$ for generalized matricization and an arbitrary N, which we used to prove Lemma 1:

6.3 Lebesgue Measure

At the time of our formalization work, Isabelle’s analysis library defined only the Borel measure on $\mathbb {R}^n$ but not the closely related Lebesgue measure. The Lebesgue measure is the completion of the Borel measure. The two measures are identical on all sets that are Borel measurable, but the Lebesgue measure can measure more sets. Following the proof by Cohen et al., we can show that the set $S$ defined in Theorem 4 is a subset of a Borel null set. It follows that $S$ is a Lebesgue null set, but not necessarily a Borel null set.

To resolve this mismatch, we considered three options:

• 1. Prove that $S$ is a Borel null set, which we believe is the case, although it does not follow trivially from $S$’s being a subset of a Borel null set.

• 2. Define the Lebesgue measure, using the already formalized Borel measure and measure completion.

• 3. Use the Borel measure whenever possible and use the almost-everywhere quantifier ($\forall _{\mathrm {ae}}$) otherwise.

We chose the third approach, which seemed simpler. Theorem 4, as expressed in Sect. 4, defines $S$ as the set of configurations in the weight space of the deeper network that express functions also expressible by the shallower network, and then asserts that $S$ is a null set. In the formalization, we state this as follows: almost everywhere in the weight space of the deeper network, the deeper network expresses functions not expressible by the shallower network. This formulation is equivalent to asserting that $S$ is a subset of a null set, which we can easily prove for the Borel measure as well.

There is, however, another issue with the definition of the Borel measure from Isabelle’s analysis library:

The type ${\alpha }$ specifies the number of dimensions of the measure space. In our proof, the measure space is the weight space of the deeper network, and its dimension depends on the number N of inputs and the size $r_l$ of the weight matrices. The number of dimensions is a term in our proof. We described a similar issue with Isabelle’s matrix library already.

The solution is to introduce a new notion of the Borel measure whose type does not fix the number of dimensions. This multidimensional Borel measure is the product measure ($\prod _\mathsf {M}$) of the one-dimensional Borel measure ($\mathsf {lborel} \,{:}{:}\, real \; measure$) with itself:

The argument $n$ specifies the dimension of the measure space. Unlike with $\mathsf {lborel}$, the measure space of ${\mathsf {lborel}_\mathsf {f}}\; n$ is not the entire universe of the type: only functions of type ${\textit{nat}\Rightarrow \textit{real}}$ that map to a default value for numbers greater than or equal to $n$ are contained in the measure space, which is available as $\mathsf {space}\;({\mathsf {lborel}_\mathsf {f}}\; n )$. With the above definition, we could prove the main lemmas about ${\mathsf {lborel}_\mathsf {f}}$ from the corresponding lemmas about $\mathsf {lborel}$ with little effort.

6.4 Multivariate Polynomials

Several multivariate polynomial libraries have been developed to support other formalization projects in Isabelle. Sternagel and Thiemann [40] formalized multivariate polynomials designed for execution, but the equality of polynomials is a custom predicate, which means that we cannot use Isabelle’s simplifier to rewrite polynomial expressions. Immler and Maletzky [26] formalized an axiomatic approach to multivariate polynomials using type classes, but their focus is not on the evaluation homomorphism, which we need. Instead, we chose to extend a previously unpublished multivariate polynomial library by Lochbihler and Haftmann [22]. We derived induction principles and properties of the evaluation homomorphism and of nested multivariate polynomials. These were useful to formalize Lemma 2:

The variables of polynomials are represented by natural numbers. The function $\mathsf {insertion}$ is the evaluation homomorphism. Its first argument is a function $x \,{:}{:}\, {\textit{nat} \Rightarrow \textit{real}}$ that represents the values of the variables; its second argument is the polynomial to be evaluated.

7 Formalization of the Fundamental Theorem

With the necessary libraries in place, we undertook the formal proof of the fundamental theorem of network capacity, starting with the CACs. A recursive datatype is appropriate to capture the hierarchical structure of these networks:

To simplify the proofs, $\mathsf {Pool}$ nodes are always binary. Pooling layers that merge more than two branches are represented by nesting $\mathsf {Pool}$ nodes to the right.

The type variable $\alpha$ can be used to store weights. For networks without weights, it is set to ${\textit{nat} \times \textit{nat}}$, which associates only the matrix dimension with each $\mathsf {Conv}$ node. For networks with weights, $\alpha$ is $real\;mat$, an actual matrix. These two network types are connected by $\mathsf {insert\_weights}$, which inserts weights into a weightless network, and its inverse $\mathsf {extract\_weights}\,{:}{:}\, bool \Rightarrow real\;mat\;cac \Rightarrow nat \Rightarrow real$, which retrieves the weights from a network containing weights.

The first argument of these two functions specifies whether the weights should be shared among the $\mathsf {Conv}$ nodes of the same layer. The weights are represented by a function w, of which only the first k values $w\>0,\, w\>1,\,\dots , w\>(k - 1)$ are used. Given a matrix, $\mathsf {flatten\_matrix}$ creates such a function representing the matrix entries. Sets over ${\textit{nat}\Rightarrow \textit{real}}$ can be measured using ${\mathsf {lborel}_\mathsf {f}}$. The $\mathsf {count\_weights}$ function returns the number of weights in a network.

The next function describes how the networks are evaluated:

where $\otimes _\mathsf {mv}$ multiplies a matrix with a vector, and $\mathsf {component\_mult}$ multiplies vectors componentwise.

The $cac$ type can represent networks with arbitrary nesting of $\mathsf {Conv}$ and $\mathsf {Pool}$ nodes, going beyond the definition of CACs. Moreover, since we focus on the fundamental theorem, it suffices to consider a deep model with $d_1=\log _2 N$ and a shallow model with $d_2=1$. These are specified by generating functions:

Two examples are given in Fig. 5. For the deep model, the arguments $Y \mathrel \# r \mathrel \# rs$ correspond to the weight matrix sizes $[r_{1,d}\,({=}\,Y),\,r_{1,d-1},\,\dots ,\,r_{1,0},\,r_{1,-1}\,({=}\,M)]$. For the shallow model, the arguments $Y$, $Z$, $M$ correspond to the parameters $r_{2,1} \,({=}\,Y)$, $r_{2,0}$, $r_{2,-1} \,({=}\,M)$, and $N$ gives the number of inputs minus 1.

Fig. 5

A deep and a shallow network represented using the $cac$ datatype. a$\mathsf {deep\_model}\; Y \; r _{\mathrm {1}}\; [ r _{\mathrm {0}}{,}\> M ]$ and b$\mathsf {shallow\_model}\; Y \; Z \; M \;3$

The rest of the formalization follows the proof sketch presented in Sect. 5.

Step I The following operation computes a list, or vector, of tensors representing a network’s function, each tensor standing for one component of the output vector:

For an $\mathsf {Input}$ node, we return the list of unit vectors of length M. For a $\mathsf {Conv}$ node, we multiply the weight matrix A with the tensor list computed for the subnetwork m, using matrix–vector multiplication. For a $\mathsf {Pool}$ node, we compute, elementwise, the tensor products of the two tensor lists associated with the subnetworks $m_1$ and $m_2$. If two networks express the same function, the representing tensors are the same:

The fundamental theorem is a general statement about deep networks. It is useful to fix the deep network parameters in a locale:

The list $\mathsf {rs}$ completely specifies one specific deep network model:

The parameter $\mathsf {shared}$ specifies whether weights are shared across $\mathsf {Conv}$ nodes within the same layer. The other parameters of the deep network can be defined based on $\mathsf {rs}$ and $\mathsf {shared}$:

The shallow network must have the same input and output sizes as the deep network to express the same function as the deep network. This leaves only the parameter $Z = r_{2,0}$, which specifies the weight matrix sizes in the $\mathsf {Conv}$ nodes and the size of the vectors multiplied in the $\mathsf {Pool}$ nodes of the shallow network:

Following the proof sketch, we consider a single output component $y_i$. We rely on a second locale that introduces a constant $\mathsf {i}$ for the index of the considered output component. We provide interpretations for both locales.

Then we can define the tensor $\mathscr {A}_\mathsf {i}$, which describes the behavior of the function expressed by the deep network at the output component $y_i$, depending on the weight configuration w of the deep network:

We want to determine for which w the shallow network can express the same function, and is hence represented by the same tensor.

Step II We must show that if a tensor $\mathscr {A}$ represents the function expressed by the shallow network, then $\smash {r_{2,d_2-1}\ge {{\mathrm{CP-rank\,}}}(\varphi (\mathscr {A}))}$. For the fundamental theorem, $\varphi$ is the identity and $d_2 = 1$. Hence, it suffices to prove that $\smash {Z=r_{2,0}\ge {{\mathrm{CP-rank\,}}}(\mathscr {A})}$:

This lemma can be proved easily from the definition of the CP-rank.

Step III We define the polynomial p and prove that it has properties IIIa and IIIb. Defining p as a function is simple:

where $[\mathscr {A}_{\,\mathsf {i}}\;w]$ abbreviates the standard matricization $\mathsf {matricize}\;\{ n .~\mathsf {even}\; n \}\;(\mathscr {A}_{\,\mathsf {i}}\;w)$, and $\mathsf {rows\_}$$\mathsf {with\_1}$ is the set of row indices with 1s in the main diagonal for a specific weight configuration w defined in step IIIb. Our aim is to make the submatrix as large as possible while maintaining the property that p is not the zero polynomial. The bound on Z in the statement of the final theorem is derived from the size of this submatrix.

The function ${\mathsf {p}_\mathsf {func}}$ must be shown to be a polynomial function. We introduce a predicate $\mathsf {polyfun}$ that determines whether a function is a polynomial function:

This predicate is preserved from constant and linear functions through the tensor representation of the CAC, matricization, choice of submatrix, and determinant:

Step IIIa We must show that if $p(w)\not =0$, then ${{\mathrm{CP-rank\,}}}(\mathscr {A}_\mathsf {i}(w))\ge \smash {r^{\nicefrac {N}{2}}}$. The Isar proof is sketched below:

Step IIIb To prove that p is not the zero polynomial, we must exhibit a witness weight configuration where p is nonzero. Since weights are arranged in matrices, we define concrete matrix types: matrices with 1s on their diagonal and 0s elsewhere ($\mathsf {id\_matrix}$), matrices with 1s everywhere ($\mathsf {all1\_matrix}$), and matrices with 1s in the first column and 0s elsewhere ($\mathsf {copy\_first\_matrix}$). For example, the last matrix type is defined as follows:

For each matrix type, we show how it behaves under multiplication with a vector:

Using these matrices, we can define the deep network containing the witness weights:

The network’s structure is identical to $\mathsf {deep\_model}$. For each $\mathsf {Conv}$ node, we carefully choose one of the three matrix types we defined, so that the representing tensor of this network has as many 1s as possible on the main diagonal and 0s elsewhere. This in turn ensures that its matricization has as many 1s as possible on its main diagonal and 0s elsewhere. The $\mathsf {rows\_with\_1}$ constant specifies the row indices that contain the 1s.

We extract the weights from the $\mathsf {witness}$ network using the function $\mathsf {extract\_weights}$:

We prove that the representing tensor of the $\mathsf {witness}$ network, which is equal to the tensor $\mathscr {A}_{\,\mathsf {i}}\;\mathsf {witness\_weights}$, has the desired form. This step is rather involved: we show how the defined matrices act in the network and perform a tedious induction over the witness network. Then we can show that the submatrix characterized by $\mathsf {rows\_with\_1}$ of the matricization of this tensor is the identity matrix of size $\mathsf {r}^\mathsf {N\_half}$:

As a consequence of this lemma, the determinant of this submatrix, which is the definition of ${\mathsf {p}_\mathsf {func}}$, is nonzero. Therefore, p is not the zero polynomial:

Fundamental Theorem The results of steps II and III can be used to establish the fundamental theorem:

Here, ‘$\forall _{\mathrm {ae}}\,x~\mathrm {w.r.t.}~m.\;P_{\!x}$’ means that the property $P_{\!x}$ holds almost everywhere with respect to the measure m. The $r^{\mathsf {N\_half}}$ bound corresponds to the size of the identity matrix in the $\textit{witness}\_\textit{submatrix}$ lemma above.

8 Discussion

We formalized the fundamental theorem of network capacity. Our theorem statement is independent of the tensor library (and hence its correctness is independent of whether the library faithfully captures tensor-related notions). The generalized theorem is mostly a straightforward generalization. To formalize it, we would need to define CACs for arbitrary depths, which our datatype allows. Moreover, we would need to define the function $\varphi$ and prove some of its properties. Then, we would generalize the existing lemmas. We focused on the fundamental theorem because it contains all the essential ideas.

The original proof is about eight pages long, including the definitions of the networks. This corresponds to about 2000 lines of Isabelle formalization. A larger part of our effort went into creating and extending mathematical libraries, amounting to about 5000 lines.

We often encountered proof obligations that Sledgehammer could solve only using the smt proof method [11], especially in contexts with sums and products of reals, existential quantifiers, and $\lambda$-expressions. The smt method relies on the SMT solver Z3 [20] to find a proof, which it then replays using Isabelle’s inference kernel. Relying on a highly heuristic third-party prover is fragile; some proofs that are fast with a given version of the prover might time out with a different version, or be unreplayable due to some incompleteness in smt. For this reason, until recently it has been a policy of the Archive of Formal Proofs to refuse entries containing smt proofs. Sledgehammer resorts to smt proofs only if it fails to produce one-line proofs using the metis proof method [36] or structured Isar proofs [8]. We ended up with over 60 invocations of smt, which we later replaced one by one with structured Isar proofs, a tedious process. The following equation on reals is an example that can only be proved by smt, with suitable lemmas:

$$\begin{aligned} \sum \limits _{i\in I} \sum \limits _{j\in J} a \cdot b \cdot f(i) \cdot g(j) =\left( \sum \limits _{i\in I} a \cdot f(i)\right) \cdot \left( \sum \limits _{j\in J} b \cdot g(j)\right) \end{aligned}$$

We could not solve it with other proof methods without engaging in a detailed proof involving multiple steps. This particular example relies on smt’s partial support for $\lambda$-expressions through $\lambda$-lifting, an instance of what we would call “easy higher-order”.

9 Related Work

CACs are relatively easy to analyze but little used in practice. In a follow-up paper [19], Cohen et al. used tensor theory to analyze dilated convolutional networks and in another paper [17], they connected their tensor analysis of CACs to the frequently used CNNs with rectified linear unit (ReLU) activation. Unlike CACs, ReLU CNNs with average pooling are not universal—that is, even shallow networks of arbitrary size cannot express all functions a deeper network can express. Moreover, ReLU CNNs do not enjoy complete depth efficiency; the analogue of the set $S$ for those networks has a Lebesgue measure greater than zero. This leads Cohen et al. to conjecture that CACs could become a leading approach for deep learning, once suitable training algorithms have been developed.

Kawaguchi [28] uses linear deep networks, which resemble CACs, to analyze network training of linear and nonlinear networks. Hardt et al. [23] show theoretically why the stochastic gradient descent training method is efficient in practice. Tishby and Zaslavsky [42] employ information theory to explain the power of deep learning.

We are aware of a few other formalizations of machine learning algorithms, including hidden Markov models [30], perceptrons [32], expectation maximization, and support vector machines [7]. Selsam et al. [39] propose a methodology to verify practical machine learning systems in proof assistants.

Some of the mathematical libraries underlying our formalizations have counterparts in other systems, notably Coq. For example, the Mathematical Components include comprehensive matrix theories [6], which are naturally expressed using dependent types. The tensor formalization by Boender [10] restricts itself to the Kronecker product on matrices. Bernard et al. [5] formalized multivariate polynomials and used them to show the transcendence of e and $\pi$. Kam formalized the Lebesgue integral, which is closely related to the Lebesgue measure, to state and prove Markov’s inequality [27].

10 Conclusion

We applied a proof assistant to formalize a recent result in a field where they have been little used before, namely machine learning. We found that the functionality and libraries of a modern proof assistant such as Isabelle/HOL were mostly up to the task. Beyond the formal proof of the fundamental theorem of network capacity, our main contribution is a general library of tensors.

Admittedly, even the formalization of fairly short pen-and-paper proofs can require a lot of work, partly because of the need to develop and extend libraries. On the other hand, not only does the process lead to a computer verification of the result, but it can also reveal new ideas and results. The generalization and simplifications we discovered illustrate how formal proof development can be beneficial to research outside the small world of interactive theorem proving.